行星轮系的类型选择及设计的基本知识整理版
- 格式:docx
- 大小:181.02 KB
- 文档页数:4



第11章 齿轮系及其设计11.1 复习笔记本章主要介绍了定轴轮系、周转轮系和复合轮系的传动比计算,轮系的功用,以及行星轮系的效率、齿数的确定。
学习时需要重点掌握轮系传动比的计算,尤其是复合轮系的分析计算,常以计算题的形式考查。
除此之外,轮系的类型和功用、行星轮系中各齿数的确定(需要满足4个条件)等内容,常以选择题和填空题的形式考查,复习时需要把握其具体内容,重点记忆。
一、齿轮系及其分类1.定义齿轮系是由一系列的齿轮所组成的齿轮传动系统,简称轮系。
2.分类根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定,将轮系分为三大类:(1)定轴轮系运转时各个齿轮的轴线相对于机架的位置都是固定的轮系称为定轴轮系。
(2)周转轮系(见表11-1-1)表11-1-1 周转轮系图11-1-1 周转轮系二、定轴轮系的传动比(见表11-1-2)表11-1-2 定轴轮系的传动比三、周转轮系的传动比1.周转轮系的传动比设周转轮系中的两个太阳轮分别为m 和n ,行星架为H ,则其转化轮系的传动比i mn H 可表示为H Hm m H mn H n n Hm nm nωωωi ωωω-==-=±在转化轮系中由至各从动轮齿数的乘积在转化轮系中由至各主动轮齿数的乘积2.具有固定轮的行星轮系的传动比具有固定轮的行星轮系,设固定轮为n ,即ωn =0,则有i mn H =(ωm -ωH )/(0-ωH )=-i mH +1,即i mH =1-i mn H 。
四、复合轮系的传动比1.计算步骤(1)将各部分的周转轮系和定轴轮系一一分开;(2)分别列出其传动比计算式;(3)联立求解。
2.划分周转轮系(1)先要找到轮系中的行星轮和行星架(注意:轮系中行星架往往由其他功用的构件所兼任);(2)每一行星架以及连同行星架上的行星轮和与行星轮相啮合的太阳轮组成一个基本周转轮系;(3)当将所有的基本周转轮系部分找出之后,剩下的便是定轴轮系部分。

是指只具有一个自由度的轮系。
一个原动件即可确定执行件(行星齿轮)的运动,原动件通常为中心轮或系杆;即与行星齿轮直接接触的中心轮或系杆作为原动件带动行星齿轮,一方面绕着行星轮自身轴线O1-O1自转,另一方面又随着构件H(即系杆)绕一固定轴线O-O(中心轮轴线)回转。
行星轮系和差动轮系统称为周转轮系(一个周转轮系由三类构件组成1.一个系杆。
2.一个或几个行星轮。
3.一个或几个与行星轮相啮合的中心轮。
)。
行星轮系中,两个中心轮有一个固定;差动轮系中,两个中心轮都可以动(即F=2)。
工作特点行星轮系是一种先进的齿轮传动机构,具有结构紧凑、体积小、质量小、承载能力大、传递功率范围及传动范围大、运行噪声小、效率高及寿命长等优点。
运用场所行星轮系在国防、冶金、起重运输、矿山、化工、轻纺、建筑工业等部门的机械设备中,得到越来越广泛的应用工作原理行星轮系主要由行星轮g、中心轮k及行星架H组成。
其中行星轮的个数通常为2~6个。
但在计算传动比时,只考虑1个行星轮的转速,其余的行星轮计算时不用考虑,称为虚约束。
它们的作用是均匀地分布在中心轮的四周,既可使几个行星轮共同承担载荷,以减小齿轮尺寸;同时又可使各啮合处的径向分力和行星轮公转所产生的离心力得以平衡,以减小主轴承内的作用力,增加运转平稳性。
行星架是用于支承行星轮并使其得到公转的构件。
中心轮中,将外齿中心轮称为太阳轮,用符号a表示,将内齿中心轮称为内齿圈,用符号b表示。
二、行星轮系的分类根据行星轮系基本构件的组成情况,可分为三种类型:2K-H型、3K型、K-H-V型。
2K-H型具有构件数量少,传动功率和传动比变化范围大,设计容易等优点,因此应用最广泛。
3K型具有三个中心轮,其行星架不传递转矩,只起支承行星轮的作用。
行星轮系按啮合方式命名有NGW、NW、NN型等。
N表示内啮合,W表示外啮合,G表示公用的行星轮g。
行星轮系与定轴轮系的根本区别在于行星轮系中具有转动的行星架,从而使得行星轮系既有自转,又有公转。

行星轮系的设计行星轮系是传动机构的一种类型,其基本原理是通过行星齿轮的旋转进行传动。
行星轮系常用于汽车、机器人、工具机、工程机械等领域的传动中。
行星轮系由太阳轮、行星轮和内齿轮组成。
太阳轮为中心轴,行星轮绕着太阳轮公转,内齿轮则位于太阳轮与行星轮之间,同时与行星轮相互啮合。
在传动过程中,太阳轮作为动力输入端,行星轮则作为中间输出端,内齿轮则作为动力输出端。
行星轮系的设计需要考虑多个因素,包括负载、传动比、效率、噪音、寿命等。
以下是行星轮系设计时需要考虑的几个重要方面:1.行星轮组数的选择行星轮系的传动比由太阳轮、行星轮和内齿轮的齿数确定。
通常情况下,行星轮组数越多,传动比越大。
在设计行星轮系时,需要根据传动的要求来选择行星轮组数,以满足所需的传动比。
同时,行星轮组数的增加会引起摩擦损失的增加,需要考虑效率和寿命的问题。
行星轮系的负载包括静载荷和动载荷。
静载荷是在轴承之间施加的压力,主要由于行星轮、内齿轮和太阳轮的自身重量造成。
动载荷则是由传动引起的力矩变化,需要考虑传动过程中的强度和刚度问题,以确保行星轮系的正常工作。
行星轮系的效率受到多个因素的影响,包括啮合行星轮和太阳轮的啮合角度、齿轮几何形状、轮齿精度、轴承摩擦和润滑等。
在设计行星轮系时,需要进行有效的优化设计,以提高其效率和传动精度。
行星轮系在传动过程中会产生一定程度的噪音。
噪音主要是由啮合行星轮、太阳轮和内齿轮时产生的振动引起的,需要进行有效的噪声控制。
在设计行星轮系时,可以采用降噪措施,例如减小啮合角度和增加轮齿精度等。
总之,行星轮系是一种有效的传动机构,其设计需要考虑多种因素,以保证其稳定、高效、长寿、低噪声的工作。
设计师需要根据具体需求对行星轮系的结构、参数和材料进行有效的优化设计。


第五十三讲行星轮系的类型选择及设计的基本知识从传动原理出发设计行星轮系时,主要解决两个问题:1、选择传动类型。
2、确定各轮的齿数和行星轮的个数。
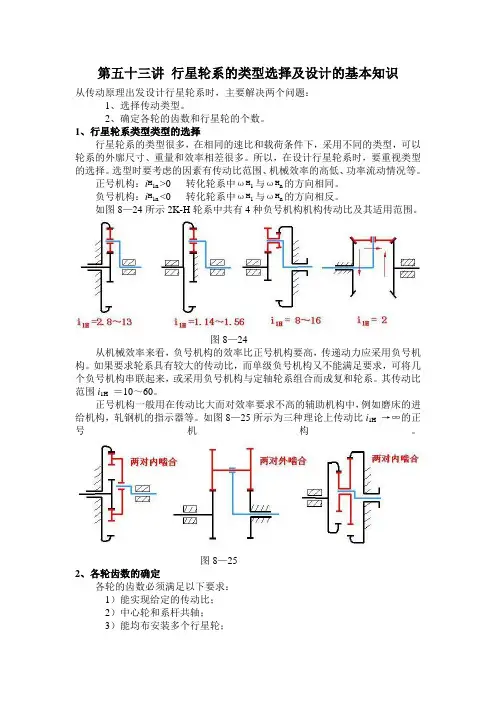
1、行星轮系类型类型的选择行星轮系的类型很多,在相同的速比和载荷条件下,采用不同的类型,可以轮系的外廓尺寸、重量和效率相差很多。
所以,在设计行星轮系时,要重视类型的选择。
选型时要考虑的因素有传动比范围、机械效率的高低、功率流动情况等。
正号机构:i H1n>0 转化轮系中ωH1与ωH n的方向相同。
负号机构:i H1n<0 转化轮系中ωH1与ωH n的方向相反。
如图8—24所示2K-H轮系中共有4种负号机构机构传动比及其适用范围。
图8—24从机械效率来看,负号机构的效率比正号机构要高,传递动力应采用负号机构。
如果要求轮系具有较大的传动比,而单级负号机构又不能满足要求,可将几个负号机构串联起来,或采用负号机构与定轴轮系组合而成复和轮系。
其传动比范围i1H=10~60。
正号机构一般用在传动比大而对效率要求不高的辅助机构中,例如磨床的进给机构,轧钢机的指示器等。
如图8—25所示为三种理论上传动比i1H→∞的正号机构。
图8—252、各轮齿数的确定各轮的齿数必须满足以下要求:1)能实现给定的传动比;2)中心轮和系杆共轴;3)能均布安装多个行星轮;4)相邻行星轮不发生干涉。
1)传动比条件如图8—26所示,13131131z z i i H H H H -=-=--=ωωωωz 1+z 3 =i 1H z 1113)1(z i z H -=∴ 2)同心条件如图8—27所示,系杆的轴线与两中心轮的轴线重合,当采用标准齿轮传动或等变位齿轮传动时有:r 3=r 1+ 2r 2 或 z 3=z 1+ 2z 2z 2=(z 3- z 1 )/2=z 1(i 1H -2)/2上式表明:两中心轮的齿数应同时为偶数或奇数。
图8—26 图8—273)均布安装条件如图8—28所示,能装入多个行星轮且仍呈对称布置,行星轮个数K 与各轮齿数之间应满足一定的条件。
行星轮介绍一.轮系的类型和应用一、轮系的分类(Classification of Gear Trains)根据轮系运转中齿轮轴线的空间位置是否固定,将轮系分为定轴轮系和周转轮系两大类。
1、定轴轮系(Ordinary Gear Trains)轮系运转时,其中各齿轮的回转轴线位置固定不动,则称之为定轴轮系。
如下图所示。
图 6-82、周转轮系(Epicyclic Gear Trains)轮系运转时,至少有一个齿轮轴线的位置不固定,而是绕某一固定轴线回转,称该轮系为周转轮系。
如图6-2所示。
又可根据自由度数的不同,将周转轮系分为差动轮系和行星轮系两类。
当轮系的自由度数为2,即需要两个原动件机构运动才能确定时,该周转轮系称为差动轮系,如图6-2a所示;自由度为1的周转轮系称为行星轮系,如图6-2b所示。
图 6-2周转轮系还可根据基本构件的不同分类。
以K表示中心轮,以H表示系杆,则图6-2所示轮系可称为2K-H型周转轮系,图6-3所示轮系则称为3K型周转轮系。
图6-3所示的轮系中有3个中心轮(图中的齿轮1、3和4)故称为3K型周转轮系,该轮系的系杆H仅起支承行星轮2-2′的作用,不传递外力矩,因而不是基本件。
图 6-3由定轴轮系和周转轮系或者由两个以上的周转轮系所组成的轮系,称为混合轮系,如图6-4所示,该机构左部由齿轮1、2、2 ′和3组成定轴轮系,而其右部则为周转轮系。
图 6-4二、轮系的功用(Functions of Gear Trains)1、实现相距较远的两轴之间的传动如下图6-5所示,若用四个小齿轮a、b、c和d代替一对大齿轮1、2实现啮合传动,既节省材料,减少占用空间,又方便于制造和安装。
图 6-52、实现分路传动图6-6为滚齿机上实现滚刀与轮坯范成运动的传动简图。
图中由轴I来的运动和动力经锥齿轮1、2传给滚刀,同时又由与锥齿轮1同轴的齿轮3经齿轮4、5、6、7传给蜗杆8,再传给蜗轮9而至轮坯。
第五十三讲行星轮系的类型选择及设计的基本知识
从传动原理出发设计行星轮系时,主要解决两个问题:
1、选择传动类型。
2、确定各轮的齿数和行星轮的个数。
1、行星轮系类型类型的选择
行星轮系的类型很多,在相同的速比和载荷条件下,采用不同的类型,可以轮系的外廓尺寸、重量和效率相差很多。
所以,在设计行星轮系时,要重视类型的选择。
选型时要考虑的因素有传动比范围、机械效率的高低、功率流动情况等。
正号机构:i H1n>0 转化轮系中3H1与3 H n的方向相同。
负号机构:i H1n<0 转化轮系中3 H1与3 H n的方向相反。
如图8—24所示2K-H轮系中共有4种负号机构机构传动比及其适用范围。
i iB=2. 8—13 i]tt=L 14—L56 2
图8 —24
从机械效率来看,负号机构的效率比正号机构要高,传递动力应采用负号机构。
如果要求轮系具有较大的传动比,而单级负号机构又不能满足要求,可将几个负号机构串联起来,或采用负号机构与定轴轮系组合而成复和轮系。
其传动比范围i1H= 10〜60。
正号机构一般用在传动比大而对效率要求不高的辅助机构中,例如磨床的进给机构,轧钢机的指示器等。
如图8—25所示为三种理论上传动比i1H -X的正号机构
图8—25
2、各轮齿数的确定
各轮的齿数必须满足以下要求:
1)能实现给定的传动比;
2)中心轮和系杆共轴;
3)能均布安装多个行星轮;
4)相邻行星轮不发生干涉。
1)传动比条件
如图8—26所示,
亠亠■ H O —CO H 1 ■z3
-丨13 = -------------- =7—1伯=—
- ■ 'H Z
1
Z1+Z3 =i lH Z i
Z3 =(i iH -1)Z i
2)同心条件
如图8—27所示,系杆的轴线与两中心轮的轴线重合,当采用标准齿轮传动或等变位齿轮传动时有:
r3= ri+ 2r2 或Z3= zi+ 2z2
z2=(Z3- zi )/2 = zi(iiH-2)/2
上式表明:两中心轮的齿数应同时为偶数或奇数。
图8—26 图8—27
3)均布安装条件
如图8—28所示,能装入多个行星轮且仍呈对称布置,行星轮个数K与各轮齿数之间应满足一定的条件。
设对称布列有K个行星轮,则相邻两轮之间的夹角为:©= 2 n /k
图8—28
在位置O i装入第一个行星轮,固定轮3,转动系杆H,使© H=© ,此时,
行星轮从位置O i运动到位置O2,而中心轮1从位置A转到位置A'转角为9。
T 9 / 0=3 1 / c^= i1H= 1+(z3 /z1 )
r Z3平乙+Z3 2兀
二0=(1+丄)9=一严
Z! 乙k
如果此时轮1正好转过N个完整的齿,则齿轮1在A处又出现与安装第一个行星轮一样的情形,可在A处装入第二个行星轮。
结论:当系杆H转过一个等份角0时,若齿轮1转过N个完整的齿,就能实
现均布安装。
对应的中心角为:9 = N (2*可)
比较得:N =(z 1+Z3)/k= z 1 i 1H /k
上式说明:要满足均布安装条件,轮1和轮3的齿数之和应能被行星轮个数K
整除。
4)邻接条件
如图8—29所示,相邻两个行星轮装入
后不发生干涉,即两行星轮中心距应大于两
齿顶圆半径之和:
O1 O2 > 2r a2
2(r1+r2)sin( 0 /2 ) > 2(r2+h*a m)
即:(z计Z2)si n( n /k)Z2+2h*a
为便于应用,将前三个条件合并得:
Z2= Z1 (i1H-2)/2
图8—29
Z
3 —(i1H -^1)z1
N=Z1 i1H /k
由此可得配齿公式:
Z1:Z2:Z3:N =Z1: Z1 (i1H: Z1(i1H 一1):^^=1:认-:(i1H 一1):區
2 k 2 k
确定各轮齿数时,应保证z1、z2、z3、N为正整数,且z1> z2、z3均大于z min
举例:已知i1H = 5, K=3,采用标准齿轮,确定各轮齿数。
解:
Z1 : Z2 : Z3
=1:(5-2)/2:(5 —1):5/3
=1:3/245/3
=6:9:24:10
若取Z1 = 18,则Z2 = 27,Z3 = 72
验算邻接条(18+27)sin n /3= >29 = Z2+2h*a,可见所选齿数满足要求。
5)行星轮系均载装置
为了减少因制造误差引起的多个行星轮所承担载荷不均匀的现象,实际应用时往往采用均载装置,如图8—30所示。
均载装置的结构特点是采用弹性元件使中心轮或系杆浮动。
图8—30
中心轮浮动。