广东中考数学专题复习尺规作图

《深圳中考专项复习》第7讲之尺规作图【考点介绍】近几年的深圳中考卷中，都有一道中等偏下难度的尺规作图识别题，考查几何5个基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）的作图痕迹识别。

【最近五年中考实题详解】1.(2020∙深圳)如图，已知AB=AC，BC=6，山尺规作图痕迹可求出BD=( )A.2B.3C.4D.5【解析】由作图痕迹可知AD为∠BAC的角平分线，而AB=AC，由等腰三角形的三线合一知D为BC重点，BD=3，故选B。

AB的长为半径画圆弧，两弧相交于点M、2.(2019∙深圳)如图，已知AB=AC，AB=5，BC=3，以AB两点为圆心，大于12N，连接MN与AC相交于点D，则△BDC的周长为（）A. 8B. 10C. 11D. 13【解析】由作图痕迹可知DM为线段AB的垂直平分线，∴AD=BD，则△BDC的周长=BC+CD+BD=BC+CD+AD=BC+AC=BC+AB=8，故选A。

3.(2018∙深圳)已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图1，菱形ADFE为△ABC的亲密菱形。

如图书2，在△CFE中，CF=6，CE=12,∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于12AD长为半径做弧，交EF于点B，AB//CD.(1)求证：四边形ACDB为△CFE的亲密菱形；(2)求四边形ACDB的面积.【解析】中等难度题型，以阅读理解题型考查菱形的证明与计算、尺规作图。

(1)证明：由尺规作图痕迹可得：AC=CD，AB=DB，BC是∠FCE的角平分线，则：∠ACB=∠DCB，又∵AB//CD，∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD，AB=DB，∴AC=CD=DB=BA，∴四边形ACDB 是菱形.∵∠ACD与∠FCE重合，它的对角∠ABD的顶点在EF上，∴四边形ACDB为△CFE的亲密菱形.(2)解：设菱形ACDB的边长为x，∵AB//CE，∴FAFC =ABCE，即6−x6=x12,解得：4x=,过A点作AH⊥CD于点H，在直角△CAH中，∠FCE=45°，AH=AC∙sin45°=4×√22=2√2,∴菱形ACDB的面积为：4×2√2=8√2.4.(2017∙深圳)如图，已知线段AB，分别以A、B为圆心，大于AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB=25°，延长AC至M，求∠BCM的度数为（）A．40° B．50° C．60° D．70°【解析】由作法可知直线l是线段AB的垂直平分线，∴AC=BC，∴∠CAB=∠CBA=25°，∴∠BCM=∠CAB+∠CBA=25°+25°=50°．故选B．5.(2016∙深圳)如图，在平行四边形ABCD中，AB=3,BC=5,以点B为圆心，以任意长为半径作弧，分别交BA、BC于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点点P、Q，再分别以P、Q为圆心，以大于12E，则DE的长为____________.【解析】由作法可知BE为角平分线，所以，∠ABE＝∠CBE，又AD∥BC，所以，∠AEB＝∠CBE，所以，∠AEB＝∠ABE，AE＝AB＝3，AD＝BC＝5，所以，DE＝5－3＝2。

广东省中考数学考点知识专题讲解与训第27讲尺规作图知识梳理与尺规作图有关的证明与计算5年真题命题点1 基本作图1．（6分）（2019•广东）如图，在△AB C中，点D是AB边上的一点．（1）请用尺规作图法，在△ABC内，求作∠ADE，使∠ADE＝∠B，DE交AC于E；（不要求写作法，保留作图痕迹）；（2）在（1）的条件下，若ADDB =2，求AEEC的值．解：（1）如图，∠ADE为所作；（2）∵∠ADE＝∠B，∴DE∥BC，∴AEEC =ADDB=2．2．（6分）（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD＝75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．解：（1）如图所示，直线EF即为所求；（2）∵四边形ABCD是菱形，∴∠ABD＝∠DBC=12∠ABC＝75°，DC∥AB，∠A＝∠C．∴∠ABC＝150°，∠ABC+∠C＝180°，∴∠C＝∠A＝30°，∵EF垂直平分线段AB，∴AF＝FB，∴∠A＝∠FBA＝30°，∴∠DBF＝∠ABD﹣∠FBE ＝45°．3．（7分）（2017•广东）如图，在△AB C中，∠A＞∠B．（1）作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连接AE，若∠B＝50°，求∠AEC的度数．解：（1）如图所示；（2）∵DE是AB的垂直平分线，∴AE＝BE，∴∠EAB＝∠B＝50°，∴∠AEC＝∠EAB+∠B＝100°．4．（6分）（2016•广东）如图，已知△AB C中，D为AB的中点．（1）请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；（2）在（1）的条件下，若DE＝4，求BC的长．解：（1）作线段AC的垂直平分线MN交AC于E，点E就是所求的点．（2）∵AD＝DB，AE＝EC，∴DE∥BC，DE=1BC，∵DE＝4，∴BC＝8．23年模拟1．（2020•罗湖区一模）如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，EF长为半径作圆弧，两分别交AB，AC于E，F两点，再分别以E，F为圆心，大于12条圆弧交于点P，连接AP，交CD于点M，若∠ACD＝110°，则∠CMA的度数为（B）A．30°B．35°C．70°D．45°2．（2020•大鹏新区一模）如图，在△AB C中，∠B＝70°，∠C＝30°，分别以点A和点AC的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点C为圆心，大于12D，连接AD，则∠BAD的度数为（C）A．40°B．45°C．50°D．60°3．（2020•恩平市模拟）已知线段a，h，小明用如图所示的方法作△ABC，他的具体作法是：①作射线AM，以点A为圆心，线段a的长为半径画弧，交射线AM于点B；②分别以点A，B为圆心，大于1AB长为半径画弧，两弧交于D，E两点；③作直线DE，交AB2于点F；④以点F为圆心，线段h的长为半径画弧，交直线DE于点C，连接AC，B C．下列关于小明作的△ABC的说法，错误的是（D）A．AF＝BF B．∠CAB＝∠CBAC．∠ACF＝∠BCF D．AB＝BCD【解析】由作图可知，DE垂直平分线段AB，∴AF＝BF，DE⊥AB，∴CA＝CB，∴∠CAB＝∠CBA，∠ACF＝∠BCF，故A，B，C正确，故选：D．4．（2020•龙华区二模）如图，矩形ABC D中，AD＝2，以A为圆心，任意长为半径作MN的长为半径作弧，弧，分别交AB、AD于M、N两点，分别以M、N为圆心，大于12两弧相交于点P，连接AP并延长交CD于点E，以A为圆心，AE为半径作弧，此弧刚好过点B，则CE的长为2√2−2．2√2−2【解析】如图，连接BE，根据作图过程可知：AE平分∠DAB，∴∠DAE＝∠EAB，∵四边形ABCD是矩形，∴DC∥AB，∠D＝90°，∴∠DAE＝∠EAB，∴∠EAB＝∠AED，∴∠DAE＝∠AED，∴DE＝AD＝2，∴DE=√AD2+DE2=2√2，∴DC＝AB＝AE＝2√2，∴CE＝DC﹣DE＝2√2−2．故答案为：2√2−2．5．（2020•禅城区二模）如图，点A是∠MON边OM上一点，AE∥ON．（1）尺规作图：作∠MON的角平分线OB，交AE于点B（保留作图痕迹，不写作法）；（2）若∠MAE＝48°，直接写出∠OBE的大小．解：（1）如图，OB为所作；（2）∵AE∥ON，∴∠MON＝∠MAE＝48°，∵OB平分∠MON，∴∠NOB=1∠MON＝24°，∵AB∥ON，2∴∠OBA＝∠NOB＝24°，∴∠OBE＝180°﹣∠OBA＝180°﹣24°＝156°．6．（2020•惠来县模拟）如图，已知锐角△ABC，AB＞B C．（1）只规作图：求作△ABC的角平分线BD；（保留作图痕迹，不写作法）（2）点E在AB边上且BC＝BE，请连接DE，求证：∠BED＝∠C．（1）解：如图，线段BD即为所求；（2）证明：∵BD平分∠ABC，∴∠EBD＝∠CBD，∵BE＝BC，BD＝BD，∴△BDE≌△BDC（SAS），∴∠BED＝∠C．7．（2020•梅州模拟）如图，已知BD是矩形ABCD的对角线．（1）用直尺和圆规作线段BD的垂直平分线，分别交AD、BC于点E和点F（保留作图痕迹，不写作法）；（2）连接BE、DF，若AB＝4，AD＝8，求四边形BEDF的周长．解：（1）如图，直线EF即为所求．（2）∵EF垂直平分线段BD，∴BE＝ED，BF＝DF，∠BEF＝∠DEF，∵AD∥BC，∴∠DEF＝∠BFE，∴∠BEF＝∠BFE，∴BE＝BF，∴BE＝DE＝DF＝BF，设BE＝x，在Rt△BAE中，AB＝4，AE＝8﹣x，可得42+（8﹣x）2＝x2，∴x＝5，∴BE+DE+DF+BF＝20，∴四边形BEDF的周长为20．8．（2020•南沙区一模）如图，AB为⊙O的直径，点C为弧A B中点，连接AC、B C．（1）利用尺规作图，作出∠BAC的角平分线，分别交BC、⊙O于点D、E，连接BE．（保留作图痕迹，不写作法）（2）若BE＝2，求AD的长度．解：（1）如图，AE即为所求；̂=BĈ，（2）∵点C为弧A B中点，∴AC∴AC＝BC，∵AB为⊙O的直径，∴∠ACB＝90°，延长BE、AC交于点F，由（1）作图可知：∠BAE＝∠CAE，∠AEB＝90°，∴AE垂直平分BF，∴BF＝2BE＝4，又∵∠DAC＝∠FBC，∠ACD＝∠BCF＝90°，AC＝BC，∴△ACD≌△BCF（ASA），∴AD＝BF＝4．9．（2020•澄海区一模）如图，在△AB C中，AB＝AC，点M在BA的延长线上．（1）按下列要求作图，并在图中标明相应的字母（尺规作图，保留作图痕迹，不要求写作法和证明）；①作∠MAC的平分线AN；②在AN上截取AD＝BC，连结C D．（2）在（1）的条件下，判断四边形ABCD的形状，并证明你的结论．解：（1）①如图，AN为所求的图形；②如图，AD为所作；（2）四边形ABCD是平行四边形．理由如下：∵AB＝AC，∴∠ABC＝∠ACB，∵AN平分∠MAC，∴∠CAD＝∠MAD，∵∠CAD+∠MAD＝∠ABC+∠ACB，∴∠MAD＝∠ABC，∴AD∥BC，∵AD＝BC，∴四边形ABCD是平行四边形．10．（2020•顺德区四模）如图，点E是▱ABCD对角线BD上的一点．（1）请用尺规作图法，过点E作EG∥CD；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，在直线EG上截取EF＝CD且点F在点E的下方，连接AE、BF、CF，若∠ABE+∠BFC＝180°，求证：四边形ABFE是菱形（1）解：如图，直线EG即为所求．（2）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∵EF∥CD，EF＝CD，∴EF＝AB，EF∥AB，∴四边形EFCD，四边形ABFE是平行四边形，∴BD∥CF，∴∠DBF+∠BFC＝180°，∵∠ABE+∠BFC＝180°，∴∠ABE＝∠DBF，∵AB∥EF，∴∠ABE＝∠BEF，∴∠BEF＝∠EBF，∴FE＝FB，∴四边形ABFE是菱形．1 / 11。

中考专题30 尺规作图问题1.尺规作图的定义：只用不带刻度的直尺和圆规通过有限次操作，完成画图的一种作图方法．尺规作图可以要求写作图步骤，也可以要求不一定要写作图步骤，但必须保留作图痕迹。

2.尺规作图的五种基本情况(1)作一条线段等于已知线段；(2)作一个角等于已知角；(3)作已知线段的垂直平分线；(4)作已知角的角平分线；(5)过一点作已知直线的垂线。

3.对尺规作图题解法写出已知，求作，作法(不要求写出证明过程)并能给出合情推理。

4.中考专题要求(1)能完成以下基本作图：作一条线段等于已知线段，作一个角等于已知角，作角的平分线，作线段的垂直平分线.(2)能利用基本作图作三角形：已知三边作三角形；已知两边及其夹角作三角形；已知两角及其夹边作三角形；已知底边及底边上的高作等腰三角形.(3)能过一点、两点和不在同一直线上的三点作圆.(4)了解尺规作图的步骤，对于尺规作图题，会写已知、求作和作法(不要求证明).【经典例题1】(2020年•台州)如图，已知线段AB ，分别以A ，B 为圆心，大于12AB 同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是( )A．AB平分∠CAD B．CD平分∠ACB C．AB⊥CD D．AB＝CD【标准答案】D【分析】根据作图判断出四边形ACBD是菱形，再根据菱形的性质：菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出标准答案．【答案剖析】由作图知AC＝AD＝BC＝BD，∴四边形ACBD是菱形，∴AB平分∠CAD、CD平分∠ACB、AB⊥CD，不能判断AB＝CD【知识点练习】(2019•丽水模拟题)如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求．连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC一定是( )A.矩形B.菱形C.正方形D.等腰梯形【标准答案】B【答案剖析】根据垂直平分线的画法得出四边形ADBC 四边的关系进而得出四边形一定是菱形。

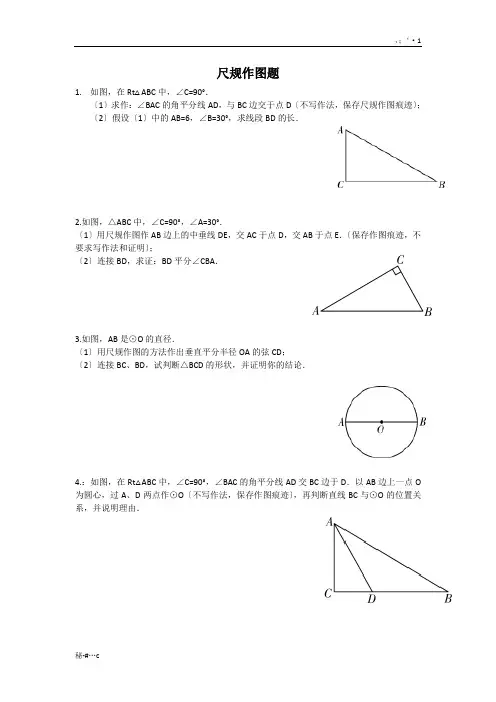
尺规作图题1.如图，在Rt△ABC中，∠C=90°．〔1〕求作：∠BAC的角平分线AD，与BC边交于点D〔不写作法，保存尺规作图痕迹〕；〔2〕假设〔1〕中的AB=6，∠B=30°，求线段BD的长．2.如图，△ABC中，∠C=90°，∠A=30°．〔1〕用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．〔保存作图痕迹，不要求写作法和证明〕；〔2〕连接BD，求证：BD平分∠CBA．3.如图，AB是⊙O的直径．〔1〕用尺规作图的方法作出垂直平分半径OA的弦CD；〔2〕连接BC、BD，试判断△BCD的形状，并证明你的结论．4.：如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB边上一点O 为圆心，过A、D两点作⊙O〔不写作法，保存作图痕迹〕，再判断直线BC与⊙O的位置关系，并说明理由．5.如图，在平面直角坐标系中，点B〔4，2〕，BA⊥x轴于A，〔1〕作出△OAB绕原点逆时针方向旋转90°后的图形△OA1B1，并写出B1的坐标及求出点B 经过的路径长。

〔2〕将△OAB平移得到△O′A′B′，点A的对应点是A′，点B的对应点B′的坐标为〔2，-2〕，在坐标系中作出△O′A′B′．6.如图8×8正方形网格中，点A、B、C和O都为格点．〔1〕利用位似作图的方法，以点O为位似中心，可将格点三角形ABC扩大为原来的2倍．请你在网格中完成以上的作图〔点A、B、C的对应点分别用A′、B′、C′表示〕；〔2〕当以点O为原点建立平面坐标系后，点C的坐标为〔-1，2〕，那么A′、B′、C′三点的坐标分别为：A′：B′：C′：．7.如图，在平行四边形ABCD中，AB＜BC．〔1〕利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等〔不写作法，保存作图痕迹〕；〔2〕假设BC=8，CD=5，求CE9.如图，BD平分∠ABF，且交AE于点D，〔1〕求作：∠BAE的平分线AP〔要求：尺规作图，保存作图痕迹，不写作法〕；〔2〕设AP交BD于点O，交BF于点C，连接CD，当AC⊥BD时，求证：四边形ABCD是菱形．10在平面直角坐标系中，点P的坐标为(－4，0)，⊙P的半径为2，将⊙P沿x轴向右平移4个单位得到⊙P1.(1)画出⊙P1，并直接判断⊙P与⊙P1的位置关系．(2)设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B，求劣弧与弦AB围成的图形的面积．(结果保存π)12.如图，△ABC是直角三角形，∠ACB=90°．〔1〕尺规作图：作⊙C，使它与AB相切于点D，与AC相交于点E，保存作图痕迹，不写作法，请标明字母．〔2〕在你按〔1〕中要求所作的图中，假设BC=3，∠A=30°，求的长．13.如图，在△ABC中，∠A=90°〔1〕请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切〔保存作图痕迹，不写作法和证明〕．〔2〕假设∠B=60°，AB=3，求⊙P的面积．14.如图，Rt△ABC的斜边AB=5，cosA=。

第27课尺规作图本节内容考纲要求考查五个基本作图和能转化为基本作图的简单尺规作图。

广东省近5年试题规律：以解答题出现，一般考查作角平分线，线段的垂直平分线和过一点直线的垂线，多与三角形、四边形问题结合一起，难度不大，但学生欠缺动手操作，是常见丢分题。

知识清单知识点一尺规作图定义只用圆规和尺子来完成的图画，称为尺规作图.基本步骤(1)已知：写出已知的线段和角，画出图形；(2)求作：求作什么图形，使它符合什么条件；(3)作法：运用五种基本作图，保留作图痕迹；(4)证明：验证所作图形的正确性；(5)结论：对所作的图形下结论.五种基本作图(1)作一条线段等于已知线段；(2)作一个角等于已知角；(3)作一个角的平分线；(4)经过一已知点作直线的垂线；(5)作已知线段的垂直平分线.课前小测1．（尺规作图的定义）尺规作图是指（）A．用直尺规范作图B．用刻度尺和圆规作图C．用没有刻度的直尺和圆规作图D．直尺和圆规是作图工具2．（作角平分线）如图，用尺规作已知角平分线，其根据是构造两个三角形全等，它所用到的判别方法是（）A．SAS B．ASA C．AAS D．SSS3．（作一个角等于已知角）小明回顾用尺规作一个角等于已知角的作图过程（如图所示），连接CD、C′D′得出了△OCD≌△O′C′D′，从而得到∠O=∠O′，其中小明作出△OCD≌△O′C′D′判定的依据是（）A．SSS B．SAS C．ASA D．AAS 4．（作垂直平分线）如图所示，已知线段AB=6，现按照以下步骤作图：①分别以点A，B为圆心，以大于12AB的长为半径画弧，两弧相交于点C和点D；②连结CD交AB于点P．则线段PB的长为．5．（作垂线）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图中正确的是（）A．B．C．D．经典回顾考点一作线段垂直平分线【例1】（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．【点拨】作线段的垂直平分线要点：①以线段两端点为圆心作弧，两弧交于两点；②再过两点作垂线．考点二作角平分线【例2】（2018•赤峰）如图，D是△ABC中BC边上一点，∠C＝∠DAC．（1）尺规作图：作∠ADB的平分线，交AB于点E（保留作图痕迹，不写作法）；（2）在（1）的条件下，求证：DE∥AC．【点拔】作角的平分线要点：①以顶点为圆心画弧交角的两边于两点；②再以这两点为圆心作弧，两弧交于一点；③最后过顶点与交点作射线．考点三作垂线【例3】（2015•广东）如图，已知锐角△AB C．（1）过点A作BC边的垂线MN，交BC于点D（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，若BC=5，AD=4，tan∠BAD=34，求DC的长．【点拨】过一点作垂线或作高线要点：①以这点为圆心，在直线上截取一条线段；②再作线段的垂直平分．考点四作一个角等于已知角【例4】（2019•广东）如图，在△ABC中，点D是AB边上的一点．（1）请用尺规作图法，在△ABC内，求作∠ADE，使∠ADE＝∠B，DE交AC 于E；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若ADDB＝2，求AEEC的值．【点拔】过一点作一个角等于已知角要点：①以角的顶点为圆心画弧交两边于两点，以这一点为圆心，相同半径作弧，交于一点；②再以两点间距离为半径，作弧，两弧交于一点；③最后过这一点于交点作射线．对应训练1．（2019•泰州）如图，△ABC中，∠C＝90°，AC＝4，BC＝8．（1）用直尺和圆规作AB的垂直平分线；（保留作图痕迹，不要求写作法）（2）若（1）中所作的垂直平分线交BC于点D，求BD的长．2．（2019•中山一模）如图，已知平行四边形ABCD，（1）作∠B的平分线交AD于E点．（用尺规作图法，保留作图痕迹，不要求写作法）（2）若平行四边形ABCD的周长为10，CD＝2，求DE的长．3．（2019•江门期末）画图题：如图，已知三角形ABC，AB＝5．（1）过点C作CD⊥AB，点D为垂足：（2）在（1）的条件下，若DB＝2，求点A到CD的距离．4．（2019•顺德期末）如图，Rt△ABC中，∠A＝90°．（1）用尺规作图法作∠ABD＝∠C，与边AC交于点D（保留作图痕迹，不用写作法）；（2）在（1）的条件下，当∠C＝30°时，求∠BDC的度数．中考冲刺夯实基础1．（2019•赤峰）已知：AC是□ABCD的对角线．（1）用直尺和圆规作出线段AC的垂直平分线，与AD相交于点E，连接CE．（保留作图痕迹，不写作法）；（2）在（1）的条件下，若AB＝3，BC＝5，求△DCE的周长．2．（2019•惠阳二模）如图，已知：AB∥CD．（1）在图中，用尺规作∠ACD的平分线交AB于E点；（不要求写作法，保留作图痕迹）（2）判断△ACE的形状，并证明．3．（2019•玉林）如图，已知等腰△ABC顶角∠A＝36°．（1）在AC上作一点D，使AD＝BD（要求：尺规作图，保留作图痕迹，不必写作法和证明，最后用黑色墨水笔加墨）；（2）求证：△BCD是等腰三角形．4．（2019•越秀一模）如图，在矩形ABCD中，AD＝AE（1）尺规作图：作DF⊥AE于点F；（保留作图痕迹，不写作法）（2）求证：AB＝DF．能力提升5．（2019•白银）已知：在△ABC中，AB＝AC．（1）求作：△ABC的外接圆．（要求：尺规作图，保留作图痕迹，不写作法）（2）若△ABC的外接圆的圆心O到BC边的距离为4，BC＝6，则S⊙O＝．6．（2019•三明模拟）如图，在△ABC中，AB＝AC．（1）尺规作图：作∠CBD＝∠A，D点在AC边上（要求：不写作法，保留作图痕迹）（2）若∠A＝40°，求∠ABD的度数．7．（2019•达州）如图，在Rt△ABC中，∠ACB＝90°，AC＝2，BC＝3．（1）尺规作图：不写作法，保留作图痕迹．①作∠ACB的平分线，交斜边AB于点D；②过点D作BC的垂线，垂足为点E．（2）在（1）作出的图形中，求DE的长．第27课尺规作图课前小测1．C．2．D．3．A．4．3．5．B．经典回顾考点一作线段垂直平分线【例1】解：（1）如图，直线EF即为所求；（2）∵四边形ABCD是菱形，∠ABC=75°，DC∥AB，∠A=∠C．∴∠ABD=∠DBC=12∴∠ABC=150°，∠ABC+∠C=180°，∴∠C=∠A=30°，∵EF垂直平分线线段AB，∴AF=FB，∴∠A=∠FBA=30°，∴∠DBF=∠ABD﹣∠FBE=45°．考点二作角平分线【例2】（1）解：如图，DE为所求；（2）证明：∵DE平分∠ADB，∴∠ADE＝∠BDE，∵∠ADB＝∠C+∠DAC，而∠C＝∠DAC，∴2∠BDE＝2∠C，即∠BDE＝∠C，∴DE∥AC．考点三作垂线【例3】解：（1）如图，MN为所求；（2）∵AD⊥BC，∴∠ADB=∠ADC=90°，∵tan∠BAD=BDAD =34，∴BD=3，∴CD=BC﹣BD=5﹣3=2．考点四作一个角等于已知角【例4】解：（1）如图，∠ADE为所作；（2）∵∠ADE＝∠B∴DE∥BC，∴AEEC ＝ADDB＝2．对应训练1．解：（1）如图直线MN即为所求．（2）∵MN垂直平分线段AB，∴DA＝DB，设DA＝DB＝x，在Rt△ACD中，∵AD2＝AC2+CD2，∴x2＝42+（8﹣x）2，解得x＝5，∴BD＝5．2．解：（1）如图，BE为所作；（2）∵四边形ABCD为平行四边形，∴AD∥BC，AB＝CD＝2，AD＝BC，∵平行四边形ABCD的周长为10∴AB+AD＝5，∴AD＝3，∵BE平分∠ABC，∴∠ABE＝∠CBE，∵AD∥BC，∴∠ABE＝∠AEB，∴AE＝AB＝2，∴DE＝AD﹣AE＝3﹣2＝1．3．解：（1）如图，CD为所作．（2）∵AB＝5，BD＝2，∴AD＝3，∴点A到CD的距离为3．4．解：（1）如图，∠ABD为所作；（2）∵∠ABC+∠C+∠A＝90°，∴∠ABC＝180°﹣90°﹣30°＝60°，∵∠ABD＝∠C＝30°，∴∠BDC＝∠ABC﹣∠ABD＝60°﹣30°＝30°，∴∠BDC＝180°﹣30°﹣30°＝120°．中考冲刺夯实基础1．解：（1）如图，CE为所作；（2）∵四边形ABCD为平行四边形，∴AD＝BC＝5，CD＝AB＝3，∵点E在线段AC的垂直平分线上，∴EA＝EC，∴△DCE的周长＝CE+DE+CD＝EA+DE+CD＝AD+CD＝5+3＝8．2．解：（1）如图即为所求：（2）△ACE是等腰三角形．证明：∵CE平分∠ACD，∴∠ACE＝∠ECD，∵AB∥CD，∴∠AEC ＝∠ECD ，∴∠ACE ＝∠AEC ，∴△ACE 是等腰三角形．3．（1）解：如图，点D 为所作；（2）证明：∵AB ＝AC ，∴∠ABC ＝∠C ＝（180°﹣36°）＝72°， ∵DA ＝DB ，∴∠ABD ＝∠A ＝36°，∴∠BDC ＝∠A +∠ABD ＝36°+36°＝72°， ∴∠BDC ＝∠C ，∴△BCD 是等腰三角形．4．（1）解：如图，F 点为所作；（2）证明：∵四边形ABCD 为矩形， ∴AD ∥BC ，∠B ＝90°，∴∠DAE ＝∠AEB ，∵DF ⊥AE ，∴∠AFD ＝90°，在△ABE 和△DFA 中B DFAAEB DAF AE AD=⎧⎪=⎨⎪=⎩∠∠∠∠，∴△ABE≌△DFA（AAS），∴AB＝DF．能力提升5．解：（1）如图⊙O即为所求．（2）25π．6．解：（1）如图，∠CBD为所作；（2）∵AB＝AC，∴∠ABC＝∠C＝1（180°﹣∠A）＝70°，2∵∠CBD＝∠A＝40°，∴∠ABD＝70°﹣40°＝30°．7．解：（1）如图，DE为所作；（2）∵CD平分∠ACB，∴∠BCD＝12∠ACB＝45°，∵DE⊥BC，∴△CDE为等腰直角三角形，∴DE＝CE，∵DE∥AC，∴△BDE∽△BAC，∴DEAC ＝BEBC，即2DE＝33DE，∴DE＝65．。

广东省中考尺规作图专题训练一、熟练掌握尺规作图题的规范语言（保留作图痕迹并描黑）1、用直尺作图的几何语言：①过点×、点×作直线××；或作直线××；或作射线××；②连结两点××；或连结××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；2、用圆规作图的几何语言：①在××上截取××＝××；②以点×为圆心，××的长为半径作圆（或弧）；③以点×为圆心，××的长为半径作弧，交××于点×；④分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、× .3、五种基本作图：①作一条线段等于已知线段；②作一个角等于已知角；③作已知线段的垂直平分线；④作已知角的角平分线；⑤过一点作已知直线的垂线；考点一：利用垂直平分线作已知线段的中点。

已知：如图，线段MN.求作：点O，使MO=NO（即O是MN的中点）.考点二：作已知角的角平分线。

已知：如图，∠AOB，求作：射线OP, 使∠AOP＝∠BOP（即OP平分∠AOB）。

考点三：作垂线（高）①如图，过点C作线段AB的垂线；②如图，过点F作线段DE的垂线.综合应用：1、如下图，已知钝角△ABC，∠B是钝角．（1）求作：BC边上的高；（2）若AB=BC，∠C=30°，AC=6，求三角形ABC的面积.2、如图，在△ABC中，AB=AC，∠ABC=720，（1）用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC的平分线BD后，求∠BDC的度数。

2025年中考数学考点分类专题归纳尺规作图1、定义（1）尺规作图是指用没有刻度的直尺和圆规作图．只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题．（2）基本要求它使用的直尺和圆规带有想像性质，跟现实中的并非完全相同．直尺必须没有刻度，无限长，且只能使用直尺的固定一侧．只可以用它来将两个点连在一起，不可以在上画刻度．圆规可以开至无限宽，但上面亦不能有刻度．它只可以拉开成你之前构造过的长度．2、基本作图有：（1）作一条线段等于已知线段．（2）作一个角等于已知角．（3）作已知线段的垂直平分线．（4）作已知角的角平分线．（5）过一点作已知直线的垂线．3、复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．4、应用与设计作图主要把简单作图放入实际问题中．首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．1．（2024•鄂尔多斯）如图，在菱形ABCD中，按以下步骤作图：①分别以点C和点D为圆心，大于CD为半径作弧，两弧交于点M，N；②作直线MN，且MN恰好经过点A，与CD交于点E，连接BE，则下列说法错误的是（）A．∠ABC＝60°B．S△ABE＝2S△ADEC．若AB＝4，则BE D．sin∠CBE2．（2024•河南）如图，已知▱AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）A．（1，2）B．（，2）C．（3，2）D．（2，2）3．（2024•郴州）如图，∠AOB＝60°，以点O为圆心，以任意长为半径作弧交OA，OB于C，D两点；分别以C，D为圆心，以大于CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上截取线段OM＝6，则M点到OB的距离为（）A．6 B．2 C．3 D．4．（2024•宜昌）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图中正确的是（）A．B．C．D．5．（2024•襄阳）如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE＝3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．19cm C．22cm D．25cm6．（2024•潍坊）如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：（1）作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；（2）以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；（3）连接BD，BC．下列说法不正确的是（）A．∠CBD＝30°B．S△BDC AB2C．点C是△ABD的外心D．sin2A+cos2D＝17．（2024•台州）如图，在▱ABCD中，AB＝2，BC＝3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（）A．B．1 C．D．8．（2024•巴中）如图，在Rt△ABC中，∠C＝90°，按下列步骤作图：①以点B为圆心，适当长为半径画弧，与AB，BC分别交于点D，E；②分别以D，E为圆心，大于DE的长为半径画弧，两弧交于点P；③作射线BP交AC于点F；④过点F作FG⊥AB于点G．下列结论正确的是（）A．CF＝FG B．AF＝AG C．AF＝CF D．AG＝FG9．（2024•昆明）如图，点A在双曲线y═（x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F （0，2），连接AC．若AC＝1，则k的值为（）A．2 B．C．D．10．（2024•安顺）已知△ABC（AC＜BC），用尺规作图的方法在BC上确定一点P，使PA+PC＝BC，则符合要求的作图痕迹是（）A．B．C．D．11．（2024•湖州）尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（）A．r B．（1）r C．（1）r D．r12．（2024•益阳）如图，在△ABC中，AB＝5，AC＝4，BC＝3．按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AC于点M，N；②分别以M，N为圆心，以大于MN的长为半径作弧，两弧相交于点E；③作射线AE；④以同样的方法作射线BF．AE交BF于点O，连接OC，则OC＝_______．13．（2024•抚顺）如图，▱ABCD中，AB＝7，BC＝3，连接AC，分别以点A和点C为圆心，大于AC的长为半径作弧，两弧相交于点M，N，作直线MN，交CD于点E，连接AE，则△AED的周长是____．14．（2024•葫芦岛）如图，OP平分∠MON，A是边OM上一点，以点A为圆心、大于点A到ON的距离为半径作弧，交ON于点B、C，再分别以点B、C为圆心，大于BC的长为半径作弧，两弧交于点D、作直线AD分别交OP、ON于点E、F．若∠MON＝60°，EF＝1，则OA＝_______．15．（2024•山西）如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB＝2，∠ABP＝60°，则线段AF的长为_______．16．（2024•东营）如图，在Rt△ABC中，∠B＝90°，以顶点C为圆心，适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D．若BD＝3，AC＝10，则△ACD的面积是____．17．（2024•淮安）如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝5，分别以点A、B为圆心，大于AB的长为半径画弧，两弧交点分别为点P、Q，过P、Q两点作直线交BC于点D，则CD的长是__．18．（2024•南京）如图，在△ABC中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE．若BC＝10cm，则DE＝___cm．19．（2024•赤峰）如图，D是△ABC中BC边上一点，∠C＝∠DAC．（1）尺规作图：作∠ADB的平分线，交AB于点E（保留作图痕迹，不写作法）；（2）在（1）的条件下，求证：DE∥AC．20．（2024•攀枝花）已知△ABC中，∠A＝90°．（1）请在图1中作出BC边上的中线（保留作图痕迹，不写作法）；（2）如图2，设BC边上的中线为AD，求证：BC＝2AD．21．（2024•牡丹江）在四边形ABCD中，∠B＝∠C＝90°，AB＝3，BC＝4，CD＝1．以AD为腰作等腰△ADE，使∠ADE＝90°，过点E作EF⊥DC交直线CD于点F．请画出图形，并直接写出AF的长．22．（2024•贵港）尺规作图（只保留作图痕迹，不要求写出作法）．如图，已知∠α和线段a，求作△ABC，使∠A＝∠α，∠C＝90°，AB＝a．23．（2024•北京）下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．已知：直线l及直线l外一点P．求作：直线PQ，使得PQ∥l．作法：如图，①在直线l上取一点A，作射线PA，以点A为圆心，AP长为半径画弧，交PA的延长线于点B；②在直线l上取一点C（不与点A重合），作射线BC，以点C为圆心，CB长为半径画弧，交BC的延长线于点Q；③作直线PQ．所以直线PQ就是所求作的直线．根据小东设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明．证明：∵AB＝____，CB＝____，∴PQ∥l（__________）（填推理的依据）．24．（2024•孝感）如图，△ABC中，AB＝AC，小聪同学利用直尺和圆规完成了如下操作：①作∠BAC的平分线AM交BC于点D；②作边AB的垂直平分线EF，EF与AM相交于点P；③连接PB，PC．请你观察图形解答下列问题：（1）线段PA，PB，PC之间的数量关系是__________；（2）若∠ABC＝70°，求∠BPC的度数．25．（2024•陇南）如图，在△ABC中，∠ABC＝90°．（1）作∠ACB的平分线交AB边于点O，再以点O为圆心，OB的长为半径作⊙O；（要求：不写做法，保留作图痕迹）（2）判断（1）中AC与⊙O的位置关系，直接写出结果．26．（2024•青岛）已知：如图，∠ABC，射线BC上一点D．求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等．27．（2024•广安）下面有4张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，请在方格纸中分别画出符合要求的图形，所画图形各顶点必须与方格纸中小正方形的顶点重合，具体要求如下：（1）画一个直角边长为4，面积为6的直角三角形．（2）画一个底边长为4，面积为8的等腰三角形．（3）画一个面积为5的等腰直角三角形．（4）画一个一边长为2，面积为6的等腰三角形．28．（2024•河南）如图，反比例函数y（x＞0）的图象过格点（网格线的交点）P．（1）求反比例函数的解析式；（2）在图中用直尺和2B铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：①四个顶点均在格点上，且其中两个顶点分别是点O，点P；②矩形的面积等于k的值．29．（2024•湖北）图①、图②都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．点O，M，N，A，B均在格点上，请仅用无刻度直尺在网格中完成下列画图．（1）在图①中，画出∠MON的平分线OP；（2）在图②中，画一个Rt△ABC，使点C在格点上．30．（2024•宁波）在5×3的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中画出线段BD，使BD∥AC，其中D是格点；（2）在图2中画出线段BE，使BE⊥AC，其中E是格点．31．（2024•济宁）在一次数学活动课中，某数学小组探究求环形花坛（如图所示）面积的方法，现有以下工具；①卷尺；②直棒EF；③T型尺（CD所在的直线垂直平分线段AB）．（1）在图1中，请你画出用T形尺找大圆圆心的示意图（保留画图痕迹，不写画法）；（2）如图2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点M，N之间的距离，就可求出环形花坛的面积．”如果测得MN＝10m，请你求出这个环形花坛的面积．32．（2024•金华）如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．。