4静力学第四章习题答案
- 格式:doc
- 大小:614.50 KB
- 文档页数:12
静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:161.2R F N==1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 3R F KN== 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)由x =∑cos 450RA F P -=15.8RA F KN∴=由Y =∑sin 450RA RB F F P +-=7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式,得:22.410RA RB F KN F KN==三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解:受力分析如图所示,取左半部分为研究对象由x=∑cos45cos450RA CBP F F--= 0Y=∑sin45sin450CB RAF F'-=联立后,解得:0.707RAF P=0.707RBF P=由二力平衡定理0.707 RB CB CBF F F P'===2-8解:杆AB,AC均为二力杆,取A点平衡由x=∑cos60cos300AC ABF F W⋅--= 0Y=∑sin30sin600AB ACF F W+-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力) 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD,AD,AB(带滑轮C,重物E和一段绳索)的受力图。
1-4构架如图所示,试分别画出杆HED,杆BDC及杆AEC的受力图。
1-5构架如图所示,试分别画出杆BDH,杆AB,销钉A及整个系统的受力图。
1-6构架如图所示,试分别画出杆AEB,销钉A及整个系统的受力图。
1-7构架如图所示,试分别画出杆AEB,销钉C,销钉A及整个系统的受力图。
1-8结构如图所示,力P作用在销钉C上,试分别画出AC,BCE及DEH部分的受力图。
参考答案1-1解:1-2解:1-3解:1-4解:1-5解:1-6解:1-7解:1-8解:第二章习题参考答案2-1解:由解析法,23cos 80RX F X P P N12sin 140RY F Y P P N故:22161.2R RX RY F F F N1(,)arccos 2944RYR RF F P F2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN 13sin 45sin 450RY F Y P P 故:223R RX RY F F F KN 方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a )由平衡方程有:0X sin 300AC AB F F 0Y cos300AC F W联立上二式,解得:0.577AB F W (拉力)1.155AC F W (压力)(b )由平衡方程有:0X cos700AC AB F F 0Y sin 700AB F W 联立上二式,解得:1.064AB F W (拉力)0.364AC F W (压力)(c )由平衡方程有:0X cos60cos300AC AB F F0Y sin 30sin 600AB AC F F W 联立上二式,解得:0.5AB F W (拉力) 0.866AC F W (压力)(d )由平衡方程有:0X sin 30sin 300AB AC F F 0Y cos30cos300AB AC F F W 联立上二式,解得:0.577AB F W (拉力) 0.577AC F W (拉力)2-4解:(a)受力分析如图所示:由x224cos45042RAF P15.8RAF KN由0Y222sin45042RA RBF F P7.1RBF KN(b)解:受力分析如图所示:由0x3cos45cos45010RARB F F P 0Y1sin 45sin 45010RA RB F F P 联立上二式,得:22.410RA RBF KN F KN2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RAF KN(压力)5RBF KN(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G ,2AC F G 由x cos 0AC rF F 12cosG G 由0Ysin 0AC NF F W 22221sinNF WG WG G 2-7解:受力分析如图所示,取左半部分为研究对象由x cos 45cos450RA CB P F F 0Ysin 45sin 450CB RA F F 联立后,解得:0.707RAF P0.707RBF P由二力平衡定理0.707RB CB CBF F F P2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x cos 60cos30AC AB F F W 0Ysin 30sin 60AB AC F F W联立上二式,解得:7.32AB F KN(受压)27.3ACF KN(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x sincos 0DB T W 0DBT Wctg (2)取B 点列平衡方程由0Y sin cos 0BD T T 230BD T T ctg WctgKN2-10解:取B 为研究对象:由0YsinBC F P sinBCP F 取C 为研究对象:由x cos sin sin 0BC DC CE F F F 由Ysin cos cos 0BC DC CE F F F 联立上二式,且有BC BCF F 解得:2cos12sincosCEPF取E 为研究对象:由0YcosNHCE F F CE CEF F 故有:22cos1cos2sin cos2sinNHP P F 2-11解:取A 点平衡:x sin 75sin 750AB AD F F 0Ycos75cos75AB AD F F P 联立后可得:2cos 75AD ABP F F 取D 点平衡,取如图坐标系:x cos5cos80AD ND F F cos5cos80NDADF F由对称性及AD ADF F cos5cos5222166.2cos80cos802cos 75N NDADP F F F KN2-12解:整体受力交于O 点,列O 点平衡由xcos cos300RA DCF F PY sin sin300RAF P联立上二式得: 2.92RAF KN1.33DCF KN(压力)列C点平衡x405DC ACF FY35BC ACF F联立上二式得: 1.67ACF KN(拉力)1.0BCF KN(压力)2-13解:(1)取DEH部分,对H点列平衡0 x25RD REF F0 Y15RDF Q联立方程后解得:5RDF Q2REF Q(2)取ABCE部分,对C点列平衡xcos450RE RAF FY sin450RB RAF F P且RE REF F联立上面各式得:22RAF Q2RBF QP(3)取BCE 部分。

4-1解:1.选定由杆OA ,O 1C ,DE 组成的系统为研究对象,该系统具有理想约束。
作用在系统上的主动力为M F F ,。
2.该系统的位置可通过杆OA 与水平方向的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
3.在图示位置,不破坏约束的前提下,假定杆OA 有一个微小的转角δθ,相应的各点的虚位移如下: δθδ⋅=A O r A ,δθδ⋅=B O r B ,δθδ⋅=C O r C 1δθδ⋅=D O r D 1,C B r r δδ=,E D r r δδ=代入可得:E Ar r δδ30=4.由虚位移原理0)(=∑i F W δ有:0)30(=⋅-=⋅-⋅E M E M A r F F r F r F δδδ对任意0≠E r δ有:F F M 30=,物体所受的挤压力的方向竖直向下。
4-4解:4a1.选杆AB 为研究对象,该系统具有理想约束。
设杆重为P,作用在杆上的主动力为重力。
2.该系统的位置可通过杆AB 与z 轴的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
由几何关系可知:θtan a h =杆的质心坐标可表示为:θθcos 2tan ⋅-=la z C3.在平衡位置,不破坏约束的前提下,假定杆AB 逆时针旋转一个微小的角度 δθ,则质心C 的虚位移:δθθδθθδ⋅+-=si n 2si n 2la z C 4.由虚位移原理0)(=∑i F W δ有:0)si n 2si n (2=+-⋅-=⋅-δθθθδla P z P C 对任意0≠δθ有:0si n 2si n 2=+-θθl a 即杆AB 平衡时:31)2arcsin(la =θ。
解:4b1.选杆AB 为研究对象,该系统具有理想约束。
设杆重为P,作用在杆上的主动力为重力。
2.该系统的位置可通过杆AB 与z 轴的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
由几何关系可知:θsi n R z A=杆的质心坐标可表示为:θθcos 2si n ⋅-=lR z C3.在平衡位置,不破坏约束的前提下,假定杆AB 顺时针旋转一个微小的角度 δθ,则质心C 的虚位移:δθθδθθθδ⋅+⋅-=si n 2cos si n 2lR z C 4.由虚位移原理0)(=∑i F W δ有:0)si n 2cos si n (2=+-⋅-=⋅-δθθθθδlR P z P C 对任意0≠δθ有:0si n 2cos si n 2=+-θθθl R 即平衡时θ角满足:0si n cos 23=-θθl R 。
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
静力学部分第一章基本概念受力图GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF2-1 解:由解析法,23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑GAGGAGAGGAFFFFAFAF故:161.2R F N ==1(,)arccos2944RY R R F F P F '∠==GAGGAGAGGAFFFFAFAF 2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN =+=方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑ sin 300AC AB F F -=0Y =∑ cos300AC F W -=0.577AB F W =(拉力) 1.155AC F W =(压力)GAGGAGAGGAFFFFAFAF(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=GAGGAGAGGAFFFFAFAF 0Y =∑ sin 700AB F W -= 1.064AB F W =(拉力)0.364AC F W =(压力) (c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -= 0Y =∑sin 30sin 600AB AC F F W +-= 0.5AB F W = (拉力)0.866AC F W =(压力) (d )由平衡方程有: 0X =∑sin 30sin 300AB AC F F -= 0Y =∑cos30cos300AB AC F F W +-=GAGGAGAGGAFFFFAFAF 0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解:(a )受力分析如图所示:GAGGAGAGGAFFFFAFAF由x =∑22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos 45cos 45010RA RB F F P --=0Y =∑sin 45sin 45010RA RB F F P -=联立上二式,得:GAGGAGAGGAFFFFAFAF22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示GAGGAGAGGAFFFFAFAF三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑ cos 0AC r F F α-=12cos G G α∴=GAGGAGAGGAFFFFAFAF由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=GAGGAGAGGAFFFFAFAF2-7解:受力分析如图所示,取左半部分为研究对象由x =∑ cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得: 0.707RA F P =0.707RB F P=由二力平衡定理 0.707RB CB CB F F F P'===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑ cos 60cos300AC AB F F W ⋅--=GAGGAGAGGAFFFFAFAF0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得: 7.32AB F KN=-(受压)27.3AC F KN=(受压)GAGGAGAGGAFFFFAFAF2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑ sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑ sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象:由x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BC BCF F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:GAGGAGAGGAFFFFAFAFx =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及 AD ADF F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡GAGGAGAGGAFFFFAFAF由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN =(拉力)GAGGAGAGGAFFFFAFAF1.0BC F KN=-(压力)2-13解:GAGGAGAGGAFFFFAFAF(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q -=联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=GAGGAGAGGAFFFFAFAF且 RE RE F F '=联立上面各式得:RA F =GAGGAGAGGAFFFFAFAF2RB F Q P=+(3)取BCE 部分。

第四章变形体静力学基础小结:1)变形体静力学研究的核心内容和主线是:力的平衡条件;变形几何协调条件;及力与变形之物理关系的研究。
2)变形体静力学研究的最简单问题是均匀连续介质、各向同性材料的小变形问题。
3)内力是物体内部某一部分与相邻部分间的相互作用力,截面法是用假想截面将物体截开,揭示并确定截面内力的方法。
对于平面问题,截面内力一般有轴力、剪力及弯矩。
4)拉伸和压缩、扭转、弯曲是杆的三类基本变形。
5)轴向拉压杆的应力、应变可表达为:应力:σ=F N /A ;应变:ε=∆L/L材料线性弹性应力—应变(物理)关系模型可用虎克定律表达为:σ=E ε在线弹性模型下,拉压杆的变形为:当杆的轴力F N 、弹性模量E 、横截面积A 发生改变时,应分段计算。
6)截面上一点的应力T 是该点处内力的集度,定义为:应力是矢量,其在截面法向的分量σ,为正应力;沿截面切向的分量τ,为剪应力。
一点的应力状态可用围绕该点截取的一个微小的单元体各面上的应力来描述。
单向拉压杆,横截面上正应力最大,45︒斜截面上的剪应力最大。
7)应变是无量纲量。
一点的线应变ε(或正应变)是过该点沿坐标方向微小线段的相对尺寸改变;形状的改变则用剪应变γ描述。
8)静定、静不定问题的同异如图4.22所示。
T FAA =→lim ∆∆∆0EALF L L N ==∆ε习题4-1试用截面法求指定截面上内力。
解:截而1:沿截而1将杆件栽开,取右役为隔离体,平衡方程F N1-2F=0F N1=2F截而2沿截而2杆件,取左段为隔离体,取左段为隔离体平衡方程F H2=4F截而3沿截而3截开杆件,取右段为隔离体,平衡议程F N3=3F 图4.22静定、静不定问题的同异变形体静力学问题研究对象受力图平衡方程能否求出约束力?静定静不定反力内力应力物理方程应变几何方程变形平衡方程物理方程几何方程联立求解反力、内力应力、应变变形…可能有温度应力、装配应力。
3F2F 2FF 321(a )2)截而1沿截而1截开杆件,取右役为隔离体根据平衡条件得:111()24AF F F M qa a ==-解:沿截而1将,杆件截杆截开,取上半部分为隔离体,平衡方程1111111000000:1x S y N M N S IF F IF F F I F a M F F M Fa=⇒==⇒+==⇒⋅+==-==求解得解:求支座反力0212y A B A B A B IF F F q L L IM F L q L F F qL =+=⋅=⋅-⋅⋅=∴==用截右而开杆件,取左段为隔离体平衡方程111211100400813:432y A S M A S IF F q F L I F M F qL M qL =-⋅-==⋅-===求解得4-6图示杆中AB 段截面面积为A 1=200mm 2,BC 段截面面积为A 2=100mm 2,材料弹性模量F(d)a 1AB L/4L q(f)1E=200GPa 。
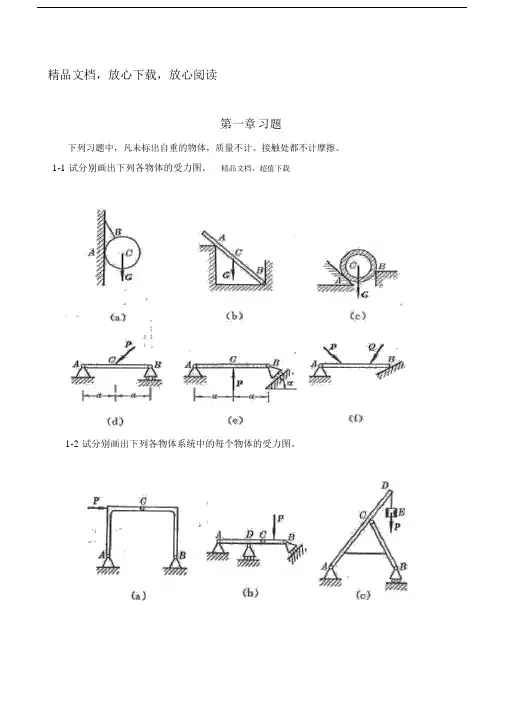
精品文档,放心下载,放心阅读第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1 试分别画出下列各物体的受力图。
精品文档,超值下载1-2 试分别画出下列各物体系统中的每个物体的受力图。
1-3 试分别画出整个系统以及杆BD ,AD ,AB(带滑轮 C,重物 E 和一段绳索)的受力图。
1-4 构架如图所示,试分别画出杆HED ,杆 BDC 及杆 AEC 的受力图。
1-5 构架如图所示,试分别画出杆BDH ,杆 AB ,销钉 A 及整个系统的受力图。
1-6 构架如图所示,试分别画出杆AEB ,销钉 A 及整个系统的受力图。
1-7 构架如图所示,试分别画出杆AEB ,销钉 C,销钉 A 及整个系统的受力图。
1-8 结构如图所示,力 P 作用在销钉 C 上,试分别画出 AC ,BCE 及 DEH 部分的受力图。
参考答案1-1 解:1-2 解:1-3 解:1-4 解:1-5 解:1-6 解:1-7 解:1-8 解:第二章 习题参考答案2-1 解:由解析法, F RX X P 2 cos P 3 80NF RYY P 1 P 2 sin 140NF R F 2 F 2 161.2N故: RX RY(F R , P 1) arccos F RY 29 44F R2-2 解:即求此力系的合力,沿OB建立 x 坐标,由解析法,有F RX X P1 cos45 P2P3 cos453KNF RY Y P1 sin45 P3 sin 450故:F R F RX2F RY23KN 方向沿OB。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a)由平衡方程有:X 0 F AC sin 30F AB0Y 0 F AC cos30W0联立上二式,解得:F AB0.577W (拉力)FAC 1.155W(压力)(b)由平衡方程有:X 0 F AC F AB cos700Y 0 F AB sin 70W0联立上二式,解得:FAB 1.064W(拉力)F AC0.364W (压力)(c)由平衡方程有:X 0 F AC cos60F AB cos300Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:FAB 0.5W(拉力)FAC 0.866W(压力)(d)由平衡方程有:X 0 F AB sin 30F AC sin 300Y 0 F AB cos30F AC cos30 W0联立上二式,解得:FAB 0.577W(拉力)FAC 0.577W(拉力)2-4 解:( a)受力分析如图所示:x 0 F RA4P cos 45 0 42由22F RA15.8 KNF RA2F RB P sin 45 042由Y 022F RB7.1KN(b)解:受力分析如图所示:由x 0 F RA 3F RB cos45 P cos45 0 10FRA 1F RB sin 45 P sin 45 0Y 010联立上二式,得:F RA22.4KNF RB10KN2-5 解:几何法:系统受力如图所示三力汇交于点 D,其封闭的力三角形如图示所以:FRA5KN(压力)F RB 5KN(与X轴正向夹150度)2-6 解:受力如图所示:已知, F R G1,F AC G2x 0F r 0由F AC coscos G1 G2由Y 0 F AC sinF N W 0F N W G2 sin W G22G122-7 解:受力分析如图所示,取左半部分为研究对象x 0由P F RA cos 45 F CB cos45 0 Y 0 F CB sin 45F RA sin 450联立后,解得:FRA0.707 PF RB0.707 P由二力平衡定理FRBFCBFCB0.707 P2-8 解:杆 AB,AC均为二力杆,取 A 点平衡x 0由F AC cos 60 F AB cos30 W 0Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:F AB7.32KN (受压)FAC 27.3KN(受压)2-9 解:各处全为柔索约束,故反力全为拉力,以D, B 点分别列平衡方程(1)取 D 点,列平衡方程x 0T DB sinW cos0由T DB Wctg0(2)取 B 点列平衡方程由Y 0 T sinT BD cos0T T BD ctg Wctg 230KN 2-10 解:取 B 为研究对象:FBC由Y 0 F BC sinP 0Psin取 C 为研究对象:x 0F DC sin F CE sin0由F BC cos由Y 0F BC sin F DC cos F CE cos0联立上二式,且有FBCFBC解得:P cos1 FCEsin2cos2取 E 为研究对象:由 Y 0 F NH F CE cos0F CE F CE 故有:F NH P cos 1 P2 sin 2 cos cos22sin 2-11 解:取 A 点平衡:x 0F AB sin 75 F AD sin 75 0Y 0 F AB cos75 F AD cos75 P 0PF AD F AB联立后可得: 2cos 75取 D 点平衡,取如图坐标系:x 0F AD cos5 F ND cos80 0cos5F ND F ADcos80由对称性及F AD F ADF N2F ND2 cos5FAD2 cos5P166.2KNcos80cos802cos 75 2-12 解:整体受力交于O点,列 O点平衡x 0由F RA cosF DC P cos30 0Y 0 F RA sin P sin 300联立上二式得:F RA 2.92 KNFDC 1.33KN(压力)列 C点平衡4x0FDC FAC53Y0FBCFAC5联立上二式得:FAC1.67KN(拉力)F BC 1.0KN (压力)2-13 解:(1)取 DEH部分,对 H点列平衡x 0 F RD 2F RE 0 5Y0FRD1Q 05联立方程后解得:FRD5QF RE2Q(2)取 ABCE部分,对 C 点列平衡x0F RE F RA cos 450Y 0 F RB F RA sin 45 P0且F RE F RE联立上面各式得:FRA2 2QF RB 2Q P(3)取 BCE 部分。
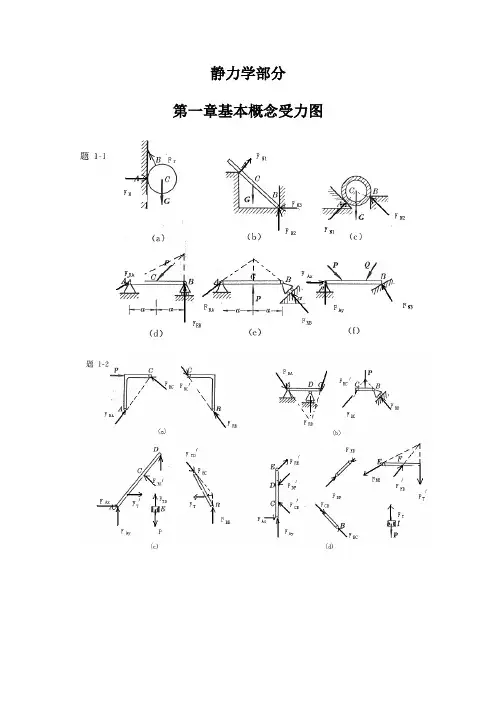
静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==o v v2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故:223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a )由平衡方程有:0X =∑sin 300AC AB F F -=o0Y =∑cos300AC F W -=o0.577AB F W=(拉力)1.155AC F W=(压力)(b )由平衡方程有:0X =∑ cos 700AC AB F F -=o0Y =∑sin 700AB F W -=o1.064AB F W=(拉力)0.364AC F W=(压力)(c )由平衡方程有:0X =∑ cos 60cos300AC AB F F -=o o0Y =∑sin 30sin 600AB AC F F W +-=o o0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=o o0Y =∑cos30cos300AB AC F F W +-=o o0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+o15.8RA F KN∴=由0Y =∑22sin 45042RA RB F F P +-=+o7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos45cos 45010RA RB F F P ⋅--=o o0Y =∑sin 45sin 45010RA RB F F P ⋅+-=o o联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN= (压力) 5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CBRA F F '-=o o联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得:2cos 75AD AB PF F ==o取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDAD PF F F KN '∴===⋅=o o o o o2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q -=联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
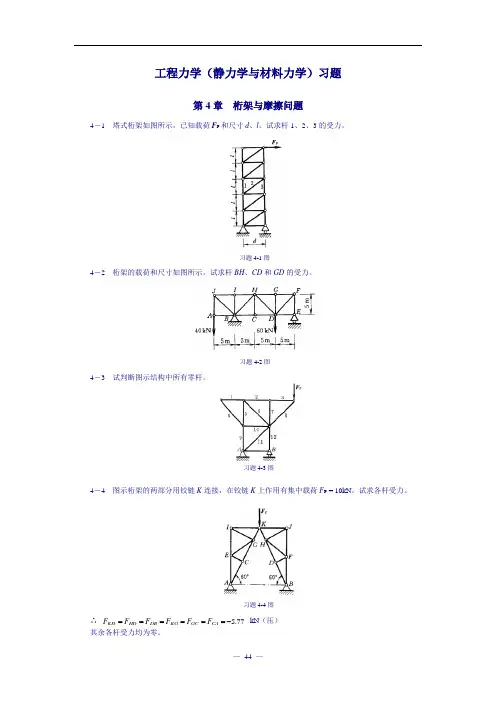
习题4-4图习题4-3图习题4-2图 习题4-1图 工程力学(静力学与材料力学)习题第4章 桁架与摩擦问题4-1 塔式桁架如图所示,已知载荷F P 和尺寸d 、l 。
试求杆1、2、3的受力。
4-2 桁架的载荷和尺寸如图所示。
试求杆BH 、CD 和GD 的受力。
4-3 试判断图示结构中所有零杆。
4-4 图示桁架的两部分用铰链K 连接,在铰链K 上作用有集中载荷F P = 10kN 。
试求各杆受力。
∴ 77.5-======CA GC KG DB HD KH F F F F F F kN (压)其余各杆受力均为零。
4-5 已知重W的物体及图示结构的尺寸。
试求杆件CF、CG的受力。
习题4-5图4-6 图示构件AE和EQ铰接在一起做成一个广告牌。
它承受给定的分布风载。
试求每个二力杆件的受力。
习题4-6图4-7 K形桁架的尺寸如图所示,已知载荷F P。
试求杆1、2受力。
F R A习题4-7图4-8 图示结构由等长构件AE、EG、BD、DK及杆DE铰接而成。
C、H分别为各等长构件的中点。
已知载荷F P。
试问这是桁架结构吗?若要求杆DE受力,可否用图示的截面法求解?习题4-8图4-9 桁架的载荷和尺寸如图所示,试求杆DE、AB和AD的受力。
解:1.整体F R G习题4-9图4-10 组合桁架由ADF和KHF两部分用铰链F连接而成。
桁架的载荷和尺寸如图所示。
试求EF和CF两杆的受力。
F AxF Ay习题4-10图4-11 图示桁架的载荷F P和尺寸d均为已知。
试求杆件FK和JO的受力。
习题4-11图4-12 图示桁架所受的载荷F P和尺寸d均为已知。
试求杆1、2、3受力。
习题4-12图4-13 复杂桁架的结构、尺寸和载荷如图所示。
试求AB 杆受力。
习题4-15图习题4-13图习题4-14图 习题4-16图 O4-14 平面桁架的结构、尺寸和载荷如图所示。
为了求杆1、2和3的受力,试确定计算方案。
(设2a EF AB ==,a DE CD BC ===)4-15 一叠纸片按图示形状堆叠,其露出的自由端用纸粘连,成为两叠彼此独立的纸本A 和B 。

工程力学(静力学与材料力学)第四版习题答案-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII静力学部分第一章基本概念受力图2-1 解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故:223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a )由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b )由平衡方程有:0X =∑cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c )由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)由x =∑22cos 45042RA F P =+15.8RA F KN∴=由Y =∑22sin 45042RA RB F F P -=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos 45cos 45010RA RB F F P --=0Y =∑sin 45sin 45010RA RB F F P -=联立上二式,得:22.410RA RB F KN F KN==三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=-2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑ sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑ sin 0BC F P α-= sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '=0Y =∑0RD F Q -=联立方程后解得:RD F2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
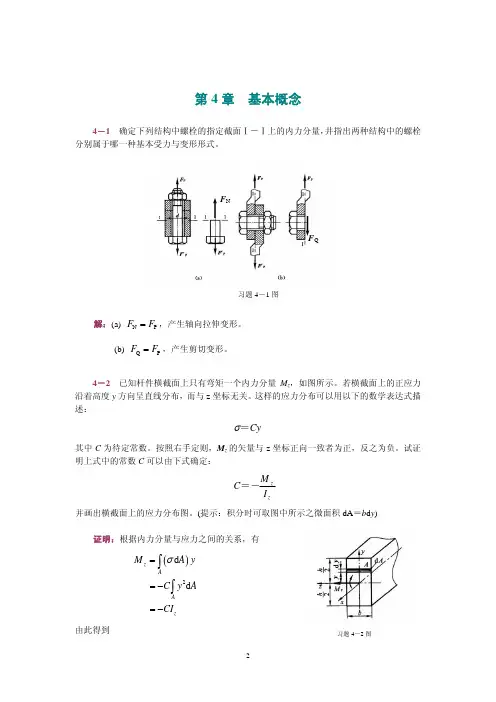
2习题4-2图第4章 基本概念4-1 确定下列结构中螺栓的指定截面Ⅰ-Ⅰ上的内力分量,井指出两种结构中的螺栓分别属于哪一种基本受力与变形形式。
解:(a) N P F F =,产生轴向拉伸变形。
(b) Q P F F =,产生剪切变形。
4-2 已知杆件横截面上只有弯矩一个内力分量M z ,如图所示。
若横截面上的正应力沿着高度y 方向呈直线分布,而与z 坐标无关。
这样的应力分布可以用以下的数学表达式描述:Cy =σ其中C 为待定常数。
按照右手定则,M z 的矢量与z 坐标正向一致者为正,反之为负。
试证明上式中的常数C 可以由下式确定:zzI M C =-并画出横截面上的应力分布图。
(提示:积分时可取图中所示之微面积dA =b d y )证明:根据内力分量与应力之间的关系,有()2d d z AAzM A yC y A CI σ==−=−∫∫由此得到习题4-1图F NF Q3习题4一3图zzI M C =-。
于是,横截面上的正应力表达式为:z zM yI σ−= 据此,可以画出横截面上的正应力分布图:4-3 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有4种答案,如图所示。
请根据弹性体横截面连续分布内力的合力必须与外力平衡这一特点,分析图示的4种答案中哪一种比较合理。
正确答案是 C 。
解:首先,从平衡的要求加以分析,横截面上的分布内力只能组成一个力偶与外加力偶矩M 平衡。
二答案(A )和(B )中的分布内力将合成一合力,而不是一力偶,所以是不正确的。
直杆在外力偶M 作用下将产生上面受拉、下面受压的变形。
根据变形协调要求,由拉伸变形到压缩变形,必须是连续变化的,因而,受拉与受压的材料之间必有一层材料不变形,这一层材料不受力。
因此,答案(D )也是不正确的。
正确的答案是(C )。
上一章 返回总目录 下一章。
第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD,AD,AB(带滑轮C,重物E和一段绳索)的受力图。
1-4构架如图所示,试分别画出杆HED,杆BDC及杆AEC的受力图。
1-5构架如图所示,试分别画出杆BDH,杆AB,销钉A及整个系统的受力图。
1-6构架如图所示,试分别画出杆AEB,销钉A及整个系统的受力图。
1-7构架如图所示,试分别画出杆AEB,销钉C,销钉A及整个系统的受力图。
1-8结构如图所示,力P作用在销钉C上,试分别画出AC,BCE及DEH部分的受力图。
参考答案1-1解:1-2解:1-3解:1-4解:1-5解:1-6解:1-7解:1-8解:第二章 习题参考答案2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:161.2R F N==1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 3R F KN==方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300ACAB FF -=0Y =∑cos300ACFW -=联立上二式,解得:0.577AB F W =(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑cos 700ACAB FF -=0Y =∑sin 700ABFW -=联立上二式,解得:1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:0.5AB F W=(拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300ABAC FF -=0Y =∑cos30cos300ABAC FF W +-=联立上二式,解得:0.577AB F W=(拉力)0.577AC F W=(拉力)2-4解:(a )受力分析如图所示:由0x =∑ cos 450RA F P =15.8RA F KN∴=由Y =∑ sin 450RA RB F F P +-=7.1RB F KN∴=(b)解:受力分析如图所示:由0x =∑cos 45cos 450RA RB F F P -= 0Y =∑sin 45sin 450RA RB F F P +-= 联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN=(压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:7.32AB F KN =-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程由0Y =∑ sin cos 0BD T T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑ sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '=故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得: 2.92RAF KN=1.33DCF KN=(压力)列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得: 1.67ACF KN=(拉力)1.0BCF KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡0x =∑0RD REF F '-=Y =∑0RD F Q -=联立方程后解得: RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡0x =∑cos 450RERA FF -=0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
工程力学(1)习题全解第4章 刚体静力学专题4-1 塔式桁架如图所示,已知载荷F P 和尺寸d 、l 。
试求杆1、2、3的受力。
解:截面法,受力如图(a ) dl=αtan ,22cos dl d +=α0=∑x F ,0cos 2P =−αF FP 222F dd l F +=(拉) 0=∑AM ,02P 1=⋅−l F d FP 12F dlF =(拉)0=∑y F ,0sin 231=++αF F FP 33F dlF −=(压)4-2 图示构件AE 和EQ 铰接在一起做成一个广告牌。
它承受给定的分布风载。
试求解:(1)先将分布载荷合成于E 点88894.2)7.7402963(8.47.740=×−+×=F N由节点C ,显然 F CQ = 0 (1) (2)截面法,图(a )0=∑D M ,08.4538.4=××+×−QG F F ,F QG = 14815 N (拉) (2)0=∑B M ,F QD = 00=∑y F ,054=+×BC QG F F ,11852−=BC F N (压) (3) (3)截面法,图(b )习题4-3图习题4-4图0=∑E M ,08.04.2)7.7402963(212.14.27.7404.253=××−−××−××−AB F2963−=AB F N (压) (4) (4)节点B ,图(c )0=∑y F ,05454=−−′BQ BC AB F F F ,05411852296354=−+×−BQ F F BQ = 11852 N (拉)(5)0=∑x F ,0)(53=++′BE BQ ABF F F ,0)118522963(53=++−BE F ,5333−=BE F N (压) (6) 又 11852−==BC CD F F N (压)(7)4-3 桁架的载荷和尺寸如图所示。
第四章习题4-1 已知F i=60N, F2=80N, F3=150N, m=转向为逆时针,B=30°图中距离单位为m。
试求图中力系向0点简化结果及最终结果。
4-2已知物体所受力系如图所示,F=10Kn, m=转向如图。
(a)若选择x轴上B点为简化中心,其主矩L B=,转向为顺时针,试求B 点的位置及主矢R'。
(b)若选择CD线上E点为简化中心,其主矩L E=,转向为顺时针,a=45°,试求位于CD直线上的E点的位置及主矢R'。
4-3 试求下列各梁或刚架的支座反力。
解:( a) 受力如图由刀M A=0 F R? 3a-Psin30 ° ? 2a-Q? a=0••• FRB=( P+Q /3「• F AX=P由刀Y=0 F Ay+FRhQ-Psin30 ° =0F Ay= ( 4Q+P /64-4 高炉上料的斜桥,其支承情况可简化为如图所示,设A 和B为固定铰,D为中间铰,料车对斜桥的总压力为Q,斜桥(连同轨道)重为W立柱BD质量不计,几何尺寸如图示,试求A 和B 的支座反力。
4-5齿轮减速箱重W=500N输入轴受一力偶作用,其力偶矩m=,输出轴受另一力偶作用,其力偶矩m2=,转向如图所示。
试计算齿轮减速箱A和B两端螺栓和地面所受的力。
4-6 试求下列各梁的支座反力。
(a) (b)4-7各刚架的载荷和尺寸如图所示,图c中m>m,试求刚架的各支座反力4-8图示热风炉高h=40m重W=4000kN所受风压力可以简化为梯形分布力,如图所示,q i=500kN/m, q2=m可将地基抽象化为固顶端约束,试求地基对热风炉的反力。
4-9起重机简图如图所示,已知P、Q a、b及c,求向心轴承A及向心推力轴承B的反力。
4-10构架几何尺寸如图所示,R=0.2m, P=1kNo E为中间铰,求向心轴承A的反力、向心推力轴承B的反力及销钉C对杆ECD 的反力。
静力学第四章部分习题解答4-1力铅垂地作用于杆AO 上,115,6DO CO BO AO ==。
在图示位置上杠杆水平,杆DC 与DE 垂直。
试求物体M 所受的挤压力M F 的大小。
解:1.选定由杆OA ,O 1C ,DE 组成的系统为研究对象,该系统具有理想约束。
作用在系统上的主动力为M F F ,。
2.该系统的位置可通过杆OA 与水平方向的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
3.在图示位置,不破坏约束的前提下,假定杆OA 有一个微小的转角δθ,相应的各点的虚位移如下: δθδ⋅=A O r A ,δθδ⋅=B O r B ,δθδ⋅=C O r C 1δθδ⋅=D O r D 1,C B r r δδ=,E D r r δδ=代入可得:E A r r δδ30=4.由虚位移原理0)(=∑i F W δ有:0)30(=⋅-=⋅-⋅E M E M A r F F r F r F δδδ对任意0≠E r δ有:F F M 30=,物体所受的挤压力的方向竖直向下。
4-4如图所示长为l 的均质杆AB ,其A 端连有套筒,又可沿铅垂杆滑动。
忽略摩擦及套筒重量,试求图示两种情况平衡时的角度θ。
解:4a1.选杆AB 为研究对象,该系统具有理想约束。
设杆重为P,作用在杆上的主动力为重力。
2.该系统的位置可通过杆AB 与z 轴的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
由几何关系可知:θtan a h =杆的质心坐标可表示为:θθcos 2tan ⋅-=l a z C3.在平衡位置,不破坏约束的前提下,假定杆AB 逆时针旋转一个微小的角度δθ,则质心C 的虚位移:δθδr Aδr Cδr B δr Dδr Eδθθδθθδ⋅+-=sin 2sin2l a z C4.由虚位移原理0)(=∑i F W δ有:0)sin 2sin(2=+-⋅-=⋅-δθθθδl a P z P C对任意0≠δθ有: 0sin 2sin2=+-θθl a即杆AB 平衡时:31)2arcsin(la =θ。
解:4b1.选杆AB 为研究对象,该系统具有理想约束。
设杆重为P,作用在杆上的主动力为重力。
2.该系统的位置可通过杆AB 与z 轴的夹角θ完全确定,有一个自由度。
选参数θ为广义坐标。
由几何关系可知:θsin Rz A =杆的质心坐标可表示为:θθcos 2sin ⋅-=lR z C3.在平衡位置,不破坏约束的前提下,假定杆AB 顺时针旋转一个微小的角度δθ,则质心C 的虚位移:δθθδθθθδ⋅+⋅-=sin 2cos sin2l R z C4.由虚位移原理0)(=∑i F W δ有:0)sin 2cos sin(2=+-⋅-=⋅-δθθθθδl R P z P C对任意0≠δθ有:0sin 2cos sin2=+-θθθl R即平衡时θ角满足:0sin cos 23=-θθl R 。
4-5被抬起的简化台式打字机如图所示。
打字机和搁板重P ,弹簧原长为2a ,试求系统在θ角保持平衡时的弹簧刚度系数值。
解:1.选整个系统为研究对象,此系统包含弹簧。
设弹簧力21,F F ,且21F F =,将弹簧力视为主动力。
此时作用在系统上的主动力有21,F F ,以及重力P 。
2. 该系统只有一个自由度,选定θ为广义坐标。
由几何关系可知:θsin ⋅==a z z B A3.在平衡位置,不破坏约束的前提下,假定有一个微小的虚位移δθ,则质心的虚位移为:δθθδδδ⋅===cos a z z z B A C弹簧的长度2sin 2θa l =,在微小虚位移δθ下:δθθδ⋅=2cosa l4.由虚位移原理0)(=∑i F W δ有:0)2coscos (22=⋅-⋅=⋅-⋅δθθθδδa F Pa l F z P C其中)22sin2(2a a k F -=θ,代入上式整理可得:02)]2cossin 2(cos 2[=--δθθθθaka P由于0≠a ,对任意0≠δθ可得平衡时弹簧刚度系数为:)2cossin 2(cos 2θθθ-=a P k4-6复合梁AD 的一端砌入墙内,B 点为活动铰链支座,C 点为铰链,作用于梁上的力kN F kN F kN F 3,4,5321===,以及力偶矩为m kN M ⋅=2的力偶,如图所示。
试求固定端A 处的约束力。
解:解除A 端的约束,代之以A Ay Ax M F F ,,,并将其视为主动力,此外系统还受到主动力M F F F ,,,321的作用。
系统有三个自由度,选定A 点的位移A A y x ,和梁AC 的转角ϕ为广义坐标。
1.在不破坏约束的前提下给定一组虚位移0,0,0==≠δϕδδA A y x ,如图所示。
由虚位移原理0)(=∑i F W δ有:0=⋅A Ax x F δ对任意0≠A x δ可得: 0=Ax F2.在不破坏约束的前提下给定一组虚位移0,0,0=≠=δϕδδA A y x ,如下图所示。
由虚位移原理0)(=∑i F W δ有:0332211=⋅+⋅-⋅+⋅+⋅-δθδδδδM y F y F y F y F A Ay(1)由几何关系可得各点的虚位移如下:A C y y y y δδδδ===31AC y y y δδδ31312==A C y y δδδθ3131==代入(1)式:0)3131(321=⋅+-++-A Ay y M F F F F δ对任意0≠A x δ可得:)(4kN F Ay =,方向如图所示。
3.在不破坏约束的前提下给定一组虚位移0,0,0≠==δϕδδA A y x ,如上图所示。
由虚位移原理0)(=∑i F W δ有:0332211=⋅+⋅-⋅+⋅+⋅-δθδδδδϕM y F y F y F M A(2)有几何关系可得各点的虚位移如下:δϕδ21=y δϕδδ33==C y yδϕδθ=δϕδθδ==2y代入(2)式:0)32(321=⋅+-++-δϕM F F F M A对任意0≠δϕ可得: )(7m kN M A ⋅=,逆时针方向。
4-7图示结构上的载荷如下:m kN q ⋅=2;力kN F 41=;力kN F 122=,其方向与水平成o60角;以及力偶,其力偶矩为m kN M ⋅=18。
试求支座处的约束力。
解:将均布载荷简化为作用在CD 中点的集中载荷3F ,大小为q 6。
1.求支座B 处的约束力解除B 点处的约束,代之以力B F ,并将其视为主动力,系统还受到主动力M F F F ,,,321的作用,如图所示。
在不破坏约束的前提下,杆AC 不动,梁CDB 只能绕C 点转动。
系统有一个自由度,选转角θ为广义坐标。
给定虚位移δθ,由虚位移原理0)(=∑i F W δ有:0150cos 45cos 330220=⋅-⋅+⋅+⋅y F y F M r F B B δδδθδ(1)各点的虚位移如下:δθδ⋅=26B rδθδ⋅=92yδθδ⋅=33y代入(1)式整理可得:0)32396(32=⋅--+δθF F M F B对任意0≠δθ可得:)(6.18kN F B =,方向如图所示。
2.求固定端A 处的约束力解除A 端的约束,代之以A Ay Ax M F F ,,,并将其视为主动力,系统还受到主动力M F F F ,,,321的作用。
系统有三个自由度,选定A 点的位移A A y x ,和梁AC 的转角θ为广义坐标。
2a.求Ax F在不破坏约束的前提下给定一组虚位移0,0,0==≠δθδδA A y x ,此时整个结构平移,如上图所示。
由虚位移原理0)(=∑i F W δ有:0120cos 02211=⋅+⋅+⋅x F x F x F A Ax δδδ (2)各点的虚位移如下:A x x x δδδ==21代入(2)式整理可得:0)5.0(21=⋅-+A Ax x F F F δ对任意0≠A x δ可得:)(2kN F Ax =,方向如图所示。
2b.求Ay F在不破坏约束的前提下给定一组虚位移0,0,0=≠=δθδδA A y x ,此时梁AC 向上平移,梁CDB 绕D 点转动,如上图所示。
由虚位移原理0)(=∑i F W δ有:030cos 02233=⋅-⋅+⋅-⋅δθδδδM y F y F y F A Ay (3)各点的虚位移如下:A C y y y y δδδδ212132===A y y δδδθ61312==代入(3)式整理可得:0)614321(23=⋅-+-A Ay y M F F F δ对任意0≠A y δ可得: )(8.3kN F Ay =,方向如图所示。
2c.求A M在不破坏约束的前提下给定一组虚位移0,0,0≠==δθδδA A y x ,此时梁AC 绕A 点转动,梁CDB 平移,如上图所示。
由虚位移原理0)(=∑i F W δ有:0120cos 02211=⋅+⋅+⋅-x F x F M A δδδθ (4)各点的虚位移如下:δθδ31=x δθδδ62==C x x代入(4)式整理可得:0)33(21=⋅-+-δθF F M A对任意0≠δθ可得:)(24m kN M A⋅-=,顺时针方向。
4-8设桁架有水平力1F 及铅垂力2F 作用其上,且KE DK BE CE DC AD =====,o30=α。
试求杆1,2和3所受的力。
解:假设各杆受拉,杆长均为a 。
1.求杆1受力去掉杆1,代之以力1P ,系统有一个自由度,选AK 与水平方向的夹角θ为广义坐标,如上图所示。
在不破坏约束的条件下给定一组虚位移,此时三角形ADK 形状不变,绕A 点转动,因此有K A r D A r K D ⊥⊥δδ,,且:δθδδθδ⋅=⋅=a r a r K D 3,滑动支座B 处只允许水平方向的位移,而杆BK 上K 点虚位移沿铅垂方向,故B 点不动。
三角形BEK 绕B 点旋转E B r E ⊥δ,且:δθδδ⋅==a r r D E对刚性杆CD 和杆CE ,由于E C r D C r E D ⊥⊥δδ,,因此0=C r δ。
由虚位移原理0)(=∑i F W δ有:060cos 60cos )(01011=⋅+⋅+E D r P r P F δδ代入各点的虚位移整理可得:0)2(11=⋅+δθa P F对任意0≠δθ可得:211F P -=(受压)。
2.求杆2受力去掉杆2,代之以力2P ,系统有一个自由度,选BK 与水平方向的夹角θ为广义坐标,如上图所示。
在不破坏约束的条件下给定一组虚位移,杆AK 绕A 点转动,因此有K A r K ⊥δ,且:δθδ⋅=a r K 3同理可知B 点不动,三角形BEK 绕B 点旋转E B r E ⊥δ,且:δθδ⋅=a r Eδθδδ⋅==a r r D E杆AD 绕A 点转动D A r D ⊥δ,由刚性杆DE 上点E 的虚位移可确定D 点位移方向如图所示,且:δθδδ⋅==a r r E D同理可知0=C r δ。