平面与点的相关位置.
- 格式:doc
- 大小:74.50 KB
- 文档页数:2

平面直角坐标系的基本概念在数学中,平面直角坐标系是用来描述平面上点的位置的一种方法。
它由两条互相垂直的直线组成,称为x轴和y轴,它们的交点被定义为原点O。
下面将介绍平面直角坐标系的基本概念和相关术语。
1. 坐标轴和原点:平面直角坐标系由两条相交于原点的直线组成,水平的直线称为x 轴,垂直的直线称为y轴。
原点O表示坐标轴的交点,同时也是平面上所有坐标的起点。
2. 坐标和有序对:在平面直角坐标系中,每个点都可以用一个有序对(x, y)表示。
其中,x是该点在x轴上的投影距离,y是该点在y轴上的投影距离。
有序对(x, y)的x称为横坐标或x坐标,y称为纵坐标或y坐标。
通过横纵坐标的组合,可以唯一确定平面直角坐标系上的每个点。
3. 象限:平面直角坐标系将平面分为四个象限,分别记作第一象限、第二象限、第三象限和第四象限。
第一象限位于x轴和y轴的正半轴部分,第二象限位于y轴的正半轴和x轴的负半轴部分,第三象限位于x轴和y轴的负半轴部分,第四象限位于x轴的正半轴和y轴的负半轴部分。
4. 距离公式:在平面直角坐标系中,两点之间的距离可以使用距离公式来计算。
设两点的坐标分别为(x1, y1)和(x2, y2),则两点之间的距离d可以通过以下公式计算:d = √[(x2 - x1)² + (y2 - y1)²]5. 中点公式:中点公式用于计算连接两点的线段的中点坐标。
设两点的坐标分别为(x1, y1)和(x2, y2),则中点的坐标为:(x, y) = [(x1 + x2) / 2, (y1 + y2) / 2]6. 斜率公式:斜率公式用于计算两点之间连线的斜率。
设两点的坐标分别为(x1, y1)和(x2, y2),则连线的斜率k可以通过以下公式计算:k = (y2 - y1) / (x2 - x1)7. 图形的方程:在平面直角坐标系中,各种图形(如直线、曲线、抛物线等)可以通过方程来表示。
例如,一条直线的方程可表示为y = mx + b,其中m 为斜率,b为y轴截距。
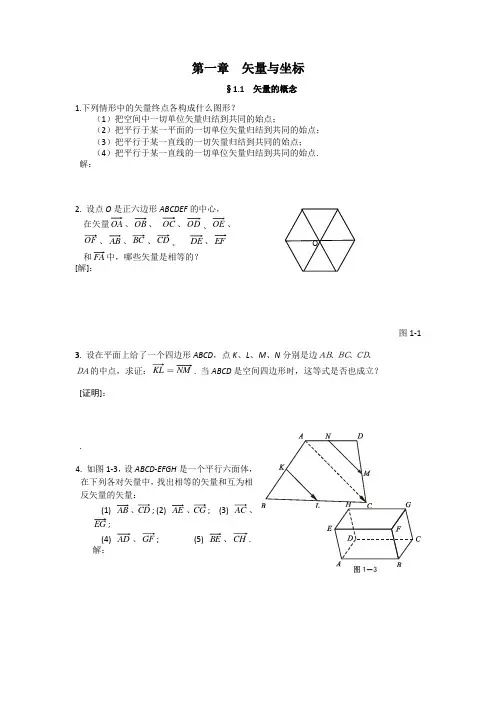
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。

平面直角坐标系中的点与直线的关系在平面直角坐标系中,点和直线之间有着密切的关系。
本文将从点到直线的不同关系进行探讨,并阐述其性质和特点。
一、点与直线的位置关系在平面直角坐标系中,点与直线的位置关系可分为三种情况:点在直线上、点在直线外部且在直线同侧、点在直线外部且在直线异侧。
1. 点在直线上当一个点的坐标恰好满足直线的方程时,我们说这个点在直线上。
以一条直线的一般方程为例,设直线的方程为Ax + By + C = 0,点的坐标为(x0, y0),如果将点的坐标带入方程后等号成立,即有Ax0 + By0 + C = 0,则点(x0, y0)在该直线上。
2. 点在直线外部且在直线同侧当一个点的坐标带入直线方程后不等号成立,且点与直线的关系满足特定条件时,我们说这个点在直线外部且在直线同侧。
以直线的斜截式方程为例,设直线方程为y = kx + b,点的坐标为(x0, y0),如果将点的坐标带入方程后不等号成立,即有y0 > kx0 + b 或 y0 < kx0 + b,且不等号的方向与直线的斜率有关,那么点(x0, y0)在直线的同侧。
3. 点在直线外部且在直线异侧当一个点的坐标带入直线方程后不等号成立,且点与直线的关系满足特定条件时,我们说这个点在直线外部且在直线异侧。
以直线的一般方程为例,设直线方程为Ax + By + C = 0,点的坐标为(x0, y0),如果将点的坐标带入方程后不等号成立,即有Ax0 + By0 + C > 0 或 Ax0 + By0 + C < 0,那么点(x0, y0)在直线的异侧。
二、点与直线之间的距离关系在平面直角坐标系中,点与直线之间的距离关系有着重要的意义。
点到直线的距离可以通过线段的长度来表示,即点到直线上的垂线段的长度。
1. 点到直线的距离公式设直线的一般方程为Ax + By + C = 0,点的坐标为(x0, y0),点到直线的距离为d。



点与平面的位置关系在数学中,点和平面是常见的几何概念,并且它们之间有着密切的位置关系。
本文将探讨点与平面之间的位置关系及其相关性质。
一、点在平面内部当一个点在平面内部时,我们可以将其描述为点属于平面。
具体而言,如果一个点的坐标满足平面方程,则该点在平面内。
例如,对于一个二维平面方程为ax+by+c=0,如果一个点(x,y)满足该方程,则该点在平面内部。
二、点在平面外部同样地,当一个点在平面外部时,我们可以将其描述为点不属于平面。
即该点的坐标无法满足平面方程。
如果一个点不满足平面方程,那么我们可以断定该点在平面外部。
三、点在平面上在数学中,点也可以位于平面上。
如果一个点同时满足平面方程,那么我们说该点位于平面上。
平面上的点与平面的关系可以用平面的方程来判断。
例如,对于一个二维平面方程为ax+by+c=0,如果一个点(x,y)满足该方程,则该点在平面上。
四、点与平面的距离点与平面之间的距离是一个重要的度量,它可以帮助我们理解点与平面之间的位置关系。
点到平面的距离是指从该点到平面上的任意一点的最短距离。
为了计算点到平面的距离,我们可以使用点到平面的法向量与点的坐标之间的关系。
具体计算公式如下:设点P(x0,y0,z0)为平面外的一点,平面的方程为ax+by+cz+d=0。
平面法向量为N(a,b,c)。
点P到平面的距离d可用公式d = |ax0+by0+cz0+d| / √(a^2+b^2+c^2) 计算得出。
五、点与平面的位置关系点与平面之间的位置关系可以分为以下几种情况:1. 点在平面上当一个点在平面上时,它既属于平面,也位于平面上。
在点和平面的相互关系中,该情况是最直观的,因为点正好与平面重合。
2. 点在平面内部如果一个点在平面内部,说明它属于平面并且位于平面内部,根据平面上点的定义,该点与平面的位置关系无疑是最紧密的。
3. 点在平面外部当一个点在平面外部时,它既不属于平面,也不位于平面上。
这种情况下,点与平面之间存在明显的分离。

第三章 平面与空间直线版权所有,侵权必究§3.1 平面的方程1.平面的点位式方程在空间给定了一点M 0与两个不共线的向量a ,b 后,通过点M 0且与a ,b 平行的平面π 就惟一被确定. 向量a ,b 叫平面π 的方位向量. 任意两个与π 平行的不共线的向量都可作为平面π 的方位向量.取标架{}321,,;e e e O ,设点M 0的向径0r =0OM ={}000,,z y x ,平面π 上任意一点M 的向径为r =OM = {x ,y ,z }(如图). 点M 在平面π上的充要条件为向量M M 0与向量a ,b 共面. 由于a ,b 不共线,这个共面的条件可以写成M M 0= u a +v b而M M 0= r -r 0,所以上式可写成r = r 0+u a +v b(3.1-1)此方程叫做平面π 的点位式向量参数方程,其中u ,v 为参数.若令a = {1X ,1Y ,1Z },b = {2X ,2Y ,2Z },则由(3.1-1)可得⎪⎩⎪⎨⎧++=++=++=vZ u Z z z v Y u Y y y vX u X x x 210210210 (3.1-2)此方程叫做平面π 的点位式坐标参数方程,其中u ,v 为参数.(3.1-1)式两边与a ×b 作内积,消去参数u ,v 得(r -r 0,a ,b ) = 0(3.1-3)此即222111000Z Y X Z Y X z z y y x x ---=0 (3.1-4)这是π 的点位式普通方程.已知平面π上三非共线点i M (i = 1,2,3). 建立坐标系{O ;e 1, e 2, e 3},设r i = i OM ={i x ,i y ,i z },i = 1,2,3. 对动点M ,设r =OM ={x ,y ,z },取21M M 和31M M 为方位向量,M 1为定点,则平面π的向量参数方程,坐标参数方程和一般方程依次为r = 1r +u(2r -1r )+v(3r -r 1)(3.1-5) ⎪⎩⎪⎨⎧-+-+=-+-+=-+-+=)()()()()()(131211312113121z z v z z u z z y y v y y u y y x x v x x u x x(3.1-6)131313121212111z z y y x x z z y y x x z z y y x x ---------= 0(3.1-7)(3.1-5),(3.1-6)和(3.1-7)统称为平面的三点式方程.特别地,若i M 是π 与三坐标轴的交点,即1M (a ,0,0),2M (0,b ,0),3M (0,0,c ),其中abc ≠0,则平面π 的方程就是caba z y a x 00---=0 (3.1-8)即1=++czb y a x (3.1-9)此方程叫平面π的截距式方程,其中a ,b ,c 称为π 在三坐标轴上的截距.2.平面的一般方程在空间任一平面都可用其上一点M 0(x 0,y 0,z 0)和两个方位向量a = {1X ,1Y ,1Z },b = {2X ,2Y ,2Z }确定,因而任一平面都可用方程将其方程(3.1-4)表示. 将(3.1-4)展开就可写成Ax +By +Cz +D = 0(3.1-10)其中A =2211Z Y Z Y ,B =2211X Z X Z ,C =2211Y X Y X由于a = {1X ,1Y ,1Z }与b = {2X ,2Y ,2Z }不共线,所以A ,B ,C 不全为零,这说明空间任一平面都可用关于a ,b ,c 的一三元一次方程来表示.反之,任给一三元一次方程(3.1-10),不妨设A ≠0,则(3.1-10)可改写成02=++⎪⎭⎫ ⎝⎛+ACz ABy A D x A即000=--+ACA B zy AD x 它显然表示由点M 0 (-D / A ,0,0)和两个不共线的向量{B ,-A ,0}和{C ,0,-A }所决定的平面. 于是有定理3.1.1 空间中任一平面的方程都可表为一个关于变数x ,y ,z 的三元一次方程;反过来,任一关于变数x ,y ,z 的三元一次方程都表示一个平面.方程(3.1-10) 称为平面π 的一般方程. 3.平面的法式方程若给定一点M 0和一个非零向量n ,则过M 0且与n 垂直的平面π也被惟一地确定. 称n 为π的法向量. 在空间坐标系{O ;i ,j ,k }下,设0r = 0OM ={x 0,y 0,z 0},n = {A ,B ,C },且平面上任一点M 的向径r =OM ={x ,y ,z },则因总有M M 0⊥n ,有n (r -r 0) = 0(3.1-11) 也就是A (x -x 0)+B (y -y 0)+C (z -z 0) = 0(3.1-12)方程(3.1-11)和(3.1-12)叫平面π 的点法式方程. (3.1-12)中的系数A ,B ,C 有简明的几何意义,它们就是平面π 的一个法向量的分量.特别地,取M 0为自O 向π 所作垂线的垂足,而n 为单位向量. 当平面不过原点时,取n 为与OP 同向的单位向量n 0,当平面过原点时取n 0的正向为垂直与平面的两个方向中的任一个.设|OP | = p ,则OP = p n 0,由点P 和n 0确定的平面的方程为 n 0(r -p n 0) = 0式中r 是平面的动向径. 由于1)(20=n ,上式可写成n 0r -p = 0(3.1-13)此方程叫平面的向量式法式方程.若设r = {x ,y ,z },n 0 = {cos α,cos β,cos γ},则由(3.1-13)得x cos α+y cos β+z cos γ-p = 0(3.1-14)此为平面的坐标法式方程,简称法式方程.平面的坐标法式方程有如下特征:1°一次项系数是单位向量的分量,其平方和等于1; 2°常数项-p ≤0(意味着p ≥ 0). 3°p 是原点到平面的距离. 4.化一般方程为法式方程在直角坐标系下,若已知π的一般方程为Ax +By +Cz +D = 0,则n = {A ,B ,C }是π的法向量,Ax +By +Cz +D = 0可写为nr +D = 0(3.1-15)与(3.1-13)比较可知,只要以2221||1CB A ++±=±=n λ 去乘(3.1-15)就可得法式方程λAx +λBy +λCz +λD = 0 (3.1-16)其中正负号的选取,当D ≠0时应使(3.1-16)的常数项为负,D =0时可任意选.以上过程称为平面方程的法式化,而将2221CB A ++±=λ叫做法化因子.§3.2 平面与点的相关位置平面与点的位置关系,有两种情形,就是点在平面上和点不在平面上. 前者的条件是点的坐标满足平面方程. 点不在平面上时,一般要求点到平面的距离,并用离差反映点在曲面的哪一侧.1.点与平面间的距离定义3.2.1 自点M 0向平面π 引垂线,垂足为Q . 向量0QM 在平面π的单位法向量n 0上的射影叫做M 0与平面π之间的离差,记作δ = 射影n 00QM(3.2-1)显然δ = 射影n 00QM = 0QM ·n 0 =∣0QM ∣cos ∠(0QM ,n 0) =±∣0QM ∣当0QM 与n 0同向时,离差δ > 0;当0QM 与n 0反向时,离差δ < 0. 当且仅当M 0在平面上时,离差δ = 0.显然,离差的绝对值|δ |就是点M 0到平面π 的距离. 定理3.2.1 点M 0与平面(3.1-13)之间的离差为δ = n 0r 0-p (3.2-2)推论1 若平面π 的法式方程为 0cos cos cos =-++p z y x γβα,则),,(0000z y x M 与π间的离差=δp z y x -++γβαcos cos cos 000(3.2-3)推论2 点),,(0000z y x M 与平面Ax +By +Cz +D = 0间的距离为()2220000,CB A DCz By Ax M d +++++=π (3.2-4)2.平面划分空间问题,三元一次不等式的几何意义 设平面π的一般方程为Ax +By +Cz +D = 0那么,空间任何一点M (x ,y ,z )与平面间的离差为=δp z y x -++γβαcos cos cos = λ (Ax +By +Cz +D )式中λ为平面π的法化因子,由此有Ax +By +Cz +D =δλ1(3.2-5)对于平面π同侧的点,δ 的符号相同;对于在平面π的异侧的点,δ 有不同的符号,而λ一经取定,符号就是固定的. 因此,平面π:Ax +By +Cz +D = 0把空间划分为两部分,对于某一部分的点M (x ,y ,z ) Ax +By +Cz +D > 0;而对于另一部分的点,则有Ax +By +Cz +D < 0,在平面π上的点有Ax +By +Cz +D = 0.§3.3 两平面的相关位置空间两平面的相关位置有3种情形,即相交、平行和重合. 设两平面π1与π2的方程分别是π1: 11110A x B y C z D +++=(1)π2: 22220A x B y C z D +++=(2)则两平面π1与π2相交、平行或是重合,就决定于由方程(1)与(2)构成的方程组是有解还是无解,或无数个解,从而我们可得下面的定理.定理3.3.1 两平面(1)与(2)相交的充要条件是111222::::A B C A B C ≠(3.3-1)平行的充要条件是11112222A B C D A B C D ==≠(3.3-2)重合的充要条件是11112222A B C D A B C D ===(3.3-3)由于两平面π1与π2的法向量分别为11112222{,,},{,,}n A B C n A B C ==,当且仅当n 1不平行于n 2时π1与π2相交,当且仅当n 1∥n 2时π1与π2平行或重合,由此我们同样能得到上面3个条件.下面定义两平面间的夹角.设两平面的法向量间的夹角为θ,称π1与π2的二面角∠(π1,π2) =θ 或π-θ为两平面间的夹角.显然有12cos (,)ππ∠=±cos θ =(3.3-4)定理3.3.2 两平面(1)与(2)垂直的充要条件是0212121=++C C B B A A(3.3-5)例 一平面过两点 1(1,1,1)M 和2(0,1,1)M -且垂直于平面x +y +z = 0,求它的方程.解 设所求平面的法向量为n = {A ,B ,C },由于12{01,11,11}{1,0,2}M M =----=--在所求平面上,有12M M n ⊥, 120M M n ⋅=,即20A C --= .又n 垂直于平面x +y +z = 0的法线向量{1,1,1},故有 A +B +C = 0 解方程组20,0,A C A B C --=⎧⎨++=⎩得2,,A CBC =-⎧⎨=⎩ 所求平面的方程为2(1)(1)(1)0C x C y C z --+-+-=,约去非零因子C 得2(1)(1)(1)0x y z --+-+-=,即2x -y -z =0§3.4 空间直线的方程1.由直线上一点与直线的方向所决定的直线方程在空间给定了一点0000(,,)M x y z 与一个非零向量v = {X ,Y ,Z },则过点M 0且平行于向量v 的直线l 就惟一地被确定. 向量v 叫直线l 的方向向量. 显然,任一与直线l 上平行的飞零向量均可作为直线l 的方向向量.下面建立直线l 的方程.如图,设M (x ,y ,z ) 是直线l 上任意一点,其对应的向径是r = { x ,y ,z },而0000(,,)M x y z 对应的向径是r 0,则因M M 0//v ,有t ∈R ,M M 0= t v . 即有r -r 0= t v所以得直线l 的点向式向量参数方程r = r 0+t v (3.4-1)以诸相关向量的分量代入上式,得⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛Z Y X t z y x z y x 000根据向量加法的性质就得直线l 的点向式坐标参数方程为⎪⎩⎪⎨⎧+=+=+=Ztz z Yt y y Xtx x 000 (3.4-2)消去参数t ,就得直线l 的点向式对称方程为Zz z Y y y X x x 000-=-=- (3.4-3)此方程也叫直线l 的标准方程.今后如无特别说明,在作业和考试时所求得的直线方程的结果都应写成对称式.例1 设直线L 通过空间两点M 1(x 1,y 1,z 1)和M 2(x 2,y 2,z 2),则取M 1为定点,21M M 为方位向量,就得到直线的两点式方程为121121121z z z z y y y y x x x x --=--=-- (3.4-4)根据前面的分析和直线的方程(3.4-1),可得到||||||||||00v M M v t =-=r r 这个式子清楚地给出了直线的参数方程(3.4-1)或(3.4-2)中参数的几何意义:参数t 的绝对值等于定点M 0到动点M 之间的距离与方向向量的模的比值,表明线段M 0M 的长度是方向向量v 的长度的 |t | 倍.特别地,若取方向向量为单位向量v 0 = {cos α,cos β,cos γ}则(3.4-1)、(3.4-2)和(3.4-3)就依次变为r = r 0+t v 0(3.4-5)⎪⎩⎪⎨⎧+=+=+=γβαcos cos cos 000t z z t y y t x x (3.4-6)和γβαcos cos cos 000z z y y x x -=-=- (3.4-7)此时因 |v | = 1,t 的绝对值恰好等于l 上两点M 0与M 之间的距离.直线l 的方向向量的方向角α,β,γ cos α,cos β,cos γ 分别叫做直线l 的方向角和方向余弦.由于任意一个与v 平行的非零向量v'都可作为直线l 的方向向量,而二者的分量是成比例的,我们一般称X :Y :Z 为直线l 的方向数,用来表示直线l 的方向.2.直线的一般方程空间直线l 可看成两平面π1和π2的交线. 事实上,若两个相交的平面π1和π2的方程分别为π1: 11110A x B y C z D +++= π2: 22220A x B y C z D +++=那么空间直线l 上的任何一点的坐标同时满足这两个平面方程,即应满足方程组111122220,0.A x B y C z D A x B y C z D +++=⎧⎨+++=⎩ (3.4-8)反过来,如果点不在直线l 上,那么它不可能同时在平面π1和π2上,所以它的坐标不满足方程组(3.4-8).因此,l 可用方程组(3.4-8)表示,方程组(3.4-8)叫做空间直线的一般方程.一般说来,过空间一直线的平面有无限多个,所以只要在无限多个平面中任选其中的两个,将它们的方程联立起来,就可得到空间直线的方程.直线的标准方程(3.4-3)是一般方程的特殊形式. 将标准方程化为一般式,得到的是直线的射影式方程.将直线的一般方程化为标准式,只需在直线上任取一点,然后取构成直线的两个平面的两个法向量的向量积为直线的方向向量即可.例1将直线的一般方程10,2340.x y z x y z +++=⎧⎨-++=⎩ 化为对称式和参数方程.解 令y = 0,得这直线上的一点(1,0,-2).两平面的法向量为a = {1,1,1},b = {2,-1,3}因a ×b = {4,-1,-3},取为直线的法向量,即得直线的对称式方程为12413x y z -+==--令t z y x =-+=-=-32141,则得所求的参数方程为 14,,23.x t y t z t =+⎧⎪=-⎨⎪=--⎩§3.5 直线与平面的相关位置直线与平面的相关位置有直线与平面相交,直线与平面平行和直线在平面上3种情形. 设直线l 与平面π 的方程分别为L :000x x y y z z X Y Z ---== (1) π :Ax +By +Cz +D = 0(2)将直线l 的方程改写为参数式⎪⎩⎪⎨⎧+=+=+=tZz z tY y y tX x x 000. (3)将(3)代入(2),整理可得(AX +BY +CZ )t = -(Ax 0+By 0+Cz 0+D )(4)当且仅当AX +BY +CZ ≠0时,(4)有惟一解CZBY AX DCz By t +++++-=000Ax这时直线l 与平面π 有惟一公共点;当且仅当AX +BY +CZ = 0,Ax 0+By 0+Cz 0+D ≠0时,方程(4)无解,直线l 与平面π 没有公共点;当且仅当AX +BY +CZ = 0,Ax 0+By 0+Cz 0+D = 0时,(4)有无数多解,直线l 在平面π 上. 于是有定理3.5.1 关于直线(1)与平面(2)的相互位置,有下面的充要条件: 1)相交: AX +BY +CZ ≠02)平行:AX +BY +CZ = 0,Ax 0+By 0+Cz 0+D ≠03)直线在平面上: AX +BY +CZ = 0,Ax 0+By 0+Cz 0+D = 0以上条件的几何解释:就是直线l 的方向向量v 与平面π 的法向量n 之间关系. 1)表示v 与n 不垂直;2)表示v 与n 垂直且直线l 上的点(x 0,y 0,z 0)不在平面π 上; 3)表示v 与n 垂直且直线l 上的点(x 0,y 0,z 0)在平面π 上. 当直线l 与平面π 相交时,可求它们的交角. 当直线不与平面垂直时,直线与平面的交角ϕ 是指直线和它在平面上的射影所构成的锐角;垂直时规定是直角.设v = {X ,Y ,Z }是直线l 的方向向量,n = {A ,B ,C }是平面π 的法向量,则令∠(l ,π ) =ϕ,∠(v ,n ) = θ ,就有ϕ=-2πθ 或 ϕ= θ-2π(θ 为锐角) 因而sin ϕ =∣cos θ∣=vn v n ⋅⋅=222222ZY X CB A CZ BY AX ++++++ (3.5-1)§3.6 空间直线与点的相关位置任给一条直线l 的方程和一点M 0,则l 和M 0的位置关系只有两种:点在直线上和点不在直线上。


解析几何课程名称:解析几何英文译名:Space Analytic Geometry课程编号:040101适用专业:小学教育专科学时数: 68 学分:4编写执笔人:黄学军审定人:刘小华编写日期:2005-4-1一、课程的性质、目的和任务《解析几何》是数学与科学方向的一门基础课,它对中小学数学教学有着指导作用。
本课程要求学生熟练掌握解析几何的基础知识和基本理论,正确地理解和使用矢量代数知识,并解决一些实际问题。
深刻理解坐标观念和曲线(面)与方程相对应的观念,熟练掌握讨论空间直线、平面、曲线、曲面的基本方法,训练学生的空间想象能力和运算能力。
二、课程教学内容及教学基本要求第一章一般二次曲线方程的研究(10课时)内容:①平面直角坐标变换;②利用坐标变换化简二次曲线方程;③二次曲线在直角坐标变换下的不变量;④利用不变量化简二次曲线方程。
要求:会用坐标变换化简二次曲线的方程,会求二次曲线的中心,了解二次曲线不变量的意义,会用不变量化简二次曲线的方程。
第二章向量代数(13课时)内容:①向量的概念;②向量的加法;③向量与数量的乘法;④共线向量与共面向量,向量的分解;⑤两向量的数量积;⑥两向量的向量积;⑦三向量的混合积。
要求:要求学生正确理解向量的概念,掌握向量的各种运算,会用向量解决几何图形的有关度量问题和相关位置问题,掌握利用向量解决初等几何问题的方法。
第三章空间直角坐标(5课时)内容:①空间直角坐标系;②用坐标进行向量运算;③曲面与空间曲线的方程。
要求:要求学生正确理解空间直角坐标系的建立方法,能用坐标来表示空间的点与向量,用方程来表示空间的图形。
第四章平面与空间直线(11课时)内容:①平面的方程;②平面与点的相关位置;③两平面的相关位置;④空间直线的方程;⑤直线与平面的相关位置;⑥空间两直线的相关位置;⑦空间直线与点的相关位置;⑧平面族。
要求:要求学生掌握平面与空间直线的各种形式的方程,学会利用方程判定直线与点、直线与直线、直线与平面以及平面与平面的相互位置关系。

七年级数学平面直角坐标系动点问题在数学中,平面直角坐标系是一个重要的概念。
它由两条垂直的坐标轴组成,分别是x轴和y轴。
在这个坐标系中,我们可以用两个数(x,y)来表示一个点的位置,其中x表示点在x轴上的位置,y 表示点在y轴上的位置。
通过这个坐标系,我们可以解决很多与点相关的问题。
本文将讨论七年级数学中与平面直角坐标系动点问题相关的内容。
我们将从点的表示、点的运动和点的坐标变化等方面进行探讨。
一、点的表示在平面直角坐标系中,我们可以用两个数(x,y)来表示一个点。
其中x表示点在x轴上的位置,y表示点在y轴上的位置。
例如,点A的坐标为(2,3),表示它在x轴上的位置是2,在y轴上的位置是3。
同样,点B的坐标为(-1,5),表示它在x轴上的位置是-1,在y轴上的位置是5。
二、点的运动在平面直角坐标系中,点可以进行各种运动。
例如,我们可以使点上下左右移动,也可以使点绕某个点旋转。
这些运动可以通过改变点的坐标来实现。
1. 点的上下左右移动当我们希望点在x轴上移动时,只需改变它的x坐标;当我们希望点在y轴上移动时,只需改变它的y坐标。
例如,如果我们希望将点A在x轴上向右移动2个单位,则可以将点A的坐标改为(4,3)。
同样,如果我们希望将点A在y轴上向上移动3个单位,则可以将点A的坐标改为(2,6)。
2. 点的旋转点的旋转是指将点绕某个点按照一定的角度进行转动。
在平面直角坐标系中,我们可以通过改变点的坐标来实现旋转。
例如,如果我们希望将点A绕原点逆时针旋转90度,则可以将点A的坐标改为(-3,2)。
三、点的坐标变化在平面直角坐标系中,点的坐标可以随着运动的变化而变化。
我们可以通过观察点的坐标变化来研究点的运动规律。
1. 点的轨迹点的轨迹是指点在平面直角坐标系中所经过的路径。
通过观察点的坐标变化,我们可以确定点的轨迹。
2. 点的速度点的速度是指点在单位时间内移动的距离。
在平面直角坐标系中,我们可以通过观察点的坐标变化来计算点的速度。

平面直角坐标系的相关概念是什么平面直角坐标系是数学中常用的一种坐标系,用于描述平面上的点的位置。
它由两个相互垂直的直线组成,其中一个称为x轴,另一个称为y轴。
通过在这两条直线上取定一个原点,确定了一个平面直角坐标系。
在平面直角坐标系中,每个点的位置可以由其在x轴和y轴上的距离表示。
1. 坐标轴:平面直角坐标系由两个相互垂直的直线组成,其中一个被称为x轴,另一个被称为y轴。
在绘制平面直角坐标系时,通常选择水平方向为x 轴,垂直方向为y轴。
两个坐标轴的交点被称为原点(O),它是平面直角坐标系的起点,也是坐标轴的零点。
2. 坐标:在平面直角坐标系中,每个点的位置可以由其在x轴和y轴上的距离表示。
假设某点的x轴距离为x,y轴距离为y,那么这个点的坐标可以表示为(x, y)。
其中,x被称为横坐标,y被称为纵坐标。
坐标是平面直角坐标系中点的唯一标识,不同点的坐标不相同。
3. 坐标系界限:平面直角坐标系有四个界限,分别是第一象限、第二象限、第三象限和第四象限。
第一象限是x轴正向和y轴正向所围成的区域;第二象限是x轴负向和y轴正向所围成的区域;第三象限是x轴负向和y轴负向所围成的区域;第四象限是x轴正向和y轴负向所围成的区域。
4. 轴对称性:在平面直角坐标系中,每一个点关于坐标轴都有对称点。
例如,点A(x, y)关于x轴的对称点是A(x, -y),关于y轴的对称点是A(-x, y),关于原点的对称点是A(-x, -y)。
5. 距离计算:平面直角坐标系中,可以使用距离公式计算两点间的距离。
假设有两点A(x1, y1)和B(x2, y2),它们之间的距离可以用以下公式表示:d = √[(x2 - x1)² + (y2 - y1)²]。
通过这个公式,我们可以求解平面上任意两点间的距离。
总结:平面直角坐标系是一种常用的坐标系,用于描述平面上的点的位置。
它由两个相互垂直的直线组成,分别称为x轴和y轴,原点是坐标轴的交点。
第3章 平面与空间直线§ 3.1平面的方程1.求下列各平面的坐标式参数方程和一般方程:(1)通过点)1,1,3(1-M 和点)0,1,1(2-M 且平行于矢量}2,0,1{-的平面(2)通过点)1,5,1(1-M 和)2,2,3(2-M 且垂直于xoy 坐标面的平面;(3)已知四点)3,1,5(A ,)2,6,1(B ,)4,0,5(C )6,0,4(D 。
求通过直线AB 且平行于直线CD 的平面,并求通过直线AB 且与ABC ∆平面垂直的平面。
解: (1) }1,2,2{21--=M M ,又矢量}2,0,1{-平行于所求平面, 故所求的平面方程为:⎪⎩⎪⎨⎧++-=-=--=v u z u y vu x 212123一般方程为:07234=-+-z y x(2)由于平面垂直于xoy 面,所以它平行于z 轴,即}1,0,0{与所求的平面平行,又}3,7,2{21-=M M ,平行于所求的平面,所以要求的平面的参数方程为:⎪⎩⎪⎨⎧+-=+-=+=v u z u y u x 317521 一般方程为:0)5(2)1(7=+--y x ,即01727=--y x 。
(3)(ⅰ)设平面π通过直线AB ,且平行于直线CD : }1,5,4{--=AB ,}2,0,1{-=CD 从而π的参数方程为:⎪⎩⎪⎨⎧+-=+=--=v u z uy vu x 235145 一般方程为:0745910=-++z y x 。
(ⅱ)设平面π'通过直线AB ,且垂直于ABC ∆所在的平面∴}1,5,4{--=AB , }1,1,1{4}4,4,4{}1,1,0{}1,5,4{==-⨯--=⨯AC AB均与π'平行,所以π'的参数式方程为:⎪⎩⎪⎨⎧+-=++=+-=v u z v u y v u x 35145 一般方程为:0232=--+z y x .2.化一般方程为截距式与参数式: 042:=+-+z y x π.解: π与三个坐标轴的交点为:)4,0,0(),0,20(),0,0,4(--, 所以,它的截距式方程为:1424=+-+-z y x . 又与所给平面方程平行的矢量为:}4,0,4{},0,2,4{-,∴ 所求平面的参数式方程为:⎪⎩⎪⎨⎧=-=++-=v z uy v u x 24 3.证明矢量},,{Z Y X v =平行与平面0=+++D Cz By Ax 的充要条件为:0=++CZ BY AX . 证明: 不妨设0≠A ,则平面0=+++D Cz By Ax 的参数式方程为:⎪⎪⎩⎪⎪⎨⎧==---=v z uy v A C u A B A D x 故其方位矢量为:}1,0,{},0,1,{ACA B --,从而v 平行于平面0=+++D Cz By Ax 的充要条件为:v ,}1,0,{},0,1,{ACA B --共面⇔01001=--AC A B Z Y X ⇔ 0=++CZ BY AX .4.已知:连接两点),12,0(),5,10,3(z B A -的线段平行于平面0147=--+z y x ,求B 里的坐标z .解: }5,2,3{z AB +-= 而AB 平行于0147=--+z y x 由题3知:0)5(427)3(=+-⨯+⨯-z 从而18=z .§ 3.2 平面与点的相关位置1.计算下列点和平面间的离差和距离:(1))3,4,2(-M , :π 0322=++-z y x ; (2))3,2,1(-M , :π 0435=++-z y x . 解: 将π的方程法式化,得:01323132=--+-z y x , 故离差为:311332431)2()32()(-=-⨯-⨯+-⨯-=M δ,M 到π的距离.31)(==M d δ(2)类似(1),可求得0354353356355)(=-++-=M δ,M 到π的距离.0)(==M d δ2.求下列各点的坐标:(1)在y 轴上且到平面02222=--+z y 的距离等于4个单位的点;(2)在z 轴上且到点)0,2,1(-M 与到平面09623=-+-z y x 距离相等的点; (3)在x 轴上且到平面01151612=++-z y x 和0122=--+z y x 距离相等的点。
点、线、面是空间几何学中的基本概念,它们存在着一定的位置关系。
向量法是解决几何问题的重要方法之一,可以有效地描述点、线、面的位置关系。
本文将探讨向量法在点、线、面位置关系中的应用,并给出相关参考内容。
一、点、线、面的向量表示向量是对空间中的点、线、面进行表示的一种数学工具。
在向量法中,我们通常使用坐标表示点的位置、用箭头表示线的方向、用平面方程表示面的位置。
具体表示如下:1.点的向量表示设点A在空间中的坐标为(Ax, Ay, Az),则A点的位置向量表示为OA = (Ax, Ay, Az)。
2.线的向量表示设直线L上一点A的位置向量为OA,且直线上一点B的位置向量为OB,则直线L的向量表示为(OA, OB)。
3.面的向量表示设平面α通过点A,并以直线L为法线,则平面α的向量表示为α: AX + BY + CZ + D = 0,其中(x, y, z)为空间中的任意一点坐标。
二、点、线、面的位置关系1.点和线的位置关系给定直线L的向量表示为(OA, OB),设点P的位置向量为OP。
点P在直线L上的充分必要条件是OP = λ1·OA + λ2·OB,其中λ1和λ2为实数。
当λ1和λ2满足该条件时,点P在线段AB上;当λ1和λ2为0或非零时,点P在线段AB的延长线上。
2.点和面的位置关系给定面α的向量表示为α: AX + BY + CZ + D = 0,设点P的位置向量为OP。
点P在平面α上的充分必要条件是OP·n = 0,其中n为α的法向量。
当OP·n = 0时,点P在平面α上;当OP·n ≠ 0时,点P在平面α的一侧。
3.线和面的位置关系给定直线L的向量表示为(OA, OB),平面α的向量表示为α: AX + BY + CZ + D = 0。
直线L与平面α的位置关系可以通过求交点进行判断。
设直线L与平面α的交点为点P,则有OP·n = 0和OP = λ1·OA + λ2·OB。
高考数学中的平面几何相关知识点详解高考数学中平面几何是一个重点和难点,需要学生在长期的学习中进行大量的练习和思维训练。
平面几何可以说是数学学科中的好入手也好深入的部分,掌握它不仅可以提高解题能力和思维能力,还可以加强对于数学知识的理解和运用。
本文将着重介绍高考数学中平面几何相关的知识点,并进行详细的分析和解释。
1. 点、线、面平面几何的基本概念有点、线和面。
点是几何中最小的概念,没有任何大小,只有位置。
线是由一组相邻的点按照一定的方向连接而成,具有长度和方向。
面是由一组相邻的线围成的区域,具有面积和形状。
在平面几何中,常常会涉及到点、线、面的相互关系。
比如,过两个点可以画出一条直线,两条相交而不共面的直线至少可以确定一个点,而两个平行的直线在平面上不相交。
此外,还有很多和点、线、面有关的基本定理和定律,需要牢记和灵活运用。
2. 直线和角的性质直线是平面几何中最简单的图形,直线上的点无限多,并没有起点和终点。
在平面几何中,直线所具有的性质有很多,比如,两条直线如果不共面,则它们不可能在任何一点相交;两个平行的直线在任何一点上的夹角都是相等的;如果一条直线上有两个垂直的线段,则它们相互垂直。
角是有大小和方向的图形,是由两条射线共同确定的。
在平面几何中,角所具有的性质也很重要,比如,同侧内角相等定理、同侧外角相等定理、对顶角相等定理等等。
掌握角的性质可以帮助学生解决许多有关平面几何的问题。
3. 相似和全等相似和全等是几何中重要的概念,也是平面几何中常用的概念。
相似是指两个图形形状相同但大小不同的关系。
在相似的图形中,对应的角度相等,对应的边长成比例关系。
全等是指两个图形大小、形状完全相同的关系。
在全等的图形中,对应的角度是相等的,对应的边长是相等的。
相似和全等是平面几何中常常会用到的概念,在解决各种几何问题时需要灵活运用。
4. 三角形和圆三角形是平面几何中最基本和重要的图形之一,具有许多特点和性质。
比如,三角形的内角和为180度,三角形的任意两边之和大于第三边,三角形的垂心、重心、外心等重要概念。
《点到平面的距离》讲义在我们的数学世界中,点到平面的距离是一个非常重要的概念。
它不仅在几何学中有着广泛的应用,还与物理学、工程学等领域密切相关。
接下来,就让我们一起深入探讨点到平面的距离。
首先,我们要明确什么是点和平面。
一个点可以用坐标(x,y,z)来表示,它在空间中是一个确定的位置。
而平面呢,则可以用一个方程来描述,比如 Ax + By + Cz + D = 0 ,其中 A、B、C 是平面的法向量的分量,D 是一个常数。
那什么是点到平面的距离呢?简单来说,就是从这个点到平面的最短距离。
想象一下,你站在一个平地上,地面就是那个平面,你所在的位置就是那个点,你到地面的垂直距离就是点到平面的距离。
那怎么来计算这个距离呢?这里我们介绍一种常用的方法。
假设点 P 的坐标为(x₀,y₀,z₀),平面的方程为 Ax + By +Cz + D = 0 。
我们先求出平面的法向量 n =(A,B,C)。
然后,我们在平面上任意取一点 Q(x₁,y₁,z₁),则向量 PQ=(x₁ x₀,y₁ y₀,z₁ z₀)。
点到平面的距离 d 就等于向量 PQ 在法向量 n 上的投影的绝对值。
根据向量的投影公式,向量 PQ 在法向量 n 上的投影为:|PQ · n| /|n| (其中“·”表示向量的点积)即:|A(x₁ x₀) + B(y₁ y₀) + C(z₁ z₀)|/√(A²+ B²+ C²)因为点 Q 在平面上,所以 Ax₁+ By₁+ Cz₁+ D = 0 ,即 Ax₁+ By₁+ Cz₁= D所以点 P 到平面的距离 d 可以表示为:|Ax₀+ By₀+ Cz₀+ D| /√(A²+ B²+ C²)为了更好地理解这个公式,我们来看几个例子。
例 1:已知点 P(1,2,3),平面方程为 2x + 3y z + 1 = 0 ,求点 P 到平面的距离。
平面直角坐标系简称平面直角坐标系,简称直角坐标系,是数学中常用的一种坐标表示方法,用于描述平面上的点和与之相关的数学问题。
它是由两条相互垂直的坐标轴组成,通常分别称为x轴和y轴。
直角坐标系的建立为我们解决各种几何、代数和分析问题提供了强有力的工具。
在直角坐标系中,每个点都可以由其在x轴上的位置和在y轴上的位置来确定。
这两个位置分别称为点的x坐标和y坐标。
以坐标原点O为参考点,每个点P可以表示为一个有序数对(x, y),其中x和y 分别代表其x坐标和y坐标,坐标原点O的坐标为(0, 0)。
这样,我们可以通过有序数对的形式来表示平面上的每个点,将其与数学问题相联系。
在直角坐标系中,我们可以进行各种几何运算,例如计算两点之间的距离、计算线段的斜率、确定两个线段是否垂直或平行等。
通过使用直角坐标系,我们可以将几何问题转化为代数问题,从而利用代数的方法进行求解。
这为我们带来了巨大的便利。
直角坐标系在代数中也起到了至关重要的作用。
通过将函数图像映射到直角坐标系上,我们可以更清晰地观察函数的性质和行为。
在直角坐标系中,函数图像可以更直观地展示出随变量变化时的规律和趋势。
通过观察函数的图像,我们可以求解方程、求导、求积分等。
直角坐标系为我们进行数学分析提供了有效的工具。
在实际问题中,直角坐标系也经常被广泛应用。
例如,在地理学中,我们可以利用直角坐标系来描述地球上的地理位置,确定不同地点的坐标。
在物理学中,直角坐标系可以用于描述物体在平面上的位置和运动。
在计算机图形学中,直角坐标系可用于描述计算机屏幕上的像素点,实现图像的显示和处理。
在学习和使用直角坐标系时,我们需要注意一些基本要点。
首先,x轴和y轴要垂直且互相正交,这是直角坐标系的基本特性。
其次,我们需要熟悉坐标轴的正方向,通常x轴向右延伸,y轴向上延伸。
同时,我们还要学会在坐标系中进行平移、旋转和缩放等操作,以适应不同问题的要求。
总之,直角坐标系是数学中一种重要的表示方法,它为我们解决各种几何、代数和分析问题提供了便捷和直观的工具。
-34-
§3.2 平面与点的相关位置
平面与点的位置关系,有两种情形,就是点在平面上和点不在平面上. 前者的条件是点的坐标满足平面方程. 点不在平面上时,一般要求点到平面的距离,并用离差反映点在曲面的哪一侧.
1.点到平面的距离
定义3.2.1 自点M 0向平面π 引垂线,垂足为Q . 向量0QM 在平面π的单位法向量n 0
上的射影叫做M 0与平面π之间的离差,记作
δ = 射影n 00QM
(3.2-1)
显然
δ = 射影n 00QM = 0QM ·n 0 =∣0QM ∣cos ∠(0QM ,n 0) =±∣0QM ∣
当0QM 与n 0同向时,离差δ > 0;当0QM 与n 0反向时,离差δ < 0. 当且仅当M 0在平面上时,离差δ = 0.
显然,离差的绝对值就是点M 0到平面π 的距离. 定理3.2.1 点M 0与平面(3.1-13)之间的离差为
δ = n 0r 0-p
(3.2-2)
推论 1 若平面π 的法式方程为 0cos cos cos =-++p z y x γβα,则),,(0000z y x M 与π
间的离差
=δp z y x -++γβαcos cos cos 000
(3.2-3)
推论2 点),,(0000z y x M 与平面Ax +By +Cz +D = 0间的距离为
()2
2
2
0000,C
B A D
Cz By Ax M d +++++=
π (3.2-4)
2.平面划分空间问题 三元一次不等式的几何意义
设平面π的一般方程为
Ax +By +Cz +D = 0
则空间中任一点M (x ,y ,z )与π间的离差为
=δp z y x -++γβαcos cos cos = λ (Ax +By +Cz +D )
-35-
式中λ为平面π的法化因子,由此有
Ax +By +Cz +D =
δλ
1
(3.2-5)
对于平面π同侧的点,δ 的符号相同;对于在平面π的异侧的点,δ 有不同的符号,而λ一经取定,符号就是固定的. 因此,平面π:Ax +By +Cz +D = 0把空间划分为两部分,对于某一部分的点M (x ,y ,z ) Ax +By +Cz +D > 0;而对于另一部分的点,则有Ax +By +Cz +D < 0,在平面π上的点有Ax +By +Cz +D = 0.
P112习题 1,2,5,8。