北师版六年级数学下册“空间与图形”过关测试题

北师大版六年级数学下册总复习《空间与图形》之“立体图形”培优卷学校:___________姓名：___________班级：___________成绩：___________一、填空题（每小题2分，共20分）1．一个圆锥的体积是9.9立方分米,和它等底同高的圆柱的体积应是（_______）．2．一个圆柱的侧面展开图是一个边长是6.28cm的正方形，这个圆柱的底面半径是（________）cm，侧面积是（________）cm2.3．一个盛满水的圆锥体容器高9厘米，如果将水全部倒入与它等底等高的圆柱体容器中，则水高（____）厘米．4．把一个圆柱体加工成一个最大的圆锥体后，它的体积减少了40立方厘米，原来圆柱体的体积是（____）立方厘米．5．自来水管的内直径是2厘米，水管内水的流速是每秒6厘米。

照这样的流速，10分钟要浪费（____）升水。

6．直角三角形的两条直角边分别是3厘米和4厘米，以3厘米的直角边为轴旋转一周，可得到一个（______）形，体积是（______）。

7．现将一个棱长为40厘米的正方体铁块锻造成一个长20厘米、宽5厘米的长方体铁块，那么这个长方体铁块的高是（______）厘米。

8．把60升水倒入一个棱长为5分米的正方体容器里，水的高度是（______）分米。

9．左图从（_____）面看和（______）面看都是。

从（________）面看是。

10．一个长方体，长、宽、高分别是8厘米、5厘米和4厘米，从中截去一个最大的正方体后，剩下的体积是（______）立方厘米。

二、选择题（20分）1．把一个长方体锯成两个完全一样的正方体后，这两个正方体的表面积和与长方体的表面积相比（）A．增加了B．减少了C．不变2．一个正方体的棱长缩小到它的12，体积将缩小到它的（）。

A．8 B．18C．143．把下图中的硬纸片折成一个正方体，与数字“3”相对的是数字“（）”。

A．2 B．4 C．5 D．64．做一个无盖的圆柱形水桶，需要多少铁皮，是求它的（）A．体积 B．侧面积 C．一个底面积+侧面积5．等底等高的圆柱、长方体、正方体的体积相比较，（）。

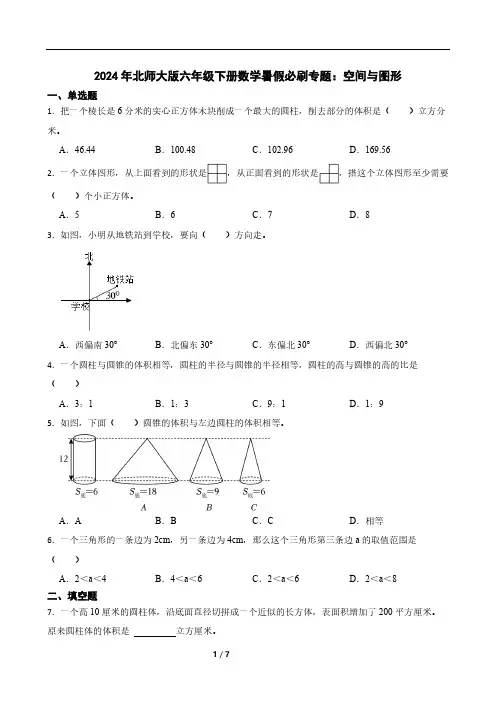
2024年北师大版六年级下册数学暑假必刷专题：空间与图形一、单选题1．把一个棱长是6分米的实心正方体木块削成一个最大的圆柱，削去部分的体积是（ ）立方分米。

A．46.44B．100.48C．102.96D．169.562．一个立体图形，从上面看到的形状是，从正面看到的形状是，搭这个立体图形至少需要（ ）个小正方体。

A．5B．6C．7D．83．如图，小明从地铁站到学校，要向（ ）方向走。

A．西偏南30°B．北偏东30°C．东偏北30°D．西偏北30°4．一个圆柱与圆锥的体积相等，圆柱的半径与圆锥的半径相等，圆柱的高与圆锥的高的比是（ ）A．3：1B．1：3C．9：1D．1：95．如图，下面（ ）圆锥的体积与左边圆柱的体积相等。

A．A B．B C．C D．相等6．一个三角形的一条边为2cm，另一条边为4cm，那么这个三角形第三条边a的取值范围是（ ）A．2＜a＜4B．4＜a＜6C．2＜a＜6D．2＜a＜8二、填空题7．一个高10厘米的圆柱体，沿底面直径切拼成一个近似的长方体，表面积增加了200平方厘米。

原来圆柱体的体积是 立方厘米。

8．一个长方体、一个圆柱体和一个圆锥体，它们的底面积和体积分别相等，如果长方体的高是12厘米，那么圆柱体的高是 厘米，圆锥体的高是 厘米。

9．如图所示，把底面直径10厘米，侧面积62.8平方厘米的圆柱切成若干等份，拼成一个近似的长方体。

这个长方体的底面积是 平方厘米，体积是 立方厘米。

10．用5个大小相等的小正方体搭成下面三个立体图形，从 面看这三个立体图形所看到的形状是完全一样的。

11．把一个棱长是a厘米的正方体锯成两个相同的长方体，表面积增加了 cm2。

12．下图中圆和长方形面积相等，圆的半径等于长方形的宽．阴影部分面积是60cm2，圆的面积是 cm2。

13．一个长方体和一个正方体的棱长总和相等，已知长方体的长、宽、高分别是3dm、2dm、4dm，那么正方体的体积是 dm3。

北师大版小学数学期末复习精华“空间与图形”过关测试题一、准确填空1．钟面上3点半时，时针与分针组成的角是（）角；9点半时，时针与分针组成的角是（）角2．一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米，平行四边形的面积是（）平方分米，三角形的面积是（）平方分米。

3. 把圆分成16等份，拼成近似的长方形，这个长方形的长是12.56厘米，那么圆的周长是（）厘米，面积是（）平方厘米。

4．把13厘米长的铁丝围成一个等腰三角形（每边为整厘米数），三条边长可能是（）、（）或（）。

5．在一个边长6厘米的正方形里剪一个最大的三角形,有( )种剪法,剪出的三角形的面积是( )平方厘米。

6．一个梯形的上底是12厘米，下底是20厘米，高是30厘米，用两个这样的梯形拼成一个平行四边形，拼成的平行四边形的底是（）厘米，面积是（）平方厘米。

7．把一个长、宽分别是15厘米和10厘米的长方形，拉成一个一条高为12厘米的平行四边形，它的面积是（）平方厘米。

8．等底等高的圆锥和圆柱容器各一个，将圆柱容器内装满水后，再倒入圆锥容器内，当圆柱容器的水全部倒光时，结果溢出36.2这升。

这时圆锥容器里有水（）毫升。

9．一个圆锥形的沙堆，底面积是18.84平方米，高1.2米，用这堆沙在10米宽的公路上铺２厘米厚的路面，能铺（）米。

10．把一个高６分米的圆柱切拼成近似的长方体，表面积比原来增加了４８平方分米。

原来圆柱的体积是（）立方分米二、慎重选择。

（将正确答案的序号填在括号里）1．一个正方体木块，从顶点上挖去一个小正方体后，表面积（），体积（）。

A、变大B、变小C、不变2．圆柱、正方体和长方体的底面周长相等，高也相等，则（）的体积最大。

A、圆柱B、正方体C、长方体3．将一个平行四边形纸片剪拼成长方形，面积（），周长（）。

A、不变B、变大C、变小4．如果两个三角形等底等高，那么这两个三角形（）。

A、形状一定相同B、面积相同C、一定能拼成一个平行四边形D、完全相同5．等腰梯形周长是48厘米，面积是96平方厘米，高是8厘米，则腰长（）。

北师大小学数学六年级下册
好的开始，是成功的一半，祝您天天进步！
发明在于发现，发现在于实践
图形与变换
一、认真思考，仔细填写。

1、旋转和平移都只是改变图形的（），而不改变图形的（）和（）。

2、右边第一张图片中的长方形向（）平移了
（）个格。

第二张图片中的三角形（）
时针旋转了（）度。

二、连一连。

三、画一画。

1、画出下面对称图形的所有对称轴。

2、请你以直线l为对称轴，画出图形的另一半。

3、将方格中的图形向右平移两个格。

4、将图形绕点O按顺时针方向旋转90°。

四、请将下面三个图形拼成一个轴对称图形。

你能想出几种拼法？
五、利用图形的平移或旋转，设计一个美丽的图案，别忘了涂上自己喜欢的颜色。

相信自己，就能走向成功的第一步
教师不光要传授知识，还要告诉学生学会生活。

数学思维可以让
他们更理性地看待人生。

2024年北师大版六年级下册数学小升初分班考必刷专题：空间与图形一、单选题1．一个圆柱体和一个圆锥体的底面周长之比是1：3，它们的体积比是1：3，圆柱体和圆锥体高的比是（）。

A．3：1B．1：9C．1：1D．3：22．直角三角形ABC （如图），以直角边AB旋转360° 后得到的是（）A．底面直径是6cm，高是8cm的圆锥B．底面直径是8cm，高是6cm的圆锥C．底面半径是8cm，高是6cm的圆锥D．底面半径是6cm，高是8cm的圆锥3．把一根长3米的圆柱形木料截成3段小圆柱后，表面积比原来增加了0.6平方米，原来这根木料的体积是（）立方米。

A．0.3B．0.4C．0.45D．0.64．把一个圆柱削成一个最大的圆锥，削去部分的体积是圆锥体积的（）A．13B．23C．2倍D．6倍5．把一个棱长是6分米的实心正方体木块削成一个最大的圆柱，削去部分的体积是（）立方分米。

A．46.44B．100.48C．102.96D．169.566．一个立体图形，从上面看到的形状是，从正面看到的形状是，搭这个立体图形至少需要（）个小正方体。

A．5B．6C．7D．8二、填空题7．将一块体积是90m3的圆柱形铁块，削成一个最大的圆锥，削成的圆锥的体积是m3。

削下的铁屑还可熔铸成个这样的圆锥。

8．一个圆锥的体积是76立方厘米，底面积是19平方厘米．这个圆锥的高是厘米．9．一个圆柱与一个圆锥，圆柱的底面积是圆锥底面积的40%，圆柱的高是圆锥高的2倍，这个圆柱和圆锥的体积之比是。

10．一个圆柱的侧面积是157cm2，高是5cm，它的底面半径是cm，表面积是cm2。

11．一个周长为20厘米的大圆内有许多小圆，这些小圆的圆心都在大圆的一个直径上．则小圆的周长之和为厘米．12．一大正方体由着千个棱长为1cm的小正方体组成，在大正方体的表面涂色，其中只有一面涂色的小正方体有24个，大正方体的表面积是平方厘米。

13．用48厘米长的铁丝焊接成个最大的正方体.这个正方体的棱长厘米，体积是立方厘米14．把一个圆柱体削成一个最大的圆锥体，体积减少了120立方厘米，那么圆锥体积是立方厘米。

北师大版六年级数学下册图形与几何、统计与概率达标检测卷一、填空。

(每空1分，共19分)1．在括号里填上合适的单位名称。

(1)学校旗杆高15( )。

(2)一瓶墨水约60( )。

(3)一张2寸登记照的面积约18( )。

2．4.5 m3＝( )dm38.06 m2＝( ) m2( ) dm23．小芳家在学校的东偏南30°方向，小芳家到学校的距离是800 m，那么学校在小芳家的( )偏( )( )°方向，学校到小芳家的距离是( ) m。

4．如左下图，正方形的面积与圆的面积的比是( )。

5．如右上图，平行四边形ABCD三个顶点A，B，C的位置用数对表示分别为(5，6)、(2，3)、(6，3)，那么顶点D的位置用数对表示是( ，)。

6．一个梯形的上底长8 cm，下底长12 cm，高10 cm，若在这个梯形中剪去一个最大的平行四边形，这个平行四边形的面积是( )cm2；若在这个梯形中剪去一个最大的三角形，剩余部分的面积是( )cm2。

7．一个长方体，高增加3 cm后就变成了一个正方体，并且表面积增加了60 cm2，原来这个长方体的体积是( )cm3。

8．把一个底面周长是25.12 dm，高10 dm的圆柱切拼成一个近似的长方体，这个长方体的表面积是( )dm2，体积是( )dm3。

9．在一个条形统计图里，用1.5 cm长的直条表示9 t，用( )cm长的直条表示24 t。

10．一个盒子里装有完全相同的红球、蓝球共10个，如果任意摸一个球，摸到红球的可能性大，则红球至少有( )个。

二、选择。

(将正确答案的序号填在括号里)(每题2分，共16分)1．下列四个图形中，不能通过基本图形平移得到的是( )。

2．下列数据中，与其他数据不相等的是( )。

A．4.05 m3 B．40500 cm3 C．4050 dm3 D．4050000 cm33．4．将完全相同的1个黑球和9个白球放在一个口袋里，从口袋里任意摸一个球，下列说法正确的是( )。

图形与儿何专项测试k 在正方形、等边二角形和圆中以扌称轴最多的是（ 「有（ ）条；对称轴竄少的是（儿有〔）条.2. •只挂钟的时针长I 。

Cm .分针长2C cin,从6时到IU 时.分针针尖其走T （ >c πι*时针扫过的面积是（ ）c∏r g3・等腰三角形的l ⅛条边分别长£ Crn . H' Cm ・那么•这个等腿一:ft 形的周长 是（）c∏U4.钟表在IQ 时整时*时甘和分针所形成的较小角是（ ）%5-如下图所示*毎个小方格的面积Jft 2 cm" <那么△八的而积是（ ^cm ;6.写出下图中外点的位齐舄 ^A （ ）,BC ）,C （）∙D （ J 四边形ABeL ）的面积症（）个小格=7. 一个氏方体•如果高増加3 Cm 就成了正方体•并且表面枳增加6）w Λ 原来这 个长方体的体积是（ 儿&看图填空。

（1）以学校为观测点•书店在（ ）偏（ K ）的方向—电影l ⅛在（）!'」 nJ /；、CJJiL2 5 5 6 7 S时间:90分钟 满T 分：1OO+10分第G 题图偏（X ［的方間上。

（2）小刖从学校去体仃馆.每分走80门“他耍定（）分・SL 如右图所示•一个棱长6 cm 的正方体内挖去-牛绘大的圆锥.剩下的体积是原止方体的（O（结果保幣一位小数｝Kh 把一段长2 In 的圆柱形木料锯成4个小圆柱.表面积帀好増加r 16 a∏r.这段木料的体积是（）dm ∖二、仔细推敲•做出判断。

（共5分）L 不相交的两条直线是平行线。

2. —个圆的半於是2 m ・这亍圆的周丘和面积相等。

3・半行四边形的IS 积等于三角形而积的Zfrto 4.冇民度分别H 2 c πι,6 Clll 、H cm 的三根小栋•这二根小楼询星相连能I 制成•个三角形。

（'）5.卜面JE-两个圆柱模型的表面展幵图。

可以判断A 圆柱的体积比B 圆柱的体积 大B（单位:Cm ）（）B三、反复比较我慎重选择门（共L 一个圆住和 个圆锥J 疋血周长的比足2：3・体积的比足5 : G.它门的髙的最 简整数比是（ ）。

空间与图形
图形的认识
（一）线与角
一、认真思考，仔细填写。

1、一条线段有（）个端点，一条射线有（）个端点，一条直线（）
端点。

2、在同一平面内，（）叫做平行线。

3、当两条直线相交成直角时，这两条直线（）。

这两条直线的交点叫做（）。

4、把锐角、钝角、平角、周角、直角按从大到小的顺序排列是（）。

二、把角送回家。

三、按要求作图。

1、画长3厘米和55毫米的线段各一条。

2、画出50°，100°，150°三个角。

四、求下面图中各角的度数。

五、按要求作图。

1、过直线外A点作已知直线的平行线。

· A
2、过直线上B点作已知直线的垂线。

·
B
六、如下图所示，小林要从A点到河边去提水，怎样走路最近，请在图上画出来。

A ·
小林。

图形与几何专项测试一、细心读题，谨慎填写。

1．在正方形、等边三角形和圆中，对称轴最多的是( )，有( )条；对称轴最少的是( )，有( )条。

2．一只挂钟的时针长10 cm，分针长20 cm，从6时到10时，分针针尖共走了( )cm，时针扫过的面积是( )cm²。

3．等腰三角形的两条边分别长5 cm、10 cm，那么，这个等腰三角形的周长是( )cm。

4．钟表在10时整时，时针和分针所形成的较小角是( )°。

5．如下图所示，每个小方格的面积是2 cm²，那么△ABC的面积是( )cm²。

6．写出下图中各点的位置。

A( )，B( )，C( )，D( )。

四边形ABCD的面积是( )个小格。

7．一个长方体，如果高增加3 cm就成了正方体，并且表面积增加60 cm²。

原来这个长方体的体积是( )。

8．看图填空。

(1)以学校为观测点，书店在( )偏( )( )的方向上，电影院在( )偏( )( )的方向上。

(2)小明从学校去体育馆，每分走80 m，他要走( )分。

9．如右图所示，一个棱长6 cm的正方体内挖去一个最大的圆锥，剩下的体积是原正方体的( )%。

（结果保留一位小数）10．把一段长2m的圆柱形木料锯成4个小圆柱，表面积正好增加了16 dm²，这段木料的体积是( )dm³。

二、仔细推敲，做出判断。

1．不相交的两条直线是平行线。

( )2．一个圆的半径是2 m，这个圆的周长和面积相等。

( )3．平行四边形的面积等于三角形面积的2倍。

( )4．有长度分别是2 cm、6 cm、6 cm的三根小棒，这三根小棒首尾相连，不能围成一个三角形。

( )5．下面是两个圆柱模型的表面展开图。

可以判断A圆柱的体积比B圆柱的体积大。

（单位：cm） ( )三、反复比较，慎重选择。

1．一个圆柱和一个圆锥，底面周长的比是2:3，体积的比是5:6。

它们的高的最简整数比是( )。

空间与图形综合复习题姓名：一、填空题。

1、从直线外一点到这条直线可以画无数条线段，其中最短的是和这条直线（）的线段。

2、一个三角形中，最小的角是46°，按角分类，这个三角形是（）三角形。

3、一个三角形三个内角度数的比是2：3：4，三个角的度数分别是（）、（）、（），它是（）角三角形。

4、一个等腰三角形的顶角是70°，它的底角是（）度；一个等腰三角形的底角是54°，它的顶角是（）。

5、经过两点可以画出（）条直线；两条直线相交有（）个交点。

6、如果等腰三角形的一个底角是53°，则它的顶角是（）；直角三角形的一个锐角是48°，另一个锐角是（）。

7、在一个等腰三角形中，一个顶角与一个底角之和是130°，这个三角形的顶角是（）度。

8、一个长方形的周长是42cm，它的长与宽的比是4∶3，它的面积是（）cm2。

9、用72cm长的铁丝焊成一个正方体框架（接口处不计），这个正方体框架的棱长是（）cm，体积是（）cm3，表面积是（）cm2。

10、一个三角形的面积是120平方分米，底是30分米，高是（）分米。

11、用两个相同的正方体木块拼成一个长方体，长方体的表面积比两个正方体的表面积的和少16平方厘米，一个正方体的表面积是（）平方厘米。

12、将一个大正方体切成大小相同的8个小正方体，每个小正方体的表面积是18平方厘米，原正方体的表面积是（）平方厘米。

13、一张长方形的纸，长是10厘米，宽是6厘米，从这张纸上剪下一个最大的正方形，剩下的纸的面积是（）平方厘米。

14、两个正方形的边长之比是2：3，它的周长之比是（），面积之比是（）。

15、把两个棱长是4cm的正方体连成一个长方体，这个长方体表面积是（）。

16、一个长方体，如果高增加2厘米，就成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是（）立方厘米。

17、一个长方体棱长总和是72cm，长宽高的比是5：3：1，这个长方体的表面积是（）cm²,体积是（）cm³。