卡诺循环与卡诺定理

§2-3 热力学第二定律2．3．1、卡诺循环物质系统经历一系列的变化过程又回到初始状态，这样的周而复始的变化过程为循环过程，简称循环。

在P-V 图上，物质系统的循环过程用一个闭合的曲线表示。

经历一个循环，回到初始状态时，内能不变。

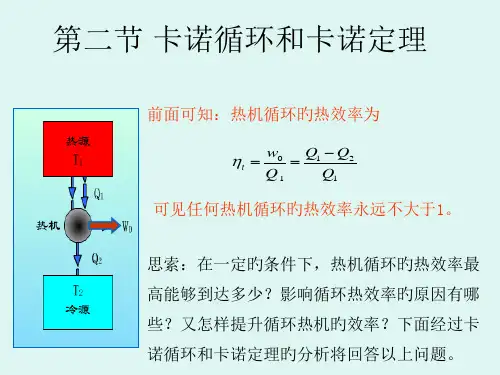
利用物质系统(称为工作物)持续不断地把热转换为功的装置叫做热机。

在循环过程中，使工作物从膨胀作功以后的状态，再回到初始状态，周而复始进行下去，并且必而使工作物在返回初始状态的过程中，外界压缩工作物所作的功少于工作物在膨胀时对外所做的功，这样才能使工作物对外做功。

获得低温装置的致冷机也是利用工作物的循环过程来工作的，不过它的运行方向与热机中工作物的循环过程相反。

卡诺循环是在两个温度恒定的热源之间工作的循环过程。

我们来讨论由平衡过程组成的卡诺循环，工作物与温度为1T 的高温热源接触是等温膨胀过程。

同样，与温度为2T 的低温热源接触而放热是等温压缩过程。

因为工作物只与两个热源交换能量，所以当工作物脱离两热源时所进行的过程，必然是绝热的平衡过程。

如图2-3-1所示，在理想气体卡诺循环的P-V 图上，曲线ab 和cd 表示温度为1T 和2T 的两条等温线，曲线bc 和da 是两条绝热线。

我们先讨论以状态a 为始点，沿闭合曲线abcda 所作的循环过程。

在abc 的膨胀过程中，气体对外做功1W 是曲线abc 下面的面积，在cda 的压缩过程中，外界对气体做功2W 是曲线cda 下面的面积。

气体对外所做的净功)(21W W W -=就是闭合曲线abcda 所围面积，气体在等温膨胀过程ab 中，从高温热源吸热121V V nRTIn Q =，气体在等温压缩过程cd 中，向低温热源放热4322V V In nRT Q =。

应用绝热方程 132121--=r r V T V T 和142111--=r r V T V T 得 4312V V V V =所以1224322V V In nRT V V InnRT Q == 2211T Q T Q = 卡诺热机的效率 112111Q Q Q Q W -=-==η 我们再讨论理想气体以状态a 为始点，沿闭合曲线adcba 所分的循环过程。

工程热力学一、基本概念（一）工质及其状态参数1、工质：实现热能与机械能相互转换的工作介质（如：水蒸汽）。

工质的状态：工质在某一瞬间宏观的物理特性。

2、工质的状态参数：描述工质状态的物理量。

常见的状态参数：温度T、压力P、比容c、内能U、焓H、熵S（1）压力：单位面积上所受的垂直作用力，p=F/A，符号为p，单位是帕斯卡，表示为“Pa”，1Pa=1N/m2，工程上常用MPa，1Mpa=10Pa，此外，还有at、atm，mmHg等。

压力的测量：压力表数据与工质实际压力的关系：（我们用p表示绝对压力，p b表示大气压力，p g表示压力表读数）绝对压力：容器内工质的的实际压力，用符号p表示；表压力：工质的绝对压力与大气压力的差值，用p g表示。

p=p b时，p g=0 p＞p b时，p=p b+p g p＜p b时，压力表（真空表）上读数称为负压或真空，p v表示，p=p b-p v电厂中有时用真空度表示真空值的大小，称为真空度。

（2）内能：内部所具有的各种微观能总和，用符号“U”表示，单位为J或kJ，U=f （T，v）主要包括：分子内动能：主要由分子不规则热运动引起，是温度的函数；分子内位能：分子间存在着作用力，与分子之间距离有关，是比容的函数。

由于内能取决于工质的温度与比容，因此，内能是状态参数（3）焓：焓为内能与流动功的总和，用H或h表示，单位为J或kJ，h=u+pv；焓是状态参数；（4）熵：ds=dq/T，单位：J/（kg.k）或kJ/(kg.k)，熵为状态参数，热力学中常用ds的正负来判断热量的大小、方向：ds＞0，q＞0，吸热；ds＜0，q＜0，放热；ds=0，q=0绝热。

3、膨胀功及p-v图4、热量及T-S图（二）热力学第一定律：热可以变为功，功也可以变为热；当一定量的热消失，必产生与之数量相当的功，消耗一定量的功，必产生相当数量的热。

热力学第一定律解析式及应用q=Δu+w（1kg工质）q：系统吸收或放出的热量。