第1章《丰富的图形世界》易错题集(01)：1.1+生活中的立体图形

第1章 丰富的图形世界（易错必刷30题8种题型专项训练）➢认识立体图形 ➢几何体的展开图 ➢正方体相对两个面上的文字 ➢简单几何体的三视图➢点、线、面、体➢展开图折叠成几何体➢截一个几何体➢简单组合体的三视图一．认识立体图形（共3小题）1．圆柱体的底面半径扩大3倍，高不变，体积扩大（ ）倍．A ．3B ．9C ．6D ．272．有一块正方体的木料，它的棱长是4cm ．把这块木料加工成一个最大的圆柱．这个圆柱的底面半径是（ ）cm ．A ．2B ．3C ．6D ．83．把一个圆柱削成一个最大的圆锥，如果圆锥的体积是72立方厘米，要削去部分是（ ）立方厘米．A ．72B ．144C ．216D ．24二．点、线、面、体（共1小题）4．观察如图，把图形绕着给定的直线旋转一周后形成的几何体可能是（ ）A ．B ．C ．D ．三．几何体的展开图（共3小题）5．如图正方体纸盒，展开后可以得到（ ）A．B．C．D．6．下列图形中，不是正方体的展开图的是（）A．B．C．D．7．下列图形不能作为一个三棱柱的展开图的是（）A．B．C．D．四．展开图折叠成几何体（共4小题）8．下列各图经过折叠后不能围成一个正方体的是（）A．B．C．D．9．小欣同学用纸（如图）折成了个正方体的盒子，里面放了一瓶墨水，混放在下面的盒子里，只凭观察，选出墨水在哪个盒子中（）A．B．C．D．10．把图中的纸片沿虚线折叠，可以围成（）A．三棱锥B．三棱柱C．五棱锥D．五棱柱11．下列图形经过折叠可以围成一个棱柱的是（）A．B．C．D．五．专题：正方体相对两个面上的文字（共6小题）12．如图是一个正方体的平面展开图，把展开图折叠成一个正方体后，有“考”字一面的相对面上的字是（）A．祝B．试C．顺D．利13．一个小立方块六个面分别标有字母A，B，C，D，E，F，从三个不同方向看到的情形如图所示，则C，D，F对面的字母分别是（）A．A、B、E B．A、E、B C．E、B、A D．F、E、B14．如图，是一个正方体的表面展开图，如果相对两个面上的两个数字之和相等，那么y x的值为（）A．8B．﹣8C．16D．﹣1615．一个正方体的六个面分别标有六个不同的点数，其展开图如图所示，则该正方体可能是（）A．B．C．D．16．一个正方体，它的各个面上分别标有数字1、2、3、4、5、6．甲、乙、丙三同学从不同角度观察这个正方体，看到的情况如图所示（不考虑数字的正、倒等），则这个正方体上标有数字1、2、3的三个面所对的面上标记的数字分别为．17．如图，一个正方体的六个面分别写着六个连续的整数，且相对面上的两个整数的和都相等，将这个正方体放在桌面，将其以如图所示的方式滚动，每滚动90°算一次，请问滚动2022次后，正方体贴在桌面一面的数字是．六．截一个几何体（共4小题）18．用一个平面去截正方体，截面图不可能是（）A．正三角形B．平行四边形C．六边形D．正八边形19．下列说法正确的是（）A．棱柱的每条棱长都相等B．棱柱侧面的形状可能是一个三角形C．长方体的截面形状一定是长方形D．经过一点可以画无数条直线20．截一个几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．如图，下列几何体的截面是．21．如图是一个几何体的展开图．（1）写出该几何体的名称：（2）用一个平面去截该几何体，截面形状可能是（填序号）；①三角形；②四边形；③五边形；④六边形（3）根据图中标注的长度（单位：cm），求该几何体的表面积和体积．七．简单几何体的三视图（共2小题）22．下列几何体中，同一个几何体从正面看和从上面看形状图不同的是（）A．B．C．D．23．下列几何体中，其主视图和左视图不相同的是（）A．B．C．D．八．简单组合体的三视图（共7小题）24．某运动会颁奖台如图所示，它的左视图是（）A．B．C．D．25．如图所示的几何体由5个大小相同的立方块搭成，从上面看到的该几何体的形状图是（）A．B．C．D．26．如图，由七个相同的小正方体拼成立体图形，若从标有①②③④的四个小正方体中取走一个或多个后，余下的几何体与原几何体的左视图相同，则取走的正方体不可能是（）A．④B．③C．②D．①27．如图，这个几何体的左视图正确的是（）A．B．C．D．28．如图，这是一个机械模具，则它的左视图是（）A．B．C．D．29．如图所示的几何体由5个完全相同的小正方体组成，它的俯视图是（）A．B．C．D．30．如图是用7块相同的小长方体搭成的几何体．若拿走一块长方体后，该几何体的主视图和左视图都没改变，则这块长方体的序号是．。

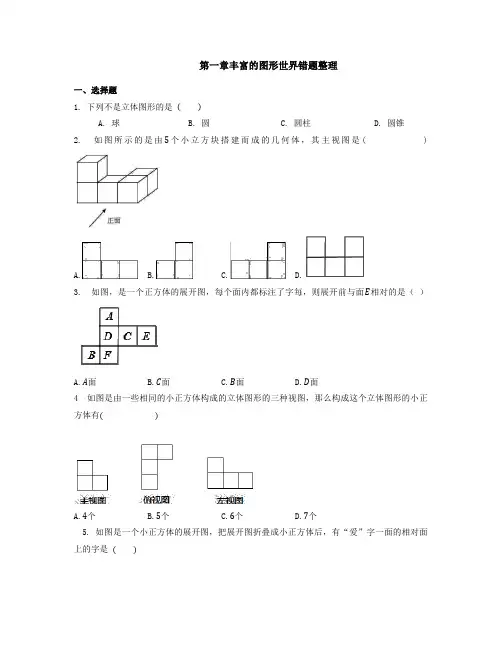
第一章丰富的图形世界错题整理一、选择题1. 下列不是立体图形的是( )A. 球B. 圆C. 圆柱D. 圆锥2. 如图所示的是由5个小立方块搭建而成的几何体，其主视图是( )A. B. C. D.3. 如图，是一个正方体的展开图，每个面内都标注了字每，则展开前与面E相对的是（）A.A面B.C面C.B面D.D面4 如图是由一些相同的小正方体构成的立体图形的三种视图，那么构成这个立体图形的小正方体有()A.4个B.5个C.6个D.7个5. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“爱”字一面的相对面上的字是( )A. 美B. 丽C. 宜D. 昌6．把图中的纸片沿虚线折叠，可以围成一个几何体，这个几何体的名称是（）A．五棱锥B．五棱柱C．六棱锥D．六棱柱7．下列图形中，不是正方体表面展开图的是（）A．B．C．D．8．在一个有盖的正方体玻璃容器内装了一些水（约占一半），把容器按不同方式倾斜，容器内水面的形状不可能是（）A．B．C．D．二、填空题9. 笔尖在纸上写字说明；车轮旋转时看起来象个圆面，这说明；一枚硬币在光滑的桌面上快速旋转形成一个球，这说明．10．如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值是．11．一个正方体盒子的展开图如图所示，如果要把它粘成一个正方体，那么与点A重合的点是．12. 如图是正方体的一种平面展开图，它的每个面上都有一个汉字，那么在原正方体的表面上，与汉字“香”相对的面上的汉字是．13. 把一个边长为2cm的立方体截成八个边长为1cm的小立方体，至少需要截次．14. 一个正方体的平面展开图如图所示，将它折成正方体后，“保”字对面的字是________．15 如图所示几何体(a)的一个视图(b)的名称是________．16. 如图是一个几何体从三个方向看所得到的形状图，则该几何体的表面积为________（结果保留π）17．图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①、②、③、④某一位置，所组成的图形不能围成正方体的位置是___．18．用一个平面去截一个几何体，截面形状为圆，则这个几何体可能为__________（填序号）．①正方体；②圆柱；③圆锥；④正三棱柱三、解答题19. 观察图所示的八个几何体，回答下列问题．（1）依次写出这八个几何体的名称：①；②；③；④；⑤；⑥；⑦；⑧；（2）在这个几何体中，不含曲面的有；含曲面的有（填序号即可）；（3）分别写出几何体⑥和⑧的两个相同点和两个不同点．20.如图，是一个正方体纸盒的两个表面展开图，请把-4，3，9，6，-1，2分别填入六个面中，使得折成正方体后，相对面上的两数之和与-5互为相反数．21.（1）写出下列立体图形的名称．（）（）（）（）（）（2）把一个正方体用刀切去一部分，能否得到正方体、长方体、三棱锥、三棱柱、四棱柱、五棱柱？22. 如图所示，根据几何体的三视图及其尺寸解答下列问题．（1）若r=3，求几何体的体积；（2）若几何体的体积为90π，求r．23. 观察如图所示的几何体，回答下列问题．（1）填写下表：（2）由此可推测n（n为大于或等于3的正整数）棱柱有多少个面?多少个顶点?多少条棱?。

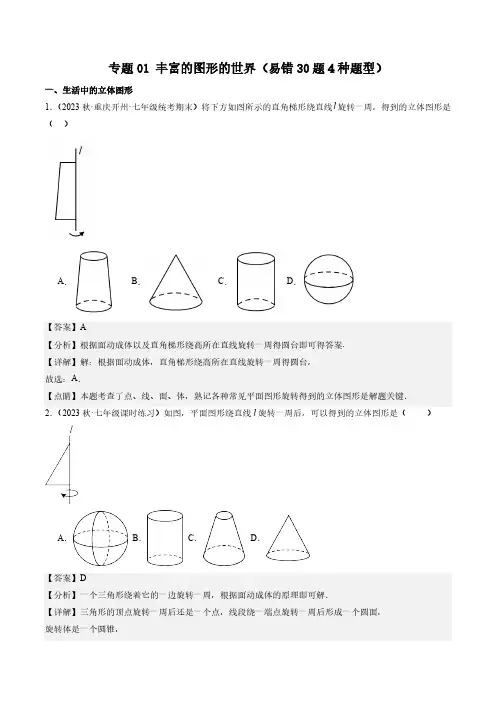
专题01 丰富的图形的世界（易错30题4种题型）一、生活中的立体图形1．（2023秋·重庆开州·七年级统考期末）将下方如图所示的直角梯形绕直线l旋转一周，得到的立体图形是（）A．B．C．D．【答案】A【分析】根据面动成体以及直角梯形绕高所在直线旋转一周得圆台即可得答案.【详解】解：根据面动成体，直角梯形绕高所在直线旋转一周得圆台，故选：A．【点睛】本题考查了点、线、面、体，熟记各种常见平面图形旋转得到的立体图形是解题关键．2．（2023秋·七年级课时练习）如图，平面图形绕直线l旋转一周后，可以得到的立体图形是（）A．B．C．D．【答案】D【分析】一个三角形绕着它的一边旋转一周，根据面动成体的原理即可解．【详解】三角形的顶点旋转一周后还是一个点，线段绕一端点旋转一周后形成一个圆面，旋转体是一个圆锥，A．河B．东C．初D．数【答案】C【分析】根据题意，理解旋转过程中，各个面的变化情况．【答案】六棱柱【分析】根据棱锥的特点可得九棱锥侧面有根据n棱柱有3n条棱可得答案．【详解】解：Q九棱锥侧面有9条棱，(1)共需要彩带多少厘米？(2)做这样一个礼品盒至少要多少硬纸？(3)这个礼品盒的体积是多少？（结果保留【答案】(1)215cm(2)()2450cm p (3)()31000cm p【点睛】本题考查认识立体图形，掌握圆柱体的特征、表面积、体积的计算方法是正确解答的前提．7．（2022秋·广东深圳·七年级校考期中）如图是一个长为4cm ，宽为3cm 的长方形纸片．(1)若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是___________，这能说明的事实是___________．(2)求：当此长方形纸片绕长边所在直线旋转一周时（如图1），所形成的几何体的体积．(3)求：当此长方形纸片绕短边所在直线旋转一周时（如图2），所形成的几何体的体积．【答案】(1)圆柱，面动成体(2)336cm p (3)348cm p 【分析】（1）根据对几何体的认识和面动成体解答即可；（2）绕长旋转得到的圆柱的底面半径为3cm ，高为4cm ，从而计算体积即可；（3）绕宽旋转得到的圆柱底面半径为4cm ，高为3cm ，从而计算体积即可．【详解】（1）解：若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体；故答案为：圆柱；面动成体．（2）解：绕长边旋转得到的圆柱的底面半径为3cm ，高为4cm ，体积233436cm p p =⨯⨯=；（3）解：绕短边旋转得到的圆柱底面半径为4cm ，高为3cm ，体积234348cm p p =⨯⨯=．【点睛】本题考查了点、线、面、体的知识，熟记常见平面图形旋转可得到什么立体图形是解决本题的关键，另外要掌握圆柱的体积计算公式．8．（2023秋·全国·七年级专题练习）18世纪瑞士数学家欧拉证明了简单多面体中顶点数（V ）、面数（F ）、棱数（E ）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题．(1)根据上面的多面体模型，直接写出表格中的m ，n 的值，则m =______，n =______．9．（2023秋·七年级课时练习）下列四组图中，每组左边的平面图形不能折叠成右边的立体图形的是（）A．①②B．①③④C．②③D．②③④【答案】B【分析】根据立体几何图形的展开图，相对面等知识即可求解．【详解】解：①不能折叠成正方体；②能折叠成长方体；③不能折成圆锥；④不能折成四棱锥；故选：B．【点睛】本题主要考查立体几何的展开图，掌握立体几何展开图，相对面等知识是解题的关键．10．（2022秋·福建宁德·七年级统考期末）如图所示的小正方形大小相同，其中有五个已经涂上阴影，若要将图中①，②，③，④中的某一个小正方形再涂上阴影，使得所有涂上阴影的小正方形组成的图形是正方体表面展开图，则可以涂上阴影的小正方形是（）A．①B．②C．③D．④【答案】A【分析】根据正方体表面展开图的基本图形，选择符合的小正方形即可．【详解】正方体表面展开图的基本图形有：141型：中间一行4个作侧面，上下两个各作为上下底面，共有6种基本图形，231型：中间一行3个作侧面，共3种基本图形，222型：中间两个面，只有1种基本图形，33型：中间没有面，两行只能有一个正方形相连，只有1种基本图形，观察发现题中只能是231型中的图（7）类型，应选小正方形①，故选：A．【点睛】本题考查了正方体的展开图，掌握正方体的展开图类型去判断是解题的关键．11．（2023春·河南驻马店·九年级校考阶段练习）2022年11月4日，第五届中国国际进口博览会在上海开幕，河南展区亮点十足，首台河南造“移动的快递柜”开进博览会．将这六个汉字分别写在某正方体的表面上，如图是它的一种展开图，则在原正方体中，与“移”字所在面相对的面上的汉字是（）A．的B【答案】B【分析】根据正方体的展开图中的隔一相对的原理判断即可．【详解】根据正方体的展开图隔一相对的原理，得到【答案】“教”【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，据此分析判断即可．【详解】解：在该正方体的展开图中，与【答案】同【分析】根据正方体展开图的形状进行判断作答即可．【详解】解：由题意知，滚动到最后一格时，最下方为∵“建”字对面是“同”，14．（2023·全国·七年级专题练习）一种产品的包装盒如图所示，为了生产这种包装盒，需要先画出其表面展开图的纸样（单位：cm ）(1)如图所示，给出三种纸样甲、乙、丙，在甲、乙、丙中正确的有______．(2)利用你所选的一种纸样，求出包装盒的表面积（侧面积和两个底面积的和）和体积．【答案】(1)乙丙(2)2238cm S =表面积，体积为3195cm ．【分析】（1）根据长方体展开图的特点进行求解即可（2）根据长方体的表面积公式和体积公式进行求解即可【详解】（1）解：由长方体展开图的特点可知乙、丙是长方体的展开图，甲不是长方体的展开图，故答案为：乙丙；（2）解：()2213313535238cm S =⨯⨯+⨯+⨯=表面积，体积为35133195cm ⨯⨯=．【点睛】本题主要考查了长方体的展开图，求长方体的表面积和提交，熟练掌握长方体的相关知识是解题的关键．15．（2023秋·全国·七年级专题练习）综合实践问题情景：某综合实践小组进行废物再利用的环保小卫士行动．他们准备用废弃的宣传单制作装垃圾的无盖纸盒．操作探究：(1)若准备制作一个无盖的正方体纸盒，图1中的___________图形经过折叠能围成无盖正方体纸盒．(2)如图2是小明的设计图，把它折成无盖正方体纸盒后与“小”字相对的是___________(3)如图3，有一张边长为40cm的正方形废弃宣传单，小华准备将其四角各剪去一个小正方形，折成无盖长方体纸盒．①请你在图3中画出示意图，用实线表示剪切线，虚线表示折痕．②若四角各剪去了一个边长为5cm的小正方形，这个纸盒的容积．【答案】(1)C(2)环(3)①见解析，②34500cm【分析】（1）根据正方体的折叠，可得有5个面，依据正方体的展开图可得答案；（2）根据正方体的表面展开图的特征，得出答案；（3）①画出相应的图形即可；②根据折叠得出高，表示底面的长和宽即可得这个纸盒的底面积；底面积乘以高求容积即可．【详解】（1）解：∵折叠成一个无盖的正方体纸盒，∴展开图有5个面，再根据正方体的展开图的特征，故A选项、B选项中图形不符合题意，选项C的图形符合题意，选项D的图形可以折叠出有盖的正方体的纸盒，故选项D不符合题意；故选项C中的图形能够折叠成一个无盖的正方体纸盒；故选：C（2）解：解：∵正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，∴与“小”字相对的字是“环”，答：折成无盖正方体纸盒后与“小”字相对的字是“环”；故答案为：环（3）解：①所画出的图形如图所示：②纸盒的容积为()23540254500cm ´-´= 答：纸盒的容积为34500cm ．【点睛】本题考查正方体的表面展开图，正方形相对两面上的字，列代数式并求值，掌握正方体的表面展开图的特征是解决问题的关键．三、截一个几何体16．（2023·江苏南京·校联考三模）在一个密闭透明的圆柱桶内装一定体积的水，将圆柱桶按不同方式放置时，圆柱桶内的水平面不可能呈现出的几何形状是（ ）A ．圆面B ．矩形面C ．梯形面D ．椭圆面或部分椭圆面【答案】C【分析】对不同的放置情况分别判断，得出结论．【详解】解：当圆柱桶竖直放置时，液面形状为圆形，故选项A 不符合题意；当圆柱桶水平放置时，液面为矩形，故选项B 不符合题意；无论圆柱桶怎样放置，圆柱桶内的水平面不可能呈现出梯形面，故选项C 符合题意；当圆柱桶倾斜放置时，若液面经过底面，则液面为椭圆的一部分，若液面不经过底面，则液面为椭圆，故选项D 不符合题意．故选：C ．【点睛】本题考查了圆柱的结构特征．关键是理解用平面去截圆柱体，所得到截面.17．（2023秋·山东临沂·七年级统考期末）如图，一圆柱形油桶中恰好装有半桶油，现将油桶由直立状态放倒成水平放置状态，在整个过程中，桶中油面的形状不可能是（ ）A ．B ．C ．D ．【答案】C【答案】21【分析】根据截去正方体一个角变成一个多面体，这个多面体多了一个面，棱数不变即可进行解答．【详解】解：根据题意得：n=m=+=，12617【答案】圆长方形【分析】根据立体图形截面特点解题即可．【详解】图①由图可知截面跟底面相同，故形状为：圆，(1)写出该几何体的名称_________：(2)用一个平面去截该几何体，截面形状可能是_________（填序号）；①三角形；②四边形；③五边形；④六边形(3)根据图中标注的长度（单位：cm），求该几何体的表面积和体积．【答案】(1)长方体(2)①②③④(3)2cm120cm，723【分析】（1）直接根据几何体的展开图判断即可；（2）根据长方体有六个面，用平面去截长方体时最多与六个面相交得六边形，最少与三个面相交得三角形即可得出结果；（3）利用长方体的表面积计算公式及体积计算公式求解即可．【详解】（1）解：根据几何体的展开图共有6个面，且各面有正方形及长方形，∴此几何体为长方体，故答案为：长方体；（2）解：∵长方体有六个面，∴用平面去截长方体时最多与六个面相交得六边形，最少与三个面相交得三角形，∴用一个平面去截长方体，截面的形状可能是三角形、四边形、五边形、六边形，故答案为：①②③④；（3）解：2264662120cmS=⨯⨯+⨯⨯=，3V=⨯⨯=，66272cm答：表面积是1202cm．cm，体积是723【点睛】题目主要考查长方体的展开图及其表面积与体积的计算方法，用平面截图的方法等，熟练掌握长方体的基本性质是解题关键．21．（2023秋·全国·七年级专题练习）如图所示，把一个底面半径是5cm，高是8cm的圆柱放在水平桌面上．(1)若用一个平面沿水平方向去截这个圆柱，所得的截面是(2)若用一个平面沿竖直方向去截这个圆柱，所得的截面是(3)若用一个平面去截这个圆柱，使截得的截面是长方形且长方形的截面面积最大，请写出截法，并求出此时截面面积．A．B．C．D．【答案】B【分析】根据从左边看得到的图形有两行，上面一行最左边有一个正方形，下面一行有三个正方形，可得答案．【详解】解：该几何体从左面看到的平面图形是“”，故选：B．【点睛】本题考查了从不同的方向看物体，解题的关键是掌握从左边看到的图形有两行，上面一行最左边有一个正方形，下面一行有三个正方形．23．（2023秋·全国·七年级专题练习）如图，下列几何体中能同时堵住图中三个空洞的几何体是（）A．B．C．D．【答案】B【分析】根据立体图形的概念和定义结合图即可解．【详解】解：能同时堵住图中三个空洞的几何体是选项B的几何体．故选：B．【点睛】本题考查了立体图形的认识．立体图形：有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一个平面内，这就是立体图形．24．（2023秋·辽宁沈阳·七年级统考期末）如图所示的两个几何体分别由7个和6个相同的小立方块搭成，A．从正面看到的形状图不同C．仅从左面看到的形状图不同【答案】D【分析】分别画出这两个几何体从正面看，从左面看，从上面看的形状图，再进行比较即可．【详解】分别画出这两个几何体从正面看，从左面看，从上面看的形状图，∴从正面、上面、左面看到的形状图都相同，故选：D．【点睛】本题考查了从不同方向看简单组合体，掌握从正面看，从左面看，从上面看的形状图的画法是解题的关键．25．（2022秋·山东淄博·六年级统考期中）如图所示，这个几何体是由若干个完全相同的小正方体搭成【答案】1740体的形状图．【答案】见解析【分析】根据正面看，左面看的图形，根据各行、各列对应的立方体的个数进行画图．【详解】解：如图所示：【点睛】本题考查了作图-三视图的画法，把握“长对正，宽相等，高平齐”是画图的关键．29．（2023秋·全国·七年级专题练习）如图，是由若干个完全相同的小正方体组成的一个几何体，请画出这个几何体从正面看、从左面看和从上面看到的平面图形．（用阴影表示）【答案】见详解【分析】想象出从三个方向看的图形，画出即可；【详解】解：三个平面图形如图所示：从正面看：从左面看：从上面看：【点睛】本题考查了几何体的从不同方向看的图形，空间想象能力是本题的解题关键．30．（2022秋·辽宁辽阳·七年级校考阶段练习）李明和同学们一起研究“从三个不同方向看几何体的形状”．(1)图1是由几个大小相同的小立方体搭成的几何体，请画出从正面看到的这个几何体的形状图；(2)图2是由几个大小相同的小立方体搭成的几何体，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示该位置的小立方体的个数．请画出从左面看到的这个几何体的形状图．【答案】(1)见解析(2)见解析【分析】（1）从正面看，画出图形即可；（2）根据左看行，找最大：图形有两列，第一列有2个小正方形，第二列有3个小正方形，画出图形即可．【详解】（1）解：从正面看到的这个几何体的形状图，如图所示：（2）解：从左面看到的这个几何体的形状图，如图所示：【点睛】本题考查从不同方向看几何体的形状．熟练掌握从不同方法看由小立方体堆砌而成的几何体，以及根据从上面看的图形，确定从左面看和从正面看的图形的方法，是解题的关键．。

【突破易错·冲刺满分】2021-2022学年七年级数学上册期末突破易错挑战满分（北师大版）易错01丰富的图形世界【易错1例题】展开与折叠1．（2021·福建七年级期末）如图是一个正方体的平面展开图，则这个正方体“美”字所在面的对面标的字是（）A．让B．生C．活D．更【答案】B【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：这是一个正方体的平面展开图，共有六个面，其中面“让”与面“活”相对，面“更”与面“好”相对，“生”与面“美”相对．故选：B．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．【易错2例题】从三个方向看物体的形状2．（2021·重庆巴蜀中学九年级三模）如图是由几个相同的小正方体堆砌成的几何体，从上面．．看到该几何体的形状图是（）A．B．C．D．【答案】D【分析】根据从上面看得到的图形可得答案．【详解】解：从上面看第一层三个小正方形，第一层两个小正方形，故D正确；故选：D．【点睛】本题考查了从不同方向观察立体图形的方法，解题的关键是熟练掌握三视图的定义．【专题训练】一、选择题1．（2021·江苏九年级一模）下列三棱柱展开图错误的是（）A．B．C．D．【答案】D【分析】根据三棱柱的两底展开是三角形，侧面展开是三个四边形，可得答案．【详解】解：A、B、C中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图.D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有.故D不能围成三棱柱.故选：D.【点睛】本题考查了几何体的展开图，注意两底面是对面，展开是两个全等的三角形，侧面展开是三个矩形．2．（2021·重庆西南大学附中七年级期末）如图，是正方体的表面展开图，若“末”在底面，则其相对面上的字是（）A．期B．油C．加D．考【答案】B【分析】利用正方体及其表面展开图的特点解题．【详解】解：这是一个正方体的平面展开图，共有六个面，相对的面之间一定相隔一个正方形，若“末”在底面，则其相对面上的字是油．故选：B．【点睛】本题考查了正方体相对两个面上的文字，注意正方体是空间图形，从相对面入手，分析及解答问题．3．（2021·辽宁中考真题）某几何体的展开图如图所示，该几何体是（）A．B．C．D．【答案】D【分析】根据几何体的展开图可直接进行排除选项．【详解】解：由该几何体的展开图可知该几何体是圆锥；【点睛】本题主要考查几何体的展开图，熟练掌握简单几何体的展开图是解题的关键．4．（2021·河南七年级期末）在本学期第一章的数学学习中，我们曾经辨认过从正面、左面、上面三个不同的方向观察同一物体时看到的形状图．如图是马老师带领的数学兴趣小组同学搭建的一个几何体，这个几何体由6个大小相同的正方体组成，你认为从左面看到的几何体的形状应该为（）A．B．C．D．【答案】B【分析】从左面看到的平面图形是该组合体的左视图，根据看到的平面图形画出左视图即可得到答案．【详解】解：从左面看该组合体，可以看到两列，左起第一列可以看到两个正方形，第二列看到一个正方形，所以该组合体的左视图是：故选：.B本题考查的是三视图的含义，掌握左视图的含义是解题的关键．二、填空题5．（考点21三视图（考点）-备战2021年中考数学考点微专题）图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①、②、③、④某一位置，所组成的图形不能围成正方体的位置是___．【答案】①【分析】由平面图形的折叠及正方体的表面展开图的特点解题．【详解】解：将图1的正方形放在图2中的①的位置出现图1正方形与图2最右边正方形重叠，所以不能围成正方体．将图1的正方形放在图2中的②④的位置是展开图的1-3-2形，可以围成正方体，将图1的正方形放在图2中的③的位置是展开图的3-3形日字连，可以围成正方体，故答案为：①．【点睛】本题考查了展开图折叠成几何体，解题时勿忘记正方体展开图的各种情形．注意：只要有“田”“凹”“一”的展开图都不是正方体的表面展开图．6．（2020·辽宁太和区第二初中七年级月考）观察下面的几何体，从上面看到的是_______，从左面看到的是_________．从正面看到的是________．【答案】③ ② ①根据几何体不同方向看到的图形判断即可．【详解】由图可知从上面看到的是,故填③;从左面看到的是,故填②;从正面看到的是,故填①．【点睛】本题考查不同方向看几何体,主要在于通过空间想象力判断．7．（2021·内蒙古七年级期末）如图是某几何体从不同方向看到的图形．若从正面看的高为10cm，从上面看的圆的直径为4cm，求这个几何体的侧面积（结果保留π）为_____．【答案】40πcm2【分析】根据题意即可判断几何体为圆柱体，再根据告诉的几何体的尺寸即可求出圆锥的侧面积．【详解】解：观察三视图可得这个几何体是圆柱；∵从正面看的高为10cm，从上面看的圆的直径为4cm，∵该圆柱的底面直径为4cm，高为10cm，∵该几何体的侧面积为2πrh＝2π×2×10＝40π（cm2）．故这个几何体的侧面积（结果保留π）为40πcm2．故答案为：40πcm2．【点睛】本题考查了从不同侧面看几何体及求圆柱的侧面积，确定几何体的形状是解题关键．8．（2019·全国九年级单元测试）如图是由一些棱长为1的小立方块所搭几何体的三种视图．若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个长方体，至少还需要______个小立方块．【答案】26【分析】先由主视图、左视图、俯视图求出原来的几何体共有10个正方体，再根据搭成的大长方体的共有4×3×3＝36个小正方体，即可得出答案．【详解】解：由主视图可知，搭成的几何体有三层，且有4列；由左视图可知，搭成的几何体共有3行；第一层有7个正方体，第二层有2个正方体，第三层有1个正方体，共有10个正方体，∵搭在这个几何体的基础上添加相同大小的小正方体，以搭成一个大长方体，∵搭成的大长方体的共有4×3×3＝36个小正方体，∵至少还需要36−10＝26个小正方体．故答案为：26．【点睛】本题考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查，关键是求出搭成的大长方体共有多少个小正方体．三、解答题9．（2021·天津实验中学七年级期末）如图，上面的图形分别是下面哪个立体图形展开的形状，请你把有对应关系的平面图形与立体图形连接起来．【答案】见解析．【分析】根据常见的各种立体几何图形的展开图的特征即可得答案．【详解】∵三个长方形和两个三角形如图摆放是三棱柱的展开图，一个扇形和一个圆是圆锥如图摆放的展开图，六个长方形如图摆放是长方体的展开图，一个长方形和两个圆如图摆放是圆柱的展开图，∵连接如图：【点睛】本题考查常见立体几何图形的展开图，熟记各立体几何图形的展开图是解题关键．10．（2021·山东七年级期末）如图，由几个相同的小正方体搭成一个几何体，请画出这个几何体的三种视图．（在所提供的方格内涂上相应的阴影即可）【答案】见解析．【分析】几何体从正面看有4列，每列小正方形数目分别为1，3，1，1；从左面看有2列，每列小正方形数目分别为3，2；从上面看有4列，每行小正方形数目分别为1，2，1，2，据此作图即可．【详解】解：如图所示：【点睛】本题考查从不同方向看几何体．几何体的三种视图就是从三个方向看到的平面图形．11．（2021·南昌市二十八中教育集团青云学校七年级期末）如图，是一个正方体纸盒的两个表面展开图，请把-4，3，9，6，-1，2分别填入六个面中，使得折成正方体后，相对面上的两数之和与-5互为相反数．【答案】答案见解析【分析】根据相反数的性质，得与-5互为相反数的数为：5，再根据有理数加法运算和正方体展开图的性质分析，即可得到答案．【详解】与-5互为相反数的数为：5根据题意计算，展开图如下：．【点睛】本题考查了有理数和立方体展开图的知识；解题的关键是熟练掌握相反数、有理数加法运算、正方体展开图的性质，从而完成求解．12．（2021·全国七年级单元测试）下面是一个多面体的表面展开图每个面上都标注了字母，（所有字母都写在这一多面体的外表面）请根据要求回答问题：（1）如果面F在前面，从左边看是B，那么哪一面会在上面？（2）如果从右面看是面C面，面D在后边那么哪一面会在上面？（3）如果面A在多面体的底部，从右边看是B，那么哪一面会在前面．【答案】（1）C面会在上面；（2）A面会在上面；（3）C面会在前面【分析】利用长方体及其表面展开图的特点解题．这是一个长方体的平面展开图，共有六个面，其中面“A”与面“F”相对，面“B”与面“D”相对，面“C”与面“E”相对．【详解】解：（1）由图可知，如果F面在前面，B面在左面，那么“E”面下面，∵面“C”与面“E”相对，∵C面会在上面；（2）由图可知，如果C面在右面，D面在后面，那么“F”面在下面，∵面“A”与面“F”相对，∵A面在上面．（3）由图可知，如果面A在多面体的底部，从右边看是B，那么“E”面在后面，∵面“C”与面“E”相对，∵ C面会在前面【点睛】考查了几何体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．13．（2020·渠县三江中学七年级月考）如图是从三个方向看几何体得到的形状图．（1）说出这个几何体的名称；（2）画出它的一种表面展开图；（3）若从正面看到的形状图的宽为4cm，长为7cm，从左面看到的形状图的宽为3cm，从上面看到的形状图中斜边长为5cm，求这个几何体所有棱长的和，以及它的表面积和体积．【答案】（1）三棱柱；（2）见解析；（3）这个几何体所有棱长的和为45cm，它的表面积为96cm2，体积为42cm3【分析】（1）根据三棱柱的三视图特征即可解答；（2）根据三棱柱的三视图特征，画出其表面展开图即可，答案不唯一；（3）根据题意可知，侧棱为7，共3条，两个底面三角形的三边长为3、4、5，继而相加即可求得棱长的和，结合表面积等于三个侧面与两个底面的面积和求得表面积，根据体积＝底面积×侧棱即可求解．【详解】解：（1）这个几何体是三棱柱，（2）表面展开图如图所示（答案不唯一）：（3）棱长和为：7×3+（3+4+5）×2=45cm×3×4×2+（3+4+5）×7=96cm2表面积为：S=S（底）+S（侧）=12×3×4×7=42cm3体积为：V=S（底）×h=12故：这个几何体所有棱长的和为45cm，它的表面积为96cm2，体积为42cm3．【点睛】本题主要考查三棱柱有关知识，解题的关键是熟练掌握三棱柱的特征，三视图，表面积及体积计算公式．。

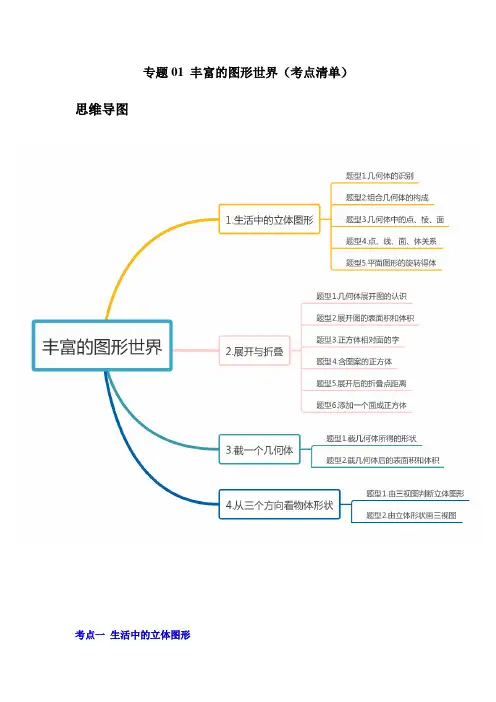
专题01 丰富的图形世界（考点清单）思维导图考点一生活中的立体图形【考试题型1】几何体的识别【典例1】下面的四个几何图形中，表示平面图形的是（）A．B．C．D．【专训1-1】下列图形中，与其他三个不同类的是（）A．B．C．D．【专训1-2】（2023秋·七年级课时练习）下面两个立体图形的名称是：．【考试题型2】组合几何体的构成【典例2】（2023秋·七年级课时练习）图中的几何体由个面围成．【专训2-1】（2023秋·七年级课前预习）如图是由棱长为1厘米的小正方体木块搭成的几何体．至少还需要个这样的小正方体才能搭成一个正方体．【专训2-2】（2022秋·全国·七年级专题练习）把4个棱长为2分米的正方体拼成长方体，拼成的长方体的表面积可能是平方分米，也可能是平方分米．【考试题型3】几何体中的点、棱、面【典例3】（2023秋·七年级课时练习）七棱柱有个顶点，有条棱，有个面．【专训3-1】（2023秋·全国·七年级专题练习）几何知识．棱．【专训3-2】（2023秋·全国·七年级专题练习）如图所示，是我们熟悉的三棱柱、五棱柱和六棱柱．(2)设n棱柱（n为正整数，且3n≥）的顶点数为a、棱数为b、面数为c，根据表中数据猜+-=________．想a c b【考试题型4】点、线、面、体关系【典例4】（2022秋·六年级单元测试）直升机的螺旋桨转起来形成一个圆形的面，这说明了．【专训4-1】（2023秋·陕西宝鸡·七年级统考期末）数学老师可以用粉笔在黑板上画出图形，这个现象说明．【专训4-2】（2022秋·辽宁沈阳·七年级统考阶段练习）把一个直角三角形绕它的一条直角边旋转360°，得到一个圆锥体．用数学知识解释为．【考试题型5】平面图形的旋转得体【典例5】（2023春·福建福州·七年级统考开学考试）下列各选项中的图形绕虚线旋转一周后，得到的几何体是圆柱的是（）A．B．C．D．a f中【专训5-1】（2023秋·七年级课时练习）如图所示的图形绕轴旋转一周，便能形成~的某个几何体，请你用线把它们连起来．【专训5-2】（2023春·河北石家庄·七年级行唐一中校考开学考试）小军和小红分别以直角梯形的上底和下底为轴，将梯形旋转一周，得到的两个立体图形．(1)你同意______的说法．(2)甲、乙两个立体图形的体积比是多少？考点二展开与折叠【考试题型1】几何体展开图的认识【典例1】（2023·四川达州·统考中考真题）下列图形中，是长方体表面展开图的是（）A．B．C．D．【专训1-1】（2021秋·广东珠海·七年级统考开学考试）下列图形，（）是正方体的展开图．A．B．C．D．【专训1-2】（2023秋·全国·七年级专题练习）如图所示的平面图形分别都是由哪种几何体展开形成的？(1)______________；(2)______________；(3)______________；(4)______________；(5)______________；(6)______________；【考试题型2】展开图的表面积和体积【典例2】（2023秋·黑龙江大庆·七年级校联考开学考试）一个长方体长20厘米，宽15厘米，高10厘米，把它切成两个完全相同的长方体，两个长方体表面积之和最大是( )平方厘米．【专训2-1】（2023秋·全国·七年级专题练习）一块长方形铁皮（如图），长25厘米，宽15厘米，从四个角分别剪去边长2厘米的小正方形，然后把四周折起来，做成没有盖子的铁盒，请你帮忙计算一下：做这样一个盒子至少需要多少铁皮？铁盒的容积是多少？【专训2-2】（2023秋·全国·七年级专题练习）如图，是一个几何体的表面展开图：(1)请说出该几何体的名称；(2)求该几何体的表面积；(3)求该几何体的体积．【考试题型3】正方体相对面的字【解题方法】【典例3】（2023春·山东泰安·六年级校考开学考试）如图，是一个小正方体的展开图，把展开图折叠成小正方体后，有“迎”字一面的相对面上的字是（）A．百B．党C．年D．喜【专训3-1】（2023秋·江苏宿迁·七年级沭阳县怀文中学校考开学考试）如图一个正方形的平面展开图如图所示，将它折成正方体后，“保”字对面的字是（）．A．碳B．低C．绿D．色【专训3-2】（2022春·上海·九年级统考自主招生）如图是正方体的一种展开图，那么在原正方体中，与“上”字所在面相对的面上的汉字是．【考试题型4】含图案的正方体【解题方法】【典例4】2023·全国·七年级专题练习）如图所示，正方体的展开图为()A．B．C．D．【专训4-1】（2023秋·河南商丘·七年级统考期末）如图，下面的图是正方体的展开图的是（）A．B．C．D．【专训4-2】（2023·全国·七年级假期作业）如图所示的正方体，它的展开图可能是下列四个选项中的（）A．B．C．D．【考试题型5】展开后的折叠点距离【解题方法】【典例5】（2023秋·全国·七年级专题练习）图①是边长为1的六个正方形组成的图形，经过折叠能围成如图①的正方体，一只蜗牛从A点沿该正方体的棱．．．．．．爬行到B点的最短距离为（）A．0B．1C．2D．3【专训5-1】（2023秋·全国·七年级专题练习）如图①是边长为2的六个小正方形组成的，在围成的正方体上图形，它可以围成如图②所示的正方体，则图①中小正方形的顶点A B的距离是．【专训5-2】（2021秋·七年级单元测试）如图所示，图（1）为一个长方体，AD=AB=10,AE=6,图2为图1的表面展开图(字在外表面上)，请根据要求回答问题：（1）面“句”的对面是面______；（2）如果面“居”是右面,面“宜”在后面,哪一面会在上面？（3）图（1）中，M、N为所在棱的中点，试在图（2）中画出点M、N的位置；并求出图（2）中三角形ABM的面积.【考试题型6】添加一个面成正方体【典例6】（2022秋·全国·七年级专题练习）如图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的情况（图中阴影部分），其中正确的是（）A．B．C．D．【专训6-1】（2023秋·七年级课时练习）如图所示的A、B、C、D四个位置的某个正方形与实线部分的五个正方形组成的图形，不能拼成正方体的是位置．【专训6-2】（2022秋·北京石景山·七年级期末）小景准备制作一个无盖的正方体盒子．请你在图中再画出一个正方形，并将添加的正方形用阴影表示，使得新图形经过折叠后能够成为一个无盖的正方体盒子．说明：至少画出2种符合上述条件的情况．考点三截一个几何体【考试题型1】截几何体所得的形状【典例1】（2023秋·七年级课时练习）小明用橡皮做了一个长方体，若用一个小刀去切该长方体，截面的形状不可能是（）A．三角形B．长方形C．五边形D．圆【专训1-1】（2023·全国·七年级专题练习）妹妹把一密闭且透明的圆柱形水杯中装一半的水，随意转动水杯，水面的形状不可能是（）A．三角形B．长方形C．圆形D．椭圆【专训1-2】（2023秋·陕西咸阳·七年级统考期末）用一个平面分别去截长方体，圆锥，三棱柱，圆柱，能得到截面是三角形的几何体有个．【考试题型2】截几何体后的表面积和体积【典例2】（2023秋·全国·七年级专题练习）若将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），则其表面积增加了（）A．25π平方厘米B．50π平方厘米C．75π平方厘米D．100π平方厘米【专训2-1】（2023秋·全国·七年级专题练习）如图所示，圆柱体的高为8，底面半径为2，则截面面积最大为 ．【专训2-2】（2022秋·江苏·七年级专题练习）已知图1为一个正方体，其棱长为12，图2为图1的表面展开图（数字和字母写在外面），请根据要求回答问题：(1)若正方体相对面上的数互为相反数，则xy =_________；(2)用一个平面去截这个正方体，下列关于截面（截出的面）的形状的结论：①可能是锐角三角形；①可能是直角三角形；①可能是钝角三角形；①可能是平行四边形．其中所有正确结论的序号是( )；A ．①B ．①①C ．①①①D ．①①①①(3)图1中，,M N 为所在棱的中点，请在图2标出点M 的位置，并求出ABM ∆的面积． 考点四 从三个方向看物体的形状【考试题型1】由三视图判断立体图形【典例1】（2022秋·江西九江·七年级统考期中）一个由小立方块搭成的几何体，从正面、左面、上面看到的形状如图所示，这个几何体是由（ ）个小立方块搭成的．A ．4B ．5C ．6D ．7【专训1-1】（2023秋·湖南岳阳·七年级校考开学考试）搭出同时符合下面要求的物体，需要（ ）个小正方体．A．10B．7C．8D．9【专训1-2】（2022秋·广东茂名·七年级校考期中）下图是由几个相同的小立方块所搭成的几何体从上面看到的形状图，请分别画出该几何体从正面、左面看到的形状图．【考试题型2】由立体图形画三视图【典例2】（2023秋·山东济南·六年级统考期末）如图，是由一些棱长都为1cm的小正方体组合成的简单几何体．该几何体从正面看到的平面图形如图所示，请在下面方格纸中分别画出从左面、上面看到的平面图形．【专训2-1】（2023秋·山东枣庄·七年级滕州育才中学校考开学考试）如图是由9个相同的小立方体组成的一个几何体，请利用下方网格画出从正面看、从左面看和从上面看的图形（一个网格为小立方体的一个面）．【专训2-2】（2023秋·全国·七年级专题练习）由8个棱长都为1cm的小正方体搭成的几何体如左图．(1)请利用图2中的网格画出这个几何体从正面看、从左面看和从上面看到的形状图．（一个网格为小立方体的一个面）(2)图1中8个小正方体搭成的几何体的表面积（包括与地面接触的部分）是cm2．(3)若要用大小相同的小立方块搭一个几何体，使得它从上面和左面看到的形状图与你在图2。

第一章丰富的图形世界1生活中的立体图形第1课时生活中的立体图形预习要点：1．写出下列几何体名称。

2．在下图中标出六棱柱的顶点、侧棱、侧面和底面3．在棱柱中，相邻两个面的交线叫做，相邻两个侧面的交线叫做，棱柱的所有长都相等，棱柱的上、下底面的形状相同。

侧面的形状都是。

4．长方体、正方体都是棱柱，棱往可以分为和，的侧面是长方形。

5．（2019•丽水）下列图形中，属于立体图形的是（）A．B．C．D．6．下列说法正确的是（）①教科书是长方形；②教科书是长方体，也是棱柱；③教科书的表面是长方形．A．①②B．①③C．②③D．①②③7．埃及金字塔类似于几何体（）A．圆锥B．圆柱C．棱锥D．棱柱8．在下列立体图形中，只要两个面就能围成的是（）A．长方体B．圆柱体C．圆锥体D．球9．六棱柱有面．10．在正方体、长方体、球、圆柱、圆锥、三棱柱这些几何体中，不属于柱体的有，属于四棱柱的有．11．若一直棱柱有10个顶点，那么它共有条棱．同步小题12道一．选择题1．下列几何图形是立体图形的是（）A．扇形B．长方形C．正方体D．圆2．下面的几何体中，属于棱柱的有（）A．1个B．2个C．3个D．4个3．下列物体的形状类似于球的是（）A．乒乓球B．羽毛球C．茶杯D．白织灯泡4．下列几何图形中，属于圆锥的是（）A．B．C．D．5．三棱柱的顶点个数是（）A．3 B．4 C．5 D．66．下列说法不正确的是（）A．长方体与正方体都有六个面B．圆锥的底面是圆C．棱柱的上下底面是完全相同的图形D．五棱柱有五个面，五条棱二．填空题7．下列图形中，是柱体的有．（填序号）8．如果一个六棱柱的一条侧棱长为5cm，那么所有侧棱之和为．9．一个棱柱的棱数恰是其面数的2倍，则这个棱柱的顶点个数是．10．若一个直棱柱共有12个顶点，所有侧棱长的和等于60，则每条侧棱的长为．三．解答题11．将下列几何体与它的名称连接起来．12．如图，一个正五棱柱的底面边长为2cm，高为4cm．（1）这个棱柱共有多少个面？计算它的侧面积；（2）这个棱柱共有多少个顶点？有多少条棱？（3）试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数．第2课时图形变换预习要点：1．图形是由点、线、面构成的。

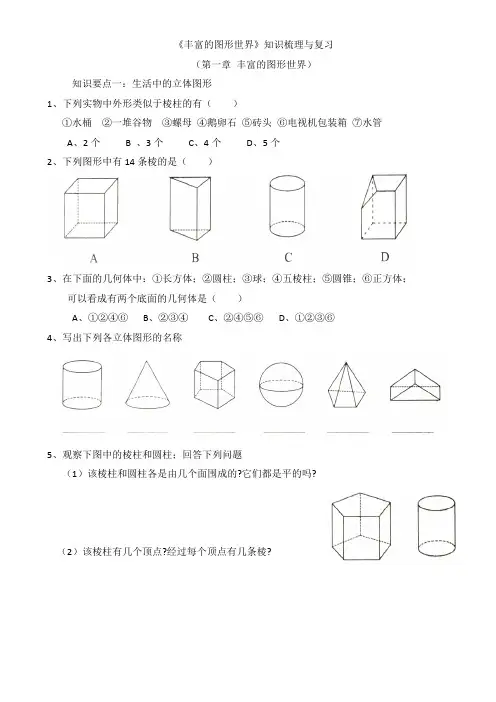
《丰富的图形世界》知识梳理与复习（第一章丰富的图形世界）知识要点一：生活中的立体图形1、下列实物中外形类似于棱柱的有（）①水桶②一堆谷物③螺母④鹅卵石⑤砖头⑥电视机包装箱⑦水管A、2个 B 、3个C、4个D、5个2、下列图形中有14条棱的是（）3、在下面的几何体中：①长方体；②圆柱；③球；④五棱柱；⑤圆锥；⑥正方体；可以看成有两个底面的几何体是（）A、①②④⑥B、②③④C、②④⑤⑥D、①②③⑥4、写出下列各立体图形的名称5、观察下图中的棱柱和圆柱；回答下列问题（1）该棱柱和圆柱各是由几个面围成的?它们都是平的吗?（2）该棱柱有几个顶点?经过每个顶点有几条棱?6、将长和宽分别为3cm 和2cm 的长方形分别绕长、宽所在的直线旋转一周得到两个几何体，哪个几何体的体积大?（2V r h π=）知识要点二：展开与折叠7、下列说法中错误的是（ ）A 、棱柱的侧面数与侧棱数相同B 、棱柱的顶点数一定是偶数C 、棱柱的面数一定是奇数D 、棱柱的棱数一定是3的倍数8、下图中不可能围成正方体的有（ ）A 、1个B 、2个C 、3个D 、4个9、小红制作了一个对面图案均相同的正方体礼品盒（如图所示），则这个正方体礼品盒的平面展开图应该为（ ）10、一个正方体的展开图如图所示，如果这个正方体相对的面上标注的数值相等，那么x = ，y = 。

11、如图所示，是两个立体图形的展开图，请写出这两个立体图形的名称（1）：（2）：12、如图是一个多面体的展开图，每个面内都标注了字母，请根据要求回答问题：（1）如果面A在多面体的底部，哪一个面会在上面?（2）如果面F在前面，从左面看是面B，那么哪一面会在上面?（3）如果面D在后面，从右面看是面C，那么哪一面会在上面?知识要点三：截一个几何体13、用平面去截一个圆柱，截面的形状不可能是（）A、三角形B、正方形C、长方形D、圆14、有下列几何体：①正方体；②长方体；③圆柱；④圆锥；⑤棱柱；⑥球这些几何体中截面可能是圆的有（）A、2种B、3种C、4种D、5种15、正方体被一个平面所截，所得边数最多的多边形是A、四边形B、五边形C、六边形D、七边形16、写出下图中截面的形状17、如图所示，有一个正方体，棱长为5cm，如果在它的左上方截去一个长、宽、高分别为5cm，3cm，2cm的长方体，求它的表面积减少了百分之几？知识要点四：从三个方向看物体的形状18、下面四个几何体中，从左面看是四边形的几何体共有（）A、1个B、2个C、3个D、4个19、如图所示是从三个方向看到的物体的形状图，对应的直观图是下列选项中的（）20、如图所示，是一个几何体从三个方向看到的形状图，根据图中标注的数据可求得这个几何体的体积为（）A、24πB、32πC、36πD、48π21、如图所示，把立方体的六个面分别涂上六种不同的颜色（红、黄、紫、蓝，白、绿），现将上述大小相同颜色分布完全一样的四个立方体拼成一个水平放置的长方体，那么立方体绿色面的对面颜色是（）A、红色B、紫色C、白色D、蓝色21、如图是由几个立方块所搭成的几何体从上面看到的形状，则该几何体从正面看有列，从左面看有行。

1. 下面几何体中，全是由曲面围成的是（）A. 圆柱B. 圆锥C. 球D. 正方体2. 下列说法错误的是（）A. 长方体、正方体都是棱柱B. 三棱柱的侧面是三角形C. 直六棱柱有六个侧面、侧面为长方形D. 球体的三种视图均为同样大小的图形3. 如图，在一个棱长为6cm的正方体上摆放另一个正方体，使得上面正方体的四个顶点恰好均落在下面正方体的四条棱上，则上面正方体体积的可能值有（）A. 1个B. 2个C. 3个D. 无数个4. 如图，左排的平面图形绕轴旋转一周，可以得到右排的立体图形，那么与甲、乙、丙、丁各平面图形顺序对应的立体图形的编号应为（）A. ③④①②B. ①②③④C. ③②④①D. ④③②①5. 在下列几何体中，由三个面围成的有____，由四个面围成的有____．（填序号）6. 如图，在直六棱柱中，棱AB与棱CD的位置关系为____，大小关系是_____．7. 用五个面围成的几何体可能是_______．8. 若一个直四棱柱的底面是边长为1cm的正方形，侧棱长为2cm，则这个直棱柱的所有棱长的和是___cm．9. 由一个平面图形绕着它的一条边所在的直线旋转一周形成的几何体，叫做旋转体．如果有一个几何体，围成它的各个面都是多边形，那么这个几何体叫做________．在你所熟悉的立体图形中，旋转体有________，多面体有________．（要求各举两个例子）10. 一只小蚂蚁从如图所示的正方体的顶点A沿着棱爬向有蜜糖的点B，它只能经过三条棱，请你数一数，小蚂蚁有__种爬行路线．11. 探究：将一个正方体表面全部涂上颜色，试回答：（1）把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体，我们把仅有i个面涂色的小正方体的个数记为x i，那么x3=____，x2=____，x1=____，x0=____；（2）如果把正方体的棱四等分，同样沿等分线把正方体切开，得到64个小正方体，与（1）同样的记法，则x3=____，x2=____，x l=____，x0=____；（3）如果把正方体的棱n等分（n≥3），然后沿等分线把正方体切开，得到n3个小正方体，与（1）同样的记法，则x3=____，x2=____，x1=____，x0=____．答案1. 【答案】C【解析】圆柱的上下底面是平的面，圆锥的底面平的面，正方体的六个面都是平的面.故选C.2. 【答案】B【解析】三棱柱的侧面都是平行四边形.故选B.3. 【答案】D【解析】上面正方体体积取决于上面立方体的棱长，由于棱长有无数种情况，则上面正方体体积的值也有无数种.故选D.4. 【答案】A【解析】甲旋转后得到③，乙旋转后得到④，丙旋转后得到①，丁旋转后得到②．故与甲乙丙丁各平面图形顺序对应的立体图形的编号应为③④①②．故选A．5. 【答案】（2）（6）【解析】正方体和长方体都是由六个面围成；圆柱由三个面围成；球是由一个面围成；圆锥由两个面围成；三棱锥由4个面围成.故由三个面围成的有（2），由四个面围成的有（6）．6. 【答案】平行相等【解析】由图形易知，棱AB与棱CD的位置关系为平行，大小关系是相等．【方法点睛】本题目是一道考查直棱柱的相关问题，比如棱的位置关系，数量关系.在棱柱中，侧棱都是平行且相等的.上下两底面相对的棱平行且相等.难度不大.7.【答案】四棱锥或三棱柱【解析】四棱锥是由4个侧面和1个底面围成，三棱柱是由3个侧面和2个底面围成.故用五个面围成的几何体可能是四棱锥或三棱柱.8. 【答案】16【解析】上下底面的棱长之和为，侧棱长之和为，则这个直棱柱的所有棱长的和是16cm．9.【答案】多面体圆柱、圆锥六棱柱、三棱锥【解析】由一个平面图形绕着它的一条边所在的直线旋转一周形成的几何体，叫做旋转体．如果有一个几何体，围成它的各个面都是多边形，那么这个几何体叫做多面体；．在你所熟悉的立体图形中，旋转体有圆柱、圆锥；多面体有六棱柱、三棱锥（所有的棱柱，棱锥）. 10. 【答案】6【解析】第一步：由A出发的棱有3条。