《编译原理》第四章试题

S→aA A→Ab|b (1) 构造识别该文法项目活前缀的DFA (2) 判定该文法是否为LR(0)文法。若是的话构造相应的LR分析 表。 (3) 对句子abbb#进行分析。、 6.已知文法G[S] S→ r D D→ D , i D→ i (1) 构造识别该文法项目活前缀的DFA (2) 判定该文法为哪类LR文法？构造相应. 对文法G[S] S→a|∧|(T) T→T,S|S (1) 给出(a,(a,a))和(((a,a),∧,(a)),a)的最左推导。 (2) 对文法G，进行改写，然后对每个非终结符写出不带回 溯的递归子程序。 (3) 经改写后的文法是否是LL(1)的?给出它的预测分析表。 (4) 给出输入串(a,a)#的分析过程，并说明该串是否为G的 句子。 2. 已知文法G[S]： S→MH|a H→LSo|ε K→dML|ε L→eHf M→K|bLM (1)求出各个非终结符的First集Follow集。 (2)判断G是否是LL(1)文法，如果是，构造LL(1)分析表。 3.已知文法G[Z] Z→aAAa A→bF’b F’→F F→cF|c (1) 求出各个非终结符的FIRSTVT 集和LASTVT集。 (2) 判断该文法是否为算符优先文法。（请以a,b,c,’,#的顺 序构造相应的算符优先矩阵。） 4. 设有文法G[S]： S→V V→T|ViT T→F|T+F F→)V*|( (1) 求出各个非终结符的FIRSTVT 集和LASTVT集。 (2) 判断该文法是否为算符优先文法。（请以i,+,*,(,),#的顺 序构造相应的算符优先矩阵） （3）给出（+（i（#的分析过程。 5. 已知文法G[s]

procedure T; begin if sym=ˊ(ˊor sym=ˊaˊ or sym=ˊbˊ or sym=ˊ∧ˊ then begin F; T end else error end;
（4）构造它的递归下降分析程序。
procedure T ; begin
if sym= ˊ(ˊ or sym= ˊaˊ or sym= ˊbˊ or sym= ˊ∧ˊ then T else if sym= ˊ*ˊ then error end;
（3）该文法不含左递归，而且每一个 非终结符的各个产生式的候选首符集两 两不相交。
FIRST(A)= {a}
FOLLOW(A)={d, #}
FIRST (A) = { ε, a} FOLLOW(A)={d, #}
FIRST(B) = {d} FOLLOW(B )={e}
FIRST(B) = {ε ,b} 法G ’
(S): S → a∣∧∣(T) T → ST ’ T’ → ,ST’ | ε
其中：过程advance把输入串指示器IP调至指向下一个输入 符号；sym是指IP当前所指的那个输入符号；error为出错诊 断处理程序。
（2）经改写后的文法是否是LL(1)的？给出它的预测分析表。
else error end else error end;
4.2 试消除下面文法G[A] 中的左递归，并提取公共左因子， 判断改写后的文法是否为LL(1)文法?
A→aABe∣a
B→Bb∣d
解: （1）首先消除左递归
A→aABe∣a B →dB B →bB | ε （2）提取公共左因子 A → aA A → ABe | ε B → dB B →bB | ε
证明：对于具有形如A|的产生式有： A → ABe | ε B →bB | ε

S-> S’ S’->(S)SS’| First( (S)SS’) = { （ } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S （ S->S’ ） S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后，发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如：( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’，所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ，所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ，所以Follow(S)加入到Follow(S’)中。 所以，Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ，当A后面的S’推导出非空时，把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ，当A后面的S’推导出空时，把Follow(S’)={$,+,*}加入到Follow(A)中。 所以，Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ，因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*，因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。

编译原理2014—2015学年第二学期第四单元测试试卷（闭卷考试）时间：45分钟满分：100分姓名班级出题人刘兵班级 2一、选择题（5*2分）（每题1分，共10分）1．编译过程中语法分析器的任务就是__________。

(1) 分析单词是怎样构成的（2）分析单词串是如何构成语句和说明的（3）分析语句和说明是如何构成程序的（4)分析程序的结构A （2）（3） B（2）（3）（4） C （1）（2）（3） D（1）（2）（3）（4）2．给定文法G[S]及其非终结符A，FIRST(A)定义为：从A 出发能推导出的终结符号的集合（S 是文法的起始符号，为非终结符）。

对于文法G[S]：S→[L] | aL→L, S| S其中，G[S]包含的四个终结符号分别为：a , [ ]则FIRST(S)的成员包括。

A. aB. a、[C. a、[和]D. a、[、]和，3．若一个文法是递归的，则它产生的句子个数是( )A．无穷个 B．不确定 C．有限个 D.根据具体情况而定4．语法分析器则可以发现源程序中的__D___。

A．语义错误 B．语法和语义错误 C．错误并校正 D．语法错误5．若文法 G 定义的语言是无限集，则文法必然是( ) 。

A．递归的 B．前后文无关的C．二义性的 D．无二义性的二、简答题（2*10分）（每题10分，共20分）1．自上而下分析的前提？2.若有文法A→(A)A|ε，说明该文法是LL(1)的文法。

三、分析题（4题共70分）1．设有文法G[E]:E→Aa|BbA→cA|eBB→bd试按照递归子程序法为该文法构造语法分析程序。

2．设有文法G[S]：S→ABA→bB|AaB→Sb|a试消除该文法的左递归。

3.计算练习4.2.2的文法的FIRST和FOLLOW集合(1)S->S(S)S|ε(2)S->(L)|a, L->L, S|S4. 正规式(ab)*a与正规式a(ba)*是否等价？请说明理由。

第五章习题5-1设有文法G[S] ：S→A/A→aA∣ AS∣/(1)找出部分符号序偶间的简单优先关系。

(2)验证 G[S] 不是简单优先文法。

5-2对于算符文法G[S] ：S→E E→ E-T∣ T T→T*F∣F F→ -P∣P P→ (E)∣i(1)找出部分终结符号序偶间的算符优先关系。

(2)验证 G[S] 不是算符优先文法。

5-3 设有文法G′[E] ：E→E E→E+T |T1T →T T→T*F|F F→(E)|i11111其相应的简单优先矩阵如题图5-3所示，试给出对符号串（i+i ）进行简单优先分析的过程。

题图 5-3 文法 G′ [E] 的简单优先矩阵5-4设有文法G[E]：E→E+T|TT→T*F|FF→(E)|i其相应的算符优先矩阵如题图5-4 所示。

试给出对符号串（i+i ）进行算符优先分析的过程。

(i*+)#(○○○○○＜＜＜＜＝i○○○○＞＞＞＞○○○○○○*＜＜＞＞＞＞○○○○○○+＜＜＜＞＞＞○○○○)＞＞＞＞○○○○#＜＜＜＜题图 5-4文法 G[E] 的算符优先矩阵5-5对于下列的文法，试分别构造识别其全部可归前缀的DFA和 LR(0) 分析表，并判断哪些是LR(0) 文法。

(1)S →aSb∣ aSc∣ ab(2)S →aSSb∣ aSSS∣c(3)S →AA→Ab∣ a5-6下列文法是否是SLR(1)文法？若是，构造相应的SLR(1) 分析表，若不是，则阐明其理由。

(1) S →Sab∣ bR R→S∣a(2) S →aSAB∣ BA A→aA∣ B B→ b(3) S →aA∣bB A→cAd∣εB→cBdd∣ε5-7对如下的文法分别构造LR(0) 及 SLR(1) 分析表，并比较两者的异同。

S→cAd∣ b A→ASc∣a5-8对于文法G[S]:S→A A→BA∣εB→ aB∣ b(1)构造 LR(1) 分析表；(2)给出用LR(1)分析表对输入符号串abab 的分析过程。

编译原理龙书第四章答案编译原理是计算机科学中的一门基础课程，是用于教授计算机程序的设计、构建和优化的学科，常常被用于编写编译器和解释器。

在编译原理课程中，龙书（Compilers: Principles, Techniques, and Tools）是一本经典的教材，其中第四章主要讲述了词法分析器的设计和实现。

以下是第四章的答案，按照列表划分：1. 什么是词法分析器？词法分析器（Lexical Analyzer）是编译器的组成部分之一，它用于将程序中的字符序列转换为一系列单词或词法单元（Lexeme），以便后续的语法分析和语义分析使用。

2. 词法分析器的工作流程是什么？词法分析器的工作流程如下：（1）读入字符序列。

（2）将字符序列划分为一个个词法单元，或者检查字符序列是否合法。

（3）生成一个词法单元序列，并将其传递给语法分析器。

3. 词法单元的定义是什么？词法单元是编程语言中的一个基本单元，它是对代码中的一个单一概念进行编码的基本方式。

例如，在C语言中，词法单元包括关键字（如int，if，while等）、标识符（Identifier，即自定义变量名）、运算符和特殊符号等。

4. 有哪些方法可以实现词法分析器？可以使用正则表达式、自动机等方法实现词法分析器。

其中，正则表达式可以表示字符串的集合，因此可以将其用于识别单词类别；自动机是根据输入字符序列转换状态的一种计算模型，因此可以用于实现有限自动机（Deterministic Finite Automaton）和非确定有限自动机（Nondeterministic Finite Automaton）等。

5. DFA和NFA分别是什么？DFA和NFA都是有限自动机的一种，但在转换动作上有所不同。

DFA 是确定的有限自动机，即在状态转换时只有唯一的一个选择；而NFA 是非确定的有限自动机，即在状态转换时可以有多个选择。

6. DFA和NFA之间有什么关系？DFA和NFA虽然在转换动作上不同，但它们可以互相转化。

3)
First( A' ) Follow ( A' ) {d , } {), b}
4.4(2)
见课后答案 规则见课本P66
问题？
Select( E gAf ) Select( E c) First( gAf ) Frist(c) {g} {c}
4.2
对下面的文法G： E→TE’ E’→+TE’|ε T→FT’ T’→*FT’|ε F→(E)|id (1)计算这个文法的每个非终结符的FIRST和FOLLOW。 (2)证明这个文法是LL(1)的。 (3)构造它的预测分析表。 (4)构造它的递归下降分析程序。
第四章习题
4.1 4.2 4.3 4.4
4.1
1、考虑下面文法G[A]： A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c （1）FIRST集和FOLLOW集 （2）是否是LL（1）文法。
4.1(1) First集
First( A) First( BCc) First( gDB) First( B) \ { } First(C ) {g} {b} First( D) \ { } {a} First(ca) {g} {b} {d } {a} {c} {g} {a, b, c, d , g}
E’→ε T→FT ’ T’→ε F→idFra bibliotekE’→ε
T’→ε
4.2(4)
规则见课本P66 见课后答案 E→TE’ T→FT’ F→(E)|id E’→+TE’|ε T’→*FT’|ε
4.3
文法G[S]: S→A A→B|AiB B→C|B+C C→)A*|( 1)改写为LL(1)文法 2)求改写后的文法的每个非终结符的First集和Follow集 3)构造相应的预测分析表

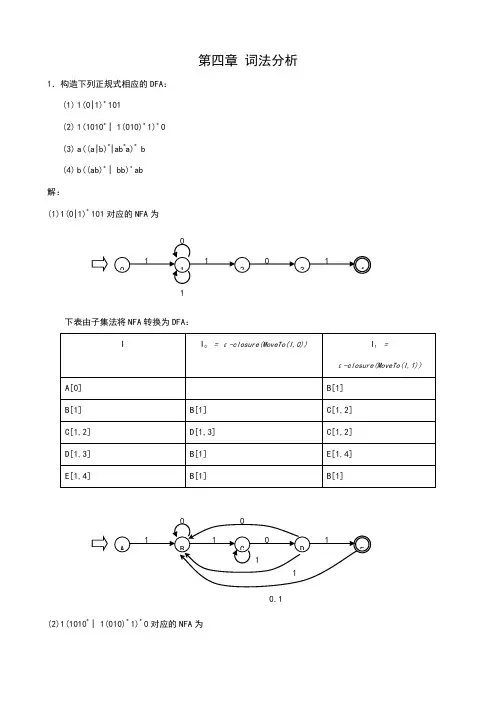
第四章 词法分析1．构造下列正规式相应的DFA ：(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解：(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA ：(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA：(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2．已知NFA=（{x,y,z},{0,1},M,{x},{z}）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。

解：根据题意有NFA 图如下下表由子集法将NFA 转换为DFA ：0，1下面将该DFA最小化：(1)首先将它的状态集分成两个子集：P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F，C等价。

由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D，E不等价（见下步），从而B与C，F可以区分。

有P21={C,F},P22={B}。

(3)区分P1:由于A，E输入0到终态，而D输入0不到终态，所以D与A，E可以区分，有P11={A,E},P12={D}。

(4)由于F(A,0)=B,F(E,0)=F,而B，F不等价，所以A，E可以区分。

(5)综上所述，DFA可以区分为P={{A}，{B}，{D}，{E}，{C，F}}。

所以最小化的DFA如下：3.将图确定化：1101111解：下表由子集法将NFA 转换为DFA ：4.把图的(a)和(b)分别确定化和最小化：(a) (b)解： (a):下表由子集法将NFA 转换为DFA ：0，1a可得图（a1），由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价，可将DFA 最小化，即：删除B ，将原来引向B 的引线引向与其等价的状态A ，有图(a2)。

1.1考虑下面文法G1S->a|^|(T)T->T,S|S消去G1的左递归。

然后对每个非终结符，写出不带回溯的递归子程序。

答:：(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的首符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的首符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的文法为LL(1)文法。

不带回溯的递归子程序如下：S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有文法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写文法为等价文法G[S’]，消除文法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合；(3)构造G[S’]的预测分析表，以此说明它是否为LL(1)文法。

(4)如果是LL(1)文法，请给出句子a*a+a*a*a的预测分析过程该文法为LL(1)文法，因为它的预测分析表中无冲突项。

========= A卷学号以1，4 ，7结尾的同学做下题=========文法G： D → TL T→ int | floatL → id R R → , id R | ε(1)构造上面文法的LL(1)分析表。

(2) 证明文法是否为LL(1)文法。

(3) 给出分析器接受int id, id的自上而下分析步骤。

========= B卷学号以2，5，8结尾的同学做下题==========文法G：S→a | ∧|(T) T→T,S | S(1) 计算S和T 的firstVT和lastVT。

(2) 获取该文法的优先关系表。

(3) 给出(a, ( a , a)) 的算符优先分析步骤。

========= C卷学号以0，3，6，9 结尾的同学做下题======文法G： E → aTd T → Eb|a(1)画出该文法识别活前缀的DFA，证明G不是LR(0)文法而是SLR(1)文法。

(2)获取SLR分析表。

(3)给出aaadbd的规范归约分析步骤。

文法G： D → TL T→ int | floatL → id R R → , id R | ε(1)构造上面文法的LL(1)分析表。

(2) 证明文法是否为LL(1)文法。

(3) 给出分析器接受int id, id的自上而下分析步骤。

First(D)=First(T)={int,float}First(L)={id}First(R)={, ε} follow(R)={#}Select(D → TL)= First(TL)= {int,float}Select(T→ int)={int}Select(T→ float)={float}Select (L → id R)= First(id R)={id}Select(R → , id R)= First(,id R)={,}Select(R →ε)= (First(ε)-{ε})∪follow(R)= {#}因为Select(T→ int)∩Select(T→ float)=∅Select(R → , id R)∩Select(R →ε)=∅所以该文法为LL（1）文法。

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

第四章1.设字母表∑={0，1}，给出∑上的正规式r=(0|10)*，请完成以下任务：1) 构造NFA M`，使得L（M`）=L（r）；2) 将NFA M`确定化、最小化，得到最简DFA M，使得L（M）=L（M`）。

解：1）M`③2) 1令T0=-closure(1)={1,2,4}, T0未被标记，加入到子集族C中2 标记T0，Move(T0,0)={2},-closure(Move(T0,0))={2,4}=T1,T1未被标记，加入到子集族C中Move(T0,1)={3},-closure(Move(T0,1))={3}=T2,T2未被标记，加入到子集族C中3 标记T1，Move(T1,0)={2},-closure(Move(T1,0))={2,4}=T1,Move(T1,1)={3},-closure(Move(T1,1))={3}=T2,4标记T2，Move(T2,0)={2},-closure(Move(T2,0))={2,4}=T1,Move(T2,1)=,-closure(Move(T2,1))=,化简后为：2.已知正规文法G1(S为开始符号)G1: S→0A|1BA→1S|1B→0S|01）该文法产生语言是什么？请用正规式表示；2）构造最简的确定有限自动机DFA，并画出状态转换图。

解：1)S=0A|1BS=(0(1S|1))|(1(0S|0))S=(01(S|))|(10(S|))S=(01|10)(S|)S=(01|10)(01|10)*2)NFA为：②③④ɛɛ①ɛ 1 0 ɛ⑤⑥⑦ɛNFA转化为DFA：1令T0=-closure(1)={1,2,5}, T0未被标记，加入到子集族C中2 标记T0，Move(T0,0)={3},-closure(Move(T0,0))={3}=T1,T1未被标记，加入到子集族C中Move(T0,1)={6},-closure(Move(T0,1))={6}=T2,T2未被标记，加入到子集族C中3 标记T1，Move(T1,0)=,-closure(Move(T1,0))=,Move(T1,1)={4},-closure(Move(T1,1))={4,8,9,10,13,17}=T3,T3未被标记，加入到子集族C中4标记T2，Move(T2,0)={7},-closure(Move(T2,0))={ 4,8,9,10,13,17}=T4,T4未被标记，加入到子集族C中Move(T2,1)=,-closure(Move(T2,1))=,5标记T3，Move(T3,0)={11},-closure(Move(T3,0))={11}=T5,T5未被标记，加入到子集族C中Move(T3,1)={14},-closure(Move(T3,1))={14}=T6,T6未被标记，加入到子集族C中6标记T4，Move(T4,0)={11},-closure(Move(T4,0))={11}=T5,Move(T4,1)={14},-closure(Move(T4,1))={14}=T6,7标记T5，Move(T5,0)=,-closure(Move(T5,0))=,Move(T5,1)={12},-closure(Move(T5,1))={9,10,12,13,16,17}=T7,T7未被标记，加入到子集族C中8标记T6，Move(T6,0)={15},-closure(Move(T6,0))={ 9,10,13,15,16,17}=T8,T8未被标记，加入到子集族C中Move(T6,1)=,-closure(Move(T6,1))=,9标记T7，Move(T7,0)={11},-closure(Move(T7,0))={11}=T5,Move(T7,1)={14},-closure(Move(T7,1))={14}=T6,10标记T8，Move(T8,0)={11},-closure(Move(T8,0))={11}=T5,Move(T8,1)={14},-closure(Move(T8,1))={14}=T6,则DFA为：②①1化简后为：②①13.将R=a(a|d)*转换成相应的正规文法。

第一章练习题（绪论）一、选择题1．编译程序是一种常用的软件。

A) 应用B) 系统C) 实时系统D) 分布式系统2．编译程序生成的目标代码程序是可执行程序。

A) 一定B) 不一定3．编译程序的大多数时间是花在上。

A) 词法分析B) 语法分析C) 出错处理D) 表格管理4．将编译程序分成若干“遍”将。

A)提高编译程序的执行效率；B)使编译程序的结构更加清晰，提高目标程序质量；C)充分利用内存空间，提高机器的执行效率。

5．编译程序各个阶段都涉及到的工作有。

A) 词法分析B) 语法分析C) 语义分析D) 表格管理6．词法分析的主要功能是。

A) 识别字符串B) 识别语句C) 识别单词D) 识别标识符7．若某程序设计语言允许标识符先使用后说明，则其编译程序就必须。

A) 多遍扫描B) 一遍扫描8．编译方式与解释方式的根本区别在于。

A) 执行速度的快慢B) 是否生成目标代码C) 是否语义分析9．多遍编译与一遍编译的主要区别在于。

A)多遍编译是编译的五大部分重复多遍执行，而一遍编译是五大部分只执行一遍；B)一遍编译是对源程序分析一遍就立即执行，而多遍编译是对源程序重复多遍分析再执行；C)多遍编译要生成目标代码才执行，而一遍编译不生成目标代码直接分析执行；D)多遍编译是五大部分依次独立完成，一遍编译是五大部分交叉调用执行完成。

10．编译程序分成“前端”和“后端”的好处是A)便于移植B)便于功能的扩充C)便于减少工作量D)以上均正确第二章练习题（文法与语言）一、选择题1．文法 G 产生的 (1) 的全体是该文法描述的语言。

A.句型B. 终结符集C. 非终结符集D. 句子2．若文法 G 定义的语言是无限集，则文法必然是 (2) A递归的 B 上下文无关的 C 二义性的 D 无二义性的3． Chomsky 定义的四种形式语言文法中， 0 型文法又称为(A)文法；1 型文法又称为(C)文法；2 型语言可由(G) 识别。

A 短语结构文法B 上下文无关文法C 上下文有关文法D 正规文法E 图灵机F 有限自动机G 下推自动机4．一个文法所描述的语言是(A)；描述一个语言的文法是(B)。

蒋⽴源编译原理第三版第四章习题与答案第4章习题14-1 消除下列⽂法的左递归性。

(1) S→SA|A A→SB|B|(S)|( ) B→[S]|[ ](2) S→AS|b A→SA|a(3) S→(T)|a|ε T→S|T,S4-2 对于如下⽂法，求各候选式的FIRST集和各⾮终结符号的FOLLOW集。

S→aAB|bA|ε A→aAb|ε B→bB|ε4-3 验证下列⽂法是否为LL(1)⽂法。

(1) S→AB|CDa A→ab|c B→dE|εC→eC|ε D→fD|f E→dE|ε(2) S→aABbCD|ε A→ASd|ε B→SAc|eC|εC→Sf|Cg|ε D→aBD|ε4-4 对于如下的⽂法G[S]：S→Sb|Ab|bA→Aa|a(1) 构造⼀个与G等价的LL(1)⽂法G′[S]；(2) 对于G′[S]，构造相应的LL(1)分析表；(3) 利⽤LL(1)分析法判断符号串aabb是否是⽂法G[S]的合法句⼦。

4-5 设已给⽂法S→SaB|bB A→S|a B→Ac(1) 构造⼀个与G等价的LL(1)⽂法G′[S]；(2) 对于G′[S]，构造相应的LL(1)分析表；(3) 利⽤LL(1)分析法判断符号串bacabc是否是⽂法G[S]的合法句⼦。

第4章习题答案4-1 解：(1) ⽂法G[S]中的S，A都是间接左递归的⾮终结符号。

将A产⽣式的右部代⼊产⽣式S→A中，得到与原⽂法等价的⽂法G′[S]：S→SA|SB|B|(S)|( )A→SB|B|(S)|( )B→[S]|[ ]⽂法G′[S]中的S是直接左递归的⾮终结符号，则消除S产⽣式的直接递归性后，我们便得到了与原⽂法等价且⽆任何左递归性的⽂法G"[S]：S→BS′|(S)S′|( )S′A→SB|B|(S)|( )B→[S]|[ ](2) ⽂法G[S]中的S，A都是间接左递归的⾮终结符号。

将A产⽣式代⼊产⽣式S→AS中，得到与原⽂法等价的⽂法G′[S]：S→SAS|aS|bA→SA|a⽂法G′[S]中的S是直接左递归的⾮终结符号，则消除S产⽣式的直接递归性后，我们便得到了与原⽂法等价且⽆任何左递归性的⽂法G"[S]：S→aSS′|bS′S′→ASS′|εA→SA|a(3) ⽂法G[S]中的T是直接左递归的⾮终结符号。

“编译技术”第四章作业4-1 已知文法G[C]：C→iEtS|iEtSeSE→ a|bS→ a+b|a*b(1)提取左公共因子；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

(3)递归下降分析程序void match(token t){if(lookahead=='t')lookahead = nexttoken;else error;}void C(){if(lookahead=='i'){match('i');E();if(lookahead=='t'){match('t');S();Cprime();}else error;}else error;}void Cprime(){if(lookahead=='e'){match('e');S();}}void E(){if(lookahead=='a')match('a');else if(lookahead=='b')match('b');else error;}void S(){if(lookahead=='a'){match('a');Sprime();}}void Sprime(){if (lookahead=='+'){match('+');if(lookahed=='b'){match('b');}else error();}else if(lookahead=='*'){match('*');if(lookahead=='b'){match('b');}else error();}}4-2 已知文法G[Z]：Z→Az|bA→ Za|a(1)删除左递归；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

第四章 习题答案1．（1）对应NFA 如图：对其进行确定化操作：T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = Ф计算ε-closure(move({S},1)) = {A}，标记为T 1 计算ε-closure(move({A},0)) = {A}=T 1计算ε-closure(move({A},1)) = {A,B}，标记为T 2计算ε-closure(move({A,B},0)) = {A,C}，标记为T 3计算ε-closure(move({A,B},1)) = {A,B}=T 2 计算ε-closure(move({A,C},0)) = {A}=T 1计算ε-closure(move({A,C},1)) = {A,B,Z}，标记为T 4 计算ε-closure(move({A,B,Z},0)) = {A,C}= T 3 计算ε-closure(move({A,B,Z},1)) = {A,B}=T 2得到的DFA 存在五种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]其中：[T 0]为初态，[T 4]为终态，对应的转换矩阵如右上表格所示，令S,A,B,C,D 分别表示这五种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：（3）对应NFA 如图：εT 0 = ε-closure({S}) = {S}计算ε-closure(move({S},a)) = {A,B,D}，标记为T 1 计算ε-closure(move({S},b)) = Ф计算ε-closure(move({A,B,D},a)) = {A,B,C,D}，标记为 计算ε-closure(move({A,B,D},b)) = {A,B,D,Z}，标记为T 3 计算ε-closure(move({A,B,C,D},a)) = {A,B,C,D}= T 2计算ε-closure(move({A,B,C,D},b)) = {A,B,C,D,Z}，标记为T 4 计算ε-closure(move({A,B,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,D,Z},b)) = {A,B,D,Z}= T 3 计算ε-closure(move({A,B,C,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,C,D,Z},b)) = {A,B,C,D,Z}= T 4 得到的DFA 存在五种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]其中：[T 0]为初态，[T 3],[T 4]为终态，对应的转换矩阵如左下表格所示，令S,A,B,C,D 分别2．根据题意，可以得其NFA 状态转换图如下图所示：T 0 = ε-closure({x}) = {x} 计算ε-closure(move({x},0)) = {z}，标记为T 1 计算ε-closure(move({x},1)) = {x}=T 0 计算ε-closure(move({z},0)) = {x, z}，标记为T 2 计算ε-closure(move({z},1)) = {y}，标记为T 3 计算ε-closure(move({x, z},0)) = {x, z}= T 2 计算ε-closure(move({x, z},1)) = {x, y}，标记为T 4 计算ε-closure(move({y},0)) = {x, y}= T 4 计算ε-closure(move({y},1)) = Ф计算ε-closure(move({x, y},0)) = {x, y, z}，标记为T 5 计算ε-closure(move({x, y},1)) = {x}= T 0计算ε-closure(move({x, y, z},0)) = {x, y, z}= T 5 计算ε-closure(move({x, y, z},1)) = {x, y}= T 4得到的DFA 存在六种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]，[T 5]其中：[T 0]为初态，[T 1],[T 2],[T 5]为终态，对应的转换矩阵如右上表格所示，令A,B,C,D,E,F 分别表示这六种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：3．状态转换图如图所示：对其进行确定化操作：T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = {V ,Q}，标记为T 1 计算ε-closure(move({S},1)) = {Q,U}，标记为T 2 计算ε-closure(move({V ,Q},0)) = {V,Z}，标记为T 3 计算ε-closure(move({V ,Q},1)) = {Q,U}= T 2计算ε-closure(move({Q,U},0)) = {V}，标记为T 4计算ε-closure(move({Q,U},1)) = {Q,U,Z}，标记为T 5 计算ε-closure(move({V,Z},0)) = {Z}= T 3 计算ε-closure(move({V,Z},1)) = {Z}= T 3计算ε-closure(move({V},0)) = {Z}=T 4 计算ε-closure(move({V},1)) = Ф计算ε-closure(move({Q,U,Z},0)) = {V ,Z}，标记为T 6 计算ε-closure(move({Q,U,Z},1)) = {Q,U,Z}= T 5 计算ε-closure(move({Z},0)) = {Z}= T 6 计算ε-closure(move({Z},1)) = {Z}= T 3得到的DFA 存在七种状态：[T 0]，[T 1]，[T 2]，[T 3]，[T 4]，[T 5]，[T 5] 其中：[T 0]为初态，[T 3],[T 5],[T 6]为终态，对应的转换矩阵如右上表格所示，令A,B,C,D,E,F,G 分别表示这七种状态，则其对应的DFA 状态转换图及状态转换矩阵分别为：4．（a ）对其进行确定化操作： T 0 = ε-closure({0}) = {0}计算ε-closure(move({0},a)) = {0,1}，标记为T 1计算ε-closure(move({0},b)) = {1}，标记为T 2计算ε-closure(move({0,1},a)) = {0,1}=T 1计算ε-closure(move({0,1},b)) = {1}= T 2计算ε-closure(move({1},a)) = {0}=T 0 计算ε-closure(move({1},b)) =Ф得到的DFA 存在三种状态：[T 0]，[T1]，[T 2]其中，[T 0]为初态，[T 0],[T 1]为终态，对应的转换矩阵如右上表格所示，令A,B,C 分别表示这三种状态，则其对应的DFA 状态转换图及状态转换矩阵如下：对其进行最小化操作：该DFA 无多余状态，进行初始划分，得终态组{A,B}，非终态组{C}对终态组{A,B}进行审查，输入符号a 后，状态A,B 均转换成状态B ；输入符号b 后，状态A,B 均转换成状态C ，由此可知，状态A,B 等价，不能再分。

第四章词法分析1．构造下列正规式相应的DFA：(1)1(0|1) * 101(2)1(1010* | 1(010) * 1)* 0(3)a((a|b) * |ab * a)* b(4)b((ab)* | bb) * ab解：(1)1(0|1) * 101 对应的 NFA为1101012341下表由子集法将NFA 转换为 DFA：I I0=ε-closure(MoveTo(I,0))I1=ε-closure(MoveTo(I,1))A[0]B[1]B[1]B[1]C[1,2]C[1,2]D[1,3]C[1,2]D[1,3]B[1]E[1,4]E[1,4]B[1]B[1]001101A B C D E110,1(2)1(1010 * | 1(010) * 1)* 0 对应的 NFA 为εε1101010 01234561εε101978ε下表由子集法将NFA 转换为 DFA：I I=ε-closure(MoveTo(I,0))I1= ε-closure(MoveTo(I,1))A[0]B[1,6]B[1,6]C[10]D[2,5,7]C[10]D[2,5,7]E[3,8]B[1,6]E[3,8]F[1,4,6,9] F[1,4,6,9]G[1,2,5,6,9,10]D[2,5,7]G[1,2,5,6,9,10]H[1,3,6,9,10]I[1,2,5,6,7] H[1,3,6,9,10]J[1,6,9,10]K[2,4,5,7] I[1,2,5,6,7]L[3,8,10]I[1,2,5,6,7] J[1,6,9,10]J[1,6,9,10]D[2,5,7]K[2,4,5,7]M[2,3,5,8]B[1,6]L[3,8,10]F[1,4,6,9] M[2,3,5,8]N[3]F[1,4,6,9] N[3]O[4]O[4]P[2,5]P[2,5]N[3]B[1,6]1L111111010B I KA D E F M00110 00C11G H J101NP O(3)a((a|b) * |ab * a)* b(略 )(4)b((ab) * | bb) * ab(略 )2．已知 NFA=（ {x,y,z},{0,1},M,{x},{z} ）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ ,M(z,1)={y},构造相应的 DFA。