21-7氢原子问题的量子力学处理

用基础量子力学解释氢原子四川师范大学本科毕业论文用基本量子力学解释氢原子——量子力学与氢原子的相遇相知相交学生姓名黄兰院系名称物理与电子工程学院专业名称物理学班级2008级 2 班学号2008070219指导教师侯邦品四川师范大学教务处二○一二年五月用基本量子力学解释氢原子本科生：黄兰指导老师：侯邦品内容摘要：主要从以下几个方面来运用基本量子力学解释氢原子。

1、氢原子的能级和能量本征函数。

首先介绍在量子力学中的波函数，再利用薛定谔方程来导出氢原子的能量本征函数，最后再分析它的物理含义。

2、氢原子的四个量子数的物理意义。

解释它们其与氢原子的能级的关系。

3、径向波函数和角度波函数。

主要是得出径向波函数和角度波函数同时给出它的物理意义。

4、简并性破除与量子激光。

氢原子的内部结构中电子在原子中受到的磁场的作用所产生的正常塞曼效应和反常塞曼效应，以及可能引起的电子跃迁。

5、氢原子的Stark效应。

氢原子在外场的作用下表现的Stark 效应，这部分将作简单的介绍。

关键词：量子量子力学氢原子 stark效应Schr?dinger方程Using quantum mechanics to explain the physical phenomena in hydrogen atomsAbstract:we shall use quantum mechanics to explain the physicalphenomena in the hydrogen atoms as follows: 1, the energy eigenfunctions for hydrogen are obtained after introducing the wave function in quantum mechanics . 2 , physical significance of the four quantum numbers in the hydrogen atoms.Here we shall focus on the hydrogen atom electron spin and its physical meaning of the four quantum numbers . 3, the radial wave function and the angle wave function . Coming to the radial wave function and the angle of the wave function at the same time we will get its physical significance. 4, the degeneracy is broken by magnetic fields. The normal and the anomalous Zeeman effect induced by magnetic field are introduced. 5, Finally, the the Stark effect in the hydrogen atomis briefly introduced.Key Words:Quantum Quantum mechanics Hydrogen atoms stark effect Schr?dinger equation目录引言 (4)1氢原子的能级和能量本征函数 (6)1.1波函数与Shr?dinger方程 (6)1.1.1波函数 (6)1.1.2波函数的归一化 (6)1.2 Shr?dinger方程 (7)1.2.1不含时Shr?dinger方程 (7)1.2.2 Shr?dinger方程的一般形式 (7)1.3中心力场中角动量守恒与径向方程 (7)1.4氢原子的能级与本征函数波函数 (8)2氢原子四个量子数 (11)2.1氢原子的定态薛定谔方程 (11)2.2 三个量子数 (12)2.3电子的自旋与第四量子数 (15)2.3.1斯特恩--盖拉赫实验(1921年) (15)3径向波函数和角度波函数 (17)3.1径向几率分布 (17)3.2电子的几率密度随角度的变化 (19)4氢原子四个量子数 ................................................................ 错误！未定义书签。

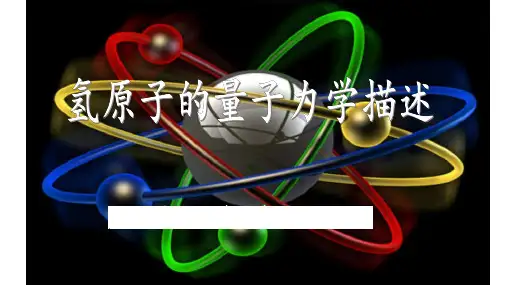
氢原子是最简单的原子，核外只有一个电子绕核运动，质子和电子之间存在库仑相互作用。

由于质子的质量是电子质量的大约2000倍，一般可以建立一个坐标系，把坐标原点取在质子上。

电子受原子核的库仑场作用，势能函数为：r e r U 024)(πε-=0222=-+∇)r ()]r (U E [m )r ( ψψ0)()4(2)(0222=++∇r r e E m r ψπεψ由于氢原子具有球对称性，可用球坐标系表示定态薛定谔方程：)(sin sin 1)(1222θψθθθψ∂∂∂∂+∂∂∂∂r r r r r 0)4(2sin 10222222=++∂∂+ψπεϕψθr e E m r 其解一般为的函数：ϕθ,,r ),,(ϕθψψr =定态薛定谔方程设波函数为)()()(),,(ϕθϕθψΦΘ=r R r 代入球坐标系的薛定谔方程，在求解波函数时，考虑到波函数应满足的单值、有限、连续以及归一化的标准化条件，可得到氢原子的量子化特征。

我们主要对一些重要的结论进行讨论。

()),3,2,1(12422204 =⋅-=n nme E n πε1. 能量量子化 主量子数求解薛定谔方程，得到氢原子的能量为n — 主量子数注意：⑴ 氢原子能量是一系列离散值 —— 反映能量量子化能级间隔随主量子的增大而减小，↓∆↑⇒E n ⑵ 最低能级对应1=n eV E 6.131-=基态能量eV nE n 26.13-=采用分离变量法，可得到三个常微分方程，分别求解出相应的函数和量子数。

n =1 基态能量eV 6.131-=E eV 6.131=-∞E E n = 2,3,… 对应的能量 称为激发态能量eV 40.32-=E eV 51.13-=E 当 n 很大时，能级间隔消失而变为连续值对应于电子被电离∞=n 当 ，0=∞E ∞=n 11E 232E 3E 454E ∞E ∞2. 角动量（动量矩）量子化 角量子数电子绕核运动 求解薛定谔方程结论：电子绕核运动的转动角动量是量子化的)1(+=l l L 角动量— l 副量子数（角量子数）氢原子的电子电离能为：eV n E n 26.13-=氢原子能量公式)1(,,2,1,0-=n l氢原子中电子的量子态n =1n =2n =3n =4n =5n =6l = 0l = 1l = 5l = 4l = 3l = 2( s )( p )( h )( g )( f )( d )1s 5f 5d 5p 5s 6s 6p 6d 6f 6g 6h 4s 3s 3p 4f 3d 4p 4d 5g 2p 2s )1(+=l l L 共有 n 个可能的取值用,,,,f d p s 分别代表 ,3,2,1,0=l 等各个量子态玻尔的旧量子论与量子力学描述电子运动的角动量量子化的区别注意：若 l = 0有 L = 0电子的概率分布具有球对称性角动量为零)1(,,2,1,0-=n l 角动量（动量矩）量子化3. 空间量子化（空间取向量子化） 磁量子数角动量空间取向是量子化的—— 电子运动具有角动量量子化波函数 电子运动相当于一圆电流圆电流具有一定磁矩 磁矩在外磁场作用下具有一定取向 电子运动的磁矩方向与其角动量方向相反 电子转动角动量方向有确定的空间取向ZB , LθμzL o 经典理论：空间取向连续θ可取π→0的任意值量子力学：空间取向不连续z L ，只取一系列的离散值 m L z =ll l l l m -----=),1(,,2,1, 角动量空间取向是量子化的 m —— 磁量子数对应一个角量子数 l ，角动量有 2 l +1个取值例 11=l 1,0±=m Z B , o -例 22=l 2,1,0±±=m Z B , o- 22- 6)1(=+=l l L 2=L 21=+=)l (l L 例 3 设氢原子处于2 p 态，试分析氢原子的能量、角动量大小及角动量的空间取向？解：2 p 态表示： n = 2, l = 1得eV 40.32-=E 角动量的大小为2)1(=+=l l L 当 l =1 时，磁量子数 m l 的可能值：-1, 0, +1，则角动量方向与外磁场的夹角的可能值为：⎪⎩⎪⎨⎧=+=4324)1(arccos πππθl l m l eV 6.132nE n -=4. 电子云 （Electron cloud ）—— 电子的概率分布电子在绕核运动中无固定点、无轨道概念，只能用各处出现的概率来描述电子运动的状态，故用电子云的密度形象地显示概率分布。

量子力学中的氢原子结构分析量子力学是一个让人感到神秘的学科，从微观角度研究原子和分子的行为和相互作用。

氢原子是量子力学中最简单的单电子原子，其结构对于研究其他多电子原子和分子具有重要意义。

本文将介绍氢原子结构的量子力学理论和现实应用。

1. 氢原子的波函数和能级量子力学中，波函数是用来描述粒子在空间中波动和存在的函数。

氢原子中电子的波函数可以用Schrodinger方程求解，得到如下公式：$\psi_{n,l,m}(r,\theta,\phi)=R_{n,l}(r)Y_{l,m}(\theta,\phi)$其中，$n$为主量子数，$l$为角量子数，$m$为磁量子数，$r$为离子半径，$Y_{l,m}$为球谐函数。

氢原子的能级也可以根据波函数求得。

具体方法是计算氢原子中电子的哈密顿算符在波函数上的期望值，得到：$E_n=-\frac{me^4}{8\epsilon_0^2h^2n^2}$其中，$m$为电子质量，$e$为电子电荷，$\epsilon_0$为真空介电常数，$h$为普朗克常数。

这个公式称为Bohr模型，与实验值相比，精度较高，但仍会有误差。

2. 氢原子的谱线和光谱学氢原子发射光线的频率可以通过与氢原子内部能级的差值相对应。

这些频率形成了光谱线，分为巴尔末系（Balmer series）、洪特姆系（Lyman series）、帕舍尼亚系（Paschen series）等。

巴尔末系中电子从$n\geq3$的能级跃迁到$n=2$的电子能级，所产生的光谱线包括Bα、Bβ等。

这些线可以被用来确定物质的组成和温度等特征。

除了发光谱线，氢原子还可以吸收谱线。

在光谱学中，通过测量吸收谱线的强度和波长，可以确定物质的成分和性质。

而通过对氢原子谱线的研究和分析，可以深入了解物质和电磁辐射之间的相互作用。

3. 氢原子的电离和激发氢原子被电离（即，从基态跃迁到自由电子状态）所需要的能量称为氢原子的电离能。

氢原子的电离能是一个常见的物理量，被用来描述和比较物质的化学性质。

用量子力学计算氢原子作者：王宏来源：《科技资讯》2013年第16期摘要：氢原子是最简单的原子，在量子力学建立过程中有着特殊地位，有必要对其进行详细的求解。

该论文用量子力学理论，通过求解氢原子在库伦势场中的定态薛定谔方程，得到氢原子的能量及能量本征函数。

关键词：量子力学氢原子能量本征函数中图分类号：O413.1 文献标识码：A 文章编号：1672-3791（2013）06（a）-0193-01从17世纪牛顿力学出现以后，直到19世纪，电动力学，热力学和统计力学也陆续被建立，从而形成了一个完整的经典物理学体系。

可是，在解决黑体辐射、光电效应等实验时，经典物理学遇到了空前的挑战，需建立全新的理论来解决面临的困难。

1900年，普朗克假说在黑体辐射上有新的突破，1905年，爱因斯坦用量子化解释了光电效应，1913年，玻尔建立“玻尔理论”。

但玻尔理论具有一定的局限性，十年之后，量子力学体系逐步建立起来，才完全解释了原子问题。

而氢原子是最简单的原子。

因此，有必要用量子力学的方法对其进行严格的求解。

1 理论计算氢原子是最简单的原子，它是由一个电荷为的原子核与一个电荷为的电子构成的。

如果取无穷远为势能的零点，则质子与电子的库仑势能为V（r）=。

则根据定态薛定谔方程可求出氢原子的能量及能量本征函。

在以下的计算中，采用自然单位。

为方便，给出氢原子的自然单位：长度的自然单位：，能量的自然单位：。

氢原子的约化质量为，质子与电子的库仑势能为V（r）=。

考虑到V（r）的球对称性，我们采用球极坐标系。

而因为[]=0，所以角动量是守恒的，在球极坐标系下，薛定谔方程可表示为：[]=E （1）由于的各分量是守恒的，而各分量不对易，则根据简并定理可知能级有简并。

是守恒量，且与的每一个分量都对易，因此体系的守恒量完全集可以方便的选为（），方程（1）的解同时选为的本征态，即： (2)代入式（1），可得出径向波函数满足方程：=0 （3）和满足方程：而为的本征值，待定。

氢原子模型交换积分在氢原子的量子力学模型中，我们假设氢原子的电子处在一个势场中，这个势场由原子核的静电场和电子的自旋磁场构成。

氢原子的量子力学模型描述了电子在这个势场中的运动和其对应的能量。

为了求解这个模型，我们需要用到交换积分。

交换积分是量子力学中非常重要的概念之一，它描述了不同粒子之间由于交换作用而产生的相互作用。

在氢原子中，电子之间由于交换作用而产生的相互作用被称为交换积分。

交换积分的计算是量子力学中一个非常复杂的问题，需要用到复杂的数学工具和物理理论来进行求解。

在氢原子的模型中，交换积分描述了电子在势场中的相互作用。

通过交换积分的计算，我们可以得到氢原子中电子的运动和其对应的能级结构。

在量子力学的框架下，我们可以用波函数的形式来描述氢原子中电子的运动，而交换积分则描述了不同波函数之间的相互作用。

因此，交换积分在氢原子模型中起着非常重要的作用。

为了求解氢原子模型中的交换积分，我们需要用到量子力学中的一些基本概念和方法。

首先，我们需要用到薛定谔方程来描述氢原子中电子的运动。

薛定谔方程是量子力学中描述粒子运动的基本方程，通过求解薛定谔方程，我们可以得到氢原子中电子的波函数。

在得到波函数之后，我们可以用到哈密顿算符来描述电子之间的相互作用。

通过对哈密顿算符的求解，我们可以得到氢原子模型中的交换积分。

在求解氢原子模型中的交换积分时，我们通常采用微扰理论来进行计算。

微扰理论是量子力学中一种非常重要的方法，它可以用来处理复杂系统的近似求解。

通过微扰理论，我们可以将复杂的问题化简为简单的近似问题，从而得到系统的近似解。

在氢原子模型中，我们可以将电子之间的相互作用看成是一个微小的扰动，通过微扰理论的方法，我们可以得到氢原子中电子的波函数和相互作用的交换积分。

在求解氢原子模型中的交换积分时，我们还需要用到一些数学工具和物理理论来进行计算。

特别是对于高阶的交换积分，我们需要用到一些复杂的积分和微分的计算方法来进行求解。

氢原子的量子力学模型概念在量子力学中，氢原子是一种重要的原子，描述它需要将它的物理原理应用到量子力学理论中。

氢原子的量子力学模型允许人们通过描述电子在能量状态下的运动，来推导出它的特性和性质。

本文将着重讨论氢原子模型的概念，用来解释氢原子在空间和动量空间的分布特性。

首先，要讨论氢原子的量子力学模型，就必须先知道原子的构成。

氢原子由一个质子和一个电子组成，它们由核周围的电磁力或强程度来绑定。

由于电子的电荷，它们会在电场的影响下产生动量。

此外，由于粒子的反离子性，它们在原子核周围会形成一个轨道系统。

因此，它们也会影响原子在空间上的分布特性。

其次，之后要讨论氢原子的量子力学模型，必须从氢原子能量状态开始。

根据量子力学的波函数原理，电子的能量状态表示其在空间的活动情况。

根据该原理，可以确定电子的能量状态，以及其对应的波函数。

当电子处于一定的能量状态时，它就会具有一定的动量特性；而当电子能量状态发生变化时，它们的波函数也会改变，从而影响其在空间和动量空间的分布特性。

再次，在探究氢原子模型的概念时，还需要关注能级在空间中的分布特性。

根据量子力学原理，电子所处的能级在空间中有一定的分布模式。

通常，电子会处于介于原子核和原子轨道的位置，即“环”的位置。

由于电子的运动轨迹有一定的循环特性，这个位置可以分解成电子轨道的半径和角度。

每个能级都有一定的半径，它们都按照一定的规律组合在原子核周围，从而构成空间分布模式。

最后，要解释氢原子模型的概念，就需要介绍动量空间的分布特性。

根据量子力学的精确的规律，可以将氢原子的运动状态分解成氢原子的动量k。

根据Schrdinger方程，氢原子的动量在空间中可以分解为两个分量，即有限的点动量和无限的连续动量。

连续动量k的分布特性取决于氢原子的总能量，而点动量k的分布特性则取决于电子在能量状态上的变化。

因此，要深入理解氢原子模型的概念，就要对电子在能量状态上的变化和它们在动量空间中的分布特性做出精确的说明与描述。

氢原子的量子力学研究进展近年来，量子力学在科学研究中扮演着越来越重要的角色。

作为量子力学研究的一个重要对象，氢原子一直是科学家们关注的焦点。

在过去的几十年里，氢原子的量子力学研究取得了许多重要的进展，为我们进一步理解量子世界提供了重要的线索。

1. 氢原子的波动性质在量子力学中，粒子的波动性质是其中一个核心概念。

氢原子作为一个简单的体系，其波动性质得到了深入的研究。

科学家发现，氢原子的电子不仅具有粒子性，还表现出波动性。

这种波动性反映在电子的波函数中，描述了电子在不同位置上的概率分布。

通过数学模型的建立和实验证明，氢原子电子的波函数具有离散的能级，即电子只能处于特定的能量状态下。

这些能量状态由主量子数（n）、角量子数（l）、磁量子数（m）等参数决定。

氢原子的波函数的解析解为球谐函数，它们描述了不同的波动模式和电子空间分布。

2. 氢原子的激发态与光谱氢原子不仅存在于基态，还可以被激发到高能态。

这些激发态可以通过吸收或发射光子的方式与基态之间发生能量的转换。

这种能量转换可通过氢原子的光谱来观察和解释。

科学家们通过对氢原子的光谱进行观察和分析，发现了许多重要的规律和现象。

例如，巴尔末系列和派兹明系列是氢原子在可见光区域的光谱线，其频率与能级之间的差别遵循一定的规律。

通过这些光谱线，科学家可以得到氢原子不同能级之间的能量差，从而进一步研究其内部结构和量子力学性质。

3. 氢原子的量子隧穿效应量子隧穿是量子力学中一个重要的现象，描述了粒子在经典物理上不可能出现的情况。

氢原子的量子隧穿效应在研究中得到了广泛的关注。

科学家们发现，当氢原子的波函数遇到势能垒时，波函数并不完全消失，而是以很小的概率透过势垒，并在另一侧重建波函数。

这种现象被称为量子隧穿，是经典物理学无法解释的。

通过量子隧穿效应的研究，科学家们不仅深入理解了氢原子的波动特性，还在其他领域中发现了类似的现象。

例如，量子隧穿在分子物理和固体物理的研究中也起到了重要的作用。