第六章 优选法及其应用

第一讲优选法一、优选法和单峰函数教学目标：1．通过丰富的生活、生产案例，使学生感受到生活中存在着大量的优选问题；2．了解优选法和单峰函数的概念。

教学重点：单峰函数的概念教学难点：单峰函数的概念的理解教学过程一、什么叫优选法？人们经常会遇到这样的问题：选取"合适"的配方；寻找"合适"的操作和工艺条件；给出产品的"合理"设计参数；把仪器调节器试到"合适"的程度；等等。

所谓"合适"、"合理"，数学上叫最优。

例如如何使产品质量最好、产量最高，或在一定质量要求下如何使成本最低、消耗原材料最少、生产周期最短等等"最优"性问题，都常常引起人们的关心。

怎样才能达到"最优"呢？举个最简单的例子，比如蒸馒头；要想蒸得好吃、不酸不黄，就要使碱适量。

假如我们现在还没有掌握使碱量的规律，而要通过直接实践的方法去摸索这个规律，怎样才能用最少的实验次数就找到最理想的结果呢？换句话说，用什么方法指导我们进行实验才能最快地找到最优方案呢？这个方法就叫作优选法。

优选法的用途很广。

上面以蒸馒头问题为例，是考虑到了它通俗易懂，而且能说明选优的问题处处有、常常见。

有许多例子说明优选法有许多更重要的用处。

例如，某仪器表研究所在制造某种仪表时，为了找到一种能去除金属表面氧化皮的酸洗液，在未掌握优选法时，在两年的时间中做了无数次试验，勉强找到了一个配方，配洗效果仍不理想；酸洗时间半小时，然后还要用刷子刷。

当掌握了优选法后，克服了盲目性，用了不到一天的时间，只做了十四次试验就找到了一种新的酸洗液配方。

按照新配方，只需三分钟，氧化皮就自然剥落，而且材料表面光滑，既不需用刷子刷，又没有腐蚀痕迹。

（1）最佳点：（2）优选问题：（3）优选法：优选法是根据生产和科学研究中的不同问题，利用数学原理，合理安排试验，以最少的试验次数迅速找到最佳点的科学试验方法。

优选法一、 一个真实案例某电子管厂从仓库中清出了积压多年的几百万米某种“废”金属丝。

为了使得这些废金属丝能够重新被利用，科研人员经过研究发现，找出准确的退火温度是使该废金属丝复活的关键。

由经验知道，退火温度的范围为[1400,1600]C C，因此，试验范围为[1400,1600]C C。

如果不考虑其他次要因素，则该金属丝的质量指标()f t 是温度t的函数，其中[1400,1600]t 。

由于目标函数()f t 的具体表达式不知道，因此，该问题的关键在于能否通过次数尽量少的调温试验，求出满足一定精度条件下的最佳退火温度。

（华罗庚先生70年代初期支援大西南三线建设期间的一个案例）分析： 尽管目标函数()f t 的具体表达式不知道，但是根据经验可知：从退火温度的最低点1400C开始，随着t 的增大，质量指标()f t 的函数值随之增大；当达到最佳退火温度0t 时，随着t 的继续增大，一直到最高点1600C，质量指标()f t 的函数值随之减少。

也就是说，()f t 是在试验区间内先增后减的单峰函数，其中只有唯一的一个最优点。

试验方法讨论： 1、 等分法通常的想法是：在试验区间[1400，1600]上均匀取点试验，就可以求得满足一定精度要求的最佳退火温度。

例如，若要求精度达到120，我们只要在 123191410,1420,1430,,1590t t t t ====各点进行试验，通过比较各点的试验结果，就能找到最佳试验点。

例如，若发现91490t =是其中最好的点，就可以断定最佳退火温度必在区间（1480，1500）上。

在生产实际中，就可以把1490C作为最佳退火温度。

问题：每一次试验都需要较高的成本，而上述等分法均匀取点，试验时没有考虑已经获得的质量指标()f t 的信息，往往需要作大量试验才能获得较好的结果。

因此等分法是一种浪费的方法。

需要找到一种更节约的方法。

2、 优选法（0.618法-黄金分割法）（受到蜂巢结构的启发） 具体步骤如下：先在试验区间的0.618处做第一次试验，第一点的温度为：(0.618160014000.61814001520C=-⨯+=-⨯+= 第一次点大小）小（）第二次试验：在第一次点关于中心对称的点，即第二次的温度为1600152014001480C =-+=-+= 第二次点大第一次点小比较上面的两次结果，如果1480C点较好，去掉1520C（称之为“坏点”）以上的温度。

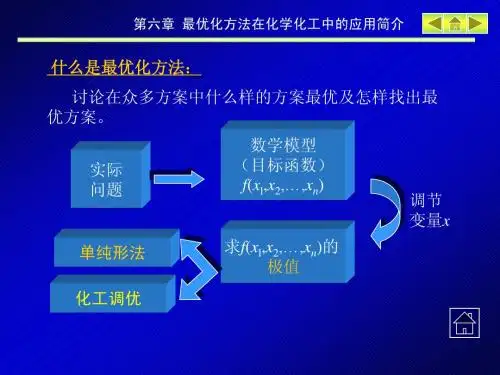
第六章最优化方法在化学化工中的应用简介什么是最优化方法：讨论在众多方案中什么样的方案最优及怎样找出最优方案。

实际问题数学模型（目标函数）f(x l,x2,…,x n)求f(xl,x2,…,x n)的极值调节变量x单纯形法化工调优单纯形规则：由反射、扩张和收缩所组成的一种逻辑运算。

通过这些运算寻找函数f (x )的最佳反响值。

单纯形：n 维空间中由n 十1个点构成的最简单的封闭图形。

基本思想：函数f (x )的导数是函数f (x )性态的反映。

如：斜量的负方向就是该函数在这点领域内最迅速下降的方向。

)()(0x x f 单纯形法的优点：不用求导，甚至没有目标函数表达式时也可使用。

6-1-1 单纯形法——基本概念6-1-2 方法原理——单纯形规则xyABCDEFG HPABC ，A 最佳，C 最差C 反射到D ，CP=PD ，AP=PB D 比A 好D 扩张到E ，PD=DEE 比B 好ABE……YYD 比B 好NABD AFD……NYD 比C 好N收缩DG=GP ABGY……N收缩PH=HC ABH…单纯形规则示意图例：色谱分离的顺序优化色谱响应函数∑==ni i p CRF 1)ln(p ——峰分离函数i ——峰个数CRF ：判断峰分离程度完全分离：p =1,CRF =0其它情形：CRF <0优化目标：使CRF 最大例：通过变化柱温和载气流速优化2，3-二甲基己烷和3-甲基庚烷的分离t /℃流量/mol·min -16011021012345678tv6-2 化工调优调优目的：调整化工生产装置的操作参数，使生产处于最佳状态。

统计调优法：用数理统计方法，从日常积累的操作数据中寻找操作条件变化对优化目标的影响，从而求得优化的操作条件。

统计调优法中的关联式型式是经验模型，描述的过程规模不宜太大，而只适用于解决某个单元设备或简单工序的问题。

模拟法调优：以描述化工过程的数学模型为基础来寻求达到某个优化目标的最佳操作条件。

优选试验设计优选法在生产和科学实验中，人们为了达到优质、高产、低消耗的目的，需要对有关因素（如配方、配比、工艺操作条件等）的最佳点进行选择，所有这些选择点的问题，都称之为优选问题。

所谓优选法就是根据生产和科研中的不同问题，利用数学原理，合理地安排试验点，减少试验次数，以求迅速地找到最佳点的一类科学方法。

优选法可以解决那些试验指标与因素间不能用数学形式表达，或虽有表达式但很复杂的那些问题。

1单因素优选法常假定f(x)是定义区间（a,b）的单峰函数，但f(x)的表达式是并不知道的，只有从试验中才能得出在某一点x0的数值f(x0)。

应用单因素优选法，就是用尽量少的试验次数来确定f(x)的最大值的近似位置。

这里f(x)指的是试验结果，区间（a,b）表示的是试验因素的取值范围。

1.1来回调试方法优选法来源于来回调试法，如图1，选取一点x1做试验得y1=f(x1),再取一点x2做试验得y2=f(x2)，假定x2>x1，如果y2>y1,则最大值肯定不在区间（a,x1）内，因此只需考虑在（x1,b）内求最大值的问题。

再在（x1,b）内取一点x3，做试验得y3=f(x3)，如果x3>x2,而y3<y2,则去掉（x3,b），再在（x1,x3）中取一点x4,……，不断做下去，通过来回调试，范围越缩越小，总可以找f(x)的最大值。

这种方法取点是相当任意的，只要取在上次剩下的范围内就行了；那么怎样取x1,x2,……，可以最快地接近客观上存在的最高点呢？也就是怎样安排试验点的方法是最好的？下面介绍几种减少试验次数的试验方法。

1.2黄金分割法（0.618法）所谓黄金分割指的是把长为L的线段分为两部分，使其中一部分对于全部之比等于另一部分对于该部分之比，这个比例就是=0.6180339887……，它的三位有效近似值就是0.618，所以黄金分割法又称为0.618法。

黄金分割法（如图2），就是将第一个试验点x1安排在试验范围内的0.618处（距左端点a），即:x1=a+(b-a)×0.618......(1)得到试验结果y1=f（x1）；再在x1的对称点x2，即：x2=b-(b×a)×0.618=a+(b-x1)=a+(b-a)×0.382 (2)做一次试验，得到试验结果y2=f(x2)；比较结果y1=f(x1)及y2=f(x2)哪个大，如果f(x1)大，就去掉（a,x2）,如图2所示，在留下的（x2,b）中已有了一个试验点x1，然后再用以上的求对称点的方法做下去，一直做到达到要求为止。

统筹法与优选法一、统筹法统筹法，又称为网络计划技术，是一种基于网络图形的科学管理工具，用于分析和优化一个复杂项目的计划和执行过程。

它帮助管理者对整个项目有一个全面、清晰的认识，并能有效协调和指导各部门的各项工作。

1.统筹法的应用范围统筹法广泛应用于各种复杂项目的计划和执行过程中，例如建筑工程、制造工厂的建设计划、新产品研发项目等。

它也可以用于日常生活中的时间管理和资源分配。

2.统筹法的优点（1）能够明确项目的目标和任务，并把任务分解为更小、更易于管理的部分。

（2）通过绘制网络图形，可以直观地显示项目的各个阶段和任务之间的关系，从而帮助管理者更好地理解项目的整体结构和流程。

（3）可以预测项目可能的风险和瓶颈，并提前采取措施进行优化。

（4）通过时间参数的计算，可以为项目制定合理的进度计划，确保项目按时完成。

3.统筹法的实施步骤（1）明确项目的目标和任务，并对其进行分解。

（2）绘制网络图形，包括任务的时间顺序、持续时间、资源分配等信息。

（3）对网络图形进行分析，找出可能的风险和瓶颈。

（4）优化网络图形，调整任务的时间安排和资源分配。

（5）制定详细的进度计划，包括任务的开始和结束时间、关键路径等。

二、优选法优选法是一种通过科学实验或统计方法来寻找最优解的方法。

它的基本思想是通过对问题的各种可能情况进行实验或统计分析，找到最优解或次优解。

1.优选法的应用范围优选法广泛应用于各种需要寻找最优解的问题中，例如工程设计、生产工艺优化、市场策略制定等。

它也可以用于日常生活中的决策问题，例如选择最佳的旅游路线、制定最佳的购物计划等。

2.优选法的优点（1）能够通过科学实验或统计分析，找到问题的最优解或次优解。

（2）可以通过反复实验或测试，验证并优化解决方案的有效性。

（3）可以避免主观臆断或片面思考，使决策更加客观和科学。

（4）能够提供一组可选的解决方案，为决策者提供更多的选择。

3.优选法的实施步骤（1）明确问题目标和限制条件。

优选法的具体实例一、 一个真实案例某电子管厂从仓库中清出了积压多年的几百万米某种“废”金属丝。

为了使得这些废金属丝能够重新被利用，科研人员经过研究发现，找出准确的退火温度是使该废金属丝复活的关键。

由经验知道，退火温度的范围为[1400,1600]C C，因此，试验范围为[1400,1600]C C。

如果不考虑其他次要因素，则该金属丝的质量指标()f t 是温度t的函数，其中[1400,1600]t 。

由于目标函数()f t 的具体表达式不知道，因此，该问题的关键在于能否通过次数尽量少的调温试验，求出满足一定精度条件下的最佳退火温度。

（华罗庚先生70年代初期支援大西南三线建设期间的一个案例）分析： 尽管目标函数()f t 的具体表达式不知道，但是根据经验可知：从退火温度的最低点1400C开始，随着t 的增大，质量指标()f t 的函数值随之增大；当达到最佳退火温度0t 时，随着t 的继续增大，一直到最高点1600C，质量指标()f t 的函数值随之减少。

也就是说，()f t 是在试验区间内先增后减的单峰函数，其中只有唯一的一个最优点。

试验方法讨论： 1、 等分法通常的想法是：在试验区间[1400，1600]上均匀取点试验，就可以求得满足一定精度要求的最佳退火温度。

例如，若要求精度达到120，我们只要在 123191410,1420,1430,,1590t t t t ====各点进行试验，通过比较各点的试验结果，就能找到最佳试验点。

例如，若发现91490t =是其中最好的点，就可以断定最佳退火温度必在区间（1480，1500）上。

在生产实际中，就可以把1490C作为最佳退火温度。

问题：每一次试验都需要较高的成本，而上述等分法均匀取点，试验时没有考虑已经获得的质量指标()f t 的信息，往往需要作大量试验才能获得较好的结果。

因此等分法是一种浪费的方法。

需要找到一种更节约的方法。

2、 优选法（0.618法-黄金分割法）（受到蜂巢结构的启发） 具体步骤如下：先在试验区间的0.618处做第一次试验，第一点的温度为：(0.618160014000.61814001520C=-⨯+=-⨯+= 第一次点大小）小（）第二次试验：在第一次点关于中心对称的点，即第二次的温度为1600152014001480C =-+=-+= 第二次点大第一次点小比较上面的两次结果，如果1480C点较好，去掉1520C（称之为“坏点”）以上的温度。

优选法与二分法、黄金分割间的联系优选法概述优选法,是以数学原理为指导，用最可能少的试验次数，尽快找到生产和科学实验中最优方案的一种科学试验的方法。

例如：在现代体育实践的科学实验中，怎样选取最合适的配方、配比；寻找最好的操作和工艺条件；找出产品的最合理的设计参数，使产品的质量最好，产量最多，或在一定条件下使成本最低，消耗原料最少，生产周期最短等。

把这种最合适、最好、最合理的方案，一般总称为最优；把选取最合适的配方、配比，寻找最好的操作和工艺条件，给出产品最合理的设计参数，叫做优选。

也就是根据问题的性质在一定条件下选取最优方案。

最简单的最优化问题是极值问题，这样问题用微分学的知识即可解决。

实际工作中的优选问题，即最优化问题，大体上有两类：一类是求函数的极值；另一类是求泛函的极值。

如果目标函数有明显的表达式，一般可用微分法、变分法、极大值原理或动态规划等分析方法求解（间接选优）；如果目标函数的表达式过于复杂或根本没有明显的表达式，则可用数值方法或试验最优化等直接方法求解（直接选优）。

优选法是尽可能少做试验，尽快地找到生产和科研的最优方案的方法,优选法的应用在我国从70年代初开始，首先由我们数学家华罗庚等推广并大量应用,优选法也叫最优化方法。

二分法一般地，对于函数f(x),如果存在实数c,当x=c时f(c)=0,那么把x=c叫做函数f(x)的零点。

解方程即要求f(x)的所有零点。

先找到a、b，使f(a)，f(b)异号，说明在区间(a,b)内一定有零点，然后求f[(a+b)/2], 现在假设f(a)<0,f(b)>0,a<b ①如果f[(a+b)/2]=0，该点就是零点，如果f[(a+b)/2]<0,则在区间（(a+b)/2，b)内有零点，(a+b)/2=>a，从①开始继续使用中点函数值判断。

如果f[(a+b)/2]>0，则在区间(a,(a+b)/2)内有零点，(a+b)/2=>b，从①开始继续使用中点函数值判断。