课程体系结构图讲解学习

建工学院
— 4 —
制的基本方法， 培养学生有效从事工程项目管理的基本能力。 先修课程： 《管理学原理Ⅰ》 、 《土木工程施工》 、 《工程管理概论》 。 掌握工程造价构成、工程造价的定额计价方法、工程计量、工程造价的 建筑工程计量与计价Ⅰ 48 第 6 学期 工程量清单计价办法，具备编制工程造价的基本能力。先修课程： 《房屋 建筑学Ⅱ》 、 《建筑结构》 、 《建筑材料Ⅰ》 、 《土木工程施工》 。 掌握房地产开发项目的策划，房地产开发市场调查，房地产开发投资， 房地产经营与管理 32 第 6 学期 以及房地产开发项目的可行性研究，掌握一些房地产制度及相应的法制 法规。先修课程： 《工程经济学Ⅰ》 掌握建设项目投资与融资选择原则和方法，掌握建设项目投资决策分析 建设项目投资与融资 40 第 6 学期 的内容和方法，初步具备根据建设项目特点进行投资决策分析和设计项 目融资方案的基本能力。 先修课程： 《工程经济学Ⅰ》 《工程项目管理Ⅰ》 、 。 掌握项目决策和实施阶段项目管理的各项具体任务及其管理方法与手 工程项目管理Ⅱ 32 第 7 学期 段，熟悉项目管理信息系统以及网络平台解决工程管理的技术方案，具 备对工程项目进行全过程信息化和网络化管理的基本能力。先修课程： 《工程项目管理Ⅰ》 。 掌握建设工程项目环境评价、建设工程项目综合评价、建设工程项目成 工程造价管理 32 第 7 学期 本管理、建设工程项目后评价的主要内容、程序和方法，使学生具备进 行建设项目全过程造价管理和造价咨询的基本能力。 先修课程： 《工程项 目管理Ⅰ》 、 《建筑工程计量与计价Ⅰ》 。 熟悉工程招投标的方式、程序及有关合同管理问题。掌握工程施工招标 工程项目招投标与合同管理 32 第 7 学期 和投标的编制，具备编制招标文件或投标文件，并能进行合同管理的能 力。先修课程： 《建设法规》 、 《建筑工程计量与计价Ⅰ》 。 专 业 拓 建筑结构 CAD 32（32） 第 5 学期 建筑 CAD 32（32） 第 3 学期 掌握 Auto CAD 基本绘图.编辑方法与技巧，能熟练运用 CAD 软件进行 建筑图形设计。先修课程： 《建筑制图》 。 使学生掌握并能运用 CAD 进行结构辅助设计的方法与技巧。 先修课程： 工程制图 建工学院 建工学院 建工学院 建工学院 建工学院 建工学院 建工学院 建工学院

信息系统方向 管理信息系统
ERP原理及应用 MIS实训
程序设计方向 Java程序设计 程序设计
数据库应用实训
网页设计方向 网页设计与制作
网页美工与动画 动态网站开发实训
测试方向 PC测试与维护 PC测试与维护实训 软件测试
IT销售及跨行业 PC组装维护 服务器配置与管理 专业选修课
专业基础课
程序设计 计算机网络基础
计算机专业英语
微机原理
SQL Server数据库应用
公基础课
全校性基础课
就业创业教育 形势教育 市场营销学 军事理论教育 计算机应用基
阅读与写作 毛泽东思想和 市场营销学 思想道德修养 大学生职业生涯
管理学原理
体育
财务管理
经济法
公共选修课
自然科学 大学英语
人文类课程 大学计算机

40 （8）
40 8（8）
32
16（16）
40
第 2 学期 第 2 学期 第 4 学期 第 4 学期 第 3 学期 第 3 学期 第 5 学期 第 5 学期 第 6 学期
第 6 学期
第 3 学期
先修课程：《宏观经济学》。 掌握会计账务处理程序和核算方法，提高学生基本会计核算和实际 业务的手工操作能力。后续课程：《财务会计学》、《财务管理Ⅰ》。 通过手工操作锻炼提高学生实际业务的账务处理能力。先修课程： 《基础会计学》。 掌握统计学的基本理论和方法，培养学生运用统计软件进行数据分 析和发现经济问题的能力。先修课程：《概率论与数理统计》。 锻炼提高学生运用统计软件分析、解决经济问题的能力。先修课程： 《统计学原理》。 系统掌握管理学的基本原理和方法，培养学生运用管理学理论与方 法分析解决管理问题的能力。先修课程：《微观经济学》，后续课程： 《企业管理学》、《管理信息系统》、《管理学原理实验》。 提高学生运用管理学理论与方法分析、解决管理问题的能力。先修 课程：《管理学原理》。 掌握企业经营管理过程中要素管理、流程管理及生产管理等内容和 方法，培养学生运用理论知识和方法分析、解决企业管理问题的能 力。先修课程：《管理学原理》。 提高学生运用企业管理知识和方法分析、解决企业管理问题的能力。 先修课程：《企业管理学》。 掌握从管理信息系统的规划和开发、系统设计、系统分析、系统实 施、系统运行和评价过程中涉及到的基本原理、技术和方法。先修 课程：《管理学原理》。 上机操作，进一步提高学生运用所学的管理信息系统规划和开发、 系统设计、系统分析等理论与方法进行规划、评价管理信息系统的 能力。先修课程：《管理信息系统》。 掌握我国目前民法、商法、经济法等经济法律制度的基础知识和主 要内容，培养学生运用经济法律解决民事权益保护、公司制度、票 据支付、企业破产等实际问题的能力。

3
计算机软件 计算机科学 计算机软件 计算机工程 计算机软件 计算机工程 计算机软件
理信学院 理信学院 理信学院 理信学院 理信学院 理信学院 理信学院
Android 程序设计Ⅰ
96（96）
Object C 编程基础
96（96）
SSH——J2EE 轻量级解决 64（64）
方案
Android 特色应用开发
培养学生对算法复杂度进行正确分析的基本能力，独立设计求解问题最优算 法的基本能力。先修课：《C 语言程序设计》、《数据结构》、《离散数学》 掌握基于计算机的知识表示、运用知识进行推理等方面的理论和技术，培养 用计算机实现人类智能的能力。先修课程：《离散数学》、《数据结构》、《概 率论与数理统计》。 掌握利用计算机进行图形的表示、 生成、处理、显示方面的知识；培养应 用计算机解决图形处理的能力、开发人机交互界面的能力。先修课：《C 语 言程序设计》、《线性代数》、《数据结构》。 培养学生掌握数据仓库的设计、开发技术和 OLAP 技术及工具的使用技能， 能运用分类、聚类、关联规则挖掘等算法发现并提取隐藏在大数据内的信息。 先修课：《C 语言程序设计》、《数据库系统原理与应用》，《人工智能》。 本课程以目前移动端 UI 发展与行业知识进行详细讲解。学生通过学习这门 课程，可以了解到（1）UI 设计师的发展之路；（2）该从何下手学习 UI 设 计；（3）在实际工作中，UI 设计的整体项目流程。 掌握密码学原理及信息安全的关键技术，培养学生的网络和信息安全的防护 能力，为今后开发、管理安全、可靠实用的计算机系统打下基础。先修课： 《数据结构》、《操作系统》、《数据库系统原理与应用》、《计算机网络原理》。 掌握计算机专业英语术语，培养学生阅读笔译计算机专业领域的英文资料、 书刊，获取专业信息和表达专业思想的初步能力。先修课：《大学英语》 培养学生用计算机求解数值计算问题的能力，如求解方程、方程组的数值解， 曲线拟合，积分值计算等。先修课：《高等数学》、《线性代数》、《C 语言程 序设计》。 充分了解云计算数据中心和虚拟化等关键概念，具备在云计算和大数据的开 发和管理能力。先修课程：《数据结构》、《数据库系统原理与应用》。 通过本课程的学习，使学生掌握 HTML5 的各种新特性，主要包括 JavaScript、 HTML5 表单及文件处理、Web 通信、支持多线程编程的 Web Workers、jQuery

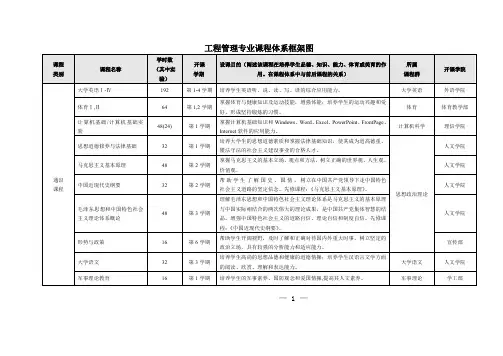
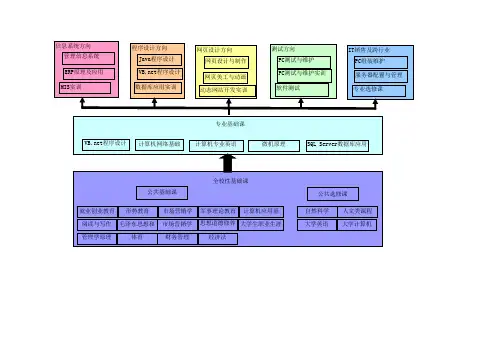
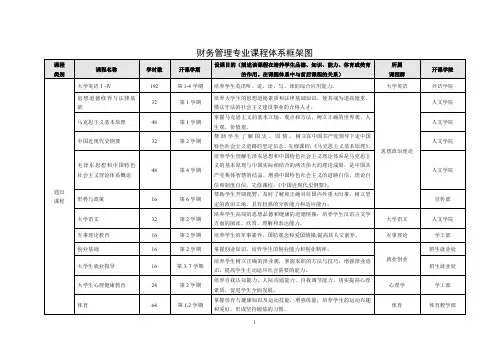
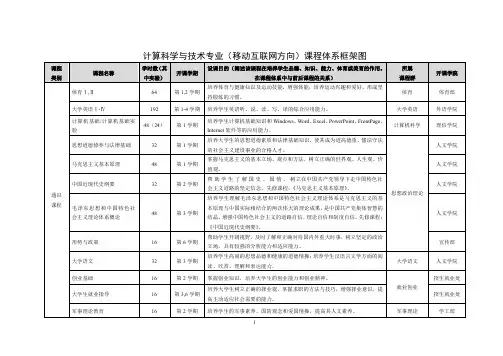
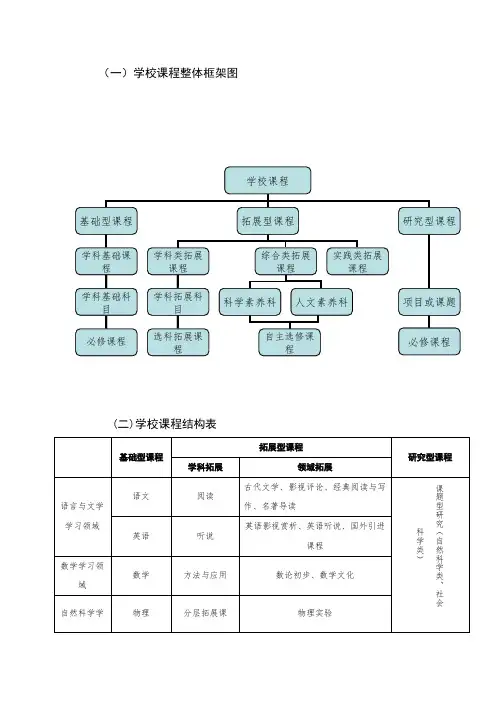
（一）学校课程整体框架图
(二)学校课程结构表
基础型课程
拓展型课程
研究型课程
学科拓展
领域拓展
语言与文学学习领域
语文
阅读
古代文学、影视评论、经典阅读与写
作、名著导读
课题型研究（自然科学类、社会
科学类）
英语
听说
英语影视赏析、英语听说、国外引进
课程
数学学习领
域 数学
方法与应用
数论初步、数学文化
自然科学学
物理
分层拓展课
物理实验
学校课程
基础型课程
拓展型课程
研究型课程
学科基础课
程 学科类拓展
课程 综合类拓展课程
实践类拓展课程
学科拓展科
目 科学素养科选科拓展课
程
人文素养科项目或课题
学科基础科
目 必修课程
必修课程
自主选修课
程。

与中国实际相结合的两次伟大的理论成果，是中国共产党集体智慧的结晶。增强 思想政治理
中国特色社会主义的道路自信、理论自信和制度自信。先修课程：《中国近现代史
论
纲要》。
帮助学生树立中国特色社会主义的共同理想，坚定对马克思主义的信念；增强学
生的爱国主义情感，做忠诚的爱国者；帮助学生正确地认识和把握人生、人生价
物理学
使学生了解生物体化学组成成分的分子结构及其性质，生命活动中发生的化学变
第 3 学期 化和调控规律，从而掌握生物化学的基础理论和基本知识。先修课程：《普通化学
Ⅰ》、《分析化学Ⅲ》、《有机化学Ⅲ》。
第 3 学期
掌握生物化学的基本实验技能，能够运用生物化学理论知识对实验问题进行分析 和讨论；学会以生物化学实验的方法和手段去解决本专业领域的问题。
体育 计算机基础/计算机基础实 验 普通化学Ⅰ
学科 （专 业）基 础课 程
分析化学Ⅲ 有机化学Ⅲ
基础化学实验Ⅰ-Ⅱ 计算机应用/计算机应用实
16 16 24 64 48（24） 48
24
48 72（72） 56（24）
第 3，7 学期
帮助学生正确地把握目前就业市场的需求形势，了解国家、各省市有关大学生就 业制度和政策，按照社会需求确立就业期待和就业心理，树立正确的择就业观念 和就业取向，了解大学生就业程序，把握一定的就业技巧，掌握求职的方法与技 巧，增强择业意识，提高主动适应社会需要的能力。
掌握主要果品、蔬菜、乳制品、肉制品和粮油食品等加工工艺和关键技术，为食
食品质量与 安全检测
食品工程
食品学院
食品学院 食品学院 食品学院 食品学院
发酵工艺学
24
发酵工艺学实验
16（16）

掌握病虫草害发生的基本规律和防治方法，提高对农药应用的能力。
掌握常见杀虫剂、杀菌剂、除草剂及植物激素等农药生物活性测定技 术的基本原理及基本方法。 熟悉常见农药室内外活性评价方法的设计、选择及实施方法。先修课 程：《农药生物活性测定》。
线性代数
大学物理Ⅲ
学科（专 业）基础
课程
大学物理Ⅲ实验 无机化学Ⅲ
化学实验Ⅰ(1)
分析化学Ⅰ
化学实验Ⅰ(2)
48（24） 16 16 144 32 48 16
64 48 48 48
第 1 学期 第 2,6 学期
培养学生计算机基础知识和 Windows、Word、Excel、PowerPoint、 FrontPage、Internet 软件的应用能力。 培养大学生树立正确的择业观，掌握求职的方法与技巧，增强择业意 识，提高主动适应社会需要的能力。
40
第 6 学期
程
化药学院
化学制药工业生产技术与管理等工作的专业技能。
掌握药厂反应设备及车间工艺学科的基本知识和基本概念，具有对工
40
第 6 学期
业反应过程进行工程学分析的初步概念，为反应器的合理选型提供理
化药学院
制药专业综合实验 概率论与数理统计
实验设计与分析
计算机在化学中的应用
专业
任
拓展
课程 选 波谱解析
数学 应用数学
化学应用 化学基础 化工基础 药学基础
药学
—5—
化药学院 理信学院 化药学院
化药学院 化药学院 化药学院 化药学院 化药学院 化药学院源自天然药物化学实验16
现代企业管理
32
化工环保及治理技术
32
生物制药
制药工程专业英语

32
英语词汇学概论
32
英汉语言对比
32
第 3 学期 第 4 学期 第 5 学期 第 5 学期 第 6 学期 第 6 学期 第 7 学期 第 3 学期 第 4 学期
通过介绍影片故事背景，欣赏经典台词，评析影视作品所表现的主题。
使学生了解历史、认识社会现实、开阔眼界、增长知识、提高艺术素养，
提升文化审美能力，扩展文化视野。
音特点、语流的规律、语调的功能，具有较标准的英语语音、语调，能
流利朗读和交际，为后续的《基础英语Ⅰ-Ⅳ》、《英语口语Ⅰ-Ⅳ》学习
打下坚实的语言基础。
通过语言基础训练与篇章讲解分析，培养和提高学生综合运用英语的能
力。使学生逐步提高语篇阅读理解能力，了解英语各种文体的表达方式
和特点，扩大词汇量和熟悉英语常用句型，具备基本的口头与笔头表达
英语口语Ⅰ-Ⅳ 英语基础写作Ⅰ-Ⅳ 英语语法与语篇
120 120(60) 120(120) 96(32)
32
第 3 学期 第 4-5 学期 第 1 学期
第 1-4 学期 第 1-4 学期 第 1-4 学期 第 1-4 学期 第 1-4 学期 第 3 学期
帮助学生熟悉中国文化，加强文化认同感和民族自豪感，提高宣传能力，
能力。
通过课内外大量阅读和训练，帮助学生扩大词汇量、吸收语言和文化背
景知识，提高学生的阅读速度和阅读理解能力；培养学生细致观察语言
的能力以及假设判断、分析归纳、推理检验等逻辑思维能力。 专业基础课程
通过多种形式的训练，帮助学生初步克服听力障碍，听懂中等难度的英
语听力材料，并用英语简要地做笔记，根据所听材料进行分析、领会说
外语学院 外语学院 外语学院
外语学院 外语学院 外语学院 外语学院 外语学院 外语学院

能，提高学生的动手、实践和创新能力，为学生从事土木工程勘测、
48(24)
思想道德修养与法律基础
32
马克思主义基本原理
48
中国近现代史纲要
32
毛泽东思想和中国特色社 48
会主义理论体系概论
形势与政策
16பைடு நூலகம்
大学语文
32
第 1,2 学期 第 1 学期 第 1 学期 第 2 学期 第 2 学期
第 3 学期
第 6 学期 第 3 学期
培养体育与健康知识及运动技能，增强体能；培养运动兴趣和爱好， 形成坚持锻炼的习惯。 培养学生计算机基础知识和 Windows、Word、Excel、PowerPoint、 FrontPage、Internet 软件的应用能力。 培养大学生的思想道德素质和法律基础知识，使其成为道高德重、懂 法守法的社会主义建设事业的合格人才。 掌握马克思主义的基本立场、观点和方法，树立正确的世界观、人生 观、价值观。 帮助学生了解国史、国情，树立在中国共产党领导下走中国特色社会 主义道路的坚定信念。先修课程：《马克思主义基本原理》。 培养学生理解毛泽东思想和中国特色社会主义理论体系是马克思主 义的基本原理与中国实际相结合的两次伟大的理论成果，是中国共产 党集体智慧的结晶。增强中国特色社会主义的道路自信、理论自信和 制度自信。先修课程：《中国近现代史纲要》。 帮助学生开阔视野，及时了解和正确对待国内外重大时事，树立坚定 的政治立场，具有较强的分析能力和适应能力。 培养学生高尚的思想品德和健康的道德情操；培养学生汉语言文学方 面的阅读、欣赏、理解和表达能力。
80（12） 第 3 学期 培养学生掌握工程材料的力学性能及受力构件的内力、变形情况，研
数、理基础 工程制图

课程设计系统框架图一、教学目标本课程的教学目标是使学生掌握第二章“代数与方程”的核心概念和基本技能。

学生将能够：1.知识目标：理解代数表达式的概念，掌握代数式的简化、求值方法；熟悉一元一次方程的解法，了解其应用场景。

2.技能目标：能够运用代数知识解决实际问题，独立完成一元一次方程的求解，并进行简单应用。

3.情感态度价值观目标：培养学生的逻辑思维能力，激发学生对数学的兴趣，培养合作探究的学习态度。

二、教学内容教学内容围绕第二章“代数与方程”进行，具体包括：1.代数表达式：介绍代数表达式的概念，讲解代数式的简化、求值方法。

2.一元一次方程：讲解一元一次方程的定义、解法，并通过实例演示其应用场景。

3.实际问题求解：培养学生运用代数知识解决实际问题的能力，巩固所学知识。

三、教学方法本课程采用多种教学方法，以激发学生的学习兴趣和主动性：1.讲授法：讲解代数表达式、一元一次方程的基本概念和解法。

2.讨论法：学生分组讨论实际问题，培养合作探究的学习态度。

3.案例分析法：通过具体案例，让学生了解代数知识在实际问题中的应用。

4.实验法：引导学生进行实际操作，验证一元一次方程的解法。

四、教学资源为了支持教学内容和教学方法的实施，丰富学生的学习体验，我们将使用以下教学资源：1.教材：《数学》。

2.参考书：提供一些关于代数与方程的拓展阅读资料。

3.多媒体资料：制作PPT、视频等，帮助学生形象地理解代数知识。

4.实验设备：提供计算器、纸笔等，方便学生进行实际操作。

五、教学评估为了全面、客观地评估学生的学习成果，本课程采用以下评估方式：1.平时表现：关注学生在课堂上的参与度、提问回答等情况，给予及时的反馈和鼓励。

2.作业：布置适量的作业，要求学生独立完成，通过作业可以看出学生的掌握程度。

3.考试：安排一次章节考试，测试学生对代数与方程知识的掌握情况。

4.实践项目：让学生运用所学知识解决实际问题，评估学生的实际应用能力。

评估结果将作为学生学习成果的重要依据，用于指导后续教学。

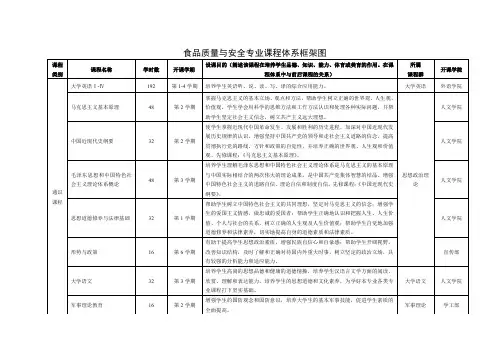
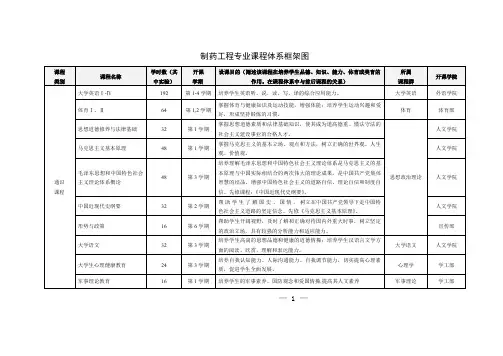
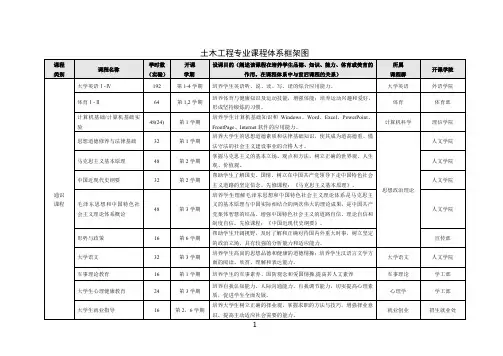
课程体系结构图
通识教育必修课程包括和中国特色社会主义理论体系概论、第二外语（日语、法语、德语）、思想道德修养与法律基础、中国近现代史纲要、马克思主义基本原理概论、形势与政策、计算机应用基础、体育、职业发展与就业指导和创新与创业。

这些课程的目的是培养学生的综合素质和基本能力。

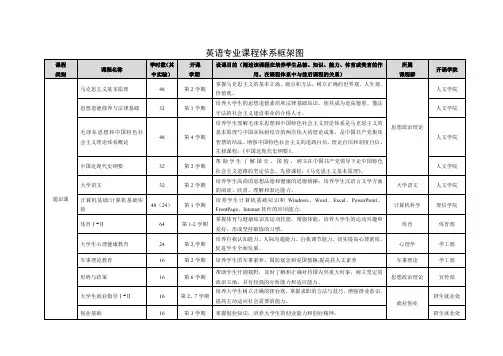
院级课程包括基础英语、英语口语、英语阅读、英语写作、英语听说、高级英语、口译、笔译、英语语法、英语语音、英美文学选读、英语国家概况、语言学概论、跨文化交际、翻译理论与实践、英语报刊选读和英语词汇学。

这些课程旨在提高学生的英语水平和语言应用能力。

专业必修课程包括心理学、教育学、英语教学法、英语学科课程与教学论和教师职业道德。

这些课程旨在提高学生的教育专业知识和教学能力。

专业选修课程包括现代教育技术应用、基础教育课程标准解读与教材分析、英语课程教学设计、教师语言、教育研究方
法和微格教学训练。

这些课程旨在提高学生的专业技能和实践能力。

集中实践环节包括综合实践和专业实践。

综合实践包括军训与军事理论、普通话水平测试、素质拓展学分和文明修身。

专业实践包括教育名著选读、二语得、英语文体学、中外教育史、英语修辞学和中国文化概论。

这些实践环节旨在提高学生的实践能力和综合素质。

经管学院 经管学院 经管学院 经管学院
40(4)
第 6 学期
经管学院
公司战略与风险管理
32
第 5 学期
风险，是注册会计师的考试科目，也是企业内部管理人员必修的一门课程。 先修课程： 《管理学原理》、《财务管理学》。
经管学院
专业拓 展课程 （选修）
高级财务管理Ⅰ/高级财 务管理Ⅰ实验 EXCEl 在会计与财务中 的应用/ EXCEl 在会计 与财务中的应用及实验 合同法
会计学专业课程体系框架图
学时数 课程类别 课程名称 （实验 数） 大学英语 I-IV 马克思主义基本原理 中国近现代史纲要 192 48 32 第 1-4 学 期 第 1 学期 第 2 学期 开课学期 设课目的（阐述该课程在培养学生品德、知识、能力 、体育或美育的作用。在课程体 系中与前后课程的关系） 所属课程 群 开课学院
培养学生英语听、说、读、写、译的综合应用能力。 掌握马克思主义的基本立场、观点和方法，树立正确的世界观、人生观、价值观。 帮助学生了解国史、国情，树立在中国共产党领导下走中国特色社会主义道路的坚定信 念。 培养学生理解毛泽东思想和中国特色社会主义理论体系是马克思主义的基本原理与中
英语
外语学院 人文学院 人文学院
40(8)
第 5 学期
经管学院
会计信息系统
24
第 5 学期
作方法和技巧，强化学生操作会计软件的专业技能。先修课程：《基础会计学》、《财 务会计学》。
经管学院
会计信息系统实验 审计学 审计学实验 高级会计学/高级会计学 实验 政府与非营利组织会计
32（32） 56 16（16） 64（8）
第 5 学期 第 7 学期 第 7 学期 第 6 学期

新课程下的高中数学课程：结构、内容及变化一、高中数学课程基本框架普通高中数学课程标准更加突出了基础性和选择性。

与以往的高中数学课程相比，高中数学课程内容由模块构成，采用学分管理的形式。

高中数学课程分为必修和选修。

必修课程由五个模块组成；选修课程有四个系列，其中系列 1、系列 2 由若干个模块组成，系列 3、系列 4由若干个专题组成；每个模块 2 学分（36学时），每个专题1学分（18学时），每两个专题可组成一个模块。

课程结构如图所示。

图1．普通高中数学新课程结构图二、高中数学课程基本内容1．必修课程必修课程是整个高中数学课程的基础，包括五个模块，共10学分。

五个模块的内容分别为：数学1：集合，函数概念与基本初等函数Ⅰ（指数函数、对数函数、幂函数）。

数学2：立体几何初步，平面解析几何初步。

数学3：算法初步，统计，概率。

注：上图中代表 模块（36学时），代表专题（18学时）数学-1 数学-2 数学-3 数学-4 数学-5选修1-1选修1-2 选修2-1选修2-2 选修2-3 选修3-1选修3-2 选修3-3 选修3-4 选修3-5选修3-6 选修4-1选修4-3 选修4-2 选修4-4 选修4-10必修模块选修系列……数学4：基本初等函数Ⅱ（三角函数），平面上的向量，三角恒等变换。

数学5：解三角形，数列，不等式。

2．选修课程普通高中数学课程标准提供了四个系列的选修课程：◆系列1：由两个模块组成。

选修1－1：常用逻辑用语，圆锥曲线与方程，导数及其应用。

选修1－2：统计案例，推理与证明，数系扩充及复数的引入，框图。

◆系列2：由三个模块组成。

选修2－1：常用逻辑用语，圆锥曲线与方程，空间中的向量与立体几何。

选修2－2：导数及其应用，推理与证明，数系的扩充与复数的引入。

选修2－3：计数原理，统计案例，概率。

◆系列3：由六个专题组成。

选修3－1：数学史选讲。

选修3－2：信息安全与密码。

选修3－3：球面上的几何。