钢结构基本原理(第二版)习题参考解答第七章
- 格式:doc
- 大小:224.00 KB
- 文档页数:5


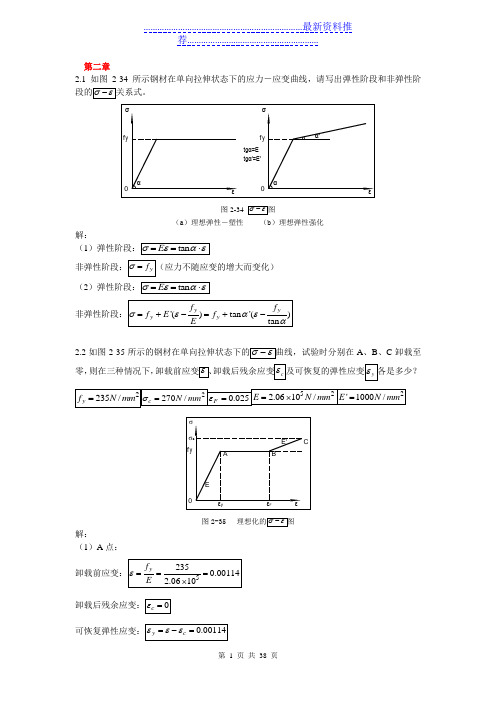
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=tgα'=E'f y 0f y 0tgα=E σf yCσF卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869c c Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶图(a)理想弹性-塑性(b )理想弹性强化解:(1(22.2如图2-35A 、B、C 卸载至零,则在三种情况下,图2-35解:(1)A 点:(2)B点:(3)C点:2.3作用时间之间的关系。
点、极限强度提高,而塑性韧性降低(时效现象)也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
2.5 解释下列名词:(1)延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy、并达到抗拉极限强度fu的破坏。
(2)损伤累积破坏指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。
(3)脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小(一般小于屈服点fy )的破坏。
(4)疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏。
(5)应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏。
(6)疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数。

习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案mm l x 60000=;mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===;mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ;4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得855.0=x ϕ(附表4-4);785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=;mm l y 30000=mm A 9500=;mm i x 0.62=;mm i y 3.119= 8.960.6260000===x x x i l λ;1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得478.0=x ϕ(附表4-5);953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。

第4章 轴心受力构件4.1 验算由2∟635⨯组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼(图4.37),钢材为Q235钢。
如截面尺寸不够,应改用什么角钢? 注:计算时忽略连接偏心和杆件自重的影响。
解:(1)强度 查表得 ∟635⨯的面积A=6.14cm 2 ,min 1.94x i i cm ==,22()2(614205)1028n A A d t mm =⨯-⋅=⨯-⨯=, N=270KN327010262.62151028n N Mpa f Mpa A σ⨯===≥=,强度不满足,所需净截面面积为32270101256215n N A mm f ⨯≥==, 所需截面积为212562057282n A A d t mm =+⋅=+⨯=, 选636⨯,面积A=7.29cm 22729mm =2728mm ≥ (2)长细比[]min3000154.635019.4o l i λλ===≤= 4.2 一块-40020⨯的钢板用两块拼接板-40012⨯进行拼接。
螺栓孔径为22mm ,排列如图4.38所示。
钢板轴心受拉,N=1350KN (设计值)。
钢材为Q235钢,解答下列问题; (1)钢板1-1截面的强度够否?(2)是否需要验算2-2截面的强度?假定N 力在13个螺栓中平均分配,2-2截面应如何验算?(3)拼接板的强度够否?解:(1)钢板1-1截面强度验算:210min (3)(400322)206680n A b d t mm =-⋅⋅=-⨯⨯=∑,N=1350KN31135010202.12056680n N Mpa f Mpa A σ⨯===≤=,强度满足。
(2)钢板2-2截面强度验算:(a ),种情况,(a )是最危险的。
22()0(5)(40080522)206463n a A l d t mm =-⋅⋅=-+⨯⨯=, N=1350KN32135010208.92056463n N Mpa f Mpa A σ⨯===≥=,但不超过5%,强度满足。

习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案;mm l x 60000=mml y 30000=mmA 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=;mm A I i x x 3.1199500135103167===mmAI i y y 0.62950036479167===;3.503.11960000===x x x i l λ4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得(附表4-4);(附表4-5)855.0=x ϕ785.0=y ϕ应根据确定柱子整体稳定的承载力y ϕkNAf P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案;mm l x 60000=mml y 30000=;;mm A 9500=mm i x 0.62=mmi y 3.119=;8.960.6260000===x x x i l λ1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得(附表4-5);(附表4-4)478.0=x ϕ953.0=y ϕ应根据确定柱子整体稳定的承载力x ϕkNAf P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶图(a)理想弹性-塑性(b )理想弹性强化解:(1(22.2如图2-35A 、B、C 卸载至零,则在三种情况下,图2-35解:(1)A 点:(2)B点:(3)C点:2.3作用时间之间的关系。
点、极限强度提高,而塑性韧性降低(时效现象)也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
2.5 解释下列名词:(1)延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy、并达到抗拉极限强度fu的破坏。
(2)损伤累积破坏指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。
(3)脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小(一般小于屈服点fy )的破坏。
(4)疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏。
(5)应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏。
(6)疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数。
钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan y y y y ff f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =tgα'=E'f y0f y 0tgα=E图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯ 卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c fE εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+=卸载后残余应变:0.05869c c E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
σf y 0Cσ答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶图(a)理想弹性-塑性(b )理想弹性强化解:(1(22.2如图2-35A 、B、C 卸载至零,则在三种情况下,图2-35解:(1)A 点:(2)B点:(3)C点:2.3作用时间之间的关系。
点、极限强度提高,而塑性韧性降低(时效现象)也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
2.5 解释下列名词:(1)延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy、并达到抗拉极限强度fu的破坏。
(2)损伤累积破坏指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。
(3)脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小(一般小于屈服点fy )的破坏。
(4)疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏。
(5)应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏。
(6)疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数。
7.1 一压弯构件长15m ,两端在截面两主轴方向均为铰接,承受轴心压力1000N kN =,中央截面有集中力150F kN =。
构件三分点处有两个平面外支承点(图7-21)。
钢材强度设计值为2
310/N mm 。
按所给荷载,试设计截面尺寸(按工字形截面考虑)。
解:选定截面如下图示:
图1 工字形截面尺寸
下面进行截面验算:
(1)截面特性计算
()23002026502021420540A mm =⨯⨯+-⨯⨯=
339411300650286610 1.45101212
x I mm =⨯⨯-⨯⨯=⨯ 63/325 4.4810x x W I mm ==⨯
337411220300610149.01101212
y I mm =⨯⨯⨯+⨯⨯=⨯ 53/150 6.0110y y W I mm ==⨯
266.2x i mm ==
66.2y i m m = (2)截面强度验算
36226100010562.510172.3/310/20540 4.4810
x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯ 满足。
(3)弯矩作用平面内稳定验算 长细比1500056.3266.2
x λ== 按b 类构件查附表4-4
,56.368.2,查得0.761x ϕ=。
2257222.061020540' 1.20101.1 1.156.3
EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 弯矩作用平面内无端弯矩但有一个跨中集中荷载作用:
371000101.00.2 1.00.20.981.2010 1.1
mx EX N N β⨯=-⨯=-⨯=⨯⨯, 取截面塑性发展系数 1.05x γ= 363611000100.98562.5100.7612054010001010.8 1.05 4.481010.8' 1.2010mx x x x x EX M N A N W N βϕγ⨯⨯⨯+=+⨯⎛⎫⎛⎫⨯-⨯⨯⨯-⨯ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭ 22189.54/310/N mm f N mm =<= ,满足。
(4)弯矩作用平面外稳定验算 长细比500075.566.2
y λ==,按b 类构件查附表4-4,
75.591.5=,查得0.611x ϕ=。
弯矩作用平面外侧向支撑区段,构件段有端弯矩,也有横向荷载作用,且端弯矩产生同向曲率,取 1.0tx β=。
弯矩整体稳定系数近似取2275.53451.07 1.070.884400023544000235y
y
b f λϕ=-⋅=-⨯=,取截面影响系数 1.0η=。
36221100010 1.0562.5101.0222.4/310/0.61120540 4.48100.88
tx x y b x M N N mm f N mm A W βηϕϕ⨯⨯⨯+=+⨯=<=⨯⨯⨯ 满足。
(5)局部稳定
a.
翼缘:
15077.1510.720b t -==<(考虑有限塑性发展),满足要求。
b.腹板 腹板最大压应力:3620max 6100010562.510610166.6/205406504.4810
x h N M N mm A W h σ⨯⨯=+⋅=+⨯=⨯ 腹板最小压应力:3620min
6100010562.51061069.2/205406504.4810x h N M N mm A W h σ⨯⨯=-⋅=-⨯=-⨯ 系数max min 0max 166.669.2 1.42166.6
σσασ-+=== [
[
061043.6160.52516 1.420.556.32562.614w w h t αλ==<++=⨯+⨯+,满足。
由以上验算可知,该截面能满足要求。
7.2 在上题的条件中,将横向力F 改为作用在高度10m 处,沿构件轴线方向,且有750mm 偏心距,图7-22,试设计截面尺寸。
7.3 一压弯构件的受力支承及截面如图7-23所示(平面内为两端铰支支承)。
设材料为Q235(2235/y f N mm =),计算其截面强度和弯矩作用平面内的稳定性。
解:
(1)截面特性计算
2
3001223761010960A mm =⨯⨯+⨯=338411300400290376 3.15101212
x I mm =⨯⨯-⨯⨯=⨯ 63/200 1.5810x x W I mm ==⨯
169.6x i mm =
(2)截面强度验算
362268001012010148.9/215/10960 1.5810
x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯,满足。
(3)弯矩作用平面外的稳定验算 长细比1200070.8169.6
x λ==,按b 类构件查附表4-4
,70.870.8=,查得0.746x ϕ=。
2256222.061010960' 4.04101.1 1.170.8
EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 弯矩作用平面内构件段有有横向荷载作用,也有端弯矩作用且端弯矩产生反向曲率,取: 21800.650.350.650.350.417120
mx M M β=+⨯=-⨯= 取截面塑性发展系数 1.05x γ=,
363616800100.417120100.746109608001010.8 1.05 1.581010.8' 4.0410mx x x x x EX M N A N W N βϕγ⨯⨯⨯+=+⨯⎛⎫⎛⎫⨯-⨯⨯⨯-⨯ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭ 22133.6/215/N mm f N mm =<=,满足。
故可知,该截面强度和平面内稳定均得到满足。
7.4 某压弯缀条式格构构件,截面如图7-24所示,构件平面内外计算长度029.3x l m =,
018.2y l m =。
已知轴压力(含自重)2500N kN =,问可以承受的最大偏心弯矩x M 为多少。
设钢材牌号为Q235,N 与x M 均为设计值,钢材强度设计值取2
205/N mm 。
解:
(1)截面特性计算 63I a :215459A mm =849.4010x I mm =⨯,741.7010y I mm =⨯,
264.6x i mm =,33.2y i mm = 12510L ⨯:2243.73A mm =,最小回转半径min 24.6i mm =
格构截面:
221545930918A mm =⨯=
()
721042 1.701015459900 2.5110x I mm =⨯⨯+⨯=⨯ 73/900 2.7910x x W I mm ==⨯
901.0x i m m = 由于截面无削弱,失稳破坏一般先于强度破坏,故这里不考虑强度破坏的问题。
(2)平面内整体稳定 虚轴方向长细比2930032.5901.0
ox x x l i λ===
换算长细比52.6ox λ== 按b 类构件查附表4-4,查得0.845x ϕ=,取弯矩等效系数 1.0mx β=。
2257222.061030918' 2.07101.1 1.152.6
EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 根据平面内整体稳定计算公式有:11'mx x
x x x EX M N f A N W N βϕϕ+≤⎛⎫- ⎪⎝⎭ ①
(3)单肢稳定 单肢最大压力:max 21800
x M N N =
+ ② 最大受压分肢弯矩平面内长细比:1180054.233.2
x λ== 最大受压分肢弯矩平面外长细比:11820073.8246.6y λ== 11y x λλ>,按轴心受压构件查附表4-4得稳定系数10.728y ϕ=
根据轴心受压构件稳定计算公式:
max 1y N f A
ϕ≤ ③ (4)缀条稳定 由缀条稳定计算公式看出,斜缀条的受力与所求x M 无关,这里不作考虑
因此,由①计算得2741x M kN m ≤⋅,由②③计算得1902x M kN m ≤⋅,取1902x M kN m =⋅。