则称事件A与事件B
,其含义是:
__________________________________
• 3.概率的几个基本性质
• (1)概率的取值范围0≤为P(A)≤1
.
• (2)必然事件的概率1为 . • (3)不加法公式:P(A)+P(B)
• 若事件A与事件B互斥,则P(A∪B)
(2)由于点数之和最小是 2,最大是 12,在 2~13 范围之 内,它是必然事件,其概率为 1.
(3)由(2)知,和是 7 是有可能的,此事件是随机事件,事 件“点数和为 7”包含的基本事件有{1,6},{2,5},{3,4}, {4,3},{5,2},{6,1}共 6 个,因此 P=6×6 6=16.
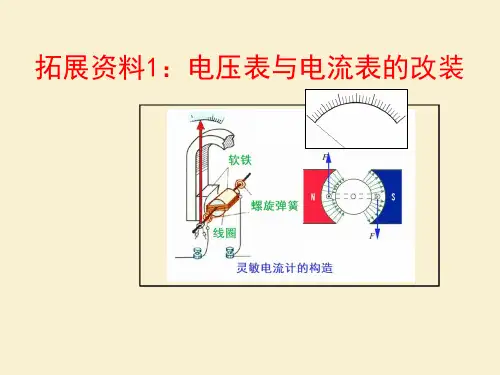
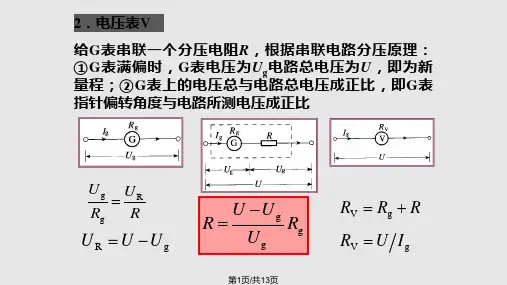
拓展:一个电流表G的内阻Rg=1kΩ,满 偏电流为Ig=500μA。
改装成双量程(0-0.6A-3A)电流表
G
R1
a
b
3A
R2
c 0.6A
则R1=
Ω,R2=
Ω.
第十章 计数原理和概率
第4课时 随机事件的概率
• 1.了解随机事件发生的不确定性和频率的 稳定性,了解概率的意义,了解频率与概率 区别.
____________在_一__定_条_件__下_不_可__能_发__生_的_事_.件
• (2)不可能事件: 在_一_定__条_件_下__可_能_发__生_也_可__能_不__发_生_的__事_件________.
• (3)随机事件: __________________________________ ______.
• (2)求甲、乙两人同在第3号车站下车的概率; • (3)求甲、乙两人同在第4号车站下车的概
• 【解析】 (1)用有序数对(x,y)表示甲在x 号车站下车,乙在y号车站下车,则甲下车 的站号记为2,3,4共3种结果,乙下车的站号 也是2,3,4共3种结果.甲、乙两个下车的所 有可能结果有9种,分别为:(2,2),(2,3), (2(,24))设,甲(、3,乙2两),人(同3时,3在),第(33,号4车)(4站,下2)车,的(事4,件3)为,A,则 (4,4).