组合数的公式
- 格式:docx
- 大小:97.05 KB
- 文档页数:2

组合数定理组合数定理是组合数学中的一个重要定理,它在排列组合问题的解决中起到了至关重要的作用。
本文将介绍什么是组合数定理、其重要性以及如何运用组合数定理解决实际问题。
首先,让我们来了解什么是组合数。
组合数是指从n个不同元素中取出r个元素(r≤n),不考虑元素的顺序,所组成的集合的个数。
用数学符号表示,组合数记作C(n, r)或者(nCr)。
组合数定理告诉我们,组合数可以通过以下公式计算出来:C(n, r) = n! / (r!(n-r)!)其中,n!表示n的阶乘,即n的所有正整数的乘积。
例如,5! =5 * 4 * 3 * 2 * 1 = 120。
组合数定理的重要性体现在以下几个方面:1. 组合数定理在概率论中的应用。
在计算概率时,有时需要计算从一个集合中选取特定数量的元素的可能性。
组合数定理提供了一种快速计算这种可能性的方法。
2. 组合数定理在组合优化中的应用。
组合优化是研究将元素排列或组合以获得最佳结果的一门学科。
组合数定理可以帮助寻找最优解的算法设计和解决问题。
3. 组合数定理在计算机科学中的应用。
在算法设计和分析中,我们经常需要计算从一个集合中选择特定数量的元素的可能性,以确定算法的复杂性。
组合数定理为计算这些可能性提供了有效的解决方法。
除了上述重要性之外,组合数定理还可以用于求解实际问题。
例如,在搭配衣服时,我们希望知道从若干种颜色中选择m种颜色进行搭配的可能性。
这时可以使用组合数定理来计算搭配的可能性。
另一个例子是在排列球队时,我们希望知道从n个球队中选择r个球队进行比赛的可能性。
同样,组合数定理可以帮助我们计算出这种选择的可能性。
综上所述,组合数定理是组合数学中重要的定理之一。
它不仅在理论研究中有着重要的地位,而且在实际问题的解决中也起到了指导作用。
通过运用组合数定理,我们可以更准确、高效地解决排列组合问题。
希望本文能为读者提供一些指导意义,帮助他们更好地掌握组合数定理的应用。

组合数公式大全组合数是组合数学中的一个重要概念,它描述了从一个集合中选择出若干元素进行组合的情况,而不考虑元素的顺序。
组合数在数学中有着广泛的应用,涉及到概率论、统计学、排列组合等领域。
本文将为您全面介绍组合数的相关理论和公式。
**一、组合数的定义**组合数通常记作C(n, k),表示从n个不同元素中选取k个元素的不同组合数目。
组合数的主要特点是不考虑元素的顺序,也就是说,选择元素a、b和选择元素b、a被视为同一种组合。
组合数的计算涉及到阶乘的概念,具体公式如下:C(n, k) = n! / (k! * (n - k)!)n!表示n的阶乘,即n的所有自然数乘积。
**二、组合数的递推公式**除了直接使用组合数的定义进行计算,还可以利用递推公式来快速计算组合数。
组合数有以下递推公式:C(n, k) = C(n-1, k) + C(n-1, k-1)这个递推公式的意义在于,从n个元素中选取k个元素的组合数,可以分解成两种情况:一种是包含第n个元素的组合,另一种是不包含第n个元素的组合。
通过这种递推关系,可以快速计算出较大规模的组合数。
**三、组合数的性质**组合数有一些重要的性质,例如:1. 对称性:C(n, k) = C(n, n-k),也就是说,从n个元素中选取k个元素的组合数等于从n个元素中选取n-k个元素的组合数。
2. 组合数的加法原理:C(n, k) + C(n, k+1) = C(n+1, k+1),也就是说,从n个元素中选取k个元素的组合数加上选取k+1个元素的组合数,等于从n+1个元素中选取k+1个元素的组合数。
3. 组合数的乘法原理:C(m, k) * C(n, r) = C(m+n, k+r),也就是说,从m个元素中选取k个元素的组合数乘以从n个元素中选取r个元素的组合数,等于从m+n个元素中选取k+r个元素的组合数。
**四、高级组合数公式**除了基本的组合数公式外,还有一些高级的组合数公式,如:1. Lucas定理:对于任意非负整数n和m以及质数p,Lucas定理表示C(n, m)对p取模的结果等于C(n%p, m%p)与C(n/p, m/p)的乘积对p取模的结果。

组合数的计算方法在数学中,组合数是一个非常重要的概念,用于计算从一组对象中选择出若干个对象的方式数量。
组合数的计算方法有多种,其中最经典且普遍适用的方法是利用组合公式或者递推公式进行计算。
本文将介绍这两种计算组合数的方法,并且针对具体问题给出应用示例。
一、组合公式的计算方法组合公式是计算组合数的一种基本方法,它适用于从n个不同的对象中选取r个对象的组合数计算。
组合公式的表达式如下:C(n, r) = n! / (r! * (n-r)!)其中,C(n, r)表示从n个不同的对象中选取r个对象的组合数,n!表示n的阶乘,即n*(n-1)*(n-2)*...*2*1,r!表示r的阶乘,(n-r)!表示(n-r)的阶乘。
这个公式的推导来源于组合数的基本原理,即从n个不同的对象中选取r个对象的组合数等于从n个不同的对象中选取1个对象,再从剩下的n-1个对象中选取r-1个对象的组合数。
通过这种递归的方式,最终可以得到组合公式。
通过组合公式,我们可以很方便地计算组合数。
下面通过一个具体的例子来展示:例:从5个不同的球中选择3个球的组合数是多少?根据组合公式,我们可以计算出:= 5! / (3! * 2!)= (5 * 4 * 3 * 2 * 1) / ((3 * 2 * 1) * (2 * 1))= 10因此,从5个不同的球中选择3个球的组合数是10。
二、递推公式的计算方法除了组合公式,另一种常用的计算组合数的方法是递推公式。
递推公式是通过前一项组合数与当前项组合数之间的关系,逐步计算得到的。
递推公式的表达式如下:C(n, r) = C(n-1, r-1) + C(n-1, r)其中,C(n, r)表示从n个不同的对象中选取r个对象的组合数。
通过递推公式,我们可以从已知的初始条件推导出任意给定的组合数。
下面通过一个具体的例子来展示:例:计算C(5, 3)的值。
根据递推公式,我们可以得到:C(5, 3) = C(4, 2) + C(4, 3)然后再继续展开:C(4, 2) = C(3, 1) + C(3, 2)继续展开:C(3, 1) = C(2, 0) + C(2, 1) = 1 + 2 = 3C(3, 2) = C(2, 1) + C(2, 2) = 2 + 1 = 3C(3, 3) = 1继续展开:C(4, 2) = 3 + 3 = 6C(4, 3) = 3 + 1 = 4最终得到:C(5, 3) = 6 + 4 = 10通过递推公式的计算,我们同样得到了从5个不同的球中选择3个球的组合数是10。

组合数常用公式
【原创版】
目录
一、组合数概念介绍
二、组合数公式推导
三、组合数公式应用举例
四、组合数在实际问题中的应用
正文
一、组合数概念介绍
组合数是离散数学中的一个重要概念,用于表示从 n 个元素中取出m 个元素的不同组合方式的数量。
组合数用符号 C(n,m) 表示,其中 n 表示元素总数,m 表示选取元素的个数。
例如,从 5 个数中选取 3 个
数的组合数为 C(5,3)=10,表示从 5 个数中选取 3 个数的不同组合方
式有 10 种。
二、组合数公式推导
组合数的计算公式为:C(n,m)=n!/[m!(n-m)!],其中 n! 表示 n 的阶乘,即 1*2*3*...*n。
推导过程如下:
假设有 n 个元素,我们要从中选取 m 个元素,我们可以先选择第 1 个元素,有 n 种选择方法;然后选择第 2 个元素,由于已经选择了一个,所以还剩下 n-1 种选择方法;以此类推,直到选择第 m 个元素,还剩下n-m+1 种选择方法。
因此,总共有 n*(n-1)*...*(n-m+1) 种选择方法。
而 n! 表示 n 的阶乘,即 1*2*3*...*n,因此,n!/(m!(n-m)!) 即为从 n 个元素中选取 m 个元素的不同组合方式的数量。
三、组合数公式应用举例
例如,有 5 个数,要求从这 5 个数中选取 2 个数,根据组合数公式,C(5,2)=5!/[2!(5-2)!]=10,表示从 5 个数中选取 2 个数的不同组合方式有 10 种。


组合计数公式组合计数公式,这可是数学里一个挺有意思的玩意儿!咱先来说说啥是组合计数公式。
简单来讲,它就是帮咱们数数,算算在一堆东西里挑出几个来,能有多少种不同的挑法。
比如说,从 5个苹果里选 2 个,有几种选法?这就得靠组合计数公式来帮忙啦。
组合计数公式里有个很重要的概念叫“组合数”,通常用 C(n, k) 来表示,意思是从 n 个不同元素中选取 k 个元素的组合数。
它的计算公式是:C(n, k) = n! / [k!(n - k)!] 。
这里面的“!”表示阶乘,比如说 5! = 5 × 4 × 3 × 2 × 1 。
我记得有一次,学校组织活动,要从班上的 20 个同学里选出 5 个参加比赛。
同学们都在那七嘴八舌地讨论到底有多少种选法。
这时候,我就跟他们说,咱们可以用组合计数公式来算算。
然后我就在黑板上写出了 C(20, 5) = 20! / [5!(20 - 5)!] ,算出来一共有 15504 种选法。
同学们都瞪大了眼睛,觉得太神奇了,原来数学能这么厉害,轻轻松松就算出了这么多种可能。
组合计数公式在生活中的应用可多啦。
比如说抽奖,从一堆号码里抽出几个中奖号码,这就是组合问题。
还有安排座位,一排有 10 个座位,选 3 个坐人,有多少种坐法,这也能用组合计数公式来解决。
再比如说,你去买水果,有 8 种水果,你只想买 3 种,那到底有多少种不同的买法?用组合计数公式一算就知道。
还有分东西,把 12 个玩具分给 4 个小朋友,每个小朋友至少一个,这也能通过组合计数公式来思考。
组合计数公式还能帮助咱们理解概率问题。
比如说扔骰子,扔两次,两次点数之和为 7 的概率是多少?这也得先通过组合计数公式算出总的可能性,再算出点数之和为 7 的可能性,最后就能算出概率啦。
在学习组合计数公式的时候,可别死记硬背,得理解它背后的道理。
多做几道题,多想想实际生活中的例子,这样才能真正掌握它。

组合数常用公式【原创版】目录一、组合数概念介绍二、组合数常用公式1.阶乘公式2.阶乘与组合数的关系3.组合数公式推导4.组合数公式应用实例正文一、组合数概念介绍组合数是一种数学概念,用来表示从一定数量的元素中选取一定数量元素的不同组合方式。
组合数通常用 C(n, m) 表示,其中 n 表示元素总数,m 表示选取元素的数量。
例如,从 5 个元素中选取 2 个元素的不同组合数可以表示为 C(5, 2)。
二、组合数常用公式1.阶乘公式阶乘是指从 1 乘到给定正整数的所有正整数的乘积。
例如,5 的阶乘表示为 5! = 5 × 4 × 3 × 2 × 1。
阶乘公式为:! = n × (n - 1) × (n - 2) ×...× 3 × 2 × 12.阶乘与组合数的关系组合数可以表示为阶乘的比值。
例如,从 5 个元素中选取 2 个元素的不同组合数 C(5, 2) 可以表示为:C(5, 2) = 5! / (2! × (5 - 2)!)3.组合数公式推导我们可以通过阶乘公式推导组合数公式。
首先,我们考虑从 n 个元素中选取 m 个元素的不同组合数。
我们可以将这个问题转化为从 n 个元素中选取 n-m 个元素的不同组合数,即:C(n, m) = C(n, n - m)然后,我们利用阶乘公式计算组合数:C(n, m) = n! / [(n - m)! × m!]4.组合数公式应用实例假设我们有一个班级,共有 5 名学生。
现在我们需要从这 5 名学生中选取 2 名学生参加一个活动。
我们可以使用组合数公式计算不同的选法:C(5, 2) = 5! / [(5 - 2)! × 2!]= 10因此,从 5 名学生中选取 2 名学生的不同选法共有 10 种。
总结一下,组合数常用公式包括阶乘公式和组合数公式。

组合数与排列数的计算技巧在数学中,组合数和排列数是常见的基本概念。
组合数指的是从$n$个元素中取$r$个元素的组合方式数,而排列数则是把$n$个元素进行全排列的方式数。
在实际问题中,我们常常需要计算这些数值。
本文将简要介绍组合数与排列数的概念及其计算技巧。
一、组合数组合数是指从$n$个不同元素中,任取$r$ $(r≤n)$个不同元素的组合数。
通常情况下,组合数表示为$\binom{n}{r}$。
1、计算公式组合数的计算公式如下:$$\binom{n}{r}=\frac{n!}{r!(n-r)!}$$其中,$n!=n(n-1)(n-2)\cdots2\times1$表示$n$的阶乘,$r!=(r(\mathrm{r}-1)(r-2)\cdots2\times1)$,$(n-r)!=(n-r)(n-r-1)(n-r-2)\cdots2\times1$。
由组合数的计算公式可知,当$n$和$r$较大时,直接计算可能会产生数值溢出。
为了解决这个问题,我们可以考虑使用对数等技巧对公式进行转化。
2、对数等技巧利用对数等技巧可以将组合数的计算公式转化为以下形式:$$\ln\binom{n}{r}=\ln n!-\ln r!-\ln(n-r)!$$使用对数等式可以大大缩小计算量,避免数值溢出的问题。
另外,我们还可以通过运用组合恒等式进一步简化计算。
3、组合恒等式组合恒等式包括加法公式和乘法公式两种。
这里简单介绍一下乘法公式:$$\binom{n}{r}=\binom{n-1}{r}+\binom{n-1}{r-1}$$乘法公式的证明可以通过重新排列组合方式进行推导。
4、实例对于有些问题,我们可以根据实际情况将组合数的计算简化。
例如,假设有5位候选人参加竞选,选出2位当选,那么选举的方式有多少种?根据组合数的定义,选举方式数为$\binom{5}{2}=\frac{5!}{2!(5-2)!}=10$种。
二、排列数排列数是指由$n$个不同元素进行的全排列方式数。

12个基本排列组合公式排列组合是数学中一个挺有意思的部分,咱们今天就来聊聊 12 个基本的排列组合公式。
先来说说排列公式,从 n 个不同元素中取出 m 个元素的排列数,记作 A(n, m) ,公式就是 A(n, m) = n! / (n - m)! 。
比如说,从 5 个不同的水果里选 3 个排成一排,那排法就有 A(5, 3) = 5! / (5 - 3)! = 60 种。
再看组合公式,从 n 个不同元素中取出 m 个元素的组合数,记作C(n, m) ,公式是 C(n, m) = n! / [m! (n - m)!] 。
就像从 10 个同学里选 4 个参加活动,选法就有 C(10, 4) = 10! / [4! (10 - 4)!] = 210 种。
我记得之前在课堂上,给学生们讲排列组合的时候,发生了一件特别有趣的事儿。
当时我出了一道题:在一个班级里有 8 个男生和 6 个女生,要选 3 个同学去参加比赛,其中至少有一个女生,有多少种选法?同学们开始埋头苦算,有的皱着眉头,有的咬着笔杆。
这时候,有个平时很调皮的男生突然举手说:“老师,这题太难啦,能不能少选几个同学啊?”大家都被他逗笑了。
我笑着说:“别着急,咱们一步步来分析。
”首先,我们可以算出总的选法有 C(14, 3) 种。
然后,算出全是男生的选法有 C(8, 3) 种。
那么至少有一个女生的选法就是总的选法减去全是男生的选法,即 C(14, 3) - C(8, 3) 。
经过一番计算和讲解,同学们终于恍然大悟。
咱们继续说排列组合公式。
还有一些特殊的情况,比如可重复排列,从 n 个不同元素中可重复地选取 m 个元素的排列数,公式是 n^m 。
还有环形排列,n 个不同元素的环形排列数是 (n - 1)! 。
在实际生活中,排列组合的应用可多啦。
比如说抽奖,从一堆号码里抽出中奖号码,这就是组合;而把获奖的人排个名次,这就是排列。
再比如安排座位,教室里有 30 个座位,让 25 个同学去坐,这也是一种排列组合的问题。

组合排列的公式
组合排列的公式是指用来计算组合和排列的数学公式。
1. 组合的公式
组合是指从一组对象中选择一部分对象组成一个集合。
计算组合的公式是:
C(n, k) = n! / (k!(n-k)!)
其中,n表示总对象数,k表示选取对象的数量,n!表示n的
阶乘(即n的所有正整数的乘积),k!表示k的阶乘,(n-k)!
表示n-k的阶乘。
C(n, k)表示从n个对象中选取k个对象的组
合数。
2. 排列的公式
排列是指从一组对象中按照一定的顺序选择一部分对象组成一个集合。
计算排列的公式是:
P(n, k) = n! / (n-k)!
其中,n表示总对象数,k表示选取对象的数量,n!表示n的
阶乘(即n的所有正整数的乘积),(n-k)!表示n-k的阶乘。
P(n, k)表示从n个对象中选取k个对象的排列数。
需要注意的是,组合和排列的计算中都使用了阶乘的计算公式。
组合数的计算公式组合数是一类有趣的数字,可以帮助我们解决许多有关组合的问题。
它也有着广泛的应用,是重要的数学工具。
组合数的计算公式作为一种重要的算法,可以帮助我们计算组合数。
首先,我们来看看组合数的定义。
组合数表示从一组候选项中选出n个元素的组合数,其中每个元素有k个可用的选择,并且顺序无关。
它可以表示为:C(n,k)=n!/(k! * (n-k!))。
其次,我们来讨论组合数计算公式的运用。
组合数的计算公式可以用来计算从一组候选项中选取特定数量的组合的个数。
它可以帮助我们解决问题,比如:有多少种从一组N个数字中选出K个数字的方式?此外,组合数计算公式也可以用来解决组合问题。
它可以帮助我们计算从一组N个数中选出K个数字的组合,并且可以用来解决关于特定组合事项的问题,比如:从一篮子苹果中,怎样可以选出3个,不改变它们原有的排列方式?组合数的计算公式也有着广泛的应用。
它可以用来计算不同形式的组合,比如两者的组合,三者的组合,四者的组合或更多。
它可以用来计算复杂的组合情况,如多组权重的组合,或组合问题的复杂重叠情况。
此外,它也可以用于计算组合期权价值,以及组合投资组合的收益率。
最后,组合数计算公式有着多种变体。
可以采用不同的方法来计算不同形式的组合,这些方法包括:加法原理、乘法原理、排列组合原理、哥德巴赫原理等。
除此之外,还可以采用数学归纳法来证明组合的计算公式的有效性。
总之,组合数计算公式是一种重要的算法,可以用来计算组合、解决组合问题,也有着广泛的应用。
它有着多种变体,可以采用不同的方式来计算组合,也可以用数学归纳法来证明其有效性。
综上所述,组合数计算公式具有实际上的价值,可以帮助我们解决复杂组合问题,从而实现更有效的计算结果。
组合数公式大全组合数公式是组合数学中重要的一部分,包括排列数、组合数、二项式定理等内容。
下面将详细介绍组合数公式的相关知识,包括概念、性质和常用公式等。
一、排列数的概念和性质排列数是组合数学中的一个重要概念,它指的是从n个不同元素中取出m(m≤n)个元素按照一定顺序排成一列的方法数。
排列数通常用P(n,m)表示,计算公式如下:P(n,m) = n! / (n-m)!n!表示n的阶乘,即n! = n×(n-1)×(n-2)×...×2×1。
排列数的性质包括以下几个方面:1. P(n,1) = n,即从n个元素中取出1个元素的排列数为n。
2. P(n,n) = n!,即从n个元素中取出n个元素的排列数为n的阶乘。
3. P(n,m) = n×P(n-1,m-1),即从n个元素中取出m个元素的排列数等于n乘以从n-1个元素中取出m-1个元素的排列数。
二、组合数的概念和性质组合数是组合数学中的另一个重要概念,它指的是从n个不同元素中取出m(m≤n)个元素,不考虑元素的排列顺序,共有多少种取法。
组合数通常用C(n,m)表示,计算公式如下:C(n,m) = n! / [m!(n-m)!]组合数的性质包括以下几个方面:1. C(n,0) = 1,即从n个元素中取出0个元素的组合数为1。
2. C(n,n) = 1,即从n个元素中取出n个元素的组合数为1。
3. C(n,1) = n,即从n个元素中取出1个元素的组合数为n。
4. C(n,m) = C(n,n-m),即从n个元素中取出m个元素的组合数等于从n个元素中取出n-m个元素的组合数。
三、二项式定理二项式定理是代数学中的一个重要定理,它给出了一个任意实数指数的二项式的展开式。
二项式定理表达式如下:(a+b)^n = C(n,0)*a^n*b^0 + C(n,1)*a^(n-1)*b^1 + C(n,2)*a^(n-2)*b^2 + ... + C(n,n-1)*a^1*b^(n-1) + C(n,n)*a^0*b^n在二项式定理中,C(n,m)表示从n个元素中取出m个元素的组合数,a和b是任意实数,n是任意非负整数。
常见组合数公式组合数在数学中可是个相当有趣的概念呢!咱今天就来好好聊聊常见的组合数公式。
咱先来说说组合数到底是啥。
比如说,从 5 个不同的苹果里选出 2 个,有几种选法?这就是组合问题,而计算选法的数量就得用到组合数。
常见的组合数公式有 C(n,m) = n! / [m!(n - m)!] 。
这看起来有点复杂是不?别慌,咱慢慢说。
n! 表示 n 的阶乘,就是从 1 乘到 n 。
比如说 5! 就是 1×2×3×4×5 。
那 m! 和 (n - m)! 也是同样的道理。
我记得有一次,我去超市买零食。
货架上有 10 种不同的零食,我只想选 3 种。
这时候就得用到组合数公式来算算有多少种不同的选择啦。
按照公式,C(10, 3) = 10! / [3!(10 - 3)!] ,算出来就是 120 种。
哇,原来有这么多可能性呢!再来说说组合数的性质。
比如 C(n,m) = C(n, n - m) 。
这啥意思呢?还是拿刚才那个例子,从 10 种零食里选 3 种,和从 10 种零食里选 7 种(因为 10 - 3 = 7 ),结果是一样的。
还有一个性质是 C(n,m + 1) = C(n,m) × (n - m) / (m + 1) 。
这个在计算的时候也能派上用场,能让计算更简便。
组合数公式在很多地方都有用呢!比如排列组合的问题、概率的计算等等。
就说抽奖吧,假如有 20 个人参加抽奖,只有 5 个中奖名额。
那计算中奖的组合数就能知道总共有多少种可能的中奖情况。
在数学竞赛里,组合数的题目也是经常出现的。
有时候题目看起来很复杂,但只要掌握了组合数公式和它的性质,就能迎刃而解。
总之,常见的组合数公式虽然看起来有点复杂,但只要多练习、多应用,就能熟练掌握,解决各种有趣的数学问题。
就像我们在生活中面对各种选择,只要找到了合适的方法,就能轻松应对,选出最适合自己的“组合”!。
组合数的公式
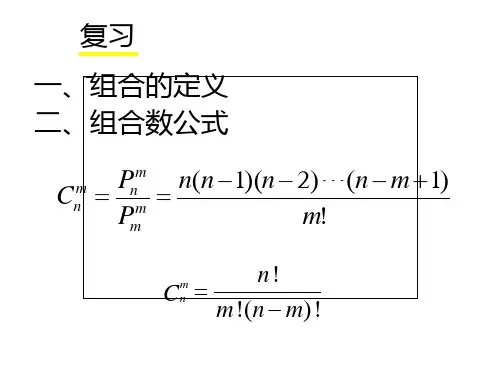
Cmn是组合数公式,Cmn=m!/[n!*(m-n)!] ,其中,n!代表n的阶乘。
组合数公式是指从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做n个不同元素中取出m个元素的组合数,用符号Cmn表示。
算法举例
1、设15000件产品中有1000件次品,从中拿出150件,求得到次品数的期望和方差。
2、设某射手对同一目标射击,直到射中R次为止,记X为使用的射击次数,已知命中率为P,求E(X)、D(X)。
这两题都要用到一些技巧。
先列出几个重要公式,证明过程中提
供变换技巧,然后把这两个题目作为例题。
先定义一个符号,用S(K=1,N)F(K)表示函数F(K)从K=1到K=N求和。
C(M-1,N-1)+C(M-1,N)=C(M,N)。
证明:
1、可直接利用组合数的公式证明。
2、(更重要的思路)。
从M个元素中任意指定一个元素。
则选出N个的方法中,包含这一个元素的有C(M-1,N-1)种组合,不包含这一个元素的有C(M-1,N)种组合。
因此,C(M-1,N-1)+C(M-1,N)=C(M,N)。