等积变形应用题练习
- 格式:ppt
- 大小:445.00 KB
- 文档页数:8

等积变形专项练习
1。
在一个底面积是31.4平方厘米的长方体玻璃容器中,有一个底面半径是1厘米的圆锥形铝块完全浸在水中,当从水中取出铝块时,容器的水面下降了0。
2厘米。
这个圆锥形铝块高多少厘米?
2。
用半径10cm高7cm的圆柱形泥巴揉成半径一样大的圆锥形,圆锥的高是多少厘米呢?
3.一个圆柱形的水桶,内部的底面半径是20厘米,高是45厘米,里面盛有30厘米深的水。
将一个底面半径是15厘米的圆锥形铁块完全沉进水里,水不溢出,水面上升了3厘米,圆锥形铁块的高是多少?
4.有一段钢可做一个底面直径8厘米,高9厘米的圆柱形零件.如果把它改制成高是12厘米的圆锥形零件,零件的底面积是多少平方厘米?
5。
一个圆柱形容器的底面半径是4分米,高6分米,里面盛满水,把水倒在棱长是8分米的正方体容器中,水深多少分米?
6.将一个底面直径是20厘米、高是9厘米的金属圆锥,全部浸没在直径是40厘米的圆柱形水槽中且水未溢出。
水槽中的水面会升高多少厘米?
7。
把一个长2米的圆柱截去4分米后,原来的表面积就减少了25.12平方分米,原来圆柱的体积是多少立方分米?
8。
在一个底面是边长为2分米的正方形的长方形水槽中,放入一块青铜(完全浸没在水中),水面上升1分米且水未溢出.(水槽厚度忽略不计)
(1)求这块青铜的体积.
(2)如果把这块青铜铸成一个底面直径是2分米的圆柱,它的高是多少?(得数保留一位小数)
9.(拓展)在一个圆柱形储水桶里,把一段半径是5cm的圆钢全部放入水中,水面就上升9cm;把圆钢竖着拉出水面8cm长后,水面就下降4cm。
求圆钢的体积。
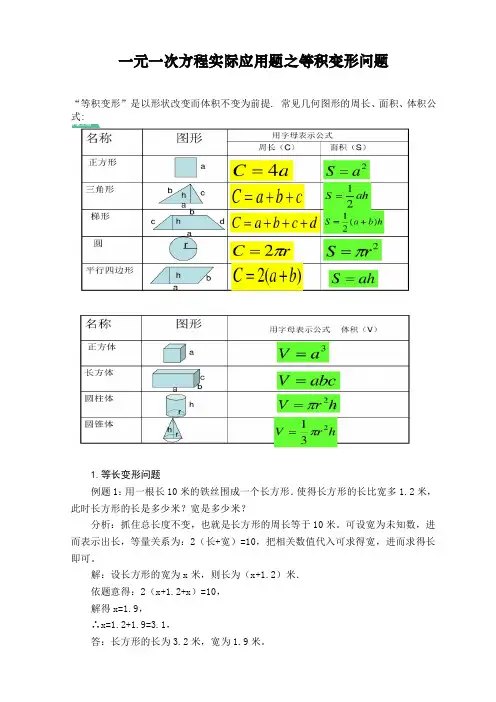
一元一次方程实际应用题之等积变形问题“等积变形”是以形状改变而体积不变为前提. 常见几何图形的周长、面积、体积公式:1.等长变形问题例题1:用一根长10米的铁丝围成一个长方形.使得长方形的长比宽多1.2米,此时长方形的长是多少米?宽是多少米?分析:抓住总长度不变,也就是长方形的周长等于10米。
可设宽为未知数,进而表示出长,等量关系为:2(长+宽)=10,把相关数值代入可求得宽,进而求得长即可。
解:设长方形的宽为x米,则长为(x+1.2)米.依题意得:2(x+1.2+x)=10,解得x=1.9,∴x=1.2+1.9=3.1,答:长方形的长为3.2米,宽为1.9米。
2.等体积变形问题例题2:要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长是多少毫米?分析:抓住锻造前后的体积不变,此题的等量关系为:锻造前的体积=锻造后的体积.据此列方程求解。
要注意的是,题目中已知直径,需要转化为半径。
解:设需截取直径为40mm的圆钢长xmm,60÷2=30(mm)、40÷2=20(mm);依题意得:π×30^2×30=π×20^2×x解得:x=67.5例题3:有一段钢材可作一个底面直径 8 厘米,高 9 厘米的圆柱形零件。
如果把它改制成高是 12 厘米的圆锥形零件,零件的底面积是多少平方厘米?分析:根据“底面直径8厘米,高9厘米的圆柱形零件”,利用圆柱体积公式,可以求出圆柱的体积,又因为把圆柱形的零件改制成圆锥形零件时,此段钢的体积不变,根据体积不变列出方程求解。
解:零件的底面积是x平方厘米。
8÷2=4(厘米)依题意得:3×π×4^2×9=x×12解得:x=36π答:零件的底面积是36π平方厘米。
3.等面积变形问题例题4:如图,某小学将一块梯形空地改成宽为30m的长方形运动场地,要求面积不变.若在改造后的运动场地,小王、小李两人同时从点A出发,小李沿着长方形边顺时针跑,小王则是逆时针跑,并且小王每秒比小李多跑2m,经过10秒钟他们相遇.(1)求长方形的长;(2)求小王、小李两人的速度分析:(1)求得原梯形的面积,利用面积不变和长方形的面积求得长方形的长即可;(2)设小李的速度是xm/s,则小王的速度是(x+2)m/s,利用10秒钟他们相遇所走的路程为长方形的周长列出方程解决问题。
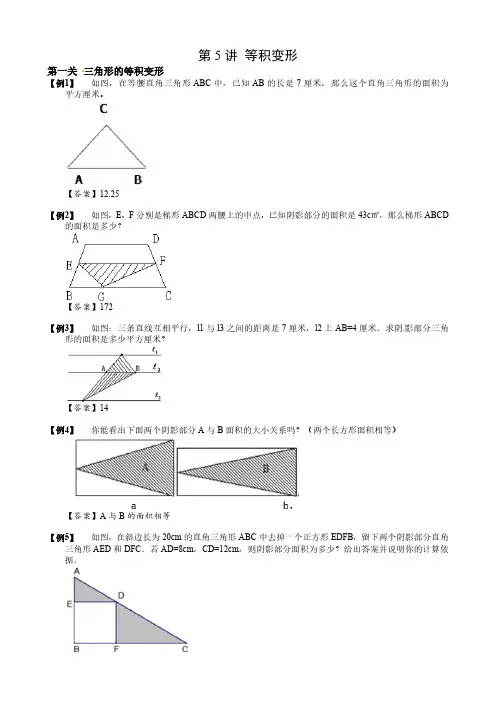
第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。

专项练习—等积变形1. 已知直角三角形的两条直角边长分别是21和28,求这个三角形内的最大正方形的边长?2. 如图,四边形ABCD 是等腰梯形,ADBE 是平行四边形,面积等于8,还知道三角形BCE 的面积是2,那么三角形CDE 的面积是多少?3. 开发商准备在一块地面上盖商品房,这块长方形地形情况如图,甲处比乙处高50厘米.现在要把这块地推平整,要从甲处取下多少厘米厚的土填在乙处上?ED CBA50厘米100米60米30米乙甲4. 如图,折线A ﹣B ﹣C ﹣D 的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分.点E 在矩形的边上,使得线段AE 也平分矩形的面积.已知线段AB =30,BC =24,CD =10,求DE 的长.5. 如图是直角三角形中有一个内接正方形,求图中阴影部分的面积.单位:厘米.提示:分拆图形时常用“分割、填补、组合、旋转”等方法.6. 雨哗哗地不停地下着.如果在雨地放一个如图1那样的长方体的容器(单位:厘米),雨水将它灌满要用1小时.雨水灌满图2容器各需多长时间?E D CBA图2图1107. 把一个底面直径是4厘米的圆柱底面分成许多相等的扇形,然后沿着直径切开,拼成一个和它体积相等的长方体,这个长方体的表面积比原来圆柱的表面积增加了20平方厘米,这个长方体的体积是多少立方厘米?8. 如图,O 是半圆的圆心,AC =BC ,CD =DB ,AB =12厘米,求阴影部分的面积.9. 如图,直角梯形ABCD 中,AB =12,BC =8,CD =9,且三角形AED 、三角形FCD 和四边形EBFD 的面积相等,求三角形DEF 的面积.BAFEDCBA10.边长分别为8cm和6cm的两个正方形ABCD与BEFG如图并排放在一起.连接DE交BG于P,则图中阴影部分APEG的面积是多少?11.有一个长方体铁块,长8分米,宽4分米,高3分米.把它完全铸成一个圆柱,圆柱的底面半径是5分米,高是多少分米?(保留一位小数)12.有两个高度相等的容器A和B,已知A容器半径是6厘米,B容器的半径是8厘米,现在把A容器装满水,然后全部倒入B容器中,测得B容器中的水深比A容器高的3 4低了3厘米.求A、B两个容器的高是多少厘米?E13. 如图,正方形ABCD 的边长为4cm ,则图中阴影部分的面积为多少平方厘米?14. 如图,有边长分别是15分米和20分米的两个正方形,一条直线把这两个相连的正方形分成甲、乙、丙、丁四部分.甲三角形的面积比丙三角形的面积大多少平方分米?15. 如图,ABCD 是等腰梯形,上底和下底分别是16厘米和24厘米,高是12厘米.阴影部分的面积是多少?丁丙乙甲CD。

一元一次方程应用题(6)(等长变形、等积
变形)
1.假设原长方形的长为x,宽为y,则根据周长公式
2(x+y)=26,可得x+y=13.将长减少1,宽增加2后得到的正方
形的边长为y+2,因此有y+2=x-1.将这两个方程联立解得x=9,y=4,所以原长方形的长为9cm,宽为4cm。
2.圆锥体的体积为1/3πr^2h,圆柱体的体积为πr^2h,两
者相等,因此可得圆柱体的高为8×(30/10)^2=72cm,所以圆
柱体内的水高为8cm。
3.设新的长方形宽为x,则根据折叠后周长不变可得
2x+10=18,解得x=4,因此新的长方形的长为9cm,宽为4cm。
4.正方体的体积为20^3=8000cm^3,盛水量筒的容积为
12×h,其中h为水面升高的高度,因此有12h=8000,解得
h=666.67cm,所以水面升高了666.67/12≈55.56cm。
5.设大长方形面积为S,则重叠部分面积为S/6,小长方
形面积为S/4,阴影部分面积为224cm^2,因此有S/6-S/4=224,解得S=1344,所以重叠部分面积为S/6=224cm^2.
6.(1) 第一个中的水体积为π(4^2)×16=256π,第二个的底
面积为π(8^2)=64π,因此第二个中的水高为256π/64π=4cm。
2) 将1插入2后,1中的水体积为π(4^2)×10=160π,2中的水体积为π(8^2)×10=640π,因此水位上升了640π-
256π=384π,所以水面升高了384π/(π(8^2))≈1.5cm。

等积变形应用题
1、把一段铁丝围成长方形;可以使它的长比宽多2cm;如果围成正方形;边长刚好为5cm.求所围成的长方形的长和宽各为多少
2、用一根20厘米的铁丝围成一个长方形1使得长方形的长比宽大2.6厘米;此时;长方形的长、宽各是多少厘米2使得长方形的长与宽相等;此时正方形的面积是多少3若围成一个圆;面积是多少
3、有一块棱长为4厘米的正方体铜块;要将它熔化后铸成长2厘米、宽4厘米的长方体铜块;铸成后的铜块的高是多少厘米不计损耗
4、某铜铁厂要锻造长、宽、高分别为260mm、150 mm、130 mm的长方体毛坯;需要截取底面积为 130 mm2的方钢多长
5、某机器加工厂要锻造一个毛胚;上面是一个直径为20毫米;高为40毫米的圆柱;下面也是一个圆柱;直径为60毫米;高为20毫米;问需要直径为40毫米的圆钢多长
6、将一罐满水的直径为40厘米;高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里;问这时水的高度是多少
7、一个直径为1.2米高为1.5米的圆柱形水桶;已装满水;向一个底面边长为1米的正方形铁盒倒水;当铁盒装满水时;水桶中的水高度下降了多少米..
8、如图所示;一个养鸡场的一边靠着墙;墙长14米;其他三边用竹篱笆围成;现有竹篱笆的长为35米;小王打算建一个养鸡场;长比宽多5米;小赵打算建一个养鸡场;长比宽多2米.你认为谁的设计较合理这时养鸡场的面积是多少。
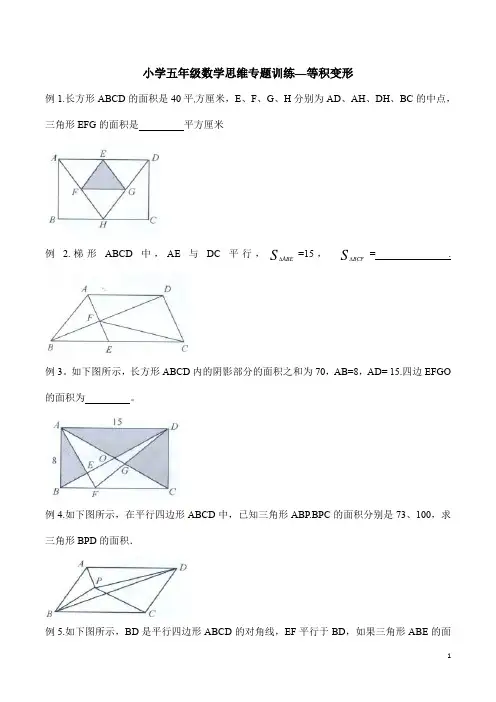
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。

一元一次方程解应用题————等积变形问题复习:常用几何图形的计算公式长方形的周长 = 长方形的面积 =三角形的周长 = 三角形的面积 =圆的周长= 圆的面积=长方体的体积 = 圆柱体的体积 =想一想:请指出下列过程中,哪些量发生了变化,哪些量保持不变?1、把一小杯水倒入另一只大杯中;2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;3、用一块橡皮泥先做成一个立方体,再把它改变成球。
问题1(1)用一根长8米的铁丝围成一个长方形.使长方形的宽比长少1米,求这个长方形的面积.(2)用一根长8米的铁丝围成一个正方形,求这个正方形的面积.(3)用一根长8米的铁丝围成一个圆,求这个圆的面积.(4)在周长相等的长方形、正方形、圆中,谁的面积最大?谁的面积最小?精讲例题1.将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是 20厘米的“矮胖”形圆柱,高变成了多少?等量关系:解设锻压后圆柱的高为x厘米,填写下表锻压前锻压后底面半径高体积练习:1、如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和90毫米的长方体毛坯底板,应截取圆钢多少(计算时思考:题目中有哪些已知量和未知量?它们之间有什么关系?如何设未知数?已知:圆钢直径(200mm)、长方体毛胚的长宽高(300mm、300mm、90mm)未知:圆钢的高相等关系:圆钢体积=长方体毛胚的体积设未知数:设应截取圆钢 x 毫米。
2.已知一圆柱形容器底面半径为0.5m,高为1.5m,里面盛有1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器水面将升高多少?小结:说说列方程解应用题的一般步骤:1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.2、用代数式表示有关的量.3、根据等量关系列出方程.4、解方程,求出未知数的值.5、检验求得的值是否正确和符合实际情形,并写出答案.等积变形是以形状改变而体积不变为前提。

七年上册数学应用题提高练习训练七年上册数学应用题提高练习训练一、等积变形问题一、等积变形问题常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变. ①圆柱体的体积公式①圆柱体的体积公式①圆柱体的体积公式 V= V= V=底面积×高=底面积×高=底面积×高=S S ·h =p r2h②长方体的体积②长方体的体积 V V V=长×宽×高==长×宽×高==长×宽×高=abc abc1.把一段铁丝围成长方形,发现长比宽多2cm 2cm;围成正方形时,边长刚好为;围成正方形时,边长刚好为4cm 4cm.求所.求所围成的长方形的长和宽各是多少?围成的长方形的长和宽各是多少?2.用一个底面半径为40mm 40mm,高为,高为120mm 的圆柱形玻璃杯向一个底面半径为100mm 的大圆柱形玻璃杯中倒水,倒了满满10杯水后,大玻璃杯的液面离杯口还有10mm 10mm,大玻璃,大玻璃杯的高度是多少?杯的高度是多少?3.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成.现有长为35米的竹篱笆,小王打算用它围成一个鸡场,其中长比宽多5米;小赵也打算用它围成一个鸡场,其中长比宽多2米.你认为谁的设计符合实际?按照他的设计,鸡场的面积是多少?多少?4.将一个装满水的内部长、宽、高分别为300毫米,毫米,300300毫米和80•80•毫米的长方体铁盒毫米的长方体铁盒中的水,倒入一个内径为200毫米的圆柱形水桶中,正好倒满,求圆柱形水桶的高(精确到0.1毫米,p ≈3.143.14)).5.在一个底面直径为5cm 5cm,高为,高为18cm 的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径是6cm 6cm、、高是10cm 的圆柱形玻璃杯中,的圆柱形玻璃杯中,能否完全装下?若装不下,能否完全装下?若装不下,能否完全装下?若装不下,那么瓶内水还那么瓶内水还剩多高?若未能装满,求杯内水面离杯口的距离.二、打折销售问题二、打折销售问题(1)商品利润=商品售价-商品成本价商品利润=商品售价-商品成本价(2)商品利润率=商品利润商品成本价×100% (3)商品销售额=商品销售价×商品销售量(4(4)商品的销售利润=(销售价-成本价)×销售量)商品的销售利润=(销售价-成本价)×销售量(5)商品打几折出售,就是按原标价的百分之几十出售,如打8折出售,即按原标价的80%80%出售.出售.出售. 1.随着计算机技术的迅猛发展,电脑价格大幅度下降,某品牌电脑今年每台售出价格为4200元,比去年降低了30%30%,问去年该品牌电脑每台售出价为多少元?,问去年该品牌电脑每台售出价为多少元?2、东方商场把进价为1890元的某商品按标价的8折出售,仍获利10%10%,则该商品的标,则该商品的标价为多少?价为多少?3、某种商品的进价是1000元,售价为1500元,元, 由于销售情况不好,商店决定降价出售,但又要售,但又要保证利润不低于5%5%,那么商店最多降多少元出售此商品。

等积变形数学题
1、把一块长19cm,宽5cm,高3cm的长方体铝块和一个棱长7cm的正方体铝
块熔铸成一个底面周长为的圆柱体铝块,求圆柱体铝块的高是多少
2、一个圆锥体沙堆,底面积是,高是,用这堆沙在10m宽的公路上铺2cm厚
的路面,能铺多少米
3、一个酸奶瓶,他的瓶身呈圆柱体(不包括瓶颈),容积是,当瓶子正放时,
瓶内酸奶高为8cm,瓶子倒放时,空余部分高为2cm,请你算一算瓶内酸奶的体积是多少cm3
4、在一个底面直径5cm,高是18cm的圆柱体杯中倒满水,倒入直径6cm,高
10cm的圆柱形杯中,若装不下,求剩下水的体积,若装得下,求水面离杯口有多高
5、在一个圆柱体水桶里,把一段半径是5cm的圆钢全部放入水中,水面就上升
9cm,把圆钢竖着拉出水面8cm长后,水面就下降4cm,求圆钢体积
6、有A、B两个圆柱体容器,最初在容器A里装有2升水,容器B是空的,现
在往两个容器中以每分钟升的流量注入水,4分钟后,两个容器的水面高度相等。
设B的底面半径是5cm,那么A的底面直径是多少cm。
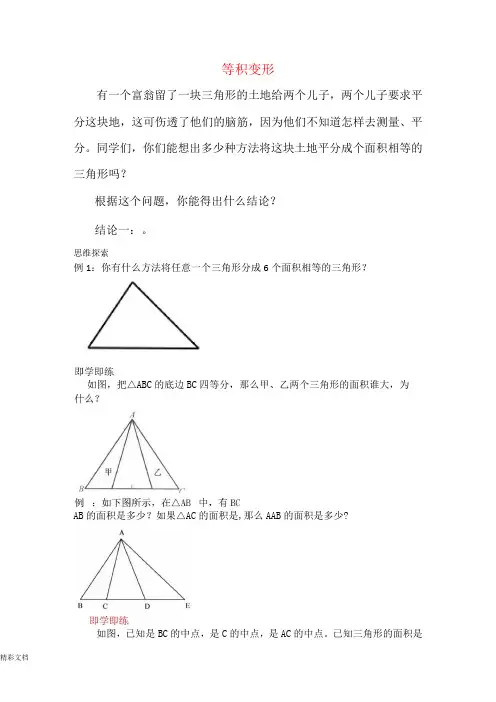
等积变形有一个富翁留了一块三角形的土地给两个儿子,两个儿子要求平分这块地,这可伤透了他们的脑筋,因为他们不知道怎样去测量、平分。
同学们,你们能想出多少种方法将这块土地平分成个面积相等的三角形吗?根据这个问题,你能得出什么结论?结论一:。
思维探索例1:你有什么方法将任意一个三角形分成6个面积相等的三角形?如图,把△ABC的底边BC四等分,那么甲、乙两个三角形的面积谁大,为AB的面积是多少?如果△AC的面积是,那么AAB的面积是多少?如图,已知是BC的中点,是C的中点,是AC的中点。
已知三角形的面积是平方厘米,那么三角形ABC的面积是多少平方厘米?A思维探索例:(平行线间的等积变形)如下图,△和厶夹在一组平行线之间,且有公共底边,那么△和厶的面积关系是怎样的?结论拓展:夹在平行线间的一组同底三角形面积相等例:如图,在梯形中共有个三角形,其中面积相等的三角形有哪几对?即学即练如下图,在梯形A中,梯形A的面积是,AA的面积融会贯通例:如图,在直角三角形A中,D、E分别是A、A的中点,如果△AED的面积是即学即练如下图,在AA中,D、E是所在边的中点,如果AA的面积是,那么△DE的面积是多少?例:如图,A和DE都是长方形,A的长是厘米,的长是厘米。
那么图中阴影部分的面积是多少平方厘米?即学即练在边长为厘米的正方形中有一点,将点分别和四条边的中点相连,如下图,求阴影部分的面积。
练习册知识导航一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状。
为便于实际问题的研究,我们还会常常用到以下结论:()等底等高的两个三角形面积相等;()底在同一条直线上并且相等,该底所对的角的的顶点是同一个点或在与底平行精彩文档如图, 是直角的直线上,这两个三角形面积相等;()若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
等积变换1、等面积图形拼接类1、小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG .请你参考小明的做法解决下列问题:(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形.要求:在图3中画出并指明拼接成的平行四边形(画出一个..符合条件的平行四边形即可);(2)如图4,在面积为2的平行四边形ABCD 中,点E 、F 、G 、H 分别是边AB 、 BC 、CD 、DA 的中点,分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ .请在图4中探究平行四边形MNPQ 面积的大小(画图..并直接写出结果).2、根据所给的图形解答下列问题:(1)如图1,△ABC 中,AB=AC ,∠BAC =90°,AD ⊥BC 于D ,把△ABD 绕点A旋转,图1图2图3图4并拼接成一个与△ABC 面积相等的正方形,请你在图1中完成这个作图;(2)如图2,△ABC 中,AB=AC ,∠BAC =90°,请你设计一种与(1)不同的方法,将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形;(3)设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形, 请你依据此矩形画出正方形,并根据你所画的图形,证明正方形面积等于矩形ABCD 的面积的结论.A BCD图3图2图1CBAAB CD2、等分面积类问题1、请作一条直线通过割补把下面的四边形变成面积相等的三角形2、如图,一块矩形的铁皮ABCD 被割去一个小矩形部分DEFG ,剩下一个五边形ABCGFE ,请作一条直线把剩下的五边形分成面积相等的两部分BCADG E D BCFAABCDAD3、(1)请过△ABC 边BC 中点D 作一条直线平分△ABC 的面积(2)请过△ABC 边BC 中点D 外任一点P 作一条直线平分△ABC 的面积4、如图,梯形纸片ABCD 中,AD ∥BC 且AB DC.设AD=a,BC=b. 过AD 中点和BC 的中点的直线可将梯形纸片ABCD 面积分成面积相等的两部分. 请你再设计一种方法:只须用剪子剪一次将梯形纸片ABCD 分割成面积相等的二部分,画出设计的图形并简要说明你的分割方法.DBCADBCAP5、如图是王大爷的一块四边形菜地,在A处有一口井,王大爷要想从A处引一条笔直的水渠,且这条笔直的水渠将四边形菜地分成面积相等的两部分.请你为王大爷设计一条引水渠的方案,画出图形,并简要写出作图的主要步骤.Welcome To Download !!!欢迎您的下载,资料仅供参考!。
等积变形题目五年级等积变形是指图形在形状发生改变的过程中,其面积大小保持不变的一种变形。
例如,一个四边形可以变成正方形、长方形、梯形或不规则的其他几边形,只要其面积大小保持不变,就是等积变形。
1.问题:有一个长方体,它的长、宽、高分别是a、b、c(a>b>c),现在进行等积变形,把长方体的长变成d,宽和高保持不变。
请问变形后的长方体与原长方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原长方体和变形后的长方体的体积是相等的。
2.问题:有一个正方体,边长为a,现在进行等积变形,把正方体的边长变成d,请问变形后的正方体与原正方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原正方体和变形后的正方体的体积是相等的。
3.问题:有一个三角形,它的底边为a,高为h,现在进行等积变形,把三角形的底边变成d,高保持不变。
请问变形后的三角形与原三角形的面积相比,是变大还是变小?解析:因为等积变形不改变三角形的面积,所以原三角形和变形后的三角形的面积是相等的。
4.问题:有一个正方形,边长为a,现在进行等积变形,把正方形的边长变成d,请问变形后的正方形与原正方形的面积相比,是变大还是变小?解析:因为等积变形不改变正方形的面积,所以原正方形和变形后的正方形的面积是相等的。
5.问题:有一个长方形,长为a,宽为b,现在进行等积变形,把长方形的长变成d,宽保持不变。
请问变形后的长方形与原长方形的面积相比,是变大还是变小?解析:因为等积变形不改变长方形的面积,所以原长方形和变形后的长方形的面积是相等的。
五年级等积变形题一、等积变形题目。
1. 一个长方体水箱,从里面量长6分米,宽5分米,高4分米。
先倒入82升水,再浸入一块棱长2分米的正方体铁块,这时水面离水箱口1分米。
求水箱的容积是多少升?- 解析:正方体铁块体积为2×2×2 = 8立方分米,因为1立方分米= 1升,所以8立方分米= 8升。
倒入水的体积是82升,此时水和铁块总体积为82+8=90升。
水面离水箱口1分米,则此时水和铁块占水箱的高度是4 - 1=3分米。
水箱底面积为6×5 = 30平方分米,根据长方体体积公式V=Sh(S是底面积,h是高),那么3分米高的水和铁块的体积对应的水箱容积部分为30×3 = 90升,所以水箱容积为90÷3×4 = 120升。
2. 有一个底面积是300平方厘米、高10厘米的长方体,里面盛有5厘米深的水。
现在把一块石头浸没到水里,水面上升2厘米。
这块石头的体积是多少立方厘米?- 解析:因为石头浸没到水中,水面上升的体积就是石头的体积。
长方体底面积是300平方厘米,水面上升了2厘米,根据长方体体积公式V = Sh,石头体积为300×2=600立方厘米。
3. 一个正方体容器棱长为6分米,里面装满水。
现将水倒入一个长0.8米、宽0.6米的长方体容器中,水面高多少分米?- 解析:首先统一单位,0.8米= 8分米,0.6米= 6分米。
正方体容器棱长6分米,则水的体积为6×6×6 = 216立方分米。
将水倒入长方体容器中,长方体容器底面积为8×6 = 48平方分米,根据h=(V)/(S)(h是高,V是体积,S是底面积),水面高度为216÷48 = 4.5分米。
4. 把一块棱长12厘米的正方体铁块熔铸成一个底面积是144平方厘米的长方体铁块,这个长方体铁块的高是多少厘米?- 解析:正方体铁块体积为12×12×12 = 1728立方厘米。
列方程解应用题之等积变形问题和利润问题等积变形问题:1、用直径为4cm的圆柱形钢材,铸造3个直径为2cm,高为16cm的圆柱形零件,问需要截取多长的圆柱形钢材?2、一个直径为10cm,高为12cm的圆柱形量杯,把它盛满水后倒入底面直径为12cm,高为10cm的圆柱形量杯,问倒入后,水面离杯口还有多少厘米?3、在一个底面直径5cm,高18cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径6cm、高10cm的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离。
4、一只直径为90毫米的圆柱形玻璃杯中装满了水,把杯中的水倒入一个底面边长为131毫米的正方形、高为81毫米的长方体铁盒中,当铁盒装满水时,玻璃杯中的水大约下降了多少?利润问题:1、某商店在元旦时实行7.5折优惠销售方案,则售价为15元的商品,标价为多少元?2、一件休闲服按标价的六折出售,店主可赚32元,已知该衣服进价为58元,则原标价为多少元?3、商店里有种衣服,每件售价600元可获利20%,现在客户以2800元总价购买了若干件衣服,而商家仍有12%的利润,问客户买了几件衣服?4、某商店因换季准备打折销售,如果按定价的7.5折出售将亏本25元,而按定价的9.5折出售将赚20元,问这种商品的定价是多少?5、一家商店将某型号彩电先按原售价提高40%,然后在广告中写上“大酬宾,八折优惠”,经顾客投诉后,执法部门按已得非法收入的10倍处以每台2700元的罚款,求每台彩电的原售价。
6、某人去年在银行存入人民币若干元,年利率为2.25%,今年到期后将获得利息360元,则他存入的人民币为多少元?7、某人想用一笔钱买年利率为2.89%的3年期国库券,如果他想3年后本息和为2万元,现在应买国库券多少万元?8、某企业向银行贷了一笔款,商定归还期为一年,年利率为6%,该企业立即用这笔款购买了一批货物,再以高于买入价的35%出售,经一年售完,用所得收入还清贷款本利,还剩14.5万元,问这笔贷款是多少万元?9、肖青的妈妈前年买了某公司的二年期债券4500元,今年到期,扣除利息税后,共得本利和约4700元,问这种债券的年利率是多少?(精确到0.01%)10、某种商品每件进价为180元,按标价的九折销售时,利润率为20%,这种商品每件标价是多少元?。