山东省威海市2016届高三第二次模拟考试文科综合试题及答案

2016年威海市高考模拟考试文科综合本试题卷共15页，48题(含选考题)。

全卷满分300分。

考试用时150分钟。

注意事项：1．本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

答题前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第I卷时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3．回答第II卷时，将答案写在答题卡上，写在试卷上无效。

4．考试结束，将本试卷和答题卡一并交回。

第I卷本卷共35小题。

每小题4分，共140分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

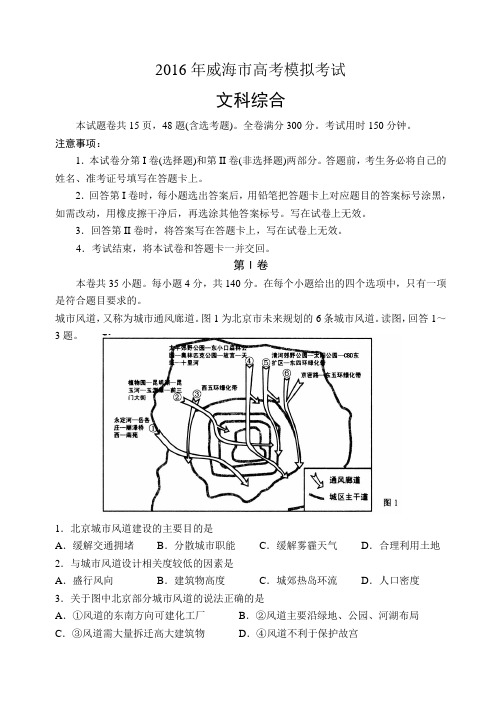
城市风道，又称为城市通风廊道。

图1为北京市未来规划的6条城市风道。

读图，回答1～3题。

1．北京城市风道建设的主要目的是A．缓解交通拥堵B．分散城市职能C．缓解雾霾天气D．合理利用土地2．与城市风道设计相关度较低的因素是A．盛行风向B．建筑物高度C．城郊热岛环流D．人口密度3．关于图中北京部分城市风道的说法正确的是A．①风道的东南方向可建化工厂B．②风道主要沿绿地、公园、河湖布局C．③风道需大量拆迁高大建筑物D．④风道不利于保护故宫极地涡旋(简称“极涡”)是指通常盘踞在极地高空的冷性大型涡旋，其位置、强度、移动对极地及高纬地区的天气影响明显。

2015年12月底，一个位于冰岛的强大风暴将北大西洋热量带向北极，迫使北极“极涡”离开极地，携带冷空气南下，造成我国大部分地区1月中下旬爆发极其罕见的超强寒潮。

图2为2016年1月2 3日北极“极涡”位置示意图。

据此完成4~6题。

4．极地涡旋的形成原因是A．冰岛低压北上，极地气流上升B．北极地区海域广阔，形成热低压C．接受太阳辐射热量少，气流下沉D．来自副极地上空的气流，在此下沉5．图示时刻，甲地高空的风向是A．东风B．东北风C．西南风D．西风6．此次“极涡”南下，说明了A．全球气候开始变冷B．厄尔尼诺现象对地球的影响变小C．西伯利亚地区不是我国冬季冷空气的唯一来源D．寒带的范围变大甘肃省是我国重要的农产品基地，其农产品种类多、品质好。

绝密★启用前2016届山东平度高三高考模拟二文综地理试卷（带解析）试卷副标题考试范围：xxx ；考试时间：34分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）图为“粤、苏、贵、桂四省区2010年和2050年老年人口比重变化趋势图”，完成下列问题。

1、导致图中老年人口变化趋势的最主要原因是（ ） A ．人口寿命的延长 B ．人口出生率的降低 C ．经济、医疗水平的提高 D ．省际人口的迁移2、据图判断，今后我国应优先建立、完善养老体系的地区是（ ） ①农村 ②城镇 ③经济欠发达省份 ④经济发达省份 A ．①③B ．①④C ．②③D ．②④3、党的十八届五中全会会议决定：全面实施一对夫妇可生育两个孩子政策，这对我国可能产生的影响有（ ） A ．可暂时缓解老龄化 B ．造成性别比失调 C ．社会养老负担进一步加重D ．人均GDP 快速增长读下表，完成下列问题。

4、关于我国不同区域农村土地流转的说法，正确的是（ ） A ．甘肃玉门土地流转方式以转让为主 B ．我国中部地区土地流转面积比东部地区大 C ．土地流转方式中苏州租赁耕地面积比株洲的大 D ．湖南株洲的耕地总面积比山西原平少5、关于促使各地进行土地流转原因的叙述，下列说法错误的是（ ） A ．大批农民工进城，导致农村大片土地撂荒，危及粮食安全 B ．原有的以家庭为单位小块经营，效率低下，农业产出低 C ．农村人口老龄化加剧，农业从业人口老化 D ．农村地区基础设施完善，农业科技进步6、下列关于农村“土地流转”的影响说法，不正确的是（ ） A ．能增加农村耕地面积 B ．可以提高农产品商品率C ．有利于农业生产的专业化、机械化D ．有利于农业生产的规模化、集约化天文日照时数是指如果一个地方一直都是晴天，太阳照射地面的时数，也就是实际日照时数的上限。

2016山东高考文综试题及答案2016年普通高等学校招生全国统一考试（山东卷）文科综合能力测试本试卷分第Ⅰ卷和第Ⅱ卷两部分，共300分。

考试时间150分钟。

第Ⅰ卷1至6页，第Ⅱ卷7至12页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题，共140分）一、选择题：本题共35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是正确的。

1. 2016年4月24日，中国首个“中国航天日”。

24年前的4月21日，中国“长征二号E”运载火箭成功发射美国制造的“澳赛特B1”通信卫星，中国航天业迈入了国际卫星发射市场。

24年后的今天，中国航天业已跻身世界前列，这得益于A. 坚持独立自主、自力更生原则B. 坚持改革开放，坚持引进来和走出去相结合C. 坚持公有制为主体、多种所有制经济共同发展的基本经济制度D. 坚持按劳分配为主体、多种分配方式并存的分配制度答案：B2. 2016年1月16日，亚洲基础设施投资银行正式开业。

亚投行的成立，将有效增加亚洲地区基础设施投资，推动区域互联互通和经济一体化进程，也有利于改善亚洲发展中成员国的投资环境，创造就业，提升中长期发展潜力，对亚洲乃至全球经济增长带来积极提振作用。

这表明A. 经济全球化实质上是以发达资本主义国家为主导的B. 发展是解决我国一切问题的基础和关键C. 经济全球化是生产力发展的产物，推动了生产力的发展D. 经济全球化使世界各国的经济联系在一起，任何国家经济都不可能孤立发展答案：C3. 2016年3月16日，第十二届全国人民代表大会第四次会议表决通过了《中华人民共和国慈善法》。

该法规定，慈善组织应当执行国家统一的会计制度，依法进行会计核算，建立健全会计监督制度，并接受政府和社会的监督。

这表明A. 人民代表大会是我国最高国家权力机关B. 全国人民代表大会具有最高立法权C. 政府接受人民代表大会的监督D. 人民代表大会制度是我国的根本政治制度答案：B4. 2016年3月4日，习近平总书记看望参加全国政协十二届四次会议的民建、工商联委员时，首次用“亲”“清”两字定位新型政商关系。

2016普通高等学校招生全国统一考试文科综合能力测试本试题卷共页，48题（含选考题）。

全卷满分300分。

考试用时150分钟。

★祝考试顺利★注意事项：1、答卷前，先将自己的姓名、准考证号填写在试题卷和答题卡上。

用合乎要求的2B 铅笔将答题卡上试卷类型A后方的方框涂黑。

2、选择题的作答：每小题选出答案后，用合乎要求的2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3、非选择题的作答：用合乎要求的签字笔直接答在答题卡上对应的答题区域内。

在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用合乎要求的2B铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

选择题共35小题，每小题4分，共140分在每小题给出的四个选项中，只有一项是符合题目要求的。

我国某地的小张同学，早晨在上学路上会习惯性地观察天空的太阳。

图中SN为南北方向，PQ垂直SN，a、b是在两个不同日期但北京时间都是7:00，小张经过空旷的P点所看到的天空中太阳的位置。

完成1-2题。

1.从以上信息可以判断P点的经度是A.95°EB.105°EC.120°ED.135°E2.在a、b这两个日期，P点当日正午太阳高度分别是Ha、Hb，且Ha<Hb则A.P点位于北温带B.P点位于热带C.P点在北回归线D.以上都有可能下图为我国某区域冬季某日8时至次日8时的降雪量和积雪深度分布图，该时段该区域风向主要为偏东风，云量分布差异不明显。

完成3-4题。

3.造成该区域东西部积雪深度差异的主要因素是A.降雪量B.温度C.光照D.地形4.图中M地积雪深度低于周围地区，该地可能是A.农田B.林地C.城区D.乡村下图为“某地区自然景观分布示意图”以及“P区域的等高线图”。

读图，回答5-6题。

5.图中P处的地貌名称是A．河漫滩 B．冲积扇 C．三角洲 D．侵蚀平原6.P处沉积作用最显著的月份是A．1月 B．3月 C．7月 D．10月1980年我国开始执行一对夫妇只能生育一胎的计划生育政策，2013年启动实施一方是独生子女的夫妇可生育两个孩子的政策。

2016年威海市高考模拟考试语文本试卷分为第I卷和第II卷两部分，共8页。

满分150分。

考试用时150分钟。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答案卡和试卷规定的位置上。

2．第I卷每小题选出答案后，用2 B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案标号。

答案不能答在试卷上。

3．第II卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上：如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

第I卷(共36分)一、(15分，每小题3分)阅读下面的文字，完成1～3题。

九寨沟的湖泊独具特色。

湖水终年碧蓝澄．澈，明丽见底，而且随着光照变化、季节推移，(呈现／表现)不同的色调与水韵。

雄浑的，碧波噌吰；平静的，水波澹澹．．。

每当风平浪静，蓝天，白云，远山，近树，倒映湖中。

一湖之中，鹅黄、黛绿、赤褐、绛红、翠碧等色彩组成不(规则／规律)的几何图形，__________。

视角移动，色彩亦变，一步一态，变幻无穷．．．．。

有的湖泊，微波细浪，璀璨成花，远视俨如燃烧的海洋；有的湖泊，湖底静伏着钙化礁堤，朦胧中仿佛姣龙游动。

整个沟内，奇湖错落，目不暇接．．．．。

九寨沟也是瀑布王国。

所有的瀑布都从密林里狂奔出来，在山岩上腾跃呼啸，几经跌宕．，形成叠瀑，声若滚雷，似一群银龙竞跃．．．．，________，化作迷茫的水雾。

朝阳照射，出现奇丽的彩虹，使人赏心悦目，(留恋／流连)忘返。

1．文中加点字的字音和字形都不正确的一项是A．澄(chéng)澈姣龙游动B．澹澹(chán) 变幻无穷C．礁堤(tī) 银龙竟跃D．跌宕(dàng) 目不暇接2．依次选用文中括号里的词语，最恰当的一项是A．表现规则留恋B．呈现规律流连C．呈现规则流连D．表现规律留恋3．在文中两处横线上依次填入语句，衔接最恰当的一项是A．相互浸染，斑驳陆离无数小水珠被激溅起来B．斑驳陆离，相互浸染激溅起无数小水珠C．斑驳陆离，相互浸染无数小水珠被激溅起来D．相互浸染，斑驳陆离激溅起无数小水珠4．下列各句中，加点成语使用正确的一项是A．“妈妈好，还是爸爸好?”这种排斥性选择往往会误导孩子挖空心思揣摩大人心理，养成随机应变．．．．的性格。

天津市武清区2015～2016学年度高三年级第二学期第三次模拟考试数学(理科)试题注意事项：1．选择题选出答案后，请用铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

2．请用黑色墨水的钢笔或签字笔解答填空题、解答题。

一．选择题（本大题共8 小题，每小题5分，共40分。

每小题给出的四个选项中，只有一项是符合题目要求的）1．若i 为虚数单位，则复数ii +3等于（ ）（A ）i 2321+- （B ）i 2321+ （C ）i 4341+-（D ）i 4341+2．已知y x ,满足约束条件⎪⎩⎪⎨⎧≤-≤-≥-+03032x y x y x ，则目标函数y x z 32-=的最大值是（ ）（A ）15（B ）5 （C）1-（D ）3- 3．如图为某算法的程序框图，该算法的程序运行后输出的结果为299，则实数M 的取值范围是（ ）（A ）299296<<M（B ）299296<≤M（C ）299296≤<M（D ）299296≤≤M4．“1<a ”是“函数()|1|||-+-=x a x x f 在区间[1,)+∞上为增函数”的( )（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件5．已知2.1424.0,6log ,3log -===c b a ，则（ ）（A ）c b a >> （B ）c a b >> （C ）b a c >> （D ）a b c >>6．已知双曲线()0,012222>>=-b a by ax 的左、右焦点分别为21,F F ，以点2F 为圆心的圆与双曲线的渐近线相切，切点为P ．若3221π=∠PF F ，则双曲线的离心率为（ ）（A ）313（B ）321（C ）5（D ）377．如图，PM 是圆O 的切线，M 为切点，PAB 是圆的割线，AD ∥PM ，点D 在圆上，AD 与MB 交于点C ．若3,4,6===AC BC AB ，则MD 等于（ ）（A ）2 （B ）38（C ）49 （D ）948．已知函数()()()221+-+--=x e x ax x f 恰有两个零点，则实数a 的取值范围是（ ）（A ）0>a （B ）21-≥a（C ）021<<-a （D ）021≤<-a二、填空题（本大题共6小题，每小题5分，共30分，把答案填在题中横线上）9．已知集合{}1|2||<-=x x A ，集合{}02|2>-=x x B ，则=B A ．10．在平面直角坐标系内，满足⎩⎨⎧≤≤-≤≤2210y x 的点()y x ,构成的区域为D ，曲线x y 42=与直线1=x 围成的封闭区域为M ．向D 内随机投入一点，该点落入M 内的概率为 ．11．如图是一个几何体的三视图，则这个几何得 分 评卷人体的体积为 ．12．从4名男生，3名女生中选派3人参加学科竞赛，一人参加数学竞赛、一人参加物理竞赛、一人参加化学竞赛，若3人中既有男生又有女生，则不同的选派方法有 种．13．已知P 是ABC ∆内一点，2141+=，PBC ∆的面积为2016，则PAB ∆的面积为 ．14．若对,[1,2]x y ∈，2xy =，总有不等式24ax y -≥-成立，则实数a 的取值范围是 ．三.解答题（本大题共6小题，共80分，解答题应写出文字说明、证明过程或演算步骤）15．（本小题满分13分）已知函数()1sin 23cos 23cos sin 322++-=x x x x x f ，R x ∈． （1）求函数()x f 的最小正周期并写出函数()x f 图象的对称轴；（2）求函数()x f 在区间⎥⎦⎤⎢⎣⎡-3,4ππ上的最大值和最小值．某人玩掷骰子移动棋子的游戏，棋盘分为BA,两方，开始时棋子放在A方，根据下列①、②、③的规定移动棋子：①骰子出现1点时，不能移动棋子；②出现2、3、4、5点时，把棋子移向对方；③出现6点时，若棋子在A方就不动，若棋子在B方就移至A方．（1）将骰子连掷2次，求掷第一次后棋子仍在A方而掷第二次后棋子在B方的概率；（2）若将骰子连掷3次，3次中棋子移动的次数记为ξ，求随机变量ξ的分布列和期望．17．（本小题满分13分）如图，四边形ABCD 为矩形，四边形BCEF 为直角梯形，BF ∥CE ，BC BF ⊥，422===AB BF CE ， 120==∠DCE ABF ，G 是AF 中点．（1）求证：AF ∥平面DCE ； （2）求证：DF BG ⊥ ；（3）若二面角A DF E --的大小为 150，求线得 分 评卷人段DF的长．18．（本小题满分13分）已知椭圆)0(12222>>=+b a by ax 的左、右焦点分别为21F F 、，在第一象限椭圆上的一点M 满足212F F MF ⊥，且||3||21MF MF =． （1）求椭圆的离心率；（2）设1MF 与y 轴的交点为N ，过点N 与直线1MF 垂直的直线交椭圆于B A ,两点，若175411=⋅+⋅F F ，求椭圆的方程．19．（本小题满分14分）已知数列{}n a 的前n 项和为n S ，21=a ，()*++∈-+=N n a a n n n n 23311． （1）求数列{}n a 的通项公式； （2）求n S ；（3）证明：存在*∈N k ，使得kk nn a a a a 11++≤．已知函数()aex=-，R+g x+xex=，()2axf x+-a∈．（1）求函数()x f的单调区间；（2）若存在[]2,0∈x ，使得()()0<-x g x f 成立，求a 的取值范围； （3）设()2121,x x x x ≠是函数()x f 的两个零点，求证021<+x x ．数学(理科)参考答案1．D 2．C 3．B 4．A 5．C 6．B 7．B 8．A 9． ()3,2 10． 32 11．3 12．180 13．4032 14．0≤a15．（本小题满分13分） （1）()1sin 23cos 23cos sin 322++-=x x x x x f ()1sin cos 232sin 2322+--=x x x 12cos 232sin 23+-=x x …………………………2分 132sin 3+⎪⎭⎫⎝⎛-=πx …………………………4分 函数()x f 的最小正周期为ππ=22． (6)分由函数()x f 图象可知函数()x f 图象的对称轴为Z k k x ∈-=,122ππ．……………7分 （2）∵函数()x f 在区间⎥⎦⎤⎢⎣⎡--12,4ππ上是减函数，在区间⎥⎦⎤⎢⎣⎡-3,12ππ上是增函数，……9分253,1312,1234=⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛-+-=⎪⎭⎫ ⎝⎛-πππf f f …………………………11分∴函数()x f 在区间⎥⎦⎤⎢⎣⎡--12,4ππ上的最大值为25，最小值为13+-………………13分16．（本小题满分13分）(1)骰子掷第一次后棋子在A方的事件记为M,则()3162==M P ………………2分骰子掷第二次后棋子在B方的事件记为N,则()3264==N P …………………………4分∵事件M 、N 互相独立，∴棋子在掷第一次后在A 方,掷第二次后在B 方的概率为()()()923231=⨯==N P M P MN P (5)分（2）ξ的可能值为0,1,2,3 ………………………6分()21686262620=⨯⨯==ξP ………………………7分()+⨯⨯==6161641ξP +⨯⨯61646221628646262=⨯⨯………………………8分 ()+⨯⨯==6265642ξP +⨯⨯656164216100656462=⨯⨯………………………9分()216806465643=⨯⨯==ξP ………………………10分随机变量ξ的分布列为………………………11分ξ123P2168 21628216100 21680613216803216100221628121680=⨯+⨯+⨯+⨯=ξE ………………………13分17．（本小题满分13分）（1）在CE 上取一点M ，使BF CM =，连FM ，∵BF ∥CE ，∴BF ∥CM ∴四边形BCMF 为平行四边形………………1分∴四边形ADMF 为平行四边形………………3分 ∴AF∥DM ，∵⊂DM 平面DCE ，⊄AF 平面DCE ，∴AF∥平面DCE (4)分（2）以C 为坐标原点，CD CB ,的方向分别为y x ,轴，建立空间直角坐标系．设a AD =，∵422===AB BF CE ， 120==∠DCE ABF ，G 是AF 中点． ∴()()()0,2,0,0,0,,0,2,D a B a A ，()()⎪⎪⎭⎫⎝⎛--23,21,,3,1,,32,2,0a G a F E ．……………6分∴()3,3,,23,21,0-=⎪⎪⎭⎫⎝⎛=a DF BG ，()32,4,0-=DE ……………7分∵()()032332103,3,23,21,0=⨯+-⨯+⨯=-⋅⎪⎪⎭⎫⎝⎛=⋅a a DF BG ，∴DF BG ⊥………8分（3）∵四边形ABCD 为矩形，∴BC AB ⊥，又∵BC BF ⊥，BF AB ,是平面ABF内的两条相交直线，∴⊥BC 平面ABF∵⊂BG 平面ABF ，∴BC BG ⊥，∴AD BG ⊥，又DF BG ⊥ ∵DFAD ,是平面ADF内的两条相交直线，∴⊥BG 平面ADF (9)分∴⎪⎪⎭⎫⎝⎛=23,21,0BG 是平面ADF 的一个法向量………………10分设平面EDF 的一个法向量为()z y x n ,,=，∴0,0=⋅=⋅DE n DF n∴⎪⎩⎪⎨⎧=+-=+-0324033z y z y ax ，令az 2=，则3,3==x a y ，即()aa n 2,3,3=………………11分∵二面角A DF E --的大小为150|150cos |=，解得26=a∴线段DF 的长为()()26333||222=+-+=a ………………13分18．（本小题满分13分）（1）由椭圆定义a MF MF 2||||21=+，∵||3||21MF MF =，∴a MF 2||42=，∴2224||16a MF = …………………2分在直角12F MF ∆中，222214||||c MF MF =-，即2224||8c MF =……………4分∴214422=a c ，即22=a c ，∴椭圆的离心率为22 (5)分（2）∵22=a c ，∴c b c a ==,2，∴椭圆方程为122222=+cy cx ，即022222=-+c y x …………………6分 易知点M 的坐标为⎪⎪⎭⎫⎝⎛c c 22,，∵点N 是线段2MF 的中点，∴点N 的坐标为⎪⎪⎭⎫⎝⎛c 42,0 ∵直线1MF 的斜率为42，∴直线AB 的斜率为22-，∴直线AB 的方程为c x y 4222+-=…………………8分 与椭圆方程联立消去y 得04741722=--c cx x (9)分设点A 的坐标为()11,y x ，点B 的坐标为()22,y x ，∴1747221⨯-=c x x∵AB 垂直平分线段1MF ，∴172711=⋅=⋅B F A F MB MA …………………10分 ∴172722,22,2211=⎪⎪⎭⎫ ⎝⎛--⋅⎪⎪⎭⎫ ⎝⎛--c y c x c y c x ∴17274222,4222,2211=⎪⎪⎭⎫ ⎝⎛---⋅⎪⎪⎭⎫ ⎝⎛---c x c x c x c x ∴()()1727422242222121=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--+--c x c x c x c x化简得17381221=+c x x ，∴173********=+⨯-c c ，∴82=c…………………12分∴8,1622222====c b c a ，∴椭圆的方程为181622=+y x …………………13分19．（本小题满分14分）（1）∵nn n n a a 23311-+=++，∴nn nn n a a ⎪⎭⎫⎝⎛-+=++323113311…………………1分令n nn a b 3=，∵21=a ，∴321=b ，∴nn n b b ⎪⎭⎫⎝⎛-=-+323111 (2)分∴()()()123121--++-+-+=n n n b b b b b b b b +=32121323113231132311-⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛⨯-+⎪⎭⎫ ⎝⎛⨯-n 1213231323132313111-⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛⨯-⎪⎭⎫ ⎝⎛⨯---+=n n13232132131-+⎪⎭⎫ ⎝⎛=-⎪⎭⎫ ⎝⎛-⨯-=n n n n…………………4分∴()n n n n a 312⨯-+=…………………5分（2）令数列{}n 2的前n 项和为)(1n S ，则221)(1-=+n n S …………………6分令数列(){}n n 31⨯-的前n 项和为)(2n S ， 则)(2n S ()()n n n n 31323231301321⨯-+⨯-++⨯+⨯+⨯=- ∴()()132)(2313231303+⨯-+⨯-++⨯+⨯=n n n n n S∴()()()112132)(23131313313332+-+⨯----=⨯--+++=-n n n nn n n S ∴)(2n S 1343249+⨯-+=n n …………………9分4123432343249221111)(2)(1++⨯-=⨯-++-=+=++++n n n n n n n n n S S S …………10分（3）通过分析，推测数列⎪⎪⎭⎫⎝⎛+n n a a 1的第一项最大，……11分 下面证明2,213121≥=<+n a a a a nn∵()n n n n a 312⨯-+=0>，∴只需证n n a a 1321<+ 即，()()[]n n n n n n 3121332211⨯-+<⨯+++ 即，()0313729>⨯-+⨯n n n∵2≥n ，∴上式显然成立，∴2,213121≥=<+n a a a a n n …………………13分∴存在1=k ，使得k k nn a a a a 11++≤12a a =对任意的*∈N k 均成立. …………………14分 20．（本小题满分14分）（1）()1-='x e x f …………………1分令()0>'x f ，得>x ，则()x f 的单调递增区间为()∞+,0；…………………2分令()0<'x f ，得<x ，则()x f 的单调递减区间为()0,∞-.…………………3分（2）记()()()x g x f x F -=，则()x F 22a a x e e x x -+--=-，()2-+='-x x e e x F (4)分∵022222=-=-⨯≥-+--x x x x e e e e ，∴()0≥'x F ，∴函数()x F 为()∞+∞-,上的增函数，…………5分∴当[]2,0∈x 时，()x F 的最小值为()20a a F -=………………………6分 ∵存在[]2,0∈x ，使得()()0<-x g x f 成立，∴()0min <x F ………………………7分即02<-a a ，解得1>a 或0<a 即为所求. ………………………8分 （3）由（1）可知，0=x 是函数()x f 的极小值点，也是最小值点，即最小值为()a f =0， 显然只有0<a 时，函数()x f 有两个零点，设21x x <，易知， 0,021><x x ．………9分 ∵)()()()(2221x f x f x f x f --=-- ()()22222222x e e a x e a x e x x x x --=++-+-=--，………………………10分 令)0(2)(≥--=-x x e e x h x x ，由（2）可知)(x h 在[)∞+,0上单调递增，…………11分 ∴)(x h 0)0(=≥h ，又∵210x x <<，∴0)(2>x h ，即02222>---x e e x x …………12分∴)()(21x f x f ->，又∵0,021<-<x x ，………………………13分 且由（1）知)(x f 在()0,∞-上单调递减，∴21x x -<，∴021<+x x ．………14分。

山东省威海市高三第二次模拟考试理综试题(含答案)2016年威海市高考模拟考试理科综合本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

第I卷1至5页，第II卷6至16页。

注意事项：1．答题前，考生务必用毫米黑色签字笔将自己的姓名、座号、考生号写在试卷和答题卡上。

考生要认真核对答题卡上粘贴的条形码的考生号、姓名、考试科目与考生本人姓名、考试号是否一致。

2．第I卷每小题选出答案后要用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

第II卷用毫米黑色签字笔在答题卡上书写作答。

在试题卷上作答，答案无效。

3．考试结束，监考员将试题卷和答题卡一并交回。

可能用到的相对原子质量：C 12 O 16 Na 23 S 32 Cl I127 Ba 137 第I卷(选择题共126分) 本卷共21小题，每小题6分，共126分。

一、选择题：本题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列叙述错误的是A．菠菜遗传物质的基本组成单位有4种B．线粒体中只能合成ATP，不能消耗ATP C．甲状腺激素发挥作用后被灭活D．每个核糖体具有两个tRNA的结合位点2．下列关于植物激素的叙述，错误的是A．在植物生长发育的过程中，几乎所有生命活动都受到植物激素的调节B．植物激素不直接参与细胞内的代谢活动C．适宜浓度的赤霉素既能促进植物细胞伸长也能促进果实成熟D．细胞分裂素和脱落酸在调节细胞分裂方面表现为拮抗作用3．下列有关实验的叙述，正确的是A．营养物质消耗、代谢产物积累是限制酵母菌种群数量增长的主要因素B．经甲基绿染色的口腔上皮细胞，可在高倍镜下观察到蓝绿色的线粒体C．用过氧化氢酶探究温度对酶活性的影响，实验的自变量是酶的用量和温度D．用于观察质壁分离与复原的洋葱表皮细胞也可以用来观察有丝分裂4．下列关于生态系统能量流动的叙述，错误的是A．能量流动包括能量的输入、传递、转化和散失过程B．分解者所需的能量可来自各营养级生物所储存的能量C．生态系统维持正常的能量流动需要不断补充能量D．生产者固定的能量除用于自身呼吸外均流入下一营养级5．疟原虫是一种单细胞生物。

山东省威海市高三文综第二次诊断考试试卷（政治部分）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2019高一上·友好期中) 随着我国居民健康意识的不断增强，“花钱买健康”的观念正在逐渐形成，体育健身娱乐业如雨后春笋般迅速发展。

上述材料表明（）A . 生产为消费创造动力B . 消费观念决定的发展C . 消费是生产的最终目的D . 新的消费热点往往会带动一个产业的形成和发展2. （2分） (2018高三上·覃塘月考) 供给侧改革的全称是“供给侧的经济结构性改革”，就是指从供给、生产端入手，通过解生产力，提升竞争力促进经济发展。

“互联网+”在扩大有效供给、提升供给能力、促进供给侧与需求侧的高效配合和精准对接等方面可以发挥重要作用。

下列能体现这一作用的新趋势有（）①建设物联网智能家居，提高居民生活质量②线上互联网企业和线下传统企加强战略合作③企业采用大数据技术调研市场，为产品研发精准定位④使用信息技术，升级企业技术设备，提高劳动生产率A . ①②B . ②③C . ①④D . ③④3. （2分）(2016·衡阳模拟) 国企改革是全面深化改革的“重头戏”。

推进国有企业改革，要有利于国有资本保值增值，有利于提高国有经济竞争力，有利于放大国有资本功能。

这三个“有利于”标准，是国企改革之“魂”。

下列对这三个“有利于”标准理解正确的是（）A . 实现国有资本保值增值，才能巩固国有经济的主体地位，更好地放大控制力B . 国有资本保值增值这一标准是三个“有利于”标准中首要的和基本的标准C . 提高国有经济的竞争力能增强其对社会资本的绝对支配力、控制力和影响力D . 放大国有资本功能发挥其对经济发展的主导作用，促进各种所有制相互竞争4. （2分）李克强总理指出，必须从改革行政审批制度入手来转变政府职能，把国务院各部门行政审批事项再削减三分之一以上，简政放权，减少微观事务管理，把错装在政府身上的手换成市场的手，切实从“越位点”退出，把“缺位点”补上。

1-5 BDBDC 6-11 CDACBA36（22分）（1）（2分）15.8℃(2)该区属于山地地形(2分)，北、东、南多山，三面地势较高(2分)，中部为谷地，地势较低(2分)。

（3）B地降水多(2分)，位于夏季风的迎风坡(2分)，C地降水少，位于夏季风的背风坡。

(2分)（4）乙村位于出山口附近，地表径流和土石容易汇集至此，所以多泥石流，甲村位于河谷中部地区，地形平坦开阔，泥石流很难到达。

(4分)乙村地形封闭,水汽不易扩散，容易成雾，甲村地形开阔,水汽容易扩散，很难成雾.(4分)37. （24分）（1）水热充足，土壤发育深厚，利于林木和农作物的生长（2分）；山地垂直分异明显，土壤类型多样，利于发展多种经营（2分）；红壤广布，土壤贫瘠，不利于农业生产（2分）；山区坡度大，表土不稳定，易出现水土流失，导致土地退化。

（2分）(2)输沙量呈下降趋势（2分）有利影响：改善河口地区水质；减轻河口泥沙淤积，提高河口通航能力。

（4 分）不利影响：河口滩涂增速减慢，海岸侵蚀加剧，三角洲退缩，海水倒灌；入海的营养物质减少，导致河口生物减少；（4分）（3）原因：江水不冻，河滩（沙洲）宽阔；河里有丰富的水生生物（水草、鱼虾等），食物充足；水质良好；人们有保护野生物种意识（为它们投食等）。

（每点2分，答3点得6分）42.（10分）【自然灾害与防治】分布特点：西部、北部山区 (2分)。

原因：西部、北部多山地、沟谷发育、地形起伏大；岩石较破碎；夏季多暴雨；地表植被覆盖率较低。

（理由答出其中两项即可得8分）43.（10分）【环境保护】表现：蒸发量增多（2分）；地表径流增多（2分）；下渗量减少（2分）。

原因：与原生林相比，橡胶林树种单一（2分），且植株间距大（2分），拦蓄径流的能力下降。

12-23 CDDA DABC CDBC38.（1）①①有利于消费者树立正确的消费观念及节能环保意识，坚持适度消费；理性消费；保护环境，绿色消费，积极发挥消费对生产的反作用。