高中数学 基础知识篇 第二章 基本初等函数(Ⅰ)同步练测 新人教A版必修1

高中数学学习材料马鸣风萧萧*整理制作资料名称: 新课标高中数学（必修1）第二章基本初等函数（1）（基础训练）测试题一、选择题1．下列函数与x y =有相同图象的一个函数是（ ）A ．2x y = B ．xx y 2=C ．)10(log ≠>=a a ay xa 且 D ．x a a y log =2．下列函数中是奇函数的有几个（ ）①11x x a y a +=- ②2l g (1)33x y x -=+- ③x y x = ④1l o g 1ax y x +=- A ．1 B ．2 C ．3 D ．43．函数y x=3与y x=--3的图象关于下列那种图形对称( ) A ．x 轴 B ．y 轴 C ．直线y x = D ．原点中心对称4．已知13x x -+=，则3322x x -+值为（ ）A .33B .25C .45D . 45-5．函数12log (32)y x =-的定义域是（ ）A ．[1,)+∞B ．2(,)3+∞C ．2[,1]3D ．2(,1]36．三个数60.70.70.76log 6，，的大小关系为（ ） A . 60.70.70.7log 66<< B . 60.70.70.76log 6<<C ．0.760.7log 660.7<< D . 60.70.7log 60.76<<7．若f x x (ln )=+34，则f x ()的表达式为（ ） A ．3ln x B ．3ln 4x + C ．3xe D ．34xe +二、填空题1．985316,8,4,2,2从小到大的排列顺序是 。

2．化简11410104848++的值等于__________。

3．计算：(log )log log 2222545415-++= 。

4．已知x y x y 224250+--+=，则log ()x xy 的值是_____________。

人教A版高中数学必修1第二章基本初等函数单元测试题(含参考答案)[1] 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（人教A版高中数学必修1第二章基本初等函数单元测试题(含参考答案)[1]）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为人教A版高中数学必修1第二章基本初等函数单元测试题(含参考答案)[1]的全部内容。

必修1第二章《基本初等函数》班级 姓名 序号 得分一．选择题．（每小题5分，共50分）1．若0m >，0n >，0a >且1a ≠，则下列等式中正确的是 ( ） A ．()m nm na a+= B ．11mma a =C ．log log log ()a a a m n m n ÷=-D ．43()mn =2．函数log (32)2a y x =-+的图象必过定点 （ ）A ．(1,2)B ．(2,2)C ．(2,3)D ．2(,2)33．已知幂函数()y f x =的图象过点(2,2,则(4)f 的值为 ( ） A ．1 B ． 2 C ．12D ．84．若(0,1)x ∈，则下列结论正确的是 （ ） A ．122lg xx x >> B ．122lg xx x >> C ．122lg xx x >> D ．12lg 2x x x >>5．函数(2)log (5)x y x -=-的定义域是 （ ） A ．(3,4) B ．(2,5) C ．(2,3)(3,5) D ．(,2)(5,)-∞+∞6．某商品价格前两年每年提高10%，后两年每年降低10%，则四年后的价格与原来价格比较，变化的情况是 ( ) A ．减少1.99% B ．增加1.99% C ．减少4% D ．不增不减7．若1005,102a b ==,则2a b += （ ） A ．0 B ．1 C ．2 D ．38． 函数()lg(101)2x xf x =+-是 （ ）A ．奇函数B ．偶函数C ．既奇且偶函数D ．非奇非偶函数9．函数2log (2)(01)a y x x a =-<<的单调递增区间是 （ ) A ．(1,)+∞ B ．(2,)+∞ C ．(,1)-∞ D ．(,0)-∞10．若2log (2)y ax =- (0a >且1a ≠）在[0,1]上是x 的减函数,则a 的取值范围是 ( ) A ．(0,1) B ．(0,2) C ．(1,2) D ．[2,)+∞ 一．选择题（每小题5分,共50分）二．填空题．(每小题5分，共25分)11．计算：459log 27log 8log 625⨯⨯= ．12．已知函数3log (0)()2(0)x x x >f x x ⎧=⎨≤⎩，， ,则1[()]3f f = ．13．若3())2f x ax bx =++，且(2)5f =,则(2)f -= ．14．若函数()log (01)f x ax a =<<在区间[,2]a a 上的最大值是最小值的3倍，则a = ． 15．已知01a <<，给出下列四个关于自变量x 的函数： ①log x y a =，②2log a y x =, ③31(log )ay x = ④121(log )ay x =．其中在定义域内是增函数的有 ． 三．解答题（6小题，共75分） 16．(12分)计算下列各式的值：（Ⅰ)4160.253216(24()849-+-⨯．(Ⅱ)21log 32393ln(log (log 81)2log log 12543++++-17．（ 12分）已知函数方程2840x x -+=的两根为1x 、2x （12x x <)． （Ⅰ)求2212x x ---的值；（Ⅱ）求112212x x ---的值．18．(共12分)（Ⅰ）解不等式2121()x x a a--> (01)a a >≠且．（Ⅱ)设集合2{|log (2)2}S x x =+≤，集合1{|()1,2}2x T y y x ==-≥-求S T ，S T ．19．（ 12分） 设函数421()log 1x x f x x x -⎧<=⎨≥⎩．（Ⅰ)求方程1()4f x =的解．（Ⅱ）求不等式()2f x ≤的解集．20．（ 13分)设函数22()log (4)log (2)f x x x =⋅的定义域为1[,4]4，（Ⅰ）若x t 2log =，求t 的取值范围；（Ⅱ）求()y f x =的最大值与最小值，并求出最值时对应的x 的值．21．(14分）已知定义域为R 的函数12()22x x bf x +-+=+是奇函数．（Ⅰ）求b 的值；(Ⅱ）证明函数()f x 在R 上是减函数;（Ⅲ）若对任意的t R ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求k 的取值范围．参考答案一．选择题二．填空题．11． 9 ． 12． 12． 13． 1． 14． 4． 15． ③,④．三．解答题:16．（Ⅰ）． 解：原式427272101=⨯+--=．(Ⅱ）解：原式33log (425)3315223223211222log ()25⨯=++⨯+=++⨯-=⨯．17． 解：由条件得：14x =-24x =+．(Ⅰ）221221122121212()()11118()()()16x x x x x x x x x x x x --+-⨯-=+-===．（Ⅱ）1122121x x---===．18．解：（Ⅰ)原不等式可化为:212x xa a-->．当1a>时，2121x x x->-⇔>．原不等式解集为(1,)+∞．当1a>时,2121x x x-<-⇔<．原不等式解集为(,1)-∞．（Ⅱ）由题设得:{|024}(2,2]S x x=<+≤=-，21{|1()1}(1,3]2T y y-=-<≤-=-．∴(1,2]S T=-, (2,3]S T=-．19．解：（Ⅰ）11()1424xxf x-<⎧⎪=⇔⎨=⎪⎩(无解）或411log4xxx≥⎧⎪⇔=⎨=⎪⎩∴方程1()4f x=的解为x=（Ⅱ）1()222xxf x-<⎧≤⇔⎨≤⎩或41log2xx≥⎧⎨≤⎩11xx<⎧⇔⎨≥-⎩或116xx≥⎧⎨≤⎩．11x⇔-≤<或116x≤≤即116x-≤≤．∴不等式()2f x≤的解集为:[1,16]-．20．解:（Ⅰ)t的取值范围为区间221[log,log4][2,2]4=-．（Ⅱ)记22()(log2)(log1)(2)(1)()(22)y f x x x t t g t t==++=++=-≤≤．∵231()()24y g t t==+-在区间3[2,]2--是减函数，在区间3[,2]2-是增函数∴当23log2t x==-即3224x-==()y f x=有最小值31()424f g=-=-；当2log2t x==即224x==时，()y f x=有最大值(4)(2)12f g==．21．解：（Ⅰ）∵()f x是奇函数，所以1(0)014bf b-==⇔=(经检验符合题设) ．(Ⅱ)由（1)知21()2(21)xxf x-=-+．对12,x x R∀∈,当12x x<时，总有2112220,(21)(21)0x x x x->++>．∴122112121212121122()()()0221212(21)(21)x x x xx x x xf x f x----=-⋅-=⋅>++++,∴12()()f x f x>．∴函数()f x 在R 上是减函数．(Ⅲ)∵函数()f x 是奇函数且在R 上是减函数，∴22222(2)(2)0(2)(2)(2)f t t f t k f t t f t k f k t -+-<⇔-<--=-．22221122323()33t t k t k t t t ⇔->-⇔<-=--．（＊） 对于t R ∀∈(*)成立13k ⇔<-．∴k 的取值范围是1(,)3-∞-．。

课时23 对数的运算(2)换底公式的应用a b c abc A ．1 B ．2 C ．3 D ．5答案 A解析 ∵log a x ＝1log x a ＝2，∴log x a ＝12. 同理log x c ＝16，log x b ＝13. ∴log abc x ＝1log x abc ＝1log x a ＋log x b ＋log x c＝1. 2．若log 34·log 48·log 8m ＝log 416，则m ＝________.答案 9解析 由换底公式，得lg 4lg 3×lg 8lg 4×lg m lg 8＝lg m lg 3＝log 416＝2，∴lg m ＝2lg 3＝lg 9，∴m ＝9.3．设3x ＝4y ＝36，求2x ＋1y的值． 解 由已知分别求出x 和y ，∵3x ＝36,4y＝36，∴x ＝log 336，y ＝log 436，由换底公式得： x ＝log 3636log 363＝1log 363，y ＝log 3636log 364＝1log 364， ∴1x ＝log 363，1y＝log 364， ∴2x ＋1y＝2log 363＋log 364＝log 36(32×4)＝log 3636＝1. 4．计算：(1)log 89×log 2732；(2)log 927；(3)log 21125×log 3132×log 513； (4)(log 43＋log 83)(log 32＋log 92)．解 (1)log 89×log 2732＝lg 9lg 8×lg 32lg 27＝lg 32lg 23×lg 25lg 33＝2lg 33lg 2×5lg 23lg 3＝109； (2)log 927＝log 327log 39＝log 333log 332＝3log 332log 33＝32； (3)log 21125×log 3132×log 513＝log 25－3×log 32－5×log 53－1＝－3log 25×(－5log 32)×(－log 53)＝－15×lg 5lg 2×lg 2lg 3×lg 3lg 5＝－15； (4)原式＝⎝⎛⎭⎪⎫lg 3lg 4＋lg 3lg 8⎝ ⎛⎭⎪⎫lg 2lg 3＋lg 2lg 9 ＝⎝ ⎛⎭⎪⎫lg 32lg 2＋lg 33lg 2⎝ ⎛⎭⎪⎫lg 2lg 3＋lg 22lg 3 ＝12＋14＋13＋16＝54.运用换底公式不熟练致误23A.14 B.12C ．2D ．4 易错分析 本题易在使用对数的运算公式时，尤其换底公式的使用过程中发生错误． 答案 D正解 log 29×log 34＝lg 9lg 2×lg 4lg 3＝2lg 3lg 2×2lg 2lg 3＝2×2＝4.一、选择题1.log 29log 23＝( )A.12 B ．2 C.32 D.92答案 B解析 由换底公式log 39＝log 29log 23.∵log 39＝2，∴log 29log 23＝2.2．已知log 23＝a ，log 37＝b ，则log 27＝() A ．a ＋b B ．a －b C ．ab D.ab答案 C解析 log 27＝log 23×log 37＝ab .3．设2a ＝5b ＝m ，且1a ＋1b ＝2，则m ＝( ) A.10 B ．10 C ．20 D ．100答案 A解析 ∵2a ＝5b ＝m ，∴a ＝log 2m ，b ＝log 5m .1a ＋1b ＝log m 2＋log m 5＝log m 10＝2，∴m 2＝10.又∵m >0，∴m ＝10，选A.4.1log 1419＋1log 1513等于( )A ．lg 3B ．－lg 3C.1lg 3 D ．－1lg 3答案 C解析 原式＝log 1914＋log 1315＝log 1312＋log 1315＝log 13110＝log 310＝1lg 3.选C. 5．已知2a ＝3b ＝k (k ≠1)，且2a ＋b ＝ab ，则实数k 的值为( )A ．6B ．9C ．12D ．18答案 D解析 a ＝log 2k ，b ＝log 3k ，由2a ＋b ＝ab 得2log 2k ＋log 3k ＝log 2k ·log 3k ，即2lg k lg 2＋lg k lg 3＝k2lg 2lg 3，得2lg 3＋lg 2＝lg k ，即k ＝18.二、填空题6．方程log 3(x －1)＝log 9(x ＋5)的解是________．答案 4解析 由换底公式得log 9(x ＋5)＝12log 3(x ＋5)．∴原方程可化为2log 3(x －1)＝log 3(x ＋5)，即log 3(x －1)2＝log 3(x ＋5)，∴(x －1)2＝x ＋5.∴x 2－3x －4＝0，解得x ＝4或x ＝－1.又∵⎩⎪⎨⎪⎧ x －1>0，x ＋5>0，∴x >1，故x ＝4.7．若log a b ·log 3a ＝4，则b 的值为________．答案 81解析 log a b ·log 3a ＝4，即log 3a ·log a b ＝4，即log 3b ＝4，∴34＝b ，∴b ＝81.8．已知2x ＝72y ＝A ，且1x ＋1y ＝1，则A 的值是________．答案 98解析 ∵2x ＝72y ＝A ，∴x ＝log 2A,2y ＝log 7A .∴1x ＋1y ＝1log 2A ＋2log 7A＝log A 2＋2log A 7＝log A 2＋log A 49＝log A 98＝1.∴A ＝98.三、解答题9．计算下列各式的值：(1)lg 2＋lg 5－lg 8lg 5－lg 4；(2)lg 5(lg 8＋lg 1000)＋(lg 23)2＋lg 16＋lg 0.06. 解 (1)原式＝1－3lg 2lg 5－2lg 2＝1－3lg 21－3lg 2＝1； (2)原式＝lg 5(3lg 2＋3)＋3(lg 2)2－lg 6＋lg 6－2＝3lg 5×lg 2＋3lg 5＋3lg 22－2＝3lg 2(lg 5＋lg 2)＋3lg 5－2＝3(lg 2＋lg 5)－2＝3－2＝1.10．已知x ，y ，z 为正数，3x ＝4y ＝6z,2x ＝py .(1)求p ；(2)求证：1z －1x ＝12y. 解 (1)设3x ＝4y ＝6z ＝k (显然k >0，且k ≠1)，则x ＝log 3k ，y ＝log 4k ，z ＝log 6k .由2x ＝py ，得2log 3k ＝p log 4k ＝p ·log 3k log 34. ∵log 3k ≠0，∴p ＝2log 34.(2)证明：1z －1x ＝1log 6k －1log 3k ＝log k 6－log k 3＝log k 2＝12log k 4＝12y ，∴1z －1x ＝12y.►2.2.2 对数函数及其性质。

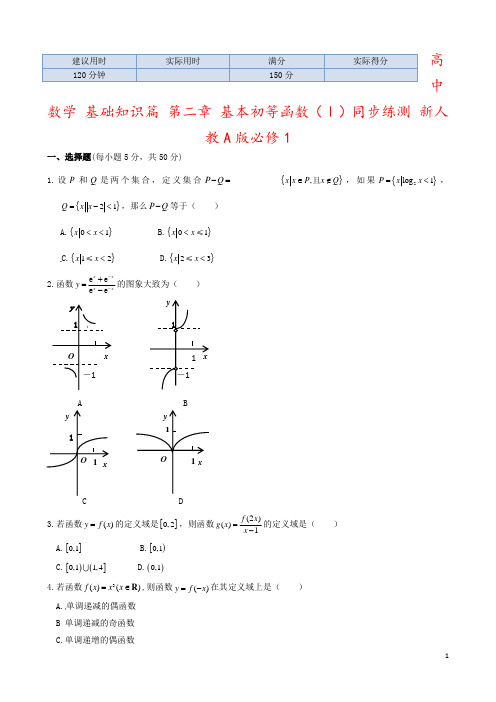
O Ox1 x11 y y O 1 x xy－1－1高中数学 基础知识篇 第二章 基本初等函数（Ⅰ）同步练测 新人教A 版必修1一、选择题(每小题5分，共50分)1.设P 和Q 是两个集合，定义集合P Q -={},x x P x Q ∈∉且，如果{}2log 1P x x =<，{}21Q x x =-<，那么P Q -等于（ ）A.{}01x x <<B.{}01x x <≤C.{}12x x <≤D.{}23x x <≤ 2.函数e e e ex xx x y --+=-的图象大致为（ ）y1 1A B1D3.若函数()y f x =的定义域是[]0,2，则函数(2)()1f xg x x =-的定义域是（ ） A.[]0,1 B.[)0,1 C.[)(]0,11,4 D.()0,14.若函数3()()f x x x =∈R ,则函数()y f x =-在其定义域上是（ ） A.单调递减的偶函数 B 单调递减的奇函数 C.单调递增的偶函数建议用时 实际用时满分 实际得分120分钟150分D.单调递增的奇函数 5.若01x y <<<，则（ ）A.33y x <B.log 3log 3x y <C.44log log x y <D.1144xy⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭6.若1()21xf x a =+-是奇函数，则a 等于（ ） A.0 B.12 C.1 D.12-7. 已知函数()f x 满足：当4x ≥时，1()2xf x ⎛⎫= ⎪⎝⎭；当4x <时，()(1)f x f x =+，则2(2log 3)f +=（ ）A.124 B.112 C.18 D.388.若()13e ,1,ln ,2ln ,ln x a x b x c x -∈=== ，则（ ） A.a b c << B.c a b << C.b a c << D.b c a <<9.定义在R 上的函数()f x 满足()()f x y f x +=+ ()2(,),(1)2f y xy x y f +∈=R ,则(3)f -等于（ ） A.2 B.3 C.6 D.910.若函数()log (01)a f x x a =<<在区间[],2a a 上的最大值是最小值的3倍，则a 的值为（ ） A.24 B.22 C.14 D.12二、填空题（每小题6分，共24分）11.函数21ln 11y x x⎛⎫=++- ⎪⎝⎭的定义域为 .12.如果函数2(0)ay x x=<的图象与函数21(0)y a x x =+<的图象有两个交点，那么a 满足的条件是 . 13.方程223x x -+=的实数解的个数是 .14.设0,1a a >≠且，若函数2lg(23)()x x f x a -+=有最大值，则不等式2log (57)0a x x -+>的解集为 .三、解答题（共76分）15.（12分）已知3227log 9,log 25p q ==，试用,p q 表示lg 5 .16.（12分）求不等式x x 283312-->⎪⎭⎫ ⎝⎛的解集.17.（12分）已知函数22xxy b a +=+(,a b 是常数且0a >，1a ≠)在区间3,02⎡⎤-⎢⎥⎣⎦上有max 3y =，min 52y =，试求a 和b 的值.18.（12分）已知函数()2lg(21)f x ax x=++，（1）若()f x的定义域是R，求实数a的取值范围及()f x的值域；（2）若()f x的值域是R，求实数a的取值范围及()f x的定义域.19.（14分）函数222()log(01)12bx xf x b bax-+=>≠+且.（1）求()f x的定义域；（2）求使()0f x≥在()0,+∞上恒成立的实数a的取值范围.20．（14分）已知定义在()0,1上的函数2()41xxf x=+.（1）求证：函数()f x在()0,1上是单调递减的；（2）求λ的取值范围，使方程()0-=在()f xλx∈上有根.0,1第二章基本初等函数（Ⅰ）（必修1人教A版）得分：一、选择题二、填空题11． 12． 13. 14.三、解答题15.16.17.18.19.20.第二章基本初等函数（Ⅰ）（必修1人教A 版）1.B 解析：由题意，得{}{}02,13P x x Q x x =<<=<<，所以{}01.P Q x x -=<≤2.A 解析：要使函数有意义，需使e e0xx--≠，其定义域为{}0,x x ≠e e e e ()()e e e ex x x xx xx x f x f x ----++-==-=---，所以函数图象关于原点对称，排除D.又因为222e e e 121e e e 1e 1x x x x x x xy --++===+---，所以当0>x 时，函数为减函数，排除B,C ，故选A.3.B 解析：因为()y f x =的定义域是[]0,2，所以要使(2)()1f x g x x =-有意义，需022,10,x x ⎧⎨-≠⎩≤≤所以01x <≤.4.B 解析：由33()()()f x x x f x -=-=-=-，得3()y f x x =-=-，结合幂函数的图象和性质即得.5.C 解析：因为3x y =在R 上是增函数，且01x y <<<，所以33x y <，故A 错误. 因为3log y x =在()0,+∞上是增函数，且01x y <<<，所以333log log log 10x y <<=， 所以33110log log x y>>，所以log 3log 3x y >，故B 错误. 因为4log y x =在()+∞,0上是增函数，且01x y <<<，所以44log log x y <，故C 正确.因为14xy ⎛⎫= ⎪⎝⎭在R 上是减函数，且01x y <<<，所以yx ⎪⎭⎫ ⎝⎛>⎪⎭⎫ ⎝⎛4141，故D 错误.6.B 解析：因为()()f x f x -=-，即112121xx a a -+=----， 所以22121221x x x x x a a a a +-•--•+=--，所以(1)22(1)x xa a a a --=-•+-，所以1,1,a a a a -=-⎧⎨-=-⎩ 所以12a =. 7.A 解析：因为22log 34+<，故222(2log 3)(2log 31)(3log 3)f f f +=++=+.又23log 34+>，故23log 3321111(3log 3)22324f +⎛⎫⎛⎫+==⨯=⎪⎪⎝⎭⎝⎭. 8.C 解析：因为11ex <<，所以1ln 0x -<<.令ln t x = ，则10t -<<，所以20,a b t t t -=-=->所以a b >. 32(1)(1)(1),c a t t t t t t t -=-=-=+-又因为10t -<<，所以011,211,t t <+<-<-<- 所以0,c a ->所以c a >，所以c a b >>.9.C 解析：因为(1)(01)(0)(1)201(0)(1)f f f f f f =+=++⨯⨯=+，所以(0)0f =. 因为(0)(11)(1)(1)2(1)1(1)(1)2f f f f f f =-+=-++⨯-⨯=-+-，所以(1)0f -=. 因为(1)(21)(2)(1)2(2)1(2)(1)4f f f f f f -=-+=-++⨯-⨯=-+-，所以(2)2f -=. 因为(2)(31)(3)(1)2(3)1(3)(1)6f f f f f f -=-+=-++⨯-⨯=-+-，所以(3)6f -=.10.A 解析：因为01a <<，所以()log a f x x =是()0,+∞上的减函数，从而有()3(2)f a f a =，即log 3log (2)a a a a =，解得24a =. 11.(]1,0 解析：列出函数有意义的限制条件，解不等式组.要是函数有意义，需2110,10,x x ⎧+>⎪⎨⎪-⎩≥即210,1,x x x +⎧>⎪⎨⎪⎩≤即10,11,x x x <->⎧⎨-⎩或≤≤解得01x <≤，所以定义域为(]1,0.12.102a -<< 解析：由题意知方程221aa x x+=有两个不同的负根，即2220a x x a +-=有两个不同的负根，所以20,10,20,a a∆⎧⎪>⎪⎪-<⎨⎪⎪->⎪⎩所以3180,0,a a ⎧+>⎨<⎩所以31,80,a a ⎧>-⎪⎨⎪<⎩所以331,20,a a ⎧⎛⎫>-⎪ ⎪⎨⎝⎭⎪<⎩所以102a -<<. 13.214.{}23x x << 解析：本题主要考查函数值域的求法以及对数不等式的解法.要使2lg(23)()xx f x a -+=有最大值，则01a <<，所以2log (57)0log 1a a x x -+>=，即22570,571,x x x x ⎧-+>⎪⎨-+<⎪⎩解得23x <<.15.解：2322log 3,log 553p q ==,lg 5=333333log 5log 515232log 10log 5log 215425q pq pq q p===+++.16.解：由已知282133x x --⎛⎫> ⎪⎝⎭，得2821133x x-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭. 因为函数13xy ⎛⎫= ⎪⎝⎭在(,)-∞+∞上是减函数，所以282x x -<，即2280x x --<，解得24x -<<.因此原不等式的解集是{}24x x -<<.17.解：令()22211u x x x =+=+－,3,02x ⎡⎤∈-⎢⎥⎣⎦，∴ 当1x =－时，min 1u =－；当0x =时，max 0.u = （1）当1a >时，013,5,2b a b a -⎧+=⎪⎨+=⎪⎩解得2,2.a b =⎧⎨=⎩ （2）当01a <<时，103,5,2b a b a -⎧+=⎪⎨+=⎪⎩解得2,33.2a b ⎧=⎪⎪⎨⎪=⎪⎩综上，2,2a b =⎧⎨=⎩或2,33.2a b ⎧=⎪⎪⎨⎪=⎪⎩18.解：（1）因为()f x 的定义域为R ，所以2210ax x ++>对一切x ∈R 成立． 所以0,440,a a ∆>⎧⎨=-<⎩解得1a >.又因为22112110ax x a x a a ⎛⎫++=++> ⎪⎝⎭－，所以()()21lg 21lg 1f x ax x a ⎛⎫=++ ⎪⎝⎭－≥，所以实数a 的取值范围是(1,)+∞,()f x 的值域是1lg 1,a ⎡⎫⎛⎫-+∞⎪ ⎪⎢⎝⎭⎣⎭.（2)因为()f x 的值域是R ，所以221u ax x =++的值域R (0,)⊇+∞. 当0a =时，21u x =+的值域为(0, )⊇+∞R ；当0a ≠时，221u ax x =++的值域(0, )⊇+∞R 等价于0,440.4a a a>⎧⎪-⎨⎪⎩≤解得01a <≤.所以实数a 的取值范围是[]0,1.当0a =时，由210x +>，得12x >－,此时()f x 的定义域是1,2⎛⎫+∞ ⎪⎝⎭－； 当01a <≤时，由2210ax x ++>，得1111a ax x +---<> 此时()f x 的定义域是⎪⎪⎭⎫⎝⎛+∞---⎪⎪⎭⎫ ⎝⎛-+-∞-,1111,a a a a .19.解：（1）因为2222(1)10x x x -+=-+>，所以120ax +>，即21ax >-. 所以若0a =，则()f x 的定义域为R ； 若0a >，则()f x 的定义域为1,2a ⎛⎫-+∞ ⎪⎝⎭； 若0a <，则()f x 的定义域为1,2a ⎛⎫-∞-⎪⎝⎭. （2）①当1b >时，在()f x 的定义域内，()0f x ≥等价于22212x x ax -++≥，即22(1)10x a x -++≥，于是问题等价于2112(1)x a x x x++=+≤在()0,+∞上恒成立. 令1()g x x x=+，则()g x 在(]0,1上递减，在[)1,+∞上递增，所以min ()(1)2g x g ==， 所以2(1)2a +≤，即0a ≤.另一方面要使()0f x ≥在()0,+∞上恒成立，则()0,+∞必是()f x 定义域的子集，由（1）可知0a ≥， 由0a ≥且0a ≤可知0a =.②当01b <<时，在()f x 的定义域内，()0f x ≥等价于22(1)1a x x ++≥，于是问题等价于12(1)a x x++≥在()0,+∞上恒成立.显然这样的实数a 不存在，故所求的a 的取值范围为0a =.20.（1）证明：设()12,0,1x x ∈，且12x x <，则12211212121222(22)(221)()()4141(41)(41)x x x x x x x x x x f x f x -•--=-=++++. 因为()12,0,1x x ∈，且12x x <，所以2112220,21,21x x x x ->>>，所以12()()0f x f x ->，即12()()f x f x >，所以()f x 在(0,1)上是单调递减的.（2）解：因为2041x x >+，所以要使()f x λ=有解，需0λ>，故42()041x x x f x λλλ-+--==+. (﹡)令2,(1,2)x t t =∈，则(﹡)式等价于方程20t t λλ-+=在(1,2)t ∈上有解. 令2()0g t t t λλ=-+=，分下列两种情况：①在(1,2)t ∈上有一解，则满足(1)(2)0g g •<，解得2152λ<<；②在(1,2)t ∈上有两解，则满足0,1(1,2),2(1)0,(2)0,g g ∆>λ⎧⎪⎪∈⎪⎨⎪>⎪>⎪⎩无解.所以当21,52λ⎛⎫∈ ⎪⎝⎭时，方程()0f x λ-=在(0,1)x ∈上有根.。

课时21 对数对数的意义①若M ＝N ，则log a M ＝log a N ； ②若log a M ＝log a N ，则M ＝N ； ③若log a M 2＝log a N 2，则M ＝N ； ④若M ＝N ，则log a M 2＝log a N 2. A ．①与② B ．②与④ C ．② D ．①②③④ 答案 C解析 对于①，当M ＝N ≤0时，log a M 与log a N 无意义，因此①不正确；对于②，对数值相等，底数相同，因此，真数相等，所以②正确；对于③，有M 2＝N 2，即|M |＝|N |，但不一定有M ＝N ，③错误；对于④，当M ＝N ＝0时，log a M 2与log a N 2无意义，所以④错误，由以上可知，只有②正确．2．求下列各式中x 的取值范围： (1)lg (x －10)； (2)log (x －1)(x ＋2)； (3)log (x ＋1)(x －1)2.解 (1)由题意有x －10>0，即x >10，即为所求； (2)由题意有⎩⎪⎨⎪⎧ x ＋2>0，x －1>0且x －1≠1，即⎩⎪⎨⎪⎧x >－2，x >1且x ≠2，∴x >1且x ≠2；(3)由题意有⎩⎪⎨⎪⎧x －2>0，x ＋1>0且x ＋1≠1，解得x >－1且x ≠0，x ≠1.3答案507解析 因为m ＝log 37，所以3m ＝7，则3m ＋3－m ＝7＋7－1＝507.4．将下列指数式化成对数式，对数式化成指数式： (1)35＝243；(2)2－5＝132；(3)log 1381＝－4；(4)log 2128＝7.解 (1)log 3243＝5；(2)log 2132＝－5；(3)13－4＝81；(4)27＝128.对数性质的应用(1)log 8x ＝－23；(2)log x 27＝34；(3)log 3(2x ＋2)＝1.解 (1)由log 8x ＝－23，得x ＝8－23＝(23)－23＝23×⎝ ⎛⎭⎪⎫－23＝2－2＝14；(2)由log x 27＝34，得x 34＝27.∴x ＝2743＝(33)43＝34＝81；(3)由log 3(2x ＋2)＝1，得2x ＋2＝3， 所以x ＝12.对数恒等式的应用(2)计算23＋log23＋35－log39.解(1)令t＝10x，则x＝lg t，∴f(t)＝lg t，即f(x)＝lg x，∴f(3)＝lg 3；(2)23＋log23＋35－log39＝23·2log23＋353log39＝23×3＋359＝24＋27＝51.一、选择题1．下列四个命题，其中正确的是( )①对数的真数是非负数；②若a>0且a≠1，则log a1＝0；③若a>0且a≠1，则log a a＝1；④若a>0且a≠1，则a log a2＝2.A．①②③ B．②③④C．①③ D．①②③④答案 B解析①对数的真数为正数，①错误；②∵a0＝1，∴log a1＝0，②正确；③∵a1＝a，∴log a a＝1，③正确；④由对数恒等式a log a N＝N，得a log a2＝2，④正确．2．2x＝3化为对数式是( )A．x＝log32 B．x＝log23C．2＝log3x D．2＝log x3答案 B解析由2x＝3得x＝log23，选B.3．化简：0.7log 0.78等于( ) A ．2 2 B ．8 C.18 D ．2答案 B解析 由对数恒等式a log aN ＝N ，得0.7log 0.78＝8.∴选B. 4．若log 2(log x 9)＝1，则x ＝( ) A ．3 B ．±3 C．9 D ．2 答案 A解析 ∵log 2(log x 9)＝1，∴log x 9＝2，即x 2＝9， 又∵x >0，∴x ＝3.5．若log a 3＝m ，log a 2＝n ，则a m ＋2n的值是( )A ．15B ．75C ．12D ．18 答案 C解析 由log a 3＝m ，得a m＝3，由log a 2＝n ，得a n＝2， ∴am ＋2n＝a m ·(a n )2＝3×22＝12.二、填空题6．已知log 2x ＝2，则x －12＝________.答案 12解析 ∵log 2x ＝2，∴x ＝22＝4， 4－12＝⎝ ⎛⎭⎪⎫1412＝12.7．若lg (ln x )＝0，则x ＝________. 答案 e解析 ∵lg (ln x )＝0，∴ln x ＝1，∴x ＝e.8．若集合{x ，xy ，lg xy }＝{0，|x |，y }，则log 8(x 2＋y 2)＝________. 答案 13解析 ∵x ≠0，y ≠0，∴lg xy ＝0，∴xy ＝1， 则{x,1,0}＝{0，|x |，y }，∴x ＝y ＝－1， log 8 (x 2＋y 2)＝log 82＝log 8813＝13.三、解答题9．(1)已知log 189＝a ，log 1854＝b ，求182a －b的值；(2)已知log x 27＝31＋log 32，求x 的值．解 (1)18a ＝9,18b＝54，182a －b＝a218b＝9254＝8154＝32； (2)∵log x 27＝31×3log 32＝31×2＝6， ∴x 6＝27，∴x ＝2716＝(33)16＝ 3.10．求下列各式中x 的值：(1)log 4(log 3x )＝0；(2)lg (log 2x )＝1； (3)log 2[log 12(log 2x )]＝0.解 (1)∵log 4(log 3x )＝0，∴log 3x ＝40＝1， ∴x ＝31＝3；(2)∵lg (log 2x )＝1，∴log 2x ＝10，∴x ＝210＝1024；(3)由log 2[log 12(log 2x )]＝0，得log 12(log 2x )＝1，log 2x ＝12，x ＝ 2.。

word1 / 7第二章 基本初等函数（Ⅰ）注意事项：1．答题前，先将自己的某某、某某号填写在试题卷和答题卡上，并将某某号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．()0a a >可以化简为（ ）A ．32aB ．18a C ．34aD ．38a2．三个数21log 5，0.12，0.22的大小关系是（ ）A ．0.10.221log <2<25B ．0.20.121log <225<C ．0.10.2212<2log 5< D ．0.10.2212<log 25< 3．设集合2R {|}x A y y x ∈＝＝，，21{|}0B x x <＝－，则A B ＝（ ）A ．()1,1-B ．()0,1C ．()1-∞，+D ．(0)∞，+4．已知23xy＝，则xy=（ ）A ．lg 2lg 3B ．lg 3lg 2C ．2lg 3D ．3lg 25．函数()ln f x x x ＝的图象大致是（ ）6．若函数()33x x f x －＝＋与()33x x g x －＝－的定义域均为R ，则（ ） A ．()f x 与()g x 均为偶函数 B ．()f x 为奇函数，()g x 为偶函数 C ．()f x 与()g x 均为奇函数 D ．()f x 为偶函数，()g x 为奇函数 7．函数121(22)m y m m x -=+-是幂函数，则m ＝（ ）A ．1B ．3-C ．3-或1D ．28．下列各函数中，值域为(0)∞，+的是（ ） A ．22x y -=B ．12y x =-C ．21y x x =++D ．113x y +=9．已知函数：①2xy ＝；②2log y x ＝；③1y x －＝；④12y x =；则下列函数图象（第一象限部分）从左到右依次与函数序号的对应顺序是（ ）A ．②①③④B ．②③①④C ．④①③②D ．④③①②10．设函数()()211log 2121x x x f x x -⎧+-<⎪=⎨≥⎪⎩，则()22log ()12f f -＋＝（ ）A ．3B ．6C ．9D ．1211．已知函数()22()1122xa xx f x x ⎧-≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩满足对任意的实数12x x ≠都有word2 / 7()()1212f x f x x x -<0-成立，则实数a 的取值X 围为（ ）A ．()2-∞，B ．13,8⎛⎤-∞ ⎥⎝⎦C ．(2]-∞，-D ．13,28⎡⎫⎪⎢⎣⎭12．如果一个点是一个指数函数与一个对数函数的图象的公共点，那么称这个点为“好点”．在下面的五个点()1,1M ，()1,2N ，()2,1P ，()2,2Q ，1G 2,2⎛⎫⎪⎝⎭中，可以是“好点”的个数为（ ） A ．0个 B ．1个C ．2个D ．3个二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．已知124(0)9a a =>，则23log a =________．14．已知函数2log 0()30xxx f x x >⎧⎪⎨≤⎪⎩，则14f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭________． 15．若函数212log (35)y x ax =-+在[)1-∞，+上是减函数，则实数a 的取值X 围是________．16．如图，矩形ABCD 的三个顶点A ，B ，C 分别在函数22logy x =，12y x =，22xy ⎛⎫= ⎪ ⎪⎝⎭的图象上，且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2， 则点D 的坐标为________．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．(10分)()31320.5log 511lg3lg91lg 812730.25-⎛⎫++-+-+ ⎪⎝⎭．18．(12分)已知函数1()=2axf x ⎛⎫⎪⎝⎭，a 为常数，且函数的图象过点()1,2-．（1）求a 的值；（2）若()42x g x -－＝，且g (x )＝f (x )，求满足条件的x 的值．word3 / 719．(12分)已知函数f (x )＝log a (1＋x )，g (x )＝log a (1－x )，(a ＞0，a ≠1)． （1）设a ＝2，函数f (x )的定义域为[3,63]，求f (x )的最值； （2）求使f (x )－g (x )＞0的x 的取值X 围．20．(12分)求使不等式2821x x a a --⎛⎫> ⎪⎝⎭成立的x 的集合(其中a >0，且a ≠1)．word4 / 721．(12分)已知函数f (x )＝2x的定义域是[0,3]，设g (x )＝f (2x )－f (x ＋2)， （1）求g (x )的解析式及定义域； （2）求函数g (x )的最大值和最小值．22．(12分)若函数f (x )满足21(log )1a a f x x x a ⎛⎫=⋅- ⎪-⎝⎭ (其中a ＞0且a ≠1)．（1）求函数f (x )的解析式，并判断其奇偶性和单调性；（2）当x ∈(－∞，2)时，f (x )－4的值恒为负数，求a 的取值X 围．word1 / 72018-2019学年必修一第二章训练卷基本初等函数（二）答案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．【答案】B【解析】因为0a >，所以B ．2．【答案】A【解析】∵21log <05，0.10.2022<<，∴0.10.221log <2<25，故选A ．3．【答案】C【解析】{}2R {|}0|x A y y x y y ∈>＝＝，＝．2{|}{1011|}B x x x x <<<＝－＝－， ∴{}0111|{|}{|}AB x x x x x x ><<>＝－＝－，故选C ．4．【答案】B【解析】由23x y ＝得lg 2lg3x y ＝，∴lg2lg3x y ＝，∴lg3lg 2x y =，故选B ． 5．【答案】A【解析】由()ln l ()n ||f x x x x x f x --＝-＝-＝-知，函数()f x 是奇函数，故排除C ，D ，又110f e e ⎛⎫=-< ⎪⎝⎭，从而排除B ，故选A ．6．【答案】D【解析】因为()()33x x f x f x --＝＋＝，()()33x x g x g x ---＝＝-，所以()f x 是偶函数， ()g x 为奇函数，故选D ．7．【答案】B【解析】因为函数121(22)m y m m x -=+-是幂函数，所以2221m m -+＝且1m ≠，解得3m ＝-．故选B ．8．【答案】A 【解析】A，22xy x -==⎝⎭的值域为(0)∞，+． B ，因为120x -≥，所以21x ≤，0x ≤，y =(0],-∞， 所以021x <≤，所以0121x ≤-<，所以y =[)0,1． C ，2213124y x x x ⎛⎫=++=++ ⎪⎝⎭的值域是3,4⎡⎫+∞⎪⎢⎣⎭，D ，因为()()1,00,1x ∈-∞+∞+，所以113x y +=的值域是()0,11()∞，+．故选A ．9．【答案】D【解析】根据幂函数、指数函数、对数函数的图象可知选D ． 10．【答案】C【解析】221log ()(())223f -+--=＝，()221216log log 2log 12226f －＝＝＝， ∴()22log (19)2f f -＋＝，故选C ．11．【答案】B【解析】由题意知函数()f x 是R 上的减函数，于是有()22012212a a -<⎧⎪⎨⎛⎫-⨯≤-⎪ ⎪⎝⎭⎩由此解得138a ≤，即实数a 的取值X 围是13,8⎛⎤-∞ ⎥⎝⎦，选B ．12．【答案】C【解析】设指数函数为()01x y a a a >≠＝，，显然不过点M 、P ，若设对数函数为()log 01b y x b b >≠＝，，显然不过N 点，故选C ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）word2 / 713．【答案】4【解析】∵124(0)9a a =>，∴2221223a ⎡⎤⎛⎫⎛⎫=⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦，即423a ⎛⎫= ⎪⎝⎭，∴422332log log 4.3a ⎛⎫== ⎪⎝⎭14．【答案】19【解析】∵14>0，∴211log 244f ⎛⎫==- ⎪⎝⎭．则104f ⎛⎫< ⎪⎝⎭，∴211349f f -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭．15．【答案】(]86-，-【解析】令()235g x x ax ＝－＋，其对称轴为直线6a x =，依题意，有()1610ag ⎧≤-⎪⎨⎪->⎩，即68a a ≤-⎧⎨>-⎩，∴86(]a ∈-，-． 16．【答案】11,24⎛⎫⎪⎝⎭【解析】由图象可知，点(),2A A x在函数y x =的图象上，所以2A x =，212A x ==⎝⎭， 点(),2B B x 在函数12y x =的图象上，所以122B x =，4B x ＝． 点()4C C y ，在函数xy =⎝⎭的图象上，所以414C y ==⎝⎭． 又12D A x x ==，14D C y y ==，所以点D 的坐标为11,24⎛⎫⎪⎝⎭．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．【答案】见解析． 【解析】原式3310.5log 5253log 1431(3)231lg3lg3lg3(3()03).5---++＝＋＋－＋＋325log 6362531＝＋＝＋＝．18．【答案】（1）1；（2）－1． 【解析】（1）由已知得122a-⎛⎫= ⎪⎝⎭，解得a ＝1．（2）由（1）知1()2xf x ⎛⎫= ⎪⎝⎭，又g (x )＝f (x )，则1422xx -⎛⎫-= ⎪⎝⎭，即112=42xx⎛⎫⎛⎫--0 ⎪ ⎪⎝⎭⎝⎭，即2112022x x ⎡⎤⎛⎫⎛⎫--=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，令12xt ⎛⎫= ⎪⎝⎭，则t 2－t －2＝0，即(t －2)(t ＋1)＝0，又t >0，故t ＝2，即122x⎛⎫= ⎪⎝⎭，解得x ＝－1．19．【答案】（1）最小值为2，最大值为6；（2）见解析．【解析】（1）当a ＝2时，f (x )＝log 2(1＋x )，在[3,63]上为增函数，因此当x ＝3时，f (x )最小值为2．当x ＝63时f (x )最大值为6． （2）f (x )－g (x )＞0即f (x )＞g (x )当a ＞1时，log a (1＋x )＞log a (1－x )，满足111010x xx x +>-⎧⎪+>⎨⎪->⎩∴0＜x ＜1当0＜a ＜1时，log a (1＋x )＞log a (1－x )，满足111010x x x x +<-⎧⎪+>⎨⎪->⎩∴－1<x ＜0综上a ＞1时，解集为{x |0＜x ＜1}，0＜a ＜1时解集为{x |－1<x ＜0}． 20．【答案】见解析． 【解析】∵22881x x a a --⎛⎫= ⎪⎝⎭，∴原不等式化为282x x a a -->，当a >1时，函数y ＝a x是增函数，∴8－x 2>－2x ，解得－2<x <4； 当0<a <1时，函数y ＝a x是减函数，∴8－x 2<－2x ，解得x <－2或x >4．故当a >1时，x 的集合是{x |－2<x <4}；当0<a <1时，x 的集合是{x |x <－2或x >4}．word3 / 721．【答案】（1）g (x )＝2222x x -＋，{x |0≤x ≤1}（2）－3，－4． 【解析】（1）∵f (x )＝2x，∴g (x )＝f (2x )－f (x ＋2)＝2222x x -＋．因为f (x )的定义域是[0,3]，所以0≤2x ≤3，0≤x ＋2≤3，解得0≤x ≤1． 于是g (x )的定义域为{x |0≤x ≤1}． （2）设g (x )＝(2x )2－4×2x＝(2x－2)2－4．∵x ∈[0,1]，∴2x∈[1,2]，∴当2x＝2，即x ＝1时，g (x )取得最小值－4； 当2x＝1，即x ＝0时，g (x )取得最大值－3． 22．【答案】（1）2()()1x x a f x a a a -=-- (x ∈R )，见解析；（2）)(21,23⎡+⎣．【解析】（1）令log a x ＝t (t ∈R )，则x ＝a t，∴2()()1t ta f t a a a -=--． ∴2()()1x xa f x a a a -=-- (x ∈R )． ∵()22()()()11x xx x a a f x a a a a f x a a ---=-=--=---，∴f (x )为奇函数． 当a ＞1时，y ＝a x为增函数，x y a -=-为增函数，且201aa >-，∴f (x )为增函数．当0＜a ＜1时，y ＝a x为减函数x y a -=-为减函数，且201aa <-， ∴f (x )为增函数．∴f (x )在R 上为增函数．（2）∵f (x )是R 上的增函数，∴y ＝f (x )－4也是R 上的增函数． 由x ＜2，得f (x )＜f (2)，要使f (x )－4在(－∞，2)上恒为负数， 只需f (2)－4≤0，即2224()1a a a a --≤-，∴422141a a a a ⎛⎫-≤ ⎪-⎝⎭，∴a 2＋1≤4a ，∴a 2－4a＋1≤0，∴22a ≤≤a ≠1， ∴a的取值X 围为)(21,23⎡+⎣．。

函数的应用1．题型为选择题或填空题，主要考查零点个数的判断及零点所在区间．2．函数的零点与方程的根的关系：方程f (x )＝0有实数根⇔函数y ＝f (x )的图象与x 轴有交点⇔函数y ＝f (x )有零点．[典题示例] 函数f (x )＝⎩⎪⎨⎪⎧x 2－1，x ≤0，x －2＋ln x ，x ＞0的零点个数为________．[解析] 令f (x )＝0，得到⎩⎪⎨⎪⎧x 2－1＝0，x ≤0，解得x ＝－1；或⎩⎪⎨⎪⎧x －2＋ln x ＝0，x ＞0，在同一个直角坐标系中画出y ＝2－x 和y ＝ln x 的图象，观察交点个数，如图所示．函数y ＝2－x 和y ＝ln x ，x ＞0，在同一个直角坐标系中交点个数是1，所以函数f (x )在x ＜0时的零点有一个，在x ＞0时零点有一个，所以f (x )的零点个数为2.[答案] 2 [类题通法]确定函数零点个数的方法(1)解方程f (x )＝0有几个根．(2)利用图象找y ＝f (x )的图象与x 轴的交点或转化成两个函数图象的交点个数． (3)利用f (a )·f (b )与0的关系进行判断．[题组训练]1．函数f (x )＝lg x －9x 的零点所在的大致区间是( ) A ．(6,7) B ．(7,8) C ．(8,9)D ．(9,10)解析：选D ∵f (6)＝lg 6－96＝lg 6－32＜0，f (7)＝lg 7－97＜0，f (8)＝lg 8－98＜0，f (9)＝lg 9－1＜0，f (10)＝lg 10－910＞0， ∴f (9) · f (10)＜0.函数的零点问题∴f (x )＝lg x －9x的零点的大致区间为(9,10)．2．已知函数f (x )＝ln x －⎝⎛⎭⎫12x －2的零点为x 0，则x 0所在的区间是( ) A ．(0,1) B ．(1,2) C ．(2,3)D ．(3,4)解析：选C ∵f (x )＝ln x －⎝⎛⎭⎫12x －2在(0，＋∞)是增函数， 又f (1)＝ln 1－⎝⎛⎭⎫12－1＝ln 1－2＜0， f (2)＝ln 2－⎝⎛⎭⎫120＜0， f (3)＝ln 3－⎝⎛⎭⎫121＞0， ∴x 0∈(2,3)．3．函数y ＝⎝⎛⎭⎫12|x |－m 有两个零点，则m 的取值范围是________． 解析：在同一直角坐标系内，画出y 1＝⎝⎛⎭⎫12|x |和y 2＝m 的图象，如图所示，由于函数有两个零点，故0＜m ＜1.答案：(0,1)1．通过对近几年高考试题的分析可以看出，对函数的实际应用问题的考查，更多地以实际生活为背景，设问新颖、灵活；题型以解答题为主，难度中等偏上；主要考查建模能力，同时考查分析问题、解决问题的能力．2．函数实际应用的示意图[典题示例] 某网店经营的某消费品的进价为每件12元，周销售量p (件)与销售价格x (元)的关系，如图中折线所示，每周各项开支合计为20元．(1)写出周销售量p (件)与销售价格x (元)的函数关系式； (2)写出利润周利润y (元)与销售价格x (元)的函数关系式；函数的应用(3)当该消费品销售价格为多少元时，周利润最大？并求出最大周利润． [解] (1)由题设知，当12≤x ≤20时，设p ＝ax ＋b ，则⎩⎪⎨⎪⎧12a ＋b ＝26，20a ＋b ＝10，∴a ＝－2，b ＝50. ∴p ＝－2x ＋50，同理得，当20＜x ≤28时，p ＝－x ＋30，所以p ＝⎩⎪⎨⎪⎧－2x ＋50，12≤x ≤20，－x ＋30，20＜x ≤28.(2)当12≤x ≤20时，y ＝(x －12)(－2x ＋50)－20＝－2x 2＋74x －620； 当20＜x ≤28时，y ＝(x －12)(－x ＋30)－20＝－x 2＋42x －380.∴y ＝⎩⎪⎨⎪⎧－2x 2＋74x －620，12≤x ≤20，－x 2＋42x －380，20＜x ≤28. (3)当12≤x ≤20时，y ＝－2x 2＋74x －620， ∴x ＝372时，y 取得最大值1292. 当20＜x ≤28时，y ＝－x 2＋42x －380， ∴x ＝21时，y 取得最大值61. ∵1292＞61，∴该消费品销售价格为372时，周利润最大，最大周利润为1292. [类题通法]建立恰当的函数模型解决实际问题的步骤(1)对实际问题进行抽象概括，确定变量之间的主被动关系，并用x ，y 分别表示． (2)建立函数模型，将变量y 表示为x 的函数，此时要注意函数的定义域． (3)求解函数模型，并还原为实际问题的解．[题组训练]1.某工厂8年来某种产品的总产量C 与时间t (年)的函数关系如图所示．以下四种说法：①前三年产量增长的速度越来越快； ②前三年产量增长的速率越来越慢； ③第三年后这种产品停止生产； ④第三年后产量保持不变． 其中说法正确的是序号是________．解析：由t ∈[0,3]的图象联想到幂函数y ＝x α(0＜α＜1)，反映了C 随时间的变化而逐渐增长但速度越来越慢．由t ∈[3,8]的图象可知，总产量C 没有变化，即第三年后停产，所以②③正确．答案：②③2．将甲桶中的a 升水缓慢注入空桶乙中，t 分钟后甲桶中剩余的水量符合指数衰减曲线y ＝a e nt .若5分钟后甲桶和乙桶的水量相等，又过了m 分钟后甲桶中的水只有a8升，则m的值为( )A ．7B ．8C ．9D ．10解析：选D 令18a ＝a e nt ，即18＝e nt ，由已知得12＝e 5n ，故18＝e 15n ，比较知t ＝15，m ＝15－5＝10.3．某企业决定从甲、乙两种产品中选择一种投资生产，打入国际市场，已知投资生产这两种产品的有关数据如表：时需上交0.05x 2万美元的特别关税．(1)写出该厂分别投资生产甲、乙两种产品的年利润y 1，y 2与生产相应产品的件数x (x ∈N)之间的函数关系式；(2)分别求出投资生产这两种产品的最大年利润．解：(1)由题知y 1＝10x －(20＋ax )＝(10－a )x －20,0≤x ≤200且x ∈N ；y 2＝18x －(40＋8x )－0.05x 2＝－0.05x 2＋10x －40＝－0.05(x－100)2＋460,0≤x ≤120且x ∈N.(2)∵3≤a ≤8，∴10－a ＞0， ∴y 1＝(10－a )x －20为增函数． 又0≤x ≤200，x ∈N ，∴x ＝200时y 1取最大值，即生产甲产品的最大年利润为(10－a )×200－20＝1 980－200a (万美元)．又y 2＝－0.05(x －100)2＋460,0≤x ≤120，x ∈N ，∴x ＝100时y 2取最大值，即生产乙产品的最大年利润为460万美元．1．已知函数f (x )＝⎩⎪⎨⎪⎧x (x ＋4)，x ＜0，x (x －4)，x ≥0，则该函数的零点的个数为( )A ．1B ．2C ．3D ．4解析：选C 当x ＜0时，令x (x ＋4)＝0，解得x ＝－4；当x ≥0时，令x (x －4)＝0，解得x ＝0或4.综上，该函数的零点有3个．2．函数f (x )＝ln(x ＋1)－2x 的零点所在的大致区间是( )A ．(1,2)B ．(0,1)C ．(2，e)D ．(3,4)解析：选A f (1)＝ln 2－2＝ln 2e 2＜ln 1＝0，f (2)＝ln 3－1＝ln 3e＞ln 1＝0，所以函数f (x )＝ln(x ＋1)－2x的零点所在的大致区间是(1,2)．3．某家具的标价为132元，若降价以九折出售(即优惠10%)，仍可获利10%(相对进货价)，则该家具的进货价是( )A ．118元B ．105元C ．106元D ．108元解析：选D 设该家具的进货价是x 元，由题意得132(1－10%)－x ＝x ·10%，解得x ＝108元．4．下列函数：①y ＝lg x ；②y ＝2x ；③y ＝x 2；④y ＝|x |－1，其中有2个零点的函数是( ) A ．①② B ．③④ C ．②③D ．④解析：选D 分别作出这四个函数的图象，其中④y ＝|x |－1的图象与x 轴有两个交点，即有2个零点，选D.5．已知函数f (x )在区间[a ，b ]上是单调函数，且f (a )f (b )＜0，则方程f (x )＝0在区间[a ，b ]内( )A ．至少有一实根B ．至多有一实根C ．没有实根D ．必有唯一实根解析：选B 由于f (a )f (b )＜0，则f (a )＜0＜f (b )或f (b )＜0＜f (a )，又函数f (x )在区间[a ，b ]上是单调函数，则至多有一个实数x 0∈[a ，b ]，使f (x 0)＝0，即方程f (x )＝0在区间[a ，b ]内至多有一实根．6．已知0＜a ＜1，则方程a |x |＝|log a x |的实根个数为( ) A ．2 B ．3C ．4D ．与a 的值有关解析：选A 设y 1＝a |x |，y 2＝|log a x |，分别作出它们的图象如图所示．由图可知，有两个交点，故方程a |x |＝|log a x |有两个根．故选A.7．长为4，宽为3的矩形，当长增加x ，宽减少x2时，面积达到最大，此时x 的值为________．解析：由题意，S ＝(4＋x )⎝⎛⎭⎫3－x 2，即S ＝－12x 2＋x ＋12，∴当x ＝1时，S 最大． 答案：18．某学校要装备一个实验室，需要购置实验设备若干套，与厂家协商，同意按出厂价结算，若超过50套就可以每套比出厂价低30元给予优惠．如果按出厂价购买应付a 元，但再多买11套就可以按优惠价结算，恰好也付a 元(价格为整数)，则a 的值为________．解析：设按出厂价y 元购买x (x ≤50)套应付a 元， 则a ＝xy .再多买11套就可以按优惠价结算恰好也付a 元，则a ＝(x ＋11)(y －30)，其中x ＋11＞50.∴xy ＝(x ＋11)(y －30)(39＜x ≤50)．∴3011x ＝y －30.又x ∈N ，y ∈N(因价格为整数)，39＜x ≤50， ∴x ＝44，y ＝150，a ＝44×150＝6 600. 答案：6 6009．若函数f (x )＝a x －x －a (a ＞0，且a ≠1)有两个零点，则实数a 的取值范围为________． 解析：函数f (x )的零点的个数就是函数y ＝a x 与函数y ＝x ＋a 交点的个数，如下图，由函数的图象可知a ＞1时两函数图象有两个交点，0＜a ＜1时两函数图象有唯一交点，故a ＞1.答案：(1，＋∞)10．某产品按质量分为10个档次，生产第一档(即最低档次)的利润是每件8元，每提高一个档次，利润每件增加2元，但每提高一个档次，在规定的时间内，产量减少3件．如果在规定的时间内，最低档次的产品可生产60件．(1)请写出规定时间内产品的总利润y 与档次x 之间的函数关系式，并写出x 的定义域； (2)在规定的时间内，生产哪一档次产品的总利润最大？并求出最大利润．解：(1)由题意知，生产第x 个档次的产品每件的利润为8＋2(x －1)元，该档次的产量为60－3(x －1)件．则规定时间内第x 档次的总利润y ＝(2x ＋6)(63－3x )＝－6x 2＋108x ＋378，其中x ∈{x ∈N *|1≤x ≤10}．(2)y ＝－6x 2＋108x ＋378＝－6(x －9)2＋864，则当x ＝9时，y 有最大值为864.故在规定的时间内，生产第9档次的产品的总利润最大，最大利润为864元．11．A 、B 两城相距100 km ，在两地之间距A 城x km 处D 地建一核电站给A 、B 两城供电，为保证城市安全．核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比，比例系数λ＝0.25.若A 城供电量为20亿度/月，B 城为10亿度/月．(1)求x 的范围；(2)把月供电总费用y 表示成x 的函数；(3)核电站建在距A 城多远，才能使供电费用最小． 解：(1)x 的取值范围为[10,90]．(2)y ＝0.25×20x 2＋0.25×10(100－x )2＝5x 2＋52(100－x )2(10≤x ≤90)．(3)由y ＝5x 2＋52(100－x )2＝152x 2－500x ＋25 000＝152⎝⎛⎭⎫x －10032＋50 0003. 则当x ＝1003km 时，y 最小． 故当核电站建在距A 城1003km 时，才能使供电费用最小．12．为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本y (元)与月处理量x (吨)之间的函数关系可近似地表示为y ＝12x 2－200x ＋80 000，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？解：设该单位每月获利为S 元， 则S ＝100x －y＝100x －⎝⎛⎭⎫12x 2－200x ＋80 000＝－12x 2＋300x －80 000＝－12(x －300)2－35 000，因为400≤x ≤600，所以当x ＝400时，S 有最大值－40 000.故该单位不获利，需要国家每月至少补贴40 000元才能不亏损．(时间120分钟 满分150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设U ＝{1,2,3,4,5}，A ＝{1,2,3}，B ＝{2,3,4}，则下列结论中正确的是( ) A ．A ⊆B B ．A ∩B ＝{2} C ．A ∪B ＝{1,2,3,4,5}D ．A ∩(∁U B )＝{1}解析：选D A 显然错误；A ∩B ＝{2,3}，B 错；A ∪B ＝{1,2,3,4}，C 错，故选D. 2．(2017·山东高考)设函数y ＝4－x 2的定义域为A ，函数y ＝ln(1－x )的定义域为B ，则A ∩B ＝( )A ．(1,2)B ．(1,2]C ．(－2,1)D ．[－2,1)解析：选D 由题意可知A ＝{x |－2≤x ≤2}，B ＝{x |x <1}，故A ∩B ＝{x |－2≤x <1}．3．设f (x )＝⎩⎪⎨⎪⎧2e x －1，x ＜2，log 3(2x－1)，x ≥2，则f (f (2))＝( ) A ．0 B ．1 C ．2D ．3解析：选C ∵f (2)＝log 3(22－1)＝1. ∴f (f (2))＝f (1)＝2e 1－1＝2.4．下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( ) A ．y ＝x －2B ．y ＝x －1C ．y ＝x 2－2D ．y ＝log 12x解析：选A ∵y ＝x－1是奇函数，y ＝log 12x 不具有奇偶性，故排除B 、D ，又函数y ＝x 2－2在区间(0，＋∞)上是单调递增函数，故排除C ，只有选项A 符合题意．5．函数y ＝log 2|1－x |的图象是( )解析：选D 函数y ＝log 2|1－x |可由下列变换得到： y ＝log 2x →y ＝log 2|x |→y ＝log 2|x －1|→y ＝log 2|1－x |.故选D.6．已知幂函数y ＝f (x )的图象过点⎝⎛⎭⎫12，22，则log 2f (2)的值为( )A.12 B ．－12C ．2D ．－2解析：选A 设f (x )＝x α，则22＝⎝⎛⎭⎫12α，∴α＝12，f (2)＝212，所以log 2f (2)＝log 2212＝12. 7．函数f (x )＝lg x －1x 的零点所在的区间是( ) A ．(0,1) B ．(1,10) C ．(10,100)D ．(100，＋∞)解析：选B ∵f (1)＝－1＜0，f (10)＝1－110＝910＞0，f (100)＝2－1100＞0， ∴f (1)·f (10)＜0，由函数零点存在性定理知，函数f (x )＝lg x －1x 的零点所在的区间为(1,10)．8．设a ＝60.4，b ＝log 0.40.5，c ＝log 80.4，则a ，b ，c 的大小关系是( ) A ．a <b <c B ．c <b <a C ．c <a <bD ．b <c <a解析：选B ∵a ＝60.4>1，b ＝log 0.40.5∈(0,1)，c ＝log 80.4<0，∴a >b >c .故选B. 9．如右图，向放在水槽底部的烧杯注水(流量一定)，注满烧杯后，继续注水，直至注满水槽，水槽中整体水面上升高度h 与注水时间t 之间的函数关系大致是下列图象中的( )解析：选B 开始一段时间，水槽底部没有水，烧杯满了之后，水槽中水面上升先快后慢．故选B.10．已知函数f (x )＝1＋x 21－x 2，则有( )A ．f (x )是奇函数，且f ⎝⎛⎭⎫1x ＝－f (x ) B ．f (x )是奇函数，且f ⎝⎛⎭⎫1x ＝f (x ) C ．f (x )是偶函数，且f ⎝⎛⎭⎫1x ＝－f (x ) D ．f (x )是偶函数，且f ⎝⎛⎭⎫1x ＝f (x ) 解析：选C ∵f (－x )＝f (x )， ∴f (x )是偶函数，排除A 、B.又f ⎝⎛⎭⎫1x ＝1＋⎝⎛⎭⎫1x 21－⎝⎛⎭⎫1x 2＝1＋x 2x 2－1＝－f (x )，故选C. 11．已知函数f (x )＝m ＋log 2x 2的定义域是[1,2]，且f (x )≤4，则实数m 的取值范围是( ) A ．(－∞，2] B ．(－∞，2) C ．[2，＋∞)D ．(2，＋∞)解析：选A 因为f (x )＝m ＋2log 2x 在[1,2]是增函数，且由f (x )≤4，得f (2)＝m ＋2≤4，得m ≤2.12．已知函数f (x )＝⎩⎪⎨⎪⎧|lg x |，0<x ≤10，－12x ＋6，x >10，若a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则abc 的取值范围是( )A ．(1,10)B ．(5,6)C ．(10,12)D ．(20,24)解析：选C 作出f (x )的大致图象．由图象知，要使f (a )＝f (b )＝f (c )，不妨设a <b <c ，则－lg a ＝lg b ＝－12c ＋6.于是lg a ＋lg b ＝0. 故ab ＝1.因而abc ＝c .由图知10<c <12，故abc ∈(10,12)．二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上) 13．设U ＝R ，已知集合A ＝{x |x ＞1}，B ＝{x |x ＞a }，且(∁U A )∪B ＝R ，则实数a 的取值范围是________．解析：∵A ＝{x |x ＞1}， ∴∁U A ＝{x |x ≤1}．由B ＝{x |x ＞a }，(∁U A )∪B ＝R 可知a ≤1. 答案：(－∞，1]14．调查表明，酒后驾驶是导致交通事故的主要原因，交通法规规定，驾驶员在驾驶机动车时血液中酒精含量不得超过0.2 mg/mL.某人喝酒后，其血液中酒精含量将上升到3 mg/mL ，在停止喝酒后，血液中酒精含量以每小时50%的速度减少，则至少经过________小时他才可以驾驶机动车．(精确到小时)解析：设n 小时后他才可以驾驶机动车，由题意得3(1－0.5)n ≤0.2，即2n ≥15，解得n ≥log 215，故至少经过4小时他才可以驾驶机动车．答案：415．已知函数f (x )＝⎩⎪⎨⎪⎧2x ＋1，x ＜1，x 2＋ax ，x ≥1，若f (f (0))＝4a ，则实数a 等于________． 解析：∵0＜1，∴f (0)＝20＋1＝2.∵2＞1，∴f (2)＝4＋2a ，∴f (f (0))＝f (2)＝4＋2a ＝4a ，∴a ＝2.答案：216．已知函数f (x )＝lg(2x －b )(b 为常数)，若x ∈[1，＋∞)时，f (x )≥0恒成立，则b 的取值范围是________．解析：∵要使f (x )＝lg(2x －b )在x ∈[1，＋∞)上，恒有f (x )≥0，∴有2x －b ≥1在x ∈[1，＋∞)上恒成立，即2x ≥b ＋1恒成立．又∵指数函数g (x )＝2x 在定义域上是增函数．∴只要2≥b ＋1成立即可，解得b ≤1.答案：(－∞，1]三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知集合A ＝{x |2＜2x ＜8}，B ＝{x |a ≤x ≤a ＋3}．(1)当a ＝2时，求A ∩B ；(2)若B ⊆∁R A ，求实数a 的取值范围．解：(1)当a ＝2时，A ＝{x |2＜2x ＜8}＝(1,3)，B ＝{x |a ≤x ≤a ＋3}＝[2,5]，故A ∩B ＝[2,3)．(2)∁R A ＝(－∞，1]∪[3，＋∞)．故由B ⊆∁R A 知，a ＋3≤1或a ≥3，故实数a 的取值范围为(－∞，－2]∪[3，＋∞)．18．(本小题满分12分)已知f (x )＝log a x (a ＞0且a ≠1)的图象过点(4,2)．(1)求a 的值；(2)若g (x )＝f (1－x )＋f (1＋x )，求g (x )的解析式及定义域；(3)在(2)的条件下，求g (x )的单调减区间．解：(1)由已知f (x )＝log a x (a ＞0且a ≠1)的图象过点(4,2)，则2＝log a 4，即a 2＝4，又a ＞0且a ≠1，所以a ＝2.(2)g (x )＝f (1－x )＋f (1＋x )＝log 2(1－x )＋log 2(1＋x )．由⎩⎪⎨⎪⎧1－x ＞0，1＋x ＞0，得－1＜x ＜1，定义域为(－1,1)．(3)g (x )＝log 2(1－x )＋log 2(1＋x )＝log 2(1－x 2)，其单调减区间为[0,1)．19．(本小题满分12分)若f (x )是定义在(0，＋∞)上的增函数，且对一切x ，y >0，满足f ⎝⎛⎭⎫x y ＝f (x )－f (y )．(1)求f (1)的值；(2)若f (6)＝1，解不等式f (x ＋3)－f ⎝⎛⎭⎫13<2.解：(1)在f ⎝⎛⎭⎫x y ＝f (x )－f (y )中，令x ＝y ＝1，则有f (1)＝f (1)－f (1)，∴f (1)＝0.(2)∵f (6)＝1，∴f (x ＋3)－f ⎝⎛⎭⎫13<2＝f (6)＋f (6)．∴f (3x ＋9)－f (6)<f (6)，即f ⎝⎛⎭⎫x ＋32<f (6)．∵f (x )是定义在(0，＋∞)上的增函数，∴⎩⎪⎨⎪⎧ x ＋3>0，x ＋32<6.解得－3<x <9， 即不等式的解集为(－3,9)．20．(本小题满分12分)随着新能源的发展，电动汽车在全社会逐渐普及开来，据某报记者了解，某市电动汽车国际示范区运营服务公司逐步建立了全市乃至全国的分时租赁服务体系，为新能源汽车分时租赁在全国的推广提供了可复制的市场化运营模式．现假设该公司有750辆电动汽车供租赁使用，管理这些电动汽车的费用是每日1 725元．调查发现，若每辆电动汽车的日租金不超过90元，则电动汽车可以全部租出；若超过90元，则每超过1元，租不出的电动汽车就增加3辆．设每辆电动汽车的日租金为x (元)(60≤x ≤300，x ∈N *)，用y (元)表示出租电动汽车的日净收入(日净收入等于日出租电动汽车的总收入减去日管理费用)．(1)求函数y ＝f (x )的解析式；(2)试问当每辆电动汽车的日租金为多少元时，才能使日净收入最多？解：(1)当60≤x ≤90，x ∈N *时，y ＝750x －1 725；当90＜x ≤300，x ∈N *时，y ＝[750－3(x －90)]x －1 725，故f (x )＝⎩⎪⎨⎪⎧750x －1 725，60≤x ≤90，x ∈N *，－3x 2＋1 020x －1 725，90＜x ≤300，x ∈N *. (2)对于y ＝750x －1 725,60≤x ≤90，x ∈N *，∵y 在[60,90](x ∈N *)上单调递增，∴当x ＝90时，y max ＝65 775.对于y ＝－3x 2＋1 020x －1 725＝－3(x －170)2＋84 975，90＜x ≤300，x ∈N *，当x ＝170时，y max ＝84 975.∵84 975＞65 775，∴当每辆电动汽车的日租金为170元时，日净收入最多．21．(本小题满分12分)已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝2x －1.(1)求f (3)＋f (－1)；(2)求f (x )的解析式；(3)若x ∈A ，f (x )∈[－7,3]，求区间A .解：(1)∵f (x )是奇函数，∴f (3)＋f (－1)＝f (3)－f (1)＝23－1－2＋1＝6.(2)设x ＜0，则－x ＞0，∴f (－x )＝2－x －1， ∵f (x )为奇函数，∴f (x )＝－f (－x )＝－2－x ＋1， ∴f (x )＝⎩⎪⎨⎪⎧2x －1，x ≥0，－2－x ＋1，x ＜0.(3)作出函数f (x )的图象，如图所示．根据函数图象可得f (x )在R 上单调递增，当x ＜0时，－7≤－2－x ＋1＜0， 解得－3≤x ＜0；当x ≥0时，0≤2x －1≤3，解得0≤x ≤2；∴区间A 为[－3,2]．22．(本小题满分12分)对于函数f (x )＝a －2b x＋1(a ∈R ，b ＞0，且b ≠1)． (1)探索函数y ＝f (x )的单调性；(2)求实数a 的值，使函数y ＝f (x )为奇函数；(3)在(2)的条件下，令b ＝2，求使f (x )＝m (x ∈[0,1])有解的实数m 的取值范围．解：(1)函数f (x )的定义域为R ，设x 1＜x 2，则f (x 1)－f (x 2)＝⎝⎛⎭⎫a －2bx 1＋1－⎝⎛⎭⎫a －2bx 2＋1＝2(bx 1－bx 2)(bx 1＋1)(bx 2＋1).当b ＞1时，由x 1＜x 2，得bx 1＜bx 2，从而bx 1－bx 2＜0，于是f (x 1)－f (x 2)＜0，所以f (x 1)＜f (x 2)，此时函数f (x )在R 上是单调增函数； 当0＜b ＜1时，由x 1＜x 2，得bx 1＞bx 2，从而bx 1－bx 2＞0，于是f (x 1)－f (x 2)＞0，所以f (x 1)＞f (x 2)， 此时函数f (x )在R 上是单调减函数．(2)函数f (x )的定义域为R ，由f (0)＝0得a ＝1. 当a ＝1时，f (x )＝1－2b x ＋1＝b x －1b x ＋1， f (－x )＝1－2b －x ＋1＝b －x －1b －x ＋1＝1－b x 1＋b x . 满足条件f (－x )＝－f (x )，故a ＝1时，函数f (x )为奇函数．(3)f (x )＝1－22x＋1， ∵x ∈[0,1]，∴2x ∈[1,2]，2x ＋1∈[2,3]，22x＋1∈⎣⎡⎦⎤23，1， ∴f (x )∈⎣⎡⎦⎤0，13， 要使f (x )＝m (x ∈[0,1])有解，则0≤m ≤13，即实数m 的取值范围为⎣⎡⎦⎤0，13.。

2019-2020学年必修1第二章训练卷基本初等函数（一）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1．下列函数不是幂函数的是（ ） A ．3y x =B ．2y x =C ．3xy =D ．12y x-=【答案】C【解析】幂函数是形如ay x =形式的函数，选项C 为指数函数，故选C ．2．若0m >，0n >，0a >且1a ≠，则下列等式正确的是（ ） A ．nnaa -=B ．log log log ()a a a m n m n ⋅=+C ．3322m m =D ．()mmm a a bb=【答案】D 【解析】1nn aa-=，故A 错误； log log log ()a a a m n mn +=，故B 错误；2323m m =，故C 错误；应选D ．3．函数log (21)3a y x =-+的图象必过点（ ） A ．1(,4)2B ．(1,3)C ．1(,3)2D ．(1,4)【答案】B【解析】当1x =时，211x -=，则log 13033a y =+=+=， ∴函数log (21)3a y x =-+的图象必过点(1,3)，应选B ． 4．计算25log 25log 16⋅=（ ） A ．8 B ．10 C ．16 D ．40【答案】A【解析】24252525log 25log 16log 5log 22log 54log 28⋅=⋅=⨯=，应选A ．5．下列函数中，在区间(0,)+∞上为减函数的是（ ）A ．2y x =B ．12y x =C ．2xy -=D ．ln y x =【答案】C【解析】选项A 、B 、D 在区间(0,)+∞均为增函数，选项C 在区间(0,)+∞上为减函数，故选C ．6．函数()ln(1)21f x x x =-+-的定义域为（ ） A ．1(,1)2B ．1[,1)2C ．1(,1]2D ．1[,1]2【答案】B【解析】由题意可知10210x x ->⎧⎨-≥⎩，解得112x ≤<，故选B ．7．已知幂函数()y f x =经过2(4,)2，则(16)f =（ ） 此卷只装订不密封班级 姓名 准考证号 考场号 座位号A ．2B ．12C ．14D ．4【答案】B【解析】设()af x x =，∵()y f x =经过2(4,)2，则242a =，得14a =-， ∴14()f x x-=，∴141(16)162f -==，故选B ． 8．三个数0.87，70.8，0.8log 7的大小顺序是（ ）A ．70.80.8log 70.87<<B ．0.870.8log 770.8<<C ．70.80.80.87log 7<< D ．0.870.870.8log 7<<【答案】A 【解析】0.871>，700.81<<，0.8log 70<，故70.80.8log 70.87<<，故选A ．9．10025a=，108b=，则3a b +=（ ） A ．12B ．13C ．2D ．3【答案】D【解析】∵10025a=，∴100log 25lg 5a ==，又∵108b=，∴lg83lg 2b ==，∴33lg53lg 23lg103a b +=+==，故选D ． 10．已知函数①ay x =，②by x =，③cy x =，④dy x =的部分图象如下图，则下列正确的是（ ）A ．a b c d <<<B ．c a d b <<<C ．c b d a <<<D ．c d b a <<<【答案】C【解析】由图可知0c <，1d =，01b <<，1a >，故c b d a <<<．应选C ． 11．若对数函数()log a f x x =的图象与函数()y g x =的图象关于y x =对称，且当0x <时()1g x >，则a 的取值范围是（ ）A ．01a <<B ．0a >且1a ≠C ．1a >D ．12a <<【答案】A【解析】由题意可知，()xg x a =，当0x <时，()1g x >，可知01a <<，故选A ．12．已知log (83)a y ax =-（0a >且1a ≠）在[0,2]上是x 的减函数，则a 的取值范围是（ ） A ．(0,1) B ．3(,1)4C ．8(1,)3D ．4(1,)3【答案】D【解析】令83t ax =-，则log a y t =，当01a <<时，log a y t =单减，而83t ax =-也是减函数， 故log (83)a y ax =-是关于x 的增函数，不合题意，舍去；当1a >时，log a y t =单增，83t ax =-单减， 故符合log (83)a y ax =-是关于x 的减函数． ∵[0,2]x ∈，∴[86,8]t a ∈-，∴860a ->得43a <，则413a <<．应选D ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．计算：8527log 27log 16log 625⨯⨯= ．【答案】163【解析】3448527253log 27log 16log 625log 3log 2log 5⨯⨯=⨯⨯2531616lg 3lg 2lg 516log 3log 2log 533lg 2lg 5lg 33=⨯⨯=⨯⨯⨯=． 14．已知函数()2log ,(0)3,(0)xx x f x x ->⎧=⎨≤⎩，则1()2f f ⎡⎤=⎢⎥⎣⎦．【答案】3【解析】211()log 122f ==-，1(1)33f -==，∴1()(1)32f f f ⎡⎤=-=⎢⎥⎣⎦， 故答案为3．15．函数21()(5)m f x m m x +=--是幂函数，且为奇函数，则实数m 的值是 ．【答案】2-【解析】∵()f x 是幂函数，∴251m m --=，∴260m m --=， 解得2m =-或3，当2m =-时，11m +=-，1()f x x -=是奇函数，符合题意； 当3m =时，14m +=，4()f x x =是偶函数，不符合题意，∴2m =-．16．若函数()log (01)a f x x a =<<在区间1,22a a ⎡⎤⎢⎥⎣⎦上的最大值是最小值的2倍，则a = ． 【答案】18【解析】∵01a <<，∴()log a f x x =在区间1,22a a ⎡⎤⎢⎥⎣⎦上是单调递减函数，∴max 111()()log ()log 1222a af x f a a ===+，min ()(2)log (2)log 21a a f x f a a ===+，max min ()2()f x f x =，∴1log 12(log 21)2a a +=+，得1log 2log 212a a -=， 即1log 18a =，解得18a =．三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．（10分）已知函数2()log ()f x mx n =+，若(3)1f =-，(10)2f =，求(4)f ． 【答案】0．【解析】∵(3)1f =-，(10)2f =，则221log (3)132log (10)2104m n m n m n m n ⎧+=-+=⎧⎪⇒⎨⎨+=⎩⎪+=⎩，解得121m n ⎧=⎪⎨⎪=-⎩，∴21()log (1)2f x x =-，则2(4)log 10f ==．18．（12分）计算下列各式的值：（1）1640.2524(2()8249--+-⨯； （2）21log 56293log (log 64)2log log 12543+++-． 【答案】（1）67；（2）152． 【解析】（1）原式132472342(28)89472672=⨯+-⨯-⨯=⨯+--=．（2）原式1333263334log 24log 54log 101ln log 625110log 2log 52log 10e +=++⨯+=+++--- 115110422=++-=． 19．（12分）解下列方程及不等式：（1）解方程：22log (31)log (95)1x x-=--；（2）解不等式：1221()xx aa--≥（0a >且1a ≠）． 【答案】（1）1x =；（2）见解析．【解析】（1）∵22log (31)log (95)1x x -=--，即222log (31)log (95)log 2xx-=--，∴95312x x--=，令3(xt t =>，则2512t t --=，即2230t t --=，解得3t =或1-（舍）， ∴33x=，解得1x =． （2）∵1221()xx aa-->，即122x x a a -->， 当01a <<时，有122x x -<-，解得1x >-； 当1a >时，有122x x ->-，解得1x <-， 综上，当01a <<时，不等式1221()xx aa-->解集为{1}x x >-； 当1a >时，不等式1221()xx aa-->解集为{1}x x <-． 20．（12分）已知幂函数213()(322)mf x m m x+=--+在(0,)+∞上为增函数．（1）求()f x 解析式；（2）若函数2()(21)1y f x a x a =-++-在区间(2,3)上为单调函数，求实数a 的取值范围．【答案】（1）2()f x x =；（2）3522a a a ⎧⎫≤≥⎨⎬⎩⎭或． 【解析】（1）∵幂函数解析式为213()(322)mf x m m x+=--+，∴23221m m --+=，即23210m m +-=，解得1m =-或13， 当1m =-时，2()f x x -=在(0,)+∞上为减函数，不合题意，舍去； 当13m =时，2()f x x =在(0,)+∞上为增函数，符合题意， ∴2()f x x =．（2）22(21)1y x a x a =-++-在区间(2,3)上为单调函数， 函数对称轴为212a x +=， ∴有2122a +≤或2132a +≥，解得32a ≤或52a ≥，∴实数a 的取值范围为3522a a a ⎧⎫≤≥⎨⎬⎩⎭或． 21．（12分）已知()y f x =是定义在R 上的偶函数，且当0x ≤时()21xf x =-． （1）求函数()f x 解析式； （2）画出函数()f x 的图象；（3）写出函数()f x 的单调区间及值域．【答案】（1）21,0()21,xxx f x x -⎧-≤⎪=⎨->⎪⎩；（2）见解析；（3）见解析．【解析】（1）当0x >时，0x -<，∵()f x 是在R 上的偶函数，∴()()21xf x f x -=-=-，∴()f x 解析式为21,0()21,xxx f x x -⎧-≤⎪=⎨->⎪⎩．（2）函数()f x 的图象如下图：（3）由图象可知()f x 单调递增区间为(,0)-∞，单调递减区间为(0,)+∞，()f x 值域为(1,0]-．22．（12分）设函数2()log (21)2()xf x ax a =++∈R ．（1）若函数()f x 是定义在R 上的偶函数，求a 的值；（2）若不等式()()f x f x mt m +-≥+对任意x ∈R ，[3,2]t ∈-恒成立，求实数m 的取值范围．【答案】（1）14a =-；（2）21,3⎡⎤-⎢⎥⎣⎦． 【解析】（1）∵()f x 是定义在R 上的偶函数，得()()f x f x =-恒成立，则22log (21)2log (21)2x xax ax -++=+-，∴222212114log log log 212(12)2x x x x x xax x ---++====-++， 即(41)0a x +=恒成立，则410a +=，故14a =-． （2）222()()log (21)2log (21)2log [(21)(21)]x x x x f x f x ax ax --+-=++++-=+⋅+2log (222)x x -=++，令2xs =，(0,)s ∈+∞，则21()()log (2)f x f x s s+-=++，令1()g s s s=+，根据双勾函数性质可知，当1s =，即0x =时，()g s 取得最小值为(1)112g =+=．此时()()f x f x +-取得最小值为2log (22)2+=． ∴2mt m +≤对任意[3,2]t ∈-恒成立，令()h t mt m =+，由(3)32(2)22h m m h m m -=-+≤⎧⎨=+≤⎩，解得213m -≤≤，故实数m 的取值单位是21,3⎡⎤-⎢⎥⎣⎦．感谢您的支持！由Ruize收集整理。

高中数学学习材料金戈铁骑整理制作高中同步创优单元测评A 卷 数 学班级：________ 姓名：________ 得分：________第二章 基本初等函数(Ⅰ)(一)(指数与指数函数) [名师原创·基础卷](时间：120分钟 满分：150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．计算[(－2)2]－ 12的结果是( )A.2 B ．－2 C.22D ．－222.⎝ ⎛⎭⎪⎫1120－(1－0.5－2)÷⎝ ⎛⎭⎪⎫278 23的值为( )A ．－13 B.13 C.43 D.733．若a >1，则函数y ＝a x 与y ＝(1－a )x 2的图象可能是下列四个选项中的()4．下列结论中正确的个数是( )①当a <0时，(a 2 23＝a 3；②na n ＝|a |(n ≥2，n ∈N )； ③函数y ＝(x －2) 12 －(3x －7)0的定义域是[2，＋∞)； ④6(－2)2＝32.A ．1B ．2C ．3D ．45．指数函数y ＝f (x )的图象经过点⎝ ⎛⎭⎪⎫－2，14，那么f (4)·f (2)等于( )A ．8B ．16C ．32D ．64 6．函数y ＝21x的值域是( ) A ．(0，＋∞) B ．(0,1) C ．(0,1)∪(1，＋∞)D ．(1，＋∞)7．函数y ＝|2x －2|的图象是( )8．a ，b 满足0<a <b <1，下列不等式中正确的是( ) A ．a a <a b B ．b a <b b C ．a a <b a D ．b b <a b9．函数f (x )的图象向右平移1个单位长度，所得图象与曲线y ＝e x 关于y 轴对称，则f (x )＝( )A ．e x ＋1B ．e x －1C ．e －x ＋1D ．e －x －110．若函数y ＝a x ＋m －1(a >0，a ≠1)的图象在第一、三、四象限内，则( )A ．a >1B ．a >1，且m <0C ．0<a <1，且m >0D ．0<a <111．函数f (x )＝2x ＋2－4x ，若x 2－x －6≤0，则f (x )的最大值和最小值分别是( )A ．4，－32B ．32，－4 C.23，0D.43，112．若函数f (x )＝3x ＋3－x 与g (x )＝3x －3－x 的定义域均为R ，则( )A ．f (x )与g (x )均为偶函数B ．f (x )为偶函数，g (x )为奇函数C ．f (x )与g (x )均为奇函数D ．f (x )为奇函数，g (x )为偶函数第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中横线上)13．已知a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系为________．14．若方程⎝ ⎛⎭⎪⎫14x ＋⎝ ⎛⎭⎪⎫12x －1＋a ＝0有正数解，则实数a 的取值范围是________．15．已知函数f (x )＝⎝ ⎛⎭⎪⎫12|x －1|，则f (x )的单调递增区间是________．16．定义区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1，已知函数y ＝2|x |的定义域为[a ，b ]，值域为[1,2]，则区间[a ，b ]的长度的最大值与最小值的差为________．三、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)解不等式a 2x ＋7<a 3x －2(a >0，a ≠1)．18．(本小题满分12分)已知函数f (x )＝3x ，且f (a )＝2，g (x )＝3ax －4x . (1)求g (x )的解析式；(2)当x ∈[－2,1]时，求g (x )的值域．19．(本小题满分12分)已知函数f (x )＝⎝ ⎛⎭⎪⎫12ax，a 为常数，且函数的图象过点(－1,2)．(1)求a 的值；(2)若g (x )＝4－x －2，且g (x )＝f (x )，求满足条件的x 的值．20．(本小题满分12分)已知函数f (x )＝a ·2x ＋b ·3x ，其中常数a ，b 为实数． (1)当a >0，b >0时，判断并证明函数f (x )的单调性； (2)当ab <0时，求f (x ＋1)>f (x )时x 的取值范围．21．(本小题满分12分)设a ∈R ，f (x )＝a －22x ＋1(x ∈R )．(1)证明：对任意实数a ，f (x )为增函数； (2)试确定a 的值，使f (x )≤0恒成立．22．(本小题满分12分)已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋2是奇函数．(1)求b 的值；(2)判断函数f (x )的单调性；(3)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．详解答案第二章 基本初等函数(Ⅰ)(一)(指数与指数函数) [名师原创·基础卷]1．C 解析：[(－2)2]－ 12＝2－12＝12＝22.2．D 解析：原式＝1－(1－22)÷⎝ ⎛⎭⎪⎫322＝1－(－3)×49＝73.故选D. 3．C 解析：a >1，∴y ＝a x 在R 上单调递增且过(0,1)点，排除B ，D ，又∵1－a <0，∴y ＝(1－a )x 2的开口向下．4．A 解析：在①中，a <0时，(a 2) 32>0，而a 3<0，∴①不成立．在②中，令a ＝－2，n ＝3，则3(－2)3＝－2≠|－2|，∴②不成立． 在③中，定义域应为⎣⎢⎡⎭⎪⎫2，73∪⎝ ⎛⎭⎪⎫73，＋∞，∴③不成立． ④式是正确的，∵6(－2)2＝622＝32，∴④正确． 5．D 解析：设f (x )＝a x (a >0且a ≠1)， 由已知得14＝a －2，a 2＝4，所以a ＝2， 于是f (x )＝2x ，所以f (4)·f (2)＝24·22＝64.解题技巧：已知函数类型，求函数解析式，常用待定系数法，即先把函数设出来，再利用方程或方程组解出系数．6．C 解析：∵1x ≠0，∴21x≠1， ∴函数y ＝21x 的值域为(0,1)∪(1，＋∞)．7．B 解析：找两个特殊点，当x ＝0时，y ＝1，排除A ，C.当x ＝1时，y ＝0，排除D.故选B.8．C 解析：∵0<a <b <1，∴a a >a b ，故A 不成立，同理B 不成立，若a a <b a ，则⎝ ⎛⎭⎪⎫a b a <1，∵0<ab <1,0<a <1，∴⎝ ⎛⎭⎪⎫a b a<1成立，故选C. 9．D 解析：与曲线y ＝e x 关于y 轴对称的曲线为y ＝e －x ，函数y ＝e －x 的图象向左平移一个单位长度即可得到函数f (x )的图象，即f (x )＝e －(x ＋1)＝e －x －1.解题技巧：函数图象的平移变换，要注意平移的方向和平移量．平移规律为：10．B 解析：由函数y ＝a x ＋m －1(a >0，a ≠1)的图象在第一、三象限知，a >1.知函数在第四象限，∴a 0＋m －1<0，则有m <0.11．A 解析：f (x )＝2x ＋2－4x ＝－(2x )2＋4·2x ＝－(2x －2)2＋4，又∵x 2－x －6≤0，∴－2≤x ≤3，∴14≤2x ≤8.当2x ＝2时，f (x )max ＝4，当2x ＝8时，f (x )min ＝－32. 12．B 解析：因为f (－x )＝3－x ＋3－(－x )＝3－x ＋3x ＝f (x )， g (－x )＝3－x －3－(－x )＝3－x －3x ＝－g (x )，所以f (x )为偶函数，g (x )为奇函数．13．c >a >b 解析：由指数函数y ＝a x 当0<a <1时为减函数知， 0．80.7>0.80.9，又1.20.8>1,0.80.7<1， ∴1.20.8>0.80.7>0.80.9，即c >a >b .14．(－3,0) 解析：令⎝ ⎛⎭⎪⎫12x＝t ，∵方程有正根，∴t ∈(0,1)．方程转化为t 2＋2t ＋a ＝0， ∴a ＝1－(t ＋1)2.∵t ∈(0,1)，∴a ∈(－3,0)．15．(－∞，1] 解析：解法一：由指数函数的性质可知，f (x )＝⎝ ⎛⎭⎪⎫12x在定义域上为减函数，故要求f (x )的单调递增区间，只需求y ＝|x －1|的单调递减区间．又y ＝|x －1|的单调递减区间为(－∞，1]，所以f (x )的单调递增区间为(－∞，1]．解法二：f (x )＝⎝ ⎛⎭⎪⎫12|x －1|＝⎩⎨⎧⎝ ⎛⎭⎪⎫12x －1，x ≥1，2x －1，x <1.可画出f (x )的图象，并求其单调递增区间．解题技巧：既可以利用复合函数的“同增异减”法则求解，也可以去绝对值符号，转化为分段函数求解．16．1 解析：作出函数y ＝2|x |的图象(如图所示)．当x ＝0时，y ＝20＝1， 当x ＝－1时，y ＝2|－1|＝2， 当x ＝1时，y ＝21＝2，所以当值域为[1,2]时，区间[a ，b ]的长度的最大值为2，最小值为1，它们的差为1.17．解：当a >1时，a 2x ＋7<a 3x －2等价于2x ＋7<3x －2， ∴x >9；当0<a <1时，a 2x ＋7<a 3x －2等价于2x ＋7>3x －2. ∴x <9.综上，当a >1时，不等式的解集为{x |x >9}； 当0<a <1时，不等式的解集为{x |x <9}． 解题技巧：注意按照底数进行分类讨论． 18．解：(1)由f (a )＝2，得3a ＝2，a ＝log 32， ∴g (x )＝(3a )x －4x ＝(3log 32)x －4x ＝2x －4x ＝－(2x )2＋2x . ∴g (x )＝－(2x )2＋2x . (2)设2x ＝t ，∵x ∈[－2,1]， ∴14≤t ≤2.g (t )＝－t 2＋t ＝－⎝ ⎛⎭⎪⎫t －122＋14，由g (t )在t ∈⎣⎢⎡⎦⎥⎤14，2上的图象可得，当t ＝12，即x ＝－1时，g (x )有最大值14； 当t ＝2，即x ＝1时，g (x )有最小值－2. 故g (x )的值域是⎣⎢⎡⎦⎥⎤－2，14.19．解：(1)由已知得⎝ ⎛⎭⎪⎫12－a ＝2，解得a ＝1. (2)由(1)知，f (x )＝⎝ ⎛⎭⎪⎫12x ，又g (x )＝f (x )，则4－x －2＝⎝ ⎛⎭⎪⎫12x ， 即⎝ ⎛⎭⎪⎫14x －⎝ ⎛⎭⎪⎫12x －2＝0，即⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12x 2－⎝ ⎛⎭⎪⎫12x －2＝0. 令⎝ ⎛⎭⎪⎫12x ＝t ，则t 2－t －2＝0，即(t －2)(t ＋1)＝0. 又t >0，故t ＝2，即⎝ ⎛⎭⎪⎫12x ＝2，解得x ＝－1. 20．解：(1)函数f (x )在R 上是增函数．证明如下： a >0，b >0，任取x 1，x 2∈R ，且x 1<x 2，(2)∵f (x ＋1)>f (x )，∴f (x ＋1)－f (x )＝(a ·2x ＋1＋b ·3x ＋1)－(a ·2x ＋b ·3x ) ＝a ·2x ＋2b ·3x >0，当a <0，b >0时，⎝ ⎛⎭⎪⎫32x >－a 2b ，则x >log 1.5⎝ ⎛⎭⎪⎫－a 2b ， 当a >0，b <0时，⎝ ⎛⎭⎪⎫32x <－a 2b ，则x <log 1.5⎝ ⎛⎭⎪⎫－a 2b .综上，当a <0，b >0时，x 的取值范围是⎝ ⎛⎭⎪⎫log 1.5⎝ ⎛⎭⎪⎫－a 2b ，＋∞； 当a >0，b <0时，x 的取值范围是⎝ ⎛⎭⎪⎫－∞，log 1.5⎝ ⎛⎭⎪⎫－a 2b . 21．(1)证明：任取x 1，x 2∈R ，且x 1<x 2，故对于任意实数a ，f (x )为增函数．(2)解：f (x )＝a －22x ＋1≤0恒成立，只要a ≤22x ＋1恒成立，问题转化为只要a 不大于22x ＋1的最小值． ∵x ∈R,2x >0恒成立，∴2x ＋1>1.∴0<12x ＋1<1,0<22x ＋1<2，∴a ≤0. 故当a ∈(－∞，0]时，f (x )≤0恒成立．22．解：(1)因为f (x )是奇函数，所以f (0)＝0， 即b －12＋2＝0，解得b ＝1.(3)因为f (x )是奇函数，f (t 2－2t )＋f (2t 2－k )<0，则f (t 2－2t )<－f (2t 2－k )＝f (k －2t 2)，因f (x )为减函数，由上式推得，t 2－2t >k －2t 2. 即对一切t ∈R 有3t 2－2t －k >0，从而判别式Δ＝4＋12k <0，解得k <－13.故k 的取值范围是⎝ ⎛⎭⎪⎫－∞，－13.。