(完整版)小学四年级奥数教程第4讲：竖式数字谜

竖式谜解题思路四年级（一）一位数的乘、除法竖式数字谜问题。

例1在左下乘法竖式的□中填入合适的数字，使竖式成立。

分析与解：由于积的个位数是5，所以在乘数和被乘数的个位数中，一个是5，另一个是奇数。

因为乘积大于被乘数的7倍，所以乘数是大于7的奇数，即只能是9(这是问题的“突破口”)，被乘数的个位数是5。

因为7×9＜70＜8×9，所以，被乘数的百位数字只能是7。

至此，求出被乘数是785，乘数是9(见右上式)。

例2在左下边除法竖式的□中填入适当的数，使竖式成立。

分析与解：由48÷8=6即8×6=48知，商的百位填6，且被除数的千位、百位分别填4，8。

又显然，被除数的十位填1。

由1□=商的个位×8知，两位数1□能被8除尽，只有16÷8=2，推知被除数的个位填6，商的个位填2。

填法如右上式。

例2是从最高位数入手分析而得出解的。

例3在右边除法竖式的□中填入合适的数字。

使竖式成立。

分析与解：从已知的几个数入手分析。

首先，由于余数是5，推知除数＞5，且被除数个位填5。

由于商4时是除尽了的，所以，被除数的十位应填2，且由于3×4=12，8×4=32，推知，除数必为3或8。

由于已经知道除数＞5，故除数=8。

(这是关键！)从8×4=32知，被除数的百位应填3，且商的百位应填0。

从除数为8，第一步除法又出现了4，8×8=64，8×3=24，这说明商的千位只能填8或3。

试算知，8和3都可以。

所以，此题有下面两种填法。

（二）两位数的竖式数字谜问题例1在下列乘法竖式的□中填入合适的数字：分析与解：(1)为方便叙述，将部分□用字母表示如左下式。

第1步：由A4B×6的个位数为0知，B=0或5；再由A4B×C=□□5，推知B＝5。

第2步：由A45×6＝1□□0知，A只可能为2或3。

但A为3时，345×6＝2070，不可能等于1□□0，不合题意，故A=2。

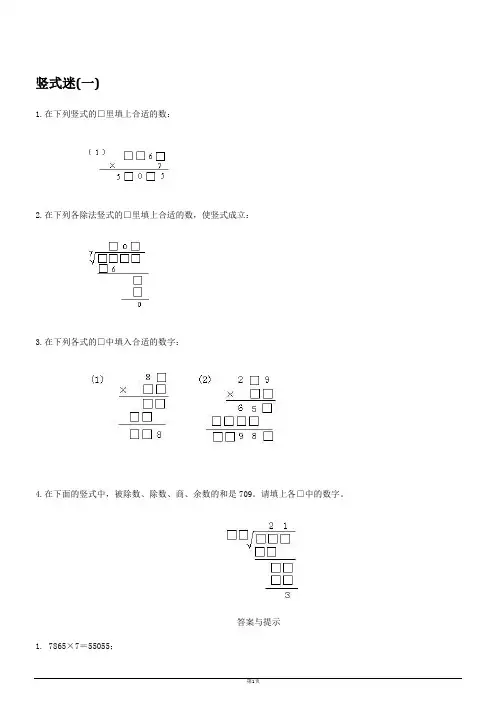
竖式迷(一)1.在下列竖式的□里填上合适的数：2.在下列各除法竖式的□里填上合适的数，使竖式成立：3.在下列各式的□中填入合适的数字：4.在下面的竖式中，被除数、除数、商、余数的和是709。

请填上各□中的数字。

答案与提示1. 7865×7＝55055；2.5607÷7=8013.提示：(1)先确定乘数是11。

(2)先确定乘数的十位数是7，再确定被乘数的十位数是1，最后确定乘数的个位是3。

4.提示：由题意和竖式知，被除数＋除数＝709－21－3＝685，再由竖式知，被除数＝除数×21＋3，所以，除数×21＋3＋除数＝685，除数×22＝685－3＝682，除数＝682÷22＝31。

被除数为31×21＋3＝654。

填法如右式。

竖式迷(二)（一）一位数的乘、除法竖式数字谜问题。

例1在左下乘法竖式的□中填入合适的数字，使竖式成立。

分析与解：由于积的个位数是5，所以在乘数和被乘数的个位数中，一个是5，另一个是奇数。

因为乘积大于被乘数的7倍，所以乘数是大于7的奇数，即只能是9(这是问题的“突破口”)，被乘数的个位数是5。

因为7×9＜70＜8×9，所以，被乘数的百位数字只能是7。

至此，求出被乘数是785，乘数是9(见右上式)。

例2在左下边除法竖式的□中填入适当的数，使竖式成立。

分析与解：由48÷8=6即8×6=48知，商的百位填6，且被除数的千位、百位分别填4，8。

又显然，被除数的十位填1。

由1□=商的个位×8知，两位数1□能被8除尽，只有16÷8=2，推知被除数的个位填6，商的个位填2。

填法如右上式。

例2是从最高位数入手分析而得出解的。

例3在右边除法竖式的□中填入合适的数字。

使竖式成立。

分析与解：从已知的几个数入手分析。

首先，由于余数是5，推知除数＞5，且被除数个位填5。

由于商4时是除尽了的，所以，被除数的十位应填2，且由于3×4=12，8×4=32，推知，除数必为3或8。

四年级下学期第四讲，数字谜第08讲复杂竖式【内容概述】重点是三位数及三位数以上的乘、除法，涉及小数乘、除法的竖式填空格问题．补填空格与破译字母相结合的竖式问题，涉及较强推理能力的竖式问题．对审题、选择突破口和试验求解三个步骤有较高要求，通过“破泽”提高推理能力和对运算法则深入、灵活的理解．【典型问题】【基础题】1.【40401】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★）请在图15-1所示乘法算式的每个方框中填入一个数字，使其成为正确的竖式．那么计算所得的乘积应是多少？2.【40402】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★）图15-2是一个乘法竖式，请在其中的10个空格内分别填入0至9这10个数字，使算式成立．3. 【40403】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★）请把图15-3所示的除法竖式中空缺的数字补上．问其中的商是多少？4. 【40404】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★★）图15-4是一个残缺的除法竖式，其中只写出了5个3．那么，这个算式的商数是多少？0 6图15-3图15-45. 【40405】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★）请在图15-5中的每个方框内填入恰当的数字，使这个除法算式成立．求其中的商数、除数与被除数．6. 【40406】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★）请补全如图15-6所示的除法竖式．问这个算式中的被除数是多少？7. 【40407】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★）在图15-7中的每个方框内填入适当的数字，使这个小数除法竖式成立．图15-53 510 图15-68. 【40408】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★）在图15-8所示算式的各方格内填入适当的数字，并将A ，B ，C ，D 分别替换为不同的数字，使算式成立．问：A ，B ，C ，D 各代表哪个数字？9. 【40409】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★）图15-9是一个正确的乘法算式，其中的每个方框和汉字都代表一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字，且“总”字所代表的数字大于2．问：“总决赛”所表示的三位数是多少？图15-710.【40410】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★★）在图15-10所示的乘法算式中，每个方框和汉字都代表一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字．那么，这个乘法算式的最后乘积是多少？11.【40411】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★）在图15-11所示的乘法算式中，每个方框和汉字都代表一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字．那么，这个乘法算式的最后乘积是多少？12.【40412】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★★）在图15-12所示的乘法算式中，每个方框和字母都代表一个数字，相同的字母代表相同的数字，不同的字母代表不同的数字．那么a+b+c等于多少？13.【40413】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★）图15-13是一个乘法算式，其中的每个方框和汉字都代表一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字．那么，当算式成立时，“巴西法国争夺冠军”这8个字所代表的八位数是多少？14.【40414】（导引偶数题，四下第04讲，复杂竖式，数字谜第08讲★★★）在如图15-14所示的算式中，每个方框和汉字都代表一个数字，相同的汉字代表相同的数字，不同的汉字代表不同的数字．那么，当算式成立时，最后的乘积是多少？15.【40415】（导引奇数题，四下第04讲，复杂竖式，数字谜第08讲★★★★）按照图15-15给出的各数字的奇偶性补全这个除法竖式．奇奇偶奇奇 6 偶偶奇奇偶偶奇偶奇奇奇奇偶偶偶奇偶偶奇偶图15-1516.【40416】（汪岩、四下第04讲，复杂竖式，数字谜第08讲★★）在图1的乘法竖式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字，那么“北京举办奥运会”所代表的七位数是什么？526×308=162008，代表的七位数是5216308。

小学数学四年级思维奥数寒假讲义-第4讲 乘法竖式谜（教师版）【课前小热身】下面的竖式谜，你还记得吗？注意寻找突破口来解题哦。

（1）43□□□⨯（2）64□□□⨯（3）□□□84⨯（4）□□□□7⨯【知识梳理】 一、末位分析乘法竖式问题中常用的突破口有：首位、末位、位数、进位及重复出现的汉字或字母。

末位分析：①×2，×4，×6，×8有两个答案，如□× 2= 4，□有2、7两个答案； ②×1，×3，×7，×9有一个答案，如□× 3= 8，□只有6一个答案； ③×5，乘积的末位为0，有5个答案；乘积的末位为5，也有5个答案； ④×0，乘积的末位只能是0，有10个答案。

【典例精讲】【例题1】如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字，请问：“爱我中华”所表示的四位数是多少？华中我爱爱华中我36⨯ 【答案】2758【解析】从末位开始，3×6=18，因此“华”代表8，然后依次进行即可，即7586×3=22758。

【训练1】如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字，请问：竖式的乘积是多少？石穿水滴水石穿水84⨯【答案】31392【解析】从末位分析，4×8=32，则“石”=2，然后依次进行即可，即3924×8=31392。

【例题2】如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字，请问：“优邦学”所表示的三位数是多少？【答案】296【解析】末位分析，学×9= 4，则“学”=6，个位向十位进位5，依次类推，“数”=9，十位向百位进位8，“爱”=2，即296×6=2664。

【训练2】如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字，请问：“一丝不苟”所表示的四位数是多少？43苟不丝苟不丝一⨯ 【答案】1428【解析】末位分析，苟×3= 4，则“苟”=8，个位向十位进位2，依次类推，“不”=2，十位没有向百位进位，“丝”=4，百位向千位进位1，“一”=1，即1428×3=4284。

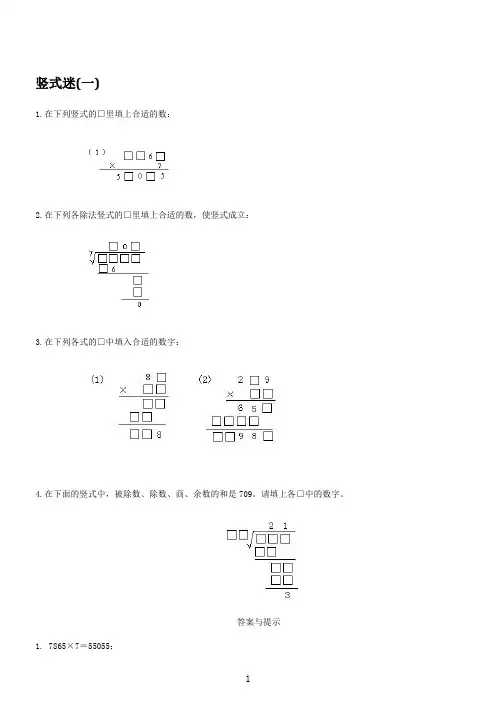
竖式迷(一)1.在下列竖式的□里填上合适的数：2.在下列各除法竖式的□里填上合适的数，使竖式成立：3.在下列各式的□中填入合适的数字：4.在下面的竖式中，被除数、除数、商、余数的和是709。

请填上各□中的数字。

答案与提示1. 7865×7＝55055；2.5607÷7=8013.提示：(1)先确定乘数是11。

(2)先确定乘数的十位数是7，再确定被乘数的十位数是1，最后确定乘数的个位是3。

4.提示：由题意和竖式知，被除数＋除数＝709－21－3＝685，再由竖式知，被除数＝除数×21＋3，所以，除数×21＋3＋除数＝685，除数×22＝685－3＝682，除数＝682÷22＝31。

被除数为31×21＋3＝654。

填法如右式。

竖式迷(二)（一）一位数的乘、除法竖式数字谜问题。

例1在左下乘法竖式的□中填入合适的数字，使竖式成立。

分析与解：由于积的个位数是5，所以在乘数和被乘数的个位数中，一个是5，另一个是奇数。

因为乘积大于被乘数的7倍，所以乘数是大于7的奇数，即只能是9(这是问题的“突破口”)，被乘数的个位数是5。

因为7×9＜70＜8×9，所以，被乘数的百位数字只能是7。

至此，求出被乘数是785，乘数是9(见右上式)。

例2在左下边除法竖式的□中填入适当的数，使竖式成立。

分析与解：由48÷8=6即8×6=48知，商的百位填6，且被除数的千位、百位分别填4，8。

又显然，被除数的十位填1。

由1□=商的个位×8知，两位数1□能被8除尽，只有16÷8=2，推知被除数的个位填6，商的个位填2。

填法如右上式。

例2是从最高位数入手分析而得出解的。

例3在右边除法竖式的□中填入合适的数字。

使竖式成立。

分析与解：从已知的几个数入手分析。

首先，由于余数是5，推知除数＞5，且被除数个位填5。

由于商4时是除尽了的，所以，被除数的十位应填2，且由于3×4=12，8×4=32，推知，除数必为3或8。

小学奥数基础教程（四年级）第1讲速算与巧算（一）第2讲速算与巧算（二）第3讲高斯求和第4讲 4，8，9整除的数的特征第5讲弃九法第6讲数的整除性（二）第7讲找规律（一）第8讲找规律（二）第9讲数字谜（一）第10讲数字谜（二）第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法（一）第15讲盈亏问题与比较法（二）第16讲数阵图（一）第17讲数阵图（二）第18讲数阵图（三）第19将乘法原理第20讲加法原理（一）第21讲加法原理（二）第22讲还原问题（一）第23讲还原问题（二）第24讲页码问题第25讲智取火柴第26讲逻辑问题（一）第27讲逻辑问题（二）第28讲最不利原则第29讲抽屉原理（一）第30讲抽屉原理（二）第1讲速算与巧算（一）计算是数学的基础，小学生要学好数学，必须具有过硬的计算本领。

准确、快速的计算能力既是一种技巧，也是一种思维训练，既能提高计算效率、节省计算时间，更可以锻炼记忆力，提高分析、判断能力，促进思维和智力的发展。

我们在三年级已经讲过一些四则运算的速算与巧算的方法，本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。

例1 四年级一班第一小组有10名同学，某次数学测验的成绩（分数）如下：86，78，77，83，91，74，92，69，84，75。

求这10名同学的总分。

分析与解：通常的做法是将这10个数直接相加，但这些数杂乱无章，直接相加既繁且易错。

观察这些数不难发现，这些数虽然大小不等，但相差不大。

我们可以选择一个适当的数作“基准”，比如以“80”作基准，这10个数与80的差如下：6，-2，-3，3，11，-6，12，-11，4，-5，其中“-”号表示这个数比80小。

于是得到总和=80×10＋（6-2-3＋3＋11-＝800＋9＝809。

实际计算时只需口算，将这些数与80的差逐一累加。

为了清楚起见，将这一过程表示如下：通过口算，得到差数累加为9，再加上80×10，就可口算出结果为809。

竖式数字迷教学目的学习根据有关的运算法则、数的性质（和差积商的位数，数的整除性、奇偶性、尾数规律等）来进行正确地推理、判断．教学内容竖式数字谜是一种猜数的游戏解竖式数字谜，就得根据有关的运算法则、数的性质（和差积商的位数，数的整除性、奇偶性、尾数规律等）来进行正确地推理、判断．解答竖式数字谜时应注意以下几点：(1)空格中只能填写0，1，2，3，4，5，6，7，8，9，而且最高位不能为0；(2)进位要留意，不能漏掉了；(3)答案有时不唯一；(4)两数字相加，最大进位为1．三个数字相加最大进位为2；(5)两个数字相乘，最大进位为8；(6)相同的字母（汉字或符号）代表相同的数字，不同的字母（汉字或符号）代表不同的数字．下面的算式中．只有5个数字已写出，请补上其他数字．在5个方格中，要各填一个数字，使算式成立，先填哪一个呢？做这类题目，要善于发现问题的“突破口”．从百位进位来看，和的千位数字只能是1．从十位相加来看，进位到百位，也只能进l．因此，□2□的百位是9，和的百位是0通过上面的分析，就找到了这道题日的“突破口”．再从15-7-6=2，11-2-1=8，就可得出算式解在下面算式的□内各填人一个合适的数字，使算式成立由于12-9=3，所以被减数的个位数字为2；再看十位，由于9-0=9，所以减数的十位数字为0；再看百位，由于9-0=9．所以差的百位数字为9；最后看千位，由于7-5-1=1．所以被减数的千位数字为7。

解本题还可以根据加、减法是互逆运算的关系，将减法算式转化成下面的加法算式：同学们自己试一试填写算式。

巩固练习1在下面竖式的空格中，各填人一个合适的数字，使竖式成立你做对了吗？答案：下面是一个六位数乘以一个一位数的算式，不同的汉字表示不同的数，相同的汉字表示相同的数，其中的六位数是_______．（第一届小学“希望杯”全国数学邀请赛试题）从“赛×赛”的个位数字为9入手，得出赛=3或7，再由999 999÷赛=小学希望杯赛，就可得出结论．解由赛×赛的个位数字为9，得赛=3或7．若赛=3，则小学希望杯赛=999 999÷3=333 333因为不同的汉字代表不同的数，所以赛≠3因此，赛=7，小学希望杯赛=999 999÷7=142 857本题抓住关键环节“赛×赛”的个位数字为9作为突破口，再巧用乘法与除法是互逆运算即可得出结论。

竖式迷(一)1.在下列竖式的□里填上合适的数：2.在下列各除法竖式的□里填上合适的数，使竖式成立：3.在下列各式的□中填入合适的数字：4.在下面的竖式中，被除数、除数、商、余数的和是709。

请填上各□中的数字。

答案与提示1. 7865×7＝55055；2.5607÷7=8013.提示：(1)先确定乘数是11。

(2)先确定乘数的十位数是7，再确定被乘数的十位数是1，最后确定乘数的个位是3。

4.提示：由题意和竖式知，被除数＋除数＝709－21－3＝685，再由竖式知，被除数＝除数×21＋3，所以，除数×21＋3＋除数＝685，除数×22＝685－3＝682，除数＝682÷22＝31。

被除数为31×21＋3＝654。

填法如右式。

竖式迷(二)（一）一位数的乘、除法竖式数字谜问题。

例1在左下乘法竖式的□中填入合适的数字，使竖式成立。

分析与解：由于积的个位数是5，所以在乘数和被乘数的个位数中，一个是5，另一个是奇数。

因为乘积大于被乘数的7倍，所以乘数是大于7的奇数，即只能是9(这是问题的“突破口”)，被乘数的个位数是5。

因为7×9＜70＜8×9，所以，被乘数的百位数字只能是7。

至此，求出被乘数是785，乘数是9(见右上式)。

例2在左下边除法竖式的□中填入适当的数，使竖式成立。

分析与解：由48÷8=6即8×6=48知，商的百位填6，且被除数的千位、百位分别填4，8。

又显然，被除数的十位填1。

由1□=商的个位×8知，两位数1□能被8除尽，只有16÷8=2，推知被除数的个位填6，商的个位填2。

填法如右上式。

例2是从最高位数入手分析而得出解的。

例3在右边除法竖式的□中填入合适的数字。

使竖式成立。

分析与解：从已知的几个数入手分析。

首先，由于余数是5，推知除数＞5，且被除数个位填5。

由于商4时是除尽了的，所以，被除数的十位应填2，且由于3×4=12，8×4=32，推知，除数必为3或8。