电路原理一经典例题重点整理(1-9章)

电路原理每章知识点总结基本元件：1. 电阻：电子元件中最基本的元器件，用来限制电流。

电阻的大小用欧姆（ohm）表示，符号为Ω。

2. 电容：由两个导体之间的绝缘材料组成，用来存储电荷。

其大小用法拉德（Farad）表示，符号为F。

3. 电感：当电流通过导线时会产生磁场，导线围绕的磁场又会产生电流。

这种现象称为电感，用亨利（Henry）表示，符号为H。

电路定律：1. 基尔霍夫电压定律（KVL）：在一段闭合回路中，各个元器件之间的电压和等于回路中电压的代数和。

2. 基尔霍夫电流定律（KCL）：在电路中，流入一个节点的电流的总和等于流出该节点的电流的总和。

3. 欧姆定律：电流与电压成正比，电阻成反比。

数学表达式为 V=IR，其中V为电压，I为电流，R为电阻。

第二章：串并联电路串联电路：所有元件依次连接起来，电流只有一个路径可走。

并联电路：所有元件并联连接，电流可以通过不同的路径流动。

电流和电压的计算：1. 串联电路中各个电阻的电压之和等于电源电压。

2. 并联电路中，各个电阻的电流之和等于总电流。

第三章：交流电路交流电路中的频率和周期：1. 交流电源的频率用赫兹（Hz）表示，一般为50Hz或60Hz。

2. 周期是指一个完整的波形所经过的时间，它与频率成反比。

周期T=1/f。

交流电路中的电压和电流：1. 交流电压：交流电压的大小可以用有效值表示，称为有效值，标识为Vrms。

2. 交流电流：交流电流的大小也可以用有效值表示，称为有效值，标识为Irms。

交流电路中的电阻、电容和电感：1. 交流电路中的电阻会产生有功功率消耗。

2. 交流电路中的电容会导致电压滞后。

3. 交流电路中的电感会导致电流滞后。

第四章：放大电路放大电路的作用是将输入信号放大到所需的大小。

常用的放大电路包括共集电极放大电路（CE）、共基极放大电路（CB）和共射极放大电路（CC）。

放大电路中的输入和输出：1. 输入端：输入信号称为小信号，其大小远远小于电源电压。

电路原理总结第一章基本元件和定律1.电流的参考方向可以任意指定，分析时：若参考方向与实际方向一致，则i>0，反之i<0。

电压的参考方向也可以任意指定，分析时：若参考方向与实际方向一致，则u>0反之u<0。

2．功率平衡一个实际的电路中，电源发出的功率总是等于负载消耗的功率。

3．全电路欧姆定律：U=E-RI4．负载大小的意义：电路的电流越大，负载越大。

电路的电阻越大，负载越小。

5．电路的断路与短路电路的断路处：I＝0，U≠0电路的短路处：U＝0，I≠0二．基尔霍夫定律1．几个概念：支路：是电路的一个分支。

结点：三条（或三条以上）支路的联接点称为结点。

回路：由支路构成的闭合路径称为回路。

网孔：电路中无其他支路穿过的回路称为网孔。

2．基尔霍夫电流定律：（1）定义：任一时刻，流入一个结点的电流的代数和为零。

或者说：流入的电流等于流出的电流。

（2）表达式：i进总和=0或： i进=i出（3）可以推广到一个闭合面。

3．基尔霍夫电压定律（1）定义：经过任何一个闭合的路径，电压的升等于电压的降。

或者说：在一个闭合的回路中，电压的代数和为零。

或者说：在一个闭合的回路中，电阻上的电压降之和等于电源的电动势之和。

（2）表达式：1或： 2或： 3（3）基尔霍夫电压定律可以推广到一个非闭合回路三．电位的概念（1）定义：某点的电位等于该点到电路参考点的电压。

（2）规定参考点的电位为零。

称为接地。

（3）电压用符号U表示,电位用符号V表示（4）两点间的电压等于两点的电位的差。

（5）注意电源的简化画法。

四．理想电压源与理想电流源1．理想电压源（1）不论负载电阻的大小，不论输出电流的大小，理想电压源的输出电压不变。

理想电压源的输出功率可达无穷大。

（2）理想电压源不允许短路。

2．理想电流源（1）不论负载电阻的大小，不论输出电压的大小，理想电流源的输出电流不变。

理想电流源的输出功率可达无穷大。

（2）理想电流源不允许开路。

《电路I 》复习题一、填空题 1、RC 串联电路从一种状态到另一种状态的转换过程中，不能突变的是 。

2、一个电路有n 个结点，b 条支路，它可以列 条KCL方程、 条KVL 方程。

3、三个3K Ω的电阻星形连接，当转换成三角形连接时其每个等值电阻为 K Ω。

4、右图所示电路电压源功率为 。

5、电阻的对偶是电导，阻抗的对偶是导纳，那么感抗的对偶是 。

6、对称三相电源是由3个同频率、等幅值、初相依次滞后120°的正弦电压源连接成 形或 形组成的电源。

7、已知电路中某支路电流为A t i )30314sin(14.14 +=，则该电流的有效值为 ，频率为 ，初相为 。

8、理想变压器将一侧吸收的能量全部传输到另一侧输出，在传输过程中，仅仅将 、 按变比作数值的变换。

9、RLC 串联电路发生谐振时的固有频率是 。

10、要提高感性负载的功率因数，可在感性负载上 并联 适当的电容。

正弦交流电的三要素是：（ 振幅 ）、（ 频率 ）、（ 初始相位 ）。

11、已知)30100cos(10 -=t i A ，)60100sin(25-=t u V ，则i 、u 之间的相位关系为 。

12、右图所示电路中I = 。

13、三相对称电路，当负载为星形接法时，相电压U P 与线电压U L 的关系为 ，相电流I P 与线电流I L 的关系为 。

14、电路中三条或三条以上支路的公共连接点称为 。

15、RL 串联电路从一种状态到另一种状态的转换过程中，不能突变的是 。

16、阻抗的对偶是导纳，电阻的对偶是电导，那么容抗的对偶是 。

17、受控源中，被控制量和控制量成正比，这种受控源称为 受控源。

18、已知电路中某支路电压为)45314sin(28.28-=t u V ，则该电压的有效值为 ，频率为 ，初相为 。

19、要提高电路功率因数，对容性负载，应并接 元件。

20、品质因素（Q 值）是分析和比较谐振电路频率特性的一个重要的辅助参数，当Q ＞1时，电感和电容两端电压将 信号源电压。

《电路原理》复习要点知识点复习：第一章电路模型和电路定理1、电流、电压的参考方向与其真实方向的关系；2、直流功率的计算；3、理想电路元件；无源元件：电阻元件R：消耗电能电感元件L：存储磁场能量电容元件C：存储电场能量有源元件：独立电源：电压源、电流源受控电源：四种线性受控源（V C V S;V C C S;C C V S;C C C S）4、基尔霍夫定律。

（1）、支路、回路、结点的概念（2）、基尔霍夫定律的内容：集总电路中基尔霍夫定律包括基尔霍夫电流定律( KCL )和基尔霍夫电压定律( KVL )。

基尔霍夫电流定律(KCL)：任意时刻，流入电路中任一节点的电流代数和恒为零。

约定：流入取负，流出取正；物理实质：电荷的连续性原理；推广：节点→封闭面（广义节点）；基尔霍夫电压定律(KVL)：任意时刻，沿任一闭合回路电压降代数和恒为零。

约定：与回路绕行方向一致取正，与回路绕行方向不一致取负；物理实质：电位单值性原理；推广：闭合路径→假想回路；（3）、基尔霍夫定律表示形式：m基尔霍夫电流定律(KCL)基尔霍夫电压定律(KVL)熟练掌握：基尔霍夫电流定律( KCL )：在集总参数电路中，任意时刻，对任意结点，流出或流入该结点电流的代数和等于零。

KCL 是电荷守恒和电流连续性原理在电路中任意结点处的反映；KCL 是对结点电流的约束，与支路上接的是什么元件无关，与电路是线性还是非线性无关；KCL 方程是按电流参考方向列写，流出结点的电流取“+”，流入结点的电流取“—”，与电流实际方向无关。

基尔霍夫电压定律 (KVL)：在集总参数电路中，任意时刻，沿任一闭合路径（回路）绕行，各支路电压的代数和等于零。

KVL 是能量守恒的具体体现(电压与路径无关)；KVL 是对回路电压加的约束，与回路各支路上接的是什么元件无关，与电路是线性还是非线性无关；KVL 方程是按电压参考方向列写，任意选定回路绕行方向（顺时针或逆时针），支路电压的参考方向与回路绕行方向一致，该电压取“+”，反之“—”，与电压实际方向无关。

部分习题解答第一章部分习题1-1在题图1-1中,已知i=2+t A，且t=0时，，试求=？电场储能W C=？(其中C=1uF )题图1-1解：1-2题图1-2是一个简化的晶体管电路，求电压放大倍数，再求电源发出的功率和负载吸收的功率。

题图1-2解：，电源发出的功率：负载吸收的功率：1-4题图1-4电路中，=0.5A，=1A，控制系数r=10，电阻R=50。

方框内为任意电路(设不短路)，试求电流I ？题图1-4解：，1－5电路各参数如题图1-5所示，试求电流I为多少？题图1-5解：如图，共有3个节点，6条支路，由KCL得：由得：，，节点，，解得：，，，，，1-15在题图1-15所示电路中，已知电流源＝2A，＝1A，R=5，＝1，＝2，试求电流I、电压U及电流源的端电压和各为多少？题图1-15解：由：1-16题图1-16所示电路中，电压源分别为＝6V，=8V，R=7，试求电流I。

题图1-16解：，1-17如题图1-17所示电路中，发出功率为36W，电阻消耗的功率为18W，试求、、的值。

题图1-17解：，1-18题图1-18所示电路中，电压源E=12V，电流源＝100mA，电压控制电压源的控制系数＝1，＝20，＝100，试求和电流源发出的功率。

题图1-18解：，1-19题图1-19所示电路中，电压源E=20V，电阻＝＝10，R=50，控制系数＝5，试求I和。

题图1-19解：，，第二章部分习题2-1、题图2－1所示电路中，给定=1，=2,=3,=4,＝5A,=6A,试用回路电流法求各支路电流。

题图2－1解：以R1 , R3 , R4所在支路为树，各支路电流：，2-2、题图2-2电路中，已知==2,==1,==3,=4,=6A,=1A,以,,,,支路为树，试求连支电流和。

题图2-2解：2-4、在题图2－4所示电路中，已知＝2，＝3，＝4，＝5，＝＝2，=4V，试用网孔电流法求和。

题图2－4解：列写网孔电流方程：，代入数据解得：2-5、电路如题图2－5所示，已知＝4，＝5，＝6，＝7A,=8A,=9A,试用网孔电流法求各支路电流。

电路原理知识点总结第1篇（1）串联电路：i=i1+i2;（2）并联电路：i=i1+i2【方法提示】1、电流表的使用可总结为（一查两确认，两要两不要）（1）一查：检查指针是否指在零刻度线上；（2）两确认：①确认所选量程。

②确认每个大格和每个小格表示的电流值。

两要：一要让电流表串联在被测电路中；二要让电流从“+”接线柱流入，从“-”接线柱流出；③两不要：一不要让电流超过所选量程，二不要不经过用电器直接接在电源上。

在事先不知道电流的大小时，可以用试触法选择合适的量程。

2、根据串并联电路的特点求解有关问题的电路（1）分析电路结构，识别各电路元件间的串联或并联；（2）判断电流表测量的是哪段电路中的电流；（3）根据串并联电路中的电流特点，按照题目给定的条件，求出待求的电流。

电路原理知识点总结第2篇电流和电路一、摩擦起电摩擦过的物体具有吸引轻小物体的现象叫摩擦起电；二、两种电荷用丝绸摩擦过的玻璃棒带的电荷叫正电荷；用毛皮摩擦过的橡胶棒带的电荷叫负电荷；三、电荷间的相互作用同中电荷相互排斥，异种电荷相互吸引；四、验电器1、用途：用来检验物体是否带电；2、原理：利用同种电荷相互排斥；五、电荷量（电荷）电荷的多少叫电荷量，简称电荷；单位是库仑，简称库，符号为C；六、元电荷1、原子是由位于中心的带正电的原子核和核外带负电的电子组成；2、最小的电荷叫元电荷（一个电子所带电荷）用e表示；e=1。

6×10—19；3、在通常情况下，原子核所带正电荷与核外电子总共所带负电荷在数量上相等，电性相反，整个原子呈中性；七、摩擦起电的实质电荷的转移。

（由于不同物体的原子核束缚电子的本领不同，所以摩擦起电并没有新的电荷产生，只是电子从一个物体转移到了另一个物体，失去电子的带正电，得到电子的带负电）八、导体和绝缘体善于导电的物体叫导体（如金属、人体、大地、酸碱盐溶液），不善于导电的物体叫绝缘体（如橡胶、玻璃、塑料等）；导体和绝缘体在一定条件下可以相互转换；九、电流电荷的定向移动形成电流；电流方向：正电荷定向移动的方向为电流的方向（负电荷定向移动方向和电流方向相反）；在电源外部，电流的方向从电源的正极流向负极；十、电路用导线将用电器、开关、用电器连接起来就组成了电路；电源：提供电能（把其它形式的.能转化成电能）的装置；用电器：消耗电能（把电能转化成其它形式的能）的装置；十一、电路的工作状态1、通路：处处连通的电路；2、开路：某处断开的电路；3、短路：用导线直接将电源的正负极连同；十二、电路图及元件符号用符号表示电路连接的图叫电路图（记住常用的符号）画电路图时要注意：整个电路图导线要横平竖直；元件不能画在拐角处。

大一电路知识点总结加例题【绪论】大一电路学科是电子信息类专业课程的基础，对于学习后续专业课程和工程实践具有重要意义。

本文将对大一电路学科中的重要知识点进行总结，并配以相关的例题，帮助读者更好地理解和掌握电路基础知识。

【第一部分：电路基础知识点】1. 电压、电流与电阻电路中的基本概念是电压、电流和电阻。

电压是指电荷在电路中移动时产生的电势差，用符号U表示，单位是伏特（V）；电流是指单位时间内通过导体断面的电荷量，用符号I表示，单位是安培（A）；电阻是指阻碍电流流动的特性，用符号R表示，单位是欧姆（Ω）。

例题1：在一个电阻为10 Ω的电路中，通过的电流为2 A，求该电路两端的电压是多少？解析：根据欧姆定律，U = I * R，代入所给数值，得到U = 2 A * 10 Ω = 20 V，所以该电路两端的电压为20 V。

2. 串联电路与并联电路电路中的元件可以串联连接或并联连接。

串联连接是指元件依次相连，电流只有一条路径可以流过，电压在各个元件之间分配；并联连接是指元件并行相连，电流在各个元件之间分流，电压相同。

例题2：如图所示是一个由两个电阻串联连接而成的电路，请计算总电阻。

解析：根据串联电阻的计算公式，总电阻为两个电阻之和，即R_total = R1 + R2。

代入所给数值，得到R_total = 8 Ω + 12 Ω = 20 Ω，所以该电路的总电阻为20 Ω。

【第二部分：电路定律与分析方法】1. 基尔霍夫电流定律和基尔霍夫电压定律基尔霍夫电流定律指出，在电路中，进入某节点的电流之和等于离开该节点的电流之和；基尔霍夫电压定律指出，在电路中，沿着闭合回路的各个电压之和等于零。

例题3：如图所示为一个闭合回路，请利用基尔霍夫电压定律计算电流I。

解析：根据基尔霍夫电压定律，电压上升的部分等于电压下降的部分。

设电流I从A点流入，根据电压计算公式，可以得到2 V - 3 V + 5 V - 4 V = 0。

电路每章知识点总结1.1 电路的基本概念电路是由电子器件（如电压源、电流源、电阻、电容、电感等）连接在一起，在其中电子流动的路径。

电路分为直流电路和交流电路。

1.2 电路元件的基本特性电路元件包括电阻、电容、电感、电源等。

电阻是电压和电流之间的关系，电容是电压与电荷之间的关系，电感是电流对电压的延迟响应。

1.3 电路的基本定律基本电路定律包括基尔霍夫电流定律、基尔霍夫电压定律和欧姆定律。

基尔霍夫电流定律是指在交汇节点处，每一支路的电流之和等于零；基尔霍夫电压定律是指在闭合回路内，各支路电压的代数和等于零；欧姆定律是指电流和电压成正比关系。

第二章：直流电路2.1 直流电路的基本特点直流电路是指电流的方向始终保持不变的电路。

在直流电路中，电流的大小和方向都是固定的。

2.2 直流电路的分析方法直流电路的分析方法包括节点分析法和支路电流分析法。

节点分析法是一种用来分析电路的计算方法，在计算中用到的量有节点电压、支路电流和等效电阻等概念。

支路电流分析法是指在电路分析中，将电路看做由一系列电流的支路构成的。

2.3 直流电路中的电压源和电流源直流电路中的电压源和电流源分别是用来提供恒定电压和恒定电流的器件。

第三章：交流电路3.1 交流电路的基本特点交流电路是指电流方向和大小在一定时间内均不是固定的电路。

在交流电路中，电流的方向和大小都是随时间变化的。

3.2 交流电路中的频率与周期频率是指单位时间内一个周期内的变化次数，单位是赫兹（Hz）。

周期是指波形图中一个完整的波形图的时间间隔。

3.3 交流电路中的交流电压与交流电流交流电压和交流电流是指在交流电路中，电压和电流都是随时间变化的。

第四章：电路分析方法4.1 等效电路分析法等效电路分析法是讲把一个复杂的电路分析成一个简单的电路，分析其特性表现。

4.2 非线性电路的分析方法非线性电路是指电路中的电压和电流之间呈现非线性关系的电路，其分析方法与线性电路不同。

4.3 交叉耦合电路的分析方法交叉耦合电路是指电路中不同元件之间存在相互影响的情况，其分析方法需考虑这些影响因素。

电路原理章节知识点总结一、电路基本概念1. 电路的定义和分类电路是指电子元件按照一定的连接方式组成的系统。

根据电流和电压的性质，电路可以分为直流电路和交流电路两种。

直流电路中电流和电压保持恒定，而交流电路中电流和电压呈周期性变化。

2. 电压、电流和电阻电压是电荷在电路中移动时产生的功率，通常用符号V表示，单位是伏特（V）。

电流是流动的电荷在电路中的数量，通常用符号I表示，单位是安培（A）。

电阻是电路对电流的阻碍程度，通常用符号R表示，单位是欧姆（Ω）。

3. 电路中的基本元件电路中的基本元件包括电源、导线、电阻、电容、电感和半导体元件等。

电源提供电压和电流，导线用于连接各个元件，电阻用来阻碍电流的流动，电容和电感则分别能储存电荷和电能。

4. 电路的基本定律基尔霍夫定律包括基尔霍夫电流定律和基尔霍夫电压定律。

电流定律指出在任意一个节点处，进入该节点的电流等于离开该节点的电流的代数和。

电压定律指出在任何一个闭合回路中，沿着回路的各段电压之和等于零。

5. 电路中的功率和能量功率是指单位时间内做功或者产生热量的能力。

在电路中，功率可以表示为电压和电流的乘积，即P=VI。

能量则是指物体具有的做功能力，电路中的能量可以以电荷的形式储存在电容和电感中。

6. 电路中的等效电路等效电路是指将一个复杂的电路简化为一个简单的电路，使得两个电路在某种意义下相等。

常见的等效电路包括Thévenin等效电路和Norton等效电路，它们可以方便地进行电路分析和设计。

二、电路分析方法1. 理想电路假设在电路分析中，常常会假设电路中的元件是理想的，即不存在内阻、耦合等非理想性质。

这样假设可以简化电路分析，但是在实际设计中必须考虑到元件的实际特性。

2. 网孔分析法网孔分析是一种电路分析方法，通过建立方程组求解电路中的各个电流。

在使用网孔分析时，需要使用基尔霍夫电流定律和欧姆定律，将电路分解成多个网孔，并通过KCL和KVL方程求解电路的未知量。

电路原理题⽬第⼀章1.图中所⽰电路中，已知a点、b点的电位分别为φa=10V,φb=5V。

则电动势E＝____V:电压U＝____V:由参考⽅向，得E=φa?φb,U=φa?φb由已知得E=10?5=5V,U=10?5=5V2.蓄电池端纽a和b两端的电压Uab和电动势Eab的关系是：E ab=U ab E ab=?U ab E ab=?U ab-由参考⽅向知道，电压Uab是指电压从a点到b点的降低。

电动势Eab是指电压从a点到b点的升⾼。

由此得Eab＝－Uab 3.图中所⽰电路中，已知a点、b点的电位分别为φa=10V,φb=5V。

则电动势E＝____V:电压U＝____V:E=φb?φa,U=φa?φb由已知得E=5?10=?5V,U=10?5=5V4.图中所⽰电路中，已知a点、b点的电位分别为φa=10V,φb=5V。

则电动势E＝____V:电压U＝____V:由参考⽅向，得E=φa?φb,U=φb?φa由已知得E=10?5=5V,U=5?10=?5V5.图中所⽰电路中，已知a点、b点的电位分别为φa=10V,φb=5V。

则电动势E＝____V:电压U＝____V:E=φb?φa,U=φb?φa由已知得E=5?10=?5V,U=5?10=?5V6.⼆端元件的端电压和流过的电流如图所⽰。

则⼆端元件发出的功率P＝____W:由电流的参考⽅向与电压降的⽅向⼀致,得，发出功率P＝－2×3＝－6W 7.⼆端元件的端电压和流过的电流如图所⽰。

则⼆端元件发出的功率P＝____W:由电流的参考⽅向与电压降的⽅向不⼀致,得，发出功率P＝2×3=6WThe reference direction of the voltage U across the resistor R is designated as: right is positive and left is negative, while the reference direction of it’s the current I is along the arrow from left to right, then the relationship of U and I is:U=RI U=RI- U=?RIresistor R are non-associated.8.For the circuit in the figure,the voltage Uab is:U ab=?14VU ab=?14V- U ab=11V U ab=?5V U ab=1V Mark the reference direction of the voltage U as shown in figure.We getU=3?1=3VAccording to KVL, the voltage is:U ab=?8+3=?5V9.For the circuit in the figure, the current I=____A:Mark the reference direction of the current I1 as shown in figure.Based on Ohm’s law,I1=12/2=6AAccording to KCL,I=4?I1=?2A10.For the circuit in the figure, the current I=____A and the voltage U=____V :Mark the reference directions of the current I1 and the voltage U1 as shown in figure.Based on Ohm’s law,I1=12/2=6AU1=3?8=24VAccording to KCL and KVL,I=8?I1=2AU=U1+12=36V11.For the circuit in the figure, the current I =____A and the voltage U1=____V，U2 =____V:Mark the reference directions of the current I1 and the voltage U3 and U4 as shown in figure.Based on Ohm’s law,I1=9/1=9AU4=2?2=4VAccording to KCL and KVL,I=3+2?I1=?4AU1=U3+9=15VU2=U4+9=13V12.For the circuit in the figure, the current I =____A and the voltage U1=____V，U2 =____V:Mark the reference directions of the current I1 and the voltage U3 and U4 as shown in figure.Based on Ohm’s law,I1=9/1=9AU4=2?2=4VAccording to KCL and KVL,I=3+2?I1=?4AU1=U3+9=15VU2=U4+9=13V13. Given the circuit as shown in the figure,(1) when I=4A，the current of current source I S＝______A ;(2) when U=9V，the current of current source I S＝______A:Write the equation applying KVL,U1=3U1+I×1According to Ohm’s law and KCL,U=3×(U1/1+I)According to Ohm’s law and KCL,I S=(U+U1)/2+U1/1+ICombine and solve the equations above by using the known values.（1）当I = 4A时，Is = 4A（2）当U = 9V时，Is = 6A14. In the figure,the current of current source I S= (A)?Write the equation applying Ohm’s law and KVL,U=?100U1+40×2=?100U1+80According to Ohm’s law,U1=0.2I SAccording to KCL and Ohm’s law,U=5(I S?2)Combining the above equations, we haveI S=3.6A15.Refer to the circuit of the figure, the power delivered by theindependent source is P= _____W.Write KCL on the upper node,U/2+U/3+0.5U=12Thus,U=9VThe power delivered by the independent source isP gen=12×9=108W16. In the following circuit, find the node voltage V3=__8.75____V. (hint: use simulation tools.)第⼆章1.As Fig2-1 shown, the input resistance of the two circuitsare______Ω and______ΩSimplify the circuit, we getThe bridge is balanced and the 5 ohm resistor can be removed, we getFrom the series-parallel formula, the solved resistance isR=10ΩSolution for (b)：Simplify the circuit, we getFrom the series-parallel formula, the solved resistance isR=10Ω2. The circuit in Fig 2-2 can be simplified as：Fig（a）, Fig（b）, Fig （c）, Fig（d）. Choose （）or（）.解析：In the Fig.2-2, the 3 ohm resistor connected in series with the 5A current source doesn’t contribute to the port voltage, it only affects the voltage of current source. So it can be removed in the simplification.Using source transformation to the circuit in Fig above, we get the circuit shown in Fig below3.The circuit in Fig 2-3 can be simplified as：Fig（a）, Fig（b）, Fig（c）, Fig（d）. Choose （）.&：Remove the 10 ohm resistor connected in parallel with the 6V voltage source, because it doesn’t contributes to the port voltage, then we getTransform the 2A current source in parallel with the 10 ohm resistor into a voltage source in series with a resistor, then we getIt’s finally simplified as4.Using source transformation to solve the current I(/A) of the circuit in the figure:Using source transformation to the 8V voltage source in series with the 4 ohm resistor, we getIt’s simplified as解析：Using source transformation to the 6A current source in parallel with the 2 ohm resistor and the 3A current source in parallel with the 3 ohm resistor respectively, then we getThe current I is solvedI=(12?9)/(2+3+5)=0.3A/doc/d918d4bac5da50e2524d7ff6.html ing source transformation to solve the current I (/A) of the circuit in the figure:解析：To simplify the circuit, remove the 10A current source in parallel with the voltage source and the 10 ohm resistor in series with the 5A current source, then we getTransform the two current voltage in parallel with resistor into voltage source in series with resistor, and we getIt’s simplified asTransform the 28V voltage source in series with the 4 ohm resistor into a 7A voltage source in parallel with a 4 ohm resistor, we getTwo 4 omega resistors in parallel is 2 ohm resistor, and transform the 7A current source in parallel with the 2 ohm resistor into a 14V voltage source in series with a 2 ohm resistor, then we getThe current I is solvedI=(14?25)/(2+3+5)=?1.1A6.The voltage U ab in the circuit shown in the figure is______V:解析：Using source transformation to the dependent source in the circuit, we getApplying the KCL and KVL, the equation is written as4(1?I)+4I=8IThe current is solvedI=0.5ABased on Ohm’s Law, the voltage isU ab=8I=0.5×8=4V。

第一套基本题1.1 求图1.1所示电路中的电压U1和电流I1，I2。

设：（1）U S=2V；（2）U S=4V；（3）U S=6V。

图1.11.2 已知图1.2所示电路中电流I5=4A。

求电流I1，I2，I3，I4和电压源电压U S。

图1.21.3 求图1.3所示电路中从电压源两端看进去的等效电阻R eq。

图1.31.4 求图1.4所示电路中各元件的功率，并校验功率守恒。

图1.4 第二套提高题1.1 已知图1.1所示电路中电压U=3V。

求由电源端看进去的电阻R eq和电阻R1的值。

图1.11.2 图1.2所示电路中，已知3A电流源两端电压为40V。

求负载吸收的功率。

图1.21.3 已知图1.3所示电路中，R1=40W，R e=27W，R b=150W，R L=1500W ，=0.98。

求电压增益u2/u1和功率增益p2/p1。

其中p1是u1供出的功率，p2是R L吸收的功率。

图1.3 第一套基本题2.1 求图2.1所示各电路的入端电阻R AB、R ab。

图2.12.2 试求图2.2所示电路中的电压U。

图2.22.3 试将图2.3所示电路化成最简单形式。

图2.32.4 图2.4所示电路中，设输入电压为U i，试求U o/ U i。

图2.4 第二套提高题2.1 求图2.1所示各电路的入端电阻R AB，R ab。

图中各电阻值均为1。

图2.1答案：2.2 求图2.2所示电路中的电压U L。

设I S，R，R L为已知。

图2.22.3 求图2.3所示电路中的电流i。

图2.32.4 图2.4所示电路由许多单元构成，每个单元包含R1和R2两个电阻。

设单元数极多，视作无穷大。

（1）设R1=2，R2=1。

求A，B处的入端电阻。

图2.4 （2）以B点为电位参考点，若每个节点电压是前一个节点电压的一半，问此时R1/R2是多少？第一套基本题3.1 在图3.1所示电路中，试用支路电流法求图示电路的各支路电流。

图3.13.2 试用回路电流法求图3.2所示电路中电流源两端电压U S。

第一章 电路模型和电路定律电路理论主要研究电路中发生的电磁现象，用电流i 、电压u 和功率p 等物理量来描述其中的过程。

因为电路是由电路元件构成的，因而整个电路的表现如何既要看元件的联接方式，又要看每个元件的特性，这就决定了电路中各支路电流、电压要受到两种基本规律的约束，即：（1）电路元件性质的约束。

也称电路元件的伏安关系（VCR ），它仅与元件性质有关，与元件在电路中的联接方式无关。

（2）电路联接方式的约束（亦称拓扑约束）。

这种约束关系则与构成电路的元件性质无关。

基尔霍夫电流定律（KCL ）和基尔霍夫电压定律（KVL ）是概括这种约束关系的基本定律。

掌握电路的基本规律是分析电路的基础。

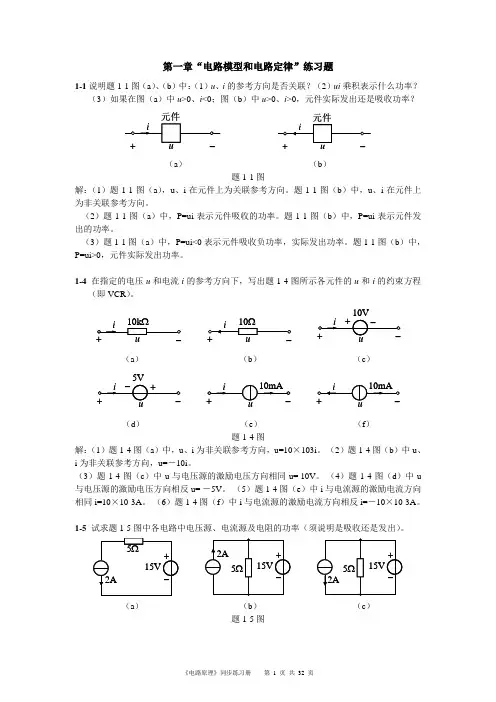
1-1 说明图（a ）,（b ）中,（1）,u i 的参考方向是否关联？（2）ui 乘积表示什么功率？（3）如果在图（a ）中0,0<>i u ；图（b ）中0,0u i <>，元件实际发出还是吸收功率？解：（1）当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端，即电流的参考方向与元件两端电压降落的方向一致，称电压和电流的参考方向关联。

所以（a ）图中i u ,的参考方向是关联的；（b ）图中i u ,的参考方向为非关联。

（2）当取元件的i u ,参考方向为关联参考方向时，定义ui p =为元件吸收的功率；当取元件的i u ,参考方向为非关联时，定义ui p =为元件发出的功率。

所以（a ）图中的ui 乘积表示元件吸收的功率；（b ）图中的ui 乘积表示元件发出的功率。

（3）在电压、电流参考方向关联的条件下，带入i u ,数值，经计算，若0>=ui p ，表示元件确实吸收了功率；若0<p ，表示元件吸收负功率，实际是发出功率。

（a ）图中，若0,0<>i u ，则0<=ui p ，表示元件实际发出功率。

在i u ,参考方向非关联的条件下，带入i u ,数值，经计算，若0>=ui p ，为正值，表示元件确实发出功率；若0<p ，为负值，表示元件发出负功率，实际是吸收功率。