预应力钢束的估算及其布置

预应力钢筋估算预应力钢筋估算是指对预应力构件中所需的钢筋数量进行计算和估算的工作。

它是预应力构件设计和施工过程中非常关键的一步，直接影响到预应力构件的质量和使用性能。

预应力钢筋估算的步骤如下：1. 确定预应力构件的设计要求：首先需要明确预应力构件的设计要求和参数，包括构件的尺寸、受力特点、预应力设计力等。

2. 分析预应力构件的受力情况：根据预应力构件的设计要求，分析构件的受力情况，确定每个截面的受力状态和受力组合，包括轴向受力、弯矩受力、剪力受力等。

3. 计算预应力筋的设计级配：根据构件的受力情况，采用合适的设计方法，计算出预应力筋的设计级配。

预应力筋的设计级配包括筋材的类型、直径、数量等。

4. 计算预应力筋的总量：根据预应力构件的设计要求和预应力筋的设计级配，计算出每个截面上预应力筋的总量。

预应力筋的总量包括每个截面上各直径预应力筋的数量和总长度。

5. 考虑预应力筋的接头：在预应力构件中，由于构件的长度通常比较大，预应力筋需要在一定的长度上作出接头。

在估算预应力钢筋的数量时，还需要考虑接头的数量和长度。

6. 估算耗损量：预应力构件在施工和使用过程中，由于各种原因会产生一定的预应力损失。

在估算预应力钢筋的数量时，还需要考虑这部分的耗损量。

7. 编制钢筋图纸和清单：根据预应力钢筋的估算结果，编制钢筋图纸和清单。

钢筋图纸和清单是预应力构件施工的重要依据，需要详细明确每个截面上各直径预应力筋的位置和数量。

总之，预应力钢筋估算是预应力构件设计和施工过程中不可或缺的一环，它的准确性和合理性直接关系到预应力构件的质量和使用性能。

通过以上步骤的计算和估算，可以获得合理的预应力钢筋数量，为预应力构件的施工提供有效的指导和依据。

4.1预应力筋的计算和布置采用符合ASTM A416-97标准的270级钢绞线, 标准强度Ryb=1860Mpa, 弹性模量Ey=1.95x105 Mpa, 松弛率为3.5%, 钢绞线规格公称直径为Φj15.20mm。

查《混凝土结构设计规范》知:1.钢绞线规格公称直径为Φj15.20mm为一束21根配置。

公称截面面积为2919mm。

2.C50混凝土的轴心抗压强度标准值为32.4 Mpa, 混凝土的弯压应力限值为32.4×0.5 Mpa =16200 Kpa。

配筋计算选用正常使用极限状态下的弯矩值配筋, 所选弯矩值如表4-1所示。

配筋弯矩值表4-1运用程序进行受弯构件配筋估算, 所得钢筋数量如表4-2所示。

预应力钢筋数量表4-2由于本桥桥跨结构对称,且本桥为连续刚构, 结合计算出来的钢筋情况, 因此只计算支点处（即41截面的预应力损失） 4.1. 1 控制应力及有关参数计算 控制应力: σcon=0.75×1860=1395(MPa)其他参数: 管道偏差系数: k ＝0.0015；摩擦系数: μ＝0.25； 4.2摩擦损失1l σ 4.2.1预应力钢束的分类将钢束分为10类, 分别为a1,a2,a3,a4,a5,a6,a7,a8,a9,a10。

因为桥跨对称,且本桥为连续刚构, 结合计算出来的钢筋情况, 因此只计算支点处（即41截面的预应力损失）下各种损失亦如此。

8.2.21l σ计算由于预应力钢筋是采用两端张拉施工, 为了简化计算, 近似认为钢筋中点截面是固定不变的, 控制截面离钢筋哪端近, 就从哪端起算摩擦损失。

摩擦损失的计算公式(参见参考文献[2]6.2.2)如下[])(11kx u con l e +--=θσσ (8-2)式中 x —从张拉端至计算截面的管道长度, 可近似地取该管道在构件地投影长度。

角 的取值如下: 通长束筋按直线布置, 角 为0；负弯矩顶板筋只算两端下弯角度为10°, 负弯矩腹板筋只考虑下弯角度15°, 不考虑侧弯角度；负弯矩腹板筋只考虑两端上弯角度13°,正弯矩腹板筋只考虑两端上弯角度25°。

预应力钢束的估算与布置在建筑和桥梁工程中，预应力技术的应用日益广泛，而预应力钢束的估算与布置则是其中至关重要的环节。

这不仅关系到结构的安全性和耐久性，还直接影响着工程的经济性和施工的可行性。

预应力钢束的估算，是基于结构在使用阶段所承受的荷载以及设计要求来进行的。

首先需要明确结构的受力情况，包括恒载（如结构自重）、活载（如人群、车辆等荷载）以及可能存在的特殊荷载（如地震、风荷载等）。

通过对这些荷载的分析和计算，确定结构在各个部位所需要的预应力大小。

在估算预应力钢束数量时，要考虑到结构的几何形状和尺寸。

例如，对于梁式结构，跨中部位通常需要较大的预应力来抵抗正弯矩，而支座附近则需要较大的预应力来抵抗负弯矩。

此外，还需要考虑混凝土的强度等级、钢材的性能等因素。

一般来说，高强度的混凝土和高强度的预应力钢材可以在一定程度上减少钢束的数量，但同时也要考虑到施工的难度和成本。

在进行预应力钢束的布置时，需要遵循一定的原则。

首先，要保证预应力钢束的布置能够有效地抵抗结构所承受的荷载，使结构在各个方向上的受力均匀。

其次，要考虑施工的便利性，尽量避免钢束的交叉和弯曲过多，以减少施工中的困难和误差。

另外，还要注意钢束的锚固位置和方式，确保锚固可靠，不出现滑移和破坏。

对于梁式结构，常见的预应力钢束布置形式有直线形、曲线形和折线形。

直线形布置简单，施工方便，但对于抵抗复杂的弯矩分布效果相对较差。

曲线形布置能够更好地适应弯矩的变化，但施工难度较大，成本也较高。

折线形布置则是在直线形和曲线形之间的一种折衷方案，兼具一定的经济性和受力性能。

在实际工程中，往往需要根据具体情况对预应力钢束进行优化布置。

例如，在大跨度桥梁中，为了减小梁体的自重和提高结构的跨越能力，可以采用悬臂施工法，并在悬臂端布置较多的预应力钢束。

而对于一些特殊形状的结构，如箱梁、T 梁等，还需要考虑钢束在腹板、顶板和底板的分布，以保证结构的整体受力性能。

预应力钢束的间距也是布置中需要考虑的重要因素。

预应力钢束的估算与布置在现代建筑和桥梁工程中，预应力技术得到了广泛的应用。

预应力钢束作为预应力结构中的关键组成部分，其合理的估算与布置对于结构的安全性、经济性和耐久性具有至关重要的意义。

一、预应力钢束估算的基本原理预应力钢束的估算主要基于结构的受力分析和设计要求。

首先，需要明确结构在使用过程中所承受的各种荷载，包括恒载（如自重）、活载（如人员、车辆等）以及可能的特殊荷载（如风载、地震作用等）。

然后，根据结构的几何形状、材料特性和约束条件，运用力学原理进行结构分析，计算出在不同荷载组合下结构各部位的内力（如弯矩、剪力、轴力等）。

在估算预应力钢束的数量和规格时，通常需要考虑预应力的效应，即通过施加预应力来抵消或减小结构在使用荷载下的拉应力，从而提高结构的承载能力和抗裂性能。

一般来说，预应力钢束所提供的预应力应足以平衡结构在最不利荷载组合下的拉应力，并留有一定的安全储备。

二、预应力钢束估算的方法1、经验公式法这是一种较为简便的估算方法，基于大量的工程实践经验和统计数据，得出了一些适用于特定结构类型和跨度的经验公式。

例如，对于常见的预应力混凝土梁，可根据梁的跨度、截面尺寸和荷载情况，利用经验公式初步估算预应力钢束的数量和面积。

然而，经验公式法具有一定的局限性，其适用范围有限，对于特殊的结构形式或复杂的荷载条件，可能会产生较大的误差。

2、荷载平衡法荷载平衡法是一种较为精确的估算方法。

它的基本思想是通过预应力钢束所产生的等效荷载来平衡结构在使用荷载下的内力。

具体来说，首先计算出结构在使用荷载下的内力分布，然后根据预应力钢束的布置形式和预应力大小，计算出预应力钢束所产生的等效荷载，通过调整预应力钢束的数量和布置，使得等效荷载与使用荷载下的内力达到平衡。

这种方法需要对结构的力学性能有深入的理解，计算过程相对复杂，但能够得到较为准确的估算结果。

3、有限元分析法随着计算机技术的发展，有限元分析方法在预应力钢束估算中得到了越来越广泛的应用。

预应力钢束的布置 1）跨中截面及锚固端截面的钢束位置①.对于跨中截面，在保证布置预留管道构造要求的前提下，尽可能使钢束群重心的偏心距大些。

本算例采用内径70mm ，外径77mm 的预留铁皮波纹管，根据《公预规》9.1.1条规定，管道至梁底和梁侧净距不应小于3cm 及管道直径1/2。

根据《公预规》9.4.9条规定，水平净距不应小于4cm 及管道直径的0.6倍，在竖直方向可叠置。

根据以上规定，跨中截面的细部构造如图2-12所示。

由此可直接得出钢束群重心至梁底距离为：cm0.182)0.92(12.55.12=++=p a②.对于锚固端截面，钢束布置通常考虑下述两个方面：一是预应力钢束合力重心尽可能靠近截面形心，是截面均匀受压；二是考虑锚头布置的可能性，以满足张拉操作方便的要求。

为使施工方便，全部3束预应力钢筋均锚于梁端，如图2-12所示。

钢束群重心至梁底距离为：cm5931409550=++=p a图2-12 钢束布置图（尺寸单位：cm ）a ） 预制梁端部；b ） 钢束在端部的锚固位置；c ） 跨中截面钢束位置2）其它截面钢束位置及倾角计算 ①钢束弯起形状、弯起角及其弯曲半径采用直线段中接圆弧线段的方式弯曲；为使预应力钢筋的预加力垂直作用于锚垫板，N1、N2和N3弯起角05.7=θ；各钢束的弯起半径为：mm R N 800001=；mm R N 250002=；mm R N 250003=。

由图2-12 a ）可得锚固点到支座中心的水平距离xi a 为：cm 2535)tan7-(50-72a x321====x x a a②钢束各控制点位置的确定以N3号钢束为例，其起弯布置如图2-13所示。

图2-13 曲线预应力钢筋布置图（尺寸单位：mm ）由0cot θ⋅=c L d 确定导线点距锚固点的水平距离mm 28485.7cot )125500(=⨯-= d L由)2/tan(02θ⋅=R L b 确定弯起点至导线点的水平距离 mm 163975.3tan 2500002=⨯=b L所以弯起点至锚固点的水平距离为mm 4486163928482=+=+=b d w L L L则弯起点至跨中截面的水平距离为mm L x w k 10204448614690)2502/29380(=-=--=根据圆弧切线的性质，图中弯止点沿切线方向至导线点的距离与弯起点至导线点的水平距离相等，所以弯止点至导线点的水平距离为mm 16255.7cos 1639cos 0021=⨯=⋅=θb b L L故弯止点至跨中截面的水平距离为mm 13468)1639162510204()(21=++=++b b k L L x同理可以计算N1、N2的控制点位置，将各钢束的控制参数汇总与表2-12。

桥梁工程课程设计第1章 设计资料及构造布置1.1设计资料1.1.1 桥梁跨径及桥宽标准跨径：30m ； 主梁全长：29.96m ； 计算跨径：29.16m ；桥面净空：净—15+2×0.75m （人行道）+2×0.25m （栏杆）；桥面坡度：不设纵坡，车行道双向横坡为2%，人行道单向坡为1.5%。

1.1.2 设计荷载：公路—Ⅰ级1.1.3 材料及施工工艺混凝土：主梁C50，人行道、栏杆、桥面铺装及混凝土三角垫层用C30； 预应力钢筋：采用《公路钢筋混凝土及预应力混凝土桥梁设计规范》（JTG D62—2004）的2.15s φ钢绞线，每束7根，全梁配6束，pk f =1860MPa 。

按后张法工艺制作主梁，采用φ70mm 金属波纹管成孔，预留孔道直径为75mm 和OVM 锚。

1.1.4 设计依据（1）《公路桥涵设计通用规范》（JTG D60—2004）简称《桥规》（2）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004） （3）《桥梁工程》 （人民交通出版社，姚铃森编）图1.1.11.2 横截面布置1.2.1 主梁间距与主梁片数主梁间距通常应随着梁高与跨径的增加而加宽为经济，由此可提高主梁截面效率指标值，采用主梁间距 2.3m，考虑人行道可以适当挑出，考虑设计资料给定的桥面净宽选用7片主梁，其横截面布置形式图1.2.1。

图1.2.11.2.2主梁尺寸拟定1.2.2.1主梁高度预应力混凝土简支梁桥的主梁高度与其跨径之比在1/15～1/25之间，标准设计中一般取为1/16～1/18。

所以梁高取用175cm。

1.2.2.2主梁腹板的厚度在预应力混凝土梁中，梁中腹板内主拉应力较小，腹板厚度翼板由布置预制孔管的构造决定，同时从腹板本身的稳定要求出发，腹板厚度一般不宜小于其高度的1/15。

本设计采用16cm.在跨中区段梁腹板下部设置马蹄，设计实践表明马蹄面积与截面面积以10%-20%为宜，马蹄宽：36cm，高：30cm。

预应力钢束规格的表示
摘要：
1.预应力钢束规格的表示方法
2.预应力钢束的理论重量计算
3.预应力钢束的布置和要素
4.预应力钢束的估算及其布置
5.预应力钢束桥博计算方法
正文：
预应力钢束规格的表示主要是通过直径和束数来描述，例如Φs15.2-19 表示公称直径为15.2mm，每组有19 根钢绞线组成一束。

这种表示方法可以清晰地传达钢束的规格信息，为后续的计算和布置提供依据。

预应力钢束的理论重量计算需要知道钢绞线的直径和每束的根数，通常采用的公式是：理论重量= 钢绞线根数× 单根钢绞线长度× 钢绞线截面面积÷ 弹性模量。

以75 的钢绞线为例，其外径为15.2mm，每米理论重量约为1.0789kg。

在预应力钢束的布置中，需要考虑满足构造要求和最小配筋率规定。

预应力钢束的元素和坐标可以通过计算得到，具体计算方法取决于桥梁的结构形式和受力特点。

预应力钢束的估算及其布置是在满足应力要求的前提下进行的。

估算公式为：钢束数= （应力要求- 混凝土抗压强度）÷ 单根钢绞线的抗拉强度。

在实际操作中，还需要考虑预应力钢材的弹性模量和张拉力等因素。

对于预应力钢束桥博计算，可以采用T 梁张拉预应力钢束计算公式：平均张拉力= p - e^(-kx) / kx，其中p 为预应力钢材张拉端的张拉力，x 为从张拉端至计算截面的孔道长度，k 为弹性模量，e 为自然对数的底数。

第5章预应力钢束的估算与布置在计算中使用的组合结果并不是桥梁的真实受力。

确定钢束需要知道各截面的计算内力，而布置好钢束前又不可能求得桥梁的真实受力状态，故只能估算。

此时与真实受力状态的差异由以下四方面引起：①未考虑预加力的作用；②未考虑预加力对徐变、收缩的影响；③未考虑（钢束）孔道的影响；④各钢束的预应力损失值只能根据经验事先拟定。

5.1 估算依据根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定，估算数量时，应满足以下三方面要求：1）正常使用极限状态下的应力要求（6.3.1）；2）承载能力极限状态下的强度要求（5.2.2）；3）施工阶段的应力要求（7.2.8）。

本次设计要求第一种种方法进行估算。

由于此时还无法求知二次内力等等，估束时可将前面计算的弯矩内力乘以1.25作为估束依据。

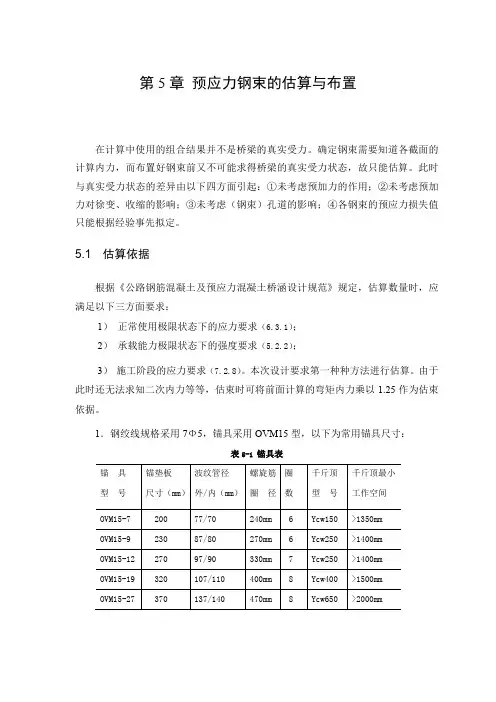
1．钢绞线规格采用7Φ5，锚具采用OVM15型，以下为常用锚具尺寸：表5-1 锚具表2．后张法预应力混凝土构件，预应力钢筋的净间距及预应力钢筋的预留管道应符合下列要求：1)采用抽拔橡胶管成型的管道，其净间距不应小于4cm ，对于大吨位的预应力筋，不小于管道直径。

2)采用预埋铁皮套管，其水平净距不应小于4cm ，竖直方向在水平段可两套叠置，叠置套管的水平净距也不应小于4cm 。

管道至构件顶面或侧面边缘的净距不应小于3.5cm ，至构件底边缘净距不小于5cm 。

3)曲线预应力钢绞线弯曲半径不小于4m ，弯起角不大于30o 。

4)锚下应设置厚度大于15mm 的钢板和钢筋网。

5.2 预应力筋的估算方法按正常使用状态计算时，拉应力满足要求估算下限；压应力满足要求估算上限。

图5-1 内力简图规范（JTG D62-2004的6.3.1条）规定，对于抗裂验算， 写成计算式为： 在最大弯矩Mmax 作用下，截面上、下翼缘混凝土应力满足08.0m a x ≥-下下W M y σ 或 max8.0M W y ≥下下σ （5-1）在最小弯矩Mmin 作用下，截面上、下翼缘混凝土应力满足08.0min ≥+上上W M y σ或min8.0M W y -≥上上σ （5-2） 可将上式改为：上上W M y min8.0-≥σ （5-3）下下W M y max 8.0≥σ （5-4）e 上N y 下e 下Y 上 Y 下M min M ma+++----+--Mmin合成式中，上y σ、下y σ——由预应力在截面上缘和下缘所产生的应力；W 上、W 下——分别截面为上、下翼缘抗弯模量（可按毛截面考虑）； m a x M 、 m in M ——荷载最不利组合时的计算截面内力，当为正弯矩时 取正值，当为负弯矩时取负值，且按代数值取大小。

预应力钢束估算及布置预应力钢束是一种用于加固混凝土结构的材料，通过施加预先设定的张力，使混凝土结构在使用过程中能够承受更大的荷载。

预应力钢束的估算和布置是预应力混凝土结构设计中非常重要的一环，下面将对其进行详细介绍。

一、预应力钢束估算预应力钢束的估算需要考虑以下几个因素：1.荷载：预应力钢束的估算需要根据混凝土结构所承受的荷载来确定。

荷载的大小和分布情况对预应力钢束的估算有着重要的影响。

2.混凝土强度：混凝土的强度对预应力钢束的估算也有着重要的影响。

强度越高的混凝土需要使用更多的预应力钢束来加固。

3.预应力钢束的材质和规格：预应力钢束的材质和规格也是估算的重要因素。

不同材质和规格的预应力钢束所能承受的荷载不同，需要根据具体情况进行选择。

4.预应力钢束的张力：预应力钢束的张力也是估算的重要因素。

张力越大的预应力钢束所能承受的荷载也越大。

在进行预应力钢束估算时，需要根据具体情况进行综合考虑，确定最终的预应力钢束数量和布置方案。

二、预应力钢束布置预应力钢束的布置需要考虑以下几个因素：1.荷载：预应力钢束的布置需要根据混凝土结构所承受的荷载来确定。

荷载的大小和分布情况对预应力钢束的布置有着重要的影响。

2.混凝土结构的形状和尺寸：混凝土结构的形状和尺寸也是预应力钢束布置的重要因素。

不同形状和尺寸的混凝土结构需要采用不同的预应力钢束布置方案。

3.预应力钢束的张力：预应力钢束的张力也是布置的重要因素。

张力越大的预应力钢束需要采用更加密集的布置方案。

4.预应力钢束的间距和跨度：预应力钢束的间距和跨度也是布置的重要因素。

不同间距和跨度的预应力钢束需要采用不同的布置方案。

在进行预应力钢束布置时，需要根据具体情况进行综合考虑，确定最终的预应力钢束布置方案。

预应力钢束估算和布置是预应力混凝土结构设计中非常重要的一环，需要根据具体情况进行综合考虑，确定最终的预应力钢束数量和布置方案。

预应力钢束的估算与布置估算与布置预应力钢束一、引言预应力钢束是一种用于加固混凝土构件的钢材，通过施加预先计算好的拉应力，使得构件在受力状态下能够承受更大的荷载。

本文将详细介绍预应力钢束的估算与布置方法，以确保工程的质量和安全性。

二、预应力钢束的估算1. 结构计算：首先需要进行结构计算，确定预应力钢束的数量和拉应力大小。

根据结构的荷载情况、材料强度和设计要求等参数，进行力学分析和计算，确定钢束的数量和拉应力的大小。

2. 钢束直径的选择：根据结构计算的结果，结合施工条件和工程要求，选择合适的钢束直径。

一般情况下，钢束直径越大，承载能力越高，但也会增加成本和施工难度。

3. 钢束布置方式：根据结构计算和现场实际情况，确定钢束的布置方式。

一般可选用单排、双排或多排等方式，具体根据结构的要求和钢束的数量来确定。

4. 钢束长度的计算：根据结构的跨度和布置方式，计算预应力钢束的长度。

一般情况下，钢束长度要略大于结构的跨度，以保证钢束的张紧长度和预应力效果。

5. 钢束搭接和锚固长度的确定：根据结构的要求和现场实际情况，确定钢束的搭接和锚固长度。

一般情况下，钢束的搭接长度要满足强度和刚度要求，锚固长度要满足预应力的要求。

三、预应力钢束的布置1. 布置方案的设计：根据结构需求和施工条件，设计合理的钢束布置方案。

主要包括钢束的位置、间距和布置方式等。

2. 钢束的定位和固定：根据布置方案，在混凝土构件中确定钢束的位置，并进行固定。

一般可以使用预留孔或预埋管等方式固定钢束。

3. 钢束张拉和固定：在混凝土构件浇筑后适当的时机，进行钢束的张拉和固定。

根据设计要求和施工规范，采用专业的预应力设备进行张拉，并在合适的时机进行固定。

4. 防护层和包覆混凝土：在钢束固定后，需要在钢束上加装防护层，并进行包覆混凝土。

防护层的主要作用是保护钢束免受外界环境的腐蚀和损伤，同时提高钢束与混凝土的粘结性能。

四、附件本文档所涉及的附件如下：- 结构计算报告- 钢束直径选择表- 钢束布置方案图- 钢束搭接和锚固长度表五、法律名词及注释1. 预应力钢束：用于加固混凝土构件的钢材，通过施加预先计算好的拉应力，使得构件在受力状态下能够承受更大的荷载。

完整版立交桥匝道现浇箱梁预应力施工参数计算立交桥匝道现浇箱梁预应力施工是指在钢筋混凝土现浇箱梁结构中，通过预应力钢束的施加，改变其应力状态，以增加结构的承载能力和使用寿命。

在进行预应力施工时，需要计算一系列参数，以确保施工的安全性和可靠性。

一、预应力钢束的计算1.张拉力计算当计算两侧预应力钢束的张拉力时，首先需要确定梁的设计跨度和悬臂长度。

根据设计要求和加载情况，计算出最大的活荷载，并在梁的最不利截面上，进行应力和挠度的计算。

根据计算结果，确定预应力钢束的截面尺寸和数量。

2.锚固力计算根据已经确定的预应力钢束的截面和数量，计算出每个预应力钢束锚固部位的锚固长度和锚固力。

根据锚固力大小和锚固长度，选择合适的承载锚具和锚固装置。

3.张拉应变计算根据已经确定的预应力钢束的长度、直径和材质，计算出预应力钢束的伸长量和相应的应变。

分别计算张拉之前和张拉之后的应变，以检验预应力钢束的可靠性。

二、传力系统的计算1.钢束对箱梁的传力计算当预应力钢束段与箱梁接触时，需要计算出传力的方式和大小。

根据预应力钢束的几何形状和箱梁的几何形状，计算出传力面积和传力方式。

同时，根据传力面积和传力方式，计算出传力的大小和作用点位置。

2.钢筋对钢束的传力计算在预应力施工中，由于外力的作用，钢筋也会对预应力钢束产生作用力。

根据钢筋布置和预应力钢束的位置，计算出钢筋对预应力钢束的传力大小和作用点位置。

三、施工工艺参数的计算1.砼配合比计算根据梁的设计要求和使用环境，确定砼的配合比。

根据配合比，计算出水灰比、砂率、密实度和流动性等参数，以满足现场施工的需要。

2.浇筑施工工艺参数的计算根据梁的几何形状和现场施工条件，计算出浇筑施工的工艺参数。

包括浇筑速度、浇筑顺序、施工温度和外界环境等。

3.预应力钢束张拉参数的计算根据预应力钢束的几何形状和现场施工条件，计算出预应力钢束的张拉参数。

包括预应力钢束的张拉力大小、张拉的步骤和张拉的持续时间等。

预应力混凝土简支T形梁桥设计计算一．设计资料与构造布置〔一〕.设计资料1．桥梁跨径与桥宽标准跨径：40m〔墩中心距离〕桥面净空：净9m+2×1.0m人行道+2×0.5m护栏=12m2．设计荷载公路-Ⅱ级，根据《公路桥涵设计通用规X》：均布荷载标准值为qk×0.75=8.0kN/m；集中荷载根据线性内插应取Pk2 ，每侧人行柱防撞栏重力作用分别为1.52kN/m和4.99kN/m。

混凝土：主梁采用C60，栏杆与桥面铺装用C30。

预应力钢筋采用《公路钢筋混凝土与预应力混凝土桥涵设计规X》〔JTG D62—2004〕的s15.2钢绞线，每束6根，全梁配7束，pkf=1860Mpa。

普通钢筋直径大于和等于12mm的采用HRB335钢筋，直径小于12mm的均用R235钢筋。

按后X法施工工艺要求制作主梁，采用内径70mm，外径77mm的预埋波纹管和夹片锚具。

〔1〕交通部颁《公路工程技术标准》〔JTG B01—2003〕，简称《标准》〔2〕交通部颁《公路桥涵设计通用规X》(JTG D60--2004),简称《桥规》(3)交通部颁《公路钢筋混凝土与预应力混凝土桥涵设计规X》(JTG B62—2004)(4)根本计算数据见下表注：考虑混凝土强度达到C45时开始X 拉预应力钢束。

ck f 和tk f 分别表示钢束X拉时混凝土的抗压，抗拉标准强度，如此：ck f a MP ，tk f a MP 。

(二)横截面布置～2.4m 或更宽。

本设计拟取翼板宽为2500mm 〔考虑桥面宽度〕。

由于宽度较大，为保证桥梁的整体受力性能，桥面板采用现浇混凝土刚性接头，因此主梁的工作截面有两种：预施应力、运输、吊装阶段的小截面(b i =1600mm)和运营阶段的大截面(b i =2500mm)，净-9m+2×1.5m 的桥宽选用五片主梁，如如下图所示。

(1) 主梁高度预应力砖简支梁桥的主梁高度与其跨径之比通常在1/15~1/25，标准设计中高跨比约在1/18~1/19。