第六章机械的平衡答案

第6章　机械的平衡6.1　复习笔记本章主要介绍了刚性转子的静平衡和动平衡计算和平面机构的完全平衡和部分平衡的计算。

学习时需要重点掌握刚性转子的静平衡和动平衡计算（质径积的计算），常以计算题的形式考查，而且几乎每年必考。

除此之外，静（动）平衡条件、完全平衡、部分平衡等内容，常以选择题、填空题和判断题的形式考查，复习时需要把握其具体内容，重点记忆。

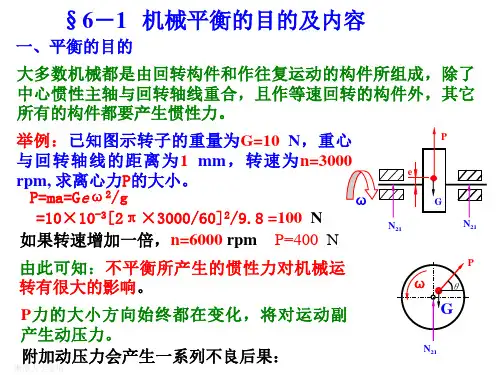
一、机械平衡的目的及内容1．机械平衡的目的（1）设法平衡构件的不平衡惯性力，以消除或减小其带来的不良影响；（2）对于利用不平衡惯性力产生的振动来工作的机械，则需研究如何合理利用不平衡惯性力。

2．机械平衡的内容（1）绕固定轴回转的构件的惯性力平衡（见表6-1-1）表6-1-1　绕固定轴回转的构件的惯性力平衡（2）机构的平衡作平面复合运动或往复移动的构件产生的惯性力无法在构件本身上找到平衡，必须研究整个机构使各运动构件惯性力的合力以及合力偶得到完全的或部分的平衡，以消除或降低最终传到机械基础上的不平衡惯性力，满足上述条件的平衡称为机械在机座上的平衡。

二、刚性转子的平衡计算（见表6-1-2）表6-1-2　刚性转子的平衡计算图6-1-1　刚性转子的平衡计算三、刚性转子的平衡实验1．静平衡实验（见表6-1-3）表6-1-3　静平衡实验2．动平衡实验试验一般需在动平衡机上进行，动平衡机的内容见表6-1-4。

表6-1-4　动平衡机3．现场平衡对于一些大型和高速转子，由于装运、蠕变、电磁场或工作温度等的影响会破坏制造期间的平衡。

若制造期间的平衡遭到破坏，可在现场直接测量机器中转子支架的振动，来确定不平衡量的大小及方位，进而进行平衡。

四、转子的许用不平衡量和许用不平衡度（见表6-1-5）表6-1-5　转子的许用不平衡量和许用不平衡度图6-1-2　许用不平衡量的分配五、平面机构的平衡。

机械原理第2、3、4、6章课后答案西北工业大学第二章机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。

解：1)取比例尺,绘制机构运动简图。

(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。

尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故 3=n 3=l p 1=h p01423323=-?-?=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。

分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。

故需增加构件的自由度。

3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。

(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。

(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。

(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。

题2-11讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。

用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。

题2-12 图a 所示为一小型压力机。

图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。

在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。

同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。

最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。

第六章 机械的平衡习题6-5解：通孔I 的失去质量为()kg b V m 766.0105014.35078004922=⨯⨯⨯⨯===-ρπφρ，I 处失去质量等效于在I 的对称处添加了一个质量为0.766kg 的质量块，因此等效后的图为质径积分别为质量I ：mm kg r m I I I .6.76100766.0=⨯==κ质量II ：mm kg r m II II II .1002005.0=⨯==κ取质径积比例尺mmm kg .01.0=κμ，作质径积多边形如图示，得平衡质量的质径积为 mm kg mr .1.1091091.10=⨯==κμκ方位为与x 轴正向夹角107o 。

但现在要制一通孔，则制在反向方位即可。

孔直径大小为mm m br b m 42042.0102005014.37800101.10944463==⨯⨯⨯⨯⨯⨯===Φ--ρπκρπ 孔的方位与x 轴反向成107o 夹角。

习题6-7解：先将质量块2、3的质径积向两个平衡面上分解，令l l l l ===342312，有cm kg l l r m I .30032301532222=⨯⨯==κcm kg l l r m II .1503130153222=⨯⨯==κcm kg l l r m I .3.133********=⨯⨯==κcm kg l l r m II .7.26632202032333=⨯⨯==κ质量块1和4在平衡面I 和II 上的质径积分别为cm kg r m I .4004010111=⨯==κ，cm kg r m I .3003010444=⨯==κ取质径积的作图比例尺mmm kg .1.0=κμ，作质径积的矢量图如下可得第I 个平衡面上所需质径积为285kg.cm ，第二个平衡面上所需质径积为381kg.cm 。

平衡质量分别为kg r m I IbI 7.550285===κ，方位：与x 轴正向夹角60。

第六章机械的平衡1 机械平衡分为哪几类？2何谓刚性转子与挠性转子？3 对于作往复移动或平面运动的构件，能否在构件本身将其惯性力平衡？4 机械的平衡包括哪两种方法？它们的目的各是什么？5 刚性转子的平衡设计包括哪两种设计？它们各需要满足的条件是什么？6 经过平衡设计后的刚性转子，在制造出来后是否还要进行平衡试验？为什么？7机械平衡的目的？8什么叫静平衡？9什么叫动平衡？10 动静平衡各需几个平衡基面？11刚性转子静平衡的力学条件是；动平衡的力学条件是。

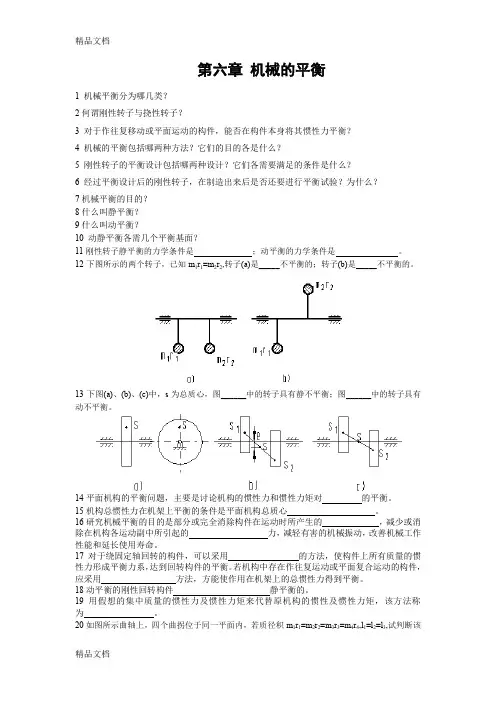
12下图所示的两个转子，已知m1r1=m2r2,转子(a)是_____不平衡的；转子(b)是_____不平衡的。

13下图(a)、(b)、(c)中，s为总质心，图______中的转子具有静不平衡；图______中的转子具有动不平衡。

14平面机构的平衡问题，主要是讨论机构的惯性力和惯性力矩对的平衡。

15机构总惯性力在机架上平衡的条件是平面机构总质心。

16研究机械平衡的目的是部分或完全消除构件在运动时所产生的，减少或消除在机构各运动副中所引起的力，减轻有害的机械振动，改善机械工作性能和延长使用寿命。

17对于绕固定轴回转的构件，可以采用的方法，使构件上所有质量的惯性力形成平衡力系，达到回转构件的平衡。

若机构中存在作往复运动或平面复合运动的构件，应采用方法，方能使作用在机架上的总惯性力得到平衡。

18动平衡的刚性回转构件静平衡的。

19用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性及惯性力矩，该方法称为。

20如图所示曲轴上，四个曲拐位于同一平面内，若质径积m1r1=m2r2=m3r3=m4r4,l1=l2=l3,试判断该曲轴是否符合动平衡条件？为什么？21图示一盘形回转体，其上有四个不平衡质量，它们的大小及质心到回转轴线的距离分别为：m 110=kg ，214kg m =，316kg m =，420kg m =，1200mm r =，r 2400=mm ，3300mm r =，4140mm r =，欲使该回转体满足静平衡条件，试求需加平衡质径积m r b b 的大小和方位。

第六章 机械的平衡题6-5 图示为一钢制圆盘，盘厚b=50mm ，位置Ⅰ处有一直径φ=50mm 的通孔，位置Ⅱ处是一质量m 2=0.5kg 的重块。

为了使圆盘平衡，你在圆盘上r=200mm 处制一通孔。

试求此孔德直径与位置。

（钢的密度γ=7.8g/cm 3）解：解法一：先确定圆盘的各偏心质量大小kg b m 7648.08.75454221-=⨯⨯⨯-=-=πγφπ kg m 5.02=设平衡孔质量γπb d m b 42-= 根据静平衡条件 02211=++b b r m r m r mmm kg r m r m r m b b b ⋅=︒-︒-=52.32210cos 135cos cos 2211θmm kg r m r m r m b b b ⋅=︒-︒-=08.104210sin 135sin sin 2211θmm kg r m r m r m b b b b b b b b ⋅=+=04.109)cos ()sin (22θθ由mm r b 200= kg m b 54.0=∴ mm b m d b2.424==γπ 在位置b θ相反方向挖一通孔︒=︒+︒=︒+⎪⎪⎭⎫⎝⎛=︒+-66.28218066.72180cos sin 1801b b b bb b b r m r m tg θθθ解法二：由质径积矢量方程式，取 mmmmkg W ⋅=2μ 作质径积矢量多边形如图6-5（b ） 平衡孔质量 kg r W m bbW b 54.0==μ 量得 ︒=6.72b θ题6-7在图示的转子中，已知各偏心质量m 1=10kg ，m 2=15kg ，m 3=20kg ，m 4=10kg ，它们的回转半径分别为r 1=40cm ，r 2=r 4=30cm ，r 3=20cm ，又知各偏心质量所在的回转平面的距离为l 12=l 23=l 34=30cm ，各偏心质量的方位角如图。

若置于平衡基面Ⅰ及Ⅱ中的平衡质量m b Ⅰ及m b Ⅱ的回转半径均为50cm ，试求m b Ⅰ及m b Ⅱ的大小和方位。

§6 机械平衡填空题：1.回转构件的直径D和轴向宽度b之比/D b符合 <=5 条件或有重要作用的回转构件，必须满足动平衡条件方能平稳地运转。

如不平衡，必须至少在 2 个校正平面上各自适当地加上或去除平衡质量，方能获得平衡。

2.只使刚性转子的惯性力得到平衡称静平衡，此时只需在 1个平衡平面中增减平衡质量；使惯性力和惯性力偶矩同时达到平衡称动平衡，此时至少要在 2个个选定的平衡平面中增减平衡质量，方能解决转子的不平衡问题。

3.刚性转子静平衡的力学条件是各偏心质量的惯性力的合力为零，而动平衡的力学条件是各偏心质量的惯性力的合力和惯性力偶矩均为零。

4.图a、b、c中，S为总质心，图 a、b 中的转子具有静不平衡，图 c 中的转子是动不平衡。

，转子a是静不平衡的，转子b是动不平衡的。

5.图示两个转子，已知mr mr1122a)b)选择题：1.设图示回转体的材料均匀，制造精确，安装正确，当它绕AA轴线回转时是处于 D 状态。

A)静不平衡B)静平衡C)完全不平衡D)动平衡2. 图示为一圆柱凸轮。

设该凸轮的材料均匀，制造精确，安装正确，则当它绕AA 轴线转动时，是处于 B 状态。

A)静不平衡B)静平衡 C)完全不平衡D)动平衡3. 图示一变直径带轮。

设该带轮的材料均匀，制造精确，安装正确，当它绕AA 轴线回转时是处于 D 状态。

A)静不平衡B)静平衡 C)完全不平衡 D)动平衡判断题：1. 若刚性转子满足动平衡条件，这时我们可以说该转子也满足静平衡条件。

(√ )2. 不论刚性回转体上有多少个平衡质量，也不论它们如何分布，只需要在任意选定两个平面内，分别适当地加平衡质量即可达到动平衡。

(√ ) 综合题1：图示为绕O 点回转的薄片圆盘，在位置1、2处钻孔，101m .r =，202m .r =，孔部分材料质量分别为110kg .m =，205kg .m =。

为进行静平衡，欲在半径05m .b r =的圆周上钻一孔。

第6章习题6.1机械为什么会产生速度波动？它有何危害？答：实际上，机械原动件的运动规律是由其各构件的质量、转动惯量和作用于其上的驱动力与阻抗力等因素而决定的，因而在一般情况下，原动件的速度和加速度是随时间而变化，机械在运动过程中会出现速度波动。

这种速度波动，会导致在运动副中产生附加的动压力，并一起机械的振动，从而降低机械的寿命、效率和工作质量。

6.2周期性速度波动应如何调节？它能否调节为恒稳定运转？为什么？答：在机械中安装一个具有很大转动惯量的回转构件——飞轮来调节周期性速度波动。

飞轮能够调速，是利用了它的储能作用。

由于飞轮转动惯量不可能为无穷大，而平均转速和最大盈亏功又都是有限值，所以安装飞轮后机械运转的速度仍有周期波动，只是波动的幅度减小而已。

6.3为什么在机械中安装飞轮就可以调节周期性速度波动？通常都将飞轮安装在高速轴上是什么原因？答：由于飞轮具有很大的转动惯量，因而要使其转速发生变化，就需要较大的能量，当机械出现盈功时，飞轮的角速度只作微小上升，即可将多余的能量吸收储存起来；当机械出现亏功时，机械运转速度减慢，飞轮又可将其储存的能量释放，以弥补能量的不足，而其角速度只作小幅度的下降。

当最大盈亏功与速度不均匀系数相同时，飞轮转动惯量与其轴的转速的平方值成反比，所以为减少飞轮的转动惯量，最好将飞轮安装在机械的高速轴上。

6.4非周期性速度波动应如何调节？为什么利用飞轮不能调节非周期性速度波动？答：机械运转的速度出现非周期性的波动，若长时间内驱动力矩大于阻抗力矩，机械将越转越快，甚至可能出现“飞车”现象，从而使机械遭到破坏；反之，若驱动力矩小于阻抗力矩，则机械会越转越慢，最后将停止不动。

飞轮只能延缓机械遭到破坏或停止不动，不能使驱动力矩和阻抗力矩恢复平衡关系。

对非周期性的速度波动进行调节，方法必须可以使机械重新回复稳定运转。

主要采取的方法是安装调速器。

6.5在什么条件下需要进行转动构件的静平衡？使转动构件达到静平衡的条件是什么？答：对于轴向尺寸很小的回转件(D/b>5,圆盘直径为D，其宽度为b)，其质量的分布可以近似地认为在同一回转面内。