不良导体导热系数的测量 (6)
- 格式:docx
- 大小:392.69 KB
- 文档页数:10

物理实验报告测量不良导体的导热系数.docx 摘要:本实验是测量不良导体的导热系数实验,主要目的是研究不同材料的导热性质,并通过实验方法测量导热系数。
实验过程中,先选取了两种不同的材料(石棉、灰铸铁)进行实验,然后分别利用导热仪和热传导仪测算材料的导热系数,并计算结果。
结果表明,两种材料的导热系数差别较大,石棉的导热系数远小于灰铸铁的导热系数。
本实验得到的结果对于进一步了解材料的物性能有重要意义。
关键词:导热系数,导热仪,热传导仪,试样,材料引言:导热系数是指在单位时间内,单位面积的材料温度梯度下,单位厚度内热量传递的能力。
导热系数是一个材料对热传导的基本反应,它是材料的一个基本物理参数,不同材料的导热系数大小差别较大,因此对于不同材料的导热系数进行测量具有重要意义。
实验项目:1.测量石棉的导热系数;实验原理:一、导热仪法导热仪法是利用导热仪来测量不同材料的导热系数。
导热仪是一种用于测量导热系数的仪器,利用它可以轻松地测量导热系数,而且测量结果比较精确。
导热仪分为静态导热仪和动态导热仪两种。
静态导热仪是指采用一定时间后的热平衡来测量材料的导热系数,它的原理是利用热传导平衡定理。
热传导平衡定理是指当物体的温度分布达到稳定状态时,所有点的温度分布相同,在每个点上的热流密度相等,因此可以根据热流密度和热传导系数的定义求得导热系数。
动态导热仪是指在一定时间内,通过测量目标材料表面和内部温度的变化来测量材料的导热系数。
动态导热仪具有快速、精确、稳定的特点,可以在室温下测量导热性能。
利用热传导仪测量材料的导热系数时,首先需要将试样放置在热源上,并使热源产生热量。
然后,利用热流计和温度计测量试样内外的温度差,从而计算出材料的导热系数。
实验步骤:1.选定两种不同材料(石棉、灰铸铁)作为试验样品;2.利用切割机将两种材料切割成长方形样品;5.利用计算机软件计算出试样的导热系数。
实验结果:(1)导热仪法:0.004 (W/mK)2.灰铸铁的导热系数:分析:通过实验结果可以看出,石棉的导热系数要小得多,而灰铸铁的导热系数则要大得多。

热 导 系 数 的 测 量实验目的:了解热传导现象的物理过程,学习用稳态平板法测量不良导体的热传导系数并用作图法求冷却速率实验原理:1. 导热系数当物体存在温度梯度时,热量从高温流向低温,传热速率正比于温差和接触面积,定义比例系数为热导系数:dQ dTdS dt dxλ=- 2. 不良导体导热系数的测量厚度为h 、截面面积为S 的样品盘夹在加热圆盘和黄铜盘之间。
热量由上方加热盘传入。
两面高低温度恒定为1T 和2T 时,传热速率为:S hT T dt dQ21--=λ 热平衡时,样品的传热速率与相同温度下盘全表面自由放热的冷却速率相等。
因此每隔30秒记录铜盘自由散热的温度,一直到其温度低于2T ,可求出铜盘在2T 附近的冷却速率dtdT。
铜盘在稳态传热时,通过其下表面和侧面对外放热;而移去加热盘和橡胶板后是通过上下表面以及侧面放热。
物体的散热速率应与它们的散热面积成正比:()()dtQ d h R R h R R dt dQ '++=222ππ 式中dtQ d '为盘自由散热速率。
而对于温度均匀的物体,有 dtdTmc di Q d =' 联立得:()()dtdT mc h R R h R R dt dQ 222++=ππ结合导热系数定义即可得出样品的导热系数表达式。
实验容:1. 用卡尺测量A 、B 盘的厚度及直径(各测三次,计算平均值及误差)。
2. 按图连接好仪器。
3. 接通调压器电源,等待上盘温度缓慢升至1T =3.2~3.4mV4. 将电压调到125V 左右加热,来回切换观察1T 和2T 值,若十分钟基本不变(变化小于0.03)则认为达到稳态,记录下1T 和2T 的值5. 移走样品盘,直接加热A 盘,使之比2T 高10℃(约0.4 mV );调节变压器至零,再断电,移走加热灯和传热筒,使A 盘自然冷却,每隔30s 记录其温度,选择最接近2T 的前后各6个数据,填入自拟表格数据处理:样品盘质量898.5m g = 上盘稳定温度1 3.17T mV = 下盘稳定温度2 2.56T mV =样品盘比热容10.3709()c kJ kg K -=⋅⋅实验前室温=21.8C T ︒室 实验后室温=22.6C T '︒室几何尺寸均使用游标卡尺测量:自由散热降温时下盘温度:下面先处理几何数据:取0.95P =,3n = 则0.95 4.30t = 1.96p k =a) 对下盘厚度A h :0.768A h cm =0.002/0.001A A h u cm σ===游标卡尺测量:C =0.002cm ∆=仪 由于下盘∆估因较小而忽略0.002cm B ∆=∆=仪0.950.006U cm ===最后:(0.7680.006)Ah cm =±0.95P =b) 对下盘直径A D :12.954A D cm = /0.002/0.001AA D u cm σ===游标卡尺测量:C =0.002cm ∆=仪 考虑直径判断误差,取0.01cm ∆=估0.01cm B ∆==0.950.012U cm ===最后:(12.9540.012)AD cm =±0.95P =c) 对样品盘厚度B h :0.757B h cm = 0.002BA h u cm σ===游标卡尺测量:C =0.002cm ∆=仪 由于样品质地较软,取0.01cm ∆=估0.01cm B ∆==0.950.014U cm ===最后:(0.7570.014)Ah cm =±0.95P =d) 对下盘直径B D :12.995B D cm = /0.006/0.003BA D u cm σ===游标卡尺测量:C =0.002cm ∆=仪 考虑直径判断误差,且样品较软,取0.02cm ∆=估0.02cm B ∆==0.950.026U cm ===最后:(12.9950.026)BD cm =±0.95P =e) 对上盘稳定温度1T :由于只测量了一次,因此只计算B 类不确定度电压表测量:3C = 0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪0.95/ 1.960.005/30.003P B U k C mV =∆=⨯=最后:1(3.170.00)T mV =±0.95P =f) 对下盘稳定温度2T :由于只测量了一次,因此只计算B 类不确定度电压表测量:3C = 0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪0.95/ 1.960.005/30.003P B U k C mV =∆=⨯=最后:1(2.560.00)T mV =±0.95P =1. 逐差法将12个数据前后分成2组,然后对应相减:(对应组数据时间差630180t s s ∆=⨯=)0.25T mV ∆= 0.02T mV σ= /0.02/0.008A T u mV σ===电压表测量:3C = 0.005mV ∆=仪 对数字万用表∆估忽略0.005B mV ∆=∆=仪等效测量次数6n =,取0.95P =,则0.95 2.57t = 1.96p k =0.950.02U mV ===最后:(0.250.02)TmV ∆=±0.95P =得出逐差法降温速度:30.25 1.38910/180dT T mV s dt t -∆===⨯∆根据公式:()()21224()2B A A B A A mch D h dTdtD T T D h λπ+=⋅-+代入数据:()()323322320.8985(0.370910)(0.75710)12.95440.76810 1.389103.14(12.99510)(3.17 2.56)12.95420.76810λ-----⨯⨯⨯⨯⨯⨯+⨯⨯=⨯⨯⨯⨯⨯-⨯+⨯⨯得到:110.240W m K λ--=⋅⋅由不确定度传递公式:()()122ln lnln ln 42ln ln 2ln ln()B A A B A A mch D h D D h V V V tλπ=+++--++∆--∆ 求微分:()()121242()242A A A A B B B A A B A A d D h d D h dh dD d V V d d V h D h D D h V V V λλ++-∆=+--+-++∆- 合并同类项:1212122()(42)4242B B A A A A B B A A A A A A A A dh dD dD dD dh dh dV dV d d V h D D h D h D h D h V V V V V λλ∆=-+-+-+-+++++∆--转化成不确定度:12222222221212222()()()[][]()()()(4)(2)(4)(2)B B A A h D A D A h V V T B B A A A A A A A A U U h U D U U U U U h D D h D h D h D h T V V V V λλ∆=++++++++++∆--即:U λ= 代入数据:U λ= 得:110.039U W m K λ--=⋅⋅0.95P =最后:11(0.2400.039)W m K λ--=±⋅⋅0.95P =2. 作图法先在2 2.56T mV =前后取点,再作一直线,使所取个点尽量均匀的分布在直线两边。

不良导体导热系数的测定一、实验目的1、 了解热传导现象的物理过程2、 学习用稳态平板法测量材料的导热系数3、 掌握—种用热电转换方式进行温度测量的方法二、实验仪器导热系数测定仪、游标卡尺等三、实验原理1、如果热量是沿着Z 方向传导,那么在Z 轴上任一位置Z 0 处取一个垂直截面积dS ,以dz dT 表示在Z 处的温度梯度,以dtdQ 表示在该处的传热速率(单位时间内通过截面积d S 的热量),那么传导定律可表示成:dS dz dT dt dQ Z 0)(λ-= (1) 式中的负号表示热量从高温区向低温区传导(即热传导的方向与温度梯度的方向相反)。
式中比例系数λ即为导热系数。
可见热导率的物理意义:在温度梯度为一个单位的情况下,单位时内垂直通过单位面积截面的热量。
可见,只要测量出样品的温度梯度和传热速率,及垂直于传热方向上样品的面积,即可求出该样品的导热系数。
2、YBF 一3导热系数测试仪实验原理 实验装置如右图,把样品加工成平板状,并把它夹在两块良导体——铜板之间,使两块铜板分别保持在恒定温度T 1和T 2,就可能在垂直于样品 表面的方向上形成温度的梯度分布。
样品厚度可做成h ≤D (样品直径)。
这样,由于样品侧面积比平板面积小得多,由侧面散去的热量可以忽略不计,认为热量是沿垂直于样品平面的方向上传导,即只在此方向上有温度梯度。
由于铜是热的良导体,在达到平衡时,可以认为同一铜板各处的温度相同,样品内同一平行平面上各处的温度也相同。
这样只要测出样品的厚度h 和两块铜板的温度T 1、T 2 ,就可以确定样品内的温度梯度。
为了维持一个恒定的温度梯度分布,必须不断地给高温侧铜板加热,热量通过样品传到低温侧铜块,低温侧铜板则要将热量不断地向周围环境散出。
当加热速率、传热速率与散热速率相等时,系统就达到一个动态平衡状态,称之为稳态。
此时低温侧铜板的散热速率就是样品内的传热速率。
这样,只要测量低温侧铜板在稳态温度T 2 下散热的速率,也就间接测量出了样品内的传热速率。


实验 六 不良导体导热系数的测定导热系数(又称热导率)是表征物质材料热传导性质的重要物理量。
材料结构的变化与所含杂质的不同对材料导热系数值都有明显的影响,因此材料的导热系数常常需要由实验去具体测定。
1804年法国物理学家毕奥通过平壁导热实验的结果最早的表述了导热定律。
稍后,1822年法国的傅立叶运用数理的方法,更准确地把它表述为后来称之为傅立叶定律的微分形式,从而奠定了导热理论。
目前测量导热系数的方法都是建立在傅立叶导热定律的基础上。
从测量的方法来说可分为两类:一类是稳态法,另一类是动态法。
在稳态法中,先利用热源在待测样品内部形成一稳定的温度分布,然后进行测量。
在动态法中,待测样品中的温度分布是随时间变化的。
例如呈周期性的变化等。
本实验采用稳态法进行测量。
【实验目的】(1)学习用稳态法测定材料的导热系数。
(2)学习如何运用实验观测的手段,尽快找到最佳的实验条件和参数,正确测出所需的实验结果的方法。
(3)学习用物体散热速率求热传导速率的实验方法。
(4)学习热电偶的测温原理和方法。
【实验原理】(1) 傅立叶热传导方程1882年法国数学、物理学家傅立叶给出了一个热导体的基本公式——傅立叶导热方程式。
该方程式指出,在物体内部,取两个垂直于热传导方向、彼此相距为h 、温度分别为1T 、2T 的平行面(设 1T >2T ),若平面面积均为 S ,在d t 时间内通过面积S 的热量d Q 满足下述表达式:dt dQ=hT T S 21-λ, (1) 式中dtdQ为热流量,λ为该物质的热导率(又称导热系数),表明物质导热的能力。
λ在数值上等于相距单位长度的两平面的温度相差1个单位时,在单位时间内通过单位面积的热量;其单位为)K m (W。
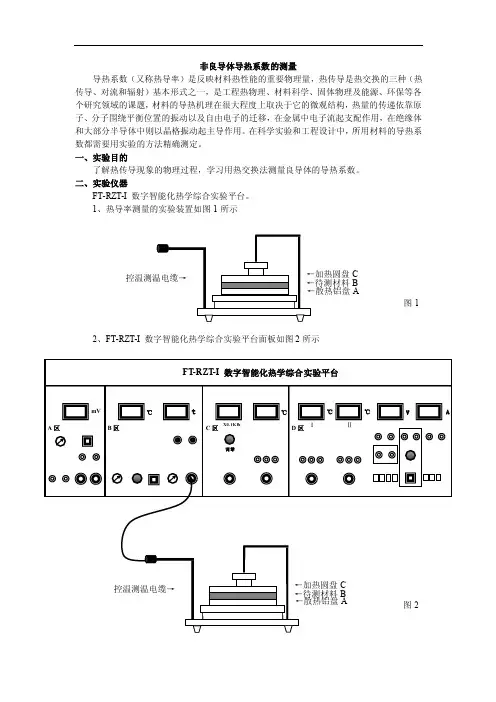
(2)本实验装置为导热系数测定仪,如图1所示。
本仪器可用于稳态法测量不良导体、金属和气体的导热系数,采用电热板加热、热电偶测温、数字毫伏表测量温差电动势。
它由电加热板、铜加热盘A,橡皮样品圆盘B,铜散热盘C 、样品支架及调节螺丝、风扇、温度传感器以及控温与测温器组成。
非良导体导热系数的测量导热系数(又称热导率)是反映材料热性能的重要物理量,热传导是热交换的三种(热传导、对流和辐射)基本形式之一,是工程热物理、材料科学、固体物理及能源、环保等各个研究领域的课题,材料的导热机理在很大程度上取决于它的微观结构,热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移,在金属中电子流起支配作用,在绝缘体和大部分半导体中则以晶格振动起主导作用。
在科学实验和工程设计中,所用材料的导热系数都需要用实验的方法精确测定。
一、实验目的了解热传导现象的物理过程,学习用热交换法测量良导体的导热系数。
二、实验仪器FT-RZT-I 数字智能化热学综合实验平台。
1、热导率测量的实验装置如图1所示2、FT-RZT-I 数字智能化热学综合实验平台面板如图2所示C B A图1三、实验原理1882年法国科学家傅立叶(J.Fourier )建立了热传导理论,目前各种测量导热系数的方法都是建立在傅立叶热传导定律的基础之上。
测量的方法可以分为两大类:稳态法和瞬态法,本实验采用的是稳态平板法测量不良导体的导热系数。
当物体内部有温度梯度存在时,就有热量从高温处传递到低温处,这种现象被称为热传导。
傅立叶指出,在dt 时间内通过dS 面积的热量dQ ,正比于物体内的温度梯度,其比例系数是导热系数,即:dS dxdTdt dQ -λ= (1) 式中dtdQ 为传热速率,dx dT 是与面积dS 相垂直的方向上的温度梯度,“-”号表示热量由高温区域传向低温区域,λ是导热系数,表示物体导热能力的大小,在SI 中λ的单位是W ·m -1·K -1。
对于各向异性材料,各个方向的导热系数是不同的(常用张量来表示)。
如图4所示,设样品为一平板,则维持上下平面有稳定的T 1和T 2(侧面近似绝热),即稳态时通过样品的传热速率为B BS h TT dt dQ 21-λ= (2) 式中h B 为样品厚度,S B =πR 2B 为样品上表面的面积,(T 1-T 2)为上、下平面的温度差,λ为导热系数。

不良导体导热系数的测量实验报告
实验目的:
1.了解不良导体的特性;
2.测量不良导体的导热系数。
实验原理:
不良导体是指导热性能较差的物质,如木材、塑料等。
导热系数是描述不良导体导热性能的一个物理量,它反映了单位面积、单位厚度、单位温度梯度下热量通过材料传导的能力。
导热系数越小,说明该材料导热性能越差。
实验仪器:
1.不良导体样品;
2.热绝缘材料;
3.热源;
4.温度计;
5.测量仪器。
实验步骤:
1.将热绝缘材料平铺在工作台上,摆放不良导体样品;
2.将热源放置在样品的一侧,使其与材料保持良好的接触;
3.在样品的另一侧放置温度计,用以测量温度变化;
4.开始记录温度的变化,记录一定时间内温度的变化曲线;
5.使用测量仪器测量材料的厚度和面积。
实验数据和结果:
根据记录到的温度数据,可以得到温度随时间的变化曲线。
根据这些数据,可以计算出材料的导热系数。
实验讨论:
在讨论中,可以对不良导体的导热性能进行评估,并分析不同因素对导热系数的影响。
实验总结:
通过本次实验,我们了解了不良导体的特性和导热系数的测量方法。
同时,我们也明白了导热系数与材料导热性能之间的关系。
这对于我们选择材料、设计热工设备等方面都具有重要意义。

不良导体导热系数的测量摘要导热系数是描述物质导热性能的重要参数,对于不良导体的导热系数的准确测量具有重要意义。
本文主要介绍了不良导体导热系数测量的原理、常用方法以及相关技术要点,旨在为不同领域的研究者提供参考和指导。
引言不良导体通常指导热性能较差的材料,其导热系数远低于金属等良导体。
不良导体导热系数的准确测量对于材料研究、热工性能评估等领域具有重要意义。
本文将介绍几种常用的不良导体导热系数测量方法,并详细介绍每种方法的原理和步骤。
原理不良导体导热系数测量的原理基于热传导定律。
热传导定律描述了物质内部的热能传递过程,其中导热系数是衡量物质传导热能的能力。
不良导体导热系数的测量可以通过测量物质中的温度变化和热流密度来间接获得。
常用方法热板法热板法是一种常用且简便的不良导体导热系数测量方法。
该方法通过在样品两侧施加热流,并测量样品表面的温度变化来计算导热系数。
具体步骤如下:1.将样品放置在两个加热板之间,确保样品与加热板之间的良好接触。
2.在样品的一侧加热板上施加固定的热流。
3.使用温度传感器测量样品表面的温度变化。
4.根据热流密度和温度变化计算样品的导热系数。
横向热流法横向热流法是另一种常用的不良导体导热系数测量方法。
该方法通过在样品两侧施加热流,并测量样品横向传导热流的温度分布来计算导热系数。
具体步骤如下:1.将样品放置在热源之间,确保样品与热源之间的良好接触。
2.在样品的一侧施加固定的热流。
3.使用温度传感器测量样品横向传导热流的温度分布。
4.根据温度分布和热流密度计算样品的导热系数。
长度法长度法是一种适用于纵向导热系数测量的方法,特别适用于长棒形状的不良导体。
该方法通过测量样品两端的温差和长度来计算导热系数。
具体步骤如下:1.将样品的一端保持恒定温度,而另一端保持绝热。
2.使用温度传感器测量样品两端的温差。
3.测量样品的长度。
4.根据温差、长度和热流密度计算样品的导热系数。
相关技术要点不良导体导热系数的测量需要注意以下技术要点:1.样品与热源之间要确保良好接触,以减小热接触电阻。

物理实验报告测量不良导体的导热系数摘要:本实验通过测量来确定不良导体的导热系数。
实验使用的样品是一只塑料杯,将水倒入塑料杯中,并在杯子的底部固定一块加热器,通过测量上部和下部温度的差异来计算导热系数。
实验结果表明,该杯的导热系数为0.14 W/(m·K),属于低导热材料。
引言:导热是一种物质从高温区域向低温区域传递热量的能力。
导体的导热系数是衡量导热能力的量。
不良导体在电学上电阻较大,而在导热方面具有低导热系数。
利用导热系数可以确定材料是否适合用于绝缘或隔热材料。
实验步骤:1.将约500毫升的水倒入小塑料杯中,然后固定一块加热器在杯底。
2.将导热计的探头插入杯底离加热器最近的位置,并在杯顶外侧的相同位置插入第二个探头。
3.等待一段时间,直到温度稳定后,读取两个探头的温度并记录下来。
4.重复以上步骤,在杯的不同位置多次测量温度。
5.根据测量结果和相应的方程计算出不良导体的导热系数。
实验结果:本实验测量了不良导体(即小塑料杯)的导热系数。
在测量过程中,使用了加热器和导热计两个重要的工具。
通过将温度探头置于加热器底部和杯顶部两个不同位置,得出了该杯的不同位置的温度分布。
通过分析温度差异,测量出不良导体的导热系数。
本实验得出的测量结果如下,小塑料杯的导热系数为0.14 W/(m·K)。
讨论:根据实验结果,可以看出不良导体在导热方面表现略差。
但是,在一些实际应用中,低导热的物质也具有一定的优势,例如用作绝缘材料、隔热材料等。
在这些应用场合中,导热系数较低的物质是非常重要的。
实验中还需要注意一些问题。
例如,在测量进行中,需要等待一定的时间使温度稳定,并且要确保温度探头与测试杯的接触良好。
此外,在实验前还需要对仪器进行了解,以保证实验过程的准确性和安全性。
准稳态法测不良导体的导热系数和比热实验报告一、实验目的(1)实验一:万用表使用测量:熟悉万用表的使用方法,学习量程的选择方法,以及根据量程得到数据精度并计算不确定度的方法。
(2)实验二:热导实验:1、了解准稳态法测量不良导体的导热系数和热比的方法;2、掌握热电偶测量温度法方法;3、加深对直线拟合处理数据方法的理解。
二、实验一:万用表使用测量计算过程:(2)交流电源有效值∆X读数精度% * 测量值+ 量程精度% * 量程= 0.2%*0.34474 + 0.05%*2 = 0.0017V =X=XX0.34474 ±0.0017V±=∆(3)交流信号的频率∆X读数精度% * 测量值+ 量程精度% * 量程= 0.01%*999.98 + 0.003%*2000 = 0.16Hz =XX999.98 ±0.16Hz=X∆=±(4)电阻∆X读数精度% * 测量值+ 量程精度% * 量程=0.020%*10.9457 + 0.004%*20 = 0.003kΩ=X==XX10.9457 ±0.003kΩ±∆(5)电容∆X读数精度% * 测量值+ 量程精度% * 量程=1%*0.930 + 0.5%*2=0.019uF ==XX0.930 ±0.019uFX±=∆(6)二极管∆X读数精度% * 测量值+ 量程精度% * 量程=0.06%*0.5735+0.020%*2 = 0.0007V =X=XX0.5736 ±0.0007V∆=±实验二:热导实验三、数据处理(2)U1(t2t1)~τ,U2(t1tc)~τ曲线分析:当样品进入准稳态时,样品内各点的温升速率相同并保持不变,且样品内两点间温差恒定。
对应的电压值变化趋势为:中心面和冷面温差U2(t1tc)线性增长,热面和中心面温差U1(t2t1)基本保持不变。

不良导体导热系数的测定[实验目的]1. 用稳定流动法测定橡皮的导热系数;2. 学习用温差电偶测量温度的方法。
[实验器材]导热系数测定仪,热电偶(铜-康铜),多量程数字电压表,橡皮样品,杜瓦瓶,游标卡尺,螺旋测微计。
[实验原理]有一粗细均匀的橡皮圆盘,上平面与发热盘接触(温度高),下平面与散热盘接触(温度低),则热量将从高温面流向低温面。
在加热一段时间后,若圆盘上各处的温度不变(但不同横截面的温度不同,存在温度差),而且向圆盘侧面散失的热量可以忽略时,则在相等的时间内,通过圆盘各横截面的热量应该相等。
当圆盘各截面有热量通过,但各处温度保持不变时,就称为达到了稳定流动状态。
在稳定流动状态下,橡皮圆盘与外界的热交换为零,即上平面从发热盘吸收的热量等于下平面向散热盘放出的热量。
由此,法国数学家、物理学家约瑟夫·傅立叶给出测定导热系数的导热方程。
该方程式指出,在物体内部垂直于导热方向上,二个相距为h ,面积为A ,温度分别为θ1、θ2的平行平面,在∆t 秒内,从一个平面传到另一个平面的热量∆Q ,满足下述表达式:hA t Q 21θθλ-⋅⋅=∆∆ (1) 式中λ定义为该物质的导热系数,亦称导热率。
由此可知,导热系数——表示物质热传导性能的物理量,其数值等于二相距单位长度的平行平面上,当温度相差一个单位时,在单位时间内,垂直通过单位面积所流过的热量。
对于样品橡皮圆盘,上平面传入的热量与由散热盘向周围环境散热的速率相等(即t Q t Q ∆∆=∆∆'),而tmc t Q ∆∆=∆∆θ',2 R A π=,所以 212 12θθπθλθθ-⋅⋅∆∆==h R t mc (2) 导热系数的SI 制单位(瓦特每米开尔文)的符号为:W/m •℃导热系数的量纲为:[][][][][][]13222--=⋅⋅⋅=∆=θθθλLMT T L L MT L t A h Q 导热系数过去常用的非SI 制单位是国际蒸汽表卡每秒厘米开(尔文):cal / (s ·cm ·℃),它与SI 单位的换算是:1cal / (s ·cm ·K )=418.68 w / (m ·K )材料的结构变化与杂质多寡对导热系数都有明显的影响。
稳态法测量不良导体的导热系数实验报告实验报告实验名称:稳态法测量不良导体的导热系数实验目的:本实验旨在通过稳态法测量不良导体的导热系数,进一步了解材料的导热性能,并提高实验操作能力。
实验原理:热传导是物质内能的传递,是由高温区向低温区传递热量的过程。
在导体中,热量的传导主要通过自由电子传导和晶格振动传导两种机制实现。
本实验通过稳态法测量不良导体的导热系数。
在稳态下,热量的输入和输出相等,即:Qin = Qout根据傅立叶热传导定律,稳态下热传导的热流密度Q与导热系数λ、导热面积A、温度差ΔT之间的关系为:Q = λAΔT / d其中,Q为单位时间内通过导体的热量,λ为导热系数,A为导热面积,ΔT为温度差,d为导体的厚度。
实验器材:1. 不良导体样品2. 直立式热传导仪3. 温度计实验步骤:1. 将热传导仪取出,并调整热电偶测温头至样品位置,并与温度计校准。
2. 将样品固定于热传导仪上,并调整加热电压至一定值,保持恒温。
3. 记录热电偶和温度计示数,计算温度差ΔT。
4. 根据所用材料的厚度测量所得,计算导热系数λ。
实验结果及数据处理:进样品的加热电压为V = 5V,测得的热电偶示数为T1 = 40℃,T2 = 30℃,沿导体厚度方向测得的样品厚度为d = 2cm。
由此可计算出温度差ΔT = T1 - T2 = 40℃ - 30℃ = 10℃。
代入傅立叶热传导定律公式Q = λAΔT / d,可得热流密度Q。
将实验中测得的其他参数代入公式,可计算得到不良导体的导热系数λ。
实验结论:通过稳态法测量不良导体的导热系数,可以得到材料的导热性能。
该实验结果为XX(具体结果),表明该不良导体具有较低的导热系数,其热传导能力较差。
实验过程中需注意:1. 实验开始前要确保热传导仪和温度计都已校准,并测得的数据准确可靠。
2. 在稳态状态下测量温度差,并注意尽量减小其他误差的影响。
3. 实验结束后及时关闭加热电源,并注意对实验器材的清理和归位。
实验6 测量不良导体的导热系数(稳态法)实验目的(1)学习一种量热方法——稳态平板法;(2) 学习用物体散热速率求热传导速率的实验方法;(3)测量不良导体橡皮样品的导热系数。
实验仪器导热系数测定仪物理天平热电偶杜瓦瓶实验原理1898年C.H.Lees首先使用平板法测量不良导体的导热系数,这是一种稳态法,实验中,样品制成平板状,如图1所示,其上端面与一个稳定的均匀发热体充分接触,下端面与一均匀散热体相接触。
由于平板样品的侧面积比平板平面小很多,可以认为热量只沿着上下方向垂直传递,横向由侧面散去的热量可以忽略不计,即可以认为,样品内只有在垂直样品平面的方向上有温度梯度,在同一平面内,各处的温度相同。
图1设稳态时,样品的上下平面温度分别为、,根据傅立叶传导方程,在时间内通过样品的热量满足下式:(1)式中为样品的导热系数,为样品的厚度,为样品的平面面积,实验中样品为圆盘状,设圆盘样品的直径为,则由(1)式得:(2)实验装置如图2所示,固定于底座的三个支架上,支撑着一个铜散热盘,散热盘可以借助底座内的风扇,达到稳定有效的散热。
散热盘上安放面积相同的圆盘样品,样品上放置一个圆盘状加热盘,其面积也与样品的面积相同。
当传热达到稳定状态时,样品上下表面的温度和不变,这时可以认为加热盘通过样品传递的热流量与散热盘向周围环境散热量相等。
因此可以通过散热盘在稳定温度时的散热速率来求出热流量。
方法如下:当测得稳态时的样品上下表面温度和后,将样品抽去,让加热盘与散热盘接触,当散热盘的温度上升到高于稳态时的值1mV左右时,移开加热盘,复上样品,让散热盘在电扇作用下冷却,记录散热盘温度随时间(每隔30秒)的下降情况,求出散热盘在时的冷却速率,则散热盘在时的散热速率为:(3)其中为散热盘的质量,为其比热容。
在达到稳态的过程中,盘的上表面并未暴露在空气中,而物体的冷却速率与它的散热表面积成正比,为此,稳态时铜盘的散热速率的表达式应作面积修正:(4)其中为散热盘的半径,为其厚度。
不良导体导热系数测定导热系数是反映材料导热性能的重要参数之一,导热系数大,导热性能较好的材料称为良导体;导热系数小、导热性能差的材料称为材料的不良导体。
一般来说,金属的导热系数比非金属要大;固体的导热系数比液体的要大;气体的导热系数最小。
本实验介绍一种比较简答的利用稳态法测定不良导体导热系数的方法。
稳态法是通过热源在样品内部形成一稳定的温度分布后,测定不良导体导热系数的方法。
一、实验目的1、掌握稳态法测定不良导体导热系数的方法2、了解物体散热速率和传热速率的关系 二、实验仪器1、TJQDC-1型导热系数测定仪2、游标卡尺3、天平4、镊子 三、实验原理 1、热传导定律当物体内部各处的温度不均匀时,就会有热量从温度较高处传递到温度较低处,这种现象叫热传导现象。
早在1882年著名物理学家傅立叶(Fourier)就提出了热传导的定律:若在垂直于热传播方向x 上作一截面S ∆,以d dxθ⎛⎫⎪⎝⎭表示0x 处的温度梯度,那么在时间t ∆内通过截面积S ∆ 所传递的热量Q ∆为:Q d S t dxθλ∆⎛⎫=-∆ ⎪∆⎝⎭(1) 式(1)中Qt∆∆为传热速率,负号代表热量传递方向是从高温区传至低温处,与温度梯度方向相反。
比例系数λ称为导热系数,其值等于相距单位长度的两平面的温度相差为一个单位时,在单位时间内通过单位面积所传递的热量,单位是瓦·米-1开-1(W ·m -1K -1).2、稳态法测传热速率测定样品导热系数的实验装置如图1所示。
图中待测样品 (圆盘) 半径 1R =60mm ,样品上表面与加热盘(位于上方的黄铜盘)的下表面接触,温度为1θ,加热盘由内部电热丝供热,热量由加热盘通过样品上表面传入样品,再从样品下表面与散热盘 (位于样品下面的黄铜盘) 的上表面相接, 温度为2θ,即样品中的热量通过下表面向散热盘散发。
样品上下表面温度可以认为是均匀分布,在1h 不很大情况下可忽略样品侧面散热的影响,则式(1)改写为:121QS t h θθλ-∆=∆ (2) 式(2)中S 为样品横截面积。
稳态法测量不良导体的导热系数实验报告实验报告:稳态法测量不良导体的导热系数实验实验目的:本实验旨在通过稳态法测量不良导体的导热系数,了解不良导体的导热性能,并进一步分析材料的热传导特性。
实验仪器:1. 实验台2. 电热器3. 铜棒样品4. 温度计5. 计时器6. 多用电表7. 导热油实验原理:稳态法测量导热系数是通过测量材料的温度梯度和热流量来计算导热系数的。
在实验过程中,首先将导热油倒入实验台中,使其充满整个实验空间。
然后,在台面上放置热源和试样,热源通过导热油将热量传递给试样,试样将热量传递给周围环境。
通过测量试样两端的温度差和热流量,可以计算出导热系数。
实验步骤:1. 准备工作: 将实验台内充填导热油,并使其达到温度平衡。
2. 将导热棒和试样一起放置在实验台上,使其与实验台接触良好。
3. 将电流通入电热器中,通过导热油将热量传递给试样,使热量在试样内传递。
4. 同时使用温度计测量试样两端的温度差,并通过多用电表测量电热器的电流和电压,计算出热流量。
5. 记录不同时间间隔的试样温度和热流量数据,并绘制温度与热流量的关系曲线。
6. 根据数据计算出导热系数。
实验结果:根据实验得到的温度-热流量关系曲线,可以通过线性拟合得到试样的斜率,即热流量值。
通过计算不同时间间隔内的温度差,可以得到导热系数的数值。
实验结论:根据实验结果,可计算出不良导体的导热系数。
导热系数是衡量材料导热性能的重要参数,通过实验可以了解不良导体的导热性能,并为材料的热传导特性分析提供参考。
实验注意事项:1. 实验过程中要注意安全,避免触电或烫伤等意外情况。
2. 导热油的量要足够充填实验台,且温度均匀平衡。
3. 实验前要对实验仪器进行检查,确保正常工作。
4. 实验操作要严格按照实验步骤进行,尽量减小误差产生。
5. 实验完成后要对实验环境进行清理和整理,保持实验台的整洁。
非金属固体材料导热系数的测量2004/04用热线法测量不良导体导热系数是一种广泛使用的方法,国家对此制定了标准——“非金属固体材料导热系数的测定——热线法”(GB/T 10297-1998)。
基本原理如图1所示,在匀质均温的物体内部放置一电阻丝,即热线,对其以恒定功率加热时,热线及其附近试样的温度将随时间变化。
根据时间与温度的变化关系,可以确定该试样的导热系数。
[1] [原理简述]由热传导理论[2]可知,恒定功率的热线对匀质物体进行热传导时,可以用一维柱坐标系的热传导方程对物体的温度场进行描述:r r rt ∂∂+∂∂=∂∂θθθα1122 (1) 边界条件为:00=r θ(t =0,r ≥0),0=∞r θ(t >0,r =∞),const.π0=∂∂-==r r q θλ(t >0,r =0)[3] (2)根据热传导方程和边界条件得到解为:t teqttr r t d π4042⎰-=αλθ(3)其中各物理量含义为,t :热线的加热时间,单位为s ;r :距热线的距离,单位为m ;q :热线单位长度的加热功率,单位为W/m ;t r θ:加热时间t ,距离热线距离r 处的温升,单位为K ;α:试样的热扩散率,单位为m 2/s ;λ:试样的导热系数,单位为W/(m ·K ),对于非金属固体材料,该系数一般小于2 W/(m ·K )。
假设t r α42→0,即r →0或αt →∞,利用Euler 公式,忽略展开后二次项以后的各项。
如果在不同时间t 1、t 2,测的同一点r 处的温升为1t r θ、2t r θ,则:12ln π412t t qt t r r λθθ=- (4) 根据(4)可以得到试样的导热系数()()12121212ln πL 4ln π4tt t t r r r r t t IU t t q θθθθλ-=-=[4](5)(5)式中,I 、U 分别热线的通电电流(单位为A )和电压(单位为V ),L 为有效加热长度(单位为m )。
实验报告一、实验题目:不良导体导热系数的测量二、实验目的了解热传导现象的物理过程,学习用稳态平板法测量不良导体的导热系数并用作图法求冷却速率。
三、实验原理 1、导热系数当物体内存在温度梯度时,热量从高温流向低温,谓之热传导或传热,传热速率正比于温度梯度以及垂直于温度梯度的面积,其比例系数为热导系数或导热率,即dQ dTdS dt dxλ=- 其中dQ dt 为传热速率,dTdx是与面积相垂直的方向上的温度梯度,“—”表示热量从高温区域传向低温区域, λ是导热系数,表示物体导热能力的大小。
2、不良导体导热系数的测量厚度为B h 、截面面积为B S 的平板形样品(橡胶板)夹在加热圆盘和黄铜盘A 之间,热量由加热盘传入。
加热盘和黄铜盘上各有一小孔,热电偶可插入孔内测量温度,两面高低温度恒定为T 1 和T 2时,传热速率为11B BT T dQS dt h λ-=- (1) 由于传热速率很难测量,但当T 1 和T 2稳定时,传入橡胶板的热量应等于它向周围的散热量。
这时移去橡胶板,使加热盘与铜盘直接接触,将铜盘加热到高于T 2约10度,然后再移去加热盘,让黄铜盘全表面自由放热。
每隔30秒记录铜盘的温度,一直到其温度低于T 2,据此求出铜盘在T 2附近的冷却速率dQ dt。
铜盘在稳态传热时,通过其下表面和侧面对外放热;而移去加热盘和橡胶板后是通过上下表面以及侧面放热。
物体的散热速率应与它们的散热面积成正比,即'A A A A A A R (R 2h )dQ dQ dt R (2R 2h )dtππ+=⋅+式中'dQ dt为盘自由散热速率。
而对于温度均匀的物体,有'dQ dT mc dt dt =。
这样,就有A A A A Cu A A A R (R 2h )dQ dT=m c dt R (2R 2h )dtππ+⋅+ (2) 比较(1)和(2)式,可以求出导热系数为A CuB A A 2B A A 12m c h (R 2h )dT=2R (R h )(T -T )dtλπ+⋅+ (3)四、实验内容1、观察和认识传热现象、过程及其规律: (1)自拟数据表格,用卡尺测量铜盘A 和样品B 的厚度及其直径,并求出平均值和误差(各测三次);(2)熟悉各仪表的使用方法,并按书上的图示连接好仪器;(3)接通调压器电源,将红外灯升压,使其从零缓慢升至200V 。
当1T 达到3.2—3.4mV 之间时,将电压调至125V 左右。
来回切换单刀双掷开关,观察1T 和2T 的值(每1—2min 记录一次)。
若10min 基本不变(变化量小于0.03mV ),则认为达到稳态,记录下1T 和2T 的值; (4)移走样本盘B ,直接加热A 盘(200V 条件下),使之比2T 高10℃(约0.4mV )。
调压器调至零,再断电。
移走加热灯和传热筒,使A 盘自然冷却,每隔30s 记录其温度(中间不要间断),选择最接近的前后各6个数据填入自拟表格。
2、用逐差法求出铜盘A 的冷却速率dTdt,并由公式(3)求出样品的导热系数λ。
3、绘出T —t 关系图,用作图法求出冷却速率dT dt 。
4、用方程回归法进行线性拟合,求解冷却速率dTdt及其误差,将结果代入公式(3),计算样品的导热系数λ及其标准差λσ。
五、实验器材(如下图所示)杜瓦瓶、传热筒、数字电压表(测温度用)、红外灯、热电偶、铜盘、橡胶圆盘(待测)、双刀双掷开关、调压器电源、支架、支杆等。
不良导热材料导热系数测定装置原理图六、数据的处理与分析1、铜盘A 和样品B 的厚度及直径(C T ο9.21=室)项目第一次第二次第三次平均值标准偏差σA盘直径DA/mm 129.90130.00129.86129.920.07A盘厚度ha/mm 7.107.187.147.140.04B盘直径DB/mm 130.02130.10130.04130.050.04B盘厚度hb/mm7.587.347.467.460.12(1)A 盘的厚度当置信概率为0.95,即P 0.95=时55A A A 0.95u (h )t 4.309.9310(m)n 3--==⨯=⨯30.0210m -∆=⨯仪, 0∆=估则 5B B A u (h ) 1.1510m C 3-∆∆===⨯ 则合成标准不确定度为224A A A B A u(h )=u (h )u (h ) 1.0010m -+=⨯所以铜盘A 的厚度为,P 0.95=(2)A 盘的直径当置信概率为0.95,即P 0.95=时30.0210m -∆=⨯仪, 0∆=估则 5B B A u (D ) 1.154710m C 3-∆∆===⨯仪则合成标准不确定度为所以铜盘A 的直径为,P 0.95=(3)B 盘的厚度当置信概率为0.95,即P 0.95=时30.0210m -∆=⨯仪, 0∆=估则 5B B B u (h ) 1.1510m C 3-∆∆===⨯仪则合成标准不确定度为所以样品B 的厚度为,P 0.95=(4)B 盘的直径当置信概率为0.95,即P 0.95=时30.0210m -∆=⨯仪, 0∆=估则 5B B B u (D ) 1.154710m C 3-∆∆===⨯仪则合成标准不确定度为所以样品B 的直径为,P 0.95=2、铜盘的比热容、质量Cu c 0.3709kJ /(kg K =⋅),(物理天平测量)不确定度的分析:对于物理天平, 0.05g ∆=m ,故可取5mA u(m )=1.66710kg 3-∆=⨯,则有 P 0.95=3、1T 、2T 的获得(本次实验的温度用电压表测量,单位为mV ,100℃对应于4mV ) 本次实验过程中,相邻两次数据测量的间隔最后十分钟的数据 T1/mv 3.37 3.37 3.37 3.37 3.36 3.36 3.36 3.36 3.36 3.36 T2/mv 2.73 2.73 2.73 2.73 2.74 2.74 2.74 2.74 2.74 2.74 此过程中1T 和2T 可认为是稳定的(变化值小于0.03mV ),故1T 和2T 最终的取值为T1=3.36mv T2=2.74mv4、2T 前后6个数据的获得(相邻两次数据测量的时间间隔约为30s ) 序号 1 2 3 4 5 6 7 8 9 10 11 12 2T (mV) 3.03 2.97 2.93 2.87 2.82 2.78 2.73 2.69 2.64 2.59 2.56 2.521)用逐差法求出冷却速率dT dt(2)绘出T —t 关系图,用作图法求出冷却速率dT dt在图上选取两个相距较远的点(35.19,3.01)和(338.98,2.54),作出的直线基本上通过这两点。
则计算得(如果有可能的话,尽量在图上把所取点标出来)(3)用方程回归法进行线性拟合求出冷却速率dTdt则得到不确定度为P0.95=则P0.95=代入得(1)使用逐差法求出的dTdt代入得(2)使用作图法求出的dTdt代入得3)使用方程回归法线性拟合求出的dTdt对λ不确定度的分析:A CuB A A 2B A A 122m c h (D /22h )dTD (D /2h )(T -T )dtλπ+=⋅+对其取对数得A CuB A AB A A 12dTln ln m +lnc +lnh ln(D /22h )ln2lnD ln(D /2h )ln(T -T )dtλ=+++--+- 微分得CuA B A A B A A 12A CuB A A A A B A A A A 1212dTddc dm dh dD dh dD dD dh dT dT d dt ++-2dT m c h D 4h D /4h D D 2h D /2h T -T T -T dtλλ=+++---+++++ 合并同类项得Cu A BA AB 12A A A Cu B A A A A A A A A B 1212dTddc dm dh 2h D /4dD dT dT d dt ++dD dh -2dT m c h (D 4h )(D 2h )(D /4h )(D /2h )D T -T T -T dtλλ=-++-+++++写成标准差公式得2U()()λλ=222222222Cu A B A A B 12A A A Cu B A A A A A A A A B 1212dT u()u(c )u(m )u(h )2h D /4u(D )u(T )u(T )dt ()+()+()(u(D ))(u(h ))()+(2)()()dT m c h (D 4h )(D 2h )(D /4h )(D /2h )D T -T T -T dt+++++++++其中由于1T 和2T 为最后的一次读数,故取312B T 0.01mVu(T )u(T )u (T) 3.3310mV 33-∆=====⨯仪() Cu c 是已给出的,故认为Cu u(c )0=将前面已求得的各项数据及其标准差代入λ的标准差公式,求得()2U 4.1310λλ-=⨯固有 P 0.95=所以橡胶的导热系数为P 0.95=七、误差分析:1,此次实验对 2,导热系数受温度的影响,实验过程中室内的温度也会对结果产生影响;3,测量铜盘和样品的直径时,不易确定它们的圆心,直径的测量存在误差;4,使用仪器和设备自身存在的系统误差;5,由于橡胶板的易形变性,其直径和厚度的测量会存在较大误差。
(用游标卡尺测量时,不能过度挤压被测物品)八、减小误差的建议:1、条件许可情况下,在实验过程中精确记录2、将室温对导热系数的影响考虑进去,对实验结果进行求解;3、确定热电偶与铜盘和热电偶接触良好;4、先采取措施确定铜盘和样品的圆心,再进行直径的测量。
九、思考题1、试分析实验中产生误差的主要因素。
(见误差分析)2、傅里叶定律dQdt(传热速率)是不易测准的量,本实验如何巧妙地避开了这一难题?答:此次实验将对dQdt 的测量转化为对dTdt(散热速率)的测量,而散热速率dTdt可以通过记录铜盘在一定原始数据评语:1)首先,我要先想你说声对不起,由于之前我不了解具体情况,导致你与陈振同学的分数过低,现在分数已经都修改过来了。
我今天收到张坤同学的邮件,已经回复了,你有空可以到他那里看看,还有,在陈振同学的报告后面也做了说明,你可以拿过来看看。
如果你们还有那些地方有异议,可以和我联系。
2)注意,最后的不确定度要跟计算值末位对齐,而且只需保留两位有效数字即可。
报告中的红色方框要多加注意。
3)误差分析以及减少误差的建议都非常好,说明观测得很仔细4)希望你继续努力,再接再厉。