下载文档原格式
第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征，特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数（R ，L ，C ）的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路，熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值（U m ，E m ，I m ）、瞬时值（u, e, i ）、有效值（U ，E ，I ）。
注：有效值与幅值的关系为：有效值2幅值=。
(2) 频率（f ）、角频率（ω）、周期（T ）。
注：三者的关系是Tf ππω22==。
(3) 相位（ϕω+t ）、初相角（ϕ）、相位差（21ϕϕ-）。
注：相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法：。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法：例如u 的波形如图2-1-1(a)所示。
(3) 相量（图）表示法：使相量的长度等于正弦量的幅值（或有效值）； 使相量和横轴正方向的夹角等于正弦量的初相角； 使相量旋转的角速度等于正弦量的角速度。
注： U U例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解：因为同频率同性质的正弦量相加后仍为正弦量，故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1：相量图法求解如下：具体步骤为三步法（如图2-1-2所示）： 第一步：画出正弦量u 1、u 2的相量12U U 、（U 1=6，U 2=4）。
第二步：在相量图上进行相量的加法，得到一个新相量U 。
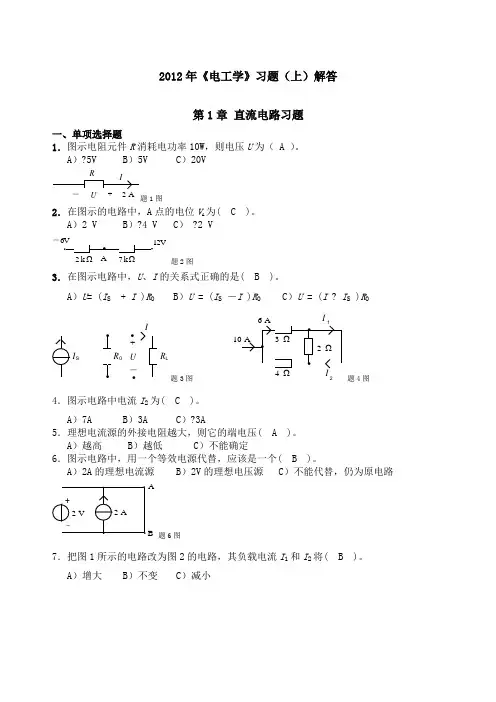
2012年《电工学》习题（上）解答第1章直流电路习题一、单项选择题1．图示电阻元件R消耗电功率10W，则电压U为（ A ）。
A）?5V B）5V C）20VU+题1图2．在图示的电路中，A点的电位V A为( C )。
A）2 V B）?4 V C）?2 V－2 k7 kΩΩ题2图3．在图示电路中，U、I的关系式正确的是( B )。
A）U= (I S+ I )R0 B）U = (I S－I )R0C）U = (I?I S)R0R L题3图I2题4图4．图示电路中电流I2为( C )。
A）7A B）3A C）?3A5．理想电流源的外接电阻越大，则它的端电压( A )。
A）越高 B）越低C）不能确定6．图示电路中，用一个等效电源代替，应该是一个( B )。
A）2A的理想电流源B）2V的理想电压源 C）不能代替，仍为原电路2 V题6图7．把图1所示的电路改为图2的电路，其负载电流I1和I2将( B )。
A）增大B）不变C）减小221Ω2V 2A图 1图2+题7图8．图示电路中，供出功率的电源是( A )。
A ）理想电压源B ）理想电流源C ）理想电压源与理想电流源U 4VS 题8图S题9图9．在图示电路中，各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ，需列出独立的电流方程数和电压方程数分别为( B )。
A ）4和3B ）3和3C ）3和410．在计算线性电阻电路的电压和电流时，用叠加原理。
在计算线性电阻电路的功率时，加原理( B )。
A ）可以用B ）不可以用C ）有条件地使用 11．在图示电路中，已知U S =12V ，I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A ）?18VB ）18VC ）?6VU I SS+题11图SA题12图12．在图示电路中，当开关S 闭合时A 点的电位V A ( C )。
A ） ?3VB ）3VC ）0V13．图示电路中，理想电流源I S1发出的电功率P 为( A )。
电工学少学时第三版张南主编课后练习答案第二章（末）电工学少学时第三版张南主编课后练习答案第二章（末）第二章正弦交流电路2.1基本要求（1）深入了解正弦量的特性，尤其是RMS、初始相位和相位差。
（2）掌握正弦量的各种表示方法及其相互关系。
(3)掌握正弦交流电路的电压电流关系及复数形式。
（4）掌握三个单参数（R、l、c）的电压、电流和功率关系。
(5)能够分析计算一般的单相交流电路，熟练运用相量图和复数法。
(6)深刻认识提高功率因数的重要性。
(7)了解交流电路的频率特性和谐振电路。
2.2基本内容2.2.1基本概念1.正弦量的三要素（1）振幅（um，EM，IM），瞬时值（U，e，I），有效值（U，e，I）。
注：有效值与振幅的关系为：有效值？振幅2。
(2)频率（f）、角频率（?）、周期（t）。
注：三者的关系是??2?f?2?。
t(3)相位（?t??）、初相角（?）、相位差（?1??2）。
注：相位差是同频率正弦量的相位之差。
2.正弦量的表示方法(1)函数式表示法：Uumsin（？t×u）；Eemsin（？t？？e）；我波形表示法：例如，u的波形如图2-1-1（a）所示。
（3）相量（图）表示：使相量的长度等于正弦量的幅值（或有效值）；使相量和横轴正方向的夹角等于正弦量的初相角；使相量旋转的角速度等于正弦量的角速度。
uuum？U我我0我？TU（b） ?？u78。
78图2-1-1（a）图2-1-1（b）25.65？U注：① 绘制实际相量时，主要使用有效值，忽略水平轴，？11也节省了油漆，没有零参考相量（只有方向，.22没有尺寸）。
图2-1-1（b）是u和I的相量图。
64.36② 相同性质（相同频率）正弦量的加减可以用相量图来解决？UI2-1图2-6（b）示例u1?62sin(?t?30o)v,u2?42sin(?t?60o)v。
求u1?u2解：因为同频率同性质的正弦量相加后仍为正弦量，故u1？u2乐队？Uu2sin（？t？？），只有你和我？一2问题解决了。
1.2.1 求图1.01所示电路中开关S 闭合和断开两种情况下a 、b 、c 三点的电位。
解：S 闭合时 a b ac 6 V 3 V 0 V V V V ==−=S 断开时 a b ac 6 V 6 V 9 V V V V ===1.5.1 试分析图1.03所示两电路中电阻的电压和电流，以及图（a ）中电流源的电压和图（b ）中电压源的电流。
解：图(a)： S 1 V1A 2 A 0.5R R R U U U I R =====电流源的电压： S 1 V U U == 图(b)： S 1 A0.5 1 V 0.5 VR R R I I U RI ====×=电压源的电流： S 1 A I I ==1.6.1 在图1.05所示电路中，已知U S = 6 V ，I S = 2 A ，R 1 = 2 Ω，R 2 = 1 Ω。
求开关S 断开时开关两端的电压U 和开关S 闭合时通过开关的电流I （不必用支路电流法）。
解：把与电压源并联的电阻R 1断开，不影响对电路的计算。
设通过R 2的电流为I 2。
S 断开时： ()2S S 222 A612 V 4 VI I U U R I ===−=−×=S 闭合时，R 2两端电压等于U S ，故：()S222S 6 A 62 A 4 AU I R I I I ===−=−=1.7.1 用支路电流法求图1.09中各支路电流，并说明U S1和U S2是起电源作用还是起负载作用。
图中U S1 = 12 V ，U S2 = 15 V ，R 1 = 3 Ω，R 2 = 1.5 Ω，R 3 = 9 Ω。
解：1232233S21133S1000I I I R I R I U R I R I U +−=+−=+−=联立方程，解得：1230.2 A 1.6 A 1.4 A I I I =−==。
1.7.2 用支路电流法求图1.10中各支路电流。
解：列方程： 1122S S 12R I R I U I I I +=+=解方程： 121223105I I I I +=+=解得： 1 1 A I =− ，2 4 A I =1.8.1 用叠加原理求图1.10所示电路中的电流I 1和I 2。
电工学少学时1-4章课后习题答案第一章电路的基本概念和基本定律一、填空题1、电路的作用是实现电能的传输和转换，以及对电信号的传递和处理。
2、电流的实际方向规定为正电荷定向移动的方向，电压的实际方向规定为由高电位指向低电位。
3、电阻元件的伏安特性曲线是一条过原点的直线，其斜率表示电阻的大小。
4、电源的电动势是电源将其他形式的能转化为电能的能力的物理量，其方向规定为在电源内部由负极指向正极。
二、选择题1、已知空间有 a、b 两点，电压 Uab=10V，a 点电位为 Va=4V，则b 点电位 Vb 为（）A 6VB －6VC 14VD －14V答案：B解析：Vb ＝ Va Uab ＝ 4 10 ＝－6V2、一电阻元件，当其电流减为原来的一半时，其功率为原来的（）A 1/2B 1/4C 2 倍D 4 倍答案：B解析：P ＝ I²R，当 I 变为原来的一半时，P' ＝（I/2)²R ＝ 1/4 I²R三、计算题1、如图所示电路，已知 E1 ＝ 18V，E2 ＝ 12V，R1 ＝3Ω，R2 ＝6Ω，R3 ＝9Ω，求各支路电流。
解：首先设各支路电流方向如图所示。
根据基尔霍夫电压定律（KVL），对于回路①：E1 I1R1 I3R3 ＝ 0即 18 3I1 9I3 ＝ 0 （1）对于回路②：E2 I2R2 ＋ I3R3 ＝ 0即 12 6I2 ＋ 9I3 ＝ 0 （2）根据基尔霍夫电流定律（KCL），在节点 A 处：I1 ＝ I2 ＋ I3 （3）联立（1）、（2）、（3）式，解得：I1 ＝ 3A，I2 ＝ 1A，I3 ＝ 2A第二章电路的分析方法一、填空题1、支路电流法是以支路电流为未知量，应用基尔霍夫定律列出方程组求解的方法。
2、网孔电流法是以网孔电流为未知量，列写网孔的 KVL 方程进行求解的方法。
3、节点电压法是以节点电压为未知量，列写节点的 KCL 方程进行求解的方法。
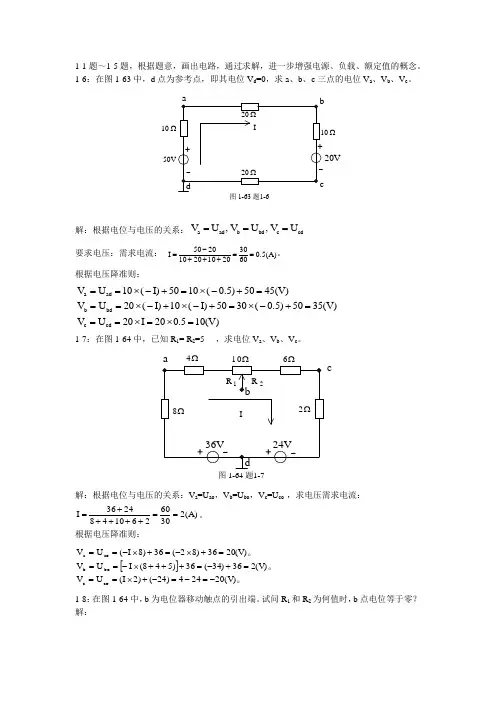
1-1题～1-5题，根据题意，画出电路，通过求解，进一步增强电源、负载、额定值的概念。
1-6：在图1-63中，d 点为参考点，即其电位V d =0，求a 、b 、c 三点的电位V a 、V b 、V c 。
20V+-Ω20图 1-63 题1-6Ω1050VΩ10Ω20+-dcbaI解：根据电位与电压的关系：a ad b bd c cd V U , V U , V U === 要求电压：需求电流： 0.5(A)6030201020102050I ==+++-=。
根据电压降准则：a adb bdc cd V U 10(I)5010(0.5)5045(V)V U 20(I)10(I)5030(0.5)5035(V) V U 20I 200.510(V)==⨯-+=⨯-+===⨯-+⨯-+=⨯-+===⨯=⨯=1-7：在图1-64中，已知R 1= R 2=5，求电位V a 、V b 、V c 。
Ω01图 1-64 题1-7Ω8Ω2+-dIΩ6+-b36V24VcΩ41R 2R解：根据电位与电压的关系：V a =U ao ，V b =U bo ，V c =U co ，求电压需求电流：2(A)30602610482436I ==+++++=。
根据电压降准则： []。
20(V )24424)(2)I (U V 。
(V)236)34(36)548(I U V 。
(V)2036)82(368)I (U V co c bo b ao a -=-=-+⨯===+-=+++⨯-===+⨯-=+⨯-==1-8：在图1-64中，b 为电位器移动触点的引出端。
试问R 1和R 2为何值时，b 点电位等于零？ 解：)6(410R 10R )4(16)/2(24R 24)(2)6(R I 0U V 2122bo b Ω=-=-=Ω=-=-+++⨯===1-9：求图1-65中的电压U ab图1-65 题1-9Ω6abU R解：本题不限方法，首先进行化简。
第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。
图1－1 题 1－1 的电路解：图（a ）中，电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图（b ）中，电流mA I 1246=+=， 各点电位 V B = 0V A = 4×1 = 4VV C =－ 2×1 = －2V图（c ）中，因S 断开，电流I = 0， 各点电位 V A = 6V V B = 6VV C = 0图（d ）中，电流mA I 24212=+=， 各点电位 V A = 2×(4+2) =12VV B = 2×2 = 4V V C = 0图（e ）的电路按一般电路画法如图，电流mA I 12466=++=，各点电位 V A = E 1 = 6VV B = (－1×4)+6 = 2V V C = －6V1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少? 解：由图1－2可知电压U 和电流I 参考方向不一致，P = －10W ＝UI 因为U ＝10V , 所以电流I ＝－1A图 1－2 题 1－2 的电路1－3 额定值为1W 、10Ω的电阻器，使用时通过电流的限额是多少？ 解：根据功率P = I 2 R A R P I 3160101.===1－4 在图1－3所示三个电路中，已知电珠EL 的额定值都是6V 、50mA ，试问哪个电珠能正常发光？图 1－3 题 1－4 的电路解：图（a ）电路，恒压源输出的12V 电压加在电珠EL 两端，其值超过电珠额定值，不能正常发光。
图（b ）电路电珠的电阻Ω=Ω==120120506K R .，其值与120Ω电阻相同，因此电珠EL 的电压为6V ，可以正常工作。
图（c ）电路，电珠与120Ω电阻并联后，电阻为60Ω，再与120Ω电阻串联，电珠两端的电压为V 4126012060＝＋⨯小于额定值，电珠不能正常发光。
1－5 图1－4所示电路中，已知电压U 1 = U 2 = U 4 = 5V ，求U 3和U CA 。
解：根据基尔霍夫电压定律，对回路ABCDA 可写出方程U 1＋U 2－U 3＋U 4 ＝0U 3= U 1＋U 2＋U 4 = 5＋5＋5＝15V 对回路ACDA 可写出方程 U CA ＋U 3－U 4＝0U CA ＝U 4－U 3＝5－15＝－10V1－6 欲使图1－5所示电路中的电流I=0，U S 应为多少？解：因为电流I=0，所以I 1＝I 2＝A 205154.＝）＋（U S ＝5×0.2＝1V图1－5 题1－6的电路1－7 在图1－6所示三个电路中，R 1 = 5Ω，R 2 = 15Ω，U S = 100V ，I 1 = 5A ，I 2 = 2A 。
若R 2电阻两端电压U ＝30V ，求电阻R 3 。
解：A R U I 2153025===A I I I 725514=+=+= Ω=⨯--=--==++5172577010051433514.I R I U U R U U R I R I S S图 1－6 题1－7的电路1－8 求图1－7所示各电路中的未知量。
图 1－7 题1－8的电路解: (a)图 Ω=-=42816R (b) 图 V U 1020103=-⨯= (c) 图 A I 60101016.=-=1－9 在图1－8所示的电路中，R 1、R 2、R 3、R 4的额定值均为6.3V 、0.3A ，R 5额定值为6.3V 、0.45A ，U = 110V 。
为使上述各电阻元件均处于额定工作状态，则选配电阻R X 和R Y 的理想阻值应为多少？解: I 1 =0.3A I =0.45AI 2 = 0.45－0.3 = 0.15AΩ=⨯=168150436..Y RΩ=⨯-=4174450536110...X R图 1－8 题1－9的电路1－10 电路如图1－9所示，求A 点的电位。
(a)(b)图 1－9 题1－10的电路解: 图（a ）的电路按一般电路画法如图(b)， A I 2514410.=+=V A =－1.25×4＝－5V 1－11 求图1－10所示电路中的电压U 、电流I 。
图 1－10 题1－11的电路解：（a ）图 U 为恒压源的输出，U ＝10VI ＝10/2＝5A（b ）图 I 为恒流源的输出，I ＝5AU ＝5×10＝50V1－12 简化图1－11所示各电路为一个等效的电压源或理想电流源。
图1－11 题1－12的电路解：（a）图两理想电流源合并为一个，电流I S＝5－3＝2A，如图（f）。
（b）图两理想电压源合并为一个，其值U S＝6－4＝2V，如图（g）。
（c）图与恒压源并联的电阻可以去掉，等效为一个理想电压源，如图（h）。
（d）图与恒流源串联的电阻可以去掉，等效为一个理想电流源，如图（j）。
（e）图与3A恒流源串联的电压源可以去掉，与5A恒流源串联的电阻可以去掉，等效为一个理想电流源，电流I S＝5－3＝2A，如图（k）。
1－13 在图1－12（a）（b）（c）所示的电路中，是哪些元件在提供功率？图1－12 题1－13的电路解：（a）图由1A电流源提供功率。
（b）图由10V电压源提供功率。
（c）图由U S电压源提供功率。
1－14 在图1－13（a）（b）（c）所示的电路中，电压U是多少？图1－13 题1－14的电路解：（a）图U＝0（b）图U＝1－3＝－2V（c）图U＝（1＋2）×120＝360V1－15 某实际电源的伏安特性如图1－14所示，试求它的电压源模型，并将其等效变换为电流源模型。
（a）图1－14 题1－15的电路解：U＝U S－IR0（1）根据图（a）可知，当I＝0时，U＝9V；带入（1）式解得U S＝9V当I＝4时，U＝6V；带入（1）式解得R0＝3/4Ω电压源模型如图（b），电流源模型如图（c）。
第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。
2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。
2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。
求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。
2-8 电路如图2-6所示，试用叠加原理求电流I。
2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。
2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。
2-11 画出图2-9所示电路的戴维宁等效电路。
2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。
当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。
试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。
今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。
现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？图3-1 t rad f /3145014.322=⨯⨯==πωAt i Vt u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25At i i t At t i f ）（，时，）（︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω本 章 小 结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。
它是以电路中的支路电流为未知量，应用基尔霍夫定律列出电路方程，通过解方程得到各支路电流。
一般地，对于具有n 个节点、b 条支路的电路可列出（n-1）个独立的节点电流方程和[b-（n-1）] 个独立的回路电压方程。
2、叠加原理是反映线性电路基本性质的一条重要定理，它可将多个电源共同作用下产生的电压和电流，分解为各个电源单独作用时产生的电压和电流的代数和。
某电源单独作用时，将其它理想电压源短路，理想电流源开路，但电源内阻必须保留。
3、戴维宁定理适合于求解电路中某一条支路电压或电流的情况。
把待求支路（或元件）单独划出来，剩下的线性有源二端网络可用一个电压源来等效替代。
此电压源中理想电压源的电压U S 等于有源二端网络的开路电压，内阻R 0等于有源二端网络中所有电源均除去后所得无源二端网络的等效内阻。
对于待求元件不要求一定是线性的。
第三章习题3-1 已知正弦电压和正弦电流的波形如图3-1所示,频率为50Hz ，试指出它们的最大值、初相位以及它们之间的相位差，并说明哪个正弦量超前，超前多少度？超前多少时间？解： u 、i 的表达式为即：u 比i 超前135°，超前2-1 某正弦电流的频率为20Hz ，有效值为 A ，在t =0时，电流的瞬时值为5A ，且此时刻电流在增加，求该电流的瞬时值表达式。
解：︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=•••••89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===AI A I V U t i A t i tV u ︒-∠=︒∠=︒∠=︒-=︒+==•••45259010022045sin10)90sin(210sin 22202121）（ωωωAt i tA i Aj jX U I Aj jX U I A R U I Hz f V U R C C L L R ）（时：当︒-==∴︒∠=-︒∠=-=︒-∠=︒∠==︒∠=︒∠===︒∠=•••••••90314sin 210314sin 2109010)22(0220)(9010220220010220220500220•R I •LI •CI •U 时Hz f 50=3-3 已知复数A 1=6+j8Ω，A 2=4+j4Ω，试求它们的和、差、积、商。
