数学建模习题课

数学建模部分课后习题解答1.在稳定的椅子问题中，如设椅子的四脚连线呈长方形，结论如何？ 解：模型假设（1） 椅子四条腿一样长，椅脚与地面接触处视为一点，四脚的连线呈长方形 （2） 地面高度是连续变化的，沿任何方向都不会出现间断（没有像台阶那样的情况），即从数学角度来看，地面是连续曲面。

这个假设相当于给出了椅子能放稳的必要条件（3） 椅子在任何位置至少有三只脚同时着地。

为了保证这一点，要求对于椅脚的间距和椅腿的长度而言，地面是相对平坦的。

因为在地面上椅脚间距和椅腿长度的尺寸大小相当的范围内，如果出现深沟或凸峰（即使是连续变化的），此时三只脚是无法同时着地的。

模型建立在上述假设下，解决问题的关键在于选择合适的变量，把椅子四只脚同时着地表示出来。

首先，引入合适的变量来表示椅子位置的挪动。

生活经验告诉我们，要把椅子通过挪动放稳，通常有拖动或转动椅子两种办法，也就是数学上所说的平移与旋转变换。

然而，平移椅子后问题的条件没有发生本质变化，所以用平移的办法是不能解决问题的。

于是可尝试将椅子就地旋转，并试图在旋转过程中找到一种椅子能放稳的情形。

注意到椅脚连线呈长方形，长方形是中心对称图形，绕它的对称中心旋转180度后，椅子仍在原地。

把长方形绕它的对称中心旋转，这可以表示椅子位置的改变。

于是，旋转角度θ这一变量就表示了椅子的位置。

为此，在平面上建立直角坐标系来解决问题。

设椅脚连线为长方形ABCD,以对角线AC 所在的直线为x 轴，对称中心O 为原点，建立平面直角坐标系。

椅子绕O 点沿逆时针方向旋转角度θ后，长方形ABCD 转至A1B1C1D1的位置，这样就可以用旋转角）0（πθθ≤≤表示出椅子绕点O 旋转θ后的位置。

其次，把椅脚是否着地用数学形式表示出来。

当椅脚与地面的竖直距离为零时，椅脚就着地了，而当这个距离大于零时，椅脚不着地。

由于椅子在不同的位置是θ的函数，因此，椅脚与地面的竖直距离也是θ的函数。

由于椅子有四只脚，因而椅脚与地面的竖直距离有四个，它们都是θ的函数，而由假设（3）可知，椅子在任何位置至少有三只脚同时着地，即这四个函数对于任意的θ，其函数值至少有三个同时为0。

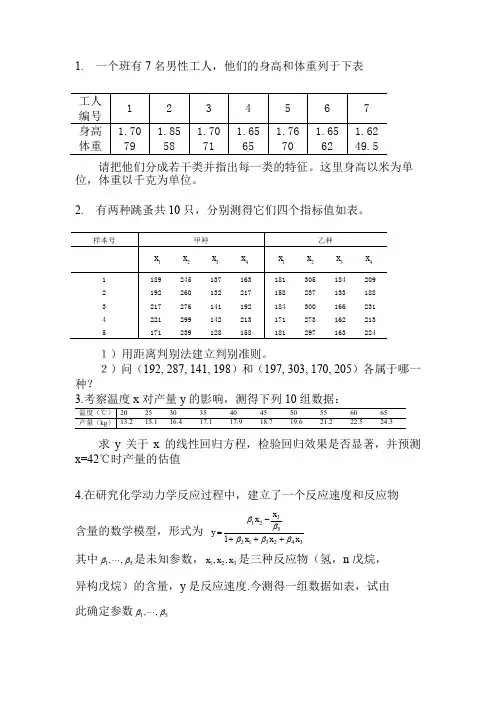
1. 一个班有7名男性工人，他们的身高和体重列于下表
请把他们分成若干类并指出每一类的特征。

这里身高以米为单位，体重以千克为单位。

2. 有两种跳蚤共10只，分别测得它们四个指标值如表。

１）用距离判别法建立判别准则。

２）问（192, 287, 141, 198）和（197, 303, 170, 205）各属于哪一种？
求y 关于x 的线性回归方程，检验回归效果是否显著，并预测x=42℃时产量的估值
4.在研究化学动力学反应过程中，建立了一个反应速度和反应物 含量的数学模型，形式为
3
423125
3
211x x x x x y βββββ+++-
=
其中51,,ββ 是未知参数，321,,x x x 是三种反应物（氢，n 戊烷， 异构戊烷）的含量，y 是反应速度.今测得一组数据如表，试由 此确定参数51,,ββ
序号反应速度y 氢x1 n戊烷x2 异构戊烷x3
1 8.55 470 300 10
2 3.79 285 80 10
3 4.82 470 300 120
4 0.02 470 80 120
5 2.75 470 80 10
6 14.39 100 190 10
7 2.54 100 80 65
8 4.35 470 190 65
9 13.00 100 300 54
10 8.50 100 300 120
11 0.05 100 80 120
12 11.32 285 300 10
13 3.13 285 190 120 5.主成分与卡方检验已课件为主。

综合题目参考答案1. 赛程安排(2002年全国大学生数学建模竞赛D 题)(1)用多种方法都能给出一个达到要求的赛程.(2)用多种方法可以证明支球队“各队每两场比赛最小相隔场次n r 的上界”(如=5时上界为1)是n ⎥⎦⎤⎢⎣⎡-23n ,如: 设赛程中某场比赛是,i j 两队, 队参加的下一场比赛是,两队(≠i i k k j ),要使各队每两场比赛最小相隔场次为r ,则上述两场比赛之间必须有除i ,j ,以外的2k r 支球队参赛,于是,注意到32+≥r n r 为整数即得⎥⎦⎤⎢⎣⎡-≤23n r . (3)用构造性的办法可以证明这个上界是可以达到的,即对任意的编排出达到该上界的赛程.如对于n =8, =9可以得到: n n 1A 2A 3A 4A 5A 6A 7A 8A 每两场比赛相隔场次数 相隔场次总数1A× 1 5 9 13 17 21 25 3,3,3,3,3,3 18 2A 1 × 20 6 23 11 26 16 4,4,4,3,2,2 193A 5 20 × 24 10 27 15 2 2,4,4,4,3,2 19 4A 9 6 24 × 28 24 3 19 2,2,4,4,4,3 19 5A 13 23 10 28 × 4 18 7 2,2,2,4,4,4 18 6A 17 11 27 14 4 × 8 22 3,2,2,2,4,4 177A 21 26 15 3 18 8 × 12 4,3,2,2,2,4 178A25 16 2 19 7 22 12 × 4,4,3,2,2,2 17w w w .k h d a w .c o m 课后答案网1A 2A 3A 4A 5A 6A 7A 8A 9A 每两场比赛相隔场次数 相隔场次总数1A× 36 6 31 11 26 16 21 1 4,4,4,4,4,4,4, 28 2A 36 × 2 27 7 22 12 17 32 4,4,4,4,4,4,3 27 3A 6 2 × 35 15 30 20 25 10 3,3,4,4,4,4,4 26 4A 31 27 35 × 3 18 8 13 234,4,4,4,3,3,3 25 5A 11 7 15 3 × 34 24 29 193,3,3,3,4,4,4 24 6A 26 22 30 18 34 × 4 9 144,4,3,3,3,3 23 7A16 12 20 8 24 4 × 33 28 3,3,3,3,3,3,4 22 8A21 17 25 13 29 9 33 × 53,3,3,3,3,3,3, 21 9A 1 32 10 23 19 14 28 5 × 3,4,3,4,3,4,3 24 可以看到, =8时每两场比赛相隔场次数只有2,3,4, =9时每两场比赛相隔场次数只有3,4,以上结果可以推广,即为偶数时每两场比赛相隔场次数只有n n n 22-n ,12-n ,2n ,n 数时只有为奇23-n ,21-n . 量赛程优劣其他指标如(4)衡的平均相隔场次 记第i 队第j 个ij c ,2,2,1,,,2,1-==n j n i ,间隔场次数为则平均相隔场次为∑∑=n i 1-=n r 21 =-j n n 1)2(ij c r 是赛程整体意义下的指标,它越大越好.可以计算=8,=9的n n r ,并讨论它是否达到上界. 相隔场次的最大偏差 定义||,r c Max f ij j i -=∑---=2)2(|n r n c Max g =1|j ijw w w .k h d a w .c o m 课后答案网f 为整个赛程相隔场次的最大偏差, 为球队之间相隔场次的最大偏差,它们都是越小越好.可以计算=8,=9的,g ,并讨论它是否达到上界.g n n f 参考文献工程数学学报第20卷第5期20032. 影院座位设计建立满意度函数),(βαf ,可以认为α和β无关, ()()βαβαh g f -=),(,g ,取尽量简单的形式,h 如αα=)(g ;0)(=βh (),030≤β0)(h h =β)30(0>β.(1)可将作为必要条件,以030≤βα最大为最佳座位的标准.在上图中以第1排座位为坐标原点建立坐标轴x ,可以得到 ⎪⎭⎫ ⎝⎛+----⎪⎭⎫ ⎝⎛+--=⎪⎭⎫ ⎝⎛+--=d x x h c H d x x c H d x x c H θθαθβtan arctan tan arctan ,tan arctan β是x 的减函数.可得x ≈1.7m,即第3(或4)排处.又通过计算或分析可知030=βα也是x 的减函数,所以第3(或4)排处是最佳座位.(2)设定一个座位间隔(如0.5m), l x 从0(或处)到030≤βd D -按离散,对于计算l )20~0(00θα的平均值,得时其值最大. 020=θ(3)可设地板线是x 的二次曲线,寻求,b 使2bx ax +a α的平均值最大. 实际上,还应考虑前排不应挡住后排的视线. 3.节水洗衣机(1996年全国大学生数学建模竞赛B 题) 该问题不要求对洗衣机的微观机制(物理、化学方面)深入研究,只需要从宏观层次去把握.宏观上洗衣的基本原理是用洗涤剂通过漂洗把吸附在衣物上的污物溶于水中,再脱去污水带走污物;洗衣的过程是通过“加水——漂洗——脱水”程序的反复运行,使残留在衣物的污物越来越少,直到满意的程度;洗涤剂也是不希望留在衣物上的东西,可将“污物”定义为衣物上原有污物与洗涤剂的总和. w w w .k h da w .c o m 课后答案网假设每轮漂洗后污物均匀地溶于水中;每轮脱水后衣物含水量为常数.~初始污水量,第轮加水量,~第k 轮脱水量c 0x ~k u k k x ),,2,1( =k .设每轮脱水前后污物在水中的浓度不变.于是cx c u x u c x n n n =+==--111,,, c x 2c x +21u x 10, 得到)()(210c u c u u c x x n n n ++= . 在最终污物量与初始污物量之比小于给定的清洁度条件下,求各轮加水量,使总用水量最小,即0/x x n k u ),,1(n k =∑=nk k u u Min k 1()ε<++)(..21c u c u u c t s n n 等价于)()(21c u c u u Min n u k +++++ α=++)()(..21c u c u u t s na 为常数可得c u c u u n +==+= 21,即第轮加水量n ~2u u k =(常数),第1轮加水量.c u u +=1令,问题简化为cx u =nx Min u n , ε<⎪⎭⎫ ⎝⎛+n x t s 11.. 其解为,即,而0→x 0→u ∞→n n .这与实际上是不合理的.应该加上对u 的限制:.则得n ,其中 21v u v ≤≤max min n n ≤≤max min n n ≤≤,1+)/1ln(2min ⎥⎦⎤⎢⎣⎡+=c v n αn 这样,为有限的几个数,可一一比较,具体数据计算从略.参考文献:《数学的实践与认识》第27卷第1期,1997w w w .k h d a w .c o m 课后答案网4.教师工资调整方案(1995年美国大学生数学建模竞赛B 题)题目对职称提升年限表述得不甚清楚(如未提及助理教授的提升),教龄也未区分是什么职称下工作的年限,所以应该作出一些相应的简化假设.按所给信息,工资仅取决于职称和教龄.建立新方案的一种办法是将职称折合成教龄,如定义x=教龄t+7×k (对于讲师、助理教授、副教授、教授,k 分别取值0,1,2,3),然后寻求工资函数I(x),使之满足题目的要求,如I(0)=27000,I(7)=32000等,以及x 较大时022<dxI d .另一种办法是职称、教龄分别对待,工资函数J(k,t)从多种函数中选择,如最简单的线性函数J(k,t)=k k k k b a t b a ,,+(k=0,1,2,3)根据一定条件确定.按照第一种办法得到的新工资方案,以职称和教龄综合指标为x 的教师的工资都应为I(x),而人们的目前工资会低于或高于它.根据题目要求,高工资不应降低,低工资则应逐渐提高,尽快达到理想值I(x).需要做的只是根据每人(目前)工资与(理想值的)差额,制定学校提供的提薪资金的分配方案.它应该是简单、合理、容易被人接受的. 按以上原则可以建立不同的模型,应通过检验比较其恶劣.检验可基于题目所给数据,按照提薪计划运行若干年,考察接近理想方案的情况,即用过渡时期的情况检验模型;也可进行随机模拟,按照一定规则随机产生数据(可以包括聘用、提职、解聘、退休的人数和时间等),再按照提薪计划运行,考察接近理想方案的情况.参考文献：叶其孝，《大学生数学建模竞赛辅导教材》（四），湖南教育出版社，20015. 一个飞行管理问题（1995年全国大学生数学建模竞赛A 题）设为第i 架飞机与第j 架飞机的碰撞角（即ij a )8arcsin(ij ij r a =其中为这两架飞机连线的长度），ij r ij β为第i 架飞机相对于第j 架飞机的相对速度（矢量）与这两架飞机连线（从i 指向j 的矢量）的夹角（以连线矢量为基准，逆时针方向为正，顺时针方向为负），i θ为第架飞机飞行方向角调整量. 本问题中的优化目标函数可以有不同的形式：如使所有飞机的最大调整量最小；所有飞机的调整量绝对值之和最小等.以所有飞机的调整量绝对值之和最小，可以得到如下的数学规划模型：w w w .k h d a w .c o m 课后答案网∑=61i i Min θ s.t. ,)(21ij j i ij a >++θθβ j i j i ≠=,6,,1,30≤i θ , 6,,1 =i 为了利用LINGO 求解这个数学规划模型，可以首先采用其他数学软件计算出ij α和ij β.其实，ij α和ij β也是可以直接使用LINGO 来计算的，这相当于解关于ij α和ij β的方程，只是解方程并非LINDO 软件的特长，这里我们作为一个例子，看看如何利用LINGO 计算ij α，可输入如下模型到LINGO 求解ij α：MIDEL ：1]SETS:2] PLANE/1..6/：x0,y0; 3] link(plane,plane):alpha,sin2: 4]ENDSETS5] @FOR(LINK(I,J)|I#NE#J:6] sin2(I,J)=64/((X0(I)-X0(J))*(X0(I)-X0(J))+7] (Y0(I)-Y0(J))*(Y0(I)-Y0(J)));8] ）；9] @FOR(LINK(I,J)|I#NE#J: 10] (@SIN(alpha*3.14159265/180.0))^2=SIN2; 11] ); 12]DATA:13] X0=150,85,150,145,130,0; 14] Y0=140,85,155,50,150,0; 15]endataEND计算结果如下：w w w .k h d a w .c o m 课后答案网ij a j=1 2 3 4 5 6i=1 0.000 0 5.3912 32.231 05.091 8 20.963 4 2.234 5 2 5.391 2 0.000 0 4.8046.613 5 5.807 9 3.815 9 3 32.231 0 4.804 0 0.0004.364 7 22.833 7 2.125 5 45.091 86.613 5 4.36470.000 0 4.4.537 2.989 8 5 20.963 4 5.807 922.8337 4.537 70.000 0 2.309 8 6 2.234 5 3.815 9 2.125 5 2.989 82.309 80.000 0 ij β也可类似地利用LINGO 求得，计算结果如下： ij β j=1 2 3 4 5 6 i=1 0.000 0 109.263 6 -128.250 0 24.1798173.065 1 14.474 9 2 109.263 6 0.000 0-88.871 1 -42.2436-92.304 8 9.000 03 -128.250 0 -88.871 1 0.000 012.4763-58.786 2 0.310 84 24.179 8 -42.243 6 12.476 30.000 0 5.969 2-3.525.65 173.065 1 -92.304 8 -58.78625.969 20.000 0 1.914 4614.474 9 9.000 00.310 8-3.5256 1.914 4 0.000 0w w w .k h d a w .c o m 课后答案网于是，该飞机管理的数学规划模型可如下输入LINGO 求解：MODEL:1]SETS2] plane/1..6/:cita:3] link(plane,plane):alpha,beta;4]ENDSETS5] min=@sum(plane:@abs(cita));6] @for(plane(I):7] @bnd(-30,cita(I),30);8] );9] @fpr(link(I,j)|I#NE#J:10] @ABS(beta(I,J)+0.5*cit(I)+0.5*cita(J))11] >alpha(I,J);12] ）;13]DATA:14] A;[JA=0.000 0 5.391.2….. …2.309 8 0.000 020] ;21] BETA=0.000 010 9.263 6………1.914 4 0.000 027] ;28]enddata END[注] alpha,beta 中数据略去，见上面表格. 求解结果如下： OPTIMUM FOUND AT STEP 197 SOLUTION OBJECTIVE V ALUE= 3.630 V ARIABLE V ALUE REDUCED COST CITA(1) 0.2974033E-06 -1.000 000 CITA(2) -0.1424833E-05 -0.715 033 4 w w w .k h d a w .c o m 课后答案网CITA(3) 2.557 866 1.000 000 CITA(4) -0.3856641E-04 0.0000000E+00CITA(5) 0.2098838E-05 -1.000 000CITA(6) 1.071 594 0.0000000E+00………. (以下略)由此可知最优解为： （其它调整角度为0）. ︒︒≈≈07.1,56.263θθ 评注：如果将目标改为最大调整量最小，则可进一步化简得到线形规划模型，也可用LINDO 或LINGO 求解.参考文献：《数学的实践与认识》第26卷第1期，19966. 降落伞的选择这个优化问题的决策变量是降落伞数量n 和每一个伞的半径r ，可先将n 和r 看作连续变量，建立优化模型，求得最优解后，再按题目要求作适当调整. 目标函数之降落伞的费用，可以根据表1数据拟合伞面费用与伞的半径r 的关系。

数学建模（I ）习题习 题 31．一个包裹从100米高的气球上掉下，当时，气球的上升速度为2米/秒，请根据以下两种情况计算包裹落到地面上约需多少时间：（1）空气阻力不计（2）空气阻力与包裹的速度成正比，阻力系数为0.05。

2．大气压强p 可用对海拔高度h 的变化率dh dp 与p 成正比来建模，且位于海平面的压强为1013毫巴（大约每平方英尺7.14磅），位于海拔高度20公里处的压强为90毫巴。

)(a 解初始值问题:微分方程： kp dh dp = （k 是一个常数） 初始条件： 0p p = （当0=h ）得到通过h 表示p 的表达式。

根据海拔高度—压强的给定数据确定0p 和k 的值。

（b ）在海拔高度50=h 公里处大气压强是多少?（c ）在海拔高度是多少公里处大气压强等于900毫巴？3．在某化学反应中，物质的数量随着时间的改变率与其当前的数量成正比。

例如，δ-醣蛋白内酯变成葡萄糖酸，当时间t 以小时为单位时，化学反应方程式是 y dtdy 6.0-= 如果当0=t 时，有δ-醣蛋白内酯100克，那么一小时后还剩下多少？4．从惠蒂尔峡谷的油井中抽走了一定数量的石油，会使加利福尼亚的石油产量每年以10%的比率减少。

试问什么时候加利福尼亚的石油产量将降到当前值得五分之一？5．一个放电的电容器，电压的改变率和终端电压成正比，并且时间t 以秒为单位时，其满足的方程是V dt dV 401-= 解此方程，用0V 表示当0=t 时的V 值。

试问经过多长时间电压将降落到初始值得10%？6．粗糖的加工过程中，有一个步骤称为转化，这一步骤将改变粗糖的分子结构。

反应一旦开始，粗糖量的改变速率和粗糖量成正比，如果1000公斤粗糖在10 小时后只剩下100公斤，那么再过14小时还剩下多少？7．在海洋表面下方x 英尺处的光的强度)(x L 满足微分方程kL dxdL -= 潜水者根据经验知道，在加勒比海潜水到18 英尺深时光线强度大约降低到水面上的一半。

数学建模课后习题数学建模课后习题：探索斐波那契数列的奥秘数学建模，一项充满挑战与乐趣的实践活动，让我们的思维在理论联系实际的道路上飞驰。

在完成了一系列的课堂学习后，我们迎来了第一道课后习题——探索斐波那契数列的奥秘。

斐波那契数列，一个古老而神奇的话题，早在中世纪就引起了数学家的关注。

这个数列由0和1开始，后续的数字是前两个数字之和，即0, 1, 1, 2, 3, 5, 8, 13, 21, 34，等等。

这些数字在数学界被称为“斐波那契数”，而在生物学界，它们则被称为“黄金分割数”。

我们首先需要理解这个数列的定义和性质。

例如，斐波那契数列的每个数字都是前两个数字之和，且每个数字都无限接近于一个黄金分割比。

这些性质使得斐波那契数列在自然界的许多领域中都有应用，如植物生长、动物繁衍，甚至在人类的艺术和建筑设计中也有体现。

为了更好地理解和应用斐波那契数列，我们需要通过编程来实现它。

Python语言提供了一种简单的方法。

以下是一段Python代码，用于生成斐波那契数列：通过调用fibonacci(n)函数，我们可以得到前n个斐波那契数。

在完成这个函数之后，我们可以进一步思考如何利用斐波那契数列解决实际问题。

例如，我们可以使用斐波那契数列来优化矩阵乘法。

在传统的矩阵乘法中，我们需要进行一系列的加法和乘法操作，而这些操作的时间复杂度是O(n^3)。

然而，通过利用斐波那契数列，我们可以将时间复杂度降低到O(n)。

这是一个巨大的优化，尤其是在处理大规模数据时。

总的来说，斐波那契数列是一个充满挑战和乐趣的数学主题。

通过完成这个课后习题，我们不仅可以加深对数学建模的理解，还可以将所学知识应用于实际问题，实现从理论到实践的跨越。

让我们一起继续探索斐波那契数列的奥秘吧！数学建模习题及答案数学建模是一种将数学方法应用于实际问题求解的技能。

通过数学建模，我们可以将现实世界中的问题转化为数学问题，并运用数学工具和计算机技术进行求解。

数学建模课后习题第⼀章课后习题6.利⽤节药物中毒施救模型确定对于孩⼦及成⼈服⽤氨茶碱能引起严重中毒和致命的最⼩剂量。

解：假设病⼈服⽤氨茶碱的总剂量为a ，由书中已建⽴的模型和假设得出肠胃中的药量为：)()0(mg M x =由于肠胃中药物向⾎液系统的转移率与药量)(t x 成正⽐，⽐例系数0>λ，得到微分⽅程M x x dtdx=-=)0(,λ（1）原模型已假设0=t 时⾎液中药量⽆药物，则0)0(=y ，)(t y 的增长速度为x λ。

由于治疗⽽减少的速度与)(t y 本⾝成正⽐，⽐例系数0>µ，所以得到⽅程：0)0(,=-=y y x dtdyµλ（2）⽅程（1）可转换为：tMe t x λ-=)(带⼊⽅程（2）可得：)()(t t e e M t y λµµλλ----=将01386=λ和1155.0=µ带⼊以上两⽅程，得：针对孩⼦求解，得：严重中毒时间及服⽤最⼩剂量：h t 876.7=，mg M 87.494=；致命中毒时间及服⽤最⼩剂量：h t 876.7=，mg M 8.4694= 针对成⼈求解：严重中毒时间及服⽤最⼩剂量：h t 876.7=，mg M 83.945= 致命时间及服⽤最⼩剂量：h t 876.7=，mg M 74.1987=课后习题7.对于节的模型，如果采⽤的是体外⾎液透析的办法，求解药物中毒施救模型的⾎液⽤药量的变化并作图。

解：已知⾎液透析法是⾃⾝排除率的6倍，所以639.06==µut e t x λ-=1100)(，x 为胃肠道中的药量，1386.0=λ解得：()2,274.112275693.01386.0≥+=--t e et z t t⽤matlab 画图:图中绿⾊线条代表采⽤体外⾎液透析⾎液中药物浓度的变化情况。

从图中可以看出，采取⾎液透析时⾎液中药物浓度就开始下降。

T=2时，⾎液中药物浓度最⾼，为；当z=200时，t=，⾎液透析⼩时后就开始解毒。

入门级数学建模练习题2. 假设在一所大学中，一位普通教授以每天一本的速度开始从图书馆借出书。

再设图书馆平均一周收回借出书的1/10，若在充分长的时间内，一位普通教授大约借出多少年本书？3. 一人早上6：00从山脚A上山，晚18：00到山顶B；第二天，早6：00从B下山，晚18：00到A。

问是否有一个时刻t,这两天都在这一时刻到达同一地点？4. 如何将一个不规则的蛋糕I平均分成两部分？5. 兄妹二人沿某街分别在离家3公里与2公里处同向散步回家，家中的狗一直在二人之间来回奔跑。

已知哥哥的速度为3公里/小时，妹妹的速度为2公里/小时，狗的速度为5公里/小时。

分析半小时后，狗在何处？6. 甲乙两人约定中午12：00至13：00在市中心某地见面，并事先约定先到者在那等待10分钟，若另一个人十分钟内没有到达，先到者将离去。

用图解法计算，甲乙两人见面的可能性有多大？7. 设有n个人参加某一宴会，已知没有人认识所有的人，证明：至少存在两人他们认识的人一样多。

8. 一角度为60度的圆锥形漏斗装着10端小孔的面积为0.59. 假设在一个刹车交叉口，所有车辆都是由东驶上一个1/100的斜坡，计算这种情下的刹车距离。

如果汽车由西驶来，刹车距离又是多少？10. 水管或煤气管经常需要从外部包扎以便对管道起保护作用。

包扎时用很长的带子缠绕在管道外部。

为了节省材料，如何进行包扎才能使带子全部包住管道而且带子也没有发生重叠。

:顶=1：a:b，选坐v>0,而设语雨速L,v≤x vv+1),v>x.解：由于教授每天借一本书，即一周借七本书，而图书馆平均每周收回书的1/10，设教授已借出书的册数是时间t的函数小x的函数，则它应满足其中初始条件表示开始时教授借出数的册数为0。

解该线性问题得X=70[1-e?t]由于当∞时，其极限值为70,故在充分长的时间内，一位普通教授大约已借出70本书。

3.解：我们从山脚A点为始点记路程，设从A到B路程函数为f,即t时刻走的距离为f;同样设从B点到A点的路程为函数g。

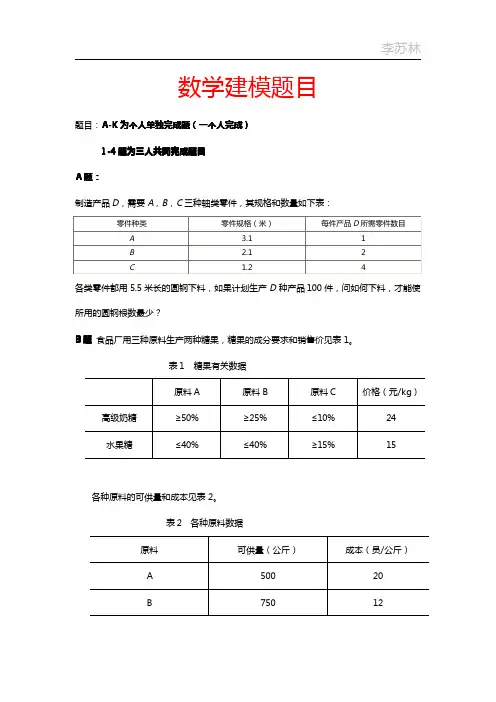
数学建模题目题目：A-K为个人单独完成题（一个人完成）1-4题为三人共同完成题目B题食品厂用三种原料生产两种糖果，糖果的成分要求和销售价见表1。

表1糖果有关数据原料A原料B原料C价格（元/kg）高级奶糖≥50%≥25%≤10%24水果糖≤40%≤40%≥15%15各种原料的可供量和成本见表2。

表2各种原料数据原料可供量（公斤）成本（员/公斤）A50020B75012该厂根据订单至少需要生产600公斤高级奶糖，800公斤水果糖，为求最大利润，试建立线性规划模型并求解。

C 题：某商业公司计划开办5家新商店。

为了尽早建成营业，商业公司决定由5家建筑公司分别承建。

已知建筑公司i A （5,4,3,2,1=i）对新商店j B （5,4,3,2,1=j ）的建造费用的报价（万元）为ij c （5,4,3,2,1,=j i ），见表3。

商业公司应当对5家建筑公司怎样分配建造任务，才能使总的建造费用最少？表3各建筑公司的建筑费用数据1B 2B 3B 4B 5B 1A 48715122A 791714103A 6912874A 67146105A 6912106D 题上海医科大学病理生理教研室曾做过小鼠肉瘤的增长实验，并得到了如表4所示的数据。

表4小鼠肉瘤的实验数据时间069111315171921232527体积0.0040.0310.0610.0740.1030.1520.2100.3390.5200.8131.269 1.558（1）若t 时刻肿瘤的体积)(t v 满足指数模型⎪⎩⎪⎨⎧==0)0(v v rv dt dv 请拟合参数r 。

（2）若t 时刻肿瘤的体积)(t v 满足Logistic 模型⎪⎩⎪⎨⎧=−=02)0(v v v v dt dv βα请拟合参数βα,。

E 题已知数据见表5。

试求y 对321,,x x x 的线性回归方程并检验回归效果，能否剔除一个变量？表5回归分析数据序号1x 2x 3x y序号1x 2x 3x y10.453158641012.6581125120.423163601110.937111763 3.11937711223.1461149640.634157611323.150134775 4.72459541421.64473936 1.765123771523.1561689579.444468116 1.93614354810.131117931726.858202168911.629173931829.95112499F 题：炼钢厂出钢时所用的盛钢水的钢包，由于钢水对耐火材料的侵蚀作用，随着使用次数的增加，容积不断增大，实测得到15组数据如表6。

P594•学校共1002名学生，237人住在A 宿舍，333人住在B 宿舍，432 人住在C 宿舍。

学生要组织一个10人的委员会，使用Q 值法分配各 宿舍的委员数。

解:设P 表示人数，N 表示要分配的总席位数。

i 表示各个宿舍（分别取 A,B,C ）， p i 表 示i 宿舍现有住宿人数， n i 表示i 宿舍分配到的委员席位。

首先，我们先按比例分配委员席位。

23710 A 宿舍为:n A ==2.365 1002 333"0 B 宿舍为：n B =3.323 1002 432X0 C 宿舍为：n C =4.3111002现已分完9人，剩1人用Q 值法分配。

经比较可得，最后一席位应分给 A 宿舍。

所以，总的席位分配应为： A 宿舍3个席位，B 宿舍3个席位，C 宿舍4个席位。

QA23722 3= 9361.5 Q B33323 4 = 9240.7 Q C4322 4 5=9331.2商人们怎样安全过河傻麴删舫紬削＜ I 11山名畝臥蹄峨颂禮训鋤嫌邂 韻靖甘讹岸讎鞍輯毗匍趾曲展 縣確牡GH 錚俩軸飙奸比臥鋪謎 smm 彌鯉械即第紘麵觎岸締熾 x^M 曲颁M 删牘HX …佛讪卜过樹蘇 卜允棘髒合 岡仇卅毘冋如;冋冋1卯;砰=口 於广歎煙船上觸人敦% V O J U;xMmm朗“…他1曲策D 咿川| thPl,2卜允隸策集合 刼為和啊母紳轉 多步贱 就匚叫=1入“山使曲并按 腿翻律由汩3』和騒側），模型求解 -穷举法〜编程上机 ■图解法S={(x ?jOI x=o, j-0,1,2,3;X =3? J =0,1,2,3； X =»*=1,2}J规格化方法，易于推广考虑4名商人各带一随从的情况状态$=（xy¥）~ 16个格点 允许状态〜U ）个。

点 , 允许决策〜移动1或2格； k 奇）左下移；&偶，右上移. 右，…，必I 给出安全渡河方案评注和思考［廿rfn片,rfl12 3xmm賤縣臓由上题可求：4个商人，4个随从安全过河的方案。

第一章 课后习题6.利用节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。

解：假设病人服用氨茶碱的总剂量为a ，由书中已建立的模型和假设得出肠胃中的药量为：)()0(mg M x =由于肠胃中药物向血液系统的转移率与药量)(t x 成正比，比例系数0>λ，得到微分方程M x x dtdx=-=)0(,λ （1） 原模型已假设0=t 时血液中药量无药物，则0)0(=y ，)(t y 的增长速度为x λ。

由于治疗而减少的速度与)(t y 本身成正比，比例系数0>μ，所以得到方程：0)0(,=-=y y x dtdyμλ （2） 方程（1）可转换为：tMe t x λ-=)(带入方程（2）可得：)()(t t e e M t y λμμλλ----=将01386=λ和1155.0=μ带入以上两方程，得： 针对孩子求解，得：严重中毒时间及服用最小剂量：h t 876.7=，mg M 87.494=； 致命中毒时间及服用最小剂量：h t 876.7=，mg M 8.4694= 针对成人求解：严重中毒时间及服用最小剂量：h t 876.7=，mg M 83.945= 致命时间及服用最小剂量：h t 876.7=，mg M 74.1987=课后习题7.对于节的模型，如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液用药量的变化并作图。

解：已知血液透析法是自身排除率的6倍，所以639.06==μut e t x λ-=1100)(，x 为胃肠道中的药量，1386.0=λ解得：()2,274.112275693.01386.0≥+=--t e et z t t用matlab 画图:图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。

从图中可以看出，采取血液透析时血液中药物浓度就开始下降。

T=2时，血液中药物浓度最高，为；当z=200时，t=，血液透析小时后就开始解毒。

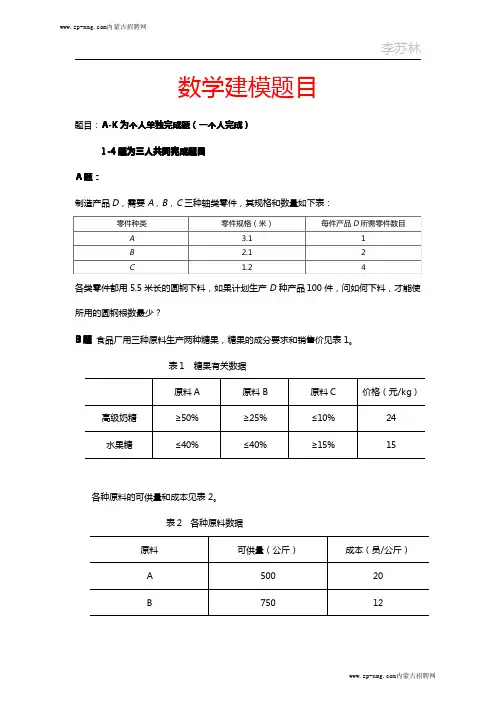
数学建模题目题目：A-K为个人单独完成题（一个人完成）1-4题为三人共同完成题目B题食品厂用三种原料生产两种糖果，糖果的成分要求和销售价见表1。

表1糖果有关数据原料A原料B原料C价格（元/kg）高级奶糖≥50%≥25%≤10%24水果糖≤40%≤40%≥15%15各种原料的可供量和成本见表2。

表2各种原料数据原料可供量（公斤）成本（员/公斤）A50020B75012该厂根据订单至少需要生产600公斤高级奶糖，800公斤水果糖，为求最大利润，试建立线性规划模型并求解。

C 题：某商业公司计划开办5家新商店。

为了尽早建成营业，商业公司决定由5家建筑公司分别承建。

已知建筑公司i A （5,4,3,2,1=i）对新商店j B （5,4,3,2,1=j ）的建造费用的报价（万元）为ij c （5,4,3,2,1,=j i ），见表3。

商业公司应当对5家建筑公司怎样分配建造任务，才能使总的建造费用最少？表3各建筑公司的建筑费用数据1B 2B 3B 4B 5B 1A 48715122A 791714103A 6912874A 67146105A 6912106D 题上海医科大学病理生理教研室曾做过小鼠肉瘤的增长实验，并得到了如表4所示的数据。

表4小鼠肉瘤的实验数据时间069111315171921232527体积0.0040.0310.0610.0740.1030.1520.2100.3390.5200.8131.269 1.558（1）若t 时刻肿瘤的体积)(t v 满足指数模型⎪⎩⎪⎨⎧==0)0(v v rv dtdv 请拟合参数r 。

（2）若t 时刻肿瘤的体积)(t v 满足Logistic 模型⎪⎩⎪⎨⎧=−=02)0(v v v v dt dv βα请拟合参数βα,。

E 题已知数据见表5。

试求y 对321,,x x x 的线性回归方程并检验回归效果，能否剔除一个变量？表5回归分析数据序号1x 2x 3x y序号1x 2x 3x y10.453158641012.6581125120.423163601110.937111763 3.11937711223.1461149640.634157611323.150134775 4.72459541421.64473936 1.765123771523.1561689579.444468116 1.93614354810.131117931726.858202168911.629173931829.95112499F 题：炼钢厂出钢时所用的盛钢水的钢包，由于钢水对耐火材料的侵蚀作用，随着使用次数的增加，容积不断增大，实测得到15组数据如表6。

考试内容分布：1、线性规划2题，有1题需编程；2、非线性规划2题，有1题需编程；3、微分方程1题，需编程；4、差分方程2题，纯计算，不需编程；5、插值2题，拟合1题，纯计算，不需编程；；6、综合1题(4分)，纯计算，不需编程。

一、列出下面线性规划问题的求解模型，并给出matlab计算环境下的程序1.某车间有甲、已两台机床，可用于加工三种工件，假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400,600和500，且已知用两种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。

问怎样分配车床的加工任务，才能即满足加工工件的要求，又使加工费用最低。

（答案见课本P35, 例1）2.有两个煤厂A,B，每月进煤分别不少于60t、100t，它们负责供应三个居民区的用煤任务，这三个居民区每月需用煤分别为45t, 75t, 40t。

A厂离这三个居民区分别为10km, 5km, 6km，B厂离这三个居民区分别为4km, 8km, 15km，问这两煤厂如何分配供煤，才能使总运输量最小？(1)问题分析设A煤场向这三个居民区供煤分别为x1,x2,x3;B煤场向这三个居民区供煤分别为x4,x5,x6，则min f=10*x1+5*x2+6*x3+4*x4+8*x5+15*x6，再根据题目约束条件来进行解题。

(2) 模型的求解>> f=[10 5 6 4 8 15];>> A=[-1 -1 -1 0 0 00 0 0 -1 -1 -1-1 0 0 -1 0 00 -1 0 0 -1 00 0 -1 0 0 -1];>> b=[-60;-100;-45;-75;-40];>> Aeq=[];>> beq=[];>> vlb=zeros(6,1);>> vub=[];>> [x,fval]=linprog(f,A,b,Aeq,beq,vlb,vub)Optimization terminated.(3) 结果分析x =0.0000 20.0000 40.0000 45.0000 55.0000 0.0000 fval = 960.0000即A 煤场分别向三个居民区供煤0t,20t,40t ；B 煤场分别向三个居民区供煤45t,55t,0t 可在满足条件下使得总运输量最小。

选修课——数学建模部分习题详细解答【陈文滨】1、在稳定的椅子问题中，如设椅子的四脚连线呈长方形，结论如何？【模型假设】（1）椅子四条腿一样长，椅脚与地面接触处视为一点，四脚的连线呈长方形．（2）地面高度是连续变化的，沿任何方向都不会出现间断 (没有像台阶那样的情况)，即从数学的角度看，地面是连续曲面．这个假设相当于给出了椅子能放稳的必要条件．（3）椅子在任何位置至少有三只脚同时着地．为保证这一点，要求对于椅脚的间距和椅腿的长度而言，地面是相对平坦的．因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内，如果出现深沟或凸峰(即使是连续变化的)，此时三只脚是无法同时着地的。

【模型建立】在上述假设下，解决问题的关键在于选择合适的变量，把椅子四只脚同时着地表示出来．首先，引入合适的变量来表示椅子位置的挪动．生活经验告诉我们，要把椅子通过挪动放稳，通常有拖动或转动椅子两种办法，也就是数学上所说的平移与旋转变换．然而，平移椅子后问题的条件没有发生本质变化，所以用平移的办法是不能解决问题的．于是可尝试将椅子就地旋转，并试图在旋转过程中找到一种椅子能放稳的情形．注意到椅脚连线呈长方形，长方形是中心对称图形，绕它的对称中心旋转180度后，椅子仍在原地．把长方形绕它的对称中心O旋转，这可以表示椅子位置的改变。

于是，旋转角度θ这一变量就表示了椅子的位置．为此，在平面上建立直角坐标系来解决问题．如下图所示，设椅脚连线为长方形ABCD，以对角线AC所在的直线为x轴，对称中心O为原点，建立平面直角坐标系．椅子绕O点沿逆时针方向旋转角度θ后，长方形ABCD转至A1B1C1D1 的位置，这样就可以用旋转角θ（0≤θ≤π）表示出椅子绕点O旋转θ后的位置．其次，把椅脚是否着地用数学形式表示出来．我们知道，当椅脚与地面的竖直距离为零时，椅脚就着地了，而当这个距离大于零时，椅脚不着地．由于椅子在不同的位置是θ的函数，因此，椅脚与地面的竖直距离也是θ的函数．由于椅子有四只脚，因而椅脚与地面的竖直距离有四个，它们都是θ的函数．而由假设(3)可知，椅子在任何位置至少有三只脚同时着地，即这四个函数对于任意的θ，其函数值至少有三个同时为0．因此，只需引入两个距离函数即可．考虑到长方形ABCD是中心对称图形，绕其对称中心 O沿逆时针方向旋转180°后，长方形位置不变，但A,C和B,D对换了．因此，记A、B两脚与地面竖直距离之和为f（θ），C、D两脚与地面竖直距离之和为g（θ），其中θ∈[0，π]，从而将原问题数学化。

数学建模习题及答案课后习题第⼀部分课后习题1.学校共1000名学⽣，235⼈住在A宿舍，333⼈住在B宿舍，432⼈住在C宿舍。

学⽣们要组织⼀个10⼈的委员会，试⽤下列办法分配各宿舍的委员数：（1）按⽐例分配取整数的名额后，剩下的名额按惯例分给⼩数部分较⼤者。

（2）节中的Q值⽅法。

（3）d’Hondt⽅法：将A，B，C各宿舍的⼈数⽤正整数n=1，2，3，…相除，其商数如下表：将所得商数从⼤到⼩取前10个（10为席位数），在数字下标以横线，表中A，B，C⾏有横线的数分别为2，3，5，这就是3个宿舍分配的席位。

你能解释这种⽅法的道理吗。

如果委员会从10⼈增⾄15⼈，⽤以上3种⽅法再分配名额。

将3种⽅法两次分配的结果列表⽐较。

（4）你能提出其他的⽅法吗。

⽤你的⽅法分配上⾯的名额。

2.在超市购物时你注意到⼤包装商品⽐⼩包装商品便宜这种现象了吗。

⽐如洁银⽛膏50g装的每⽀元，120g装的元，⼆者单位重量的价格⽐是：1。

试⽤⽐例⽅法构造模型解释这个现象。

（1）分析商品价格C与商品重量w的关系。

价格由⽣产成本、包装成本和其他成本等决定，这些成本中有的与重量w成正⽐，有的与表⾯积成正⽐，还有与w⽆关的因素。

（2）给出单位重量价格c与w的关系，画出它的简图，说明w越⼤c越⼩，但是随着w的增加c减少的程度变⼩。

解释实际意义是什么。

3.⼀垂钓俱乐部⿎励垂钓者将调上的鱼放⽣，打算按照放⽣的鱼的重量给予奖励，俱乐部只准备了⼀把软尺⽤于测量，请你设计按照测量的长度估计鱼的重量的⽅法。

假定鱼池中只有⼀种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼⾝的最⼤周长）：⾝长（cm）重量76548211627374821389652454（g）胸围（cm）先⽤机理分析建⽴模型，再⽤数据确定参数4.⽤宽w的布条缠绕直径d的圆形管道，要求布条不重叠，问布条与管道轴线的夹⾓应多⼤（如图）。

若知道管道长度，需⽤多长布条（可考虑两端的影响）。

如果管道是其他形状呢。

考试内容分布：1、线性规划2题，有1题需编程；2、非线性规划2题，有1题需编程；3、微分方程1题，需编程；4、差分方程2题，纯计算，不需编程；5、插值2题，拟合1题，纯计算，不需编程；；6、综合1题(4分)，纯计算，不需编程。

一、列出下面线性规划问题的求解模型，并给出matlab计算环境下的程序1.某车间有甲、已两台机床，可用于加工三种工件，假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400,600和500，且已知用两种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。

问怎样分配车床的加工任务，才能即满足加工工件的要求，又使加工费用最低。

（答案见课本P35, 例1）2.有两个煤厂A,B，每月进煤分别不少于60t、100t，它们负责供应三个居民区的用煤任务，这三个居民区每月需用煤分别为45t, 75t, 40t。

A厂离这三个居民区分别为10km, 5km, 6km，B厂离这三个居民区分别为4km, 8km, 15km，问这两煤厂如何分配供煤，才能使总运输量最小？(1)问题分析设A煤场向这三个居民区供煤分别为x1,x2,x3;B煤场向这三个居民区供煤分别为x4,x5,x6，则min f=10*x1+5*x2+6*x3+4*x4+8*x5+15*x6，再根据题目约束条件来进行解题。

(2) 模型的求解>> f=[10 5 6 4 8 15];>> A=[-1 -1 -1 0 0 00 0 0 -1 -1 -1-1 0 0 -1 0 00 -1 0 0 -1 00 0 -1 0 0 -1];>> b=[-60;-100;-45;-75;-40];>> Aeq=[];>> beq=[];>> vlb=zeros(6,1);>> vub=[];>> [x,fval]=linprog(f,A,b,Aeq,beq,vlb,vub)Optimization terminated.(3)结果分析x =0.0000 20.0000 40.0000 45.0000 55.0000 0.0000fval = 960.0000即A 煤场分别向三个居民区供煤0t,20t,40t ；B 煤场分别向三个居民区供煤45t,55t,0t 可在满足条件下使得总运输量最小。