改进阻力系数法(水闸渗流)

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用1. 引言1.1 背景介绍水闸在水利工程中扮演着重要的角色，控制着水流的流动和水位的变化。

而水闸的设计与维护中，对水闸周围的渗流情况进行准确的计算和分析至关重要。

传统的计算方法往往存在一定的局限性，无法完全满足工程实际需求。

研究改进的计算方法对水闸渗流的准确性和效率性具有重要意义。

改进阻力系数法是一种基于实际工程经验的计算方法，通过考虑水流在渗流过程中受到的各种阻力的影响，对水闸渗流进行计算分析。

与传统方法相比，改进阻力系数法在考虑更多因素的基础上，能够更加准确地预测水流的渗漏情况。

Autobank有限元分析是一种基于数值模拟的技术，通过建立数学模型对水流在水闸周围的渗流过程进行模拟。

该方法能够考虑更多复杂的因素，并且在计算精度和计算效率上都有较大优势。

改进阻力系数法和Autobank有限元分析在水闸渗流计算中的应用具有重要意义，有助于提高水利工程设计的准确性和效率性。

1.2 研究意义水资源是人类生存和发展的重要基础资源，水闸在水资源管理领域发挥着至关重要的作用。

在水闸设计和维护过程中，水渗流计算是一项关键的技术。

而改进阻力系数法和Autobank有限元分析作为两种常用的计算方法，在水闸渗流计算中具有重要的应用价值。

研究意义主要体现在以下几个方面：通过对改进阻力系数法和Autobank有限元分析方法在水闸渗流计算中的应用进行深入研究和分析，可以为水资源管理和工程设计提供更为准确和可靠的计算结果，从而提高水闸的设计和维护水平。

通过比较改进阻力系数法和Autobank有限元分析方法的优劣势，可以为工程技术人员选择合适的计算方法提供参考，同时也可以为改进和完善这两种方法提供指导和借鉴。

对改进阻力系数法和Autobank有限元分析方法在水闸渗流计算中的应用进行研究，有助于推动水资源管理技术的进步，为我国水资源的可持续利用和保护提供技术支持和保障。

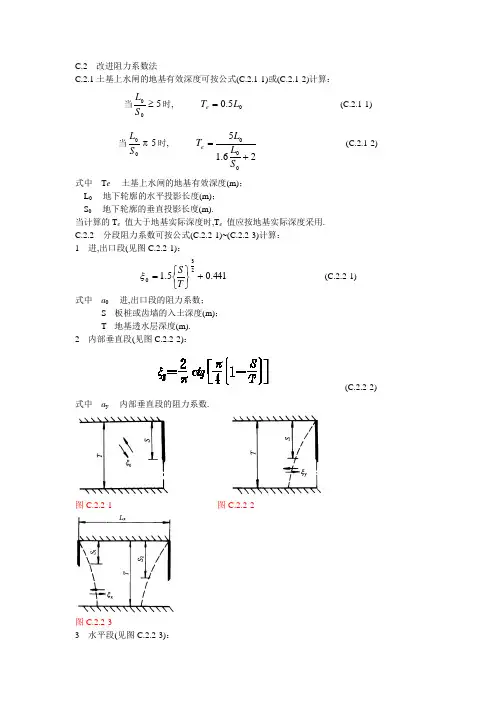
C.2 改进阻力系数法C.2.1土基上水闸的地基有效深度可按公式(C.2.1-1)或(C.2.1-2)计算： 当500≥S L 时, 05.0L T e = (C.2.1-1) 当500 S L 时, 26.15000+=S L L T e (C.2.1-2) 式中 T e ---土基上水闸的地基有效深度(m)；L 0 ---地下轮廓的水平投影长度(m)；S 0 ---地下轮廓的垂直投影长度(m).当计算的T e 值大于地基实际深度时,T e 值应按地基实际深度采用.C.2.2 分段阻力系数可按公式(C.2.2-1)~(C.2.2-3)计算：1 进,出口段(见图C.2.2-1)：441.05.1230+⎭⎬⎫⎩⎨⎧=T S ξ (C.2.2-1)式中 a 0 ---进,出口段的阻力系数；S---板桩或齿墙的入土深度(m)；T---地基透水层深度(m).2 内部垂直段(见图C.2.2-2)：(C.2.2-2)式中 a y ---内部垂直段的阻力系数. 图C.2.2-1 图C.2.2-2图C.2.2-33 水平段(见图C.2.2-3)：()TS S L x x 217.0+-=ξ (C.2.2-3) 式中 a x ---水平段的阻力系数；L x ---水平段长度(m)；S 1 ,S 2 ---进,出口段板桩或齿墙的入土深度(m).C.2.3 各分段水头损失值可按公式(C.2.3)计算：∑=∆=n i ii i H h 1ξξ (C.2.3) 式中 h χ ---各分段水头损失值(m)；a i ---各分段的阻力系数；n---总分段数.以直线连接各分段计算点的水头值,即得渗透压力的分布图形.C.2.4 进,出口段水头损失值和渗透压力分布图形可按下列方法进行局部修正： 1 进,出口段修正后的水头损失值可按公式(C.2.4-1)~(C.2.4-3)计算(见图C.2.4-1)：0''0h h β= (C.2.4-1)∑==ni i h h 10 (C.2.4-2)⎭⎬⎫⎩⎨⎧+⎥⎥⎦⎤⎢⎢⎣⎡+⎭⎬⎫⎩⎨⎧-=059.0212121.1'2''T S T T β (C.2.4-3) 图C.2.4-1式中 h '0 ---进,出口段修正后的水头损失值(m)；h 0 ---进,出口段水头损失值(m)；β'---阻力修正系数,当计算的β′≥1.0时,采用β′＝1.0；S ' ---底板埋深与板桩入土深度之和(m)；T '---板桩另一侧地基透水层深度(m).2 修正后水头损失的减小值,可按公式(C.2.4-4)计算：()0'1h h β-=∆ (C.2.4-4)式中 Δh---修正后水头损失的减小值(m).3 水力坡降呈急变形式的长度可按公式(C.2.4-5)计算：T I HhL N i X ∑=∆∆=ξ1'(C.2.4-5)式中 L'x ---水力坡降呈急变形式的长度(m).4 出口段渗透压力分布图形可按下列方法进行修正如图C.2.4-2所示,图C.2.4-2中的QP ′为原有水力坡降线,根据公式(C.2.4-3)和(C.2.4-4)和公式(C.2.4-5)计算的⑽h 和L'x 值,分别定出P 点和O 点,连接QOP,即为修正后的水力坡降线.图C.2.4-2C.2.5 进,出口段齿墙不规则部位可按下列方法进行修正(见图C.2.5-1和图C.2.5-2)： 图C.2.5-1 图C.2.5-21 当h x ≥Δh 时,可按公式(C.2.5-1)进行修正：h h h x x ∆+=' (C.2.5-1)式中 h x ---水平段的水头损失值(m)；h'x ---修正后的水平段水头损失值(m).2 当h x ＜Δh 时,可按下列两种情况分别进行修正：1)若h x +h y ≥Δh,可按公式(C.2.5-2)和公式(C.2.5-3)进行修正：x x h h 2'= (C.2.5-2)h h h h y y -∆+='(C.2.5-3)式中 h y ---内部垂直段的水头损失失值(m)；h'y ---修正后的内部垂直段水头损失值(m).2)若h x +h y ＜Δh,可按公式(C.2.5-2),公式(C.2.5-4)和公式(C.2.5-5)进行修正：y y h h 2'= (C.2.5-4)()y x cd cd h h h h h +-∆+=' (C.2.5-5)式中 h cd ---图C.2.5-1和图C.2.5-2中CD 段的水头损失值(m)；h'cd ---修正后的C Ρ段水头损失值(m).以直线连接修正后的各分段计算点的水头值,即得修正后的渗透压力分布图形.C.2.6 出口段渗流坡降值可按公式(C.2.6)计算：''0Sh J = (C.2.6) 式中 J---出口段渗流坡降值.。

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用随着水利工程建设的不断推进，水文水资源工作也在不断发展，为了更好地保护水资源和有效利用水资源，人们对水文水资源的测算、分析和预测的需求也不断增加。

水闸渗流计算是水利工程建设和管理中的一个重要环节，合理准确的渗流计算结果对于水闸的设计与管理具有关键性的作用。

传统的水闸渗流计算方法采用阻力系数法，该方法基于经验公式，计算简便，但由于忽略了细部结构的影响以及对潜水、厚地层的处理不够合理，导致了计算结果的精度较低。

为了克服传统阻力系数法的不足，有限元分析技术被引入水闸渗流计算中，其精度和可靠性得到了大幅提升，从而为水闸渗流计算提供了新的思路与方法。

改进阻力系数法是传统阻力系数法的一种改进版本，它考虑了土体细部结构的影响，并根据地层的不同特性给出了不同的阻力系数，因而提高了计算结果的准确性。

而有限元分析则采用数学模型和计算机模拟，能够准确地描述水流的变化情况，同时考虑了土体单元的不均匀性和弹性模量的影响，从而提高了计算结果的精度。

改进阻力系数法与有限元分析技术的结合应用已经在水闸渗流计算中得到了广泛的应用。

以混凝土重力坝为例，传统阻力系数法对于较为简单的坝体结构可以得到满意的结果，但对于细部结构复杂的坝体则无法满足精度要求。

而改进阻力系数法可以通过对不同结构和不同区域的阻力系数进行合理设定，得到更加准确的渗流计算结果。

有限元分析技术则可以在考虑土体细部结构和非均质性的基础上，通过建立适当的数学模型，对不同条件下的水流进行详细模拟，从而提高了计算结果的精度。

在实际工程中，对于水闸渗流计算管理人员必须根据实际情况合理选用改进阻力系数法或有限元分析技术进行渗流计算。

对于较为简单的水闸渗流计算问题，改进阻力系数法可以提供较为准确的计算结果，计算简便，符合实际的需要。

而对于较为复杂的水闸渗流计算问题，有限元分析技术可以提供更加精确的计算结果，但计算步骤相对较为复杂和繁琐，需要具备一定的专业知识和计算机模拟能力。

4.2.3.2 闸基渗流计算1、渗流计算的目的和计算方法计算闸底板各点渗透压力，验算地基土在初步拟定的底下轮廓线下的渗透稳定性。

计算方法有直线的比例法、流网法和改进阻力系数法，由于改进阻力系数法计算结果精确，因此采用此法进行渗流计算。

1）用改进阻力系数法计算闸基渗流 （1）地基有效深度的计算根据S L 与5比较得出，0L 为地下轮廓线水平投影的长度，为33m ；0S 为地下轮廓线垂直投影的长度，为7m 。

则571.473300<==S L ，所以地基有效深度m S L L T e 29.1726.150=+=。

（2）分段阻力系数的计算为了计算的简便，特将地下轮廓线进行简化处理，通过底下轮廓线的各角点和尖端将渗流区域分成8个典型段，如图4.2.3.2-1所示。

其中Ⅰ、Ⅷ段为进口段和出口段，用公式441.0)(5.1230+=T Sζ计算阻力系数，Ⅱ、Ⅳ、Ⅴ、Ⅶ段为内部垂直段，用公式)1(4ln 2TSctgy -=ππζ计算阻力系数，Ⅲ、Ⅵ段为水平段，用公式TS S L x )(7.021+-=ζ计算阻力系数。

其中21,,S S S 为板桩的入土深度，各典型段的水头损失按公式∑=∆=ni iii Hh 1ξξ计算，对于进出口段的阻力系数修正，按公式0''0h h β=，式中)059.0(2)(12121.1'2''+⎥⎦⎤⎢⎣⎡+-=T S T T β，0')1(h h β-=∆计算，其中'0h 为进出口段修正后的水头损失值，0h 为进出口段损失值，'β为阻力修正系数，当0.1'≥β时，取0.1'=β，'S 为底板埋深与板桩入图深度之和，'T 为板桩另一侧地基透水层深度。

其计算见表2.3.2-1：图4.2.3.2-1 渗流区域分段图 （单位：m ）表4.3.2.2-1 各段渗透压力水头损失 单位：（m ）表4.3.2.2-2 进出口段的阻力系数修正表 单位：（m ）Ⅷ（3）计算各角点的渗透压力值用上表所计算的水头损失进行计算，总的水头差分别为4.0m 和4.5m ，各段后角点渗压水头=该段前点渗压水头—此段的水头损失，结果列入表4.3.2.2-3：表4.3.2.2-3 闸基各角点渗透压力值 单位：（m ）（4）算渗流逸出坡降①出口段的逸出坡降分别为14.02.6859.0''===S h J 和16.02.6966.0''===Sh J ，由《水闸设计规范》可查得[]5.0=J ，则都小于地基土出口段允许渗流坡降值[]5.0=J ，满足要求，不会发生渗透变形。

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用【摘要】本文研究了改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用，并结合两种方法进行了案例分析及结果讨论。

研究发现，改进阻力系数法在水闸渗流计算中具有较高的准确性和可靠性，Autobank有限元分析则可以更全面地考虑水流的复杂性。

结合两者可提高水闸渗流计算的精度和效率。

未来的研究应该进一步探讨两种方法的优势及在不同情境下的适用性，为水利工程设计和管理提供更多参考依据。

本文总结了改进阻力系数法与Autobank有限元分析的结合优势，展望了未来的研究方向，并对本研究的意义和贡献做了总结。

【关键词】水闸、渗流计算、改进阻力系数法、Autobank有限元分析、结合应用、案例分析、结果讨论、结合优势、未来研究、总结。

1. 引言1.1 研究背景水闸是用于调节水位和流量的重要设施，对于水资源管理和防洪工程具有重要意义。

在水闸的设计和运行过程中，需要对其渗流进行准确的计算和分析。

传统的计算方法往往存在一定的局限性，因此需要引入新的方法来提高计算的精准度和效率。

改进阻力系数法是一种基于水力学原理的计算方法，通过考虑水流的阻力特性来计算水闸的渗流。

该方法能够较好地模拟水流在水闸结构中的流动情况，对于提高计算准确度具有一定的优势。

Autobank有限元分析是一种计算机辅助的数值分析方法，能够对复杂的水流场进行精确的模拟和分析。

通过将水闸结构建模并进行数值计算，可以得到更加准确的渗流结果。

综合考虑改进阻力系数法和Autobank有限元分析的优势，结合两种方法来进行水闸渗流计算将能够提高计算的精准度和效率，为水资源管理和防洪工程提供更为可靠的技1.2 研究目的研究的目的是通过对改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用进行深入研究，探索其在水文工程领域的优势和潜力。

具体包括通过比较两种方法在水闸渗流计算中的精度、效率和适用范围，评估其在实际工程中的应用价值，为水闸渗流计算提供更加准确、快速和可靠的方法与工具。

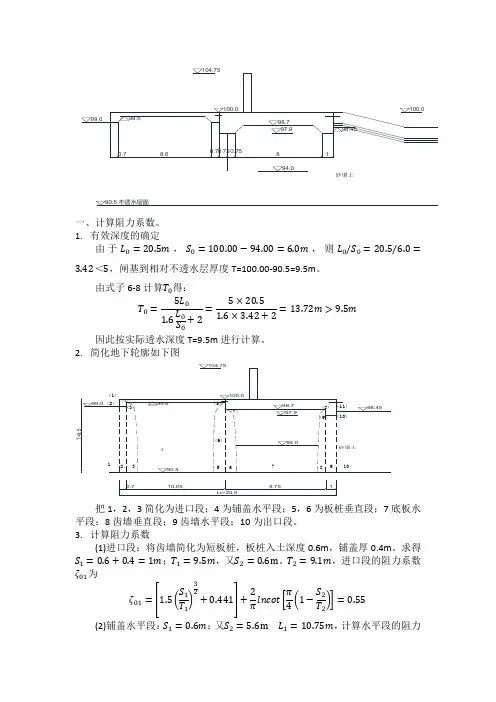
90.5 不透水层面一、计算阻力系数。

1.有效深度的确定由于L0=20.5m，S0=100.00−94.00=6.0m，则L0/S0=20.5/6.0= 3.42＜5，闸基到相对不透水层厚度T=100.00-90.5=9.5m。

由式子6-8计算T0得：T0=5L01.6L0S0+2=5×20.51.6×3.42+2=13.72m>9.5m因此按实际透水深度T=9.5m进行计算。

2.简化地下轮廓如下图把1，2，3简化为进口段；4为铺盖水平段；5，6为板桩垂直段；7底板水平段；8齿墙垂直段；9齿墙水平段；10为出口段。

3.计算阻力系数(1)进口段：将齿墙简化为短板桩，板桩入土深度0.6m，铺盖厚0.4m。

求得S1=0.6+0.4=1m；T1=9.5m，又S2=0.6m。

T2=9.1m，进口段的阻力系数ζ01为ζ01=[1.5(S1T1)32+0.441]+2πlncot[π4(1−S2T2)]=0.55(2)铺盖水平段：S1=0.6m；又S2=5.6m L1=10.75m，计算水平段的阻力系数ζx1为ζx1=L 1−0.7(S 1+S 2)T=0.67(3)板桩垂直段：左侧S 1=5.6m ；T 1=9.1m ，S 2=4.7m ；T 2=8.2m ，板桩垂直段阻力系数ζy1为ζy1=2πlncot [π4(1−S 1T 1)]+2πlncot [π4(1−S 2T 2)]=1.41 (4)底板水平段：S 1=4.7m ；又S 2=0.8m L 2=8.75m T =8.2m ，计算水平段的阻力系数ζx2为ζx2=L 2−0.7(S 1+S 2)T=0.60(5)齿墙垂直段：左侧S =0.8m ；T =8.2m ，板桩垂直段阻力系数ζy2为 ζy1=2πlncot [π4(1−ST)]=0.10 (6)齿墙水平段：S 1=S 2=0； L 3=1.0m T =7.4m ，计算水平段的阻力系数ζx3为ζx3=L 3−0.7(S 1+S 2)T=0.14(7)出口段：S =0.55m ，T =7.95m ，阻力系数ζ02为ζ02=1.5（S T）3/2+0.441=0.47二、渗透压力的计算1.各个分段渗透压水头损失值由式（6-7）ℎi =ζi ΔH∑ζin 1，其ΔH =4.75m ，∑ζi 71=0.55+0.67+1.41+0.60+0.10+0.14+0.47=3.94。

水闸渗流计算方法的探讨摘要：运用ANSYS软件有限单元法和改进阻力系数法对水闸闸基渗流进行计算，通过对比，证明了ANSYS软件在计算渗流场的可行性，它完善的求解器和前、后处理能力以及可视化的模型建立给设计提供了一个计算渗流场数值的有效方法。

关键词：有限单元法；改进阻力系数法；ANSYS；渗流；闸基引言:上游的水压力是水工建筑物要承受的主要荷载之一，而且地基和混凝土也不是完全不透水的材料，在水头的长期作用下，水即将会通过地基和坝体向下游流去，因此，在地基内和闸坝体内有一个渗流场的存在。

渗流分析给合理的选择渗流控制方法和对闸坝工程的安全可靠性的评价提供一定的根据，水闸闸基渗流为剖面的平面渗流运动，既有水平的分速度，同时也有垂直的分速度，可以近似的看做为二维流。

闸基渗流经常用到的计算方法包括有限元法、流网法、直线比例法（渗径系数法）、电网络法［1，2］和改进阻力系数法。

改进阻力系数法［3，4］为分段法，把地基渗流沿着地下轮廓线划分成水平的和垂直的几个段，进行单独的解决。

把各分段的阻力系数计算出来，再进一步把渗透流速、渗透压力、渗透坡降及渗流量求出。

这是一种近似的流体力学的解法，有较高的计算精度，对计算复杂的地下轮廓的渗流量也同样有很大的的现实意义，在国内外已经得到广泛的运用，水闸设计规范计算闸基渗流就是运用了这种方法。

把求解的渗流区域划分为有限个互相联系的子区域的方法就是有限单元法，它用子区域内连续的分区近似水头函数来代替待定的水头函数。

随着计算机的发展，其应用于数值计算的有限元法也得到了快速的发展，可以很好的把条件复杂的渗流问题模拟出来。

现在，有很多有限元软件都可以用来计算渗流，包括GEO－SLOPE、MARC、SEEPAGE、ANSYS、ADINA、FLAC、ABQUS等。

本文主要研究运用ANSYS软件有限单元法和改进阻力系数法对水闸闸基渗流进行计算，通过对比，证明了ANSYS软件在计算渗流场的可行性，它完善的求解器和前、后处理能力以及可视化的模型建立给设计提供了一个计算渗流场数值的有效方法。

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用水闸是一种常见的水利工程设施，用于控制水流量和水位，以确保水利工程的正常运行和安全。

在水闸工程设计和运行过程中，对水闸渗流进行准确的计算和分析是至关重要的。

目前在水闸渗流计算中，常用的方法包括阻力系数法和有限元分析，它们分别具有一定的优势和局限性。

为了提高水闸渗流计算的精度和效率，本文将探讨改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用，以期为水闸工程的设计和运行提供更科学、更有效的方法。

一、阻力系数法在水闸渗流计算中的应用阻力系数法是一种简单、经济、实用的水流计算方法，适用于各种类型的水流情况，包括水闸渗流。

该方法通过测定水流与固定物体表面的阻力关系来计算水流速度和流量，通常采用阿奇森公式等相关公式进行计算。

阻力系数法在水闸渗流计算中的应用主要包括以下几个步骤：1. 确定水闸渗流的边界条件，包括输入流量、出口水位、水闸结构的几何形状和材料特性等。

2. 通过实验或经验确定水流与水闸表面的阻力关系，包括渗透系数、摩擦系数等。

3. 根据所得的阻力关系和水流边界条件，利用相关公式计算水闸渗流的速度和流量。

阻力系数法的优点在于简单易行，对水流边界条件的要求较低，适用于水流速度较低、水流性质较稳定的情况。

阻力系数法也存在一些局限性，主要包括对水流非线性、流动边界复杂等情况的处理能力较弱。

Autobank有限元分析是一种基于有限元理论的数值计算方法，适用于复杂流动情况和复杂边界条件下的水闸渗流计算。

该方法将水流场分割为有限个小单元，通过离散化和数值求解得到水流场的速度、压力等相关参数。

Autobank有限元分析在水闸渗流计算中的应用主要包括以下几个步骤：2. 将水流场离散化为有限个单元，建立有限元网格。

3. 通过数值求解方法，计算水流场的速度、压力等相关参数。

Autobank有限元分析的优点在于能够适应复杂流动情况和复杂边界条件，计算精度高，结果可靠。

例 7-3 用改进阻力系数法进行闸基的渗流计算。
用[例 7 - 3 ]的有关资料：挡水时，假设水闸最大水头差 H 5.0m ，及闸底板顶高程
50.0m ；根据地基钻探报告：闸基土质在高程 50.0 ~ 40.5m 之间为沙壤土，渗透系数
K 1 2.4 10 4 cm / s ；高程 40.50m 以下为粘壤土，渗透系数 K 2 2.5 10 6 cm / s 。因 k 2 2.5 10 6 1.04 10 2 ，故认为高程 40.5m 以下的粘壤土是不透水的。 4 k 1 2.4 10
地 基 为 砂 壤 土 ， 闸 板 顺 水 流 方 向 长 度 可 取 ( 2.0 3.5) 5.0m ， 现 取 底 板 长 度 为
2.5 5.0 12.5m 。底板上、下游端均设齿墙、齿墙底宽分别为 1.5m 及 1.0m 。
铺盖：选用混凝土铺盖。长度参考现有工程资料，采用 10.0m ；厚度为 0.4m 。 铺盖上、下游端设齿墙，齿墙底宽 0.6m ，齿深 0.5m 。 板桩：采用钢筋混凝土板桩、粘壤土表层距底板齿墙底为 48.4 - 40.5 7.90( m) ，采用 “悬挂式”位于上游齿墙底中部，距齿墙上、下游端各 0.75m ，入土深度为 4.4m （未计入 桩顶伸进齿墙内的长度 0.2m 和桩尖部分的长度 0.4m ） 。 排水设施：为减小作用于闸底板上的渗透压力，降排水尽量靠上游布置，将其置于底板 之后的护坦下面，而首部紧接底板下游齿墙。 按上述布置，可绘出用改进阻力系数法计算各渗流要素的计算简图（图见 7 - 22 ） 。
3 / 2
2 0 . 441 In cot 0 . 54

0 .5 1 4 9 .1

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用阻力系数法与Autobank有限元分析是目前水闸渗流计算中常用的两种方法，它们在水工领域中有着广泛的应用。

本文将探讨这两种方法在水闸渗流计算中的应用，并对其进行改进，以提高计算的精度和准确性。

一、阻力系数法在水闸渗流计算中的应用阻力系数法是一种常用的水闸渗流计算方法，其基本原理是利用不同类型的水流构件及其对应的流态阻力系数，通过公式计算出流态阻力，并结合流量、水头等参数，进行水流的计算。

该方法适用范围较广，计算简单、直观，因此在水闸渗流计算中有着较为广泛的应用。

阻力系数法在实际应用中存在一些问题，例如在计算过程中需要对水流的流态进行大量的假设和简化，导致计算结果与实际情况存在一定的误差；而且在水流构件类型复杂或者流态变化较大的情况下，阻力系数法的计算精度也会受到较大的限制。

需要对阻力系数法进行改进，以满足水闸渗流计算的精度要求。

Autobank有限元分析是一种利用有限元方法对水力学问题进行数值计算和分析的技术。

相比传统的计算方法，Autobank有限元分析具有更强的适用性和计算精度，能够较好地模拟水流在水闸渗流过程中的复杂流态和水流构件的变形变化，因此在水闸渗流计算中有着较大的潜力。

Autobank有限元分析也存在一些问题，例如在计算过程中需要大量的计算资源，计算时间较长，且对计算模型的建立和参数选择要求较高，对用户的专业水平和技术要求也比较高。

需要对Autobank有限元分析进行改进，以提高其计算效率和便利性，使其能够更好地应用于水闸渗流计算中。

1. 对阻力系数法进行改进，可以尝试引入更加精确的流态阻力系数计算方法，结合实际情况对水流构件类型进行更加详细的分类和计算，以提高计算精度和准确性；2. 对Autobank有限元分析进行改进，可以尝试优化计算算法和计算模型，提高计算效率和准确性，使其能够更好地应用于水闸渗流计算中；3. 在改进过程中，可以结合实际案例进行验证和优化，以确保改进后的方法在水闸渗流计算中能够满足工程实际需求，提高水闸渗流计算的精度和准确性。

改进阻力系数法在水闸渗流计算中的运用张亚;李乃回;代晴【摘要】闸基渗流是水闸设计的一个重要内容.对于闸基的防渗设计,《水闸设计规范》(SL265-2001)推荐改进阻力系数法或流网法进行防渗计算.文章主要阐述了改进阻力系数法在丰县黄楼闸除险加固工程中闸基渗流计算中的运用,通过阐述改进阻力系数法的基本原理、地下轮廓线的布置并进行相关的渗流计算,最后得出结论,该设计满足规范要求.【期刊名称】《治淮》【年(卷),期】2016(000)010【总页数】4页(P21-24)【关键词】水闸;渗流系数;渗流坡降;改进阻力系数法【作者】张亚;李乃回;代晴【作者单位】徐州市水利建筑设计研究院徐州 221000;徐州市水利建筑设计研究院徐州 221000;徐州市水利建筑设计研究院徐州 221000【正文语种】中文复新河是南四湖湖西一条流域性河道，发源于安徽省砀山县玄帝庙村西，沿废黄河北堤东流至董庄东北流入丰县，纵贯丰县境内，下游经山东省鱼台县于西姚村流入昭阳湖，丰县境内长度53.9km，流域面积1098km2。

复新河是纵贯丰县南北的一条主要排涝河道，主要有太行堤河、苏北堤河、西支河、子午河、苗城河等14条支流。

1973年淮委划定复新河流域总面积1812km2，其中安徽境内170 km2，山东境内459km2，江苏境内丰县1098km2，沛县85km2。

复新河分三个梯级，从下至上分别为李楼闸站、丰城闸站及黄楼闸。

黄楼闸位于复新河上游，宋楼镇黄楼村北，承担上游116.8km2排涝和2万亩农田灌溉任务，是复新河第三级梯级控制工程，具有防洪、排涝、蓄水、灌溉等多种功能。

根据《水闸设计规范》（SL265-2001）、《水利水电工程等级划分及洪水标准》（SL252-2000）以及《防洪标准》（GB50201-2014），确定黄楼闸设计排涝标准为10年一遇，防洪标准为20年一遇。

黄楼闸为中型涵闸，工程等别为Ⅲ等，主要建筑物的级别为3级，次要建筑物为4级，临时建筑物为5级。

你知道水闸设计的渗流计算方法吗渗流是指水在岩土空隙之间的运动，在水利工程、石油化工、环境保护等方面都有广泛的应用。

在水闸设计与工作中加入渗流理论，主要还是为计算水闸中水流动向、水的渗透过程以及渗透引起的水闸结构变化。

对水闸渗流问题进行研究有助于合理的评价水坝安全指标，提升水闸稳定性，对社会的稳定与发展有重要的意义。

1．渗流对水闸的影响水闸对于调节水坝水流有着重要的作用，而渗流又对水闸工作有重要的影响。

许多水闸由于设备不完善，技术不完备，渗流问题十分突出，需要人们进行深入的研究和探讨。

1.1影响水闸挡水和泄洪渗流是河流、湖泊、水井集水廊道、水库、水坝等水体周围常见的现象，尤其是水闸周围，由于长时间处于工作或建设阶段，大部分会使水体周边土质松软，水体发生渗流现象的可能性更大。

有时水闸处于关闭状态进行挡水，但由于周边土地经常被水体浸泡，再加上水闸建设和日常工作活动，造成附近土质松软，加剧了水的渗透，影响挡水效果。

泄洪时也是一样，由于水在岩土缝隙之间的大量运动，容易使周边土壤储存大量水分，影响开闸泄洪的放水效果。

1.2渗流在闸基不均匀沉降中的作用实际上，我国大部分大坝都有不同程度的渗水现象，很大程度上是受水的渗流作用影响。

水的渗流现象会使大量水分渗入大坝内部，造成大坝身体的湿陷，而每当雨季来临，上游来水猛增，泄洪量骤然增大，水位提升，渗流会加剧对大坝的不利影响。

同时，渗流所产生的扬压力会冲击水闸工作质量，极有可能会造成水闸抗滑稳定性下降。

而且渗流带来的影响不止在抗滑稳定性方面，对主体大坝的应力分布也有重要影响。

1.3对抗滑稳定性的影响抗滑稳定性是衡量一个大坝安全与否的重要指标，这一指标的提升也就意味着水闸结构的稳定性的提升。

闸基滑动需要以连续的软弱面作为支撑，下游有足够的临空面供其衔接，很多时候由于水分渗流现象严重，岩土含水量提升，土质变松软，并且会造成岩土之间空隙增大，摩擦力减小，产生大面积的临空面，加剧闸基的滑动。

改进阻力系数法改进阻力系数法是在阻力系数法的基础上发展起来的，这两种方法的基本原理非常相似。

主要区别是改进阻力系数法的渗流区划分比阻力系数法多，在进出口局部修正方面考虑得更详细些。

因此，改进阻力系数是一种精度较高的近似计算方法。

1．基本原理如下图1所示，有一简单的矩形断面渗流区，其长度为L ，透水土层厚度为T ，两断面间的测压管水位差为h 。

根据达西定律，通过该渗流区的单宽渗流量q 为TL hkq = （1）或k qT L h =（2）令L ／T ＝ξ，则得k q h /ξ= （3）式中ξ称为阻力系数，ξ值仅和渗流区的几何形状有关，它是渗流边界条件的函数。

图1矩形渗流区图 图2 改进阻力系数法计算对于比较复杂的地下轮廓，需要把整个渗流区大致按等势线位置分成若干个典型渗流段，每个典型渗流段都可利用解析法或试验法求得阻力系数ξ，其计算公式见表1。

如图2所示的简化地下轮廓，可由2、3、4、5、6、7、8、9、10点引出等势线，将渗流区划分成10个典型流段，并按表1的公式计算出各段的ξi 。

再由式 (6) 得到任一典型流段的水头损失h i 。

对于不同的典型段，ξ值是不同的，而根据水流的连续原理，各段的单宽渗流量应该相同。

所以，各段的q ／K 值相同，而总水头H 应为各段水头损失的总和，于是得kq h i /ξ= (4)∑∑====mi imi i k q h H 11ξ (5) 将式(5)代人式(4）得各段的水头损失为∑==mi iii Hh 1ξξ (6)表1 典型流段的阻力系数求出各段的水头损失后，再由出口处向上游方向依次叠加，即得各段分界点的渗压水头。

两点之间的渗透压强可近似地认为呈直线分布。

进出口附近各点的渗透压强，有时需要修正。

如要计算q ，可按式（4）进行。

2．计算步骤（1）确定地基计算深度。

上述计算方法对地基相对不透水层较浅时可直接应用，但在相对不透水层较深时，须用有效深度T e 作为计算深度T c 。

基于改进阻力系数法的大沙河某拦河水闸渗流分析研究◎ 王朝1 纪凤杰1 郭连峰2 刘攀1 周星岑11.徐州市水利建筑设计研究院有限公司；2.盐城市水利勘测设计研究院有限公司摘 要：本文以黄河故道大沙河夹河闸扩改建工程的水闸渗流稳定计算为研究对象，深入分析改进阻力系数法计算结果影响因素以及在水闸稳定分析计算中的应用情况，所得结论如下：1）从计算机理以及案例计算均表明阻力系数的大小主要取决于渗流区域的几何条件，尤其计算段的长度，且水头损失与阻力系数之间呈现正相关；2）通过采用修正系数法对夹河闸进行渗流分析结果表明计算各段渗透坡降最大出现在出口段，平均渗透坡降为0.585，水闸抗渗稳定满足规范要求。

本文研究内容对进一步优化改进阻力系数法以及水闸渗流稳定计算均具有借鉴意义。

关键词：改进阻力系数法；渗流分析；大沙河；拦河水闸1. 前言水闸作为水利工程中应用十分广泛的一种水工建筑物形式，广泛应用于我国各类河道中，在我国灌溉、生态景观、河道治理等方面有着不可或缺的作用[1]。

在水闸设计建设以及运行过程中，最为突出的问题为渗流稳定分析问题，对于水闸等小型水工建筑物而言，渗流控制不当极易出现渗流破坏造成人民群众生命财产损失[2]。

针对水闸设计工作中的渗流稳定计算相关问题，常采用的方法包括：改进阻力系数法、有限元法、相应面法[3]、直线比例法等方法。

其中改进阻力系数法为一种分段方法，以近似流体力学的解法将计算范围进行分段计算，具有计算精度较高且能适应复杂地下轮廓[4]。

众多专家学者[5，6]对改进阻力系数法进行了丰富且深入的研究，尤其对于其应用场景以及应用效果等方面，但对于阻力系数的影响因素等并未进行深入研究。

基于此，为进一步明确阻力系数影响因素，本文以实际工程计算为对象对改进阻力系数法在水闸稳定分析中的应用情况进入深入研究。

2. 工程概况2.1工程简介夹河闸是大沙河上的一座重要控制工程，位于大沙河镇东北侧，其主要作用是蓄水灌溉、生态景观、负担大沙河上游1658平方公里的防洪除涝任务，同时还起到调蓄当地径流和徐州市境内的东水西调任务，形成河川水库，解决丰县高亢地区水资源缺乏的局面。

第８期２０２０年８月广东水利水电ＧＵＡＮＧＤＯＮＧＷＡＴＥＲＲＥＳＯＵＲＣＥＳＡＮＤＨＹＤＲＯＰＯＷＥＲＮｏ８Ａｕｇ．２０２０改进阻力系数法的适用性分析贾　杰（广东珠荣工程设计有限公司，广东广州　５１０６１０）摘　要：改进阻力系数法是规范推荐的一种土基渗流计算的方法。

该文通过ＧｅｏＳｔｕｄｉｏ有限元分析法和改进阻力系数法的对比分析，提出改进阻力系数法的适用范围，避免该方法被误用而导致设计不合理。

根据分析成果，改进阻力系数法适用于简单地层和上部相对强透水层、下部相对弱透水层的双层地层，不应用于上部相对弱透水层、下部相对强透水层的双层地层和复杂地层。

关键词：改进阻力系数法；渗流计算；ＧｅｏＳｔｕｄｉｏ中图分类号：ＴＶ２２３ ６ 文献标识码：Ｂ 文章编号：１００８－０１１２（２０２０）０８－００７６－０７ 收稿日期：２０２０－０５－０８；修回日期：２０２０－０６－０５作者简介：贾杰（１９８８－），男，本科，工程师，主要从事水利水电工程水工结构设计工作。

１　概况改进阻力系数法是《水闸设计规范》（ＳＬ２６５—２０１６）［１］（下文简称“规范”）推荐的土基水闸基底渗流计算的方法，同时广泛应用于泵站、防洪墙等水工建筑物基底的渗流计算，该方法可方便的计算出建筑物基底各个位置的渗透压力、渗透比降等。

计算闸坝地基渗流常用的方法有柯斯拉的独立变数法、巴甫洛夫斯基的分段法、努麦罗夫的渐近线法以及丘加也夫的阻力系数法，改进阻力系数法是沿用阻力系数概念并各取其优点总结分析提出的一种方法［２］。

本文旨在利用ＧｅｏＳｔｕｄｉｏ有限元分析法（下文简称“有限元法”）验证改进阻力系数法的合理性，通过对比分析两种计算方法在简单地层、双层地层以及复杂地层等条件下的计算成果，提出改进阻力系数法的适用范围，以便在中小型水利工程设计过程中尽量减少对改进阻力系数法的误用。

２　计算方法１）改进阻力系数法根据规范６ ０ ２，土基上水闸基底渗透压力计算可采用改进阻力系数法或流网法；复杂土质地基上的重要水闸，应采用数值计算方法［１］；根据《水工设计手册（第２版）第７卷泄水与过坝建筑物》，闸基渗流计算可求解出渗流区域内的渗透压力、渗透坡降、渗透流速及渗流量，一般用改进阻力系数法进行。

改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用随着科技的不断发展，水利工程领域的水闸设计和分析方法也在不断地更新迭代。

阻力系数法和有限元分析是两种常用的计算方法。

在水闸渗流计算中，这两种方法都有其独特的优势和局限性。

本文将探讨改进阻力系数法与Autobank有限元分析在水闸渗流计算中的应用，分析这两种方法对水闸渗流计算的影响和潜在的发展空间。

阻力系数法是一种经验性的计算方法，适用于水闸渗流计算中的水流速度、水位和流量等参数的估算。

该方法通过测量水流速度和水深，再根据一系列的经验公式和系数来计算水流的状态和特性。

在水闸渗流计算中，改进阻力系数法通常包括以下几个步骤：1.测量水深和水流速度。

通过实地测量或者数值模拟等方法，获取水流的深度和速度数据。

2.选择相应的阻力系数。

根据水流的特性和流态选择合适的阻力系数。

3.计算水流速度和流量。

根据所选的阻力系数和水流的深度、速度等参数，计算水流的速度和流量。

改进阻力系数法的优势在于简单易行，不需要复杂的数学模型和计算工具，适用于一般的水闸渗流计算。

该方法也存在一些局限性，如只能进行局部的计算，难以适用于复杂的水流状态和结构体系。

有限元分析是一种数值计算方法，适用于复杂结构和水流状态的计算。

Autobank是一款专业的水利工程有限元分析软件，广泛应用于水文水利领域的工程设计和分析中。

1.建立水流领域模型。

通过Autobank软件，建立水流领域的有限元模型，包括水闸的结构、水流的状态和边界条件等。

2.进行计算分析。

根据建立的有限元模型，进行水流的数值计算，得出水流速度、水位和水压等参数。

3.结果分析和优化设计。

根据计算结果，对水流状态和水闸结构进行分析和优化设计。

改进阻力系数法和Autobank有限元分析是两种不同的水闸渗流计算方法，各有其独特的优势和局限性。

在实际工程应用中，可以根据具体的工程需求和计算条件选择合适的方法。

在一般的水闸渗流计算中，改进阻力系数法是一种简单易行的计算方法，可快速估算水流的横截面流量和流速等参数，适用于一般的工程设计和分析。

【例2】 用改进阻力系数法计算例1中各渗流要素。

某水闸地下轮廓布置及尺寸如图4-28所示。

混凝土铺盖长10.50m ，底板顺水流方向长10.50m ，板桩入土深度4.4m 。

闸前设计洪水位104.75m ，闸底板堰顶高程100.00m 。

闸基土质在高程100.00～90.50m 之间为砂壤土，渗透系数K 砂=2.4×10-4cm/s ，可视为透水层，90.50m 以下为粘壤土不透水层。

试用渗径系数法验算其防渗长度，并用直线比例法计算闸底板底面所受的渗透压力。

（一）阻力系数的计算 （二）1.有效深度的确定 由于)m (5.205.10100=+=L ，)m (0.600.9400.1000=-=S ，故542.30.65.2000<==S L ，按式（4-19）计算e T)m (5.95.9000.100m 72.13242.36.15.20526.15000=-=>=+⨯⨯=+=T S L L T e故按实际透水层深度m 5.9=T 进行计算。

2.简化地下轮廓 将地下轮廓划分成十个段，如图4-29（a ）所示。

3.计算阻力系数[ 图4-29（b ）]（1）进口段：将齿墙简化为短板桩，板桩入土深度为0.5m ，铺盖厚度为0.4m ，故)(9.04.05.0m S =+=，m T 5.9=。

按表（4-3）计算进口段阻力系数01ξ为48.044.05.99.05.144.05.12/32/301=+⎪⎭⎫⎝⎛⨯=+⎪⎭⎫⎝⎛⨯=T S ξ（2）齿墙水平段：021==S S ，m 6.0=L ，m 6.8=T，按表（4-3）计算齿墙水平段阻力系数1x ξ为()07.06.86.07.0211==+-=T S S L x ξ（3）齿墙垂直段：m 5.0=S，m 1.9=T 。

按表（4-3）计算齿墙垂直段的阻力系数1y ξ为06.01.95.014ctg ln 214ctg ln 21=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=ππππξT S y（4）铺盖水平段：m 5.01=S ，m 6.52=S ，m 75.10=L ，按表（4-3）计算铺盖水平段阻力系数2x ξ为()()71.01.96.55.07.075.107.0212=+⨯-=+-=T S S L x ξ（5）板桩垂直段：m 6.5=S ，m 1.9=T ，根据表（4-3），板桩垂直段阻力系数2y ξ为74.01.96.514ln 22=⎪⎭⎫⎝⎛-=ππξctgy （6）板桩垂直段：m 9.4=S ，m 4.8=T ，根据表（4-3），板桩垂直段阻力系数3y ξ为69.04.89.414ln 23=⎪⎭⎫⎝⎛-=ππξctgy （7）底板水平段：m 9.41=S ，m 5.02=S ，m 75.8=L ，m 4.8=T ，故底板水平段阻力系数3x ξ为()59.04.85.09.47.075.83=+-=x ξ（8）齿墙垂直段：m 5.0=S ，m 4.8=T ，根据表（4-3），则齿墙垂直段的阻力系数4y ξ为06.04.85.014ln 24=⎪⎭⎫⎝⎛-=ππξctgy （9）齿墙水平段：021==S S ，m 0.1=L ，m 9.7=T ，按表（4-3）计算齿墙水平段阻力系数4x ξ为13.09.70.14==x ξ （10）出口段：出口段中m 55.0=S ，m 45.8=T ，按表（4-3）计算其阻力系数02ξ为46.044.045.855.05.12/302=+⎪⎭⎫ ⎝⎛⨯=ξ（二）渗透压力计算1.求各分段的渗压水头损失值 根据式（4-18） ∆H ∑=iii h ξξ，其中m 75.4=∆H ，且 99.346.013.006.059.069.074.071.006.007.048.071=+++++++++=∑=i i ξ（1）进口段)m (57.048.019.148.099.375.411=⨯=⨯=∆H ∑=ξξh（2）齿墙水平段 )m (08.007.019.12=⨯=h （3）齿墙垂直段 )m (07.006.019.13=⨯=h （4）铺盖水平段 )m (85.071.019.14=⨯=h（5）板桩垂直段 )m (88.074.019.15=⨯=h （6）板桩垂直段 )m (82.069.019.16=⨯=h（7）底板水平段 )m (70.059.019.17=⨯=h（8）齿墙垂直段 )m (07.006.019.18=⨯=h （9）齿墙水平段 )m (16.013.019.19=⨯=h （10）出口段 )m (55.046.019.110=⨯=h2. 进出口水头损失值的修正（1）进口处按式（4-20）计算修正系数1β'为⎥⎦⎤⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛'⨯-='059.0212121.121TS T T β66.0059.05.99.025.96.812121.12=⎥⎦⎤⎢⎣⎡+⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛⨯-= 0.166.01<='β，应予修正。