高一数学对数以及对数函数人教版

对数与对数函数一、目标认知学习目标1．掌握对数的概念、常用对数、对数式与指数式互化，对数的运算性质、换底公式与自然对数；2．掌握对数函数的概念、图象和性质.重点对数式与指数式的互化及对数的性质，对数运算的性质与对数知识的应用；理解对数函数的定义，掌握对数函数的图象和性质.难点正确使用对数的运算性质；底数a对图象的影响及对数函数性质的作用.二、知识要点梳理知识点一、对数及其运算我们在学习过程遇到2x=4的问题时，可凭经验得到x=2的解，而一旦出现2x=3时，我们就无法用已学过的知识来解决，从而引入出一种新的运算——对数运算.(一)对数概念：1．如果，那么数b叫做以a为底N的对数，记作：log a N=b.其中a叫做对数的底数，N叫做真数.2．对数恒等式：3．对数具有下列性质：(1)0和负数没有对数，即；(2)1的对数为0，即；(3)底的对数等于1，即.(二)常用对数与自然对数通常将以10为底的对数叫做常用对数，.以e为底的对数叫做自然对数，.(三)对数式与指数式的关系由定义可知:对数就是指数变换而来的，因此对数式与指数式联系密切，且可以互相转化.它们的关系可由下图表示.由此可见a，b，N三个字母在不同的式子中名称可能发生变化.(四)积、商、幂的对数已知(1)；推广：(2)；(3).(五)换底公式同底对数才能运算，底数不同时可考虑进行换底，在a>0，a≠1，M>0的前提下有:(1)令log a M=b，则有a b=M，(a b)n=M n，即，即，即：.(2) ，令log a M=b，则有a b=M，则有即，即，即当然，细心一些的同学会发现(1)可由(2)推出，但在解决某些问题(1)又有它的灵活性.而且由(2)还可以得到一个重要的结论：.知识点二、对数函数1．函数y=log a x(a>0，a≠1)叫做对数函数.2．在同一坐标系内，当a>1时，随a的增大，对数函数的图像愈靠近x轴；当0<a<1时，对数函数的图象随a的增大而远离x轴.(见图1)(1)对数函数y=log a x(a>0，a≠1)的定义域为(0，+∞)，值域为R(2)对数函数y=log a x(a>0，a≠1)的图像过点(1，0)(3)当a>1时，三、规律方法指导容易产生的错误(1)对数式log a N=b中各字母的取值范围(a>0 且a¹1，N>0，bÎR)容易记错.(2)关于对数的运算法则，要注意以下两点：一是利用对数的运算法则时，要注意各个字母的取值范围，即等式左右两边的对数都存在时等式才能成立.如：log2(-3)(-5)=log2(-3)+log2(-5)是不成立的，因为虽然log2(-3)(-5)是存在的，但log2(-3)与log2(-5)是不存在的.二是不能将和、差、积、商、幂的对数与对数的和、差、积、商、幂混淆起来，即下面的等式是错误的：log a(M±N)=log a M±log a N，log a(M·N)=log a M·log a N，log a.(3)解决对数函数y=log a x (a>0且a¹1)的单调性问题时，忽视对底数a的讨论.(4)关于对数式log a N的符号问题，既受a的制约又受N的制约，两种因素交织在一起，应用时经常出错.下面介绍一种简单记忆方法，供同学们学习时参考.以1为分界点，当a，N同侧时，log a N>0；当a，N异侧时，log a N<0.经典例题透析类型一、指数式与对数式互化及其应用1．将下列指数式与对数式互化：(1)；(2)；(3)；(4)；(5)；(6).举一反三：【变式1】求下列各式中x的值：(1)(2)(3)lg100=x (4)类型二、利用对数恒等式化简求值2．求值：举一反三：【变式1】求的值(a，b，c∈R+，且不等于1，N>0)类型三、积、商、幂的对数3．已知lg2=a，lg3=b，用a、b表示下列各式.(1)lg9 (2)lg64 (3)lg6 (4)lg12 (5)lg5 (6) lg15举一反三：【变式1】求值(1)(2)lg2·lg50+(lg5)2 (3)lg25+lg2·lg50+(lg2)2【变式2】已知3a=5b=c，，求c的值.【变式3】设a、b、c为正数，且满足a2+b2=c2.求证：.【变式4】已知：a2+b2=7ab，a>0，b>0. 求证：.类型四、换底公式的运用4．(1)已知log x y=a，用a表示；(2)已知log a x=m，log b x=n，log c x=p，求log abc x.举一反三：【变式1】求值：(1)；(2)；(3).类型五、对数运算法则的应用5．求值(1) log89·log2732(2)(3)(4)(log2125+log425+log85)(log1258+log254+log52)举一反三：【变式1】求值：【变式2】已知：log23=a，log37=b，求：log4256=?类型六、函数的定义域、值域求含有对数函数的复合函数的定义域、值域，其方法与一般函数的定义域、值域的求法类似，但要注意对数函数本身的性质（如定义域、值域及单调性）在解题中的重要作用.6. 求下列函数的定义域：(1)；(2).举一反三：【变式1】求下列函数的定义域.(1) y=(2) y=ln(a x-k·2x)(a>0且a¹1，kÎR).【变式2】函数y=f(2x)的定义域为[-1，1]，求y=f(log2x)的定义域.类型七、函数图象问题7．作出下列函数的图象：(1) y=lgx，y=lg(-x)，y=-lgx；(2) y=lg|x|；(3) y=-1+lgx.类型八、对数函数的单调性及其应用利用函数的单调性可以：①比较大小；②解不等式；③判断单调性；④求单调区间；⑤求值域和最值.要求同学们：一是牢固掌握对数函数的单调性；二是理解和掌握复合函数的单调性规律；三是树立定义域优先的观念.8. 比较下列各组数中的两个值大小：(1)log23.4，log28.5(2)log0.31.8，log0.32.7(3)log a5.1，log a5.9(a>0且a≠1).举一反三：【变式1】（2011 天津理7）已知则（）A．B．C．D．9. 证明函数上是增函数.举一反三：【变式1】已知f(log a x)=(a>0且a≠1)，试判断函数f(x)的单调性.10．求函数y=(-x2+2x+3)的值域和单调区间.类型九、函数的奇偶性11. 判断下列函数的奇偶性.(1)(2).类型十、对数函数性质的综合应用12．已知函数f(x)=lg(ax2+2x+1).(1)若函数f(x)的定义域为R，求实数a的取值范围；(2)若函数f(x)的值域为R，求实数a的取值范围.13．已知函数h(x)=2x(x∈R)，它的反函数记作g(x)，A、B、C三点在函数g(x)的图象上，它们的横坐标分别为a，a+4，a+8(a>1)，记ΔABC的面积为S.(1)求S=f(a)的表达式；(2)求函数f(a)的值域；(3) 判断函数S=f(a)的单调性，并予以证明；(4)若S>2，求a的取值范围.学习成果测评基础达标一、选择题1.下列说法中错误的是( )A.零和负数没有对数B.任何一个指数式都可化为对数式C.以10为底的对数叫做常用对数D.以e为底的对数叫做自然对数2.有以下四个结论：①lg(lg10)=0；②ln(lne)=0；③若10=lgx，则x=10；④若e=lnx，则x=e2，其中正确的是( )A.①③B.②④C.①②D.③④3.下列等式成立的有( )①；②；③；④；⑤；A.①②B.①②③C.②③④D.①②③④⑤4.已知，那么用表示是( )A. B. C. D.5.（2011 天津文6）设，，，则（）．A. B. C. D.6.已知，且等于( )A. B. C. D.7.函数的图象关于( )A.轴对称B.轴对称C.原点对称D.直线对称8.函数的定义域是( )A. B.C. D.9.函数的值域是( )A. B. C. D.10.下列函数中，在上为增函数的是( )A. B.C. D.二、填空题11.3的_________次幂等于8.12.若，则x=_________；若log2003(x2-1)=0，则x=_________.13.(1)=_______；(2) 若_______；(3)=_______；(4)_______；(5)=_______；14.函数的定义域是__________.15.函数是___________(奇、偶)函数.三、解答题16.已知函数，判断的奇偶性和单调性.17.已知函数，(1)求的定义域；(2)判断的奇偶性.18.已知函数的定义域为，值域为，求的值.能力提升一、选择题1．设a，b，c为正数，且3a=4b=6c，则有( )A. B. C. D.2．已知，那么a的取值范围是( )A. B. C. D.或a>13.图中曲线是对数函数y=log a x的图象，已知a值取，则相应于C1，C2，C3，C4的a值依次为( )A. B.C. D.4.（2011 重庆理5）下列区间中，函数在其上为增函数的是A. B. C. D.5.设偶函数f(x)=log a|x-b|在(-∞，0)上是增函数，则f(a+1)与f(b+2)的大小关系是( )A.f(a+1)=f(b+2)B.f(a+1)>f(b+2)C.f(a+1)<f(b+2)D.不能确定6.设方程2x+x-3=0的根为，方程log2x+x-3=0的根为，则的值是( )A.1B.2C.3D.6二、填空题7.已知函数y=log a(kx2+4kx+3)，若函数的定义域为R，则k的取值范围是__________；若函数的值域为R，则k的取值范围是________.8.（2011 辽宁理9）设函数f(x)＝则满足f(x)≤2的x的取值范围是A．[－1，2]B．[0，2]C．[1，＋)D．[0，＋).9．已知a=0.33，b=30.3，c=log30.3，d=log0.33，则a，b，c，d的大小关系是______.三、解答题10.设log a c，log b c是方程x2-3x+1=0的两根，求的值.11.设1)判断f(x)的单调性，并给出证明；2)若f(x)的反函数为f-1(x)，证明f-1(x)=0有唯一解；3)解关于x的不等式.12.光线通过一块玻璃板，其强度要损失10%，把几块这样的玻璃板重叠起来，设光线原来的强度为a，通过x块玻璃板以后强度值为y.1)试写出y关于x的函数关系式；2)通过多少块玻璃板以后，光线强度减弱到原来的以下.。

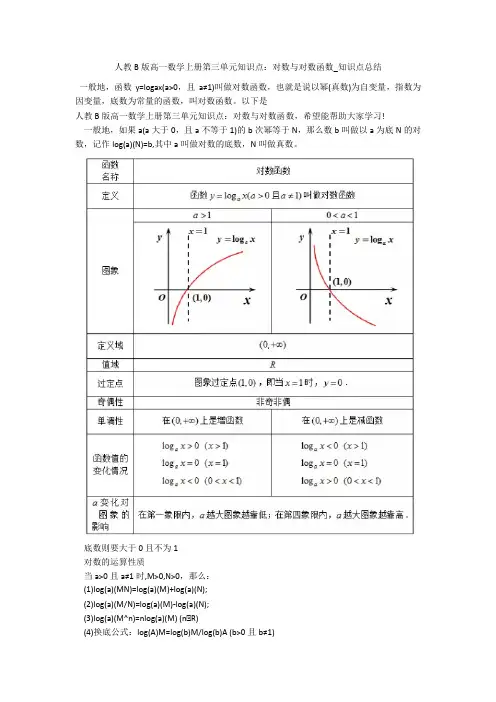
人教B版高一数学上册第三单元知识点：对数与对数函数_知识点总结一般地，函数y=logax(a>0，且a≠1)叫做对数函数，也就是说以幂(真数)为自变量，指数为因变量，底数为常量的函数，叫对数函数。

以下是人教B版高一数学上册第三单元知识点：对数与对数函数，希望能帮助大家学习!一般地，如果a(a大于0，且a不等于1)的b次幂等于N，那么数b叫做以a为底N的对数，记作log(a)(N)=b,其中a叫做对数的底数，N叫做真数。

底数则要大于0且不为1对数的运算性质当a>0且a≠1时,M>0,N>0，那么：(1)log(a)(MN)=log(a)(M)+log(a)(N);(2)log(a)(M/N)=log(a)(M)-log(a)(N);(3)log(a)(M^n)=nlog(a)(M) (n∈R)(4)换底公式：log(A)M=log(b)M/log(b)A (b>0且b≠1)对数与指数之间的关系当a>0且a≠1时,a^x=N x=㏒(a)N常用简略表达方式(1)常用对数:lg(b)=log(10)(b)(2)自然对数:ln(b)=log(e)(b)(3) log(a)+(b)=log(a)(b)e=2.718281828...通常情况下只取e=2.71828对数函数的定义对数函数的一般形式为y=㏒(a)x，它实际上就是指数函数的反函数(图象关于直线y=x对称的两函数互为反函数)，可表示为x=a^y。

因此指数函数里对于a的规定(a>0且a≠1)，同样适用于对数函数。

右图给出对于不同大小a所表示的函数图形：可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

定义域：(0，+∞)值域：实数集R定点：函数图像恒过定点(1，0)。

单调性：a>1时，在定义域上为单调增函数，并且上凸;0奇偶性：非奇非偶函数周期性：不是周期函数零点：x=1知识拓展：16世纪末至17世纪初的时候，当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算，于是数学家们为了寻求化简的计算方法而发明了对数。

目录对数函数 (2)模块一：对数与对数运算 (2)考点1：对数运算 (3)模块二：对数函数图像与性质的应用 (3)考点2：对数比较大小 (4)模块二：对数型复合函数 (5)考点3：对数函数相关的复合函数 (5)课后作业： (7)对数函数模块一：对数与对数运算1.对数的概念：一般地，如果b a N =(0a >，且1)a ≠，那么我们把b 叫做以a 为底N 的对数，记作log a b N =，其中a 叫做对数的底数，N 叫做真数．2.常用对数与自然对数对数log a N （0a >且1a ≠），当底数 （1）10a =时，叫做常用对数，记做lg N ；（2）e a =时，叫做自然对数，记做ln N （e 为无理数，e 2.71828≈）． 3.对数的运算性质：如果，且，那么： （1）；（积的对数等于对数的和） 推广（2） ；（商的对数等于对数的差） （3） ．（幂的对数等于底数的对数乘以幂指数）4.换底公式：（）．5.换底公式的几个基本使用： ①； ②；③；④. 0a >100a M N ≠>>，，log ()log log a a a M N M N ⋅=+1212log ()log log log a k a a a kN N N N N N ⋅⋅⋅=+++log log log aa a MM N N=-log log ()a a M M ααα=∈R log log log a b a NN b=010a b a b N >≠>，，，，log log 1a b b a ⋅=log log log a b a b c c ⋅=1log log n a a b b n=log log n m a a mb b n=考点1：对数运算例1.（1）化简求值：253948(log 212)(log 313)2log og og +++； 【解答】解：2539482233231113525(log 212)(log 313)2()()5(1)()55323223232223264log lg lg lg lg lg lg og og lg lg lg lg lg lg +++=+++=+++=⨯+= （2）2525(2)lg lg lg lg ++= ．【解答】解：2525(2)52(52)521lg lg lg lg lg lg lg lg lg lg ++=++=+=． 故答案为：1．例2.（1）若496m n ==，则11m n+= ． 【解答】解：由496m n ==， 得4log 6m =，9log 6n =， 即614log m =，61log 9n=， 所以66611log 4log 9log 362m n+=+==， 故答案为：2．（2）已知72p =，75q =，则2lg 用p ，q 表示为 ． 【解答】解：72p =，75q =， 72plg lg ∴=，75qlg lg =，∴2512qlg lg lg p==-， 化为2plg p q =+， 故答案为：pp q+． 模块二：对数函数图像与性质的应用1.对数函数：我们把函数且）叫做对数函数，其中是自变量，函数的定义域是，值域为实数集．2.对数函数的图象与性质：log (0a y x a =>1a ≠x (0)+∞，R考点2：对数比较大小例3.（1）若log 0.5log 0.50m n >>，则( ) A ．1m n <<B ．1m n <<C ．1n m <<D ．1n m <<【解答】解：log 0.5log 0.50m n >>；∴0.50.5110log m log n>>；0.50.5log log 0n m ∴>>；1n m ∴<<．故选：D ．（2）设4log 9a =，4log 25b =，5log 9c =，则( ) A ．a b c >> B ．c a b >> C ．b c a >> D ．b a c >>【解答】解：454995log log log =； 44log 9log 51>>；∴444995log log log <； 54log 9log 9∴<；又44log 9log 25<； b a c ∴>>．故选：D ．（3）已知2log 6a =，3log 2b =，3log 6c =，则( ) A ．a b c <<B ．b c a <<C ．a c b <<D ．c b a <<【解答】解：22log 6log 42>=，330log 2log 31<<=，3331log 3log 6log 92=<<=； b c a ∴<<．故选：B ．例4.求不等式2log (583)2x x x -+>的解集． 【解答】解：133252⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭，，模块二：对数型复合函数单调性、定义域、值域、奇偶性为本模块重点考点3：对数函数相关的复合函数例5.函数212log (12)y x x =--的单调增区间是 ．【解答】解：由2120x x -->得3x <-或4x >． 令2()12g x x x =--，则当3x <-时，()g x 为减函数，当4x >时，()g x 为增函数函数．又12y log u =是减函数，故212(12)y log x x =--在(,3)-∞-为增函数．故答案为：(,3)-∞-． 例6.（1）求函数21124log log 5⎛⎫=-+ ⎪⎝⎭y x x 在[]24，上的最值． 【解答】解：max10=y ，min 132=y ．（2）已知()32log ([19])f x x x =+∈，，求函数22[()]()y f x f x =+的最大值与最小值． 【解答】解：1x =时，y 有最小值6；3x =时，y 有最大值13．例7.已知函数22()log 2xf x x+=- （Ⅰ）求()f x 的定义域； （Ⅱ）讨论()f x 的奇偶性；（Ⅲ）求使()0f x >的x 的取值范围． 【解答】解：()I 由对数函数的定义知202xx+>-． 如果2020x x +>⎧⎨->⎩，则22x -<<；如果2020x x +<⎧⎨-<⎩，则不等式组无解．故()f x 的定义域为(2,2)- 2222()()()22x xII f x log log f x x x-+-==-=-+-， ()f x ∴为奇函数． 22()log 02x III x +>-等价于212x x+>-，① 而从()I 知20x ->，故①等价于22x x +>-，又等价于0x >．∴当(0,2)x ∈时有()0f x >例8.已知函数()log (1)log (1)a a f x x x =+--，其中0a >且1a ≠． （1）求函数()f x 的定义域；（2）判断()f x 的奇偶性，并说明理由；（3）若3()25f =，求使()0f x >成立的x 的集合．【解答】解：（1）要使函数有意义，则1010x x +>⎧⎨->⎩，解得11x -<<，即函数()f x 的定义域为(1,1)-； （2）()log (1)log (1)[log (1)log (1)]()a a a a f x x x x x f x -=-+-+=-+--=-，()f x ∴是奇函数． （3）若3()25f =，33log (1)log (1)log 4255a a a ∴+--==，解得：2a =，22()log (1)log (1)f x x x ∴=+--，若()0f x >，则22log (1)log (1)x x +>-， 110x x ∴+>->，解得01x <<，故不等式的解集为(0,1)．课后作业：1．计算2(2)205lg lg lg +⨯的结果是( ) A ．1B ．2C ．2lgD ．5lg【解答】解：因为22(2)205(2)(12)(12)1lg lg lg lg lg lg +⨯=++-=， 故选：A ．2．若3412a b c ==，且0abc ≠，则c ca b+等于( ) A ．4B ．3C ．2D ．1【解答】解：设3412a b c k ===， 则3log a k =，4log b k =，12log c k =， 则12123434112k k k log log log k log k c c a b log k log k log ++=+==． 故选：D ．3．已知52log a =，122b =，c =( )A ．a c b >>B ．a b c >>C ．c a b >>D ．c b a >>【解答】解：5512log log 32log 22a b =>==，7log 3c =，a c ∴>，52log 41b =<，72log 91c =>，c b ∴>．a cb ∴>>．故选：A ．4．若函数()log (0a f x x a =>且1)a ≠在区间[a ，22]a 上的最大值比最小值多2，则(a =) A ．2B ．3或13C ．4或12D ．2或12【解答】解：由22(21)0a a a a -=->，有12a >且1a ≠， ①当1a > 时，2(2)2a a log a log a -=，得2a =，②当112a << 时，2(2)2a a log a log a -=，得a ， 故2a =，故选：A ．5．已知函数()(2)(2)f x lg x lg x =++-．（1）求函数()f x 的定义域并判断函数()f x 的奇偶性； （2）记函数()()103f x g x x =+，求函数()g x 的值域； （3）若不等式()f x m >有解，求实数m 的取值范围． 【解答】解：（1）函数()(2)(2)f x lg x lg x =++-， ∴2020x x +>⎧⎨->⎩，解得22x -<<．∴函数()f x 的定义域为(2,2)-．()(2)(2)()f x lg x lg x f x -=-++=， ()f x ∴是偶函数．（2）22x -<<，2()(2)(2)(4)f x lg x lg x lg x ∴=++-=-． ()()103f x g x x =+，∴函数22325()34()24g x x x x =-++=--+，(22)x -<<，325()()24max g x g ∴==，()(2)6min g x g →-=-， ∴函数()g x 的值域是(6-，25]4． （3）不等式()f x m >有解，()max m f x ∴<， 令24t x =-，由于22x -<<，04t ∴< ()f x ∴的最大值为4lg ．∴实数m 的取值范围为{|4}m m lg <．。

人教版高一对数函数知识点对数函数是高等数学中的重要概念，它在数学和实际生活中都有广泛的应用。

本文将介绍人教版高一对数函数的一些重要知识点。

一、定义和性质对数函数是指以一个正实数作为底数，另一个正实数作为真数的幂等于某个给定的正实数。

对数函数的定义可以表示为y=logₐx，其中a为底数，x为真数，y为对数。

对数函数的性质包括：1. 对数函数定义域：对数函数对于底数a来说，定义域为正实数集合。

2. 对数函数值域：对数函数的值域为实数集合。

3. 对数函数的图像特点：对数函数的图像呈现出一条曲线，其特点是，在定义域的左半部分和右半部分都为无穷大时，函数值趋于负无穷；在定义域的中间部分，函数值逐渐增加，但增长趋势逐渐变缓。

二、对数函数的表示方法1. 指数幂函数与对数函数的关系：对数函数和指数幂函数是互为反函数关系。

即logₐx=y等价于a^y=x。

这里的a为底数，x为真数，y为对数。

2. 常见的对数函数表示方法：常见的对数函数有自然对数函数（底数为e）和常用对数函数（底数为10）。

自然对数函数表示为y=lnx，其中ln表示以e为底的对数。

常用对数函数表示为y=log₍₁₀₎x，其中log表示以10为底的对数。

三、对数函数的基本性质1. 对数函数的单调性：自然对数函数和常用对数函数都是单调递增函数，即随着变量的增大，函数值也递增。

2. 对数函数的性质之一：对数函数满足性质logₐM+N=logₐM+logₐN。

即对数函数中的加法可以转化为对数函数的乘法。

3. 对数函数的性质之二：对数函数满足性质logₐM-N=logₐM-logₐN。

即对数函数中的减法可以转化为对数函数的除法。

四、对数函数的应用对数函数在实际生活和数学中都有广泛应用，下面简要介绍几个常见的应用。

1. 对数函数在生物学中的应用：对数函数可以描述生物种群的增长规律，如人口增长、微生物繁殖等。

2. 对数函数在经济学中的应用：对数函数可以用来描述经济增长的规律，如GDP增长、财富分布等。

对数与对数函数考点分解：1、 理解对数的概念及运算性质2、 能用换底公式将一般对数转化为常用对数3、 理解对数函数的概念，理解对数函数的单调性，能利用单调性比较大小、求最值4、 掌握对数函数经过的特殊点，会进行简单的图像变换5、 会求复合函数的单调性、定义域、值域知识梳理：1、已知23834x y ==，log ，则x y +2的值为（ ） A. 3 B. 8 C. 4 D. log 482、 已知log log 5534==a b ，，则log 2512是（ ）A. a b +B. 12()a b +C. abD. 12ab 3、.三个数0.377,0.3,ln 0.3a b c ===大小的顺序是（ ）A ．a b c >> B. a c b >> C ．b a c >> D. c a b >>4、（2010湖北文）函数0.51log (43)y x =-的定义域为（ ） （A ）( 34,1) （B ）(34,∞) （C ）（1，+∞） （D ） ( 34,1)∪（1，+∞） 5、（2010山东文）(3)函数()()2log 31x f x =+的值域为（ ）；A. ()0,+∞B. )0,+∞⎡⎣C. ()1,+∞D. )1,+∞⎡⎣6、函数)6(log 221--=x x y 的单调增区间为知识归纳：1、 对数的定义：2、 对数的运算性质：3、 两种重要的对数：4、 对数函数的图像及性质：经典例题：例题1：设M N a a a a==-{}{lg }01112，，，，，，是否存在实数a ，使得M N ={}1？例题2、已知函数()ln()(10)x x f x a b a b =->>>.(1) 求函数()f x 的定义域I ；(2) 判断函数()f x 在定义域I 上的单调性，并说明理由；（3）当,a b 满足什么关系时，()f x 在[)1+∞，上恒取正值。

人教 B 版高一数学上册第三单元知识点：对数与对数函数一般地，函数 y=logax(a>0 ，且 a≠1)叫做对数函数，也就是说以幂 (真数 )为自变量，指数为因变量，底数为常量的函数，叫对数函数。

以下是人教 B 版高一数学上册第三单元知识点：对数与对数函数，希望能帮助大家学习 !一般地，假如 a(a 大于 0，且 a 不等于 1) 的 b 次幂等于 N ，那么数 b 叫做以 a 为底 N 的对数，记作 log(a)(N)=b, 此中 a 叫做对数的底数， N 叫做真数。

底数则要大于 0 且不为 1对数的运算性质当 a>0 且 a≠1时 ,M>0,N>0 ，那么：(1)log(a)(MN)=log(a)(M)+log(a)(N);(2)log(a)(M/N)=log(a)(M)-log(a)(N);(3)log(a)(M^n)=nlog(a)(M) (n∈R)(4)换底公式： log(A)M=log(b)M/log(b)A (b>0且b≠ 1)对数与指数之间的关系当 a>0 且 a≠1时 ,a^x=N x= ㏒ (a)N常用简单表达方式(1)常用对数 :lg(b)=log(10)(b)(2)自然对数 :ln(b)=log(e)(b)(3) log(a)+(b)=log(a)(b)e=2.718281828...往常状况下只取e=2.71828对数函数的定义对数函数的一般形式为 y=㏒ (a)x ，它实质上就是指数函数的反函数 (图象对于直线 y=x 对称的两函数互为反函数 )，可表示为 x=a^y 。

所以指数函数里对于 a 的规定 (a>0 且 a≠1)，相同合用于对数函数。

右图给出对于不一样大小a 所表示的函数图形：能够看到对数函数的图形只可是的指数函数的图形的对于直线 y=x 的对称图形，由于它们互为反函数。

定义域：(0，+∞)值域：实数集 R定点：函数图像恒过定点(1， 0)。