最新-北京各区初三期末28题几何综合汇总

2020年北京初三各区上学期期末几何综合学生版1西城27. △ABC是等边三角形，点P在BC的延长线上，以P为中心，将线段PC逆时针旋转n°（0 ＜n＜180）得线段PQ，连接AP，BQ．（1）如图1，若PC=AC，画出当BQ∥AP时的图形，并写出此时n的值；（2）M为线段BQ的中点，连接PM. 写出一个n的值，使得对于BC延长线上任意一点P，总有并说明理由．图1 备用图解：（1）如图．当BQ∥AP时，n = 60．（2）n = 120．证明：延长PM至N，使得MN=PM，连接BN，AN，QN，如图．∵ M为线段BQ的中点，∴ 四边形BNQP是平行四边形．∴ BN∥PQ，BN=PQ．∴∠NBP=60°．∵ △ABC是等边三角形，∴ AB=AC，∠ABC =∠ACB = 60°．∴∠ABN=∠ACP =120°．∵ 以P 为中心，将线段PC 逆时针旋转120°得到线段PQ ， ∴ PQ =PC ． ∴ BN =PC ． ∴△ABN ≌△ACP ． ∴∠BAN =∠CAP ，AN=AP ． ∴∠NAP =∠BAC = 60°． ∴ △ANP 是等边三角形． ∴ PN =AP ．又 MP =PN ，∴ MP． ············································································ 7分2东城区27．在△ABC 中，∠BAC =45°，CD ⊥AB 于点D ，AE ⊥BC 于点E ，连接DE ． （1）如图1，当△ABC 为锐角三角形时，①依题意补全图形，猜想∠BAE 与∠BCD 之间的数量关系并证明； ②用等式表示线段AE ，CE ，DE 的数量关系，并证明;（2）如图2，当∠ABC 为钝角时，依题意补全图形并直接写出线段AE ，CE ，DE 的数量关系．图1图2解：（1）①依题意，补全图形，如图1所示. 猜想：∠BAE =∠BCD. 理由如下：12∵CD⊥AB,AE⊥BC，∴∠BAE﹢∠B=90°,∠BCD﹢∠B=90°.∴∠BAE=∠BCD.…………………………2分图1②证明：如图2，在AE上截取AF=CE.连接DF.∵∠BAC=45°,CD⊥AB,∴△ACD是等腰直角三角形.∴AD=CD.又∠BAE=∠BCD,∴△ADF≌△CDE（SAS）.∴DF=DE,∠ADF=∠CDE.∵AB⊥CD, 图2 ∴∠ADF﹢∠FDC=90°.∴∠CDE﹢∠FDC=∠EDF=90°.∴△EDF是等腰直角三角形.∴EF∵AF+EF=AE,∴CE+DE=AE. …………………………5分（3）依题意补全图形，如图3所示.线段AE，CE，DE的数量关系：CE-DE=AE.……………………………7分3朝阳27．已知∠MON=120°，点A，B分别在ON，OM边上，且OA=OB，点C在线段OB上（不与点O，B 重合），连接CA. 将射线CA绕点C逆时针旋转120°得到射线CA´，将射线BO绕点B逆时针旋转150°与射线CA´交于点D.(1)根据题意补全图1；(2)求证：①∠OAC=∠DCB；②CD=CA（提示：可以在OA上截取OE=OC，连接CE）；(3)点H在线段AO的延长线上，当线段OH，OC，OA满足什么等量关系时，对于任意的点C都有∠DCH=2∠DAH，写出你的猜想并证明.（1）解：补全图形，如图.（2）证明：①根据题意∠ACD=120°.∴∠DCB+∠ACO=60°.∵∠MON=120°，∴∠OAC +∠ACO=60°.∴∠OAC=∠DCB.②在OA上截取OE=OC，连接CE.∴∠OEC=30°.∴∠AEC=150°.∴∠AEC=∠CBD.∵OA=OB，∴AE=BC.∴△AEC≌△CBD.∴CD=AC.(3) OH-OC= OA.证明：在OH上截取OF=OC，连接CF，∴△OFC 是等边三角形，FH=OA.∴CF=OC，∠CFH=∠COA=120°.∴△CFH≌△COA.∴∠H=∠OAC.∴∠BCH =60°+∠H =60°+∠OAC . ∴∠DCH =60°+∠H +∠DCB=60°+2∠OAC .∵CA =CD ，∠ACD =120°， ∴∠CAD =30°. ∴∠DCH =2∠DAH .4大兴区27.已知：如图，B,C,D 三点在 上，︒=∠45BCD ，PA 是钝角 △ABC 的高线，PA 的延长线与线段CD 交于点E. (1) 请在图中找出一个与∠CAP 相等的角，这个角是 ； (2) 用等式表示线段AC ，EC ，ED 之间的数量关系， 并证明.5石景山区27．如图，在正方形ABCD 中，P 是边BC 上的一动点（不与点B ，C 重合），点B 关于 直线AP 的对称点为E ，连接AE ．连接DE 并延长交射线AP 于点F ，连接BF ． （1）若BAP α∠=，直接写出ADF ∠的大小（用含α的式子表示）； （2）求证：BF DF ⊥；（3）连接CF ，用等式表示线段AF ，BF ，CF 之间 的数量关系，并证明． （1）………………………… 2分（21．4分 （3FEP DC BA图1NMA………………………… 5分 2．，………………………… 7分6丰台区26．如图，∠90MAN =︒，B ，C 分别为射线AM ，AN 上的两个动点，将线段AC 绕点A 逆时针．．．旋转30︒到AD ，连接BD 交AC 于点E ．（1）当∠ACB =30°时，依题意补全图形，；（2）写出一个∠ACB 的度数，并证明．解：（1）正确补全图形；………………1分………………3分（2 ……………………………………………………4分图2……………………………………………………………5分∠…………………………………………………………7分7顺义区27．已知：如图，在正方形ABCD 中，点E 在AD 边上运动，从点A 出发向点D 运动，到达D 点停止运动．作射线CE ，并将射线CE 绕着点C 逆时针旋转45°，旋转后的射线与AB 边交于点F ，连接EF . （1） 依题意补全图形；（2） 猜想线段DE ，EF ，BF 的数量关系并证明；（3） 过点C 作CG ⊥EF ，垂足为点G ，若正方形ABCD 的边长是4，请直接写出点G 运动的路线长．CCF BC D E A（备用图）解：（1）补全图形如图1． …………………………………………… 1分图1 图2（2）线段DE ，EF ，BF 的数量关系是 EF=DE+BF ．……… 2分 证明：延长AD 到点H ，使DH=BF ，连接CH （如图2）． 易证△CDH ≌△CBF ．∴CH= CF ，∠DCH =∠BCF ． ∵∠ECF =45°，∴∠ECH =∠ECD +∠DCH= ∠ECD +∠BCF =45°． ∴∠ECH =∠ECF =45°． 又∵CE= CE ， ∴△ECH ≌△ECF ． ∴EH= EF ．∴EF=DE+BF ． …………………………………………… 6分（3）点G 运动的路线长为 2π ． ……………………… 7分8平谷区27．如图，正方形ABCD ，将边BC 绕点B 逆时针旋转60°，得到线段BE ，连接AE ，CE ． （1）求∠BAE 的度数；（2）连结BD ，延长AE 交BD 于点F ． ①求证：DF=EF ；②直接用等式表示线段AB ，CF ，EF 的数量关系．（1）解：∵AB=BE ，∴∠BAE =∠BEA ． ······································································· 1 ∵∠ABE =90°－60°=30°∴∠BAE =75°． (2)（2）证明：∴∠DAF =15°． (3)连结CF ．由正方形的对称性可知，∠DAF =∠DCF =15°． ······························· 4 ∵∠BCD =90°，∠BCE =60°， ∴∠DCF =∠ECF =∠DAF =15°． ∵BC=EC ，CF=CF ，∴△BCF ≌△ECF ． ···································································· 5 ∴BF=EF ． ··············································································· 6 （3 (7)9昌平区27.已知等边△ABC ，点D 为BC 上一点，连接AD .（1）若点E 是AC 上一点，且CE ＝BD ，连接BE ，BE 与AD 的交点为点P ，在图（1）中根据题意补全图形，直接写出∠APE 的大小；（2）将AD 绕点A 逆时针旋转120°，得到AF ，连接BF 交AC 于点Q ，在图（2）中根据题意补全图形，用等式表示线段AQ 和CD 的数量关系，并证明.（1）补全图形. ………………………………………………………… 1分 ∠APE =60° ……………………………………………………………… 2分（2）补全图形.………………………………………………………………3分ABDCDCBA..………………………………………………………………4分证明：在△ABD 和△BEC 中， ⎪⎩⎪⎨⎧=︒=∠=∠=CEBD C ABD BC AB 60∴△ABD ≌△BEC （SAS ）∴∠BAD =∠CBE .∵∠APE 是△ABP 的一个外角，∴∠APE =∠BAD +∠ABP =∠CBE +∠ABP =∠ABC =60°.∵AF 是由AD 绕点A 逆时针旋转120°得到，∴AF =AD ，∠DAF =120°. ∵∠APE =60°， ∴∠APE +∠DAP =180°.∴AF ∥BE...……………………………………………………………………………………………5分 ∴∠1=∠2∵△ABD ≌△BEC ， ∴AD =BE . ∴AF =BE .在△AQF 和△EQB 中，⎪⎩⎪⎨⎧=∠=∠∠=∠BEAF EQB AQF 21△AQF ≌△EQB （AAS ）∴AQ =QE ..……………………………………………………………………………………………6分∵AE=AC－CE，CD=BC－BD，且AE=BC，CD=BD.∴AE=CD...……………………………………………………………………………………………7分10通州11门头沟27．如图，∠MON =60°，OF 平分∠MON ，点A 在射线OM 上， P ，Q 是射线ON 上的两动点，点P 在点Q 的左侧，且PQ=OA ，作线段OQ 的垂直平分线，分别交OM ，OF ，ON 于点D ，B ，C ，连接AB ，PB ． （1）依题意补全图形；（2）判断线段 AB ，PB 之间的数量关系，并证明；（3）连接AP ，当P 和Q 两点都在射线ON 上移动时，k 是否存在最小值？若存在，请直接写出k 的最小值，备用图（本小题满分7分）（1）补全图形正确．………………………………1分 （2）AB =PB ．………………………………………2分证明：如图，连接BQ ．∵BC 的垂直平分OQ ，∴ OB =BQ ，……………………3分 ∴∠BOP =∠BQP ． 又∵ OF 平分∠MON ， ∴∠AOB = ∠BOP ．∴∠AOB = ∠BQP ．…………4分 又∵PQ=OA ，∴ △AOB ≌△PQB ，…………………………………………………………5分 ∴AB =PB ．（37分12房山区27.在△ABC中，∠ACB＝90°，AC＝BC以点B为圆心、1为半径作圆，设点M为⊙B 上一点，线段CM绕着点C顺时针旋转90°，得到线段CN，连接BM、AN．（1）在图27-1中，补全图形，并证明BM＝AN .（2）连接MN，若MN与⊙B相切，则∠BMC的度数为________________.（3）连接BN，则BN的最小值为___________；BN的最大值为___________27-1 备用图备用图（1）如图27-1，补全图形…………1分证明：⸪∠ACB＝∠MCN＝90°∴∠MCB＝∠NCA …………2分⸪CM＝CN，CB＝CA∴△MCB≌△NCA∴BM＝AN…………3分图27-1（2） 45°或135°…………4分（3） 1 ； 3 …………6分13密云区27. 已知：在Rt △ABC 中，∠BAC=90°，AB=AC ，点D 为BC 边中点．点M 为线段B C 上的一个动点（不与点C ，点D 重合），连接AM ，将线段AM 绕点M 顺时针旋转90°，得到线段ME ，连接EC ． （1）如图1，若点M 在线段BD 上． ① 依据题意补全图1；② 求∠MCE 的度数．（2）如图2，若点M 在线段CD 上，请你补全图形后，直接用等式表示线段AC 、CE 、CM 之间的数量关系 ．(1) ① 补全图1：………………………………2分② 解：过点M 作BC 边的垂线交CA 延长线于点F ∴ ∠FMC =90° ∴ ∠FMA+∠AMC=90°∵将线段AM 绕点M 顺时针旋转90°，得到线段ME ∴∠AME=90°∴ ∠CME+∠AMC=90°∴∠FMA= ∠CME ………………………………3分在Rt △FMC 中,∠FCM=45°∴∠F=∠FCM=45°图1∴FM=MC ………………………………4分在△FMA和△CME中∴∴∠MCE=∠F=45°……………5分（2……………7分14海淀27．在Rt△ABC中，∠ACB=90°，AC=1, 记∠ABC=α，点D为射线BC上的动点，连接AD，将射线DA 绕点D顺时针旋转α角后得到射线DE，过点A作AD的垂线，与射线DE交于点P，点B关于点D的对称点为Q，连接PQ．（1）当△ABD为等边三角形时，① 依题意补全图1；② PQ 的长为_____________；（2）如图2，当α=45°，, 求证：PD =PQ ；（3）设BC = t , 当PD =PQ 时，直接写出BD 的长.（用含t 的代数式表示）（1）解：①补全图形如下图所示.② PQ =2.（2）作PF BQ ⊥于F ，AH PF ⊥于H .∵PA AD ⊥, ∴∠PAD =90°.由题意可知∠1=45°. ∴2901451∠=︒-∠=︒=∠. ∴PA AD =. ∵90ACB ∠=︒, ∴90ACD ∠=︒∵AH PF ⊥，PF BQ ⊥， ∴90AHP AHF PFC ∠=∠=∠=︒. ∴四边形ACFH 是矩形.∴90,CAH AH CF ∠=︒=.图 121 ∵90,CAH DAP ∠=∠=︒∴3490DAH DAH ∠+∠=∠+∠=︒. ∴34∠=∠.又∵90,ACD AHP ∠=∠=︒∴ACD AHP ≌△△.∴1AH AC ==.∴1CF AH ==.B ，Q 关于点D 对称，∴F 为DQ 中点.∴PF 垂直平分DQ .∴PQ =PD .（3。

海淀区九年级第二学期末练习数 学2024.05学校_____________ 姓名______________ 准考证号______________第一部分 选择题一、选择题（共16分，每题2分）第1 - 8题均有四个选项，符合题意的选项只有一个．1．截至2023年底，我国人工智能核心产业规模接近5800亿元，形成了京津冀、长三角、珠三角三大集聚发展区．将580000000000 用科学记数法表示应为 （A ）105810⨯（B ）115.810⨯（C ）125.810⨯（D ）120.5810⨯2．右图是一张长方形纸片，用其围成一个几何体的侧面，这个几何体可能是 （A ）圆柱 （B ）圆锥 （C ）球（D ）三棱锥3．五边形的内角和为 （A ）900︒（B ）720︒（C ）540︒（D ）360︒4．若a b >，则下列结论正确的是 （A ）0a b +>（B ）0a b −>（C ）0ab >（D ）0ab> 5．如图，实数5在数轴上对应的点可能是（A ）点A（B ）点B（C ）点C（D ）点D6．如图，12l l ，点A 在1l 上，以点A 为圆心，适当长度为半径画弧，分别交1l ，2l 于点B ，C ，连接AC ，BC ．若140∠=︒，则ABC ∠的大小为 （A ）80︒ （B ）75︒ （C ）70︒（D ）65︒考生须知1．本试卷共7页，共两部分，28道题，满分100分。

考试时间120分钟。

2．在试卷和答题纸上准确填写学校名称、姓名和准考证号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，请将本试卷、答题纸和草稿纸一并交回。

ABC1l 1l 20 1 2 3–1 A B CD7．九年级（1）班羽毛球小组共有4名队员，其中两名男生，两名女生．从中随机选取两人，恰好能组成一组混双搭档的概率是 （A）14（B ）13（C ）12（D ）238．某种型号的纸杯如图1所示，若将n 个这种型号的杯子按图2中的方式叠放在一起，叠在一起的杯子的总高度为H ．则H 与n 满足的函数关系可能是 （A ）0.3H n = （B ）100.3H n=（C ）100.3H n =−（D ）100.3H n =+第二部分 非选择题二、填空题（共16分，每题2分） 9． 若代数式12x −有意义，则实数x 的取值范围是 ． 10．若1x =是方程230x x m −+=的一个根，则实数m 的值为 ． 11．如图，在△ABC 中，D ，E 分别在边AB ，BC 上，DEAC ．若2AD =，4BD =，则DEAC的值为 ．12．在平面直角坐标系xOy 中，点1(1)A y ，，2(2)B y ，在反比例函数ky x=(0k ≠) 的图象上． 若12y y <，则满足条件的k 的值可以是 （写出一个即可）．13．如图所示的网格是正方形网格，A ，B ，C 是网格线的交点，C 在以AB 为直径的半圆上．若点D 在BC 上，则BDC ∠= ︒．14．一组数据3，2，4，2，6，5，6的平均数为4，方差为20s ．再添加一个数据4，得到一组新数据．若记这组新数据的方差为21s ，则21s 20s （填“＞”“＝”或“＜”）．A DBE C图1图2D CBA15．下表是n 与2n （其中n 为自然数）的部分对应值表：n5 10 15 20 25 30 35 2n321 02432 7681 048 57633 554 4321 073 741 82434 359 738 368根据表格提供的信息，计算102432768⨯的结果为 ． 16．在ABC 中，D 为边AB 的中点，E 为边AC 上一点，连接DE ．给出下面三个命题：①若AE EC =，则12DE BC =； ②若12DE BC =，则DE BC ∥； ③若DE BC ∥，则AE EC =．上述命题中，所有真命题的序号是 ．三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分） 解答写出文字说明、演算步骤或证明过程．17．计算：020242sin 45|3|8−︒+−+.18．解不等式组：532342(1).x x x x +⎧<⎪⎨⎪−>+⎩，19．已知2230m n −−=，求代数式2()2()m n n m n +−+的值.20．如图，点A ，B ，C ，D 在一条直线上，AB BC CD ==，AE EC =，四边形ECDF 是平行四边形. （1）求证：四边形EBCF 是矩形； （2）若12AD =，4cos 5A =，求BF 的长．21．我国古代著作《管子·地员篇》中介绍了一种用数学运算获得“宫商角徵羽”五音的方法．研究发现，当琴弦的长度比满足一定关系时，就可以弹奏出不同的乐音．例如，三根弦按长度从长到短排列分别奏出乐音“do ，mi ，so ”，需满足相邻弦长的倒数差相等．若最长弦为15个单位长，最短弦为10个单位长，求中间弦的长度．ODACBFE22．在平面直角坐标系xOy 中，一次函数0y kx b k =+≠（）的图象由函数12y x =的图象平移得到，且经过点(24),．（1）求这个一次函数的解析式；（2）当2x >时，对于x 的每一个值，函数y x n =+的值与一次函数0y kx b k =+≠（）的值的差大于1，直接写出n 的取值范围．23．一本图鉴中的照片由1开始连续编号，由于装订线脱落，照片散落一地．小云想利用统计学知识估计照片总数，于是从中随机抽取20张照片，将其编号作为样本，数据整理如下： a ．20张照片的编号：4，8，15，25，34，39，41，48，68，79，85，86，89，91，102，104，110，121，144，147 b ．20张照片编号的最小值、最大值、平均数和中位数：最小值 最大值 平均数 中位数 414772m（1）写出表中m 的值；（2）设照片总数为n ，所有照片编号分别为1，2，…，n ，这n 个数的平均数和中位数均为12n +． ①利用样本平均数估计全体平均数，可估算出照片的总数1n 为_________， ②利用样本中位数估计全体中位数，可估算出照片的总数2n 为_________，小云发现，有一个估算结果不合理，这个不合理的结果是_________（填“1n ”或“2n ”）； （3）小云想到还可使用样本数据的“平均间隔长度”进行估计．在下面的示意图中，用1220x x x ，，…，表示随机抽取的20张照片编号从小到大排序，则从0到20x 的平均间隔长度为2020x ，从0到n 的平均间隔长度为21n，直接写出此时估算出照片的总数3n （结果取整数）．24．如图，P 是⊙O 外一点，P A ，PB 分别切⊙O 于点A ，B ，PO 与⊙O 交于点H ，AH OH =. （1）求证：△ABP 是等边三角形；（2）过点A 作PO 的平行线，与⊙O 的另一个交点为C ，连接CP ．若6AB =，求⊙O 的半径和tan CPB ∠的值.HBAOPnx 20x 19 …x3 x 2x 125．生活垃圾水解法是一种科学处理生活垃圾的技术．有研究表明，在生活垃圾水解过程中添加一些微生物菌剂能够加快原料的水解．某小组为研究微生物菌剂添加量对某类生活垃圾水解率的影响，设置了六组不同的菌剂添加量，分别为0%，2%，4%，6%，8%，10%，每隔12h 测定一次水解率，部分实验结果如下：a ．不同菌剂添加量的生活垃圾，在水解48 h 时，测得的实验数据如下图所示：为提高这类生活垃圾在水解48 h 时的水解率，在这六组不同的菌剂添加量中，最佳添加量 为 %；b ．当菌剂添加量为p %时，生活垃圾水解率随时间变化的部分实验数据记录如下：时间t （h ）1224364860728496108120水解率y （%）0 28.0 35.1 39.4 42.5 44.9 46.8 48.5 50.0 51.2 52.3通过分析表格中的数据，发现当菌剂添加量为p %时，可以用函数刻画生活垃圾水解率y 和时间t 之间的关系，在平面直角坐标系中画出此函数的图象．结合实验数据，利用所画的函数图象可以推断，当水解132 h 时，生活垃圾水解率超过54%（填“能”或“不能”）．根据以上实验数据和结果，解决下列问题： （1）直接写出p 的值；（2）当菌剂添加量为6%时，生活垃圾水解率达到50%所需的时间为0t 小时，当菌剂添加量为p %时，生活垃圾水解0(48)t +小时的水解率 50%（填“大于”“小于”或“等于”）.t (h)1224364860728496108120132O菌剂添加量 （%）水解率 （%）25 30 35 40 4550 55 46810220 O26．在平面直角坐标系xOy 中，抛物线2y ax bx c =++（0a >）的对称轴为x t =，点1()2A t m ，，(2)B t n ，，00()C x y ，在抛物线上．（1）当2t =时，直接写出m 与n 的大小关系；（2）若对于067x <<，都有0m y n <<，求t 的取值范围．27．在ABC △中，AB AC =，60A ∠<︒，点D 在边AC 上（不与点A ，C 重合），连接BD ，平移线段BD ，使点B 移到点C ，得到线段CE ，连接DE ．（1）在图1中补全图形，若2BAC E ∠=∠，求证：CBD ∠与CDE ∠互余；（2）连接AE ，若AC 平分BAE ∠，用等式表示CBD ∠与BAE ∠之间的数量关系，并证明.图1 备用图28．在平面直角坐标系xOy 中，⊙O 的半径为1，AB 是⊙O 的一条弦，以AB 为边作平行四边形ABCD ．对于平行四边形ABCD 和弦AB ，给出如下定义：若边CD 所在直线是⊙O 的切线，则称四边形ABCD 是弦AB 的“弦切四边形”．（1）若点(01)A −，，(10)C ，，四边形ABCD 是弦AB 的“弦切四边形”，在图中画出“弦切四边形”ABCD ，并直接写出点D 的坐标；（2）若弦AB 的“弦切四边形”为正方形，求AB 的长；（3）已知图形M 和图形N 是弦AB 的两个全等的“弦切四边形”，且均为菱形，图形M 与N 不重合．P ，Q 分别为两个“弦切四边形”对角线的交点，记PQ 的长为t ，直接写出t 的取值范围．海淀区九年级第二学期期末练习数学试卷参考答案第一部分选择题一、选择题（共16分，每题2分）第二部分非选择题二、填空题（共16分，每题2分）9．2x≠10．211．2312．答案不唯一，0k<即可13．135 14．<15．33 554 432 16．①③三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17. 解：原式1232=−⨯++………………………………………………………………..4分13=+4=+…………………………………………………………………5分18. 解：原不等式组为56342 2.x xx x+<⎧⎨−>+⎩，①②解不等式①，得1x>. ………………………………………………………………….2分解不等式②，得6x>. …………………………………………………………………..4分∴原不等式组的解集为6x>. ……………………………………………………………..5分19. 解：原式222222m mn n mn n=++−−22m n=−. ……………………………………………………………………….3分∵2230m n −−=，∴223m n −=. …………………………………………………………………………4分∴原式3=. ………………………………………………………………………… 5分 20．（1）证明：∵四边形ECDF 为平行四边形，∴EF // CD ，EF CD =. …………………………………………………………1分 ∵B ，C ，D 在一条直线上，BC CD =， ∴EF // BC ，EF =BC .∴四边形EBCF 为平行四边形. ……………………………………………………2分 ∵AE EC =，AB BC =， ∴EB AC ⊥.∴90EBC ∠=.∴四边形EBCF 为矩形. …………………………………………………………3分（2）解：∵A ，B ，C ，D 在一条直线上，AB BC CD ==，12AD =，∴4AB =. …………………………………………………………………….4分 ∵EB AC ⊥. ∴90EBA ∠=. ∵4cos 5A =. ∴5cos ABAE A==. …………………………………………………………………….5分 ∵AE EC =， ∴5EC =.∵四边形EBCF 为矩形， ∴5BF EC ==.∴BF 的长为5. ………………………………………………………………….6分21. 解：设中间弦的长度为x 个单位长. …………………………. ………………. ………………..1分由题意可得11111510x x−=−. …………………………………………………………….3分 解得 12x =. ……………………………………………………………………………. 4分 经检验，12x =是原方程的解且符合题意. ………………………………………………. 5分 答：中间弦的长度为12个单位长. ……………………………………………………….6分22．解：（1）∵一次函数(0)y kx b k =+≠的图象由函数12y x =的图象平移得到， ∴12k =. .…..…..……………………………………………………………………..1分 ∵一次函数(0)y kx b k =+≠的图象经过点(24)，，∴1242b ⨯+=. ∴3b =. .…..…..……………………………………………………………………..2分 ∴该一次函数的解析式为132y x =+. …………………...………………………..3分 （2）3n ≥. ….….….….…………………………………………………………………..5分23．解：（1）82； ….…….……………………………………..…………………………………..1分（2）143，163，1n ； ………………………………………………………………………... 4分 （3）154. ………………………………………………………………………….…..5分24.（1）证明：连接OA ，如图.∵OA OH =，AH OH =， ∴OA OH AH ==. ∴△AOH 为等边三角形.∴60AOH ∠=︒. …………………………………………………………………..….1分 ∵P A 切O 于点A ， ∴PA AO ⊥. ∴90PAO ∠=︒.∴30APO ∠=︒. ………………………………………………………………..….2分 ∵P A ，PB 分别切O 于点A ，B ， ∴PA PB =，30APO BPO ∠=∠=︒. ∴60APB ∠=︒.∴△ABP 为等边三角形. …………………………………………………………….3分（2）解：如图，连接BC .∵△ABP 为等边三角形，6AB =， ∴6PA PB AB ===.由（1）得，在Rt △P AO 中，90PAO ∠=︒，30APO ∠=︒.P∴tan 3063OA PA =︒=⨯= ∴O的半径为. ……………………………..…………………………4分 ∵△AOH 为等边三角形. ∴60HAO HOA ∠=∠=︒.由（1）得PA PB =，APO BPO ∠=∠， ∴PO AB ⊥. ∵AC // PO ， ∴AC AB ⊥. ∴90BAC ∠=︒.∴BC 是O 的直径. ………………………..…………………………5分∴BC = ∵PB 切O 于点B ， ∴PB BC ⊥. ∴90PBC ∠=︒.∴tan BC CPB PB ∠===………………………..…………………………6分 25.解：a . 6； ………………………………………………………..……………………………..1分b . 图象如下图.………………………………………..…………………………………....2分 不能. ……………………………………………………..……………………………..3分y（h ）P（1） 4； …………………………………………………………..……………………………..4分 （2） 小于. ……………………………………………..……………………………..……..5分 26.解：（1） ＜； ………………………………………………………………………………………2分（2）∵0a >， 抛物线的对称轴为x t =，∴ 当x t ≥时，y 随x 的增大而增大；当x t ≤时，y 随x 的增大而减小. ① 当7t ≥时，122t t t <<.点(2)B t n ，关于抛物线对称轴x t =的对称点为'(0)B n ，， 此时点,',A B C 均在抛物线对称轴左侧. ∵对于067x <<，都有0m y n <<，∴06,17.2t ≤⎧⎪⎨≥⎪⎩解得 14t ≥. ② 当67t <<时，取0x t =，此时0y 为最小值，与0m y <矛盾，不符合题意. ③ 当06t <≤时，122t t t <<.点1()2A t m ，关于抛物线对称轴x t =的对称点为3'()2A t m ，， 此时点',,ABC 均在抛物线对称轴右侧. ∵对于067x <<，都有0m y n <<， ∴36,227.t t ⎧≤⎪⎨⎪≥⎩解得742t ≤≤. ④ 当0t =时，122t t t ==，m n =，不符合题意. ⑤ 当0t <时，122t t t <<.点(2)B t n ，关于抛物线对称轴x t =的对称点为'(0)B n ，， 此时点',B C 在抛物线对称轴右侧. ∵'06B x x <<， ∴0n y <，不符合题意.综上所述，t 的取值范围是742t ≤≤或14t ≥. …………………………………………6分 27.（1）补全图形如图1：图1…………………………………………………………………………………………1分 证明：设E α∠=，则22BAC E α∠=∠=.∵AB AC =， ∴180902BACABC ACB α︒−∠∠=∠==︒−.由平移可知，BC // DE ，BC DE =.∴四边形BCED 为平行四边形. ……………………………………………………2分 ∴CBD E α∠=∠=. ∵BC // DE ，∴90CDE ACB α∠=∠=︒−. ∴90CBD CDE ∠+∠=︒.∴CBD ∠与CDE ∠互余. ………………………………………………………3分（2）CBD ∠与BAE ∠之间的数量关系为12CBD BAE ∠=∠. …………………4分解：如图2，连接BE ，交AC 于点O ，延长AC 至F ，使OF OA =，连接EF .图2BB由（1）可得，四边形BCED 为平行四边形.∴OB OE =.∵OA OF =，BOA EOF ∠=∠，∴△BOA ≌△EOF .∴AB FE =，BAO EFO ∠=∠. ∵AC 平分BAE ∠，∴12BAO EAO BAE ∠=∠=∠.∴EFO EAO ∠=∠. ∴AE FE =.∴AB AE =. ………………………………………………………………………5分 ∵OB OE =， ∴AC BE ⊥.∴四边形BCED 为菱形.∴BD BC =. ……………………………………………………………………………6分 ∴BDC BCD ∠=∠.∴在△BCD 中，2180CBD BCD ∠+∠=︒. ∵在△ABC 中，2180BAC BCD ∠+∠=︒. ∴BAC CBD ∠=∠.∴12CBD BAE ∠=∠. ………………………………………………………………7分28.（1）如图，四边形ABCD 即为所求.……………………………………………………………………………………………….1分x点D 的坐标为(1,2)D −. …………………………………………………………………..2分 （2）如图，弦AB 的弦切四边形为正方形ABCD ，设正方形ABCD 的边长为a ，CD 与O 的切点为E ，连接EO 并延长交AB 于点F . ∵CD 与O 的切点为E ，EF 经过圆心O ， ∴EF CD ⊥.∵四边形ABCD 为正方形， ∴AB // CD ，AB BC a ==. ∴EF AB ⊥. ∴1122AF AB a ==，EF BC a ==. ∵1OE =， ∴1OF a =−.在Rt △OAF 中，由勾股定理得，222OA OF AF =+.∴22211(1)()2a a =−+.解得 85a =. ∴AB 的长为85. ………………………………………………………………………..5分（3）05t <≤或2t =. ………………………………………………………………………..2分。

2023北京初三（上）期末数学汇编解直角三角形三、解答题4．（2023秋·北京密云·九年级统考期末）2022年11月29日，搭载神舟十五号载人飞船的运载火箭在酒泉65，在点45，其中，线段的距离为5.5．根据这些数据，请计算旗杆)≈≈≈650.9,cos650.4,tan65 2.16．（2023秋·北京平谷·90，AD ⊥于点E点D，DE AB九年级北京市十一学校校考期末）如图，在ABC中，9．（2023秋·北京西城·九年级北京市第六十六中学校考期末）从西双版纳傣族自治州走出丛林，一路北上，历经波“观象热潮”．象群北移途经峨山县时，一头亚洲象曾脱离象群．如图，位置和独象位置．经测量，象群在峨山县西北方向约东30°方向的交汇处，请你计算此时独象距离象群多少公里？（结果保留根号）30,37,90,AB ABH AHB 结合sin37,AH AB再解方程即可【详解】解：由题意得：30,37,90,AB ABH AHBsin 37,AH AB 300.6018AH m ，故答案为：18【点睛】本题考查的是解直角三角形的实际应用，掌握关键.Rt AOC 中，求出Rt AOC 中，由10km ，进一步即可得到两个雷达站之间的距离．Rt AOC中，AC C=cos20∠=ABORt AOC中，45==10kmBO AOBC OC BO=−⨯−10 1.73210、C两个雷达站之间的距离为7.32km【点睛】此题考查了解直角三角形的应用，数形结合并准确计算是解题的关键．12米90，DE在Rt△ABD中∵AB=12，∠BAD=45°。

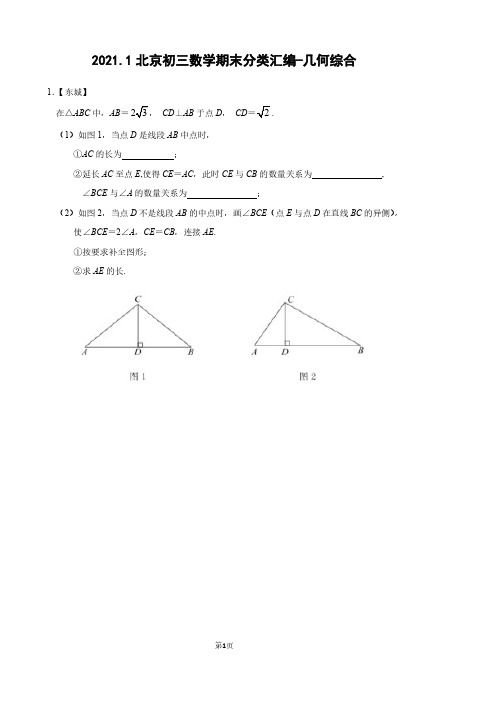
2021_2012东城区九年级上期末数学分类汇编——几何综合一．解答题（共9小题）1．在△ABC中，AB＝2，CD⊥AB于点D，CD＝．（1）如图1，当点D是线段AB的中点时，①AC的长为；②延长AC至点E，使得CE＝AC，此时CE与CB的数量关系是CE＝CB，∠BCE与∠A的数量关系是∠BCE＝2∠A；（2）如图2，当点D不是线段AB的中点时，画∠BCE（点E与点D在直线BC的异侧），使∠BCE＝2∠A，CE＝CB，连接AE．①按要求补全图形；②求AE的长．【分析】（1）①利用勾股定理求解即可．②利用线段的垂直平分线的性质以及三角形的外角的性质解决问题即可．（2）①根据要求作出图形即可．②如图2中，在AC的上方作△ACT，使得CT＝CA，∠ACT＝∠BCE，过点C作CH⊥AT于H．证明△ACE≌△TCB（SAS），推出AE＝BT，可得结论．【解答】解：（1）①如图1中，∵AD＝DB＝AB＝，CD⊥AB，∵CD＝，∴AC＝＝＝．故答案为：．②连接BE．∵CA＝CE，CA＝CB，∴CE＝CB，∵CA＝CB，∴∠A＝∠CBA，∴∠ECB＝∠A+∠CBA＝2∠A，故答案为：CE＝CB，∠BCE＝2∠A．（2）①图形如图2所示：②如图2中，在AC的上方作△ACT，使得CT＝CA，∠ACT＝∠BCE，过点C作CH⊥AT于H．∵CA＝CT，CH⊥AT，∴AH＝HT，∠ACH＝∠TCH，∵∠BCE＝2∠CAB，∠ECB＝∠ACT，∴∠ACH＝∠CAB，∴CH∥AB，∵CD⊥AB，∴∠ADC＝90°，∴四边形ADCH是矩形，∴CD＝AH＝HT＝，∴AT＝2AH＝2，∵∠ACT＝∠ECB，∴∠ACE＝∠TCB，∵CA＝CT，CE＝CB，∴△ACE≌△TCB（SAS），∴AE＝BT，∵BT＝＝＝2，∴AE＝BT＝2．【点评】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，线段的垂直平分线的性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常常考题型．2．在△ABC中，∠BAC＝45°，CD⊥AB于点D，AE⊥BC于点E，连接DE．（1）如图1，当△ABC为锐角三角形时，①依题意补全图形，猜想∠BAE与∠BCD之间的数量关系并证明；②用等式表示线段AE，CE，DE的数量关系，并证明；（2）如图2，当∠ABC为钝角时，依题意补全图形并直接写出线段AE，CE，DE的数量关系．【分析】（1）①依题意补全图形，由直角三角形的性质得出∠B+∠BAE＝∠B+∠BCD＝90°，即可得出∠BAE＝∠BCD②作DG⊥DE，交AE于G，则∠EDG＝90°＝∠CDA，得出∠ADG＝∠CDE，证出△ACD是等腰直角三角形，得出AD＝CD，由①得出∠DAG＝∠DCE，证明△ADG≌△CDE （ASA），得出AG＝CE，DG＝DE，证出△DEG是等腰直角三角形，得出EG＝DE，即可得出结论；（2）作DG⊥DE，交AE的延长线于G，则∠EDG＝90°＝∠CDA，证出△ACD是等腰直角三角形，得出AD＝CD，证明△ADG≌△CDE（ASA），得出AG＝CE，DG＝DE，得出△DEG是等腰直角三角形，证出EG＝DE，即可得出结论．【解答】解：（1）①依题意补全图形，如图1所示：猜想∠BAE＝∠BCD，理由如下：∵CD⊥AB于点D，AE⊥BC于点E，∴∠CDB＝∠CDA＝∠AEB＝90°，∴∠B+∠BAE＝∠B+∠BCD＝90°，∴∠BAE＝∠BCD；②AE＝CE+DE，理由如下：作DG⊥DE，交AE于G，如图1﹣1所示：则∠EDG＝90°＝∠CDA，∴∠ADG＝∠CDE，∵∠BAC＝45°，∴△ACD是等腰直角三角形，∴AD＝CD，由①得：∠DAG＝∠DCE，在△ADG和△CDE中，，∴△ADG≌△CDE（ASA），∴AG＝CE，DG＝DE，∴△DEG是等腰直角三角形，∴EG＝DE，∵AE＝AG+EG，∴AE＝CE+DE；（2）依题意补全图形如图2所示：CE＝AE+DE，理由如下：作DG⊥DE，交AE的延长线于G，则∠EDG＝90°＝∠CDA，∴∠ADG＝∠CDE，∵∠BAC＝45°，∴△ACD是等腰直角三角形，∴AD＝CD，同①得：∠DAG＝∠DCE，在△ADG和△CDE中，，∴△ADG≌△CDE（ASA），∴AG＝CE，DG＝DE，∴△DEG是等腰直角三角形，∴EG＝DE，∵AG＝AG+EG，∴CE＝AE+DE．【点评】本题是四边形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、直角三角形的性质等知识；本题综合性强，证明三角形全等是解题的关键．3．如图，M为正方形ABCD内一点，点N在AD边上，且∠BMN＝90°，MN＝2MB．点E 为MN的中点，点P为DE的中点，连接MP并延长到点F，使得PF＝PM，连接DF．（1）依题意补全图形；（2）求证：DF＝BM；（3）连接AM，用等式表示线段PM和AM的数量关系并证明．【分析】（1）根据题意可以画出完整的图形；（2）由MN＝2MB，点E为MN的中点可知，要证明DF＝BM，只要证明DF＝EM即可，要证明DF＝EM，只要证明△MPE≌△FPD即可，然后根据题目中的条件和全等三角形的判定即可证明结论成立；（3）首先写出线段PM和AM的数量关系，然后根据题意作出合适的辅助线，利用全等三角形的判定和性质、正方形的性质即可证明结论成立．【解答】解：（1）如右图所示；（2）∵点P为线段DE的中点，∴DP＝EP在△MPE和△FPD中，∴△MPE≌△FPD（SAS），∴DF＝EM，∵E为MN的中点，∴MN＝2ME，∵MN＝2MB，∴MB＝ME＝DF，∴DF＝BM；（3）结论：，证明：连接AF，由（2）可知：△MPE≌△FPD，∴∠DFP＝∠EMP，∴DF∥ME，∴∠FDN＝∠MND，在正方形ABCD中，AD＝AB，∠BAD＝90°，又∵∠BMN＝90°，∴∠MBA+∠MNA＝180°，又∵∠MNA+∠MND＝180°，∴∠MBA＝∠MND，∴∠FDN＝∠MBA，在△F AD和△MAB中，，∴△F AD≌△MAB（SAS），∴∠F AD＝∠MAB，F A＝MA，∴∠F AM＝∠DAB＝90°，∴△F AM为等腰直角三角形，∴又∵FM＝2PM，∴．【点评】本题考查全等三角形的判定与性质、等腰直角三角形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．4．点P是矩形ABCD对角线AC所在直线上的一个动点（点P不与点A，C重合），分别过点A，C向直线BP作垂线，垂足分别为点E，F，点O为AC的中点．（1）如图1，当点P与点O重合时，请你判断OE与OF的数量关系；（2）当点P运动到如图2所示位置时，请你在图2中补全图形并通过证明判断（1）中的结论是否仍然成立；（3）若点P在射线OA上运动，恰好使得∠OEF＝30°时，猜想此时线段CF，AE，OE 之间有怎样的数量关系，直接写出结论不必证明．【分析】（1）根据矩形的性质以及垂线，即可判定△AOE≌△COF（AAS），得出OE＝OF；（2）先延长EO交CF于点G，通过判定△AOE≌△COG（ASA），得出OG＝OE，再根据Rt△EFG中，OF＝EG，即可得到OE＝OF；（3）根据点P在射线OA上运动，需要分两种情况进行讨论：当点P在线段OA上时，当点P在线段OA延长线上时，分别根据全等三角形的性质以及线段的和差关系进行推导计算即可．【解答】解：（1）OE＝OF．理由：如图1，∵四边形ABCD是矩形，∴OA＝OC，∵AE⊥BP，CF⊥BP，∴∠AEO＝∠CFO＝90°，∵在△AOE和△COF中，，∴△AOE≌△COF（AAS），∴OE＝OF；（2）补全图形如右图2，OE＝OF仍然成立．证明：延长EO交CF于点G，∵AE⊥BP，CF⊥BP，∴AE∥CF，∴∠EAO＝∠GCO，又∵点O为AC的中点，∴AO＝CO，在△AOE和△COG中，，∴△AOE≌△COG（ASA），∴OG＝OE，∴Rt△EFG中，OF＝EG，∴OE＝OF；（3）CF＝OE+AE或CF＝OE﹣AE．证明：①如图2，当点P在线段OA上时，∵∠OEF＝30°，∠EFG＝90°，∴∠OGF＝60°，由（2）可得，OF＝OG，∴△OGF是等边三角形，∴FG＝OF＝OE，由（2）可得，△AOE≌△COG，∴CG＝AE，又∵CF＝GF+CG，∴CF＝OE+AE；②如图3，当点P在线段OA延长线上时，∵∠OEF＝30°，∠EFG＝90°，∴∠OGF＝60°，同理可得，△OGF是等边三角形，∴FG＝OF＝OE，同理可得，△AOE≌△COG，∴CG＝AE，又∵CF＝GF﹣CG，∴CF＝OE﹣AE．【点评】本题属于四边形综合题，主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定，解决问题的关键是构建全等三角形和证明三角形全等，利用矩形的对角线互相平分得全等的边相等的条件，根据线段的和差关系使问题得以解决．5．已知，在等边△ABC中，AB＝2，D，E分别是AB，BC的中点（如图1）．若将△BDE 绕点B逆时针旋转，得到△BD1E1，设旋转角为α（0°＜α＜180°），记射线CE1与AD1的交点为P．（1）判断△BDE的形状；（2）在图2中补全图形，①猜想在旋转过程中，线段CE1与AD1的数量关系并证明；②求∠APC的度数；（3）点P到BC所在直线的距离的最大值为2．（直接填写结果）【分析】（1）由D，E分别是AB，BC的中点得到BE＝BC，BD＝BA，加上△ABC 为等边三角形，则∠B＝60°，BA＝BC，所以BD＝BE，于是可判断△BDE为等边三角形；（2）①根据旋转的性质得△BD1E1为等边三角形，则BD1＝BE1，∠D1BE1＝60°，而∠ABC＝60°，所以∠ABD1＝∠CBE1，则路旋转的定义，△ABD1可由△CBE1绕点B逆时针旋转得到，然后根据旋转的性质得CE1＝AD1；②由于△ABD1可由△CBE1绕点B逆时针旋转得到∠BAD1＝∠BCE1，然后根据三角形内角和定理和得∠APC＝∠ABC＝60°；、（3）由于∠APC＝∠D1BE1＝60°，则可判断点P、D1、B、E1共圆，于是可判断当BP ⊥BC时，点P到BC所在直线的距离的最大值，此时点E1在AB上，然后利用含30度的直角三角形三边的关系可得点P到BC所在直线的距离的最大值．【解答】解：（1）∵D，E分别是AB，BC的中点，∴BE＝BC，BD＝BA，∵△ABC为等边三角形，∴∠B＝60°，BA＝BC，∴BD＝BE，∴△BDE为等边三角形；（2）①CE1＝AD1．理由如下：∵△BDE绕点B逆时针旋转，得到△BD1E1，∴△BD1E1为等边三角形，∴BD1＝BE1，∠D1BE1＝60°，而∠ABC＝60°，∴∠ABD1＝∠CBE1，∴△ABD1可由△CBE1绕点B逆时针旋转得到，∴CE1＝AD1；②∵△ABD1可由△CBE1绕点B逆时针旋转得到，∴∠BAD1＝∠BCE1，∴∠APC＝∠ABC＝60°；（3）∵∠APC＝∠D1BE1＝60°，∴点P、D1、B、E1共圆，∴当BP⊥BC时，点P到BC所在直线的距离的最大值，此时点E1在AB上，在Rt△PBC中，PB＝AB＝×2＝2，∴点P到BC所在直线的距离的最大值为2．故答案为2．【点评】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了等边三角形的性质．6．在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．请直接写出AC1与BD1的数量关系和位置关系．（2）如图2，若四边形ABCD是菱形，AC＝6，BD＝8，判断AC1与BD1的数量关系和位置关系，并给出证明；（3）如图3，若四边形ABCD是平行四边形，AC＝6，BD＝12，连接DD1，设AC1＝kBD1，请直接写出k的值和AC12+（kDD1）2的值．【分析】（1）如图1，根据正方形的性质得OC＝OA＝OD＝OB，AC⊥BD，则∠AOB＝∠COD＝90°，再根据旋转的性质得OC1＝OC，OD1＝OD，∠COC1＝∠DOD1，则OC1＝OD1，利用等角的补角相等得∠AOC1＝∠BOD1，然后根据“SAS”可证明△AOC1≌△BOD1；由∠AOB＝90°，则∠OAB+∠ABP+∠OBD1＝90°，所以∠OAB+∠ABP+∠OAC1＝90°，则∠APB＝90°所以AC1⊥BD1；（2）如图2，根据菱形的性质得OC＝OA＝AC，OD＝OB＝BD，AC⊥BD，则∠AOB ＝∠COD＝90°，再根据旋转的性质得OC1＝OC，OD1＝OD，∠COC1＝∠DOD1，则OC1＝OA，OD1＝OB，利用等角的补角相等得∠AOC1＝∠BOD1，加上＝，根据相似三角形的判定方法得到△AOC1∽△BOD1，得到∠OAC1＝∠OBD1，由∠AOB＝90°得∠OAB+∠ABP+∠OBD1＝90°，则∠OAB+∠ABP+∠OAC1＝90°，则∠APB＝90°，所以AC1⊥BD1；然后根据相似比得到＝＝＝＝＝．（3）与（2）一样可证明△AOC1∽△BOD1，则＝＝＝，所以k＝；根据旋转的性质得OD1＝OD，根据平行四边形的性质得OD＝OB，则OD1＝OB＝OD，于是可判断△BDD1为直角三角形，根据勾股定理得BD12+DD12＝BD2＝144，所以（2AC1）2+DD12＝144，于是有AC12+（kDD1）2＝36．【解答】解：（1）AC1＝BD1，AC1⊥BD1；理由：如图1，∵四边形ABCD是正方形，∴OC＝OA＝OD＝OB，AC⊥BD，∴∠AOB＝∠COD＝90°，∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OC1＝OC，OD1＝OD，∠COC1＝∠DOD1，∴OC1＝OD1，∠AOC1＝∠BOD1＝90°+∠AOD1，在△AOC1和△BOD1中，∴△AOC1≌△BOD1（SAS）；∴AC1＝BD1，∵∠AOB＝90°，∴∠OAB+∠ABP+∠OBD1＝90°，∴∠OAB+∠ABP+∠OAC1＝90°，∴∠APB＝90°，则AC1⊥BD1；故AC1与BD1的数量关系是：AC1＝BD1；AC1与BD1的位置关系是：AC1⊥BD1；（2）AC1＝BD1，AC1⊥BD1．理由：∵四边形ABCD是菱形，∴OC＝OA＝AC，OD＝OB＝BD，AC⊥BD．∵△C1OD1由△COD绕点O旋转得到，∴O C1＝OC，O D1＝OD，∠CO C1＝∠DO D1．∴O C1＝OA，O D1＝OB，∠AO C1＝∠BO D1，∴＝．∴＝．∴△AO C1∽△BOD1．∴∠O AC1＝∠OB D1．又∵∠AOB＝90°，∴∠O AB+∠ABP+∠OB D1＝90°．∴∠O AB+∠ABP+∠O AC1＝90°．∴∠APB＝90°．∴AC1⊥BD1．∵△AO C1∽△BOD1，∴＝＝＝＝＝．即AC1＝BD1，AC1⊥BD1．（3）如图3，与（2）一样可证明△AOC1∽△BOD1，∴＝＝＝，∴k＝；∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OD1＝OD，而OD＝OB，∴OD1＝OB＝OD，∴△BDD1为直角三角形，在Rt△BDD1中，BD12+DD12＝BD2＝144，∴（2AC1）2+DD12＝144，∴AC12+（kDD1）2＝36．【点评】本题考查了四边形的综合题：熟练掌握平行四边形和特殊平行四边形的性质、旋转的性质；会运用三角形全等的判定与性质、三角形相似的判定与性质．7．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B＝∠E＝30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1＝S2，证明你的结论；（2）猜想论证当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想．【分析】（1）①根据旋转的性质可得AC＝CD，然后求出△ACD是等边三角形，根据等边三角形的性质可得∠ACD＝60°，然后根据内错角相等，两直线平行解答；②根据等边三角形的性质可得AC＝AD，再根据直角三角形30°角所对的直角边等于斜边的一半求出AC＝AB，然后求出AC＝BD，再根据等边三角形的性质求出点C到AB 的距离等于点D到AC的距离，然后根据等底等高的三角形的面积相等解答；（2）根据旋转的性质可得BC＝CE，AC＝CD，再求出∠ACN＝∠DCM，然后利用“角角边”证明△ACN和△DCM全等，根据全等三角形对应边相等可得AN＝DM，然后利用等底等高的三角形的面积相等证明．【解答】解：（1）①DE∥AC，理由如下：∵△DEC绕点C旋转点D恰好落在AB边上，∴AC＝CD，∵∠BAC＝90°﹣∠B＝90°﹣30°＝60°，∴△ACD是等边三角形，∴∠ACD＝60°，又∵∠CDE＝∠BAC＝60°，∴∠ACD＝∠CDE，∴DE∥AC；②∵∠B＝30°，∠C＝90°，∴CD＝AC＝AB，∴BD＝AD＝AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2；故答案为：DE∥AC；S1＝S2；（2）如图3，∵△DEC是由△ABC绕点C旋转得到，∴BC＝CE，AC＝CD，∵∠ACN+∠BCN＝90°，∠DCM+∠BCN＝180°﹣90°＝90°，∴∠ACN＝∠DCM，在△ACN和△DCM中，，∴△ACN≌△DCM（AAS），∴AN＝DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2．【点评】本题考查了全等三角形的判定与性质，三角形的面积，等边三角形的判定与性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟练掌握等底等高的三角形的面积相等，以及全等三角形的面积相等是解题的关键．8．如图1，在等腰直角△ABC中，∠BAC＝90°，AB＝AC＝2，点E是BC边上一点，∠DEF＝45°且角的两边分别与边AB，射线CA交于点P，Q．（1）如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q．设BP为x，CQ为y，试求y与x的函数关系式，并写出自变量x的取值范围；（2）如图3，点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．【分析】（1）根据条件由勾股定理可以求出BC的值，再求出∠DEB＝∠EQC，就可以得出△BPE∽△CEQ，由相似三角形的性质就可以得出结论；（2））由∠AEF＝∠B＝∠C，且∠AQE＞∠C可以得出∠AQE＞∠AEF．从而有AE≠AQ，再分类讨论，当AE＝EQ时和AQ＝EQ时根据等腰三角形的性质和全等三角形的性质就可以求出BE的值．【解答】解：（1）∵∠BAC＝90°，AB＝AC＝2，∴∠B＝∠C，．又∵∠FEB＝∠FED+∠DEB＝∠EQC+∠C，∠DEF＝∠C，∴∠DEB＝∠EQC，∴△BPE∽△CEQ，∴．设BP为x，CQ为y，∴．∴，自变量x的取值范围是0＜x＜1；（2）∵∠AEF＝∠B＝∠C，且∠AQE＞∠C，∴∠AQE＞∠AEF．∴AE≠AQ．当AE＝EQ时，∴∠EAQ＝∠EQA，∵∠AEQ＝45°，∴∠EAQ＝∠EQA＝67.5°，∵∠BAC＝90°，∠C＝45，∴∠BAE＝∠QEC＝22.5°．∵在△ABE和△ECQ中，，∴△ABE≌ECQ（AAS）．∴CE＝AB＝2．∴BE＝BC﹣EC＝；当AQ＝EQ时，可知∠QAE＝∠QEA＝45°，∴AE⊥BC．∴点E是BC的中点．∴BE＝．综上，在∠DEF运动过程中，△AEQ能成等腰三角形，此时BE的长为或．【点评】本题考查了等腰直角三角形的性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，全等三角形的判定及性质的运用，解答时合理利用相似三角形的性质和全等三角形的性质是关键．9．已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连接DF、CF．（1）如图1，当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD＝1，AC＝，求此时线段CF的长（直接写出结果）．【分析】（1）根据“直角三角形斜边上的中线等于斜边的一半”可知DF＝BF，根据∠DFE＝2∠DBF，∠CFE＝2∠CBF，得到∠EFD+∠EFC＝2∠DBC＝90°，DF⊥BF．（2）延长DF交BC于点G，先证明△DEF≌△GCF，得到DE＝CG，DF＝FG，根据AD＝DE，AB＝BC，得到BD＝BG又因为∠ABC＝90°，所以DF＝CF且DF⊥CF．（3）延长DF交BA于点H，先证明△DEF≌△HBF，得到DE＝BH，DF＝FH，根据旋转条件可以△ADH为直角三角形，由△ABC和△ADE是等腰直角三角形，AC＝，可以求出AB的值，进而可以根据勾股定理可以求出DH，再求出DF，由DF＝CF，求出得CF的值．【解答】解：（1）∵∠ACB＝∠ADE＝90°，点F为BE中点，∴DF＝BE，CF＝BE，∴DF＝CF．∵△ABC和△ADE是等腰直角三角形，∴∠ABC＝45°∵BF＝DF，∴∠DBF＝∠BDF，∵∠DFE＝∠ABE+∠BDF，∴∠DFE＝2∠DBF，同理得：∠CFE＝2∠CBF，∴∠EFD+∠EFC＝2∠DBF+2∠CBF＝2∠ABC＝90°，∴DF＝CF，且DF⊥CF．（2）（1）中的结论仍然成立．证明：如图，此时点D落在AC上，延长DF交BC于点G．∵∠ADE＝∠ACB＝90°，∴DE∥BC．∴∠DEF＝∠GBF，∠EDF＝∠BGF．∵F为BE中点，∴EF＝BF．∴△DEF≌△GBF．∴DE＝GB，DF＝GF．∵AD＝DE，∴AD＝GB，∵AC＝BC，∴AC﹣AD＝BC﹣GB，∴DC＝GC．∵∠ACB＝90°，∴△DCG是等腰直角三角形，∵DF＝GF．∴DF＝CF，DF⊥CF．（3）延长DF交BA于点H，∵△ABC和△ADE是等腰直角三角形，∴AC＝BC，AD＝DE．∴∠AED＝∠ABC＝45°，∵由旋转可以得出，∠CAE＝∠BAD＝90°，∵AE∥BC，∴∠AEB＝∠CBE，∴∠DEF＝∠HBF．∵F是BE的中点，∴EF＝BF，∴△DEF≌△HBF，∴ED＝HB，∵AC＝，在Rt△ABC中，由勾股定理，得AB＝4，∵AD＝1，∴ED＝BH＝1，∴AH＝3，在Rt△HAD中由勾股定理，得DH＝，∴DF＝，∴CF＝∴线段CF的长为．【点评】主要考查了旋转的性质，等腰三角形和全等三角形的判定，及勾股定理的运用．要掌握等腰三角形和全等三角形的性质及其判定定理并会灵活应用是解题的关键．。

编者的话：北京目前主流的初中数学版本为京改版、人教版、北师大版，本专辑针对京改版进行整理汇编，另外两个版本请参考已经上线的人教版通用版本及北师大版通用版本，本专辑选材于京改版近两年最新月考、期中、期末、一二模、中考真题（已标注出处），包含详细解析、思路点拨等，对于期末考试的复习成系统性，把每个章节重难点考察内容进行总结，分选择题、填空题、解答题三种类型，难度为压轴，欢迎下载使用。

【玩转压轴题】考点1：相似三角形问题综合（解析版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，已知ABC V ，6AB =，4AC =，D 为AB 边上一点，且2AD =，E 为AC 边上一点（不与A 、C 重合），若ADE V 与ABC V 相似，则(AE = )A ．2B ．43C ．3或34D ．3或43【标准答案】D 【思路点拨】根据题意，△ADE 与△ABC 相似，由于题中没有指明对应边，故应该分两种情况讨论求解．【精准解析】解：①当△ADE ∽△ABC 时，有AD ：AE=AB ：AC ，∵AB=6，AC=4，AD=2，∴AE=43；②当△AED ∽△ABC 时，有AD ：AE=AC ：AB ，∵AB=6，AC=4，AD=2，∴AE=3，所以AE 等于3或43．故选D ．【名师指导】此题考查学生对相似三角形的性质的掌握情况，注意分类讨论思想的运用．2．如图，下面方格纸中小正方形边长均相等.ABC D 和DEP D 的各顶点均为格点（小正方形的顶点），若ABC D ~PDE D 且两三角形不全等，则P 点所在的格点为（）A ．P 1B ．P 2C ．P 3D ．P 4【标准答案】D 【思路点拨】根据三角形相似ABC D ∽PDE D ，然后利用DE=2，BC=1，所以DP=4，则易得点P 落在P 4处．【精准解析】若ABC ∽PDE D 且两三角形不全等，则DE BC =PDAB=2．所以DP=4．则易得点P 落在P 4处．故选D 【名师指导】本题考查了三角形相似的性质,掌握该性质是解答本题的关键.3．（2021·北京市古城中学九年级月考）如图，已知点P 在ABC D 的边AC 上，下列条件中，不能判断ABP ACB D D ∽的是 ( )A ．ABP C Ð=ÐB ．APB ABC Ð=ÐC ．2AB AP AC =·D ．AB ACBP CB=【标准答案】D 【思路点拨】根据相似三角形的判定定理（①有两角分别相等的两三角形相似，②有两边的比相等，并且它们的夹角也相等的两三角形相似）逐个进行判断即可．【精准解析】A 、∵∠A ＝∠A ，∠ABP ＝∠C ，∴△ABP ∽△ACB ，故本选项错误；B 、∵∠A ＝∠A ，∠APB ＝∠ABC ，∴△ABP ∽△ACB ，故本选项错误；C 、∵∠A ＝∠A ，AB 2＝AP•AC ，即AB ACAP AB=，∴△ABP ∽△ACB ，故本选项错误；D 、根据AB ACBP CB=和∠A ＝∠A 不能判断△ABP ∽△ACB ，故本选项正确；故选：D ．【名师指导】此题考查了相似三角形的性质．此题比较简单，解题的关键是掌握有两角对应相等的三角形相似与两边对应成比例且夹角相等的三角形相似定理的应用．4．大约在两千四五百年前，如图1墨子和他的学生做了世界上第一个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm ，像距为15cm ，蜡烛火焰倒立的像的高度是6cm ，则蜡烛火焰的高度是（ ）A ．3cmB ．4cmC ．6cmD ．9cm【标准答案】B 【思路点拨】根据小孔成像的性质及相似三角形的性质求解即可．【精准解析】根据小孔成像的性质及相似三角形的性质可得：蜡烛火焰的高度与火焰的像的高度的比值等于物距与像距的比值，设蜡烛火焰的高度为xcm ，则10615x =，x=4，即蜡烛火焰的高度为4cm ，故答案为：B ．【名师指导】本题考查了相似三角形性质的应用，解题的关键在于理解小孔成像的原理得到相似三角形．5．已知ABC V ，2，则与ABC V 相似的三角形的三边长可能是（ ）A ．1B ．1C ．1D ．1【标准答案】A 【思路点拨】根据相似三角形的判定定理即可得到结论．【精准解析】解：∵△ABC ，2，∴△ABC 2=1∴△ABC 相似的三角形三边长可能是1故选：A ．【名师指导】本题考查了相似三角形的判定，熟练掌握相似三角形的判定定理是解题的关键．6．如图，在正方形ABCD 中，点M 是AB 上一动点，点E 是CM 的中点，AE 绕点E 顺时针旋转90°得到EF ，连接DE ，DF 给出结论：①DE EF =；②45CDF Ð=°；③AMDF④若正方形的边长为2，则点M 在射线AB 上运动时，CF ．其中结论正确的是（ ）A ．②③④B ．①②③C ．①③④D ．①②④【标准答案】D 【思路点拨】延长AE 交DC 的延长线于点H ，由“AAS ”可证△AME ≌△HCE ，可得AE =EH ，由直角三角形的性质可得AE =EF =EH ，可判断①；由四边形内角和定理可求2∠ADE +2∠EDF =270°，可得∠ADF =135°，可判断②；由垂线段最短，可得当CF ⊥DF 时，CF 有最小值，由等腰直角三角形的性质可求CF 的最小值，可判断④；由连接AC ，过点E 作EP ⊥AD 于点P ，过点F 作FN ⊥EP 于N ，交CD 于G ，连接CF ，由梯形中位线定理可求PE =12（AM +CD ），由“AAS ”可证△APE ≌△ENF ，可得AP =NE =12AD ，即可求AM =2DG =2=，可判断③，即可求解．【精准解析】解：如图，延长AE交DC的延长线于点H，Q点E是CM的中点，ME EC\=，Q，//AB CDÐ=Ð，\Ð=Ð，AME HCEMAE H\D@D，()AME HCE AAS\=，AE EH又90Q，Ð=°ADH\==，DE AE EH∵绕点E顺时针旋转90°得到EF，AE\=，90AE EFÐ=°，AEF\==，故①正确；AE DE EFQ，AE DE EF==Ð=Ð，\Ð=Ð，EDF EFDDAE ADEQ，Ð+Ð+Ð+Ð+Ð=°AEF DAE ADE EDF EFD360\Ð+Ð=°，22270ADE EDFADF\Ð=°，135CDF ADF ADC\Ð=Ð-Ð=°-°=°，故②正确；1359045如图，连接AC，过点E作EP AD⊥于N，交CD于G，连接⊥于点P，过点F作FN EPCF，EP AD ⊥Q ，FN EP ⊥，90ADC Ð=°，\四边形PDGN 是矩形，PN DG \=，90DGN Ð=°，45CDF Ð=°Q ，\点F 在DF 上运动，\当CF DF ^时，CF 有最小值，2CD =Q ，45CDF Ð=°，CF \的最小值==④正确；EP AD ⊥Q ，AM AD ⊥，CD AD ⊥，////AM PE CD \，\1AP MEPD EC==，AP PD \=，PE \是梯形AMCD 的中位线，1()2PE AM CD \=+，45FDC Ð=°Q ，FNCD ⊥，45DFG FDC \Ð=Ð=°，DG GF \=，DF =，90AEP FEN Ð+Ð=°Q ，90AEP EAP Ð+Ð=°，FEN EAP \Ð=Ð，又AE EF =Q ，90APE ENF Ð=Ð=°，()APE ENF AAS \D @D ，12AP NE AD \==，11()22PE AM CD NE NP AD NP =+=+=+Q ，\12AM NP DG ==，22AM DG\===，\AMDF=，故③错误；故选：D．【名师指导】本题考查了正方形的性质，全等三角形的判定和性质，矩形的判定和性质，旋转的性质，平行线分线段成比例，梯形中位线的定理等知识，灵活运用这些性质解决问题是本题的关键．7．（2021·北京东城·一模）一个直角三角形木架的两条直角边的边长分别是30cm，40cm．现要做一个与其相似的三角形木架，如果以60cm长的木条为其中一边，那么另两边中长度最大的一边最多可达到（）A．60cm B．75cm C．100cm D．120cm【标准答案】C【思路点拨】根据勾股定理求出斜边的长，以60cm长的木条为直角边，设相似的三角形中斜边长为xcm，利用相似三角形的对应边的比相等列分式方程，解方程即可得到答案．【精准解析】∵直角三角形两条直角边分别是30cm，40cm，∴斜边50==，∵要做一个与其相似的三角形木架，∴两个三角形对应边成比例，∵直角三角形中斜边最大，∴以60cm长的木条为直角边，设相似的三角形中斜边长为xcm，则有2种情况，①3050=60x，解得：100x=，②4050=60x，解得：75x=，∴另两边中长度最大的一边最多可达到100cm，故选：C．【名师指导】本题考查了相似三角形的性质及勾股定理，利用相似三角形的性质即相似三角形的对应边的比相等进行计算是解题的关键．8．（2021·北京·清华附中九年级月考）如图，在ABC V 中，90ABC Ð=°，30C Ð=°，以点A 为圆心，以AB 的长为半径作弧交AC 于点D ，连接BD ，再分别以点B ，D 为圆心，大于12B D 的长为半径作弧，两弧交于点P ，作射线AP 交BC 于点E ，连接DE ，则下列结论中不正确的是（）A ．BE DE =B ．DE 垂直平分线段AC C．EDC ABC S S △△D ．2BD BC BE=×【标准答案】C 【思路点拨】由题中作图方法易证AP 为线段BD 的垂直平分线，点E 在AP 上，所以BE=DE ，再根据，90ABC Ð=°，30C Ð=°得到ABD n 是等边三角形，由“三线合一”得AP 平分BAC Ð，则30PAC C Ð=Ð=°，AE CE =,且30°角所对的直角边等于斜边的一半，故12AB AD AC ==，所以DE 垂直平分线段AC ，证明~EDC ABC D D 可得ED CDAB BC=即可得到结论．【精准解析】由题意可得：AD AB =，点P 在线段BD 的垂直平分线上AD AB =Q ，\点A 在线段BD 的垂直平分线上\AP 为线段BD 的垂直平分线Q 点E 在AP 上，\BE=DE ，故A 正确；Q 90ABC Ð=°，30C Ð=°，60BAC \Ð=°且12AB AD AC ==ABD \D 为等边三角形且AD CD =AB AD BD \==，AP \平分BACÐ1302EAC BAC \Ð=Ð=°，AE EC \=，ED \垂直平分AC ，故B 正确；30ECD ACB Ð=Ð=°Q ，90EDC ABC Ð=Ð=°，EDC ABC \D D ∽，ED CD AB AB BC BC \===，213EDC ABC s s D D \==，故C 错误；ED BE =Q ，AB CD BD==BE BDBD BC\=，2BD BC BE \=×，故D 正确故选C ．【名师指导】本题考查30°角的直角三角形的性质、线段垂直平分线的判定和性质，相似三角形的判定和性质，掌握这些基础知识为解题关键．9．（2021·北京·清华附中九年级月考）如图，在菱形ABCD 中，点E ，F 分别在AB ，CD上，且22BE AE DF CF ==，，点G ，H 分别是AC 的三等分点，则EHFG ABCD S S 四边形菱形的值为（）A ．12B ．16C ．13D ．19【标准答案】D 【思路点拨】由题意可证EG ∥BC ，EG ＝2，HF ∥AD ，HF ＝2，可得四边形EHFG 为平行四边形，即可求解．【精准解析】解：∵BE ＝2AE ，DF ＝2FC ，∴12AE BE =，12CF DF =，∵G 、H 分别是AC 的三等分点，∴12AG GC =，12CH AH =，∴AE AGBE GC=，∴EG ∥BC ，∴13EG AE BC AB ==，同理可得HF ∥AD ，13HF AD =，∴四边形EHGF 为平行四边形，由题意，AEG HEG S S =V V ，∵13EG AE BC AB ==，∴19AEG HEG ABC S S S ==V V V ，根据平行四边形和菱形的性质可得：2129EHFG HEG ABC ABCD S S S S ==V V 四边形菱形，故选：D ．【名师指导】本题考查了菱形的性质，以及平行线分线段成比例定理等，由题意可证EG ∥BC ，HF ∥AD 是本题的关键．10．已知∠PAQ=36°，点B 为射线AQ 上一固定点，按以下步骤作图：①分别以A ，B 为圆心，大于12AB 的长为半径画弧，相交于两点M ，N ；②作直线MN 交射线AP 于点D ，连接 BD ；③以B 为圆心，BA 长为半径画弧，交射线AP 于点C ； 根据以上作图过程及所作图形，下列结论中错误的是（）A．∠CDB=72°B．△ADB∽△ABC C．CD：AD=2：1D．∠ABC=3∠ACB【标准答案】C【思路点拨】根据垂直平分线的性质、等腰三角形的性质及判定，相似三角形的判定一一判断即可．【精准解析】解：由作图可知，MN垂直平分AB，AB＝BC，∵MN垂直平分AB，∴DA＝DB，∴∠A＝∠DBA，∵∠PAQ＝36°，∴∠CDB＝∠A＋∠DBA＝72°，（A正确）∵AB＝BC，∴∠A＝∠ACB＝36°，∴∠ABD＝∠ACB，又∵∠A＝∠A，∴△ADB∽△ABC，（B正确）∵∠A＝∠ACB＝36°，∴∠ABC＝180°－∠A－∠ACB＝108°，∴∠ABC＝3∠ACB，（D正确）∵∠ABD＝36°，∠ABC＝108°，∴∠CBD＝∠ABC－∠ABD＝72°，∴∠CBD＝∠CDB＝72°，∴CD＝BC，∵∠A＝∠ACB＝36°，∴AB ＝BC ，∴CD ＝AB ，∵AD ＋DB ＞AB ，AD ＝DB∴2AD ＞AB∴2AD ＞CD ，（C 错误）故选：C【名师指导】本题考查作图﹣复杂作图，线段的垂直平分线的性质，等腰三角形的性质及判定、相似三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．二、填空题11．（2021·北京朝阳·一模）如图，ABC V 中，BC BA >，点D 是边BC 上的一个动点（点D 与点,B C 不重合），若再增加一个条件，就能使ABD △与ABC V 相似，则这个条件可以是____（写出一个即可）．【标准答案】答案不唯一，如：BAD CÐ=Ð【思路点拨】根据题目特点，结合三角形相似的判定定理，添加合适的条件即可．【精准解析】∵∠DBA =∠CBA ，根据两边对应成比例及其夹角相等的两个三角形相似，∴添加的条件是DB ：BA =AB ：BC ；∵∠DBA =∠CBA ，根据两组对应角对应相等相等的两个三角形相似，∴添加的条件是BAD C Ð=Ð；故答案为：DB：BA=AB：BC或BAD CÐ=Ð．【名师指导】本题考查了三角形相似的判定定理，熟练掌握三角形相似的判定定理是解题的关键．12．（2021·北京顺义·二模）如图所示的网格是正方形网格，A，B，C是网格线的交点，D，E是AC，BC分别与网格线的交点，若小正方形的边长为1，则DE的长为________．【标准答案】2【思路点拨】根据格点的特征可得12CM CDCN AC==，再证明△CDE∽△CAB，根据相似三角形的性质可得12DE CDAB AC==，由此即可求得DE=2．【精准解析】如图，∵DM//AN，∴12 CM CDCN AC==，∵DE//AB，∴△CDE∽△CAB，∴12 DE CDAB AC==，∵AB=4，∴DE=2．故答案为：2．【名师指导】本题考查了相似三角形的判定及性质，根据格点的特征证得△CDE∽△CAB是解决问题的关键．13．（2021·北京市十一学校九年级期末）如图，在矩形ABCD中，将边BC翻折，翻折后的线段BE正好落在对角线BD所在的直线上，折痕为BF，已知CF＝1，BC＝2，则矩形ABCD的面积为___．【标准答案】16 3【思路点拨】根据△DEF∽△DCB，可得CD=2DE，设DE=x，则CD=2x，在Rt△DEF中，根据勾股定理列出方程即可解决问题．【精准解析】解：∵将矩形ABCD的边BC翻折，∴CF=EF=1，∠DEF=∠C=90°，∵∠FDE=∠BDC∴△DEF∽△DCB，∴12 EF DEBC CD==，∴CD=2DE，设DE=x，则CD=2x，∴DF =2x -1，在Rt △DEF 中，由勾股定理得：DE 2+EF 2=DF 2，∴x 2+12=（2x -1）2，解得x =43或x =0（舍），∴CD =2x =83，∴S 矩形ABCD =CD ×BC =83×2=163，故答案为：163．【名师指导】本题主要考查了矩形的性质、翻折的性质、以及三角形相似的判定与性质，勾股定理等知识，用方程思想是解题的关键．14．（2021·北京市第十三中学九年级期中）在平面直角坐标系中，A （3，﹣3），B （1，0），C （3，0），点P 在y 轴的正半轴上运动，若以点O 、B 、P 为顶点的三角形与三角形ABC 相似，则点P 的坐标为 ____．【标准答案】（0，23）或（0，32）．【思路点拨】利用点A 、B 、C 的坐标特征得到∠ACB ＝90°，CB ＝2，CA ＝3，设P 点坐标为（0，t ），由∠POB ＝∠ACB ，推出当OP OB BC CA =时，△OPB ∽△CBA ，即123t =；当OP OB CA CB =时，△OPB ∽△CAB ，即132t =，分别求出t 的值，从而得到点P 的坐标.【精准解析】∵B （1，0）、A （3，﹣3）、C （3，0），∴∠ACB ＝90°，CB ＝2，CA ＝3，设P 点坐标为（0，t ），∵∠POB ＝∠ACB ＝90°，∴当OP OB BC CA =时，△OPB ∽△CBA ，即123t =，解得t ＝±23，此时P 点坐标为（0，23），当OP OB CA CB =时，△OPB ∽△CAB ，即132t =，解得t ＝±32，此时P 点坐标为（0，32），综上所述，若以O 、B 、P 为顶点的三角形与△ABC 相似，则点P 的坐标为（0，23）或（0，32）．故答案为（0，23）或（0，32）．【名师指导】本题考查了相似三角形的判定，根据比例线段列出方程是解题的关键.15．（2021·北京·清华附中九年级月考）如图，把边长为3的正方形OABC 绕点O 逆时针旋转n °()090n <<得到正方形ODEF ，DE 与BC 交于点P ，ED 的延长线交AB 于点Q ，交OA 的延长线于点M ．若:3:1BQ AQ =，则AM =______．【标准答案】25．【思路点拨】连接OQ ，OP ，利用HL 证明Rt △OAQ ≌Rt △ODQ ，得QA=DQ ，同理可证：CP=DP ，设CP=x ，则BP =3-x ，PQ=x +34，在Rt △BPQ 中，利用勾股定理列出方程（3-x ）2+（94）2=（x +34）2，解方程得x =94，再利用△AQM ∽△BQP 可求解．【精准解析】解：连接OQ ，OP ，∵将正方形OABC 绕点O 逆时针旋转n °（0＜n ＜90）得到正方形ODEF ，∴OA =OD ，∠OAQ =∠ODQ =90°，在Rt △OAQ 和Rt △ODQ 中，OQ OQ OA OD=ìí=î ，∴Rt △OAQ ≌Rt △ODQ （HL ），∴QA =DQ ，同理可证：CP =DP ，∵BQ ：AQ =3：1，AB =3，∴BQ =94，AQ =34，设CP=x ，则BP =3-x ，PQ=x +34，在Rt △BPQ 中，由勾股定理得：（3-x ）2+（94）2=（x +94）2，解得x =95，∴BP =65，∵∠AQM =∠BQP ，∠BAM =∠B ，∴△AQM ∽△BQP ，∴AM AQ BP BQ =＝13，∴1635AM =，∴AM =25．故答案为：25．【名师指导】本题主要考查了旋转的性质，全等三角形的判定与性质，勾股定理，相似三角形的判定与性质等知识，利用全等证明QA =DQ ，CP =DP是解题的关键．16．（2021·北京·牛栏山一中实验学校九年级月考）如图，已知点P是边长为4的正方形ABCD内一点，且PB＝3，BF⊥BP，垂足是点B，若在射线BF上找一点M，使以点B，M，C为顶点的三角形与△ABP相似，则BM的长为___．【标准答案】163或3【思路点拨】由于∠ABC=∠PBF=90°，同时减去∠PBC后可得到∠ABP=∠CBF，若以点B，M，C为顶点的三角形与△ABP相似，那么必有：AB BMPB BC=或AB BCPB BM=，可据此求得BM的值．【精准解析】解：∵四边形ABCD是正方形，∴∠ABC=90°，AB=BC=4；又∵∠PBF=90°，∴∠ABP=∠CBF=90°-∠CBP；若以点B，M，C为顶点的三角形与△ABP相似，则：①AB BMPB BC=，即434BM=，解得BM=163；②AB BCPB BM=，即443BM=，解得BM=3；故答案为：163或3．【名师指导】本题考查了相似三角形的判定和性质，应注意相似三角形的对应顶点不明确时，要分类讨论，不要漏解．17．（2021·北京·牛栏山一中实验学校九年级月考）如图，正方形ABCD中，点E是对角线BD上一点，且BE＝2DE，连接AE并延长交CD于G，点F是BC边上一点，且CF＝2BF，连接AF、EF、FG．下列四个结论：①DG＝CG；②AF＝AG；③S△ABF ＝S△FCG；④AE＝EF．其中正确的结论是___．（写出所有正确结论的序号）【标准答案】①③④【思路点拨】由正方形的性质证明,DEG BEA V V ∽再利用相似三角形的性质可判断①；如图，设BF =m ，而CF ＝2BF ，则CF =2m ，AB =AD =3m ，DG =CG =32m ，再利用勾股定理计算可判断②；过点E 作AB 的平行线，交AD 于M ，交BC 于N ，利用矩形与相似三角形的性质求解AM =2m ，DM =m ，NC =m ， 则BN =BC -NC =2m ，FN =BN -BF =m ， ME =m ，EN =2m ，再利用勾股定理计算可判断④ ；再利用三角形的面积公式进行计算可判断③，从而可得答案.【精准解析】解：Q 正方形,ABCD //,,AB CD AB CD \=,DEG BEA \V V ∽ 而2,BE DE =1,2DG DE EG AB BE AE\=== 11,22DG AB CD \== ,DG CG \= 故①正确；如图，设BF =m ，而CF ＝2BF ，则CF =2m ，AB =AD =3m ，DG =CG =32m ，在Rt △ABF 中， ,AF ==而,AG =,AF AG \¹ 故②错误；过点E 作AB 的平行线，交AD 于M ，交BC 于N ， 可得四边形MNCD 是矩形，△AME ∽△ADG ，2,3AM AE AD AG \== ∵AD =3m ，∴AM =2m ，DM =m ，NC =m ， 则BN =BC -NC =2m ，FN =BN -BF =m ，∵MD ∥BN ，∴△MDE ∽NBE ， 且相似比12，∴ME =m ，EN =2m ，在Rt △EFN 中， EF = ,=在Rt △AME 中， ,AE ==,AE EF \= 故④正确；2211311333,2,2222222ABF FCG S AB BF m m m S FC CG m m m ==´´===´=V V Q g g g ,ABF FCG S S \=V V 故③正确；综上：正确的有：①③④故答案为：①③④【名师指导】本题考查的是勾股定理的应用，正方形的性质，矩形的判定与性质，相似三角形的判定与性质，熟练的应用相似三角形的性质解决问题是关键.18．（2021·北京·清华附中九年级月考）如图，一个由8个正方形组成的“C ”型模板恰好完全放入一个矩形框内，模板四周的直角顶点M ，N ，O ，P ，Q 都在矩形ABCD 的边上，若8个小正方形的面积均为1，则边AB 的长为__________．【思路点拨】如图，延长,NO QP 交于点E ，连接,OE PE ，根据题意求得OP 的长，设,MB a AM b ==，先证明AMN BQM △≌△，再证明AMN DNO △∽△，PQC QMB △∽△，分别求出矩形的四边，根据矩形对边相等列方程组求得,a b 的值，进而求得AB 的值．【精准解析】Q 小正方形的面积为11=，如图，延长,NO QP 交于点E ，连接,OE PE ，Q 4MN MQ ==，90ONM NMQ MQP Ð=Ð=Ð=°，\四边形MNEQ 是正方形，2,1NO PQ ==Q ，42,4413OE NO PE PQ \=-==-=-=，OP ===设,MB a AM b ==，Q 四边形ABCD 是矩形，\90A B C D Ð=Ð=Ð=Ð=°，90NMQ A Ð=Ð=°Q ，90,90AMN BMQ AMN ANM \Ð+Ð=°Ð+Ð=°，ANM BMQ \Ð=Ð，A B Ð=ÐQ ，MN MQ =，AMN BQM \△≌△，AN BM a \==，BQ AM b ==，90MNO A Ð=Ð=°Q ，90,90ANM DNO AMN ANM \Ð+Ð=°Ð+Ð=°DNO AMN\Ð=A DÐ=ÐQ AMN DNO\△∽△2142DN DO NO AM AN MN \====11112222DO AN a DN AM b \====，90MQP C D Ð=Ð=Ð=°Q 90MQB BMQ MQB PQC \Ð+Ð=Ð+Ð=°PQC QMB\Ð=ÐPQC QMB\△∽△14PQ QC PC MQ MB QB \===1111,4444PC QB b QC MB a \====AB DC=Q DO OP PC AB\++=即1124a b a b +=+①Q AD BC=2b a b +=联立12a b a ì+ïïíïïî解得a b ìïïíïïîAB a \=【名师指导】本题考查了矩形的性质，正方形的性质，全等三角形的性质与判定，相似三角形的性质与判定，解二元一次方程组，勾股定理，综合运用以上知识是解题的关键．19．（2021·北京市陈经纶中学分校九年级月考）在V ABC 中，D ，E 分别是AC ，BC 的中点，点F 在边AB 上，BD 与FC 相交于点G ，连接EG ，若13BF AB =，则BFG BEGS S =△△________．【标准答案】23【思路点拨】取AF 的中点H ，连接DH ，可证得G 为BD 中点，由中位线性质证明//EG AC ，继而证明BGE BDC V :V ，再根据相似三角形的性质得到14BEG BCD S S =V V ，结合等底等高的面积相等解题即可．【精准解析】解：取AF 的中点H ，连接DH ，如图，13BF AB H =，Q 为AF 的中点，13BF FH AH AB \===Q D 为AC 的中点，H 为AF 的中点，DH 是AFC △的中位线，//DH FC\BF FH=Q G \为BD 中点，E Q 为BC 的中点，//EG AC\BGE BDC\V :V 21()4BEG BCD S BE S BC \==V V 14BEG BCD S S \=V V Q D 为AC 的中点，12BCD ABC S S \=△△18BEG ABC S S \=V V 设BFG S a=V 6ABD S a\=V Q D 为AC 的中点，162ABD ABC S S a \==V V 12ABC S a\=V 112BFG ABC S S \=VV1212138ABC BFGBEG ABC S S S S \==△△△△，故答案为：23．【名师指导】本题考查三角形中位线性质、相似三角形的判断与性质、等底等高三角形的面积等知识，是重要考点，掌握相关知识是解题关键．20．（2021·北京·清华附中九年级月考）如图，ABC V 中，3AC =，4BC =，5AB =．四边形ABEF 是正方形，点D 是直线BC 上一点，且1CD =．P 是线段DE 上一点，且23PD DE =．过点P 作直线l 于BC 平行，分别交AB ，AD 于点G ，H ，则GH 的长是__________．【标准答案】13或59．【思路点拨】结合勾股定理逆定理判断ABC D 是直角三角形，通过证明GBM BCA D D ∽，AGH ABD D D ∽，然后利用相似三角形的性质求解，然后分当点D 位于C 点左侧时，当点D 位于C 点右侧时，进行分类讨论．【精准解析】解：ABC D Q 中，3AC =，4BC =，5AB =，2225AC BC \+=，225AB =，222AC BC AB \+=，ABC D ∴为直角三角形，①当点D 位于C 点左侧时，如图：设直线l 交BE 于点M，//l BC Q ，\11D P BM BE D E=，MGB ABC Ð=Ð，又Q 四边形ABEF 是正方形，且1123PD D E =，5BE AB \==，90EBA а=，即253BM =，解得：103BM =，MGB ABC Ð=ÐQ ，90EBA ACB Ð=Ð=°，GBM BCA \D D ∽，\GB BC BM AC=，\41033GB =，解得：409GB =，59AG AB GB \=-=，//l BC Q ，1AGH ABD \D D ∽，\1GH AG BD AB=，11CD =Q ，113BD BC CD \=-=，\5935GH =，解得：13GH =；②当点D 位于C 点右侧时，如图：与①同理，此时215CD BC CD =+=，\5955GH =，解得：59GH =，综上，GH 的长为13或59，故答案为：13或59．【名师指导】本题考查勾股定理逆定理，相似三角形的判定和性质，理解题意，证明出GBM BCA D D ∽，特别注意分类思想的运用是解题关键．三、解答题21．如图，Rt ABC V 中，90B =o ∠，点D 在边AC 上，且DE AC ⊥交BC 于点E ．（1）求证：~CDE CBA V V ．（2）若3AB =，5AC =，E 是BC 中点，求DE 的长．【标准答案】（1）见解析；（2）65DE =【思路点拨】（1）由DE ⊥AC ，∠B ＝90°可得出∠CDE ＝∠B ，再结合公共角相等，即可证出△CDE ∽△CBA ；（2）在Rt △ABC 中，利用勾股定理可求出BC 的长，结合点E 为线段BC 的中点可求出CE 的长，再利用相似三角形的性质，即可求出DE 的长．【精准解析】（1）,90DE AC B °^Ð=Q 90CDE B °\Ð=Ð=C CÐ=ÐQ ~CDE CBAD D \（2）Q 在Rt ABC D 中，3,5AB AC ==4BC \===又Q 点E 是BC 的中点114222CE BE BC \===´=由（1）知~CDE CBAD D CE DE CA BA \=253DE \= 65DE \=【名师指导】本题考查了相似三角形的判定与性质以及勾股定理，解题的关键是：（1）利用“两角对应相等两三角形相似”证出两三角形相似；（2）利用相似三角形的性质求出DE 的长．22．如图，正方形ABCD 的边长为4，E 是CD 中点，点P 在射线AB 上，过点P 作线段AE 的垂线段，垂足为F ．（1）求证：PAF AED △∽△；（2）连接PE ，若存在点P 使PEF V 与AED V 相似，直接写出PA 的长____．【标准答案】（1）见解析；（2）2或5【思路点拨】（1）根据两角对应相等两三角形相似证明即可．（2）分两种情形：当PA=PB=2时，易知PE ∥AD ，此时∠DAE=∠PEF ，∠D=∠PFE=90°，可得△PEF ∽△EAD ．当∠AED=∠PEF ，∠D=∠PFE 时，△ADE ∽△PFE ，分别求解即可．【精准解析】（1）证明：在正方形ABCD 中，90D Ð=°，//CD AB ，∴DEA PAE Ð=Ð．∵PF AE ⊥，∴D AFP Ð=Ð．∴PAF AED △∽△．（2）当PA=PB=2时，∵DE=EC ，AP=PB ，∴PE ∥AD ，此时∠DAE=∠PEF ，∠D=∠PFE=90°，可得△PEF ∽△EAD ．当∠AED=∠PEF ，∠D=∠PFE 时，△ADE ∽△PFE ，∵CD ∥AB ，∴∠AED=∠EAP=∠AEP ，∴PA=PE ，∵PF ⊥AE ，∴AF=FE ，∵AD=4，DE=EC=2，∠D=90°，∴===AE∴AF =∵△PAF ∽△AED ，∴PA AF AE DE=，=∴PA=5，综上所述，满足条件的PA 的值为2或5．故答案为：2或5．【名师指导】本题考查相似三角形的判定和性质，正方形的性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．23．（2021·北京市古城中学九年级月考）如图，AB BC ⊥，EC BC ⊥，点D 在BC 上，1AB =，2BD =，3CD =，6CE =．（1）求证：ABD DCE :△△；（2）求ADE Ð的度数．【标准答案】（1）见解析；（2）90°【思路点拨】（1）证两边成比例，再用两边成比例夹角相等证相似即可；（2）根据相似三角形的性质，得出BAD EDC Ð=Ð，可证90度．【精准解析】（1）证明：∵AB BC ⊥，EC BC ⊥，∴90ABD DCE Ð=Ð=o∵1AB =，2BD =，3CD =，6CE =∴13AB DC =，13BD CE =∴AB BD DC CE=∴ABD DCED D :（2）∵ABD DCED D :∴BAD EDCÐ=Ð∵90BAD ADB Ð+Ð=o∴90ADB EDC Ð+Ð=o∴18090ADE ADB EDC Ð=-Ð-Ð=o o【名师指导】本题考查了相似三角形的判定与性质，解题关键是熟练运用相似三角形的判定定理证明，用性质定理求角．24．已知：如图，△ABC ∽△ACD ，CD 平分∠ACB ，AD ＝2，BD ＝3，求AC 、DC 的长．【标准答案】AC=；DC=3．【思路点拨】根据相似三角形的性质及角平分线的定义即可求解．【精准解析】证明：如图∵△ABC∽△ACD，∴∠1=∠B，AD AC AC AB=又∵CD是平分∠ACB，∴∠1=∠2，∴∠2=∠B，∴BD=DC．∵BD=3，∴DC=3；又∵AD =2，BD =3，∴AB=5由AD AC AC AB=得2AC AD AB=g即2AC=2×5=10∴AC=．【名师指导】本题主要考查了相似三角形的性质即角平分线性质，解题关键是熟练掌握相似三角形的性质及角平分线的定义．25．（2021·北京·清华附中九年级期末）如图，在Rt ABC △中，90B °Ð=，以AC 为边作Rt ACE △，90ACE °Ð=，AC CE =，延长BC 至点D ，作DE CE ⊥．（1）求证：ABC CED ∽△△；（2）若4AB =，2BC =，求DE 的长．【标准答案】（1）见解析；（2）DE =【思路点拨】（1）根据垂直可知，∠B=∠DEC ，再证明∠BAC ＝∠DCE ．然后根据相似三角形的判定方法可判断△ABC ∽△CED ；（2）根据△ABC ∽△CED ，列出比例式即可求出DE ．【精准解析】（1）证明：∵DE CE ⊥，∴∠DEC=90º，∵90B °Ð=，∴B DECÐ=Ð∵90B °Ð=，90ACE °Ð=，∴90BAC BCA °Ð+Ð=，90BCA DCE °Ð+Ð=．∴BAC DCE Ð=Ð．∴ABC CED ∽△△．（2）∵90B °Ð=，4AB =，2BC =，∴AC ==∵CE AC =，∴CE =∵ABC CED ∽△△，∴AB BC CE DE=，2DE=，∴DE【名师指导】本题考查了相似三角形的判定、相似三角形的性质以及勾股定理，选择正确的判定方法是解题关键．26．（2021·北京东城·九年级期末）如图，AM 平分BAD Ð，作//BF AD 交AM 于点F ，点C 在BF 的延长线上，CF BF =，DC 的延长线交AM 于点E ．（1）求证：AB BF =；（2）若1,4AB AD ==，求:EFC EAD S S V V 的值．【标准答案】（1）见解析；（2）116．【思路点拨】（1）由角平分线的性质得出∠BAF=∠DAF ，再根据平行线的性质得出∠BAF=∠AFB ，最后得出结果；（2）先证△EFC ∽△EAD ，再利用相似三角形的性质求解即可．【精准解析】（1）证明：∵AM 平分BAD Ð，∴∠BAF=∠DAF ，∵//BF AD ，∴∠AFB=∠DAF ，∴∠BAF=∠AFB ，∴AB BF =；（2）∵CF BF =，AB BF =，∴AB=CF=1∵//BF AD ，1,4AB CF AD ===，∴△EFC ∽△EAD ，∴1=4FC EF AD AE = ，∴:EFC EAD S S V V =211()416=．【名师指导】本题考查了角平分线的性质，平行线的性质及相似三角形的判定与性质，解题的关键是熟练掌握这些性质．27．（2021·北京市古城中学九年级月考）已知：如图，在△ABC 中，AB ＝AC ，点P ，D 分别是BC 、AC 边上的点，且∠APD ＝∠B ．求证：AC •CD ＝CP •BP ．【标准答案】见解析．【思路点拨】证明ABP PCD V V ∽即可．【精准解析】∵在ABC V 中，AB AC =，∴B C Ð=Ð，∵APC B BAP Ð=Ð+Ð，APC APD CPD Ð=Ð+Ð，∴B BAP APD CPD Ð+Ð=Ð+Ð．∵APD B Ð=Ð，∴BAP CPD Ð=Ð，∴ABP PCD V V ∽，∴BP BA CD CP=．∵AB AC =，∴AC CD CP BP ×=×．【名师指导】本题考查了等腰三角形的性质，三角形相似的判定和性质，熟练掌握三角形判定相似的定理和性质是解题的关键．28．（2021·北京房山·九年级期中）如图，AD 是ABC V 的中线，点O 是AD 上任一点，连接BO 并延长，交AC 于点E ．（1）如图1，当12=AO AD 时，求AE AC 的值；（2）如图2，当13AO AD =时，求AE AC的值．【标准答案】（1）31AE AC =；（2）15AE AC =【思路点拨】（1）过点D 作BE 的平行线DF ，利用平行线分线段成比例可推理得到,CF EF EF AE ==，从而得到答案；（2）过点D 作BE 的平行线DG ，利用平行线分线段成比例可推理得到EG =CG ，EG =2AE ，从而得到答案．【精准解析】解：（1）如图1，过点D 作//DF BE ，交AC 于点F∵AD 是ABC V 中线∴BD =CD∵//DF BE ∴1CD CF BD EF==，AO AE OD EF = 又∵12=AO AD ，+AO OD AD =∴1AO AE OD EF==∴,CF EF EF AE==又∵AE EF CF AC++=∴3AC AE =即：31AE AC =（2）如图2，过点D 作//DG BE ，交AC 于点G∵ //DG BE ∴,AO AE BD EG OD EG CD CG==∵AD 是ABC V 中线，13AO AD =，+AO OD AD =∴BD =CD , 12AO AE AD EG ==∴EG =CG ，EG =2AE又∵AE EG CG AC++=∴5AE =AC ∴15AE AC =【名师指导】本题考查平行线段分线成比例，利用数形结合思想解题是解此类题的关键．29．（2021·北京丰台·九年级期末）如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE 于点F ，连接FC．（1）求证：∠FBC=∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．【标准答案】(1)见解析；(2) ①见解析；②BF=DF+CG，理由见解析．【思路点拨】（1）由∠FBC+∠COB=90°，∠CDF+∠DOF=90°，根据等角的余角相等证明即可；（2）①根据题意画出图形即可；②结论：BF=DF+CG．利用截长补短法，构造相似三角形解决问题即可；【精准解析】（1）如图1中，设CD交BF于点O．∵四边形ABCD是正方形，∴∠BCO=90°，∵BF⊥DE，∴∠OFD=∠OCB=90°，∴∠FBC+∠COB=90°，∠CDF+∠DOF=90°，∵∠DOF=∠BOC，∴∠FBC=∠CDF．（2）①如图2，②结论：BF=DF+CG．理由：在线段FB上截取FM，使得FM=FD．∵∠BDC=∠MDF=45°，∴∠BDM=∠CDF，∵BD DM DC DF==∴△BDM ∽△CDF ，∴BM DM CF DF==∠DBM=∠DCF ，∴，∴∠CFE=∠FCD+∠CDF=∠DBM+∠BDM=∠DMF=45°，∴∠EFG=∠EFC=45°，∴∠CFG=90°，∵CF=FG ，∴CF ，∴BM=CG ，∴BF=BM+FM=CG+DF ．【名师指导】本题考查了正方形的性质，余角的性质，轴对称作图，相似三角形的判定与性质，勾股定理，通过截长补短法作出辅助线构造相似三角形是解答本题的关键．30．（2021·北京海淀·一模）如图，四边形ABCD 是矩形，点E 是边BC 上一点，AE ED ⊥．（1）求证：ABE ECD ∽△△；（2）F 为AE 延长线上一点，满足EF EA =，连接DF 交BC 于点G ．若2,1AB BE ==，求GC 的长．【标准答案】（1）证明见解析 ；（2）32．【思路点拨】（1）由矩形的性质和垂直的定义，得到90B C Ð=Ð=°，BAE CED Ð=Ð，即可得到结论成立；（2）由相似三角形的性质和矩形的性质，求出4EC =，5BC =，再证明AFD EFG V V ∽，再利用相似三角形的性质，即可求出GC 的长．。

2019-2020初三上期末考试几何综合汇总1、（19-20朝阳期末）27．已知∠MON=120°，点A，B分别在ON，OM边上，且OA=OB，点C在线段OB 上（不与点O，B重合），连接CA. 将射线CA绕点C逆时针旋转120°得到射线CA´，将射线BO绕点B逆时针旋转150°与射线CA´交于点D.(1)根据题意补全图1；(2)求证：①∠OAC=∠DCB；②CD=CA（提示：可以在OA上截取OE=OC，连接CE）；(3)点H在线段AO的延长线上，当线段OH，OC，OA满足什么等量关系时，对于任意的点C都有∠DCH=2∠DAH，写出你的猜想并证明.图1备用图2、（19-20东城期末）27．在△ABC中，∠BAC=45°，CD⊥AB于点D，AE⊥BC于点E，连接DE．（1）如图1，当△ABC为锐角三角形时，①依题意补全图形，猜想∠BAE与∠BCD之间的数量关系并证明；②用等式表示线段AE，CE，DE的数量关系，并证明;（2）如图2，当∠ABC为钝角时，依题意补全图形并直接写出线段AE，CE，DE的数量关系．图1图23、（19-20西城期末）27. △ABC是等边三角形，点P在BC的延长线上，以P为中心，将线段PC逆时针旋转n°（0<n<180）得线段PQ，连接AP，BO.（1）如图1，若PC=AC，画出当BQ∥AP时的图形，并写出此时n的值；AP，（2）M为线段BQ的中点，连接PM.写出一个n的值，使得对于BC延长线上任意一点P，总有MP=12并说明理由.4、（19-20海淀期末）27．在Rt △ABC 中，∠ACB =90°，AC =1, 记∠ABC =α，点D 为射线BC 上的动点，连接AD ，将射线DA 绕点D 顺时针旋转α角后得到射线DE ，过点A 作AD 的垂线，与射线DE 交于点P ，点B 关于点D 的对称点为Q ，连接PQ ．（1）当△ABD 为等边三角形时，① 依题意补全图1； ② PQ 的长为_____________； （2）如图2，当α=45°，且43BD时, 求证：PD =PQ ； （3）设BC = t , 当PD =PQ 时，直接写出BD 的长.（用含t 的代数式表示）图 1图 2备用图N5、（19-20丰台期末）26．如图，∠90MAN =︒，B ，C 分别为射线AM ，AN 上的两个动点，将线段AC绕点A 逆时针．．．旋转30︒到AD ，连接BD 交AC 于点E ． （1）当∠ACB =30°时，依题意补全图形，并直接写出DE BE的值；（2）写出一个∠ACB 的度数，使得12DE BE，并证明．6、（19-20石景山期末）27．如图，在正方形ABCD 中，P 是边BC 上的一动点（不与点B ，C 重合），点B 关于直线AP 的对称点为E ，连接AE ．连接DE 并延长交射线AP 于点F ，连接BF ．（1）若BAP α∠=，直接写出ADF ∠的大小（用含α的式子表示）； （2）求证：BF DF ⊥；（3）连接CF ，用等式表示线段AF ，BF ，CF 之间的数量关系，并证明．FEP DCBA7、（19-20大兴期末）27.已知：如图，B,C,D 三点在⨀A 上，︒=∠45BCD ，PA 是钝角△ABC 的高线，PA 的延长线与线段CD 交于点E. (1) 请在图中找出一个与∠CAP 相等的角，这个角是 ；(2) 用等式表示线段AC ，EC ，ED 之间的数量关系，并证明.8、（19-20房山期末）27.在△ABC 中，∠ACB ＝90°，AC ＝BC ＝2，以点B 为圆心、1为半径作圆，设点M 为⊙B 上一点，线段CM 绕着点C 顺时针旋转90°，得到线段CN ，连接BM 、AN ．（1）在图27-1中，补全图形，并证明BM ＝AN .（2）连接MN，若MN与⊙B相切，则∠BMC的度数为________________. （3）连接BN，则BN的最小值为___________；BN的最大值为___________图27-1 备用图备用图9、（19-20门头沟期末）27．如图，∠MON=60°，OF平分∠MON，点A在射线OM上， P，Q是射线ON上的两动点，点P在点Q的左侧，且PQ=OA，作线段OQ的垂直平分线，分别交OM，OF，ON于点D，B，C，连接AB，PB．（1）依题意补全图形；（2）判断线段 AB，PB之间的数量关系，并证明；（3）连接AP，设APkOQ，当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．备用图10、（19-20密云期末）27. 已知：在Rt△ABC中，∠BAC=90°，AB=AC，点D为BC边中点．点M为线段B C上的一个动点（不与点C，点D重合），连接AM，将线段AM绕点M顺时针旋转90°，得到线段ME，连接EC．（1）如图1，若点M在线段BD上．①依据题意补全图1；②求∠MCE的度数．图1（2）如图2，若点M在线段CD上，请你补全图形后，直接用等式表示线段AC、CE、CM之间的数量关系．图211、（19-20平谷期末）27．如图，正方形ABCD，将边BC绕点B逆时针旋转60°，得到线段BE，连接AE，CE．（1）求∠BAE的度数；（2）连结BD，延长AE交BD于点F．Array①求证：DF=EF；②直接用等式表示线段AB，CF，EF的数量关系．12、（19-20顺义期末）27．已知：如图，在正方形ABCD中，点E在AD边上运动，从点A出发向点D运动，到达D点停止运动．作射线CE，并将射线CE绕着点C逆时针旋转45°，旋转后的射线与AB边交于点F，连接EF.（1）依题意补全图形；（2）猜想线段DE，EF，BF的数量关系并证明；（3）过点C作CG⊥EF，垂足为点G，若正方形ABCD的边长是4，请直接写出点G运动的路线长．C C（备用图）13、（19-20通州期末）27.如图，MO⊥NO于点O,△OAB为等腰直角三角形，∠OAB=90°，当△OAB绕点O旋转时，记∠MOA=a(0°≤a≤90°)。

九年级上册数学期末试卷 几何综合1．（昌平18期末27）已知，△ABC 中，∠ACB =90°，AC =BC ，点D 为BC 边上的一点. （1）以点C 为旋转中心，将△ACD 逆时针旋转90°，得到△BCE ，请你画出旋转后的图形；（2）延长AD 交BE 于点F ，求证：AF ⊥BE ；（3）若，BF =1，连接CF ，则CF 的长度为 .27．（1）补全图形…………………… 2分 （2）证明：∵ΔCBE 由ΔCAD 旋转得到，∴ΔCBE ≌ΔCAD ，……………… 3分∴∠CBE =∠CAD ，∠BCE =∠ACD =90°，……………4分 ∴∠CBE +∠E =∠CAD +∠E ， ∴∠BCE =∠AFE =90°，∴AF ⊥BE ．……………………………………5分（3………………………………………………7分2．（朝阳18期末25）△ACB 中，∠C =90°，以点A 为中心，分别将线段AB ，AC 逆时针旋转60°得到线段AD ，AE ，连接DE ，延长DE 交CB 于点F . （1）如图1，若∠B =30°，∠CFE 的度数为 ；（2）如图2，当30°<∠B <60°时，①依题意补全图2；②猜想CF 与AC 的数量关系，并加以证明.图1 图23．（西城18期末27）如图1，在Rt △AOB 中，∠AOB =90°，∠OAB =30°，点C 在线段OB上，OC =2BC ，AO 边上的一点D 满足∠OCD =30°．将△OCD 绕点O 逆时针旋转α度（90°<α<180°）得到△OC D ''，C ，D 两点的对应点分别为点C '，D '，连接AC '，BD '，取AC'的中点M，连接OM．（1）如图2，当C D''∥AB时，α=°，此时OM 和BD'之间的位置关系为；（2）画图探究线段OM和BD'之间的位置关系和数量关系，并加以证明．4．（丰台18期末27）如图，∠BAD=90°，AB=AD ，CB=CD ，一个以点C 为顶点的45°角绕点C 旋转，角两边与BA ，DA 交于点M ，N ，与BA ，DA 延长线交于点E ，F ，连接AC . （1）在∠FCE 旋转的过程中，当∠FCA =∠ECA 时，如图1，求证：AE =AF ； （2）在∠FCE 旋转的过程中，当∠FCA ≠∠ECA 时，如图2，如果∠B=30°，CB=2，用等式表示线段AE ，AF 之间的数量关系，并证明.27.解：（1）证明：∵AB=AD ，BC=CD ，AC=AC ，∴△ABC ≌△ADC . …1分∴∠BAC =∠DAC =45°，可证∠FAC =∠EAC =135°. ……2分 又∵∠FCA =∠ECA ，∴△ACF ≌△ACE . ∴AE =AF . ……3分 其他方法相应给分.（2）过点C 作CG ⊥AB 于点G ，求得AC =2.……4分∵∠FAC =∠EAC =135°，∴∠ACF +∠F =45°. 又∵∠ACF +∠ACE =45°，∴∠F =∠ACE . ∴△ACF ∽△AEC. ……5分 ∴ACAF AE AC =，即AF AE AC ⋅=2. ……6分 ∴2=⋅AF AE . ……7分5．（怀柔18期末27）在等腰△ABC 中，AB =AC ，将线段BA 绕点B 顺时针旋转到BD，使图1图2BD⊥AC于H，连结AD并延长交BC的延长线于点P.（1）依题意补全图形；（2）若∠BAC=2α，求∠BDA的大小（用含α的式子表示）；（3）小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.27.解：(1)如图……………………………………………1分(2) ∵∠BAC=2α，∠AHB=90°∴∠ABH=90°-2α…………………………………………………………………………… 2分∵BA=BD∴∠BDA=45°+α………………………………………………………………………………3分(3)补全图形，如图………………4分证明过程如下：∵D关于BC的对称点为E，且DE交BP于G∴DE⊥BP，DG=GE，∠DBP=∠EBP，BD=BE；…………………………………………5分∵AB=AC，∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH=90°-2α∠DBP=90°-α-（90°-2α）=α∴∠DBP=∠EBP=α∴∠BDE=2α∵AB=BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP .………………………………………………………………………………7分6．（平谷18期末27）如图，在Rt △ABC 中，∠BAC =90°，AB=AC ．在平面内任取一点D ，连结AD （AD ＜AB ），将线段AD 绕点A 逆时针旋转90°得到线段AE ，连结DE ，CE ，BD ．（1）请根据题意补全图1；（2）猜测BD 和CE 的数量关系并证明；（3）作射线BD ，CE 交于点P ，把△ADE 绕点A 旋转，当∠EAC =90°，AB =2，AD =1时，补全图形，直接写出PB 的长．27．解：（1）如图 (1)（2）BD 和CE 的数量是：BD =CE ；·················································································2B图1B备用图∵∠DAB +∠BAE =∠CAE +∠BAE =90°，∴∠DAB=∠CAE ． ················································································································· 3 ∵AD=AE ，AB=AC ， ∴△ABD ≌△ACE ．∴BD =CE ． (4)（3）PB ． (7)7．（密云18期末27）如图，已知Rt ABC ∆中，90ACB ∠=︒，AC=BC ，D 是线段AB 上的一点（不与A 、B 重合）. 过点B 作BE ⊥CD ，垂足为E.将线段CE 绕点C 顺时针旋转90︒，得到线段CF ，连结EF.设BCE ∠度数为α.（1）①补全图形； ②试用含α的代数式表示CDA ∠.（2）若EF AB = ，求α的大小. （3）直接写出线段AB 、BE 、CF 之间的数量关系.27.（1）①补全图形.……………………………..1分②45α︒+ ……………………………..3分 （2）在FCE ∆和ACB ∆中，45CFE CAB ∠=∠=︒ ，90FCE ACB ∠=∠=︒ F C E ∆∽ ACB ∆CF EFAC AB =EF AB =2CF AC = ………………………………..5分 连结FA.90,ECB 90FCA ACE ACE ∠=︒-∠∠=︒-∠ECB FCA ∠=∠=α在Rt CFA ∆中，90CFA ∠=︒，cos FCA ∠=30FCA ∠=︒即30α=︒. ………………………………6分（3）22222AB CF BE =+ …………………………………………8分8．（石景山18期末27）在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．（1）当点P在线段AC上时，如图1．①依题意补全图1；②若EQ=BP，则∠PBE的度数为，并证明；（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）27．（本小题满分7分）（1）解：①正确作图………………………1分②45°………………………2分连接PD，PE易证△CPD≌△CPB∴DP=BP，∠CDP=∠CBP∵P、Q关于直线CD对称∴EQ=EP∵EQ=BP∴DP=EP∴∠C D P=∠D E P………………………………………………3分∵∠CEP+∠DEP=180°∴∠CEP+∠CBP=180°∵∠BCD=90°∴∠BPE=90°∵BP=EP∴∠PBE =45°． …………………………………………………………4分 （2）解：连接PD ，PE易证△CPD ≌△CPB ∴DP =BP ，∠1=∠2 ∵P 、Q 关于直线CD 对称， ∴EQ =EP ，∠3=∠4 ∵EQ =BP ， ∴DP =EP ∴∠3=∠1， ∴∠3=∠2 ∴∠5=∠BCE =90° ∵BP =EP ， ∴∠PEB =45° ∴∠3=∠4=22.5°，在△BCE 中，已知∠4=22.5°，BC =1，可求BE 长． ……………7分9．（东城18期末27）如图1，在△ABC 中，∠ACB =90°，AC =2，BC =B 为圆心，为半径作圆．点P 为B 上的动点，连接PC ，作PCPC '⊥，使点P '落在直线BC 的上方，且满足:P C PC '=BP ，AP '． （1）求∠BAC 的度数，并证明△AP C '∽△BPC ； （2）若点P 在AB 上时，①在图2中画出△AP’C ； ②连接BP '，求BP '的长；图1图2（3）点P 在运动过程中，BP '是否有最大值或最小值？若有，请直接写出BP '取得最大值或最小值时∠PBC 的度数；若没有，请说明理由．备用图10．（顺义18期末27）综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB= ；（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．27．（1）AB ；……………………….2分（2）解：过点E 作横线的垂线，交l 1，l 2于点M ，N ，……………………………..….3分∴∠DME =∠EDF = 90°，∵∠DEF =90°，∴∠2+∠3=90°，∵∠1+∠3=90°，∴∠1=∠2，∴△DME ∽△ENF ，………….…….4分 ∴DM ME DE EN NF EF==， ∵EF =2DE ， ∴12DM ME DE EN NF EF ===， ∵ME =2，EN =3，∴NF =4，DM =1.5，根据勾股定理得DE =2.5，EF =5，DF =……………………….5分 （3）EG=2.5．…………………………………………………………..…….7分11．（门头沟18期末27）如图1有两条长度相等的相交线段AB 、CD ，它们相交的锐角中有一个角为60°，为了探究AD 、CB 与CD (或AB )之间的关系，小亮进行了如下尝试：（1）在其他条件不变的情况下使得AD BC ∥，如图2，将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系：____________________；(直接写出结果)（2）根据小亮的经验，请对图27-1的情况（AD 与CB 不平行）进行尝试，写出AD 、CB 与CD (或AB )之间的关系，并进行证明；（3）综合（1）、（2）的证明结果，请写出完整的结论 __________________________.27．（本小题满分7分）（1） AD CB AB += ……………………………………………1分（2）补全图形正确 ………………………………………2分结论：AD CB AB +＞………………………………………3分理由：如图：将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,联结BE 、CE ，且可得AB DE ∥且AB DE =∴四边形A 、B 、E 、D 是平行四边形………………………4分∴AD BE =∵AB CD =∴DE CD =∵AB DE ∥,60AOD ∠=︒∴DCE △是等边三角形……………………………………5分∴CE AB =由于AD 与CB 不平行，所以C 、B 、E 构成三角形∴BE CB CE +＞……………………………………………6分∴AD CB AB +＞（3）AD CB AB +≥ …………………………………………7分12．（通州18期末24）如图1，在矩形ABCD 中，点E 为AD 边中点，点F 为BC边中点；图1 图2点G ，H 为AB 边三等分点，I ，J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点，如图2，图3所示.那么，图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗？（1）小瑞的探究过程如下在图2中，小瑞发现， ABCD GKLH S S _______=；在图3中，小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整： 设a S DEP =△，b S AKG =△∵AF EC ∥∴DAK DEP ∽△△，且相似比为2:1，得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△，且相似比为3:1，得到b S ABM 9=△ 又∵ABCD DAG S b a S 614=+=△，ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=，b S ABCD _____=，b S KPOL _____=∴ABCD KPOL S S _____=，则GKLH KPOL S S ____（填写“”，“”或“”）（2）小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.13．（海淀18期末28）在△ABC 中，∠A 90°，ABAC ．（1）如图1，△ABC 的角平分线BD ，CE 交于点Q ，请判断“QB =”是否正确：_______（填“是”或“否”）；（2）点P 是△ABC 所在平面内的一点，连接P A ，PB ，且P A ．①如图2，点P 在△ABC 内，∠ABP 30°，求∠P AB 的大小；②如图3，点P 在△ABC 外，连接PC ，设∠APCα，∠BPCβ，用等式表示α，β之间的数量关系，并证明你的结论．图1 图2图3 28．解：（1）否. ………………1分（2）① 作PD ⊥AB 于D ，则∠PDB =∠PDA =90°，∵ ∠ABP =30°，∴ 12PD BP =. ………………2分∵ PB =，∴ 2PD PA =.∴ sin PD PAB PA ∠== 由∠P AB 是锐角，得∠P AB =45°. ………………3分 另证：作点P 关于直线AB 的对称点'P ，连接',',B P P A P P ，则',',','P B A P B A P A B P A B B P B P A P A P∠=∠∠=∠==.∵∠ABP =30°，∴'60P BP ∠=︒.∴△'P BP 是等边三角形.∴'P P BP =.∵PB =，∴'P P =. ………………2分 ∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒，证明如下： ………………4分 作AD ⊥AP ，并取AD =AP ，连接DC ，DP .∴ ∠DAP =90°.∵ ∠BAC =90°，∴ ∠BAC +∠CAP =∠DAP +∠CAP ,即 ∠BAP =∠CAD .∵ AB =AC ，AD =AP ，∴ △BAP ≌△CAD .∴ ∠1=∠2，PB =CD . ………………5分 ∵ ∠DAP =90°，AD =AP ，∴ PD =，∠ADP =∠APD =45°.∵ PB =，∴ PD =PB =CD .∴ ∠DCP =∠DPC .∵ ∠APCα，∠BPCβ，∴ 45DPC α∠=+︒，12αβ∠=∠=-.∴ 31802902DPC α∠=︒-∠=︒-.∴ 139045ADP αβ∠=∠+∠=︒--=︒.∴45αβ+=︒. ………………7分。

1．在△ABC 中，AB =AC ，∠BAC =α，点P 是△ABC 内一点，且2PAC PCA α∠+∠=．连接PB ，试探究P A ，PB ，PC 满足的等量关系．（1）当α=60°时，将△ABP 绕点A 逆时针旋转60°得到ACP '△，连接PP '，如图1所示．由ABP △≌ACP '△ 可以证得'APP △是等边三角形，再由30PAC PCA ∠+∠=︒可得∠APC 的大小为 度，进而得到CPP '△是直角三角形，这样可以得到P A ，PB ，PC 满足的等量关系为 ；（2）如图2，当α=120°时，请参考（1）中的方法，探究P A ，PB ，PC 满足的等量关系，并给出证明； （3）P A ，PB ，PC 满足的等量关系为 ．2．在Rt △ABC 中，∠ACB =90°，AC =BC ，C D 为AB 边上的中线．在Rt △AEF 中，∠AEF =90°，AE =EF ，AF < AC ．连接BF ，M ，N 分别为线段AF ，BF 的中点，连接MN ． （1）如图1，点F 在△ABC 内，求证：CD = MN ；（2）如图2，点F 在△ABC 外，依题意补全图2，连接CN ，EN ，判断CN 与EN 的数量关系与位置关系，并加以证明；（3）将图1中的△AEF 绕点A 旋转，若AC =a ，AF =b （b <a ），直接写出EN 的最大值与最小值．图1 图2 备用图3. 点P 是矩形ABCD 对角线AC 所在直线上的一个动点（点P 不与点A ，C 重合），分别过点A ，PAB C P'AB C P图1 图2C 向直线BP 作垂线，垂足分别为点E ，F ，点O 为AC 的中点．（1）如图1，当点P 与点O 重合时，请你判断OE 与OF 的数量关系；（2）当点P 运动到如图2所示位置时，请你在图2中补全图形并通过证明判断（1）中的结论是否仍然成立；（3）若点P 在射线OA 上运动，恰好使得∠OEF =30°时，猜想此时线段CF ，AE ，OE 之间有怎样的数量关系，直接写出结论不必证明．4．已知△ABC 是等边三角形，点D ，E ，F 分别是边AB ，BC ，AC 的中点，点M 是射线EC 上的一个动点，作等边△DMN ，使△DMN 与△ABC 在BC 边同侧，连接NF . （1）如图1，当点M 与点C 重合时，直接写出线段FN 与线段EM 的数量关系；（2）当点M 在线段EC 上（点M 与点E ，C 不重合）时，在图2中依题意补全图形，并判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；（3）连接DF ，直线DM 与直线AC 相交于点G ，若△DNF 的面积是△GMC 面积的9倍，8AB ，请直接写出线段CM 的长.5．在Rt △ABC 中，∠ACB=90°，O 为AB 边上的一点，且tan B =21，点D 为AC 边上的动点（不 图1 图2 备用图与点A ，C 重合），将线段OD 绕点O 顺时针旋转90°，交BC 于点E .如图1，若O 为AB 边中点， D 为AC 边中点，则OE OD的值为 ；（2）若O 为AB 边中点， D 不是AC 边的中点，①请根据题意将图2补全；②小军通过观察、实验，提出猜想：点D 在AC 边上运动的过程中，（1）中OE OD的值不变.小军把这个猜想与同学们进行交流，通过讨论，形成了求OE OD的值的几种想法：想法1：过点O 作OF ⊥AB 交BC 于点F ，要求OE OD的值，需证明△OEF ∽△ODA .想法2：分别取AC ，BC 的中点H ，G ，连接OH ，OG ，要求OE OD的值，需证明△OGE ∽△OHD .想法3：连接OC ，DE ，要求OE OD的值，需证C ，D ，O ，E 四点共圆.......请你参考上面的想法，帮助小军写出求OE OD的值的过程(一种方法即可)；（3）若1BO BAn（n ≥2且n 为正整数），则OE OD的值为 （用含n 的式子表示）.6．如图1，在△ABC 中，∠ACB =90°，点P 为△ABC 内一点．（1）连接PB ，PC ，将△BCP 沿射线CA 方向平移，得到△DAE ，点B ，C ，P 的对应点 图2图1ED分别为点D ，A ，E ，连接CE ． ① 依题意，请在图2中补全图形；② 如果BP ⊥CE ，BP =3，AB =6，求CE 的长．（2）如图3，连接PA ，PB ，PC ，求PA+PB+PC 的最小值．小慧的作法是：以点A 为旋转中心，将△ABP 顺时针旋转60°得到△AMN ，那么就将PA+PB+PC 的值转化为CP +PM +MN 的值，连接CN ，当点P 落在CN 上时，此题可解．请你参考小慧的思路，在图3中证明PA +PB +PC =CP +PM +MN ． 并直接写出当AC =BC =4时，PA +PB +PC 的最小值．7．在等边△ABC 中，E 为BC 边上一点，G 为BC 延长线上一点，过点E 作∠AEM =60°，交∠ACG的平分线于点M .(1)如图（1），当点E 在BC 边的中点位置时,通过测量AE ，EM 的长度，猜想AE 与EM 满足的数量关系图1B图2B图3NBM (2) 如图（2），小晏通过观察、实验，提出猜想：当点E 在BC 边的任意位置时，始终有AE =EM .小晏把这个猜想与同学进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：在BA 上取一点H 使AH =CE ，连接EH ，要证AE =EM ， 只需证△AHE ≌△ECM .想法2：找点A 关于直线BC 的对称点F ，连接AF ，CF ，EF .（易证∠BCF +∠BCA +ACM =180°，所以M ，C ，F 三点在同一直线上）要证AE =EM ，只需证ΔMEF 为等腰三角形.想法3：将线段BE 绕点B 顺时针旋转60°，得到线段BF ，连接CF ，EF ，要证AE =EM ，只需证四边形MCFE 为平行四边形.请你参考上面的想法，帮助小晏证明AE =EM .（一种方法即可）8.已知在Rt △ABC 中，∠ABC ＝90°，点P 是AC 的中点.（1）当∠A=30°且点M 、N 分别在线段AB 、BC 上时，∠MPN =90°，请在图1中将图形补充完整，并且 直接写出PM 与PN 的比值；（2）当∠A=23°且点M 、N 分别在线段AB 、BC 的延长线上时，（1）中的其他条件不变，请写出PM 与PN 比值的思路.9．在等边△ABC 中，E 是边BC 上的一个动点（不与点B ，C 重合），∠AEF =60°，EF 交△ABC 外角平分线CD 于点F .（1）如图1，当点E 是BC 的中点时，请你补全图形，直接写出AECF的值，并判断AE 与(2)ABC GEM(1)ME CBA图1 图2EF 的数量关系；（2）当点E 不是BC 的中点时，请你在图（2）中补全图形，判断此时AE 与EF 的数量关系，并证明你的结论.图1 图210．在△ABC 中，∠B =45°，∠C =30°． （1）如图1，若AB =52，求BC 的长；（2）点D 是BC 边上一点，连接AD ，将线段AD 绕点A 逆时针旋转90°，得到线段AE ．①如图2，当点E 在AC 边上时，求证：CE =2BD ； ②如图3，当点E 在AC 的垂直平分线上时，直接写出CEAB的值．11.已知：△ABC 中，AC =6，BC=8，AB =10,点D 是边AB 上的一点，过C ，D 两点的⊙O 分别与边CA ，CB 交于点E ，F . （1）若点D 是AB 的中点，①在图1中用尺规作出一个．．符合条件的图形（保留作图痕迹，不写作法）； ②如图2,连结EF ，若EF ∥AB ,求线段EF 的长; BBD图1图2图3③请写出求线段EF长度最小值的思路.（2）如图3，当点D在边AB上运动时，线段EF长度的最小值是_________.12．如图，在△ABC中，∠BAC=90°，AB=AC，点D是△ABC内一动点（不包括△ABC的边界），连接AD．将线段AD绕点A顺时针旋转90°，得到线段AE．连接CD，BE．（1）依据题意，补全图形；（2）求证：BE=CD．（3）延长CD交AB于F，交BE于G．①求证：△ACF∽△GBF；②连接BD，DE，当△BDE为等腰直角三角形时，请你直接．．写出AB：BD的值．【2017.1海淀期末】1．（1）150， -----------------------------------------------------1分222PA PC PB +=． ----------------------------------3分（2）如图，作120PAP '∠=°，使AP AP '=，连接PP '，CP '．过点A 作AD ⊥PP '于D 点． ∵120BAC PAP '∠=∠=°， 即BAP PAC PAC CAP '∠+∠=∠+∠， ∴BAP CAP '∠=∠． ∵AB =AC ，AP AP '=，BB备用图∴BAP CAP '△≌△. --------------------------------4分∴P C PB '=，180302APD AP D PAP '∠=∠='-∠=o °． ∵AD ⊥PP '， ∴90ADP ∠=°.∴在Rt APD △中，cos 3PD AP APD AP =⋅∠=. ∴23PP PD '==．∵60PAC PCA ∠+∠=°， ∴180120APC PAC PCA ∠=∠-∠=-o °. ∴90P PC APC APD '∠=∠-∠=°． ∴在Rt P PC '△中，222P P PC P C ''+=.∴2223PA PC PB +=． --------------------------------------------------------------------------------6分（3）22224sin 2PA PC PB α+=． ---------------------------------------------------------------7分【2017.1西城期末】2．解：（1）证明：在Rt △ABC 中，∵ CD 是斜边AB 上的中线． ∴ CD =21AB ．在△ABF 中，点M ，N 分别是边AF ，BF 的中点， ∴ MN =21AB ， ∴CD = MN ．（2）答：CN 与EN 的数量关系CN = EN ，CN 与EN 的位置关系CN ⊥EN ． ······································ 3分 证明：连接EM ，DN ，如图．与（1）同理可得 CD = MN ， EM = DN ．在Rt △ABC 中， CD 是斜边AB 边上的中线， ∴ CD ⊥AB ．在△ABF 中，同理可证EM ⊥AF ． ∴ ∠EMF =∠CDB = 90︒．∵D ，M ，N 分别为边AB ，AF ，BF 的中点， ∴ DN ∥AF ，MN ∥AB ．∴ ∠FMN =∠MND ，∠BDN =∠MND ．DP'P A∴ ∠FMN = ∠BDN ．∴ ∠EMF +∠FMN =∠CDB +∠BCN ． ∴ ∠EMN =∠NDC ． ∴ △EMN ≌△DNC ． ∴ CN = EN ，∠1 =∠2． ∵ ∠1 +∠3 +∠EMN = 10︒， ∴ ∠2 +∠3 +∠FMN = 90︒．∴ ∠2 +∠3 +∠DNM = 90︒，即∠CNE = 90︒．∴ CN ⊥EN ． ·································································· 5分（3）EN 的最大值为22b a +，最小值为22ba -. ······························ 7分 【2017.1东城期末】3.解：（1）OE =OF . …………1分（2）补全图形如右图. …………2分OE =OF 仍然成立. …………3分 证明：延长EO 交CF 于点G . ∵ AE ⊥BP ， CF ⊥BP ， ∴ AE ∥CF . ∴ ∠EAO =∠GCO.又∵ 点O 为AC 的中点，∴ AO =CO. ∵ ∠AOE=∠COG ， ∴ △AOE ≌△COG.∴ OE =OF.…………5分（3）CF OE AE =+或CF OE AE =-. …………7分【2017.1石景山期末】4．（1）FN EM =.（2）补全图形，如图1所示. (2)更多精品文档NDFA B CM 结论成立.证明：连接ED ，EF ，DF ，如图2.∵△ABC 是等边三角形，∴AB BC AC a ===.∵D ，E ，F 分别是边AB ，BC ，AC 的中点，∴12DF DE EF a ===. ∴60FDE ∠=︒.又∵△DMN 是等边三角形，∴DN DM =，60MDN ∠=︒. ∴FDN EDM ∠=∠.∴△DFN ≌△DEM . ……………………………… 4分 ∴FN EM =. ……………………………… 5分（3）CM 的长为1或2. ……………………………… 7分【2017.1朝阳期末】5.解：(1) 1.(2) ①如图.②法1:如图，过点O 作OF ⊥AB 交BC 于点F ， ∵∠DOE =90°，∴∠AOD +∠DOF =∠DOF +∠FOE =90°. ∴∠AOD =∠FOE . ∵∠ACB =90°，∴∠A +∠B =∠OFE +∠B =90°. ∴∠A =∠OFE . ∴△OEF ∽△ODA .∴OE OF OD OA=. ∵O 为AB 边中点， ∴OA =OB .在Rt △FOB 中，tan B =21， ∴12OF OB =. ∴1.2OF OA = ∴12OE OD =. FED ED 图1图2更多精品文档法2:如图，分别取AC ，BC 的中点H ，G ，连接OH ，OG ，∵O 为AB 边中点，∴OH ∥BC ，OH =12BC ，OG ∥AC .∵∠ACB =90°，∴∠OHD =∠OGE =90°. ∴∠HOG =90°. ∵∠DOE =90°，∴∠HOD +∠DOG =∠DOG +∠GOE =90°. ∴∠HOD =∠GOE . ∴△OGE ∽△OHD . ∴OE OG OD OH=. ∵tan B =21，∴1.2OG GB = ∵OH =GB ， ∴1.2OG OH = ∴12OE OD =. 法3:如图，连接OC ，DE ，∵∠ACB =90°，∠DOE =90°，∴DE 的中点到点C ，D ，O ，E 的距离相等. ∴C ，D ，O ，E 四点共圆. ∴∠ODE =∠OCE . ∵O 为AB 边中点， ∴OC =OB . ∴∠B =∠OCE . ∴∠ODE =∠B .∵tan B =21，∴12OE OD =. (3) 122n -.【2017.1昌平期末】6．解：（1）①如图1……………………… 1分②如图2，连接BD 、CD∵△BCP 沿射线CA 方向平移，得到△DAE EDBP更多精品文档∴BC ∥AD 且BC =AD∵∠ACB =90°∴四边形BCAD 是矩形……………………… 2分 ∴CD =AB =6∵BP =3∴DE = BP =3∵BP ⊥CE ，BP ∥DE∴DE ⊥CE ……………………… 3分 ∴在Rt △DCE 中，CE===……………………… 4分 （2）证明：∵以点A 为旋转中心，将△ABP 顺时针旋转60°得到△AMN .∴△AMN ≌△ABP ， ∴MN =BP ，PA =AM ，∠PAM =60° ∴△PAM 是等边三角形. ∴PA =PM∴ PA +PB +PC =CP +PM +MN …………………… 6分当AC =BC =4时，PA +PB +PC=． (8)【2017.1怀柔期末】7．(1)相等；…………1分 (2)想法一：∵△ABC 是等边三角形， ∴AB =BC , ∠B =60°. …………2分 ∵AH =CE ,∴BH =BE . ∴∠BHE =60°.∴AC //HE .∴∠1=∠2. (3)分在△AOE 和△COM 中,∠ACM =∠AEM =60°,∠AOE =MOE , ∴∠1=∠3.∴∠2=∠3. ……………………………5分 ∵∠BHE =60°,∴∠AHE =120°.∵∠ECM =120°.∴∠AHE =∠ECM . ……………………………6分 ∵AH =CE ,∴△AHE ≌△ECM （AAS ）. ∴AE =EM . ……………………………7分（或根据一线三等角证△ABE ∽△ECO ,得∠BAE =∠CEM , 再证∠AHE =∠ECM ,得△AHE ≌△ECM （ASA ）） 图3NBE图2B(2)E更多精品文档EM 想法二：∵在△AOE 和△COM 中, ∠ACM =∠AEM =60°, ∠AOE =∠COM ,∴∠EAC =∠EMC . ……………………………3分 又∵对称△ACE ≌△FCE ,∴∠EAC =∠EFC , AE =EF . …………5分 ∴∠EMC =∠EFC .∴EF =EM .∴AE =EM . …………7分 想法三：∵将线段BE 绕点B 顺时针旋转60°,∴可证△ABE ≌△CBF （SAS ）. …………………2分 ∴∠1=∠2 AE =CF . …………………3分 ∵∠AEM =∠CBA =60°,∴∠1=∠CEM .∴∠2=∠CEM .∴EM //CF . …………4分 ∵∠CBF =60°,BE =BF ,∴∠BEF =60°,∴∠MCE =∠CEF =1200.∴CM //EF . …………………5分 ∴四边形MCFE 为平行四边形. ∴CF =EM .∴AE =EM . …………………7分【2017.1门头沟期末】8.（1）补充图形正确 ……………………………………………1分PM PN =……………………………………………2分（2）作出示意图 ……………3分思路：在Rt △ABC 中，过点P 作PE ⊥AB 于E ，PF ⊥BC 于点F由PF ⊥BC 和∠ABC ＝90º可以得到AB PF ∥，∠PFC ＝90º进而得到∠A ＝∠FPC ；由∠PFC ＝∠AEP= 90º, AP=PC 可以得到 △AEP ≌ △PFC ，进而推出AE=PF ；由点P 处的两个直角可以得到∠EPM ＝∠FPN ，进而可以得到△MEP ∽ △NPF ，由此可以得到PF PE ＝PNPM 等量代换可以得到PM PEPN AE=；在Rt △AEP 中 tan PE A AE ∠=,可以得到tan 23PMPN=︒………………7分 【2017.1通州期末】9.解：（1）……………………..(1分)MECB更多精品文档33=AE CF ；……………………..(2分) AE 与EF 的数量关系为AE =EF ……………………..(3分)证明：（2）连接AF ，EF 与AC 交于点G .Θ在等边△ABC 中，CD 是它的外角平分线. ∴∠ACF =60°=∠AEF ，Θ∠AGE =∠FGC ，∴△AGE ∽△FGC ……………………..(5分)∴GF GAGC GE = ∴GF GC GA GE = Θ∠AGF =∠EGC∴△AGF ∽△EGC ……………………..(6分) Θ∠AFE =∠ACB=60°， ∴△AEF 为等边三角形 ∴AE =EF ……………………..(7分)【2017.1延庆期末】10.（1）如图1中，过点A 作AH ⊥BC 于H ．∴∠AHB =∠AHC =90°，在Rt △AHB 中，∵AB =52，∠B =45°，∴BH =ABcosB =5， AH=ABsinB =5，在Rt △AHC 中，∵∠C=30°，∴AC=2AH =10，CH =ACcosC =5，∴BC=BH+CH =5+53． ………………………………3分（2）①证明：如图1中，过点A 作AP ⊥AB 交BC 于P ，连接PE ，∴△ABD ≌△APE ，∴BD=PE ，∠B =∠APE =45°，B更多精品文档∴∠EPB =∠EPC =90°，∵∠C=30°， ∴CE =2PE ，∴CE =2BD ． …………………………5分 ③213 …………………………6分 【2017.1大兴期末】11. （1）①…………………………………2分 ②如图,连结CD ，FD ∵AC =6，BC =8，AB =10 ∴AC 2+BC 2=AB 2∴△ABC 是直角三角形，∠ACB =90°∴EF 是⊙O 的直径……………………………3分 ∵D 是AB 中点∴DA =DB =DC =5∴∠B =∠DCB ，∵EF ∥AB ∵∠CDF =∠CEF∴∠A =∠CDF∵∠A +∠B =90°∴∠CDF +∠DCB =90° ∴∠CFD =90° ∴CD 是⊙O 的直径 ∴EF =CD =5………………4分FE ACO 图1图2③由AC2+BC2=AB2可得∠ACB=90°,所以，EF是⊙O的直径.由于CD是⊙O的弦,所以，有EF≥CD，所以，当CD是⊙O的直径时，EF最小…………6分24.………………………………………………8分图3（2）5更多精品文档。

2024年1月九上期末——圆的综合1.【东城】24．如图，AB 为⊙O 的直径，点C 在⊙O 上，∠ACB 的平分线CD 交⊙O 于点D.过点D 作DE ∥AB ，交CB 的延长线于点E ．(1)求证：直线DE 是⊙O 的切线；(2)若∠BAC =30°，BC =CD 的长．2.【西城】24．如图，AB 是O 的直径，AB BC =，AC 交O 于点D ，点F 在OD 的延长线上且12FAD ABC ∠=∠．（1）求证：AF 是O 的切线；（2）若8AF =，4DF =，求AC 的长．3.【海淀】25.如图，AB 为半圆O 的直径，点C ，D 在半圆O 上，直线CM 与半圆O 相切于点C ，//CM AD .（1）若MCD ∠α=，求COA ∠的大小（用含α的式子表示）；（2）过点O 作OE CD ⊥交CM 于点E ，交CD 于点F ，若//CD AB ，6AB =，求CE 的长.4.【朝阳】24．如图，AC ，BD 是圆内接四边形ABCD 的对角线，AC ⊥BD 于点E ，BD 平分∠ADC .（1）求∠BAD 的度数；（2）点P 在DB 的延长线上，P A 是该圆的切线.①求证：PC 是该圆的切线；②若PA =AC =3，直接写出PD 的长.5.【石景山】24．如图，在ABC △中，AB AC =，以AB 为直径的O 交BC 于点D ，交AC 于点E ，点F 在AC 的延长线上，12CBF BAC ∠=∠．（1）求证：BF 是O 的切线；（2）若5AB =，1tan 2CBF ∠=，求CE 的长．6.【丰台】24．如图，△ABC 中，AB =AC ，以AB 为直径作⊙O 交BC 于点D ，作DE ⊥AC 交AC 于点E ，延长ED 与AB 的延长线交于点F ．（1）求证：DE 是⊙O 的切线；（2）若△ABC 为等边三角形，AE=3，求⊙O 半径的长．7.【昌平】24.如图，AB 是⊙O 的直径，点C 在⊙O 上，点D 为 AC 的中点，过点D 作⊙O 的切线，交BC 延长线于点P ，连接OD 交AC 于点E .（1）求证：四边形DECP 是矩形；（2）作射线AD 交BC 的延长线于点F ，若tan ∠CAB =43，BC =6，求DF 的长.8.【通州】25．如图，点C 在以AB 为直径的O 上，CD 平分ACB ∠交O 于点D ，交AB 于点E ，过点D 作DF AB ∥交CO 的延长线于点F ．（1）求证：直线DF 是O 的切线；（2）若30A ∠=︒，43AC =，求DF 的长．24题图9.【房山】24.如图,AB是⊙O的直径，AC，BC是弦，点D在AB的延长线上，且DCB DAC∠=∠，⊙O的切线AE与DC的延长线交于点E．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，30∠=︒，求AE的长.D10.【大兴】24.如图，AB是⊙O的直径，点C在⊙O上，连接AC，BC，过点O作OD⊥BC于点D,过点C作直线CE交OD的延长线于点E,使得∠E=∠B.(1)求证：CE是⊙O的切线.(2)若DE=6,CE=35,求OD的长.11.【门头沟】25.如图，△ABC内接于⊙O，AB为直径，点D在⊙O上，过点D作⊙O切线与AC的延长线交于点E，ED∥BC，连接AD交BC于点F.（1）求证：∠BAD=∠DAE；（2）若AB=6，AD=5，求DF的长.12.【燕山】24．如图，在△ABC中，∠ACB＝90°，点D在AB上，以AD为直径作⊙O与BC相切于点E，连接DE并延长交AC的延长线于点F．(1)求证：AF＝AD；(2)若CE＝4，CF＝2，求⊙O的半径．13.【顺义】25．如图，AB为⊙O的弦，点C为AB的中点，CO的延长线交⊙O于点D，连接AD，BD，过点D作⊙O的切线交AO的延长线于点E．（1）求证：DE∥AB；（2）若⊙O的半径为3，tan∠ADC＝，求DE的长．14.【密云】24.如图，⊙O是△ABC的外接圆，∠ABC=45°，连接OC交AB于点E，过点A作OC的平行线交BC延长线于点D．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为4，AD=6，求线段CD的长．15.【平谷】24.如图，AB 为⊙O 的直径，弦CD ⊥AB 于H ，连接AC 、AD ，过点A 作⊙O 的切线与∠ADC 的平分线相交于点E ，DE 交AB 于点G ，交AC 于点F ，交⊙O 于点M ，连接AM ．（1）求证：AC=AD ；（2）若22tan =∠AMD ，CD=4，求AF 长．。