【2019秋人教必修2】第六章平面向量及其应用章末复习课

1 / 3人教A 版数学必修第二册第六章《平面向量及其应用》同步讲义第六章 平面向量及其应用 知识点总结1. 向量：既有大小，又有方向的量．数量：只有大小，没有方向的量．有向线段的三要素：起点、方向、长度．零向量：长度为的向量．单位向量：长度等于个单位的向量．平行向量（共线向量）：方向相同或相反的非零向量．零向量与任一向量平行．相等向量：长度相等且方向相同的向量．2. 向量加法运算：⑴三角形法则的特点：首尾相连．⑵平行四边形法则的特点：共起点．⑶三角形不等式：．⑷运算性质：①交换律：；②结合律：；③．⑸坐标运算：设，，则．3. 向量减法运算：⑴三角形法则的特点：共起点，连终点，方向指向被减向量．⑵坐标运算：设，，则．设、两点的坐标分别为，，则．4. 向量数乘运算：⑴实数与向量的积是一个向量的运算叫做向量的数乘，记作．①；②当时，的方向与的方向相同；当时，的方向与的方向相反；当时，．⑵运算律：①；②；③．⑶坐标运算：设，则．5. 向量共线定理：向量与共线，当且仅当有唯一一个实数，使．01a b a b a b -≤+≤+a b b a +=+ ()()a b c a b c ++=++ 00a a a +=+=()11,a x y =()22,b x y = ()1212,a b x x y y +=++ ()11,a x y =()22,b x y = ()1212,a b x x y y -=-- A B ()11,x y ()22,x y ()1212,x x y y AB =--λa a λa a λλ=0λ>a λ a 0λ<a λ a 0λ=0a λ=()()a a λμλμ= ()a a a λμλμ+=+()a b a b λλλ+=+ (),a x y = ()(),,a x y x y λλλλ==()0a a ≠ b λb a λ=2 / 3设，，其中，则当且仅当时，向量、共线．6. 平面向量基本定理：如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．（不共线的向量、作为这一平面内所有向量的一组基底）7. （选讲）分点坐标公式：设点是线段上的一点，、的坐标分别是，，当时，点的坐标是．8. 平面向量的数量积：⑴．零向量与任一向量的数量积为．⑵性质：设和都是非零向量，则①．②当与同向时，；当与反向时，；或．③．⑶运算律：①；②；③．⑷坐标运算：设两个非零向量，，则．若，则，或设，，则．设、都是非零向量，，，是与的夹角，则．9. 正弦定理：在中，、、分别为角、、的对边，为的外接圆的半径，则有．10. 正弦定理的变形公式（1），，；（2），，；（3）；（4）．11. 三角形面积公式：．12. 余弦定理：在中，有，，()11,a x y = ()22,b x y = 0b ≠ 12210x y x y -=a ()0b b ≠1e 2e a1λ2λ1122a e e λλ=+1e 2e P 12P P 1P 2P ()11,x y ()22,x y 12λP P =PPP 1212,11x x y y λλλλ++⎛⎫⎪++⎝⎭()cos 0,0,0180a b a b a b θθ⋅=≠≠≤≤0a b 0a b a b ⊥⇔⋅= a b a b a b ⋅= a ba b a b ⋅=- 22a a a a ⋅== a = a b a b ⋅≤a b b a ⋅=⋅()()()a b a b a b λλλ⋅=⋅=⋅ ()a b c a c b c +⋅=⋅+⋅ ()11,a x y =()22,b x y = 1212a b x x y y ⋅=+ (),a x y = 222a x y =+ a =()11,a x y =()22,b x y = 12120a b x x y y ⊥⇔+= a b()11,a x y = ()22,b x y = θa b cos a ba b θ⋅==C ∆AB a b c A B C R C ∆AB 2sin sin sin a b c R C===A B 2sin a R =A 2sin b R =B 2sin c R C =sin 2a R A =sin 2b R B =sin 2c C R=::sin :sin :sin a b c C =A B sin sin sin sin sin sin a b c a b cC C++===A +B +A B 111sin sin sin 222C S bc ab C ac ∆AB =A ==B C ∆AB 2222cos a b c bc =+-A 2222cos b a c ac =+-B3 / 3．13. 余弦定理的推论：，，．14. 设、、是的角、、的对边，则：（1）①若，则；（2）若，则；（3）若，则2222cos c a b ab C =+-222cos 2b c a bc +-A =222cos 2a c b ac +-B =222cos 2a b c C ab+-=a b c C ∆AB A B C 222a b c +=90C =222a b c +>90C <222a b c +<90C >。

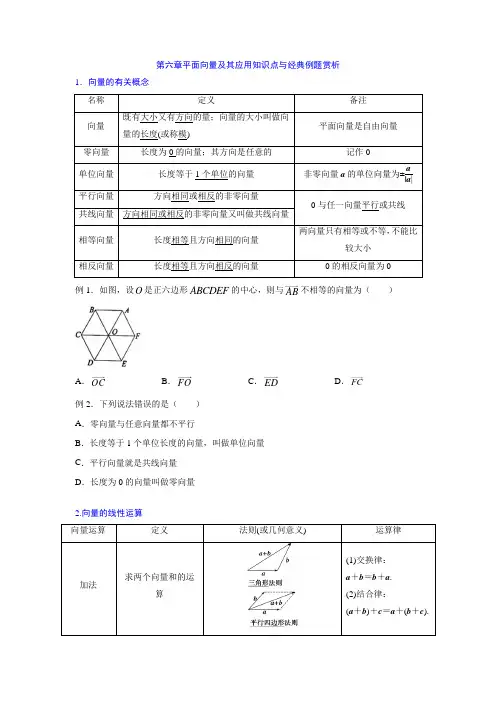
第六章平面向量及其应用知识点与经典例题赏析1．向量的有关概念 名称 定义备注向量 既有大小又有方向的量；向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量 长度为0的向量；其方向是任意的记作0单位向量 长度等于1个单位的向量 非零向量a 的单位向量为±a |a |平行向量方向相同或相反的非零向量0与任一向量平行或共线 共线向量 方向相同或相反的非零向量又叫做共线向量 相等向量 长度相等且方向相同的向量 两向量只有相等或不等，不能比较大小 相反向量长度相等且方向相反的向量0的相反向量为0例1．如图，设O 是正六边形ABCDEF 的中心，则与AB 不相等的向量为（ ）A ．OCB ．FOC ．EDD ．FC例2．下列说法错误的是（ ） A ．零向量与任意向量都不平行B ．长度等于1个单位长度的向量，叫做单位向量C ．平行向量就是共线向量D ．长度为0的向量叫做零向量2.向量的线性运算 向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律：a ＋b ＝b ＋a . (2)结合律：(a ＋b )＋c ＝a ＋(b ＋c ).减法求a 与b 的相反向量－b 的和的运算叫做a 与b 的差三角形法则a －b ＝a ＋(－b )数乘求实数λ与向量a 的积的运算(1)|λa |＝|λ||a |；(2)当λ>0时，λa 的方向与a 的方向相同；当λ<0时，λa 的方向与a 的方向相反；当λ＝0时，λa ＝0λ(μa )＝(λμ)a ； (λ＋μ)a ＝λa ＋μa ； λ(a ＋b )＝λa ＋λb例3．AB CD DA BC +++=（ ） A ．BDB ．ACC ．0D ．AB 例4．在平行四边形ABCD 中，AB CB DC +-等于（ ） A ．BC B ．AC C ．DAD ．BD例5．若5a =，b 与a 的方向相反，且7b =，则a 等于（ ） A ．57b B ．57b -C ．75b D ．75b -3.共线向量定理向量a (a ≠0)与b 共线，当且仅当有唯一一个实数λ，使b ＝λa .11．如图，OA ，OB 不共线，且()AP t AB t =∈R ，用OA ，OB 表示OP ．4．平面向量基本定理如果e 1、e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1、λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1、e 2叫做表示这一平面内所有向量的一组基底． 例6．设12,e e 是平面内两个不共线的向量，则向量,a b 可作为基底的是（ ）A ．1212,a e e b e e =+=--B ．1212112,24a e eb e e =+=+ C ．1212,a e e b e e =+=-D ．12122,24a e e b e e =-=-+例7．在边长为1的正方形ABCD 中，M 为AB 上靠近B 的三等分点，N 为BC 的中点.若MN AB AD λμ=+(,λμ∈R )，则32λμ+=（ ） A ．0B ．56C ．2D ．136例8．已知向量(3,),(,3),9a m b n a b ==⋅=，则m n +=（ ） A ．0 B ．3 C ．1D ．1-5．平面向量的坐标运算(1)向量加法、减法、数乘及向量的模设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21.(2)向量坐标的求法①若向量的起点是坐标原点，则终点坐标即为向量的坐标．②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)，|AB →|＝(x 2－x 1)2＋(y 2－y 1)2. 6．平面向量共线的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，其中b ≠0.a ∥b ⇔x 1y 2－x 2y 1＝0.例9．已知向量()1,a m =，()2,4b =，若//a b ，则a b +=（ ）A ．3B C ．D 例10．已知向量(1,2),(2,3)a b =-=，若()a ma b ⊥-，则m =（ ） A ．54B ．54-C ．45D ．45-7．平面向量的数量积已知两个非零向量a 与b ，它们的夹角为θ，则数量|a ||b |cos θ叫做a 与b 的数量积(或内积)，记作a ·b ＝|a ||b |cos θ.规定：零向量与任一向量的数量积为__0__.两个非零向量a 与b 垂直的充要条件是 a·b ＝0，两个非零向量a 与b 平行的充要条件是 a·b＝±|a||b|.例11．向量()()1,,2,1a x b ==-，若a b ⊥，则2a b +=（ ）A ．2B C ．3D ．5例12．已知(0,1),(1,3)A B --，则||AB =（ ）A B ．17C ．5D8．平面向量数量积的几何意义数量积a·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos θ的乘积． 9．平面向量数量积的重要性质(1)e·a ＝a·e ＝|a |cos θ； (2)非零向量a ，b ，a ⊥b ⇔a·b ＝0； (3)当a 与b 同向时，a·b ＝|a||b|；当a 与b 反向时，a·b ＝－|a||b|，a·a ＝|a |2，|a |＝a·a ； (4)cos θ＝a·b |a||b|； (5)|a·b |__≤__|a||b|.10．平面向量数量积满足的运算律(1)a·b ＝b·a (交换律)； (2)(λa )·b ＝λ(a·b )＝a ·(λb )(λ为实数)； (3)(a ＋b )·c ＝a·c ＋b·c . 11．平面向量数量积有关性质的坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a·b ＝x 1x 2＋y 1y 2，由此得到 (1)若a ＝(x ，y )，则|a |2＝x 2＋y 2或|a |＝x 2＋y 2.(2)设A (x 1，y 1)，B (x 2，y 2)，则A 、B 两点间的距离|AB |＝|AB →|＝(x 2－x 1)2＋(y 2－y 1)2. (3)设两个非零向量a ，b ，a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ⊥b ⇔x 1x 2＋y 1y 2＝0. 12．向量在平面几何中的应用(1)用向量解决常见平面几何问题的技巧：例13．已知||4a =，||3b =，,150a b <>=.求（1）()a b b -⋅； （2）求||a b +.例14．已知平面上三点A ，B ，C ．()2,3BC k =-，()2,4AC =-． （1）若三点A ，B ，C 不能构成三角形，求实数k 应满足的条件； （2）若ABC 中角C 为钝角，求k 的取值范围．例15．平面内给定三个向量(3,2)a =，(1,2)b =-，(4,1)c =. （1）求满足a mb nc =-的实数m ，n ； （2）若()//(2)a kc b a +-，求实数k 的值.例16．如图，在ABC 中，AB a =，AC b =，D ，F 分别为BC ，AC 的中点，P 为AD 与BF 的交点，且2AE EB =．（1）试用a ，b 表示BP ； （2）若3AB =，4AC =，3BAC π∠=，求BP ED ⋅．10，正弦定理： 1.正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，并且都等于外接圆的直径，即 RC cB b A a 2sin sin sin ===（其中R 是三角形外接圆的半径） 2.变形：1）sin sin sin sin sin sin a b c a b cC C ++===A +B +A B ．2）化边为角：C B A c b a sin :sin :sin ::=；;sin sin B A b a = ;sin sin C B c b = ;sin sin C A c a =3）化边为角：C R c B R b A R a sin 2,sin 2,sin 2===4）化角为边： ;sin sin b a B A =;sin sin c b C B =;sin sin c aC A = 5）化角为边： RcC R b B R a A 2sin ,2sin ,2sin ===二.三角形面积1.B ac A bcC ab S ABC sin 21sin 21sin 21===∆例17．已知a ，b ，c 分别是ABC 的三个内角A ､B ､C 的对边，若ABC 2c =，60A =︒，求a ，b 及角C 的值.例18．已知△ABC 的内角A ，B ，C 所对边分别为a ，b ，c ，且()3cos cos cos B a B b A c +=．（1）求cos B ；（2）若2AB =，sin sin A B =，求△ABC 的面积．例19．已知ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，sin cos a B b A c +=. （1）求B ；（2）设a =，2b =，求c .11，余弦定理 1.余弦定理：三角形中任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的2倍，即A bc c b a cos 2222-+=B ac c a b cos 2222-+= C ab b a c cos 2222-+=2.变形：bc a c b A 2cos 222-+=ac b c a B 2cos 222-+=ab c b a C 2cos 222-+=注意整体代入，如：21cos 222=⇒=-+B ac b c a利用余弦定理判断三角形形状：设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边，则：①若，，所以为锐角②若为直角A a b c ⇔=+222③若， 所以为钝角，则是钝角三角形三角形中常见的结论三角形三角关系：A+B+C=180°；C=180°—(A+B)； 三角形三边关系：两边之和大于第三边：，，； 两边之差小于第三边：，，；在同一个三角形中大边对大角：B A b a B A sin sin >⇔>⇔> 4) 三角形内的诱导公式：sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-)2sin()2cos()22cos()22sin()22tan(2tan C CC C C B A =--=-=+πππ7) 三角形的五心：垂心——三角形的三边上的高相交于一点 重心——三角形三条中线的相交于一点 外心——三角形三边垂直平分线相交于一点 内心——三角形三内角的平分线相交于一点旁心——三角形的一条内角平分线与其他两个角的外角平分线交于一点例20．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c cos sin B b A = （1）求角B 的大小；（2）若cos A =，求sin(2)A B -的值； （3）若2b =，2c a =，求边a 的值.例21．ABC 内角A 、B 、C 的对边分别为a 、b 、c ，设22()b c a bc -=- （1）求角A ；（22b c +=，求sin C ．例22．在ABC 中，A ，B ，C 的对边分别是a ，b ，c ，且3,cos b c b A c ===． （1）求a 的值；（2）若A B >，求AC 边上的高的长．参考答案1．D 【分析】由正六边形的性质结合平面向量相等的概念即可得解. 【详解】由题意，C B FO ED A O ===，2AB FC =. 故选：D. 2．A 【分析】根据零向量与单位向量及共线向量的定义判断可得； 【详解】解：模为0的向量叫做零向量，规定：零向量与任意向量平行，长度为1个单位长度的向量，叫做单位向量，故A 错误，BCD 正确． 故选：A 3．C 【分析】根据向量加法的运算法则可得. 【详解】0AB CD DA BC AB BC CD DA +++=+++=，故选：C. 4．C 【分析】直接由向量加减法法则即可得结果． 【详解】在平行四边形ABCD 中，,==AB DC CB DA ， 所以()==+--+AB CB DC AB DC C DA B ． 故选：C5．B 【分析】由向量反向可知()0a b λλ=<，即a b λ=-，由此构造方程求得λ，即可得到结果. 【详解】b 与a 的反向，()0a b λλ∴=<，a b λ∴=-，即75λ-=，解得：57λ=-，57a b ∴=-.故选：B. 6．C 【分析】逐项判断向量,a b 是否共线，若,a b 不共线，则可以作为基底 【详解】解：对于A ，因为1212()b e e e e a =--=-+=-，所以,a b 共线，所以,a b 不能作为基底，所以A 不合题意； 对于B ，因为12121111(2)2444b e e e e a =+=+=，所以,a b 共线，所以,a b 不能作为基底，所以B 不合题意；对于C ，若,a b 共线，则存在唯一实数λ，使a b λ=，即121212)(e e e e e e λλλ=+=--，所以1λ=且1λ=-，所以λ不存在，所以,a b 不共线，所以,a b 可以作为基底，所以C 符合题意；对于D ，因为1212242(2)2b e e e e a =-+=--=-，所以,a b 共线，所以,a b 不能作为基底，所以D 不合题意， 故选：C 7．C 【分析】以,AB AD 为基底表示出MN ，由此求得,λμ，进而求得32λμ+. 【详解】1132MN MB BN AB AD =+=+，所以3211211,,32λμλμ==+=+=. 故选：C8．B【分析】利用平面向量数量积运算求解即可.【详解】339a b n m ⋅=+=，所以3m n +=．故选：B.9．C【分析】由//a b ，可得1420m ⨯-=，求出m 的值，从而可求出a b +的坐标，进而可求出a b +【详解】因为//a b ，所以1420m ⨯-=，解得2m =，所以()3,6a b +=， 所以223635a b +=+=故选：C.10．C【分析】根据向量垂直的坐标表示，列出方程，即可求解.【详解】由题意，向量(1,2),(2,3)a b =-=，可得25,4a a b =⋅=-因为()a ma b ⊥-，可得2()540ma a b b ma m a =+-⋅-=⋅=，解得45m =. 故选：C.11．D【分析】 由a b ⊥，得0a b ⋅=，解出x 的值，进而可求得2a b +的坐标，根据向量模长公式即可求解.【详解】解：因为向量()1,a x =，()2,1b =-，a b ⊥，所以()1210a b x ⋅=⨯-+⨯=，解得2x =， 所以()()()1,22,102,52a b +-+==，所以2205a b +=+=， 故选：D.12．A【分析】首先求出AB 的坐标，再根据向量模的坐标公式计算可得；【详解】解：因为(0,1),(1,3)A B --，所以()()()1,30,11,4AB =---=-，所以(AB =-=故选：A13．（1）9-；（2.【分析】 （1）由已知求a b ⋅，结合向量数量积的运算律，即可求()a b b -⋅； （2）由2()a b a b +=+，利用向量数量积的运算律求值即可. 【详解】（1）4,3,,150a b a b ==<>=cos ,43(6a b a b a b ∴⋅=<>=⨯⨯=-，∴2()639a b b a b b -⋅=⋅-=--=-.（2）2()a b a b +=+222a a b b =+⋅+==14．（1）72k =；（2）,4,7722⎛⎫⎛⎫- ⎪ ⎪+∞⎝⎭⎝⎭． 【分析】 （1）由题意可得向量BC 与AC 平行，根据平行的坐标表示即可求出答案；（2）由题意0AC BC ⋅<，且向量BC 与AC 不平行，根据数量积的坐标运算即可求出结论．【详解】解：（1）由三点A ，B ，C 不能构成三角形，得A ，B ，C 在同一直线上，即向量BC 与AC 平行，∴()42230k ---⨯=，解得72k =； （2）当角C 是钝角时，0AC BC ⋅<， ∴()()22340k ⨯-+⨯-<，解得4k >-，又向量BC 与AC 不平行，则72k ≠， 综上：k 的取值范围是,4,7722⎛⎫⎛⎫- ⎪ ⎪+∞⎝⎭⎝⎭． 15．（1）59m =，89n =-；（2）1613k =-. 【分析】（1）依题意求出mb nc -的坐标，再根据向量相等得到方程组，解得即可；（2）首先求出a kc +与2b a -的坐标，再根据向量共线的坐标表示计算可得；【详解】解：（1）因为(3,2)a =，(1,2)b =-，(4,1)c =，且a mb nc =- (3，2)(1a mb nc m ==-=-，2)(4n -，1)(4m n =--，2)m n -.∴4322m n m n --=⎧⎨-=⎩，解得59m =，89n =-. （2）(3a kc +=，2)(4k +，1)(34k =+，2)k +.22(1b a -=-，2)(3-，2)(5=-，2).5(2)2(34)0k k ∴-+-+=，解得1613k =-. 16．（1）2133BP a b =-+；（2）43BP ED ⋅=. 【分析】 （1）依题意首先表示出BF ，再根据重心的性质得到23BP BF =，即可得解； （2）首先根据平面向量数量积的定义求出a b ⋅，再表示出ED ，最后根据向量数量积的运算律计算可得；【详解】解：（1）因为12BF AF AB a b =-=-+． 因为点P 为ABC 的重心，所以2212133233BP BF a b a b ⎛⎫==-+=-+⎪ ⎭⎝． （2）因为3AB =，4AC =，3BAC π∠=，所以cos 63a b a b π⋅=⋅=．又因为2AE EB =，所以)(11113262ED EB BD a b a a b =+=+-=-+． 2221111174336296183BP ED a b a b a b a b ⎛⎛⎫⎫⋅=-+⋅-+=+-⋅=⎪⎪ ⎭⎭⎝⎝．17．a ；b =1；2C π=【分析】由正弦定理的面积公式可先求出b ，再结合余弦定理可求出a ，再由正弦定理求出角C .【详解】 1sin 2ABC S bc A =，所以12sin 6022b =⨯，所以b =1ABC 中，由余弦定理得a 2=b 2+c 2-2bccosA =3，所以a ，由正弦定理sin sin a c A C =2sin C =，解得sin 1C =， 所以2C π=.18．（1）1cos 3B =；（2）【分析】 （1）由正弦定理边角互化及两角和正弦公式可得3cos sin()sin B A B C +=，而A B C π++=且sin 0C ≠，即可求cos B .（2）由（1）易得tan B =A B =即可求AB 上的高，进而求△ABC 的面积．【详解】（1）由题设，()3cos sin cos cos sin sin B A B A B C +=，∴3cos sin()3cos sin sin B A B B C C +==，又sin 0C ≠， ∴1cos 3B =.（2）由（1）知：sin 3B =，则tan B = ∵sin sin A B =，又0A B π<+<，∴A B =，故△ABC 在AB 上的高1||tan 2h AB B ==∴1||2ABC S h AB ==19．（1）4π；（2）2. 【分析】（1）由题设，根据正弦定理得sin sin sin cos sin A B B A C +=，结合三角形内角的性质得tan 1B =，即可求B ；（2）由余弦定理，结合已知条件列方程，即可求c .【详解】（1）由正弦定理得：sin sin sin cos sin A B B A C +=，而()()sin sin sin sin cos cos sin C A B A B A B A B π=-+=+=+⎡⎤⎣⎦，∴sin sin sin cos A B A B =，又sin 0A ≠，cos 0B ≠，∴tan 1B =，又0B π<<，即4B π=.（2）由余弦定理2222cos b c a ac B =+-，即a =，∴222422c c =+-⨯，解得2c =.20．（1）3B π=；（2（3. 【分析】（1sin B B =，结合三角形内角性质即可求角B . （2）由两角差、倍角公式展开sin(2)A B -，根据已知条件及（1）的结论即可求值. （3）根据余弦定理列方程即可求a 的值.【详解】（1cos sin sin A B B A =，而A 为ABC 的内角，sin B B =，即tan B =0B π<<，可得3B π=，（2）2sin(2)sin 2cos cos 2sin 2sin cos cos (2cos 1)sin A B A B A B A A B A B -=-=--，∵cos 3A =，0A π<<，可得sin 3A =，而1cos ,sin 22B B ==，∴sin(2)91818A B -=+=， （3）由余弦定理知：2222cos a c ac B b +-=，又2b =，2c a =，1cos 2B =，∴234a =，可得3a =21．（1）3A π=；（2）sin C =【分析】（1）利用余弦定理计算可得；（2）利用正弦定理将边化角，再利用和差角的正弦公式计算可得；【详解】解：（1）2222()2b c b c bc a bc -=+-=-，∴2222cos b c a bc bc A +-==， 所以1cos 2A =，因为()0,A π∈，∴3A π=．（22b c +=，sin 2sin A B C +=，sin 2sin 33c C ππ⎛⎫++= ⎪⎝⎭sin 2sin 23C C π⎛⎫++= ⎪⎝⎭，sin cos cos sin 2sin 33C C C ππ++=，3sin 2C C =，∴1cos sin 226C C C π⎛⎫=-=- ⎪⎝⎭，∴64C ππ-=，∴512C π=，sin sin sin cos cos sin 6464644C ππππππ⎛⎫=+=+= ⎪⎝⎭．22．（1）3a =或6；（2）【分析】（1）利用余弦定理将cos b A c =-化为2222b c a b c bc +-⋅=，化简后再利用余弦定理可求出6B π=，由222c a b +-=结合已知条件可求出a 的值；（2）由于A B >，所以a b >，可得6a =，然后利用三角形的面积公式可求出面积，再利用面积法可求出AC 边上的高的长【详解】解：因为cos 2b A c a =-，所以22222b c a b c a bc +-⋅=-，所以22222b c a c +-=-，即222c a b +-=．由余弦定理可得222cos 2c a b B ac +-==， 因为(0,)B π∈，所以6B π=．（1）因为222,3,c a b b c +-=== 所以29180a a -+=，解得3a =或6． （2）因为A B >，所以6a =，1sin 2ABC S ac B ==△，所以AC 边上的高的长为2ABC S b =△。