22光的衍射
- 格式:ppt
- 大小:1.91 MB
- 文档页数:59









光的衍射说课稿一、说教材11 教材的地位和作用“光的衍射”是高中物理光学部分的重要内容。
它是在学生学习了光的直线传播、光的反射和折射等知识的基础上,进一步深入研究光的波动性的表现。
光的衍射现象不仅为理解光的波动性提供了有力的证据,也为后续学习光的干涉、偏振等内容奠定了基础。
12 教学目标121 知识与技能目标学生能够理解光的衍射现象,知道光发生明显衍射的条件;了解衍射条纹的特点和衍射现象在生活中的应用。
122 过程与方法目标通过观察实验现象,培养学生的观察能力和分析问题的能力;通过对衍射现象的分析和推理,培养学生的逻辑思维能力和科学探究能力。
123 情感态度与价值观目标激发学生对物理学科的兴趣,培养学生的科学态度和创新精神;让学生体会物理知识与生活实际的紧密联系,增强学生的应用意识。
13 教学重难点131 教学重点光的衍射现象和光发生明显衍射的条件。
132 教学难点对光的衍射现象的微观解释。
二、说教法21 实验演示法通过演示光的衍射实验,让学生直观地观察到衍射现象,从而激发学生的学习兴趣和探究欲望。
22 问题引导法设置一系列问题,引导学生思考和讨论,培养学生的思维能力和合作精神。
23 多媒体辅助教学法利用多媒体课件展示衍射条纹的图片和动画,帮助学生更好地理解衍射现象的特点和规律。
三、说学法31 观察法让学生仔细观察实验现象,获取感性认识。
32 讨论法组织学生进行小组讨论,交流各自的观点和想法,培养学生的合作学习能力。
33 归纳总结法引导学生对所学知识进行归纳总结,形成系统的知识体系。
四、说教学过程41 导入新课通过播放一段激光束照射狭缝的视频,引导学生观察光在通过狭缝后的传播情况,提出问题:光在通过狭缝后为什么会发生弯曲?从而引入新课“光的衍射”。
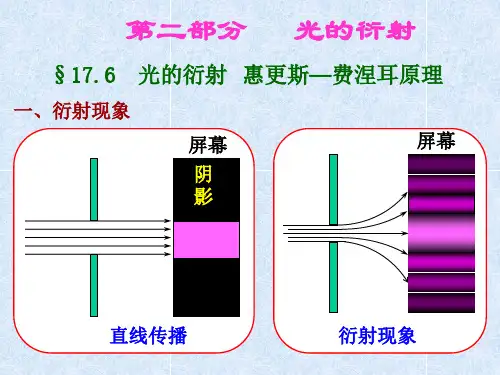
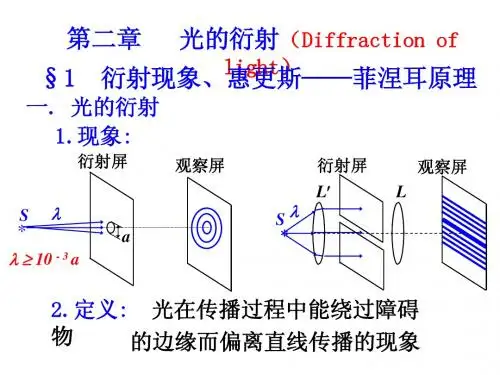
42 新课教学421 光的衍射现象演示单缝衍射实验,让学生观察光通过单缝后的衍射条纹。
然后,演示圆孔衍射实验,让学生观察光通过圆孔后的衍射现象。
引导学生比较单缝衍射和圆孔衍射条纹的特点,总结光的衍射现象的特征。
光学光的衍射和干涉光学:光的衍射和干涉在光学领域,光的衍射和干涉是重要的研究内容,它们展示了光的波动性质以及干涉现象的产生和应用。
光的衍射和干涉不仅在科学研究中有着广泛的应用,还在光学仪器设计和技术发展中发挥着重要作用。
本文将分析光的衍射和干涉的基本原理以及其在日常生活和科学研究中的应用。
一、光的衍射光的衍射是指光线通过一个较小孔隙或在物体边缘形成的小孔隙时,发生与直线传播不同的现象。
光线通过小孔隙后不再是直线传播,而是发生弯曲并产生一系列明暗相间的圆环或条纹。
这种现象可以通过菲涅尔衍射公式来描述。
菲涅尔衍射公式是描述光通过小孔隙时的干涉效应的数学表达式。
根据该公式,当光通过孔径较小的障碍物时,形成的衍射图样由中央明亮的主极大区域和周围一系列暗纹和明纹组成。
这一现象是由光的波动性质决定的,表明光是一种波动性质的电磁辐射。
光的衍射在光学研究中有着广泛应用。
例如,光的衍射可以用于显微镜和望远镜等光仪器的设计中,以增强光学成像的分辨率。
此外,在天文学领域,光的衍射还被用于测量星星的角直径和确定星体的位置等重要观测任务中。
光的衍射还被应用于红外线光谱学和生物医学成像等其他领域。
二、光的干涉光的干涉是指两束或多束光线相遇形成的明暗条纹的现象。
当光线从不同方向或不同路径到达一个点时,会出现互相增强或互相抵消的干涉效应,形成明暗相间的干涉纹。
光的干涉在两种典型情况下可以发生:干涉薄膜和杨氏干涉。
干涉薄膜是指薄膜表面反射的两束光线相遇形成的干涉现象。
当光线从介质中斜入射到薄膜表面上时,部分光线被反射,部分光线被透射,形成两束相干光线。
这两束光线再次相遇时,会发生干涉现象。
根据薄膜的厚度和光的波长,干涉纹的亮暗变化可以被用来分析薄膜的厚度和光的性质。
杨氏干涉是由两束光线的干涉引起的现象,其中一束光线通过一个狭缝,而另一束光线是绕过狭缝的。
当这两束光线再次相遇时,会形成干涉条纹。
杨氏干涉现象被广泛应用于科学研究和实验中,例如用于测量光的波长、质量和测量材料的折射率。