小学图形与几何测试题
- 格式:docx
- 大小:101.44 KB
- 文档页数:5
新苏教版六年级下册期末总复习第二单元《图形与几何》测试卷(二)姓名: 班级: 得分:一、选择题(5分)1.时针从3:00到9:00是围绕钟面中心旋转了()。
A.360° B.180°C.90° D.60°2.用一根铁丝围成正方形、长方形、正三角形和圆,那么面积最大的是()。
A.长方形B.正方形C.正三角形 D.圆3.下列图形不是轴对称图形的是()。
A.扇形B.环形 C.平行四边形D.菱形4.一根长30cm、宽3cm的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后纸条两端超出点P的长度相等,则最初折叠时,MA的长应为()。
A.7.5cm B.9cm C.12cm D.10. 5cm5.下列图中,每个大正方形都是由四个边长为1的小正方形组成,其中阴影面积不等于2的图形是()。
A.B.C.D.二、填空题(32分)6.图中共有______个三角形.7.一张长方形图片,长12厘米,宽9厘米.按1:3的比缩小后,新图片的长是(______)厘米,宽是(______)厘米,这张图片(______)不变,大小(______).8.长方形有(_____)条对称轴,正方形有(_____)条对称轴,圆有(_____)条对称轴,等边三角形有(____)条对称轴,半圆有(_____)条对称轴。
9.看图填一填。
(1)小帆船先向(______)平移了(______)格,再向(______)平移了(______)格.(2)三角形先向(______)平移了(______)格,再向(______)平移了(______)格.10.若一个角的余角比它的补角的还多1°,则这个角的大小是__________.11.如图,长方形ABCD长6cm,宽4cm,阴影部分甲和乙也是长方形。
已知甲的面积是△ABD面积的,那么乙的面积是(_______)。
12.图中多边形的周长是(________)厘米。

六年级数学下册第九章几何图形初步综合测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,在观测站O 发现客轮A ,货轮B 分别在它北偏西50°,西南方向,则∠AOB 的度数是( )A .80°B .85°C .90°D .95°2、如果A 、B 、C 三点在同一直线上,线段4cm AB =,2cm BC =,那么A 、C 两点之间的距离为( )A .2cmB .6cmC .2cm 或6cmD .无法确定3、如图所示,点A ,O ,B 在同一直线上,∠COA =90°,若∠1=∠2,则图中互余的角共有( )A.5对B.4对C.3对D.2对4、如图所示,已知∠AOB=4024'︒,OC平分∠AOB,∠BOD与∠AOC互为余角,则∠BOD的度数为()A.5958'︒︒D.6958'︒C.5948'︒B.6948'5、下列说法错误的是()A.直线AB和直线BA是同一条直线B.若线段AM=2,BM=2,则M为线段AB的中点C.画一条5厘米长的线段D.若线段AB=5,AC=3,则BC不可能是16、下面四个图形中,经过折叠能围成如图所示的几何图形的是()A.B.C.D.7、下面图形是棱柱的是()A.B.C.D.8、下列4个角中,最有可能与65°角互补的角是()A.B.C.D.9、如图,一副三角尺按不同的位置摆放,其中符合∠α=∠β的图形共有()A.4个B.3个C.2个D.1个10、下列几何图形与相应语言描述不相符的有()A.如图1所示,直线a和直线b相交于点AB.如图2所示,延长线段BA到点CC .如图3所示,射线BC 不经过点AD .如图4所示,射线CD 和线段AB 有交点第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、已知α∠与β∠互余,且3812α'∠=︒,则β∠=____________.2、如图,点A ,B ,C 在数轴上表示的有理数分别为a ,b ,c ,点C 是AB 的中点,原点O 是BC 的中点,现给出下列等式: ①c a c b =--; ②2a b c =-; ③()14c a b =--; ④a b c a b c +-=--.其中正确的等式序号是____________.3、计算:3545'7219'︒+︒=__________.4、用一个平面去截一个几何体,若截面是长方形,则该几何体可能是______(写三个).5、若∠α=135°,则∠α的补角是_____.三、解答题(5小题,每小题10分,共计50分)1、如图,线段8AB =,点C 是AB 的中点,D 是BC 的中点,E 是AD 的中点.(1)求线段BD 的长;(2)求线段EC 的长.2、如图,点A ,O ,B 在同一条直线上,射线OD 和射线OE 分别平分∠AOC 和∠BOC , 图中哪些角互为余角?哪些角互为补角?3、已知线段AB a (如图),延长BA 至点C ,使2AC AB =,延长AB 至点D ,使12BD AB =.(1)请按上述要求画全图形;(2)求线段CD 的长(用含a 的代数式表示);(3)若E 是CD 的中点, 3AE =,求a 的值.4、如图,已知点A 和线段BC ,请用直尺和圆规作图(不要求写作图过程,保留作图痕迹).(1)作线段AB 、射线CA ;(2)延长BC 至点D ,使得BD BC AC BA =+-.5、如图1,在AOB ∠内部作射线OC ,OD ,OC 在OD 左侧,且2AOB COD ∠=∠.(1)图1中,若160AOB ∠=︒,OE 平分AOC ∠,OF 平分BOD ∠,则EOF ∠______°;(2)如图2,OE 平分AOD ∠,探究BOD ∠与COE ∠之间的数量关系,并证明;(3)设COD m ∠=︒,过点O 作射线OE ,使OC 为AOE ∠的平分线,再作COD ∠的角平分线OF ,若3EOC EOF ∠=∠,画出相应的图形并求AOE ∠的度数(用含m 的式子表示).-参考答案-一、单选题1、B【解析】【分析】根据西南方向即为南偏西45︒,然后用180︒减去两个角度的和即可.【详解】由题意得:180(4550)85AOB ∠=︒-︒+︒=︒,故选:B .【点睛】本题考查有关方位角的计算,理解方位角的概念,利用数形结合的思想是解题关键.2、C【解析】【分析】根据题意,利用分类讨论的数学思想可以求得A、C两点间的距离.【详解】解:∵A、B、C三点在同一条直线上,线段AB=4cm,BC=2cm,∴当点C在点B左侧时,A、C两点间的距离为:4-2=2(cm),当点C在点B右侧时,A、C两点间的距离为:4+2=6(cm),故选C.【点睛】本题考查两点间的距离,解答本题的关键是明确题意,利用分类讨论的数学思想解答.3、B【解析】【分析】由∠AOC=90°,可求∠BOC=90°,推出∠1+∠AOE=90°,∠2+∠DOC=90°,求出∠DOC=∠AOE,推出∠1+∠COD=90°,∠2+∠AOE=90°,根据余角的定义得出即可.【详解】解∵∠COA=90°∠AOC+∠BOC=180°∴∠BOC=180°-90°=90°∴∠AOC=∠BOC=90°,∴∠1+∠AOE=90°,∠2+∠COD=90°.∵∠1=∠2,∴∠COD=∠AOE,∴∠1+∠COD=90°,∠2+∠AOE=90°,∴图中互余的角共有4对.故选B.【点睛】本题考查了邻补角,互余的应用,关键是熟悉:如果∠A和∠B互余,则∠A+∠B=90°.4、B【解析】【分析】由OC平分∠AOB,可求出∠AOC,再由∠BOD与∠AOC互为余角,即可求出∠BOD.【详解】∵∠AOB=4024'︒,OC平分∠AOB∴∠AOC=12∠AOB =2012'︒又∵∠BOD与∠AOC互为余角∴∠BOD=90°-∠AOC=6948'︒故选:B.【点睛】本题主要考查了角平分线的意义、余角的意义,掌握角平分线和余角的有关概念是解题的关键.5、B【解析】【分析】根据直线、线段以及线段中点的性质进行判定即可得出答案.【详解】解:A.因为直线AB和直线BA是同一条直线,所以A选项说法正确,故A选项不符合题意;B.如图1,AM=BM,但点M不是线段AB的中点.故B选项说法错误,故B选项符合题意.C.因为画一条5cm的线段,如图2所以C选项说法正确,故C选项不符合题意;D.因为如图3AB=5,AC=3,所以2≤BC≤8,BC不可能是1,故D选项说法正确,故D选项不符合题意.故选:B.【点睛】本题主要考查了两点间的距离,直线、射线、线段,熟练掌握两点的距离计算的方法及直线、射线、线段的性质进行判定是解决本题的关键.6、B【解析】【分析】根据图中三角形,圆,正方形所处的位置关系即可直接选出答案.【详解】三角形图案所在的面应与正方形的图案所在的面相邻,而选项A与此不符,所以错误;三角形图案所在的面应与圆形的图案所在的面相邻,而选项C与此也不符;三角形图案所在的面应与圆形的图案所在的面相邻,而选项D与此也不符,正确的是B.故选B.【点睛】此题主要考查了展开图折叠成几何体,可以动手折叠一下,有助于空间想象力的培养.7、A【解析】【分析】根据棱柱的两个底面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行进行判断.【详解】解:A、六棱柱,满足题意;B、三棱锥,不满足题意;C、球,不满足题意;D、圆柱,不满足题意.故选:A.【点睛】本题考查棱柱的定义,掌握棱柱的特征是解题的关键.8、D【解析】【分析】︒-︒=︒,为钝角,看选项只有D符合钝两个角互补,相加为180︒,与65︒互补的角的度数为18065115角的要求.【详解】︒-︒=︒,115︒为钝角,大于90︒.65︒互补的角的度数为18065115A、小于90︒为锐角,不符合要求;B、小于90︒为锐角,不符合要求;C、小于90︒为锐角,不符合要求;D、大于90︒为锐角,符合要求;故选D.【点睛】本题考查补角的性质,以及角的判断,熟悉补角的性质,掌握角的类型判断是本题的解题关键.9、B【解析】【分析】根据直角三角板可得第一个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第三个图形中∠α=∠β,第四个图形∠α和∠β互补.【详解】解:根据角的和差关系可得第一个图形∠α=∠β=45°,根据同角的余角相等可得第二个图形∠α=∠β,根据等角的补角相等可得第三个图形∠α=∠β,因此∠α=∠β的图形个数共有3个,故选:B.【点睛】此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.10、B【解析】【分析】根据直线、射线、线段的相关概念可直接进行排除选项.【详解】解:A、如图1所示,直线a和直线b相交于点A,几何图形与相应语言描述相符,故不符合题意;B、如图2所示,延长线段BA到点C,几何图形与相应语言描述不相符,故符合题意;C、如图3所示,射线BC不经过点A,几何图形与相应语言描述相符,故不符合题意;D、如图4所示,射线CD和线段AB有交点,几何图形与相应语言描述相符,故不符合题意;故选B.【点睛】本题主要考查直线、射线与线段,熟练掌握直线、射线与线段的相关概念是解题的关键.二、填空题︒1、5148'【解析】【分析】根据互余的定义(和为90︒的两个角互余)即可得.【详解】解:因为α∠与β∠互余,且3812α'∠=︒,所以9038125148β''∠=︒-︒=︒,故答案为:5148'︒.【点睛】本题考查了互余,熟练掌握互余的定义是解题关键.2、①②④【解析】【分析】先根据数轴的性质、线段中点的定义可得,,0b c c a b c a c b -=-=-<<<,再根据绝对值的性质逐个判断即可得.【详解】解:由题意得:,,0b c c a b c a c b -=-=-<<<, 则22a c b c b b c c c c c c --=--=+=-+=-=,即等式①正确;由,b c c a b c -=-=-得:22a c b b c =-=-+,0a <,20b c ∴-+<,22b a b c c ∴=-+=-,即等式②正确;由,b c c a b c -=-=-得:223a c b b b b =-=--=-, 则()()11344a b b b b c --=---==-,即()14c a b =-,等式③错误;+,3325+=+-=-=+a b c bb b bb b-+,--=--=+=+=3445b b b b ba b c b b b∴,即等式④正确;a b c a b c+-=--综上,正确的等式序号是①②④,故答案为:①②④.【点睛】本题考查了数轴、线段中点、绝对值、整式的加减,熟练掌握数轴和绝对值运算是解题关键.3、1084︒'【解析】【分析】两个度数相加,度与度,分与分对应相加,分的结果若满60则转化为度.【详解】解:35°45'+72°19'=108°4'故答案为:108°4' .【点睛】本题考查的知识点是角度的计算,注意度分秒之间的进率为60即可.4、长方体、正方体、圆柱(答案不唯一)【解析】【分析】截面的形状是长方形,说明从不同的方向看到的立体图形的形状必有长方形或正方形,由此得出长方体、正方体、圆柱用一个平面去截一个几何体,可以得到截面的形状是长方形.解:用一个平面去截一个几何体,如果截面的形状是长方形,原来的几何体可能是长方体、正方体、圆柱.故答案为:长方体、正方体、圆柱(答案不唯一).【点睛】此题考查用平面截几何体,解题的关键是掌握截面的形状既与被截的几何体有关,还与截面的角度和方向有关.5、45°##45度【解析】【分析】根据补角的定义:如果两个角的和等于180°(平角),就说这两个角互为补角,即可求解.【详解】解:∵∠α=135°,∴∠α的补角=180°-∠α=180°-135°=45°,故答案为:45°.【点睛】本题考查了补角的定义,熟练掌握补角的定义是解题的关键.三、解答题1、 (1)2(2)1【解析】(1)由点C 是AB 的中点可得AC =BC =4,由点D 是BC 的中点可得BD =CD =2即可;(2)由(1)可知AE 、AD 的长,再根据EC =AC −AE ,即可得出线段EC 的长.(1)解:因为点C 是AB 的中点,8AB =, 所以142AC BC AB ===, 又因为点D 是BC 的中点, 所以122BD CD BC ===.(2)解:由(1)得4AC =,6AD AC CD =+=,因为E 是AD 的中点, 所以132AE ED AD ===, 所以431EC AC AE =-=-=.【点睛】本题考查了两点间的距离以及线段中点的定义,利用线段的和差是解题关键.2、∠COD 和∠COE ,∠AOD 和∠BOE , ∠AOD 和∠COE ,∠COD 和∠BOE 互为余角;∠AOD 和∠BOD ,∠COD 和∠BOD ,∠BOE 和∠AOE ,∠COE 和∠AOE 互为补角【解析】【分析】和为90°的两角互余,和为180°的两角互补,根据两角和即可找出互余与互补的角.【详解】解:由题意知11=22AOD DOC AOC COE EOB BOC ∠=∠∠∠=∠=∠, ∵180AOD DOC COE EOB AOC BOC ∠+∠+∠+∠=∠+∠=︒∴∠AOC 和∠BOC 互为补角; ∴()11190222COD COE AOC BOC AOC BOC ∠+∠=∠+∠=∠+∠=︒ ∴∠COD 和∠COE 互为余角;同理,∠AOD 和∠BOE , ∠AOD 和∠COE ,∠COD 和∠BOE 也互为余角;∠AOD 和∠BOD ,∠COD 和∠BOD ,∠BOE 和∠AOE ,∠COE 和∠AOE 也互为补角;∴∠COD 和∠COE ,∠AOD 和∠BOE , ∠AOD 和∠COE ,∠COD 和∠BOE 互为余角;∠AOC 和∠BOC ,∠AOD 和∠BOD ,∠COD 和∠BOD ,∠BOE 和∠AOE ,∠COE 和∠AOE 互为补角.【点睛】本题考查了两角互余与两角互补的关系.解题的关键在于正确的找出角度的数量关系.3、 (1)见解析 (2)72CD a = (3)12a =【解析】【分析】(1)根据题意,画出图形,即可求解;(2)根据2AC AB =,12BD AB =可得AC =2a ,12BD a =,即可求解; (3)根据E 是CD 的中点,可得1724CE CD a ==,从而得到14AE AC CE a =-=,即可求解. (1)解:如图所示:(2)解:∵AC =2AB =2a ,1122BD AB a ==, ∴17222CD AC AB BD a a a a =++=++=; (3)解:如图,∵E 是CD 的中点, ∴1724CE CD a ==, ∴71244AE AC CE a a a =-=-=, ∵AE =3,即134a =, ∴12a =.【点睛】本题主要考查了线段的和与差,有关线段中点的计算,根据题意,准确画出图形是解题的关键.4、 (1)作图见解析(2)作图见解析【解析】【分析】(1)连接,AB 以C 为端点作射线,CA 从而可得答案;(2)延长,BC 在BC 的延长线上截取,CH AC 再在线段HB 上截取,HD AB 则线段BD 即为所求.(1) 解:如图,线段,AB 射线CA 是所求作的线段与射线,(2)解:如(1)图,线段BD 即为所求作的线段.【点睛】本题考查的是作线段,作射线,作一条已知线段等于几条线段的和与差,掌握基本作图语言与作图方法是解本题的关键.5、 (1)120(2)BOD 2COE ∠=∠(3)AOE ∠的度数为34m ︒或32m ︒ 【解析】【分析】(1)根据角平分线的性质得到11,22AOE COE AOC DOF BOF BOD ∠=∠=∠∠=∠=∠,再结合已知条件即可得出答案;(2)根据角平分线的性质与已知条件进行角之间的加减即可证明出结论;(3)根据角平分线的性质结合已知条件进行角度之间的加减运算,分类讨论得出结论即可.(1)∵160AOB ∠=︒,2AOB COD ∠=∠,∴80COD ∠=︒,∴80AOC BOD ∠+∠=︒ ,∵OE 平分,AOC OF ∠平分BOD ∠, ∴11,22AOE COE AOC DOF BOF BOD ∠=∠=∠∠=∠=∠, ∴1()402COE DOF AOC BOD ∠+∠=∠+∠=︒, ∴120EOF COE FOD COD ∠=∠+∠+∠=︒,故答案为:120;(2)BOD 2COE ∠=∠.证明:∵OE 平分AOD ∠,∴2AOD EOD ∠=∠,∵COD CO EOD E ,∴EOD COD COE ∠=∠-∠.∴(22)2AOD COD COE COD COE ∠=∠-∠=∠-∠. ∵2AOB COD ∠=∠,∴2AOD AOB COE ∠=∠-∠.∵BOD AOB AOD ∠=∠-∠,∴BOD 2COE ∠=∠,(3)如图1,当OE 在OF 的左侧时,∵OF 平分COD ∠,∴12COF COD ∠=∠,COD m ∠=︒, ∴12COF m ∠=︒, ∵COF COE EOF ∠=∠+∠,3COE EOF ∠=∠, ∴142COF EOF m ∠=∠=︒, ∴18EOF m ∠=︒, ∴338COE EOF m ∠=∠=︒. ∵OC 为AOE ∠的平分线,∴2AOE COE ∠=∠. ∴34AOE m ∠=︒;如图2,当OE 在OF 的右侧时,∵OF 平分COD ∠, ∴12COF COD ∠=∠, ∵COD m ∠=︒, ∴12COF m ∠=︒,∵COF COE EOF ∠=∠-∠,3COE EOF ∠=∠, ∴122COF EOF m ∠=∠=︒, ∴14EOF m ∠=︒, ∴334COE EOF m ∠=∠=︒. ∵OC 为AOE ∠的平分线,322AOE COE m ∠=∠=︒.综上所述,AOE ∠的度数为34m ︒或32m ︒. 【点睛】本题主要考查了角平分线的性质与角度之间的加减运算,关键在于根据图形分析出各角之间的数量关系.。

六年级下册图形和几何测试试卷一、填空题。
1、一个平行四边形的面积是1.2平方分米,它的高是0.6分米,底是()分米。
2、一个长方体的长、宽、高分别是3cm、2cm、4cm,这个长方体的棱长总和是( ),表面积是(),体积是()。
3、一个半圆的直径是6厘米,它的面积是()平方厘米,周长是()厘米。
4、6时整时,钟面上分针和时针所组成的角是( )°,它是一个()角;9时整时,分针和时针所组成的夹角是()°,它是一个()角,能形成这样的角的时刻还有()时整。
5、两个正方形的边长比是1∶2,它们的周长比是(),面积比是();两个圆的周长比是1∶3,则它们的半径比是(),面积比是()。
6、圆柱的体积一定,它的底面积和高成()比例关系。
7、把长为8cm,宽为6cm,高为4cm的长方体木块切成棱长是2cm的小正方体,能切出()块。
8、0.6dm3=( )cm3 3.02公顷=( )平方米530dm2=()m2二、选择题。
1、下面的图形中,不能折成正方体的是()C.2、一个正方体的棱长缩小到原来的21,表面积就会缩小到原来的( ),体积缩小到原来的( )。
A.21 B.41 C.81 3、小朋友喜欢玩的跷跷板的运动是( )。
A.旋转B.平移C.轴对称C.三、判断题。
1、在同一幅地图上,图上距离越大,实际距离也就越大。
( )2、长方体、正方体、圆柱和圆锥的体积计算公式可以统。
( )3、只有两个角是锐角的三角形一定是钝角三角形。
( )4、把一个长方形框架拉成一个平行四边形,它的周长不变,面积变大了。
( )5、甲在乙的东偏北30°方向,乙在甲的西偏南30°方向。
( )四、我会画。
(1)在下图中找出各点位置,并按顺序进行连线。
(5,1)(2,1)(2,4) (1,4)(3,6)(5,6)2、以图中的虚线为对称轴,画出图形的另一半。
五、解答题。
1、李叔叔家里要进行房屋装修,其中客厅长为5米,宽为4米,高为3米。

图形与几何专题测试卷一、估计下面图形的面积。
(每个小方格的面积为1cm2)(共9分)树叶的面积约占()cm2桃的面积约占()cm2花瓶的面积约占()cm2二、填空题。
(除标注外,每空1分,共20分)1.一个平行四边形面积是38 cm2,底是9.5 cm,高是()cm。
2.一个平行四边形的面积是10 m2,若底和高都扩大到原来2倍,它的面积是()m2。
3.一个梯形的面积是6.5 dm2,上下底之和是13 cm,这个梯形的高是()。
4.左图是由一个()形和一个()形组合成的,也可以看作由两个 ()组合而成的。
5.图中,阴影部分甲的面积比乙大4 cm2。
求三角形ABC的面积是()cm2。
6.一个三角形原来的底是14cm,如果将底增加2cm,面积就增加2cm2。
原来三角形的面积是()cm2。
7.一个直角梯形的上底、下底和高分别是10 cm、12 cm、8 cm,在里面画一个最大的正方形,正方形的面积是()cm2。
8.写出下列图形的面积。
(小方格的边长是 1 cm)(8分)9.在两条平行线间有三个不同的图形(如图),把它们按面积从大到小的顺序排列,依次是图( )>图()>图()。
三、选择题。
(共10分)1.一个梯形的面积是27cm2,高是4cm,上底长是下底长的2倍,这个梯形的上底是()cm。
A.4B.6C.8D.92.在下图中,若三角形甲的面积是20cm2,则三角形乙的面积是()cm2。
A.80 B.60 C.40 D.1603.右图中的正方形和平行四边形面积相比,()。
A.相等 B.正方形的面积大C.平行四边形的面积大 D.不能确定4.正方形、等边三角形、半圆形的对称轴的条数分别为x条,y条,z条,则x+y+z等于()。
A.5 B.7 C.8 D.195.如下图,如果梯形的面积是960cm2,上底是30cm,下底是50cm,那么阴影部分的面积是()。
A.120cm2 B.60cm2C.240cm2 D.180cm2四、按要求做题。

1.用4个边长是1厘米的小正方形,拼成如下的图形,周长最大的是()。
A B C D2.下列运动是平移的是()。
A B C D3.下列交通标志图案中, 不是..轴对称图形的是()。
A. B. C. D.4.下面()图中的阴影部分表示0.5。
A B C D5.下图一共有多少个小三角形?正确的算式是()。
A.5×4×3 B.5×5×3 C.4×4×3 D.4×(3+5)6.如右图所示,这张报纸放满了黄豆,估一估,这张纸上大约有()粒黄豆。
A.1200 B.1500 C.1000 D.8007. 用)个才能拼搭成一个从上面、正面、侧面看到的都是。
8.找一找图中黑格子排列的规律,在第四个图中涂黑格子。
9.如图:用小棒按如下方式搭着玩, 拼搭5个正方形,要用( )根小棒。
(把你的思考过程写在答题卡指定的位置上)10.下图中每个小三角形面积为8平方厘米,计算整个图形的面积。
(5分)11.下面几幅图共有(。
A .1200B .120C .1002D .102012.下面这些图形中,选项(13、下面哪些图形通过平移可以互相重合?()A.1和7 B.2和8 C.3和6 D.4和514.课堂上,老师要求用12个相同的小正方形拼出一个周长最小的长方形,下面选项()是正确的。
ABCD1 2 3 45 6 7 8北荷花池15.小红身高1.5米,她站在一幢3层楼房旁边,这幢楼房大约高( )米。
A .3 B .9 C .90 D .30016、从荷花池到大门,可以先向东走,再向 走;也可以先向 走,再向东走。
17、在一张边长10厘米的正方形中,小明小红分别从中剪去一部分。
1010108282(1) 剪去部分的图形面积相等吗?各是多少?(2) 剩下部分的图形周长相等吗?各是多少?18.下列图形中,( )是轴对称图形。
A . B. C. D.19.一个茶杯最多盛果汁600克,下面( )杯里的果汁大约重200克。

随堂测试6.2 图形与几何一、选择题1.至少用()个同样的正方体才能拼成一个新的正方体。
A.4B.8C.16D.272.9:30时,钟面上时针和分针所夹的角是()。
A.锐角B.钝角C.直角D.平角3.一个梯形中最多有()个直角。
A.4B.2C.14.以下图形中不是轴对称图形的是()。
A.平行四边形B.正方形C.等腰三角形D.圆5.下面的图形()不能由下面图形通过旋转得到。
A.B.C.D.二、填空题6.在两条平行线之间可以画( )条与平行线垂直的线段,这些垂直线段的长度( )。
7.过一点最多可以画( )条直线,过两点最多可以画( )条直线。
8.一个等腰三角形,它的顶角是50°,它的一个底角是( )。
9.把一个棱长为12dm的正方体削成一个最大的圆锥,这个圆锥的体积是( )3dm。
10.如图,平行四边形被分成甲、乙、丙三个三角形,甲的面积比乙多218cm,乙与丙的面积比是2∶3,这个平行四边形的面积是( )2cm。
三、判断题11.半径是2cm的圆,它的周长和面积的大小是相等的。
( )12.两个面积相同的三角形能拼成一个平行四边形。
( )13.两条不相交的直线一定是平行线。
( )14.小于180°的角一定是钝角。
( )四、解答题15.小东从一棵小树旁出发,先向西走60m,沿逆时针方向旋转90°,再向前走40m,又沿逆时针方向旋转90°,接着向前走80m,最后向西走20m。
此时小东在小树的什么方向?距离小树多少米?16.有一张长方形铁皮,剪下两个圆及一个长方形(如下图),正好可以做成一个圆柱。
这个圆柱的体积是多少立方厘米?17.如下图,把底面直径为4cm的圆柱切成若干等份,拼成一个近似的长方体。
这时表面积比原来增加240cm。
那么这个近似的长方体的表面积是多少平方厘米?18.下图中圆的面积与长方形的面积相等,圆的周长是25.12dm,求阴影部分的面积。
19.林玲做了一个长方体收纳盒,展开图如下。

图形与几何素养形成卷一、充满信心,顺利填空。
(26分)1.经过纸上一点,能画( )条直线;经过纸上两点,能画( )条直线。
2.一个等腰三角形的顶角与一个底角的和是150°,它的顶角是( )°。
3.下图中阴影部分的周长是( ),面积是( )。
4.一个正方体的棱长总和是36cm,它的表面积是( )cm2,体积是( )cm3。
5.一个直角三角形,三条边的长度分别是3cm、4cm、5cm,这个三角形的面积是( )cm2,斜边上的高是( )cm。
6.一个长方形的宽和长的比是4:5,这个长方形的周长是54dm,面积是( )dm2。
7.如右图,圆的直径是( )cm;长方形的长是( )cm;阴影部分的面积是( )cm2。
8.大圆的半径是4cm,小圆的半径是2cm,大、小圆的周长比是( ),面积比是( )。
9.从一个体积是120cm3的圆柱中挖去一个最大的圆锥,剩余部分的体积是( )cm3。
10.如右图,以明明家为中心:(1)超市在( )偏( )( )°方向上,距离是( )m。
(2)图书馆在( )偏( )( )°方向上,距离是( )m。
(3)学校在( )方向上,距离是( )m。
二、将正确答案的序号填在括号里。
(18分)1.用圆规画一个周长是12.56cm的圆,则圆规两脚间的距离是( )cm。
A.6.28B.4C.2D.3.142.下列现象中,属于平移的是( ),属于旋转的是( )。
①升国旗②拧开瓶盖③拉出抽屉④转动方向盘⑤电梯的升降A.①③⑤B.①③④C.②④D.①②3.下面的几何体从侧面看,图形是的是( )A.(1)(2)(4)B.(2)(3)(4)C.(1)(3)(4)D.(1)(2)(3)4.在比例尺是1:1000的地图上,量得一块三角形地的底是3.5cm,高是2cm,这块地的实际面积是( )m2。
A.700B.70000C.350D.350005.右图是底面半径为5cm的圆柱沿横截面截成相等的两部分后得到的图形,那么这个图形的体积是( )cm3。

苏教版六年级数学上册归类培优测试卷3.图形与几何一、填空。
(每空1分,共25分)1.3.04 立方分米=()立方厘米20 升=()立方米690 立方厘米=()毫升8 立方分米=()毫升2.一块橡皮的体积是6()一盒牛奶的体积是250()一间教室的体积是180()浴缸的容积大约是400() 3.小华在一个无盖的长方体玻璃容器中,摆了若干个体积为1立方厘米的小正方体。
做这个玻璃容器至少要用()平方厘米的玻璃,它的容积是()立方厘米。
4.一个长方体冰箱长6分米,宽5分米,高1.8米,这个冰箱的棱长总和是()分米,包装这个冰箱至少要用()平方分米的硬纸板,它所占的空间是()立方分米。
5.至少要用()个同样的小正方体才能拼成一个大正方体。
如果一个小正方体的棱长是6厘米,那么用它拼成的最小的大正方体的表面积是()平方厘米,体积是()立方厘米。
6.每瓶药水50毫升,装这样的200瓶,需要药水()升,如果有3.5升药水,一共可以装()瓶。
7.把一个正方体,切成三个完全相同的长方体后,表面积增加了2.4平方分米,原来这个正方体的表面积是()平方分米。
8.用一根36厘米长的铁丝焊成一个长方体框架,长、宽、高的比是4∶3∶2,如果在框架的外面糊一层纸,至少要用()平方厘米的纸。
9.把一个长8厘米,宽6厘米,高5厘米的长方体木块锯成两个相同的小长方体,表面积至少增加()平方厘米;最多增加()平方厘米。
10.用1立方厘米的小正方体摆一个棱长5厘米的正方体,需要()个。
摆成的正方体的底面积是()平方厘米。
11.小林用棱长为1厘米的正方体摆成一个物体(如图),这个物体的表面积是()平方厘米。
二、选择。
(将正确答案的字母填在括号里)(每题2分,共16分) 1.一个正方体的棱长总和是60厘米,它的表面积是()。
A.21600平方厘米B.150平方厘米C. 125平方厘米D.3600平方厘米2.将下图沿虚线折叠,可折成一个正方体,这时与6号面相对的是()号面。

北师大版五年级数学下册归类达标测试卷3.图形与几何一、认真审题,填一填。
(第1题4分,第3题3分,其余每小题2分,共23分)1.3.8 mL=( )cm34500 dm3=( )m38.5 m3=( )L 2600 dm2=( )m22.小明把一个长9 dm、宽8 dm、高6 dm的长方体木块削成最大的正方体,这个正方体的体积是( )。
3.猫发现一只老鼠,如果它朝( )偏( )( )°方向跑( )m就能捉住老鼠。
猫在老鼠的( )偏( )60°的方向上。
4.一块规格是30 cm×30 cm×6 cm的地砖,所占的空间是( )cm3,能铺地面的面积是( )cm2。
5.一个长方体容器从里面量棱长总和是96 cm,长是10 cm,宽是8 cm,高是( )cm。
如果将这个容器装满水,可以装( )mL水。
6.把两个棱长是2 cm的正方体拼成一个长方体,表面积减少( )cm2,把一个棱长为6 cm的正方体平均切成3个长方体,表面积增加( )cm2。
7.至少需要( )cm长的铁丝,才能做一个底面周长是18 cm,高是3 cm的长方体框架。
8.如图,在高为6 dm、宽为2.4 dm的楼梯上铺地毯,已知A点距墙根的距离是6 dm,至少需要地毯( )dm2。
9.把45升的水倒入长5分米、宽3分米、高4分米的鱼缸内,水面距鱼缸顶部还有( )分米。
10.一个正方体的棱长扩大到原来的2倍,这个正方体的表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
二、仔细推敲,选一选。
(将正确答案的序号填在括号里)(每小题2分,共16分)1.棱长为2 dm的正方体纸盒(纸盒厚度不计)里面能装( )个1 cm3的小正方体纸盒。
A.2000 B.4000 C.80002.下面图形折叠后能围成正方体的是( )。
3.如图是一些棱长为1 dm的小正方体堆在墙角,露在外面的面的面积总共是( )。
A.13 dm2B.14 dm2C.15 dm2D.12 dm24.下午放学,苗苗从家出发向北偏西55°方向走到学校,苗苗家在学校的( )方向上。

图形与几何测试卷(2)时间:90分钟满分:100分分数:一、填空。
(22分)1.一个圆柱和与它等底等高的圆锥的体积和是144 cm3。
圆柱的体积是( )cm3,圆锥的体积是( )cm3。
2.有一个圆环,外圆半径是6厘米,内圆半径是4厘米,圆环的面积是( )平方厘米。
3.看图数一数,填一填。
(如右图,每个方格的面积按1 cm2计算)A图( )cm2B图( )cm2C图( )cm2D图大约( )cm24.把一个高为10厘米的圆柱沿底面半径切成若干等份,拼成一个近似的长方体。
如果这个长方体的底面积是50平方厘米,那么圆柱的体积是( )立方厘米。
5.一个梯形的面积是8 cm2 ,如果它的上底、下底和高各扩大到原来的2倍,它的面积是( )cm2 。
(导学号03766120)6.两个圆的半径分别是3厘米和5厘米,它们周长的比是( ),面积的比是( )。
二、判断。
(对的在括号里画“√”,错的画“✕”)(12分)1.在一个三角形中,只要两个内角和小于另一个内角,这个三角形一定是钝角三角形。
( )2.一条直线上的两点把这条直线分成两条射线和一条线段,所以射线比直线短。
( )3.长方形、正方形、圆、等腰梯形都是轴对称图形。
( )4.圆有无数条对称轴,而半圆只有一条对称轴。
( )三、选择。
(把正确答案的选项填在括号里)(12分)1.下面各组线段中,能围成三角形的是( )。
A. 1 cm 1 cm 2 cmB. 1 cm 2.5 cm 3 cmC. 0.9 dm 1 dm 2 dmD. 4 m7 m 2 m2.一个正方形的边长和圆的半径相等,已知正方形的面积是20平方米,则圆的面积是( )平方米。
A. 15.7B. 62.8C. 12.56D. 25.123.学校传达室的门坏了,下图分别是木工师傅修门的4种方案,( )种修理方案可以使这扇门最牢固。
四、画出下图关于直线的轴对称图形。
(10分)五、看图计算。
(14分)1.求右图阴影部分的面积。
苏教版五年级数学下册归类培优测试卷3.图形与几何、统计与概率一、做一做。
(第5题3分,第7题5分,其余每空1分,共24分)1.当圆规两脚之间的距离是6厘米时,画出的圆的直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
2.有大、小两个圆,大圆的直径是小圆半径的4倍,则大圆半径是小圆半径的( ),大圆周长是小圆周长的( ),大圆面积是小圆面积的( )。
3.将一张半径是2 cm的圆形纸片,连续对折三次,得到的图形的圆心角是( )度,周长是( )cm。
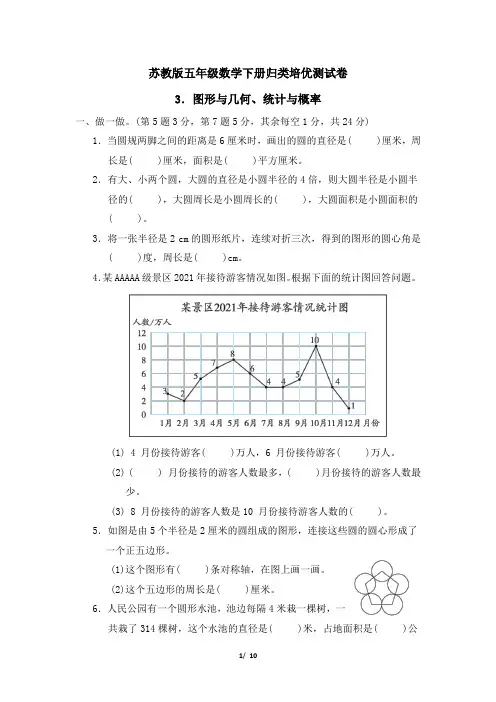
4.某AAAAA级景区2021年接待游客情况如图。
根据下面的统计图回答问题。
(1) 4 月份接待游客( )万人,6 月份接待游客( )万人。
(2) ( ) 月份接待的游客人数最多,( )月份接待的游客人数最少。
(3) 8 月份接待的游客人数是10 月份接待游客人数的( )。
5.如图是由5个半径是2厘米的圆组成的图形,连接这些圆的圆心形成了一个正五边形。
(1)这个图形有( )条对称轴,在图上画一画。
(2)这个五边形的周长是( )厘米。
6.人民公园有一个圆形水池,池边每隔4米栽一棵树,一共栽了314棵树,这个水池的直径是( )米,占地面积是( )公顷。
7.测量右图中的有关数据,并求出图中圆的面积。
(1)需要测量出( )的长度,从而得出圆的直径是( )厘米。
(2)圆的半径是( )厘米。
(3)要求圆的面积,可列式计算为:________________8.如图,一个半径为2厘米的圆在一个长16厘米、宽12厘米的长方形内滚动一周后(无滑动),又回到了原来的位置,这个圆的圆心共移动了( )厘米。
二、选择。
(将正确答案的字母填在括号里)(每小题2分,共12分)1.下面不适合制作成折线统计图的是( )。
A.某地每天的气温变化情况B.轩轩家每月的用电量的变化情况C.某校各年级的男、女生人数D.某校一年级新生入学人数变化情况2.圆的直径是正方形的对角线,则正方形的面积( )圆的面积。
人教版数学六年级下册:期末总复习第2单元《图形与几何》测试卷(一)姓名: 班级: 得分:一、选择题(5分)1.两根同样长的铁丝,一根铁丝做成长、宽、高分别是5cm、4cm、3cm的长方体框架(铁丝没有多余),另一根做成最大的正方体框架,这个正方体棱长是( )厘米。
A.3 B.4 C.5 D.62.把10厘米长的吸管剪两次,截成3段,首尾相接围成三角形,这三段长度可能是( )。
(单位:厘米)A.3,3,3 B.1,4,5 C.2,3,5 D.4,4,23.将如图沿折线围成一个正方体,这个正方体共顶点的三个面上的数字之积最大的是().A.120 B.90 C.72 D.604.底面积相等的圆柱和圆锥,它们的体积比是2∶1,圆锥的高是9厘米,圆柱的高是( )厘米。
A.3 B.6 C.8 D.25.在下面四句话中,正确的一句是()A.小于90度的角都是锐角,大于90度的角都是钝角B.在比例中,两个外项互为倒数,则两个内项成反比例C.一只热水瓶的容积是500毫升D.在c=πd中,c和π成正比例二、填空题(25分)6.一块平行四边形的草坪中有一条长8米、宽1米的小路,草坪的面积是________平方米.如果铺每平方米草坪的价格是16元,那么铺好这些草坪需要________元钱.7.要画一个周长是12.56厘米的圆,圆规两脚间的距离应定为(____)厘米,这个圆的面积是(____)平方厘米。
8.用三个完全一样的正方体,拼成一个长方体,长方体的表面积是70平方分米,原来一个正方体的表面积是(_____)平方分米。
9.大圆的直径是4厘米,小圆的直径是2厘米,大圆和小圆周长的最简整数比是________,大圆和小圆面积的最简整数比是________。
10.两个长、宽、高分别是5分米、4分米、3分米的长方体,拼成一个大的长方体,表面积至少要减少(_______)平方分米。
11.以学校为观测点,小红家在学校的南偏西30°方向,距离学校500米,那么以小红家为观测点,学校在小红家(_____)偏(_____)(_____)°的方向。
三年级数学下册图形与几何专项测试卷时间:60分钟总分:100分一、填空题。
(每空1分,共24分)1.常用的面积单位有( )、( ) 和( )。
2.当你面向东面时,背对着的方向是( )面,右边是( ) 面。
3.旗杆的影子在旗杆的西面,那么阳光是从( ) 照过来的4.一个边长是2米的正方形的面积是( )平方米。
5.在( )里填上合适的单位。
一棵大树高约6( ) 小明的身高约140( )课桌面的面积约是24( ) 游泳池的面积约300( )6.8平方米=( )方分米520平方分米= ( )平方米42平方分米=( )平方厘米600平方厘米=( )平方分米7.在○里填上“>”“<”或“=”。
5平方米○45平方分米10平方米○1000平方分米7平方米○7平方厘米20平方厘米○20平方分米8.一块长方形菜地的面积是84平方米,宽是4米,它的长是( )米,周长是( ) 米。
9.一个正方形的周长是24分米,它的边长是( )分米,面积是( )平方分米。
10.文文上学要向北走800米,放学回家要向( )走800米。
二、选择题。
(把正确答案的序号填在括号里)(10分) 1.刮东南风时,彩旗向( ) 向飘。
A. 东南B. 东北C. 西南D. 西北2.下面每个小格的面积是1平方厘米,阴影部分面积最大的是( ) A. B. C. D.3.一块正方形手帕的边长是40厘米,它的面积是16( ),周长是160( )。
A. 平方厘米 B.平方分米 C.厘米 D . 分米4.如右图所示,长方形被分为甲、乙两部分,这两部分( ) A. 周长相等,面积不相等 B.周长和面积都不相等 C. 周长和面积都相等 D.周长不相等,面积相等5.一个长方形的长和宽都扩大到原来的2倍,那么它的面积就扩大到原来的( )倍。
A.2B.4C.8D.16 三、算一算,填一填。
(8分)四、操作应用。
(12分)1.在下面的方格纸上画出面积相等的长方形和正方形各一个,并标出长方形的长和宽及正方形边长的长度。
人教版六年级数学上册图形与几何专项复习卷满分:100分试卷整洁分:2分(65分)一、填一填。
(每空1分,共24分)1.[图形的周长]右图中,每个圆的周长是()cm,长方形的周长是()cm。
2.[对称轴]圆有()条对称轴,半圆有()条对称轴,圆环有()条对称轴。
3.[圆的面积公式的推导]把一个直径是4cm的圆,剪成若干个扇形,再拼成一个近似长方形,这个近似长方形的长是()cm,宽是()cm,面积是()cm2。
4.[圆的周长和面积的应用]一个时钟的分针长6cm,经过1小时,它的尖端走了()cm,分针扫过部分的面积是()cm2。
5.[圆的画法、周长、面积]如果圆规两脚之间的距离是4cm,那么画出的圆的半径是()cm,周长是()cm,面积是()cm2。
6.[圆的半径与周长、面积的关系]两个圆的半径之比为1∶3,它们的周长比是(),面积比是()。
7.[圆环的面积]一个圆形花坛,半径6m,外面有一条宽1m的小路,小路的面积是()m2。
8.[位置与方向]看图填一填。
(1)从共青城看,少年宫位于()偏()()°方向()m处。
(2)从少年宫看,共青城位于()偏()()°方向()m处。
二、判断。
(对的打“√”,错的打“×”)(5分)1.[正方形与圆的关系]如果一个正方形与一个圆的周长相等,则它们的面积也必然相等。
( )2.[圆的面积与直径、半径的关系]若两个圆的面积相等,则两个圆的直径、半径都相等。
( )3.[圆的周长与面积]半径是2dm的圆,其周长和面积相等。
( )4.[圆的周长]同一个圆的周长和半径的比是2π∶1。
( )5.[圆的认识]两端都在圆上的线段是圆的直径。
( )三、选一选。
(将正确答案的字母填在括号里)(10分)1.[半圆的周长]直径是6cm的半圆的周长是( )cm。
A.18.84B.9.42C.15.42D.12.422.[圆的面积]在一张长为6dm,宽为4dm的长方形纸板上剪下一个最大的圆,所剪圆的面积是( )dm2。
……装……○…………订………________姓名_______班级:_________考号:_____……装……○…………订………青岛版六年级下册总复习图形与几何达标测试考试范围:xxx ;考试时间:100分钟;命题人:xxx注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 一、选择题1.下列图形中,( )是由一个基本图形经过旋转得到的。
A .B .C .2.下面三幅图中不能折成正方体的是( )。
A .B .C .3.一个三角形的三个内角的度数的比是1∶4∶5,这个三角形是( )。
A . 锐角三角形 B . 直角三角形 C . 钝角三角形4.右图中,每个小方格都是边长相等的正方形,则甲和乙两部分面积的关系是( )。
A . 甲>乙B . 甲=乙C . 甲<乙5.一个长方体的长、宽、高分别是a 米、b 米、h 米。
如果高增加2米,体积比原来增加( )立方米。
A . 2abB . 2abhC . (h +2)ab 二、填空题6.在等腰三角形中,顶角是 80°,一个底角是(______)。
7.从直线外一点到这条直线所画的________最短。
…………○…………○……答※※题※※…………○…………○……9.数一数,在中有(____)条直线,(____)条射线,(____)条线段。
10.有两根小棒,分别长5 cm和6 cm,如果再取一根围成三角形,小棒最长是(____)cm,最短是(_____)cm。
(填整数)11.把一个长方形的长和宽分别按5∶1的比例放大后,长方形的面积扩大到原来的(____)倍。
12.有一个用正方体木块搭成的立体图形。
从前面看到的图形是,从左面看到的图形是,要搭成这样的立体图形,至少要用(_____)个正方体木块。
13.棱长总和是96厘米的正方体的表面积是(_____)平方厘米,体积是(_____)立方厘米。
14.一个圆的周长和一个正方形的周长相等,正方形的周长是12.56 dm,那么圆的面积是(______)dm2。
北师大版六年级数学下册总复习《图形与几何》测试卷(本卷满分100分,考试时间90分钟)一、选择题(每小题2分,共16分)1.计算鱼缸能装水多少升,是求鱼缸的()。
A.表面积B.棱长总和C.体积D.容积2.营养学家建议:儿童每天水的摄入量应不少于1500mL。
要达到这个要求,小明每天用底面直径6cm,高10cm的圆柱形水杯喝水,至少喝水()杯。
A.4 B.5 C.6 D.73.两个圆柱形容器内原来的水面高度都是6cm。
它们的底面直径都是10cm。
①号容器内放入一个小球后,水面高度为10cm。
②号容器内放入一个小球和一个大球,水面高度为16cm。
两个容器内的小球完全相同,水也均未溢出,小球的体积与大球的体积的比是()。
A.5∶8 B.2∶5 C.2∶3 D.5∶124.制作一个无盖的圆柱形容器,应该选择()。
A.①和③B.①和④C.②和③D.②和④5.下面各图中,()是不正确的。
A.B.C.D.6.如图是由7个立方体摆成的几何体,从右面观察到的图形是()。
A.B.C.D.7.一个三角形,三个内角度数比是2∶3∶1,这个三角形按角分是()。
A.钝角三角形B.锐角三角形C.直角三角形D.无法确定8.如图,甲与乙的周长相比,()。
A.甲的周长>乙的周长B.甲的周长<乙的周长C.甲的周长=乙的周长D.无法比较二、填空题(每小题2分,共24分)1.如图,有两个边长是6厘米的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。
旋转其中一个正方形,重叠部分的面积是( )平方厘米。
2.将一个长方体的高增加3厘米后变成一个正方体,它的表面积比原来增加84平方厘米,原来长方体的体积是( )立方厘米。
3.在一幅比例尺为1∶3000的图纸上,量得一个三角形菜地的底是20厘米,高15厘米,这块菜地的实际面积是( )公顷。
4.一顶帽子,上面是直径2dm,高1dm的圆柱形(有帽顶),帽檐部分是一个宽1dm的圆环,做这顶帽子,至少要用( )的布料。
人教版五年级数学下册图形与几何专项复习卷(含答案)满分:100分试卷整洁分:2分(72分)一、用心思考,正确填写。
(第1、2小题各4分,其余每空2分,共30分)1.[旋转](1)放( )kg的物品,指针顺时针旋转45°。
(2)放( )kg的物体,指针顺时针旋转90°。
(3)放4 kg物品,指针( )时针旋转( )°。
2.[单位换算]在括号里填上合适的数。
2.8 m3=( )dm3 1.05 dm3=( )cm31800 mL=( )L 540 L=( )dm33.[长方体的体积]一根长2 m的长方体钢材,沿横截面截成两段后,表面积增加了0.6 dm2,这根长方体钢材的体积是( )dm3。
4.[长方体的体积]一个长方体包装箱,相交于一个顶点的三条棱的长度分别是5 dm、3 dm、4 dm,这个包装箱的占地面积最大是( )dm2,体积是( )dm3。
5.[长方体体积公式的应用]一个长方体容器,从里面量长4 dm,宽3 dm,能容纳30 L水。
这个长方体容器的高是( )dm。
6.[旋转]从8时55分到9时15分,分针旋转了( )°。
7.[长方体的表面积和体积]一个长方体的长、宽、高都扩大到原来的2倍,这个长方体的表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
8.[探索图形]右图是用小正方体拼成的大正方体,在它的表面涂色。
三面涂色的小正方体有( )个,没有涂色的小正方体有( )个。
9.[观察物体]一个立体图形从正面看到的形状是,从左面看到的形状是,搭这个立体图形至少要( )个小正方体,最多要( )个小正方体。
二、认真辨析,合理选择。
(将正确答案的序号填在括号里)(10分)1.[旋转]图形绕点O旋转以后,得到的图形可能是( )。
A. B. C. D.2.[表面积]右图是由同样大小的正方体组成的两个图形,它们的表面积相比较,( )。
A.一样大B.①大C.②大D.无法比较3.[观察物体]小明搭的积木从上面看到的形状是,上面的数字表示在这个位置上所用正方体的个数。
《图形与几何》测试题
(总分100分时间80分钟)
一、填空.(28分每空一分)
1.明明晚上10:00睡觉,第二天早上7:00起床,时针转了()°丽丽早上7:30分上学, 他就到达了学校时,分针刚好转了120°他上学用了()分钟。
2 .一个圆柱的底面周长是厘米,高是6厘米,那么底面半径是()厘米,一个底面的面积是()平方厘米,侧面积是()平方厘米,体积是()立方厘米。
3.连线题:把从侧面看是图A的连起来,从正面看是图B的连起来。
5、把一段圆柱形木料削成一个最大的圆锥体,削去部分的体积是圆锥体的(
6 .有12个1立方分米的立方体商品,请你为它设计一个长方体包装箱,共有()种不同的包装方法。
当包装箱的长是()分米、宽是()分米、高是()分米时,最
节省包装纸,至少需要包装纸()。
(接头处忽略不计)
7、把3米长的木料,锯成同样长的小段,共锯7次,每段占全长的(),每段长(
)
米。
如果锯成两段,需2分钟,锯成5段共需()分钟。
&周长相等的圆、长方形和正方形,()的面积最大。
9、体积和底面积都相等的圆柱和圆锥,圆柱的高与圆锥的高的比是()。
10、有9个外形颜色完全相同的零件,其中一个是次品,次品比正品重,用天平称,至少称()次可以确保把次品找出来。
11、一个圆锥体的体积是12立方分米,底面积是3平方分米,高是
迟H 重
4、0. 3立方米=()立方分米250毫升=()升
4平方米5平方分米=()平方米公顷=()平方米
正方体,它的表面积是()cm2,体积是(
).
()。
12、右图是用棱长是1厘米的小正方体搭成的,它共用了()个小
A.0.4 D约
、判断题。
(12
分)
1、 角的大小与角的边长无关。
(
)
2、 钝角三角形的两个锐角之和一定小于 90度。
( )
3、 圆柱的体积是圆锥体积的 3倍。
(
)
4、 两个面积相等的三角形,一定能拼成一个平行四边形。
(
)
5、 圆的半径和圆的面积成正比例。
(
)
6、 一个冰箱的容积是 200毫升。
(
)
三、选择题。
(把正确答案的序号填在括号里)(
10分)
1 .如果用“表示一个立方体,用 “表示两个立方体叠加,用
“表示三个立方体叠加,那么
图中由7个立方体叠加的几何体,从正面观察,可画出的平面图是(
)。
2 •下面不能组成等腰三角形的有(
)组。
第一组
器二组
第三组
第四组
弟一抿小稱 馄米 1分米
5厘米
第二抿小棒 涯米
8厘米
第三抿屮特
绸米
5厘栄
9曜米
3 •下列图形中,不能由图(1)经过一次平移或旋转得到的是(
IX
4•五名园林工人分别驾驶割草机同时给一个周长是
257米的半圆形草坪割草,小时割完。
若工人割草的效率相同,照这样计算,每名工人驾驶割草机给
500平方米的草坪割草需要
()小时。
(-取)
.品 B 甘
A.
B.
)。
A.0.4 D 约
5 .如图是测量一颗玻璃球体积的过程: (1 )将300 cm 的水倒进一个容量为 500 cm 的杯子
中;(
2)将4颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入
水中,结果水满溢出。
根据以上过程,推测这样一颗玻璃球的体积的范围为(
)。
B. 30 cm 以上,40 cm 以下 D. 50 cm 以上,60 cm 以下
四操作题。
(20分)
1•在下图中选用合适的比例尺画出汽车站、电影院和游乐场的位置。
(
9 分)
(1) 汽车站在学校正北 200米处;
(2) 电影院在学校的北偏东 65°方向,距离300米; (3) 游乐场在汽车站东偏南 15°方向,距离100米。
2、(11分,每空1分,一个图3分)
(1) 把下图中的长方形绕 A 点逆时针旋转90°画出旋转后的图形。
旋转后,B 点的位置用 数对表示是( ,)。
(2)
按1 : 2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的(
)。
(3) 如果1个小方格表示1平方厘米,请在方格纸上画一个面积是
10平方厘米的梯形。
五、解答(30分)
Z2
cm 以上,30 cm 以下 cm 以上,50 cm 以下
1 •如图是一个操场的示意图,如果按 1 : 2000的比例尺画在图纸上,操场的一条直道长多
少厘米一条弯道长多少厘米在这张图纸上操场一周的长度和面积分别是多少
2、把一个底面周长是分米,高9分米的圆柱体铁块熔铸成一个底面半径是6分米的圆锥体,
圆锥的高是多少分米
3•一个小正方形内接于一个圆,而这个圆则内接于一个大正方形(如图所示),若外面的大正方形的边长是3厘米,则阴影部分的面积是多少(取)
4.如图,四边形ABCD是直角梯形,其中AE=EB=CD=3厘米,BC=ED=2厘米。
以CD边为轴将该梯形旋转一周,形成的物体体积是多少
A
E
B
c
5、•用一根长72分米的铁丝做成一个长方体框架,使它的长、宽、高的比是4:32在这个长方体框架外边糊一层纸,至少需要多少平方分米的纸
6、如图,在一个长方体蓄水糟里,把一段底面半径是
升9cm ;把圆钢竖着拉出水面8cm后,水面就下降
5cm的圆钢全部浸入水中,水面就上
4cm,求圆钢的体积。