独立基础四棱台的计算公式
- 格式:doc
- 大小:34.00 KB
- 文档页数:1
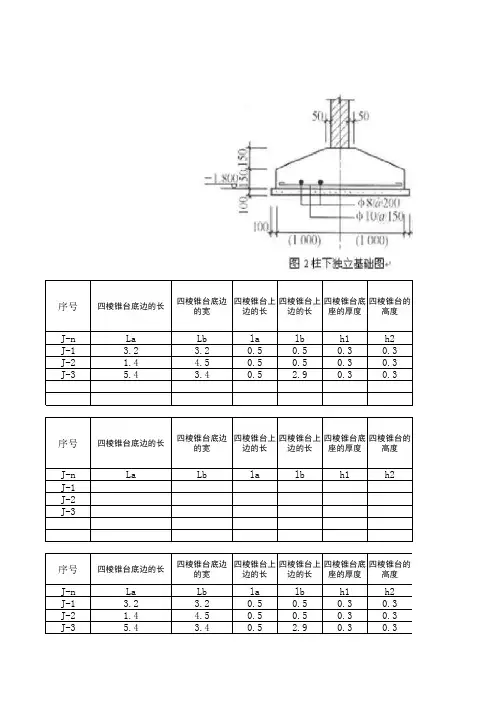
![[策划书]四棱台体积计算公式](https://uimg.taocdn.com/cf974658777f5acfa1c7aa00b52acfc789eb9fc9.webp)
四棱台体积公式:①、[S上+S下+√(S上×S下)]*h /3 (可以用于四棱锥)[上面面积+下面面积+根号(上面面积×下面面积)]×高÷2②、(S上+S下)*h/2 (不能用于四棱锥)(上面面积+下面面积)x高÷2第②个最简便的公式,可以把正方体当作四棱台验证。
注意:如果把四棱锥可以看成上面面积为0的四棱台,第①个公式仍然可以用,但是四棱锥不能用第②个公式,切记!!!!!!!!。
拟棱台:对于一个多面体,如果有两个面互相平行,而其余的面均为顶点全在这两个平行面上的三角形、平行四边形或梯形,这样的多面体叫拟棱台。
若上下底面和中截面的面积分别是S1、S2、S0,高为H,则体积V=1/6(s1+s2+4s0)H正四棱台体积V=底面积S×高H圆锥体体积=底×高÷3长方形的周长=(长+宽)×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=(上底+下底)×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=(长×宽+长×高+宽×高)×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体(正方体、圆柱体)的体积=底面积×高平面图形名称符号周长C和面积S正方形—边长C=4S=2长方形和b-边长C=2(+b)S=b三角形,b,c-三边长h-边上的高s-周长的一半,B,C-内角其中s=(+b+c)/2 S=h/2=b/2·sinC=[s(s-)(s-b)(s-c)]1/2=2sinBsinC/(2sin)四边形d,D-对角线长α-对角线夹角S=dD/2·sinα平行四边形,b-边长h-边的高α-两边夹角S=h=bsinα菱形-边长α-夹角D-长对角线长d-短对角线长S=Dd/2=2sinα梯形和b-上、下底长h-高m-中位线长S=(+b)h/2=mh圆r-半径d-直径C=πd=2πrS=πr2=πd2/4扇形r—扇形半径—圆心角度数C=2r+2πr×(/360)S=πr2×(/360)弓形l-弧长b-弦长h-矢高r-半径α-圆心角的度数S=r2/2·(πα/180-sinα) =r2rccos[(r-h)/r] - (r-h)(2rh-h2)1/2=παr2/360 - b/2·[r2-(b/2)2]1/2=r(l-b)/2 + bh/2≈2bh/3圆环R-外圆半径r-内圆半径D-外圆直径d-内圆直径S=π(R2-r2)=π(D2-d2)/4椭圆D-长轴d-短轴S=πDd/4立方图形名称符号面积S和体积V正方体-边长S=62V=3长方体-长b-宽c-高S=2(b+c+bc)V=bc棱柱S-底面积h-高V=Sh棱锥S-底面积h-高V=Sh/3棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S1)1/2]/3 拟柱体S1-上底面积S2-下底面积S0-中截面积h-高V=h(S1+S2+4S0)/6圆柱r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱R-外圆半径r-内圆半径h-高V=πh(R2-r2)直圆锥r-底半径h-高V=πr2h/3圆台r-上底半径R-下底半径h-高V=πh(R2+Rr+r2)/3球r-半径d-直径V=4/3πr3=πd2/6球缺h-球缺高r-球半径-球缺底半径V=πh(32+h2)/6=πh2(3r-h)/32=h(2r-h)球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/6圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2=π2Dd2/4桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15评论(14) | 80 12012-08-12 16:31 我只是碗馄饨| 四级体积的话叫棱台S1=上面的面积S2=下面的面积H是高V是体积V=(S1+S2+根号(S1×S2))×H ÷3评论(6) | 52 22012-05-08 23:50 绿锦小学| 十三级答:梯形是平面图形,没有体积,只有面积。

四棱台公式体积
四棱台是一种几何体,它由一个四边形底面和四个三角形侧面组成。
四棱台的体积可以用一个简单的公式来计算,即底面积乘以高度再除以3。
四棱台的体积计算公式是V = (底面积 × 高度)/3。
底面积指的是四棱台底面的面积,可以是任意形状的四边形,比如正方形、长方形、梯形等。
高度指的是从底面到顶面的垂直距离。
通过四棱台的体积公式,我们可以计算出任意形状的四棱台的体积。
例如,如果底面是一个边长为5的正方形,高度为8,则四棱台的体积为(5 × 5 × 8)/3 = 66.67立方单位。
四棱台的体积公式非常简单易懂,只需要知道底面积和高度即可计算出体积。
这个公式在很多实际问题中都有应用,比如建筑物的体积计算、容器的容积计算等。
通过计算四棱台的体积,我们可以更好地理解这个几何体的空间大小。
体积是物体所占据的空间大小的量度,它可以帮助我们比较不同物体的大小,也可以帮助我们解决实际问题。
四棱台的体积公式是数学中的基础知识,它在几何学、物理学等学科中都有广泛的应用。
掌握这个公式可以帮助我们更好地理解和解决与四棱台相关的问题。
四棱台的体积公式是通过底面积和高度来计算的,它是数学中的一个基本公式,在实际问题中有着广泛的应用。
通过计算四棱台的体积,我们可以更好地理解和解决与四棱台相关的问题。

基坑四棱台体积公式
基坑四棱台体积公式是计算基坑四棱台体积的数学公式。
基坑四棱台是指有四个不等高的等边三角形作为侧面的几何体。
计算基坑四棱台体积的公式如下:V = (A1 + A2 + sqrt(A1 * A2)) * H / 3
其中,V表示基坑四棱台的体积,A1和A2表示上下底面的面积,H表示基坑四棱台的高度。
这个公式的推导过程基于基本的几何原理。
我们可以将基坑四棱台视为两个平行的等边三角形和一个梯形的组合体。
底面的面积是两个等边三角形的面积之和,再加上两个底面的乘积的平方根。
最后乘以高度,再除以3,即可得到基坑四棱台的体积。
使用这个公式,我们可以方便地计算基坑四棱台的体积。
只需将具体数值代入公式中,即可得到准确的计算结果。
需要注意的是,在应用公式时,要确保输入的数值单位一致。
例如,面积的单位应该是平方米,高度的单位应该是米,以确保最终的体积单位是立方米。
总之,基坑四棱台体积公式是计算基坑四棱台体积的数学公式,通过将上下底面的面积和高度代入公式,可以得到准确的体积计算结果。
这个公式在土木工程等领域中具有重要的应用价值。

四梭台体积计算
鲁班算量2006在计算独立基础时,发现所有的正四棱台计算正确,而计算有长边与短边的四棱台时,就不对了,量都偏大的原因:
独立基础体积正确的计算公式为:
四棱台计算公式为(s1+s2+sqr(s1*s2))*h/3,sqr(x)对x求根
或
A*B*H+h/6*(AB+ab+(A+a)(B+b))其中A、B、H分别为独立基础下部长方体的长、宽、高;
a、b、h分别为四棱台的长、宽、高,当然,A与a、B与b相对应。
用A*B*H+h/6*(AB+ab+(A+a)(B+b))是偏小
实际工作中,这两种公式都有人用,结果有时是不一样.
而使用鲁班算量计算结果偏大,计算不等边长的四梭台与计算公式算出结果不一样是因为我们预算中的四梭台计算公式是近似的计算方法,而鲁班用的是微积分算法,结果相差很小
另外鲁班的带马牙槎的构造柱计算结果也与实际算法有差别,其实我们算构造柱时是按如果有两边有马牙槎的为边长上加6cm计算,鲁班算量考虑了层高的不同与马牙槎的高度位也考虑了(马牙槎在板底时正好为退时鲁班的计算结果就会小,但其实鲁班算的是实际的量)。

四棱台体计算公式
四棱台是一种立体几何体,它有四个侧面是等边三角形,底面是一个四边形。
四棱台的计算公式有很多,下面我将介绍其中一种计算四棱台体积和表面积的方法。
我们需要知道四棱台的底面边长和高。
假设底面边长为a,高为h。
那么四棱台的侧面积可以通过计算底面边长和高的乘积再乘以2来得到,即侧面积=2ah。
底面积可以通过计算底面边长的平方再乘以根号3再除以4来得到,即底面积=a^2√3/4。
所以四棱台的表面积等于侧面积加上底面积的两倍,即表面积=2ah+a^2√3/2。
接下来是计算四棱台的体积。
四棱台的体积可以通过计算底面积再乘以高再除以3来得到,即体积=a^2√3h/3。
通过上述计算公式,我们可以得到四棱台的表面积和体积。
这些计算公式可以帮助我们更好地理解和计算四棱台的相关问题。
在实际生活中,我们可以应用这些计算公式来解决一些与四棱台相关的实际问题,如建筑设计、物体容量计算等。
四棱台是一种具有特殊形状的几何体,通过合理运用计算公式,我们可以计算出它的表面积和体积。
这些计算公式为我们解决实际问题提供了便利,同时也帮助我们更好地理解和认识四棱台这一立体几何体。

四棱锥独立基础计算公式四棱锥独立基础,这可是建筑工程里一个挺重要的部分呢。
要计算它,咱们得先搞清楚一些基本的概念和公式。
咱先来说说啥是四棱锥独立基础。
简单来讲,它就像是一个倒扣在地上的四棱锥。
想象一下,一个金字塔形状,但是底部是平的,这就是四棱锥独立基础啦。
那计算它的公式是啥呢?一般来说,四棱锥独立基础的体积计算公式是:V = 1/3 × S × h 。
这里的 V 表示体积,S 表示底面积,h 表示锥体的高。
底面积 S 的计算方法得看四棱锥独立基础底面的形状。
如果底面是正方形,那 S = a²,这里的 a 是正方形的边长。
要是底面是长方形,S = a × b ,a 和 b 分别是长方形的长和宽。
接下来咱说个真实的事儿。
之前我去一个建筑工地,看到工人们正在浇筑四棱锥独立基础。
那个施工师傅特别认真,拿着图纸,嘴里还念念有词,算着各种数据。
我凑过去一听,嘿,他就是在算这个四棱锥独立基础的体积呢。
只见他一会儿量量这边的边长,一会儿又看看那边的高度,忙得不亦乐乎。
我就好奇地问他:“师傅,这计算难不难呀?”师傅抬头看了我一眼,笑着说:“不难不难,只要公式记得牢,数据量得准,就没问题。
”然后他跟我详细地讲了讲他是怎么一步步计算的。
他说:“你看啊,这个底面是个边长为 3 米的正方形,高度是 2米。
那先算底面积,3×3 = 9 平方米,然后体积就是 1/3×9×2 = 6 立方米。
” 我听着,感觉还挺有意思的。
在实际工程中,准确计算四棱锥独立基础的体积非常重要。
如果算少了,材料不够,基础不牢固,那可就麻烦啦;要是算多了,又会造成浪费。
所以啊,这个计算公式可得牢记在心,并且在测量数据的时候要特别仔细,一点都不能马虎。
总之,四棱锥独立基础的计算公式虽然看起来简单,但实际应用中需要我们认真对待,这样才能保证工程的质量和安全。
希望大家以后在遇到相关计算的时候,都能轻松搞定,不出差错!。

建筑工程施工工程量计算方法一、独立基础1、独立基础工程量(1)独立基础垫层的体积(2)独立基础体积(3)独立基础垫层基模板(4)独立基础模板(5)基坑的土方体积(6)槽底钎探工程量2、独立基础手工计算方法⑴、独立基础垫层的体积垫层体积=垫层面积X垫层厚度⑵、独立基础垫层模板垫层模板=垫层周长X垫层高度⑶、独立基础体积独立基础体积=各层体积相加(用长方体和棱台公式)四棱台体积=1/3X H X(S上+sq帝下)⑷、独立基础模板独立基础模板=各层周长X各层模板高(5)基坑土方工程量基坑土方的体积应按基坑底面积乘以挖土深度计算。
基坑底面积应以基坑底的长乘以基坑底的宽,基坑底长和宽是指混凝土垫层外边线加工作面,如有排水沟者应算至排水沟外边线。
排水沟的体积应纳入总土方量内。
当需要放坡时,应将放坡的土方量合并于总土方量中。
(6)槽底钎探工程量槽底钎探工程量,以槽底面积计算。
2、独立基础工程量的计算难点①异形独立基础体积不好计算。
②独立基础与其他基础相交时扣减量不好计算。
③土方量计算时考虑工作面及放坡,计算扣减比较麻烦。
承台基础1、承台基础工程量(1)承台基础垫层的体积(2)承台基础体积(3)承台基础垫层基模板(4)承台基础模板(5)基坑的土方体积(6)槽底钎探工程量2、独立基础手工计算方法⑴、承台基础垫层的体积垫层体积=垫层面积X垫层厚度⑵、承台基础垫层模板垫层模板=垫层周长X垫层高度⑶、承台基础体积独立基础体积=各层体积相加(用长方体和棱台公式)⑷、承台基础模板独立基础模板=各层周长X各层模板高(5)基坑土方工程量基坑土方的体积应按基坑底面积乘以挖土深度计算。
基坑底面积应以基坑底的长乘以基坑底的宽,基坑底长和宽是指混凝土垫层外边线加工作面,如有排水沟者应算至排水沟外边线。
排水沟的体积应纳入总土方量内。
当需要放坡时,应将放坡的土方量合并于总土方量中。
(6)槽底钎探工程量槽底钎探工程量,以槽底面积计算。
3、承台基础工程量的计算难点①异形承台基础体积不好计算。

独立基础棱台计算公式独立基础棱台,这玩意儿在建筑和数学里可都是相当重要的角色呢!咱先来说说啥是独立基础棱台。
简单来讲,它就像是一个有上底和下底的“梯形盒子”,不过是立体的哦。
比如说,咱盖房子的时候,那个支撑房子的底座,有不少就是独立基础棱台的形状。
那独立基础棱台的计算公式是啥呢?它的体积公式是:V = 1/3 × h× (S1 + S2 + √(S1 × S2)) 。
这里面的“V”代表体积,“h”呢就是棱台的高,“S1”和“S2”分别是上底面积和下底面积。
听起来是不是有点晕乎?别着急,我给您举个例子您就明白啦。
有一回,我去一个建筑工地溜达,看到工人们正在打地基,做独立基础棱台。
我就好奇地凑过去瞧。
那个师傅特别热心,跟我讲:“小伙子,你看啊,咱们这个独立基础棱台,上底是边长 2 米的正方形,下底是边长 3 米的正方形,高度是 1.5 米,你能算算这体积不?”我当时就想,这不是正好用上咱刚学的公式嘛。
先算上底面积 S1,就是 2×2 = 4 平方米;下底面积 S2 呢,就是 3×3 = 9 平方米。
然后把这些数往公式里一代,体积 V = 1/3 × 1.5 × (4 + 9 + √(4 × 9)) 。
这时候先算根号里的,√(4 × 9) = √36 = 6 。
接着算括号里的,4 + 9+ 6 = 19 。
最后再算乘法和除法,1/3 × 1.5 × 19 = 0.5 × 19 = 9.5 立方米。
我把结果跟师傅一说,师傅笑着点点头:“不错不错,看来你还真会!” 那一刻,我心里那个美哟!在实际生活中,比如修水坝、建桥梁,都能用到独立基础棱台的计算公式。
要是算错了,那可就麻烦大啦!所以啊,咱们可得把这个公式掌握好。
多做几道练习题,遇到实际问题的时候就能轻松应对啦。
您说是不是这个理儿?总之,独立基础棱台计算公式虽然看起来有点复杂,但只要咱们多琢磨琢磨,多联系实际,就一定能把它拿下!不管是在考试中还是在实际工作里,都能派上大用场。

四棱台体积公式土建四棱台体积公式在土建领域那可是相当重要的啦!咱先来说说啥是四棱台。
想象一下,有一个四棱锥,就像金字塔似的,然后从中间截一刀,上面小,下面大,这就形成了四棱台。
在土建工程中,经常会碰到四棱台形状的结构体。
比如说,有些建筑物的基础,或者是一些特殊形状的水池啥的。
四棱台体积公式是:V = [S1 + S2 + √(S1 × S2)] × h / 3 。
这里面的S1 是上底面积,S2 是下底面积,h 是四棱台的高。
我记得有一次去一个建筑工地,看到工人们正在浇筑一个四棱台形状的地基。
那个负责人拿着图纸,嘴里不停地念叨着这个体积公式,一边指挥着工人干活。
我凑过去看了看,他正拿着计算器,认真地算着上底面积、下底面积还有高度,然后按照公式算出体积,来确定需要多少混凝土。
他那认真的模样,让我深深感受到这个公式在实际工作中的重要性。
要是算错了,要么材料不够耽误工期,要么材料多了造成浪费。
在学习这个公式的时候,可别死记硬背,得理解着来。
比如说,为啥要除以 3 呢?其实就是把四棱台看成是由一个大的四棱锥减去一个小的四棱锥得到的,而四棱锥的体积公式是底面积乘以高再除以 3 ,这么一推导,是不是就好理解多啦。
而且,在实际应用中,要注意测量数据的准确性。
哪怕一点点的误差,都可能会在最后的结果中被放大。
咱再回到土建领域,比如说设计一个花坛,要是能熟练运用四棱台体积公式,就能准确算出需要多少土来填充,还能预估出成本啥的。
还有啊,在建造桥梁的桥墩时,很多时候也是四棱台的形状。
这时候就得用这个公式来计算混凝土的用量,确保桥墩的稳固和质量。
总之,四棱台体积公式虽然看起来简单,但在土建中却有着大用处。
无论是小小的花坛,还是宏伟的建筑,都离不开它的默默贡献。
所以,小伙伴们,一定要把这个公式学好、用好,为咱们的土建事业添砖加瓦哟!。

四棱承台正确的体积计算公式承台基础1、承台基础工程量(1)承台基础垫层的体积(2)承台基础体积(3)、承台基础垫层基模板(4)、承台基础模板(5)基坑的土方体积(6)槽底钎探工程量2、独立基础手工计算方法⑴、承台基础垫层的体积垫层体积=垫层面积×垫层厚度⑵、承台基础垫层模板垫层模板=垫层周长×垫层高度⑶、承台基础体积独立基础体积=各层体积相加(用长方体和棱台公式)⑷、承台基础模板独立基础模板=各层周长×各层模板高(5)基坑土方工程量基坑土方的体积应按基坑底面积乘以挖土深度计算。
基坑底面积应以基坑底的长乘以基坑底的宽,基坑底长和宽是指混凝土垫层外边线加工作面,如有排水沟者应算至排水沟外边线。
排水沟的体积应纳入总土方量内。
当需要放坡时,应将放坡的土方量合并于总土方量中。
(6)槽底钎探工程量槽底钎探工程量,以槽底面积计算。
1、承台基础工程量的计算难点①异形承台基础体积不好计算。
②承台基础与其他基础相交时扣减量不好计算。
③土方量计算时考虑工作面及放坡,计算扣减比较麻烦四棱台体积公式:①、[S上+S下+√(S上×S下)]*h /3 (可以用于四棱锥)[上面面积+下面面积+根号(上面面积×下面面积)]×高÷2②、(S上+S下)*h/2 (不能用于四棱锥)(上面面积+下面面积)x高÷2第②个最简便的公式,可以把正方体当作四棱台验证。
注意:如果把四棱锥可以看成上面面积为0的四棱台,第①个公式仍然可以用,但是四棱锥不能用第②个公式,切记!!!!!!!!。
钢丝网片长度的计算规则GCL8.0经过大量用户的调查,将用户手工算钢丝网片的长度的计算规则进行总结,并内置于软件,软件自动根据相交构件的材质,自动计算钢丝网片的长度,其计算规则如下:1、软件在哪些地方计算了钢丝网片的?非圈梁与非砼墙、非构造柱与非砼墙、砼墙与非砼墙、圈梁与女儿墙、非砼墙与分层梁。
四棱台体积公式计算公式四棱台是一种几何体,它由一个四边形底面和四个三角形侧面组成。
计算四棱台的体积是一项基本的几何计算,可以通过使用四棱台体积公式来实现。
四棱台体积公式如下:V = (1/3) * A * h其中,V表示四棱台的体积,A表示四边形底面的面积,h表示四棱台的高。
为了更好地理解四棱台体积公式,我们可以通过一个具体的例子来说明。
假设有一个四棱台,其底面是一个长方形,长6cm,宽4cm。
同时,四棱台的高为10cm。
现在我们来计算这个四棱台的体积。
我们需要计算底面的面积A。
根据长方形的面积公式,我们可以得到:A = 长 * 宽= 6cm * 4cm = 24cm²接下来,我们将A和h代入四棱台体积公式中,可以得到:V = (1/3) * 24cm² * 10cm = 80cm³因此,这个四棱台的体积为80立方厘米。
除了上述例子,四棱台体积公式还可以适用于其他类型的四棱台。
无论四棱台的底面是什么形状,只要知道底面的面积和四棱台的高,就可以使用这个公式来计算体积。
需要注意的是,四棱台体积公式只适用于正四棱台,即四个侧面的三角形是等腰三角形且底面是一个平行四边形。
如果四棱台不满足这些条件,那么就不能使用这个公式来计算体积。
还有一种特殊情况是当四棱台的高为0时,它将变成一个平行四边形,其体积为0。
这是因为在没有高的情况下,四棱台变成了一个平面图形,没有体积可言。
总结起来,四棱台体积公式是计算四棱台体积的基本工具。
通过知道底面的面积和四棱台的高,可以轻松地计算出四棱台的体积。
这个公式对于解决实际问题和进行几何计算非常有用。
希望通过本文的介绍,读者能够对四棱台体积公式有更深入的理解。
棱台计算公式
四棱台的公式是:
V=()H(S上+S下+√[S上×S下])
当是正四棱台时带入上述公式,简化后就是:
V=(h/3)(a2+ab+b2)﹝其中a,b,h分別为正四棱台的上、下底边及高的大小)
挖土方需放坡计算公式现在接触已经有三个了
1、(A+2C+KH)(B+2C+KH)
(K2:放坡系数大平方;H3:高度三次方)
2、H/3(F1+F2+ㄏF1*F2)
(F1:上底面积;F2:下底面积;ㄏF1*F2:上底面积乘以下底面积开根)
3、H/6 [ A1*B1+A*B+(A1+A)(B1+B)]
(A1:上底面积一个边长;B1:上底面积另一个边长)
(A:
下底面积一个边长;B:
下底面积另一个边长)
1公式:
是建筑预算员常用的基坑土方计算公式,直接套用放坡系数;
2公式:
是中学生计算棱台的体积公式;用于土方计算时需先计算边长,再计算面积,再计算体积;
3公式:
是棱台体积公式的延伸,当A1/A=B1/B时成立。
也不够方便,可用于现场测量结果的计算(施工计算),土方工程量近似计算。
独立基础四棱台的计算公式独立基础四棱台是一种棱和面都不平行于对面棱和面的四棱台。
它有六个面,其中两个是平行四边形,另外四个是三角形,以及八个顶点和十二条棱。
当其中四个顶点都固定时,可通过改变其他四个顶点的位置来改变四棱台的形状。
计算四棱台的体积、表面积和高度的公式如下:1.体积:四棱台的体积可以通过计算底面积乘以高度得到。
公式为:V=(A1+A2+√(A1*A2))*h/3其中,A1和A2分别是底面的面积,h是四棱台的高度。
2.表面积:四棱台的表面积可以通过计算底面积、侧面积和顶面积之和得到。
公式为:S=A1+A2+(s1+s2+s3+s4)*l/2其中,A1和A2分别是底面的面积,s1、s2、s3、s4分别是四个侧面的面积,l是四棱台的斜高。
为了更好地理解这些公式,我们来看一个具体的例子。
假设我们有一个四棱台,它的底面是一个边长为5的正方形,顶面是一个边长为3的正方形,而侧面是由边长为5的等腰三角形组成。
四棱台的高度为4首先计算底面的面积:A1=5*5=25然后计算顶面的面积:A2=3*3=9接下来计算侧面的面积:s1=(5+5+√(5*5))*4/2=(10+5)*4/2=30s2=s1s3=s1s4=s1再计算四棱台的斜高:l=√(h^2+(a1-a2)^2/4)=√(4^2+(5-3)^2/4)=√(16+4/4)=√(16+1)=√17接下来可以计算四棱台的体积和表面积:V=(A1+A2+√(A1*A2))*h/3=(25+9+√(25*9))*4/3=(25+9+√(225))*4 /3=(25+9+15)*4/3=49*4/3=196/3≈65.33S=A1+A2+(s1+s2+s3+s4)*l/2=25+9+(30+30+30+30)*√17/2=34+120*√17/2=34+60√17≈513.91因此,这个四棱台的体积约为65.33,表面积约为513.91总结起来,独立基础四棱台的计算公式为:体积公式V=(A1+A2+√(A1*A2))*h/3,表面积公式S=A1+A2+(s1+s2+s3+s4)*l/2、根据这些公式,可以根据四棱台的底面、顶面、侧面和高度来计算出其体积和表面积。
四棱台通用公式一、四棱台的体积公式。
1. 公式。
- 设四棱台的上底面面积为S_1,下底面面积为S_2,高为h,则四棱台的体积V=(1)/(3)h(S_1 + S_2+√(S_1S_2))。
2. 推导思路(简单了解)- 可以通过将四棱台补成棱锥,利用大棱锥与小棱锥体积之差来推导。
- 设小棱锥(由四棱台上底面向上延伸得到)的高为x,大棱锥(包含整个四棱台)的高为x + h。
- 根据棱锥体积公式V=(1)/(3)Sh,对于小棱锥体积V_1=(1)/(3)S_1x,大棱锥体积V_2=(1)/(3)S_2(x + h)。
- 四棱台体积V = V_2-V_1=(1)/(3)S_2(x + h)-(1)/(3)S_1x=(1)/(3)[S_2x+S_2h - S_1x]。
- 又因为根据相似三角形的性质,(S_1)/(S_2)=(x^2)/((x + h)^2),通过这个关系求出x并代入前面的式子化简后就可以得到V=(1)/(3)h(S_1 + S_2+√(S_1S_2))。
二、四棱台的表面积公式。
1. 公式。
- 四棱台的表面积S = S_上底+S_下底+S_侧。
- 其中S_上底和S_下底分别为上底面和下底面的面积(对于正方形底面,若上底面边长为a,则S_上底=a^2;若下底面边长为b,则S_下底=b^2)。
- S_侧为侧面积,若四棱台的侧面为梯形,设梯形的高为h_侧(也叫斜高),四棱台侧面梯形的上底之和为l_1,下底之和为l_2,则S_侧=(1)/(2)(l_1 +l_2)h_侧。
- 在四棱台的上下底面为正方形的情况下,若上底面边长为a,下底面边长为b,斜高为h_侧,则S_侧=2(a + b)h_侧,表面积S=a^2 + b^2+2(a + b)h_侧。
2. 斜高的计算(以正四棱台为例)- 设正四棱台的高为h,上底面边长为a,下底面边长为b(b > a)。
- 根据勾股定理,斜高h_侧=√(h^2+<=ft(frac{b - a){2})^2}。
独立基础计算办法一:混凝土体积计算:假设此基础为一四棱台,杯内为一圆柱体第一步:计算垫层体积V1=a*b*ha:垫层长b:垫层宽h:垫层高第二步:计算基层体积V2=a1*b1*h1-(a2*b2+a3*b3+sqrt{a2*b2*a3*b3})*h2/3=基础体积-杯体积a1:基底长b1:基底宽h1:基础高a2:杯底长a3:杯底宽b2:杯口长b3:杯口宽h2:杯高第三步:计算二次灌浆体积V3=(a2*b2+a3*b3+sqrt{a2*b2*a3*b3})*h2/3-π*r2*r2*h3=杯体积-被保护体积r2: 被保护圆柱半径h3:被保护圆柱在基础内高第四步:计算保护帽体积1.圆柱计算V4=π*(r1*r1-r2*r2)*h4r1:超出基面保护帽半径r2:被保护圆柱半径h4:保护帽高V混=V1+V2+V3+V4具体要根据混凝土不同配比按定额分别套用。
二:混凝土包裹占用体积(外运体积)第一步:计算垫层占用体积V垫=a*b*ha:垫层长b:垫层宽c:垫层高第二步:计算基层占用体积V基=a1*b1*h1第三步:计算保护帽占用体积V保=π*r1*r1*h4V占= V垫+V基+V保三:挖方体积V挖=(a1+2c+kH)(b1+2c+kH)H+1/3*k2H3c:工作面增加宽度k:放坡系数H:总高。
1/3*k2H3为基坑四角的角锥的体积四:回填体积计算V回= V挖-V占五:杯芯打毛面积S=(a2+a3)*sqrt[{(a3-a2)/2}2+h2*h2}+(b2+b3)*sqrt[{(b3-b2)/2}2+h2*h2}六:钢筋配网;按配筋图计算。
工作面宽度砖基按每边增加20cm,砼基按每边增加30cm,毛石基按每边增加15cm,放坡系数根据下表查用:套用定额时注意事项:1.注意混凝土配比。
以及粒径说明。
2.注意基础深度,套用不同子目。
3.回填土体积还要套用基础夯实定额。
4.垫层面积还需套用原土夯实。