计量经济学之模型估计方法的比较

计量经济学期末重点知识归纳1.普通最小二乘法：已知一组样本观测值{}n i Y X i i ,2,1:),(⋯=，普通最小二乘法要求样本回归函数尽可以好地拟合这组值，即样本回归线上的点∧i Y 与真实观测点Yt 的“总体误差”尽可能地小。

普通最小二乘法给出的判断标准是：被解释变量的估计值与实际观测值之差的平方和最小。

2.广义最小二乘法GLS ：加权最小二乘法具有比普通最小二乘法更普遍的意义，或者说普通最小二乘法只是加权最小二乘法中权恒取1时的一种特殊情况。

从此意义看，加权最小二乘法也称为广义最小二乘法。

3.加权最小二乘法WLS ：加权最小二乘法是对原模型加权，使之变成一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数。

4.工具变量法IV ：工具变量法是克服解释变量与随机干扰项相关影响的一种参数估计方法。

5.两阶段最小二乘法2SLS, Two Stage Least Squares ：两阶段最小二乘法是一种既适用于恰好识别的结构方程，以适用于过度识别的结构方程的单方程估计方法。

6.间接最小二乘法ILS ：间接最小二乘法是先对关于内生解释变量的简化式方程采用普通小最二乘法估计简化式参数，得到简化式参数估计量，然后过通参数关系体系，计算得到结构式参数的估计量的一种方法。

7.异方差性Heteroskedasticity ：对于不同的样本点，随机干扰项的方差不再是常数，而是互不相同，则认为出现了异方差性。

8.序列相关性Serial Correlation ：多元线性回归模型的基本假设之一是模型的随机干扰项相互独立或不相关。

如果模型的随机干扰项违背了相互独立的基本假设，称为存在序列相关性。

9.多重共线性Multicollinearity ：对于模型i k i i X X X Y μββββ++⋯+++=i k 22110i ，其基本假设之一是解释变量X 1,X 2,…,Xk 是相互独立的。

如果某两个或多个解释变量之间出现了相关性，则称为存在多重共线性。

AR（p）模型参数估计方法比较和实证分析陈杨林;刘业【摘要】对时间序列AR（p）模型的参数估计YULE-WALKER法、最小二乘法、最大似然法三种估计方法进行分析和比较，从模型推导出最小二乘估计、最大似然估计实质上是同一种估计方法，应用MATLAB软件对我国CPI数据建立AR（2）模型并应用3种方法对其参数进行估计、模型检验、预测结果比较，得出的结论与理论推导相符，实证上说明 AR（p）模型参数估计使用最小二乘法和最大似然法估计的结果是一样的。

%By analyzing and comparing YULE-WALKER,least squares method and maximum likelihood es-timation method of time series AR (p)model,least squares method and maximum likelihood estimation method are found essentially the same kind of estimate method.Building China's CPI data AR (2)model by using MATLAB software and then applying three methods to estimate the parameters,check the models and compare the prediction results,the conclusion obtained are found consistent with the theoretical deriva-tion.The empirical analysis shows the estimated results of AR (p)model parameter are the same by using least squares method and maximum likelihood method.【期刊名称】《南昌大学学报（理科版）》【年(卷),期】2014(000)002【总页数】4页(P124-127)【关键词】AR(p)模型;最小二乘估计;最大似然估计【作者】陈杨林;刘业【作者单位】九江职业技术学院，江西九江 332007;九江职业技术学院，江西九江 332007【正文语种】中文【中图分类】O211.61时间序列分析是数理统计中的一个重要分支是用数理统计和随机过程研究随机数据的规律最早起源于1927年，它在经济、信息等领域的研究和应用越来越活跃，George E.P.Box和 Gwilym M.Jenkins（1979）合著的《Time Series Anaysis －Forecasting and Control》一书［1］引起广泛的重视，但在我国，时间序列分析从70年代末到80年代中后期才得以深入研究和应用。

计量经济学的模型方法本文就计量经济学模型方法的几个哲学基础问题进行讨论。

（一）计量经济学模型的检验与发现一般认为的“只能检验，不能发现”，对于狭义的计量经济学模型方法，即模型检验而言是成立的，但广义的或者说完整的计量经济学模型方法，包括模型设定和模型检验两个阶段，是一个能够作出科学发现的研究过程。

狭义的计量经济学，它以模型估计和模型检为核心内容，说到底，就是回归分析。

那么它显然处于对假说进行检验的位置。

回归分析是一种统计分析方法，它针对已经设定的总体回归模型，按照随机抽样理论抽取样本观测值，采用适当的模型估计方法估计模型参数，并进行严格的检验，得到样本回归函数，从而完成统计分析的全过程。

统计分析给出的只是必要条件而非充分条件。

经济行为中客观存在的经济关系，一定能够通过表征经济行为的数据的统计分析而得到检验。

如果不能通过必要性检验，在表征经济行为的数据是准确的和采用的统计分析方法是正确的前提下，只能质疑所设定的经济关系的合理性和客观性。

但是反过来，如果在统计分析中发现了新的数据之间的统计关系，并不能就此说发现了新的经济行为关系，因为统计关系不是经济关系的充分条件。

毫无疑问，从这个意义上讲，计量经济学模型只能检验理论而不能发现理论。

尽管狭义的计量经济学模型方法的功能是有局限的，只能检验，不能发现，但它仍然是任何科学的经济学研究所不可或缺的。

经济研究以至于整个社会科学研究的一个显著特点是没有实验室，不可能通过实验室的实验来检验理论假设，那么回归分析就成为不可替代的检验方法。

广义的计量经济学，是经济理论、统计学和数学的结合。

计量经济学模型研究的完整框架是：关于经济活动的观察即行为分析关于经济理论的抽象即理论假说建立总体回归模型获取样本观测数据估计模型检验模型应用模型。

我们不妨称之为“广义的计量经济学模型理论与方法”。

大量有价值的应用计量经济学模型的实证经济研究成果，并不是“没有理论的检验”，都是首先提出理论假说，然后进行检验。

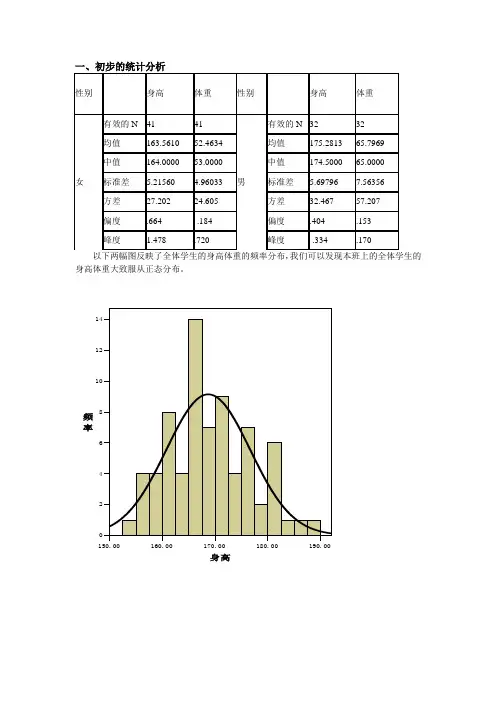
二、均值分析1、分性别对身高进行的比较假设男女身高相等，否定假设可认为男生身高明显高于女生。

2、分南北地区进行比较（1）身高假设两者均值相等，检验结果不能否定原假设，因而不能认为南北方身高有显著差异。

（2）体重通过假设两者均值相等，检验结果无法否定原假设，因而认为南北方体重没有明显差异。

3、分出生年份月份进行比较年份性别身高体重84 男均值172.00 56.00N 1 1总计均值172.00 56.00N 1 185 男均值180.33 70.67N 3 3女均值161.00 51.00N 2 2总计均值172.60 62.80N 5 586 男均值174.20 65.40N 20 20女均值162.11 52.28N 18 18总计均值168.47 59.1887 男均值178.50 66.58N 6 6女均值164.83 52.83N 18 18总计均值168.25 56.27N 24 2488 男均值170.50 65.00N 2 2女均值167.00 53.50N 2 2总计均值168.75 59.25N 4 489 女均值165.00 50.00N 1 1总计均值165.00 50.00N 1 1总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表可看出，各年份出生的人身高体重无显著性差异。

总计均值171.00 64.00N 6 6 3 男均值174.50 69.50N 4 4 女均值160.25 50.75N 4 4 总计均值167.38 60.13N 8 8 4 男均值181.25 68.50N 4 4 女均值162.25 52.00N 4 4 总计均值171.75 60.25N 8 8 5 男均值169.50 65.25N 2 2 女均值156.00 43.00N 1 1 总计均值165.00 57.83N 3 3 6 男均值175.00 63.00N 1 1 女均值171.50 57.50N 4 4 总计均值172.20 58.60N 5 5 7 男均值171.00 64.33N 3 3 女均值167.00 50.50N 2 2 总计均值169.40 58.80N 5 5 8 男均值179.20 64.90N 5 5 女均值161.50 52.50N 2 2 总计均值174.14 61.36N 7 7 9 男均值171.67 58.00N 3 3 女均值163.33 54.33N 3 3 总计均值167.50 56.1710 男均值174.67 61.83N 3 3总计均值174.67 61.83N 3 311 女均值162.50 51.67N 12 12总计均值162.50 51.67N 12 1212 男均值171.00 66.50N 2 2女均值167.00 57.00N 1 1总计均值169.67 63.33N 3 3总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表同样可得出，各月出生的人身高体重无显著性差异。

计量经济学回归分析模型计量经济学是经济学中的一个分支，通过运用数理统计和经济理论的工具，研究经济现象。

其中回归分析模型是计量经济学中最为常见的分析方法之一、回归分析模型主要用于确定自变量与因变量之间的关系，并通过统计推断来解释这种关系。

回归分析模型中的关系可以是线性的，也可以是非线性的。

线性回归模型是回归分析中最为常见和基础的模型。

它可以表示为:Y=β0+β1X1+β2X2+...+βkXk+ε其中，Y代表因变量，X1,X2,...,Xk代表自变量，β0,β1,β2,...,βk代表回归系数，ε代表随机误差项。

回归模型的核心是确定回归系数。

通过最小二乘法估计回归系数，使得预测值与实际观测值之间的差异最小化。

最小二乘法通过使得误差的平方和最小化来估计回归系数。

通过对数据进行拟合，我们可以得到回归系数的估计值。

回归分析模型的应用范围非常广泛。

它可以用于解释和预测经济现象，比如价格与需求的关系、生产力与劳动力的关系等。

此外，回归分析模型还可以用于政策评估和决策制定。

通过分析回归系数的显著性，可以判断自变量对因变量的影响程度，并进行政策建议和决策制定。

在实施回归分析模型时，有几个重要的假设需要满足。

首先，线性回归模型要求因变量和自变量之间存在线性关系。

其次，回归模型要求自变量之间不存在多重共线性，即自变量之间没有高度相关性。

此外，回归模型要求误差项具有同方差性和独立性。

在解释回归分析模型的结果时，可以通过回归系数的显著性来判断自变量对因变量的影响程度。

显著性水平一般为0.05或0.01，如果回归系数的p值小于显著性水平，则说明该自变量对因变量具有显著影响。

此外，还可以通过确定系数R^2来评估模型的拟合程度。

R^2可以解释因变量变异的百分比，值越接近1，说明模型的拟合程度越好。

总之，回归分析模型是计量经济学中非常重要的工具之一、它通过分析自变量和因变量之间的关系，能够解释经济现象和预测未来走势。

在应用回归分析模型时，需要满足一定的假设条件，并通过回归系数和拟合优度来解释结果。

计量经济模型的参数估计方法-计量经济学论文-经济学论文——文章均为WORD文档，下载后可直接编辑使用亦可打印——摘要：计量经济模型的参数估计是实证经济分析的关键，其在建模技术中处于核心的地位。

估计模型参数属于统计学中的参数估计内容。

常用的估计方法主要包括最小二剩法、极大似然估计法、矩估计法和贝叶斯估计法等。

而这些方法的应用，取决于计算机及其软件的编程。

利用R 软件可以很容易的实现对模型参数的估计，不论是线性模型，还是非线性模型，主要使用lm、glm 和nls等几个命令函数来实现。

关键词：经济建模；参数估计；经济参数；R的使用。

一位朋友获得到了一笔意想不到的奖金，于是计划着买一件观注已久的名贵消费品。

而同事同样也得到了一笔工资之外的收入，他却将这笔钱用于了投资。

用经济学的术语就是前者的消费倾向很高，而后者的消费倾向较低。

然而一个地区的消费倾向，应该是该地所有居住者的平均消费倾向。

它往往反映着该地区的生活水平和经济发达的程度，是人们比较关心的话题。

这类信息又不可能直接调查获得，因为哪些收入是新增的，以及个人之间的倾向差异较大，抽样的代表性很难保证。

所以此类信息的获得主要是通过模型测算的，即以观测得到的消费为被解释变量，收入为解释变量来构建回归方程，其回归系数就是收入的边际消费倾向。

在经济模型的各构成要件中，参数是用来表述具体经济关系的重要因素，如消费倾向就是收入决定消费模型中最重要的经济参数。

在现实的经济观察中，人们较易观测到收入和消费支出的数据，却很难直接观测到消费倾向的数据，因此我们通过建模来推算。

而这种对模型参数进行推算的过程，常被称为模型的估算。

一、经济参数估计及主要方法。

经济模型是用来描绘经济关系方程式或方程组，在经济模型中的各种变量是我们看得到的经济现实，模型中的每一个方程都表述着各变量之间的经济关联。

而变量之间精确关系的规律性反映，主要是由模型中伴随着变量存在的参数来承担的。

既然是规律性的东西，就是固定不变的。

计量经济学方法论
计量经济学是一门研究经济现象的科学方法，其主要特点是运用统计学理论和方法，对经济学中的理论模型进行检验和推断。

而计量经济学方法论则是指，对计量经济学方法的基本原理和应用进行系统化的研究和总结，包括以下方面：
1. 理论基础：计量经济学的方法论基础是建立在经济学理论基础之上的，因此对经济学理论，尤其是微观经济学和宏观经济学的基本原理必须了解和把握。

2. 模型假设：在计量经济学中，模型假设是非常重要的，因为只有合理的模型假设才能得到有意义的计量结果。

例如，线性回归模型中常用的假设有无自相关、正态性、同方差性等。

3. 数据的选择和处理：计量经济学需要进行数据的收集和处理，因此需要对数据的选择、测量和处理方法进行深入研究。

例如，对数据进行预处理，消除异常值等。

4. 模型估计：模型估计是计量经济学的核心内容，需要掌握参数估计的各种方法，如最小二乘法、极大似然法等，在估计过程中要注意模型诊断以及处理。

5. 模型检验和推断：计量经济学的目的是对经济现象进行定量检验和推断，因此需要对模型检验方法进行研究，如F检验、t检验等。

6. 模型应用：计量经济学的方法论需要与实际应用相结合，因此需要探讨如何将计量经济学方法应用于实际问题的解决中。

例如，利用计量经济学方法评估政策效果。

总之，计量经济学方法论是指对计量经济学的方法、技巧、理论基础和应用进行分析和总结，从而为实际应用提供更为有效的指导。

经济学研究中的计量经济学模型评估在经济学研究中，计量经济学是一种重要的方法论，通过建立和评估经济模型来研究经济现象和政策效果。

计量经济学模型评估是对经济模型有效性和可靠性的评估，它在经济研究中扮演着至关重要的角色。

首先，计量经济学模型评估需要建立适当的经济模型。

构建经济模型时，需要明确关注的经济问题、变量的选择和理论依据。

经济模型应该能够准确地描述经济现象，并具有可估计的参数，为后续的模型评估奠定基础。

接下来，模型评估的一项重要任务是进行模型的参数估计。

参数估计是通过收集和分析可用数据来确定模型中的未知参数。

常见的参数估计方法包括最小二乘估计、极大似然估计等。

参数估计的质量对模型评估的准确性和可靠性至关重要。

在进行模型参数估计之后，评估模型的拟合优度也是计量经济学模型评估的重要任务之一。

拟合优度反映了经济模型对现实世界数据的拟合程度。

常用的拟合优度指标包括R平方、调整R平方等。

较高的拟合优度表明模型能够较好地解释和预测数据，增强了模型评估的可信度。

此外，计量经济学模型评估还需要进行模型的假设检验。

模型假设检验的目的是验证模型的合理性和有效性。

常见的假设检验方法包括t检验、F检验等。

假设检验能够帮助我们判断模型中的变量是否具有统计显著性，从而评估模型的可用性。

除了对模型的参数估计、拟合优度和假设检验进行评估外，计量经济学模型评估还需要考虑模型的稳健性。

稳健性评估是通过对模型进行敏感性分析，检验模型在参数值或某些条件变化时的稳定性和鲁棒性。

稳健性评估可以增加模型评估的可靠性和泛化能力。

此外，计量经济学模型评估还需要进行模型的预测和验证。

模型的预测性能是评估模型性能的重要指标之一。

通过对模型进行预测，可以验证模型的有效性和可靠性。

在模型预测中，可以运用回归分析、时间序列分析等方法进行验证。

最后，计量经济学模型评估还需要进行模型结果的解释和政策分析。

对模型结果的解释是为了从理论角度深入理解模型产生结果的原因和机制。

空间计量模型选择、估计、权重、检验（Spatialeffect）应读者的要求，推送⼀篇关于空间计量⽅⾯的⽂章。

空间计量模型，主要⽤来解决空间被解释变量⾃相关和测量误差⽅⾯的问题；⽽且两个空间事物存在交互效应和异质性，因此，存在常系数回归和变异系数的回归区分。

空间计量经济学是计量经济学的⼀个分⽀，研究的是如何在横截⾯数据和⾯板数据的回归模型中处理空间相互作⽤（空间⾃相关）和空间结构（空间不均匀性）结构分析。

它与地学统计和空间统计学相似。

从某种程度上⽽⾔，空间计量经济学与空间统计学之间的不同和计量经济学与统计学之间的不同⼀样。

由于对其理论上的关⼼以及将计量经济模型应⽤到新兴⼤型编码数据库中的要求，近年来这个领域获得了快速发展。

空间数据分析和建模技巧与GIS的结合，现已⼴泛应⽤于经济政策分析中，尤其是实产和房地产经济[Anselin (1998a), Can(1998)], 环境和资源经济[Bockstael (1996), Geoghegan, Waingerand Bockstael (1997)], 发展经济[Nelson and Gray (1997)].当⾯临空间⾃相关时，标准的计量分析技巧通常会失效，⽽这种情形经常在地理或横截⾯数据集中出现，这也是空间计量得以迅速发展的原因之⼀。

传统的统计理论是⼀种建⽴在独⽴观测值假定基础上的理论。

然⽽，在现实世界中，特别是遇到空间数据问题时，独⽴观测值在现实⽣活中并不是普遍存在的（Getis, 1997）。

对于具有地理空间属性的数据，⼀般认为离的近的变量之间⽐在空间上离的远的变量之间具有更加密切的关系（Anselin & Getis，1992）。

正如著名的Tobler地理学第⼀定律所说：“任何事物之间均相关，⽽离的较近事物总⽐离的较远的事物相关性要⾼。

”（Tobler，1979）地区之间的经济地理⾏为之间⼀般都存在⼀定程度的Spatial Interaction，Spatial Effects）：Spatial Dependenceand Spatial Autocorrelation）。

计量经济学简单模型分析计量经济学是经济学领域中的一个重要分支，它借助数学和统计学的方法，通过建立模型来描述、解释和预测经济现象。

简单模型分析是计量经济学的基础，本文将介绍如何进行计量经济学简单模型分析。

首先，进行计量经济学简单模型分析需要明确研究问题和目标。

确定研究问题需要考虑实际背景和理论依据，确定模型的目标是为了回答研究问题。

其次，需要收集相关数据，包括时间序列数据、横截面数据等。

在收集数据时，需要注意数据的准确性、完整性和可比较性。

接下来，需要选择合适的模型。

简单线性回归模型是计量经济学中最简单的模型之一，适用于单一自变量和因变量的分析。

简单线性回归模型的数学形式为：y = β0 + β1x + ε，其中y是因变量，x是自变量，β0和β1是模型的参数，ε是误差项。

建立模型后，需要进行模型的估计和检验。

普通最小二乘法（OLS）是估计简单线性回归模型最常用的方法，它通过最小化残差平方和来估计模型的参数。

模型的检验包括拟合优度检验、统计检验和计量经济学检验等。

拟合优度检验用于评估模型对数据的拟合程度，统计检验用于检验模型的假设条件是否成立，计量经济学检验用于评估模型的可靠性、稳定性和预测能力。

最后，需要对模型进行分析和解释。

模型的参数估计值是解释模型的关键，β1表示自变量x每增加一个单位时因变量y的平均增加量。

需要分析模型的假设条件是否成立，以及模型的预测能力。

如果模型存在不足之处，需要进行相应的调整和改进。

总之，计量经济学简单模型分析是经济学研究的重要基础。

通过简单模型分析，我们可以描述、解释和预测经济现象，为经济决策提供科学依据。

随着数据科学和机器学习的发展，计量经济学的方法和技术将不断得到完善和创新，为经济学研究提供更加精确和实用的工具。

计量经济学模型方法
计量经济学是一种应用数学和统计学原理来研究经济现象的方法。

计量经济学模型是一种用来描述经济关系的数学模型。

常用的计量经济学模型方法包括：
1. 线性回归模型（Linear Regression Model）：线性回归模型是最常用的计量经济学模型之一，用于描述一个或多个自变量与因变量之间的线性关系。

该模型可以用来估计变量之间的关系，并进行预测和因果推断。

2. 面板数据模型（Panel Data Model）：面板数据模型是一种用于分析来自多个观察单位的经济数据的模型。

它结合了时间序列数据和截面数据的特点，可以考虑个体间的异质性和个体内的序列相关性。

3. 时间序列模型（Time Series Model）：时间序列模型用于分析随时间变化的经济数据。

它考虑到数据的序列相关性和趋势，可以用来预测未来的值和分析数据的长期趋势。

4. 非线性回归模型（Nonlinear Regression Model）：非线性回归模型用于描述自变量和因变量之间的非线性关系。

它可以更准确地拟合实际经济数据，但参数估计和推断方法更复杂。

5. 非参数模型（Nonparametric Model）：非参数模型是一种不对数据分布做出假设的模型，它不依赖于具体的函数形式，通过比较观测值之间的相对顺序来估计变量之间的关系。

这些方法可以根据具体问题的需要进行选择和应用。

在实际研究中，常常会结合多种方法和模型，以得到更全面和准确的分析结果。

计量经济学4种常用模型计量经济学是经济学的一个重要分支，主要研究经济现象的数量关系及其解释。

在计量经济学中，常用的模型有四种，分别是线性回归模型、时间序列模型、面板数据模型和离散选择模型。

下面将对这四种模型进行详细介绍。

第一种模型是线性回归模型，也是计量经济学中最常用的模型之一。

线性回归模型是通过建立自变量与因变量之间的线性关系来解释经济现象的模型。

在线性回归模型中，自变量通常包括经济学理论认为与因变量相关的变量，通过最小二乘法估计模型参数，得到经济现象的解释。

线性回归模型的优点是简单易懂，计算方便，但其前提是自变量与因变量之间存在线性关系。

第二种模型是时间序列模型，它主要用于分析时间序列数据的模型。

时间序列模型假设经济现象的变化是随时间演变的，通过分析时间序列的趋势、周期性和随机性，可以对经济现象进行预测和解释。

时间序列模型的常用方法包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）等。

时间序列模型的优点是能够捕捉到时间的动态变化，但其局限性是对数据的要求较高，需要足够的时间序列观测样本。

第三种模型是面板数据模型，也称为横截面时间序列数据模型。

面板数据模型是将横截面数据和时间序列数据结合起来进行分析的模型。

面板数据模型可以同时考虑个体间的差异和时间的变化，因此能够更全面地解释经济现象。

面板数据模型的常用方法包括固定效应模型、随机效应模型等。

面板数据模型的优点是能够控制个体间的异质性，但其需要对个体间的相关性进行假设。

第四种模型是离散选择模型，它主要用于分析离散选择行为的模型。

离散选择模型假设个体在面临多种选择时，会根据一定的规则进行选择，通过建立选择概率与个体特征之间的关系，可以预测和解释个体的选择行为。

离散选择模型的常用方法包括二项Logit模型、多项Logit模型等。

离散选择模型的优点是能够分析个体的选择行为，但其局限性是对选择行为的假设较强。

综上所述，计量经济学中常用的模型有线性回归模型、时间序列模型、面板数据模型和离散选择模型。

计量经济模型确定供需关系大类商品预测方法在市场经济中，准确预测供需关系对于企业决策和市场调控至关重要。

大类商品的供需关系预测可以帮助市场参与者更好地进行生产安排、销售策略制定和价格调整。

计量经济模型是一种常用的工具，可以帮助预测大类商品的供需关系，并为决策者提供有效的参考。

计量经济模型是一种建立在经济理论基础上的统计模型，通过对历史数据进行分析和拟合，以确定各种经济因素对供需关系的影响程度。

以下将介绍一些常见的计量经济模型，用于预测大类商品的供需关系。

1. 多元线性回归模型多元线性回归模型是一种简单而常用的计量经济模型，可以用于研究不同因素对供需关系的影响。

该模型基于一个或多个自变量与一个因变量之间的线性关系进行建模。

在预测大类商品的供需关系时，可以选择合适的自变量，如价格、收入水平、人口数量等，来解释大类商品的需求和供给变化。

模型建立后，可以使用历史数据对模型进行估计，然后应用估计得出的模型参数进行预测。

2. 时间序列模型时间序列模型是一种专门用于预测时间序列数据的计量经济模型。

在预测大类商品的供需关系时，可以将历史数据按照时间顺序排列，利用时间序列模型进行分析和预测。

常见的时间序列模型包括移动平均模型、指数平滑模型和自回归移动平均模型（ARIMA）。

这些模型可以帮助我们捕捉到大类商品供需关系中的季节性、趋势性和周期性变化，从而更准确地预测供需关系。

3. 面板数据模型面板数据模型是一种将时间序列数据和截面数据结合起来的计量经济模型。

在预测大类商品的供需关系时，可以将多个年份或多个地区的数据汇总，并使用面板数据模型进行分析和预测。

面板数据模型可以帮助我们探索不同因素对供需关系的影响，并考虑到时间和空间的变化。

常见的面板数据模型包括固定效应模型和随机效应模型，它们可以提供更准确的预测结果，并帮助决策者更好地理解供需关系。

上述三种计量经济模型是预测大类商品供需关系常用的方法，但在实际应用中，需要根据具体情况选择合适的模型。

计量经济学试题计量经济模型的评价与比较计量经济学是应用数学和统计学原理来分析经济现象的学科，它通过建立经济模型来研究经济问题，并运用计量方法对模型进行评价和比较。

本文将对计量经济模型的评价与比较进行探讨。

一、计量经济模型评价的基本方法评价计量经济模型的方法有很多，主要包括模型适用性评价和模型效果评价两个方面。

模型适用性评价是指评估模型是否适用于研究问题。

一般来说，模型应该符合经济理论，能够解释经济现象，并具有可操作性。

此外，模型的数据要求也是评价的一个重要方面，数据的质量、可获取性以及样本的大小等都会影响模型的适用性。

模型效果评价是指评估模型在解释和预测经济现象方面的准确性和效果。

常用的评价指标有拟合优度、残差分析、样本外预测等。

拟合优度是用来衡量模型对样本内数据的拟合程度，通常使用R方或调整后的R方进行度量。

残差分析用来评估模型的拟合残差是否存在问题，一般应该服从正态分布、无自相关性和异方差性。

样本外预测是评估模型对新样本的预测能力，通常采用均方根误差等指标进行度量。

二、常见的计量经济模型评价方法1. 线性回归模型评价线性回归模型是计量经济学中最常用的模型之一，在评价线性回归模型时，可以使用模型适用性评价和模型效果评价两个方法。

在模型适用性评价方面，线性回归模型要求因变量和自变量之间存在线性关系，且自变量之间应该具有较弱的多重共线性。

此外，模型的错误项应该满足线性回归模型的基本假设，即误差项应该服从正态分布、无自相关性和异方差性。

在模型效果评价方面，线性回归模型的拟合优度可以通过R方或调整后的R方进行评估。

残差分析可以用来检验模型的基本假设是否成立，例如，正态性可以通过残差的分布图或正态概率图进行判断。

2. 时间序列模型评价时间序列模型是用来分析时间序列数据的模型，常用的包括ARMA 模型、ARIMA模型等。

在时间序列模型的评价中，模型适用性评价包括检验序列的平稳性、白噪声性等。

平稳性可以通过单位根检验、ADF检验等进行判断。