初一数学下提高练习题

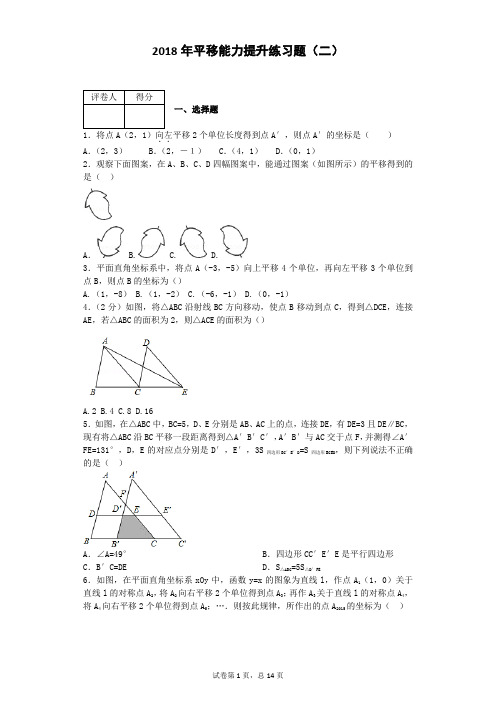
2018年平移能力提升练习题（二）一、选择题1．将点A（2，1）向左．．平移2个单位长度得到点A′，则点A′的坐标是（）A．（2，3） B．（2，－１） C．（4，1） D．（0，1）2．观察下面图案，在A、B、C、D四幅图案中，能通过图案（如图所示）的平移得到的是（）A． B. C. D.3．平面直角坐标系中，将点A（-3，-5）向上平移4个单位，再向左平移3个单位到点B，则点B的坐标为（）A.（1，-8）B.（1，-2）C.（-6，-1）D.（0，-1）4．（2分）如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A.2B.4C.8D.165．如图，在△ABC中，BC=5，D、E分别是AB、AC上的点，连接DE，有DE=3且DE∥BC，现有将△ABC沿BC平移一段距离得到△A′B′C′，A′B′与AC交于点F，并测得∠A′FE=131°，D，E的对应点分别是D′，E′，3S四边形BC′E′D=S四边形BCED，则下列说法不正确的是（）A．∠A=49° B．四边形CC′E′E是平行四边形C．B′C=DE D．S△ABC=5S△D′FE6．如图，在平面直角坐标系xOy中，函数y=x的图象为直线l，作点A1（1，0）关于直线l的对称点A2，将A2向右平移2个单位得到点A3；再作A3关于直线l的对称点A4，将A4向右平移2个单位得到点A5；…．则按此规律，所作出的点A2015的坐标为（）A、（1007，1008）B、（1008，1007）C、（1006，1007）D、（1007，1006）7．（3分）如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A 在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（）A．（4， B．（3， C．（4， D．（3，8．线段CD是由线段AB平移得到的，点A（﹣1，4）的对应点为C（2，3），则点B（﹣4，﹣1）的对应点D的坐标为（）A．（﹣7，﹣2） B．（﹣7，0） C．（﹣1，﹣2） D．（﹣1，0）9．如图，在方格纸中，线段a，b，c，d的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有（）A．3种 B．6种 C．8种 D．12种10．如图，将△ABC沿BC方向向右平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．32cm 11．如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线( )A．a户最长B．b户最长C．c户最长D．三户一样长12．在下列生活现象中，不是平移现象的是( )A．电梯的上下移动B．左右推动的推拉窗帘C．钟摆的运动D．急刹车中汽车在路面上的滑动13．如图，两个边长为5的正方形拼合成一个矩形，则图中阴影部分的面积是( )A．5B．25C．50D．以上都不对14．将长度为5cm的线段向上平移10cm所得的线段的长度是( )A．10cmB．5cmC．0cmD．无法确定15．如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．规定“把正方形ABCD 先沿x 轴翻折，再向左平移1个单位”为一次变换，如此这样，连续经过2014次变换后，正方形ABCD 的对角线交点M 的坐标变为（ ）A 、（-2012，2）B 、（-2012，-2）C 、（-2013，-2）D 、（-2013，2）二、填空题16．（3分）已知△ABC 的顶点A 的坐标为（1，2），经过平移后的对应点A′的坐标为（﹣1，3），则顶点B （﹣2，1）平移后的对应点B′的坐标为 ．17．平移小菱形◇可以得到美丽的“中国结”图案，下面四个图案是由◇平移后得到的类似“中国结”的图案，按图中规律，第20个图案中，小菱形的个数是 个．18．如图，A B C '''△是由ABC △沿射线AC 方向平移2cm 得到，若AC ＝3cm ，则A C '＝ cm ．19．（5分）如图，将周长为8的△ABC 沿BC 方向向右平移1个单位得到△DEF ，则四边形ABFD 的周长为 ．20．如图，当半径为30cm 的转动轮转过120°角时，转动带上的物体A 平移的距离为 cm （物体A 不打滑）．21．如图，A、B的坐标分别为（1，0）（0，2），若将线段AB平移到至A1B1， A1、B1的坐标分别为（2，a）（b，3），则a+b= ．22．如图1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置，得到图2，则阴影部分的周长为．23．如图，是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片，经测得FG=9cm,则这个剪出的图形的周长是 cm24．如图所示，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为2 米，其他部分均种植花草，则种植花草的面积是____________米2；25．如图，将面积为5的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中的四边形△CED的面积为________．26．如图所示，第1个图案是由黑白两种颜色的正六边形地面砖组成，第2个、第3个图案可以看作是第1个图案经过平移而得，那么第4个图案中有白色六边形地面砖________块，第n 个图案中有白色地面砖________块．27．（3分）如图，直线33y x =-+与x 轴交于点B ，与y 轴交于点A ，以线段AB 为边，在第一象限内作正方形ABCD ，点C 落在双曲线ky x=（0k ≠）上，将正方形ABCD 沿x 轴负方向平移a 个单位长度，使点D 恰好落在双曲线ky x=（0k ≠）上的点D 1处，则a= ．28．如图中图形的操作过程（本题中四个矩形的水平方向的边长均为a ，竖直方向的边长均为b ）：在图（1）中，将线段A1A2向右平移1个单位长度到B1B2，得到封闭图形A1A2B2B1（即阴影部分）；在图（2）中，将折线A1A2A3向右平移1个单位长度到B1B2B3，得到封闭图形A1A2A3B3B2B1（即阴影部分）．（1）在图（3）中，请你类似地画一条有两个折点的折线，同样向右平移1个单位长度，从而得到一个封闭图形，并画上阴影；（2）请你分别写出上述三个图形中除去阴影剩余部分的面积：S1＝________，S2＝________，S3＝________；（3）联想探索如图（4），在一长方形草地上，有条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分的草地面积是多少，并证明你的猜想．三、解答题29．（本题12分）在边长为1的小正方形组成的网格中，把一个点先沿水平方向平移|a|格（当a为正数时，表示向右平移；当a为负数时，表示向左平移），再沿竖直方向平移|b|格（当b为正数时，表示向上平移；当b为负数时，表示向下平移），得到一个新的点，我们把这个过程记为（a，b）．例如，从A到B记为：A→B（+l，+3）；从C到D记为：C→D（+1，－2），回答下列问题：（1）如图1，若点A的运动路线为：A→B→C→A，请计算点A运动过的总路程．（2）若点A运动的路线依次为：A→M（+2，+3），M→N（+1，－1），N→P（－2，+2），P→Q（+4，－4）．请你依次在图2上标出点M、N、P、Q的位置．（3）在图2中，若点A经过（m，n）得到点E，点E再经过（p，q）后得到Q，则m与p满足的数量关系是；n与q满足的数量关系是．30．（8分）如图，在平面直角坐标系中，将三角形⊿ABC向下平移5个单位长度，再向右平移3个单位长度，请画出图形⊿ A1B1C1,并写出A1,B1,C1的坐标．31．作图题（本小题满分8分）请将下图中的“小鱼”向左平移5格。

数学初一下册题数学初一下册题一、整数运算整数运算是初一下册数学的基础内容之一。

通过整数运算的练习，可以帮助学生熟练掌握整数的加减乘除法。

1. 整数加法：题目一：计算 (-5) + 7 = ?解题思路：在数轴上，从原点向左移动5个单位，然后向右移动7个单位，得到的最终位置是2。

故答案是2。

题目二：计算 (-9) + 3 = ?解题思路：在数轴上，从原点向左移动9个单位，然后向右移动3个单位，得到的最终位置是6。

故答案是6。

2. 整数减法：题目一：计算 10 - (-3) = ?解题思路：减去一个负数相当于加上一个正数，所以相当于计算 10 + 3 = 13。

故答案是13。

题目二：计算 (-4) - 6 = ?解题思路：减法可以转化为加法，即计算 (-4) + (-6) = -10。

故答案是-10。

3. 整数乘法：题目一：计算 (-2) × (-5) = ?解题思路：两个负数相乘，结果为正数，即 2 × 5 = 10。

所以答案是10。

题目二：计算 3 × (-8) = ?解题思路：一个正数乘以一个负数，结果为负数，即 3 × (-8) = -24。

所以答案是-24。

4. 整数除法：题目一：计算 (-21) ÷ 7 = ?解题思路：一个负数除以一个正数，结果为负数，即 (-21) ÷ 7 = -3。

所以答案是-3。

题目二：计算 45 ÷ (-5) = ?解题思路：一个正数除以一个负数，结果为负数，即 45 ÷ (-5) = -9。

所以答案是-9。

二、代数方程初一下册还学习了一些简单的代数方程，这是数学学习中的重要概念，通过练习代数方程，可以提高学生的逻辑思维能力。

1. 一元一次方程：题目一：解方程 2x + 3 = 9。

解题思路：将方程中的常数项移到等号右边，得到 2x = 9 - 3，化简后可得 x = 3。

所以方程的解是 x = 3。

七年级数学培优题库
七年级数学培优题库如下：
1. x是任意有理数，则2x不大于零的选项是：
A. 大于零
B. 小于零
C. 不小于零
D. 不大于零
2. 比较255、344、533、622四个数的大小，最小的数是：
A. 255
B. 344
C. 533
D. 622
3. 某超市为了促销，先将彩电按原价提高了40%，然后在广告中写上“节大酬宾，八折优惠”，结果每台彩电比原价多赚了270元，那么每台彩电的原价为：
A. 1750元
B. 2200元
C. 2250元
D. 2300元
4. 已知abc>0，则b的正方体，在地面上堆叠成什么样的立体：
A. 三维图形
B. 二维图形
C. 一维图形
D. 以上都不是
5. 北京奥运会期间，体育馆要对观众进行安全检查。

设某体育馆在安检开始时已有若干名观众在馆外等候安检，安检开始后，到达体育馆的观众人数按固定速度增加。

又设各安检人员的安检效率相同。

若用3名工作人员进行安检，需要25分钟才能将等候在馆外的观众检测完，使后来者能随到随检；若用6名工作人员进行安检，时间则缩短为10分钟。

现要求不超过5分钟完成安检工作，需要多少名工作人员：
A. 4名
B. 5名
C. 6名
D. 7名
以上题目仅供参考，每个学生的学习情况和理解能力都不一样，所以最好结合课堂上的教学内容和个人的学习进度来制定针对性的学习计划，这样才能更有效地提高数学成绩。

初一数学练习题6篇初一数学练习题6篇初一数学练习题(1)初一数学立方根练习题一、选择题1.下列说法中正确的是（）A．是一个无理数B．函数的自变量x的取值范围是x＞1C．8的立方根是±2D．若点P（-2，a）和点Q（b，-3）关于x轴对称，则a+b的值为5 2.下列各式计算正确的是（）A．B．（a＜1）C．D．3.下列等式不成立的是（）A．B．C．D．4.下列命题中为真命题的是（）A．同位角相等B．的立方根是±C．若a是无理数，a2则为有理数D．等腰三角形两腰上的高相等5.8的立方根是（）A．2B．-2C．3D．46.64的立方根是（）A．8B．±8C．4D．±47.在实数范围内，下列判断正确的是（）A．若|x|=|y|，则x=yB．若x＞y，则x2＞y2C．若|x|=（）2，则x=yD．若=，则x=y*更多试题请搜索：迅学堂初一数学练习题(2)一、选择题1、数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画一条长15厘米的线段AB，则AB盖住的整数点的个数共有（? ）个?A．13或14个 B.14或15个 C.15或16个? D.16或17个3、如下图是某风景区的旅游路线示意图，其中，，为风景点，为两条路的交叉点，图中数据为相应两点的路程（单位：千米）．一学生从处出发，以千米／时的速度步行观览景色，每个景点的逗留时间约为小时．（1）当他沿着路线游览回到处时，共用了小时，求的长；（2）若此学生打算从处出发，步行速度与在景点的逗留时间保持不变，且在最短时间内游览完三个景点返回处，请你为他设计一条步行路线，并说明这样设计的理由．（不考虑其他因素）4、如图，从A到B最短的路线是（）?A. A—G—E—B? ? B. A—C—E—B?C. A—D—G—E—B? D. A—F—E—B5、已知线段AB=10cm，直线AB上有点C，且BC=4cm，M是线段AC的中点，则AM=? cm。

初一数学下册综合算式专项练习题带括号的四则运算练习题一：计算下列算式的值1. (5 + 3) × 2 - 7解析：根据括号内的运算先计算括号内的算式，即5 + 3 = 8。

然后继续按照乘法和减法的顺序计算，8 × 2 - 7 = 16 - 7 = 9。

答案：92. 7 × (4 + 2) + 3解析：同样先计算括号内的算式，4 + 2 = 6。

然后进行乘法和加法的运算，7 × 6 + 3 = 42 + 3 = 45。

答案：453. 6 - (2 - 1) × 5解析：先计算括号内的算式，2 - 1 = 1。

然后进行乘法和减法的运算，1 × 5 = 5，6 - 5 = 1。

答案：1练习题二：根据题意写出带括号的算式1. 雅虎公司一共有50名员工，其中男性员工占总数的四分之三，求男性员工的数量。

解析：根据题意可知，男性员工占总数的四分之三，即为50的四分之三。

所以，男性员工的数量可以表示为：(50 × 4) ÷ 3。

答案：(50 × 4) ÷ 32. 某种草花的株数比玫瑰花株数的两倍还多10株，如果玫瑰花株数为20株，请你写出求草花株数的算式。

解析：题目中提到草花的株数比玫瑰花株数的两倍还多10株，我们可以表示草花株数为：(20 × 2) + 10。

答案：(20 × 2) + 10练习题三：解决实际问题1. 小明在一家超市买了一些食品，其中一种饼干的价格为每包5元，他一共购买了10包饼干。

若小明使用200元购买这些饼干，请问他还剩下多少钱。

解析：小明购买了10包饼干，每包5元，总价为10 × 5 = 50元。

而他使用了200元购买这些饼干，所以他还剩下的钱可以表示为：200 - 50。

答案：200 - 502. 小玲每天上学需要骑车9公里，她在一周内上学的总里程是多少？解析：小玲每天上学需要骑车9公里，一周共7天，所以她一周上学的总里程可以表示为：9 × 7。

初一下册数学练习题及答案一、选择题1. 已知a、b、c是三角形的三边长，且满足a^2 + b^2 = c^2，那么这个三角形是：A. 等边三角形B. 直角三角形C. 等腰三角形D. 不规则三角形答案：B2. 下列哪个数是无理数？A. πB. 0.33333...C. √2D. 1答案：A二、填空题1. 如果一个数的平方根是2，那么这个数是______。

答案：42. 一个数的立方根是3，那么这个数是______。

答案：27三、计算题1. 计算下列各题，并写出计算过程。

(1) (-3)^2答案：(-3)^2 = 9(2) √(16) + √(4)答案：√(16) + √(4) = 4 + 2 = 6四、解答题1. 已知一个长方体的长、宽、高分别为a、b、c，求证：长方体的体积是abc。

证明：长方体的体积V=长×宽×高，即V=a×b×c，所以长方体的体积是abc。

2. 一个直角三角形的两条直角边分别为3和4，求斜边的长度。

解：根据勾股定理，斜边c的长度为c = √(a^2 + b^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5。

五、应用题1. 某工厂生产一批零件，每个零件的成本为5元，如果工厂计划生产x个零件，那么总成本是多少元？答案：总成本为5x元。

2. 一个水池的长是15米，宽是10米，求水池的面积。

答案：水池的面积为长×宽=15×10=150平方米。

通过这些练习题，同学们可以巩固初一数学的基本概念和计算方法，提高解题能力。

希望同学们能够认真完成这些练习，并对照答案检查自己的解题过程。

初一数学七下二元一次方程所有知识点总结和常考题型练习题二元一次方程组知识点二元一次方程的解是指能够使二元一次方程的左右两边相等的两个未知数的值。

二元一次方程组是指含有两个未知数（x和y），并且含有未知数的项的次数都是1的方程组。

二元一次方程组的解是指二元一次方程组中的几个方程的公共解。

二元一次方程组的解有三种情况：无解、只有一组解和有无数组解。

例如，x+y=6和x+y=1就没有解；x+y=1和2x+y=2只有一组解；x+y=1和2x+2y=2有无数组解。

解二元一次方程组的方法有代入消元法和加减消元法。

代入消元法是指将一个方程的未知数用含另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解。

加减消元法是指两个二元一次方程中同一个未知数的系数相反或相等时，把这两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程。

三元一次方程组是指方程组中一共含有三个未知数，含未知数的项的次数都是1，并且方程组中一共有两个或两个以上的方程。

解三元一次方程组的关键也是“消元”：三元→二元→一元。

列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步：（1）审题，把实际问题抽象成数学问题，分析已知数和未知数；（2）设法找出能够表示题意两个相等关系；并用字母表示其中的两个未知数；（3）根据这两个相等关系列出必需的代数式，从而列出方程组；（4）解这个方程组，求出两个未知数的值；（5）在对求出的方程的解做出是否合理判断的基础上，写出答案。

二元一次方程组练一、选择题1、下列各式是二元一次方程的是（）。

2、若x=3，y=2是关于x、y的二元一次方程3x-ay=的一个（组）解，则a的值为（）。

3、对于二元一次方程x-2y=1有无数个解，下列四组值不是该方程的解的一组是（）。

4、二元一次方程x+2y=7在正整数范围内的解有（）。

二、填空题1、二元一次方程组x+y=5，2x+3y=11的解为（，）。

初一数学有理数难题与提高练习和培优综合题压轴题（含解析）初一数学有理数难题与提高练习和培优综合题压轴题(含解析)一．选择题（共12小题）1．1纳米相当于1根头发丝直径的六万分之一．则利用科学记数法来表示，头发丝的半径是（）A．6万纳米B．6×104纳米C．3×106米D．3×105米2．足球循环赛中，红队胜黄队4：1，黄队胜蓝队2：1，蓝队胜红队1：0，则下列关于三个队净胜球数的说法正确的是（）A．红队2，黄队2，蓝队0 C．红队3，黄队3，蓝队1 3．要使A．奇数B．红队2，黄队1，蓝队1 D．红队3，黄队2，蓝队0为整数，a只需为（）B．偶数C．5的倍数D．个位是5的数4．体育课上全班女生进行了百米测验，达标成绩为18秒，下面是第一小组8名女生的成绩记录，其中“+”表示成绩大于18秒，“”表示成绩小于18秒，“0”表示刚好达标，这个小组的达标率是（） 1 +0.8 0 1.2 0.1 0 +0.5 0.6 A．25% B．37.5% C．50% D．75%5．有一列数a1，a2，a3，a4，。

，an，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a1=2，则a2022年值为（）A．2B．1 C．D．2022年++=（）6．有理数a，b，c都不为零，且a+b+c=0，则A．1B．±1 C．1 D．07．计算机中常用的十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数符号，这些符号与十进制的数的对应关系如下表：16进制0 10进制0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 A B C D E F 10 11 12 13 14 15 例如，用十六进制表示5+A=F，3+F=12，E+D=1B，那么A+C=（）第1页（共39页）A．16 B．1C C．1A D．228．若ab＞0，且a+b＜0，那么（）A．a＞0，b＞0 B．a＞0，b＜0 C．a＜0，b＜0 D．a＜0，b＞09．如图，在日历中任意圈出一个3×3的正方形，则里面九个数不满足的关系式是（）A．a1+a2+a3+a7+a8+a9=2（a4+a5+a6）B．a1+a4+a7+a3+a6+a9=2（a2+a5+a8）C．a1+a2+a3+a4+a5+a6+a7+a8+a9=9a5D．（a3+a6+a9）（a1+a4+a7）=（a2+a5+a8）10．为确保信息安全，信息需加密传输，发送方由明文?密文（加密），接收方由密文?明文（解密），已知有一种密码，将英文26个小写字母a，b，c，。

初一数学好用的练习题数学是一门需要不断练习的学科，通过大量的练习题可以帮助初一学生建立起数学基础，提高解题能力。

本文将介绍一些初一数学中常见且好用的练习题，帮助学生更好地掌握数学知识。

一、整数运算题整数运算是初一数学中的重要内容，既涉及到数的四则运算，又涉及到整数的加减乘除规则。

以下是一些好用的整数运算题：1. 计算题：（1）求5 + (-8)的值是多少？（2）计算：(-3) + 6 - (-4)。

（3）计算：(-2) × 7 + 16 ÷ (-4)。

2. 应用题：（1）小明的钱包里有50元钱，他去超市买了商品，总共花费了32元。

这时他又从钱包里拿出20元钱，请问他还剩几元钱？（2）某天，餐馆共卖出54盘炒饭，其中29盘被顾客吃掉了。

请问还剩下多少盘炒饭？二、分数运算题分数是初一数学中的重要概念，通过分数运算题可以帮助学生掌握分数的加减乘除运算规则，并提高分数计算的能力。

以下是一些好用的分数运算题：1. 计算题：（1）计算：2/5 + 3/4。

（2）计算：5/6 - 1/3。

（3）计算：2/3 × 3/4。

（4）计算：3/4 ÷ 2/5。

2. 应用题：（1）小明买了一块巧克力，他吃掉了其中的1/4。

请问他还剩下多少比重的巧克力？（2）某班有32名学生，其中4/8的学生是男生。

请问男生人数有多少名？三、代数方程题代数方程是初一数学中的重要内容，通过解代数方程题可以帮助学生提高代数运算和方程解法的能力，培养逻辑思维。

以下是一些好用的代数方程题：1. 求解方程：（1）求解方程3x - 5 = 10。

（2）求解方程2y + 7 = -5。

（3）求解方程4x + 3 = 2x - 5。

2. 应用题：（1）一辆汽车以每小时60千米的速度行驶，行驶了t小时后，行驶的总路程为D千米，可以用方程60t = D表示。

如果已知t的值为5，求D的值。

（2）某物品原价为x元，打折后的价格为原价的80%。

1、证明线段相等或角相等
两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。

很多其它问题最后都可化归为此类问题来证。

证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。

说明：利用三角形全等证明线段求角相等。

常须添辅助线，制造全等三角形，这时应注意：
（1）制造的全等三角形应分别包括求证中一量；（2）添辅助线能够直接得到的两个全等三角形。

说明：当一个三角形中出现角平分线、中线或高线重合时，则此三角形必为等腰三角形。

我们也可以理解成把一个直角三角形沿一条直角边翻折（轴对称）而成一个等腰三角形。

说明：有等腰三角形条件时，作底边上的高，或作底边上中线，或作顶角平分线是常用辅助线。

证明二：如图5所示，延长ED到M，使DM＝ED，连结FE，FM，BM
说明：证明两直线垂直的方法如下：
（1）首先分析条件，观察能否用提供垂直的定理得到，包括添常用辅助线，见本题证二。

（2）找到待证三直线所组成的三角形，证明其中两个锐角互余。

（3）证明二直线的夹角等于90°。

2. 分析：本题从已知和图形上看好象比较简单，但一时又不知如何下手，那么在证明一条线段等于两条线段之和时，我们经常采用“截长补短”的手
法。

“截长”即将长的线段截成两部分，证明这两部分分别和两条短线段相等；“补短”即将一条短线段延长出另一条短线段之长，证明其和等于长的线段。