最新华理大学物理第5章习题课讲解学习
- 格式:ppt
- 大小:518.50 KB
- 文档页数:25


第五章课后习题答案5.1 解:以振动平衡位置为坐标原点,竖直向下为正向,放手时开始计时。
设t 时刻砝码位置坐标为x ,由牛顿第二定律可知: 220)(dtx d mx x k mg =+-其中0x 为砝码处于平衡位置时弹簧的伸长量,所以有 0kx mg = 解出0x 代入上式,有:022=+x mk dtxd 其中 mk =ω可见砝码的运动为简谐振动简谐振动的角频率和频率分别为: s r a d x g mk /9.90===ω Hz 58.12==πων振动微分方程的解为)c o s (ϕω+=t A x由起始条件 t =0 时,,1.00m x x -=-= 0=v得: A =0.1m ,πϕ=振动方程为:)9.9cos(1.0π+=t x5.2 证明:取手撤去后系统静止时m 的位置为平衡位置,令此点为坐标原点,此时弹簧伸长为x ,则有: 0sinkx mg =θ (1)当物体沿斜面向下位移为x 时,则有: ma T mg =-1sin θ (2) βJ R T R T =-21 (3) )(02x x k T += (4)R a β= (5) 将(2)与(4)代入(3),并利用(5),可得: k x R R kx mgR a RJ mg --=+0sin )(θ利用(1)式可得 x RJ mR kR dtx d a +-==22所以物体作简谐振动因为 R J mR kR +=ω 所以振动周期为 ωπ2=T5.3 解: 因为 mk ππων212==所以 :1221m m =νν22121)(m m νν==2 Kg5.4 解:(1) 由振动方程)420cos(01.0ππ+=t x 可知:振幅A =0.01m ;圆频率 πω20=; 周期 s T 1.02==ωπ频率Hz 10=ν ;初相40πϕ=(2)把t =2s 分别代入可得:2005.0)420cos(01.0|2=+==ππt x t m2314.0)420sin(2.0|2-=+-===πππt dt dx v t m/s)420sin(4|22πππ+===t dtdv a t5.5 解: T =2s ,ππω==T2设振动方程为:)cos(10ϕπ+=t x则速度为:)s i n (10ϕππ+-=t v加速度为: )c o s (102ϕππ+-=t a根据t =0 时,x =5cm ,v < 0 的条件,得振动的初相为 3πϕ=,故振动方程为:)3cos(10ππ+=t x设在 1t 时刻振子位于cm x 6-=处,并向x 轴负方向运动,则有:53)3'c o s (-=+ππt 54)3's i n (=+ππt故有 s cm t v /1.25)3'sin(10-=+-=πππ22/2.59)3'cos(10s cm t a =+-=πππ设弹簧振子回到平衡位置的时刻为2t ,则有πππ2332=+t ,从上述位置回到平衡位置所需时间为: st t 8.0/)]3)53(arccos()323[(12=----=-ππππ5.6。




第五章 波 动1、一频率为500HZ 的平面波,波速为350m/s ,求: (1)在波传播方向上位相差为π/3的两点相距多远?(2)介质中任意一点在时间间隔10-3s 内两位移间的位相差是多少? 解:(1)λπ=∆ϕ∆2x m 12.050035061u 232x ==νππ=λπϕ∆=∆ (2)0x =∆π=⨯⨯π=∆πν=∆ω=ϕ∆-3105002t 2t2、一横波沿细绳传播时的波动方程为 y=0.20cos π(2.5t-x)(SI),求: (1)波的振幅、速度、频率和波长;(2) x=L 处质点振动的初位相以及与该处质点速度大小相同但方向相反的其它各质点位置。
解:(1))]5.2xt (5.2cos[20.0)x t 5.2cos(20.0y -π=π-π= m /s 5.2 u )m (20.0A ==∴ πν=π=ω25.2()s 125.125.2 ==ν )m (225.15.2u ==ν=λ (2))L t 5.2cos(20.0y π-π=L π-=ϕ∴ 根据旋转矢量图可知,只有反相的各点才能速度相等而方向相反 π+=π-π-π-π=ϕ∆∴)1k 2()x t 5.2()L t 5.2( )2,1,0k ()1k 2(L x ±±=++=3、如图所示,已知t=0的波形曲线Ⅰ,波沿X 轴正向传播,经过0.5s 后波形变为曲线Ⅱ。
试根据图中绘出的条件求 (1)波的表达式; (2)P 点振动表达式。
解:(1)由图可知 s 2T m 4cm 10A ==λ= 2T 2π=ϕπ=π=ω O 点振动方程 )2t c o s (1.0)t c o s (A y 0π+π=ϕ+ω=波动方程 )x 22t c o s (1.0)x 2t c o s (A y π-π+π=λπ-ϕ+ω=(cm) (2)P 点振动方程以x = 1m 代入波动方程得 t c o s 1.0)422t c o s (1.0y p π=π-π+π=(cm ) 4、一平面简谐波在媒质中以波速u=5m/s 沿x 轴正方向传播,原点O 处质元的振动曲线如图所示。


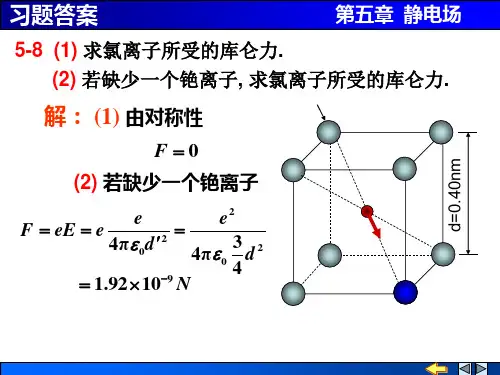
第五章作业选讲5 -8 在氯化铯晶体中,一价氯离子Cl -与其最邻近的八个一价铯离子Cs +构成如图所示的立方晶格结构.(1) 求氯离子所受的库仑力;(2) 假设图中箭头所指处缺少一个铯离子(称作晶格缺陷),求此时氯离子所受的库仑力.分析 铯离子和氯离子均可视作点电荷,可直接将晶格顶角铯离子与氯离子之间的库仑力进行矢量叠加.为方便计算可以利用晶格的对称性求氯离子所受的合力.解 (1) 由对称性,每条对角线上的一对铯离子与氯离子间的作用合力为零,故F 1 =0. (2) 除了有缺陷的那条对角线外,其它铯离子与氯离子的作用合力为零,所以氯离子所受的合力F 2 的值为N 1092.1π3π4920220212⨯===aεe r εq q F F 2 方向如图所示.5 -12 两条无限长平行直导线相距为r 0 ,均匀带有等量异号电荷,电荷线密度为λ.(1) 求两导线构成的平面上任一点的电场强度( 设该点到其中一线的垂直距离为x );(2) 求每一根导线上单位长度导线受到另一根导线上电荷作用的电场力.分析 (1) 在两导线构成的平面上任一点的电场强度为两导线单独在此所激发的电场的叠加.(2) 由F =q E ,单位长度导线所受的电场力等于另一根导线在该导线处的电场强度乘以单位长度导线所带电量,即:F =λE .应该注意:式中的电场强度E 是另一根带电导线激发的电场强度,电荷自身建立的电场不会对自身电荷产生作用力.解 (1) 设点P 在导线构成的平面上,E +、E -分别表示正、负带电导线在P 点的电场强度,则有()i i E E E xr x r ελx r x ελ-=⎪⎪⎭⎫⎝⎛-+=+=+-00000π211π2(2) 设F +、F -分别表示正、负带电导线单位长度所受的电场力,则有2002πr λλε+-==F E ii E F 002π2r ελλ-=-=+-显然有F +=F -,相互作用力大小相等,方向相反,两导线相互吸引.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅01d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数? 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d r πE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r E r <R 1 ,该高斯面内无电荷,0=∑q ,故01=ER 1 <r <R 2 ,高斯面内电荷()31323131RR R r Q q --=∑ (v=4/3Pi R3)故 ()()23132031312π4r R R εR r Q E --= +R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4r εQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B )所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-= 这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL E r <R 1 , 0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -26 电荷面密度分别为+σ和-σ的两块“无限大”均匀带电的平行平板,如图(a )放置,取坐标原点为零电势点,求空间各点的电势分布并画出电势随位置坐标x 变化的关系曲线.分析 由于“无限大”均匀带电的平行平板电荷分布在“无限”空间,不能采用点电荷电势叠加的方法求电势分布:应该首先由“无限大”均匀带电平板的电场强度叠加求电场强度的分布,然后依照电势的定义式求电势分布. 解 由“无限大” 均匀带电平板的电场强度i 02εσ±,叠加求得电场强度的分布, ()()()⎪⎪⎩⎪⎪⎨⎧><<--<=a x a x a εσa x0 2 00i E电势等于移动单位正电荷到零电势点电场力所作的功()a x a x εσV x <<--=⋅=⎰ d 0l E ()a x a εσV -<=⋅+⋅=⎰⎰- d d 0a-axl E l E ()a x a εσV >-=⋅+⋅=⎰⎰ d d 0a-axl E l E电势变化曲线如图(b )所示.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211π4π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E。