运动副中摩擦力的确定资料

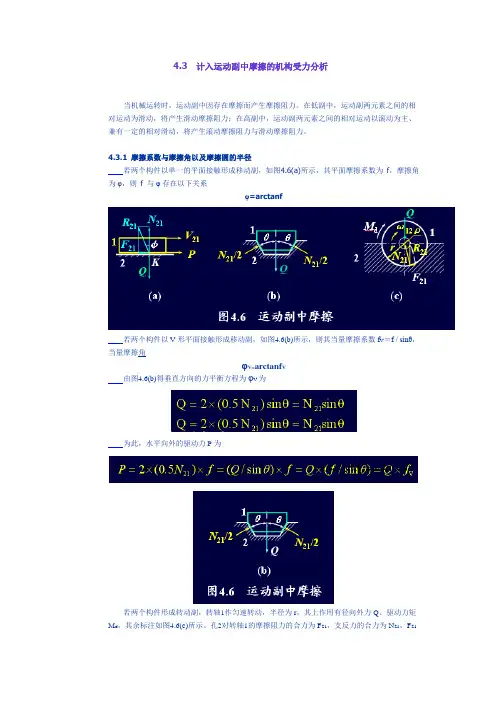
4.3计入运动副中摩擦的机构受力分析当机械运转时，运动副中因存在摩擦而产生摩擦阻力。

在低副中，运动副两元素之间的相对运动为滑动，将产生滑动摩擦阻力；在高副中，运动副两元素之间的相对运动以滚动为主、兼有一定的相对滑动，将产生滚动摩擦阻力与滑动摩擦阻力。

4.3.1摩擦系数与摩擦角以及摩擦圆的半径若两个构件以单一的平面接触形成移动副，如图4.6(a)所示，其平面摩擦系数为f，摩擦角为φ，则 f 与φ存在以下关系=arctanfφ若两个构件以V形平面接触形成移动副，如图4.6(b)所示，则其当量摩擦系数f V＝f / sinθ，当量摩擦角φV=arctanf V由图4.6(b)得垂直方向的力平衡方程为φV为为此，水平向外的驱动力P为若两个构件形成转动副，转轴1作匀速转动，半径为r，其上作用有径向外力Q、驱动力矩M d，其余标注如图4.6(c)所示。

孔2对转轴1的摩擦阻力的合力为F21，支反力的合力为N21，F21与N21的合力R21＝－Q。

由图4.6(c)得出孔2对转轴1的摩擦阻力矩Mf为M f＝r×F21＝ρ×R21(4.11)摩擦阻力F21表达为定义ρ＝f V.r ，M f为M f＝r×(Qf V)＝(f V·r)×Q＝ρ×Q(4.13)4.3.2计入运动副中摩擦时曲柄滑块机构的受力分析在图4.7(a) 中，F21、F41、M f21、M f23、M f41、Md分别为F21产生的摩擦力矩M f21为M f21＝ρ×F21(4.14) M f21阻碍相对转动ω12，以及F23产生的摩擦力矩M f23为M f23＝ρ×F23(4.15) M f23阻碍相对转动ω32，由此确定连杆2上拉力作用线的位置。

F41形成的摩擦力矩M f41为M f41＝ρ×F41曲柄1上的驱动力矩Md为M d＝h1×F12(4.17)对于滑块3，由三力汇交原理得Fr与F23的交点即为F43应通过的点，由此确定F43的位置。

§4-2 运动副中的摩擦滑动摩擦（低副）滚动摩擦（高副）—摩擦小一、移动副的摩擦根据接触面的几何形状不同，三种情况，即单一平面接触、槽面接触和圆柱面接触。

GF N -=21库仑定律)(2121大小N f fF F =滑块1的总反力212121f N R F F F +=f F fF F F N N N f ===21212121tan φfarctan =φ★总反力F R21的方向恒与相对速度V 12方向成（90°+ ϕ）1、单一平面接触总反力摩擦角ϕF R21F N21F f 212V 12P G1平面摩擦在斜面机构中的应用1）滑块沿斜面等速上升（正行程）G ——铅垂载荷；P ——水平驱动力；F R21——滑块1所受的总反力。

为使滑块沿斜面等速上升，求P 。

021=++G F P R )tan(ϕα+=G P F R21α+ϕP GF R212）滑块沿斜面等速下降（反行程）G ——驱动力；P ’——阻止滑块加速下滑的阻力；F R21——滑块1所受的总反力。

0'21=++G F P R )tan('ϕα-=G P α-ϕP’GF R21F R21α-ϕ> 0 ，说明P′>0，保持匀速状态的力；α-ϕ≤0 ，P′≤0, G 的分力不足以使滑块运动，只有工作阻力变为驱动力时,滑块才能运动。

)tan('ϕα-=G P F R212、槽面摩擦槽形角2θG F N =⋅⋅θsin 2221θsin 21G F N =V N f Gf fG fF F ===θsin 2121当量摩擦系数θsin f f V =当量摩擦角V V f arctan =φf V ≥f , 常用楔槽面增大摩擦力，如V 带传动、三角形螺纹联接等。

但注意并非实际摩擦系数增大，而是将增大的F N21折合到 f 变为f v 。

楔形滑块F N21/2F f21F N21/2不论两运动副元素的几何形状如何，两元素间产生的滑动摩擦力均可用通式：3、圆柱面摩擦F N21是沿整个接触面各处反力的总和。

5.1重点与难点5.1.1移动副中的摩擦力及总反力的确定由库仑摩擦定律知，摩擦力=f。

式中为构件2对构件1的摩擦力大小;f为摩擦系数，与构成运动副的两构件的材料有关;为构件2对构件1的正压力大小。

摩擦力总是阻碍两构件之间的相对运动的。

如图5.1所示。

因此，的方向总和相对运动速度的方向相反(为构件1相对构件2的运动速度)。

为分析问题方便，我们总是把正压力和摩擦力合成运动副总反力,与的夹角称为摩擦角φ(tanφ=f)。

因此，与的夹角总为钝角π/2+φ。

综上所述，在移动副中确定运动副总反力的方法如下:(1)运动副总反力,和正压力的夹角为φ;(2)运动副总反反力和相对速度的夹角为钝角π/2+φ。

摩擦力总是成对出现的，和总是大小相等,方向相反，在同一条直线上分别作用在不同的构件上。

而运动副总反力也总是成对出现的，和。

也是大小相等，方向相反。

在同一条直线上分别作用在不同构件上。

它们是一对作用力与反作用力。

摩擦力与外载荷的关系可以用表示。

式中，为铅垂外载荷大小；称为当量摩擦系数。

当量摩擦系数除了与摩擦系数有关外，还与运动副的形状有关。

在图5.1所示的平面移动副中，=f;在图5.2所示的槽面移动副中，=f/sinβ；在图5.3所示的柱面移动副中，=kf，k为1~1.57，k 值与运动副的接触状态有关，即在相同的外载荷作用下，运动副形状不同，生产的摩擦力不同。

这是由于运动副的形状不同，所产生的正压力不同而引起的。

5.1.2转动副中的摩擦力及总反力的确定转动副中的摩擦力=P。

如图5.4所示，摩擦力对轴颈中心的力矩即为摩擦力矩，该摩擦力矩应阻碍构件1对构件2的相对运动，因此和角速度的方向相反，=，式中，r为轴颈半径。

而正压力对轴颈中心的力矩等于零。

因此，运动副总反力对轴颈中心的力矩即为对轴颈中心的摩擦力矩，即=r=。

由力的平衡条件，=-P ，所以有=r 。

以为半径作一圆.这个圆称为摩擦圆。

运动副总反力恒切于摩擦圆。

因此，在转动副中确定运动副总反力的方法图5.4是:(1)运动副总反力，与外载荷P等值反向，并恒切于摩擦圆。

JointsIdealized JointsAbout Idealized JointsIdealized joints connect two parts. The parts can be rigid bodies, Flexible bodies, or Point mass es. You can place idealized joints anywhere in your model.Note:The joints you can attach to flexible bodies depend on the version of Adams/Solver you are using (C++ or FORTRAN). In addition, Adams/Solver (C++) does not support pointmasses.For a summary of which joints and forces are supported on flexible bodies, see Table ofSupported Forces and Joints in the Adams/Flex online help. Also refer to the Adams/Flexonline help for more information on attaching joints and forces to flexible bodies. Adams/View supports two types of idealized joints: simple and complex. Simple joints directly connect bodies and include the following:•Revolute Joints. See Revolute Joint Tool.•Translational Joints. See Translational Joint Tool.•Cylindrical Joints. See Cylindrical Joint Tool.•Spherical Joints. See Spherical Joint Tool.•Planar Joints. See Planar Joint Tool.•Constant-Velocity Joints. See Constant-Velocity Joint Tool.•Screw Joints. See Screw Joint Tool.•Fixed Joints. See Fixed Joint Tool.•Hooke/Universal Joint. See Hooke/Universal Joint Tool.Complex joints indirectly connect parts by coupling simple joints. They include:•Gears. See Gear Joint Tool.•Couplers. See Coupler Joint Tool.You access the joints through the Joint Palette and Joint and Motion Tool Stacks.Creating Idealized JointsThe following procedure explains how to create a simple idealized joint. You can select to attach the joint to parts or spline curves. If you select to attach the joint to a curve, Adams/View creates a curve marker,Adams/View2Jointsand the joint follows the line of the curve. Learn more about curve markers with Marker Modify dialogbox help. Attaching the joint to a spline curve is only available with Adams/Solver (C++). L earn aboutswitching solvers with Solver Settings - Executable dialog box help.Note that this procedure only sets the location and orientation of the joint. If you want to set the frictionof a joint, change the pitch of a screw joint, or set initial conditions for joints, modify the joint.To create a simple idealized joint:1.From the Joint palette or tool stack, select the joint tool representing the idealized joint that youwant to create.2.In the settings container, specify how you want to define the bodies the joint connects. You canselect:• 1 Location (Bodies Implicit)• 2 Bodies - 1 Location• 2 Bodies - 2 LocationsFor more on the effects of these options, see the help for the joint tool you are creating andConnecting Constraints to Parts.3.In the settings container, specify how you want the joint oriented. You can select:•Normal to Grid - Lets you orient the joint along the current Working grid, if it is displayed, or normal to the screen.•Pick Geometry Feature - Lets you orient the joint along a direction vector on a feature in your model, such as the face of a part.4.If you selected to explicitly define the bodies by selecting 2 Bodies - 1 Location or 2 Bodies - 2Locations in Step 2, in the settings container, set First Body and Second Body to how you wantto attach the joint: on the bodies of parts, between a part and a spline curve, or between two splinecurves.ing the left mouse button, select the first part or a spline curve (splines and data element curvesare all considered curves). If you selected to explicitly select the parts to be connected, select thesecond part or another curve using the left mouse button.6.Place the cursor where you want the joint to be located (for a curve this is referred to as its curvepoint), and click the left mouse button. If you selected to specify its location on each part or curve,place the cursor on the second location, and click the left mouse button.7.If you selected to orient the joint along a direction vector on a feature, move the cursor around inyour model to display an arrow representing the direction along a feature where you want the jointoriented. When the direction vector represents the correct orientation, click the left mouse button.Modifying Basic Properties of Idealized JointsYou can change several basic properties about an Idealized joints. These include:•Parts that the joint connects. You can also switch which part moves relative to another part.3Joints •What type of joint it is. For example, you can change a revolute joint to a translational joint. Thefollowing are exceptions to changing a joint's type:•You can only change a simple idealized joint to another type of simple idealized joint or to a joint primitive.•You cannot change a joint's type if motion is applied to the joint. In addition, if a joint has friction and you change the joint type, Adams/View displays an error.•Whether or not forces that are applied to the parts connected by the joint appear graphically on the screen during an animation. Learn about Setting Up Force Graphics.•For a screw joint, you can also set the pitch of the threads of the screw (translational displacement for every full rotational cycle). Learn about screw joints.To change basic properties for a joint:1.Display the Modify Joint dialog box as explained in Accessing Modify Dialog Boxes.2.If desired, in the First Body and Second Body text boxes, change the parts that the joint connects.The part that you enter as the first body moves relative to the part you enter as the second body.3.Set Type to the type of joint to which you want to change the current joint.4.Select whether you want to display force graphics for one of the parts that the joint connects.5.For a screw joint, enter its pitch value (translational displacement for every full rotational cycle).6.Select OK.About Initial Conditions for JointsYou can specify initial conditions for revolute, translational, and cylindrical joints. Adams/View uses the initial conditions during an Initial conditions simulation, which it runs before it runs a simulation of your model.You can specify the following initial conditions for revolute, translational, and cylindrical joints:•Translational or rotational displacements that define the translation of the location of the joint on the first part (I marker) with respect to its location on the second part (J marker) in units oflength. You can set translational displacement on a translational and cylindrical joint and you can set rotational displacements on a revolute and cylindrical joint.Adams/View measures the translational displacement at the origin of the I marker along thecommon z-axis of the I and J markers and with respect to the J marker. It measures the rotational displacement of the x-axis of the I marker about the common z-axis of the I and J markers with respect to the x-axis of the J marker.•Translational or rotational velocity that define the velocity of the location of the joint on the first part (I marker) with respect to its location on the second part (J marker) in units of length per unit of time.Adams/View Joints 4Adams/View measures the translational velocity of the I marker along the common z-axis of I and J and with respect to the J marker. It measures the rotational velocity of the x-axis of the I marker about the common z-axis of the I and J markers with respect to the x-axis of the J marker.If you specify initial conditions, Adams/View uses them as the initial velocity of the joint during an assemble model operation regardless of any other forces acting on the joint. You can also leave some or all of the initial conditions unset. Leaving an initial condition unset lets Adams/View calculate the conditions of the part during an assemble model operation depending on the other forces acting on the joint. Note that it is not the same as setting an initial condition to zero. Setting an initial condition to zero means that the joint will not be moving in the specified direction or will not be displaced when the model is assembled, regardless of any forces acting on it.If you impose initial conditions on the joint that are inconsistent with those on a part that the joint connects, the initial conditions on the joint have precedence over those on the part. If, however, you impose initial conditions on the joint that are inconsistent with imparted motions on the joint, the initial conditions as specified by the motion generator take precedence over those on the joint.Setting Initial ConditionsTo modify initial conditions:1.Display the Modify Joint dialog box as explained in Accessing Modify Dialog Boxes .2.Select Initial Conditions .The Joint Initial Conditions dialog box appears. Some options in the Joint Initial Conditions dialog box are not available (ghosted) depending on the type of joint for which you are setting initial conditions.3.Set the translational or rotational displacement or velocity, and then select OK .Imposing Point Motion on a JointYou can impose a motion on any of the axes (DOF) of the idealized joint that are free to move. For example, for a translational joint , you can apply translational motion along the z-axis. Learn more About Point Motion .Note:If the initial rotational displacement of a revolute or cylindrical joint varies by anywherefrom 5 to 60 degrees from the actual location of the joint, Adams/Solver issues a warningmessage and continues execution. If the variation is greater than 60 degrees, Adams/Viewissues an error message and stops execution.Note:For translational, revolute , and cylindrical joints, you might find it easier to use the jointmotion tools to impose motion. Learn about Creating Point Motions Using the Motion Tools .5JointsTo impose motion on a joint:1.Display the Modify Joint dialog box as explained in Accessing Modify Dialog Boxes.2.Select Impose Motion.The Impose Motion(s) dialog box appears. Some options in the Impose Motion dialog box are not available (ghosted) depending on the type of joint on which you are imposing motion.3.Enter a name for the motion. Adams/View assigns a default name to the motion.4.Enter the values for the motion as explained in Options for Point Motion Dialog Box, and thenselect OK.Adding Friction to Idealized JointsYou can model both static (Coulomb) and dynamic (viscous) friction in revolute, translational, cylindrical, hooke/universal, and spherical joints.Note:Using Adams/Solver (C++), you can apply joint friction to joints if they are attached to flexible bodies; using Adams/Solver (FORTRAN), you cannot. In addition, Adams/Solver(C++) does not support point masses.For a summary of which joints and forces are supported on flexible bodies, see Table ofSupported Forces and Joints in the Adams/Flex online help. Also refer to the Adams/Flexonline help for more information on attaching joints and forces to flexible bodies.To add friction to a joint:1.Display the Modify Joint dialog box as explained in Accessing Modify Dialog Boxes.2.Select the Friction tool .The Create/Modify Friction dialog box appears. The options in the dialog box change depending on the type of joint for which you are adding friction.3.Enter the values in the dialog box for the type of joint as explained below, and then select OK.•Cylindrical Joint Options•Revolute Joint Options•Spherical Joint Options•Translational Joint Options•Universal/Hooke Joint OptionsAdams/View6JointsFriction Regime Determination (FRD)Three friction regimes are allowed in Adams/View:diagram of the friction regimes available in Adams/Solver.7JointsConventions in Friction Block DiagramsThe following tables identify conventions used in the block diagrams:•Legend for Block Diagrams identifies symbols in the diagrams.•Relationship Between the Inputs Option and Switches Used in the Block Diagrams describes the relationship between the Input Forces to Friction option in the Create/Modify Friction dialog box and the switches used in the block diagrams.Legend for Block DiagramsRelationship Between the Inputs Option and Switches Used in the Block DiagramsCylindrical Joint frictionJoint reaction (F) and reaction torque (Tm) combined with force preload (Fprfrc) and torque preload (Tprfrc) yield the frictional force and torque in a cylindrical joint. As the block diagram indicates, you can turn off one or more of these force effects using switches SW1 through SW3. The frictional force inSymbol:Description: Scalar quantityVector quantitySumming junction:c=a+bMultiplication junction:c=axbMAGMagnitude of a vector quantity ABSAbsolute value of a scalar quantity FRD Friction regime determinationSwitch:Inputs are: Symbol: Acceptable values:SW1Preload Fprfrc or Tprfc On or offSW2Reaction force f or F On or off SW3Bending moment Tr On or off SW4 Torsional moment Tn On or off All or None sets all applicable switches On or off, respectivelyAdams/View8Jointsa cylindrical joint acts at the mating surfaces of the joint. The FRD block determines the direction of thefrictional force. Based on the frictional coefficient direction, the surface frictional force is broken downinto an equivalent frictional torque and frictional force acting along the common axis of translation androtation.9JointsCylindrical Joint OptionsFor the option: Do the following:Mu Static Define the coefficient of static friction in the joint. The magnitude of thefrictional force is the product of Mu Static and the magnitude of the normalforce in the joint, for example:Friction Force Magnitude, F = µNwhere µ = Mu Static and N = normal forceThe static frictional force acts to oppose the net force or torque along theDegrees of freedom of the joint.The range is > 0.Mu Dynamic Define the coefficient of dynamic friction. The magnitude of the frictionalforce is the product of Mu Dynamic and the magnitude of the normal forcein the joint, for example:Friction force magnitude, F = µNwhere µ = Mu Dynamic and N = normal forceThe dynamic frictional force acts in the opposite direction of the velocityof the joint.The range is > 0.Initial Overlap Defines the initial overlap of the sliding parts in either a translational orcylindrical joint. The joint's bending moment is divided by the overlap tocompute the bending moment's contribution to frictional forces.The default is 1000.0, and the range is Initial Overlap > 0.Adams/View Joints 10Overlap To define friction in a cylindrical joint, Adams/Solver computes the overlapof the joint. As the joint slides, the overlap can increase, decrease, or remainconstant. You can set:•Increase indicates that overlap increases as the I marker translates in the positive direction along the J marker; the slider moves to be within thejoint.•Decrease indicates that the overlap decreases with positive translationof the joint; the slider moves outside of the joint.•Remain Constant indicates that the amount of overlap does not changeas the joint slides; all of the slider remains within the joint.The default is Remain Constant.Pin Radius Defines the radius of the pin for a cylindrical joint.The default is 1.0, and the range is > 0.Stiction TransitionVelocity Define the absolute velocity threshold for the transition from dynamic friction to static friction. If the absolute relative velocity of the joint markeris below the value, then static friction or stiction acts to make the joint stick.The default is 0.1 length units/unit time on the surface of contact in thejoint, and the range is > 0.Max StictionDeformation Define the maximum displacement that can occur in a joint once the frictional force in the joint enters the stiction regime. The slightdeformation allows Adams/Solver to easily impose the Coulombconditions for stiction or static friction, for example:Friction force magnitude < static * normal forceTherefore, even at zero velocity, you can apply a finite stiction force if yoursystem dynamics require it.The default is 0.01 length units, and the range is > 0.Friction Force Preload Define the joint's preload frictional force, which is usually caused bymechanical interference in the assembly of the joint.Default is 0.0, and the range is > 0.Friction Torque Preload Define the preload friction torque in the joint, which is usually caused bymechanical interference in the assembly of the joint.The default is 0.0, and the Range is > 0.For the option:Do the following: 搭接接头丠丠JointsFor the option: Do the following:Effect Define the frictional effects included in the friction model, either Stictionand Sliding, Stiction, or Sliding. Stiction is static-friction effect, whileSliding is dynamic-friction effect. Excluding stiction in simulations thatdon't require it can greatly improve simulation speed. The default isStiction and Sliding.Input Forces to Friction Define the input forces to the friction model. By default, all user-definedpreloads and joint-reaction force and moments are included. You cancustomize the friction-force model by limiting the input forces you specify.The inputs for a translational joint are:•Preload•Reaction Force•Bending MomentFriction Inactive During Specify whether or not the frictional forces are to be calculated during aStatic equilibrium or Quasi-static simulation.Revolute Joint FrictionJoint reactions (Fa and Fr), bending moment (Tr), and torque preload (Tprfrc) determine the frictional torque in a revolute joint. You can turn off one or more of these force effects using switches SW1 through SW3. The joint reactions (Fa and Fr) are converted into equivalent torques using the respective friction arm (Rn) and pin radius (Rp). The joint bending moment (Tr) is converted into an equivalent torque usingpin radius (Rp) divided by bending reaction arm (Rb). The frictional torque (Tfrict) is applied along the axis of rotation in the direction that the FRD block computes.Joints Revolute Joint OptionsFor the option: Do the following:Mu Static Define the coefficient of static friction in the joint. The magnitude of thefrictional force is the product of Mu Static and the magnitude of the normalforce in the joint, for example:Friction Force Magnitude, F = µNwhere µ = Mu Static and N = normal forceThe static frictional force acts to oppose the net force or torque along theDegrees of freedom of the joint.The range is > 0.Mu Dynamic Define the coefficient of dynamic friction. The magnitude of the frictionalforce is the product of Mu Dynamic and the magnitude of the normal forcein the joint, for example:Friction force magnitude, F = µNwhere µ = Mu Dynamic and N = normal forceThe dynamic frictional force acts in the opposite direction of the velocityof the joint.The range is > 0.Friction Arm Define the effective moment arm used to compute the axial component ofthe friction torque. The default is 1.0, and the range is > 0.Bending Reaction Arm Define the effective moment arm use to compute the contribution of thebending moment on the net friction torque in the revolute joint. The defaultis 1.0, and the range is > 0.Pin Radius Defines the radius of the pin.The default is 1.0, and the range is > 0.Stiction Transition Velocity Define the absolute velocity threshold for the transition from dynamic friction to static friction. If the absolute relative velocity of the joint marker is below the value, then static friction or stiction acts to make the joint stick. The default is 0.1 length units/unit time on the surface of contact in the joint, and the range is > 0.Max Stiction Deformation Define the maximum displacement that can occur in a joint once the frictional force in the joint enters the stiction regime. The slight deformation allows Adams/Solver to easily impose the Coulomb conditions for stiction or static friction, for example:Friction force magnitude < static * normal forceTherefore, even at zero velocity, you can apply a finite stiction force if your system dynamics require it.The default is 0.01 length units, and the range is > 0.Friction Torque Preload Define the preload friction torque in the joint, which is usually caused bymechanical interference in the assembly of the joint.The default is 0.0, and the Range is > 0.Effect Define the frictional effects included in the friction model, either Stictionand Sliding, Stiction, or Sliding. Stiction is static-friction effect, whileSliding is dynamic-friction effect. Excluding stiction in simulations thatdon't require it can greatly improve simulation speed. The default isStiction and Sliding.Input Forces to Friction Define the input forces to the friction model. By default, all user-definedpreloads and joint-reaction force and moments are included. You cancustomize the friction-force model by limiting the input forces you specify.The inputs for a translational joint are:•Preload•Reaction Force•Bending MomentFriction Inactive During Specify whether or not the frictional forces are to be calculated during aStatic equilibrium or Quasi-static simulation.For the option: Do the following:JointsSpherical Joint FrictionThe reaction force (F) and the preload frictional torque (Tprfrc) are the two forcing effects used in computing the frictional torque on a Spherical joint. The ball radius is used to compute an equivalent frictional torque. The FRD block determines the direction of the frictional torque.Spherical Joint OptionsFor the option: Do the following:Mu Static Define the coefficient of static friction in the joint. The magnitude of thefrictional force is the product of Mu Static and the magnitude of the normalforce in the joint, for example:Friction Force Magnitude, F = µNwhere µ = Mu Static and N = normal forceThe static frictional force acts to oppose the net force or torque along theDegrees of freedom of the joint.The range is > 0.Mu Dynamic Define the coefficient of dynamic friction. The magnitude of the frictionalforce is the product of Mu Dynamic and the magnitude of the normal forcein the joint, for example:Friction force magnitude, F = µNwhere µ = Mu Dynamic and N = normal forceThe dynamic frictional force acts in the opposite direction of the velocityof the joint.The range is > 0.Ball Radius Defines the radius of the ball in a spherical joint for use in friction-force andtorque calculations.The default is 1.0, and the range is > 0.Stiction Transition Velocity Define the absolute velocity threshold for the transition from dynamic friction to static friction. If the absolute relative velocity of the joint marker is below the value, then static friction or stiction acts to make the joint stick. The default is 0.1 length units/unit time on the surface of contact in the joint, and the range is > 0.JointsTranslational Joint FrictionJoint reaction force (F), bending moment (Tm), torsional moment (Tn), and force preload (Fprfrc) are used to compute the frictional force in a translational joint. You can individually turn off the force effects using switches SW1 through SW4.Max StictionDeformation Define the maximum displacement that can occur in a joint once the frictional force in the joint enters the stiction regime. The slightdeformation allows Adams/Solver to easily impose the Coulombconditions for stiction or static friction, for example:Friction force magnitude < static * normal forceTherefore, even at zero velocity, you can apply a finite stiction force if yoursystem dynamics require it.The default is 0.01 length units, and the range is > 0.Friction Torque Preload Define the preload friction torque in the joint, which is usually caused bymechanical interference in the assembly of the joint.The default is 0.0, and the Range is > 0.Effect Define the frictional effects included in the friction model, either Stictionand Sliding, Stiction, or Sliding. Stiction is static-friction effect, whileSliding is dynamic-friction effect. Excluding stiction in simulations thatdon't require it can greatly improve simulation speed. The default isStiction and Sliding.Input Forces to FrictionDefine the input forces to the friction model. By default, all user-definedpreloads and joint-reaction force and moments are included. You cancustomize the friction-force model by limiting the input forces you specify.The inputs for a translational joint are:•Preload•Reaction Force Friction Inactive During Specify whether or not the frictional forces are to be calculated during aStatic equilibrium or Quasi-static simulation .For the option:Do the following:The bending moment (Tm) is converted into an equivalent force using the Xs block. Similarly, torsional moment is converted into an equivalent joint force using the friction arm (Rn). Frictional force (Ffrict) is applied along the axis of translation in the direction that the FRD block computes.Joints Translational Joint OptionsFor the option: Do the following:Mu Static Define the coefficient of static friction in the joint. The magnitude of thefrictional force is the product of Mu Static and the magnitude of the normalforce in the joint, for example:Friction Force Magnitude, F = µNwhere µ = Mu Static and N = normal forceThe static frictional force acts to oppose the net force or torque along theDegrees of freedom of the joint.The range is > 0.Mu Dynamic Define the coefficient of dynamic friction. The magnitude of the frictionalforce is the product of Mu Dynamic and the magnitude of the normal forcein the joint, for example:Friction force magnitude, F = µNwhere µ = Mu Dynamic and N = normal forceThe dynamic frictional force acts in the opposite direction of the velocityof the joint.The range is > 0.Reaction Arm Define the effective moment arm of the joint-reaction torque about thetranslational joint's axial axis (the z-direction of the joint's J marker). Thisvalue is used to compute the contribution of the torsional moment to the netfrictional force.The default is 1.0, and the range is > 0.Initial Overlap Defines the initial overlap of the sliding parts in either a translational orcylindrical joint. The joint's bending moment is divided by the overlap tocompute the bending moment's contribution to frictional forces.The default is 1000.0, and the range is Initial Overlap > 0.Overlap To define friction in a cylindrical joint, Adams/Solver computes the overlapof the joint. As the joint slides, the overlap can increase, decrease, or remainconstant. You can set:•Increase indicates that overlap increases as the I marker translates in thepositive direction along the J marker; the slider moves to be within thejoint.•Decrease indicates that the overlap decreases with positive translationof the joint; the slider moves outside of the joint.•Remain Constant indicates that the amount of overlap does not changeas the joint slides; all of the slider remains within the joint.The default is Remain Constant.Stiction Transition Velocity Define the absolute velocity threshold for the transition from dynamic friction to static friction. If the absolute relative velocity of the joint marker is below the value, then static friction or stiction acts to make the joint stick. The default is 0.1 length units/unit time on the surface of contact in the joint, and the range is > 0.Max Stiction Deformation Define the maximum displacement that can occur in a joint once the frictional force in the joint enters the stiction regime. The slight deformation allows Adams/Solver to easily impose the Coulomb conditions for stiction or static friction, for example:Friction force magnitude < static * normal forceTherefore, even at zero velocity, you can apply a finite stiction force if your system dynamics require it.The default is 0.01 length units, and the range is > 0.Friction Force Preload Define the joint's preload frictional force, which is usually caused bymechanical interference in the assembly of the joint.Default is 0.0, and the range is > 0.Effect Define the frictional effects included in the friction model, either Stictionand Sliding, Stiction, or Sliding. Stiction is static-friction effect, whileSliding is dynamic-friction effect. Excluding stiction in simulations thatdon't require it can greatly improve simulation speed. The default isStiction and Sliding.For the option: Do the following:。