罗尔定理与拉格朗日中值定理

拉格朗日中值定理与罗尔定理的理解
首先说明拉格朗日中值定理与罗尔定理的关系：罗尔定理可理解为特殊形式的拉格朗日中值定理，即f （a ）=f （b ），而拉格朗日中值定理中二者并不一定相等。

因此，证明拉格朗日中值定理后，罗尔定理也得以证明。

下面我将先对拉格朗日中值定理进行证明。

)(x f 满足：
设函数o a b a f a f a b n n +-++=-⇒-1)())((n 1......)(')()()(！即
)('))((n 1......))((''21)('111)(ξf o a b a f a b a f a f n n =+-++-+-！！！①
到此，我们知道了f’(ξ)用泰勒展开式表示时的大小，即证明了f’(ξ)在泰勒展开式中值的存在。

那么ξ是否在（a ，b ）区间内？我们知道泰勒公式的意义是利用已知点的函数值不断逼近所求点的函数值，所以只需知道在由a 点向b 点逼近的过程中是否遇到了ξ点，即ξ
点与b 点间是否存在余项。

用泰勒公式求解:
o x x x f x x x f x f x f n n +-++-+=-100)(000))((1)-(n 1......))((''11)('01)('！！！②将x=b ,x 0=a 代入上式，得：
o a b a f a b a f a f b f n n +-++-+=
-1)())((1)-(n 1......))((''11)('01)('！！！③
)1()3(-得：。

费马极值引理，罗尔中值定理，拉格朗⽇中值定理，柯西中值定理微分三⼤中值定理，罗尔中值定理，拉格朗⽇（Lagrange）中值定理、柯西（Cauchy）中值定理。

我对拉格朗⽇中值定理的构造函数的构造思路，进⾏了⾃⼰的猜测，⽹上没有找到类似的猜测和研究下⾯的费马定理可以看做是三⼤中值定理的引理费马定理(fermat):设f(x)在其极值点x0处可导，则f′(x0)=0*以下证明的前提，都是在(a,b)上可导，⽽不是[a,b]上可导，原因在于端点a,b两侧，[a,b]之外，未必可导，甚⾄未必有定义。

a,b的左右导数，未必等于另⼀侧导数。

即，a点左导数，不⼀定等于a点右导数*拉格朗⽇中值定理，是罗尔中值定理的推⼴，罗尔中值定理是拉格朗⽇中值定理的⼀个特例，即函数在定义域内两端点函数值相等的特例。

柯西中值定理，是拉格朗⽇中值定理的⼀个特例，即，g(x)=x,结论就变成了拉格朗⽇中值定理。

证明：因为f(x)在x0点位极值点，故∃x0的邻域U(x0,δ)，∀x∈U，有f(0)⩾f(x)在x0点的左右极限如下左极限为limδ→0f(x0)−f(x0−δ)δ⩾0右极限为limδ→0f(x0+δ)−f(x0)δ⩽0因为f(x)在x0可导，所以左极限与右极限相等，故0⩽limδ→0f(x0)−f(x0−δ)δ=f′(x0)=limδ→0f(x0+δ)−f(x0)δ⩾0可得f′(x0)=0罗尔中值定理(Rolle)设函数f在[a,b]上连续，在(a,b)内可导，且f(a)=f(b),那么⾄少存在⼀证明：因为函数 f(x) 在闭区间[a,b] 上连续，所以存在最⼤值与最⼩值，分别⽤ M 和 m 表⽰，分两种情况讨论：2. 若 M>m，则因为 f(a)=f(b) 使得最⼤值 M 与最⼩值 m ⾄少有⼀个在 (a,b) 内某点ξ处取得，从⽽ξ是f(x)的极值点，⼜条件 f(x) 在开区间 (a,b) 内可导得，f(x) 在ξ处取得极值，由费马引理，可导f'(ξ)=0。

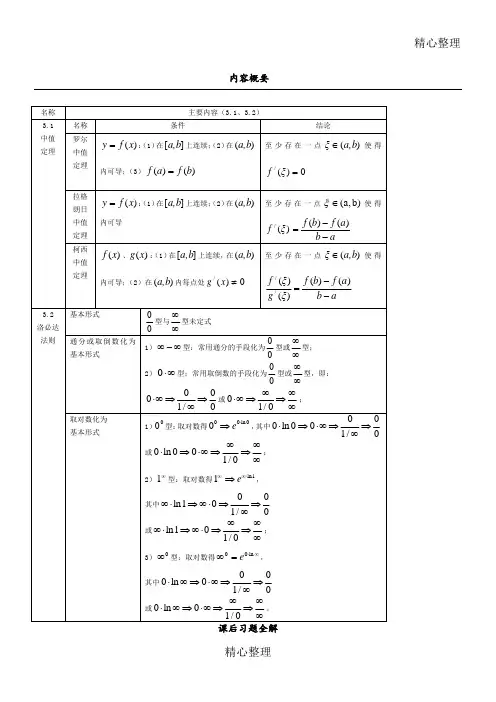
内容概要课后习题全解习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值ξ。

（1）]511[32)(2.,,x x x f ---=；（2）]30[3)(,,x x x f -=。

知识点：罗尔中值定理。

思路：根据罗尔定理的条件和结论，求解方程0)(/=ξf ，得到的根ξ便为所求。

解：（1）∵32)(2--=x x x f 在]511[.,-上连续，在)5.1,1(-内可导，且0)51()1(==-.f f ，∴32)(2--=x x x f 在]511[.,-上满足罗尔定理的条件。

令()410f ξξ'=-=得)511(41.,ξ-∈=即为所求。

（2）∵x x x f -=3)(在]30[,上连续，在)30(,内可导，且0)3()0(==f f ， ∴xx x f -=3)(在]30[,上满足罗尔定理的条件。

令()0f ξ'==，得)30(2,ξ∈=即为所求。

★2.验证拉格朗日中值定理对函数25423-+-=x x x y 在区间]10[,上的正确性。

知识点：拉格朗日中值定理。

思路：根据拉格朗日中值定理的条件和结论，求解方程(1)(0)()10f f f ξ-'=-，若得到的根]10[,ξ∈则可验证定理的正确性。

解：∵32()452y f x x x x ==-+-在]10[,连续，在)10(,内可导，∴25423-+-=x x x y 在区间]10[,上满足拉格朗日中值定理的条件。

又2)0(2)1(-=-=,f f ，2()12101f x x x '=-+，∴要使(1)(0)()010f f f ξ-'==-，只要：5(01)12,ξ=，∴5(01)12,ξ∃=∈，使(1)(0)()10f f f ξ-'=-，验证完毕。

★3.已知函数4)(x x f =在区间]21[,上满足拉格朗日中值定理的条件，试求满足定理的ξ。

罗尔中值定理与拉格朗日中值定理引言：在微积分中，有两个非常重要的定理——罗尔中值定理和拉格朗日中值定理。

它们在分析函数的性质和证明一些数学问题中起着重要的作用。

在本文中，我们将详细介绍这两个定理的概念、条件和应用。

一、罗尔中值定理（Rolle's Theorem）：罗尔中值定理是微积分中的一条基本定理，它首次由法国数学家米歇尔·罗尔于1691年提出。

该定理是一个关于导数连续函数的性质的陈述，下面是它的准确表述：定理：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导。

如果f(a) = f(b)，那么在(a, b)内至少存在一个点c，使得f'(c) = 0。

简单来说，罗尔中值定理告诉我们，如果一个函数在闭区间的端点取得相同的函数值，并且在开区间内可导，那么在这个开区间内一定存在一个点，该点的导数为零。

举例：设函数f(x) = x^3 - x^2 - x + 1，该函数在闭区间[0, 1]上连续，在开区间(0, 1)内可导。

计算f(x)在开区间(0, 1)内的某个零点。

根据罗尔中值定理，我们可以先验证f(x)在闭区间[0, 1]上的连续性，然后计算f(a)和f(b)的值，如果相等，那么就可以利用该定理证明在开区间内存在某个点c，使得f'(c) = 0。

二、拉格朗日中值定理（Lagrange's Mean Value Theorem）：与罗尔中值定理类似，拉格朗日中值定理也是微积分中的重要定理，其命名来自于法国数学家约瑟夫·拉格朗日。

下面是拉格朗日中值定理的准确表述：定理：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导。

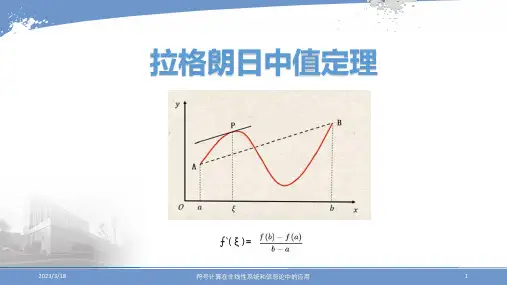
那么在(a, b)内存在一个点c，使得f(b) - f(a) = f'(c) * (b - a)。

简单来说，拉格朗日中值定理告诉我们，如果一个函数在闭区间上连续且在开区间内可导，那么在该开区间内一定存在一个点，使得函数在两个端点间的变化率等于此点的导数。

罗尔定理与拉格朗日中值定理解读罗尔定理和拉格朗日中值定理是微积分中重要的基本定理，它们在求解函数的性质和应用中起着重要的作用。

本文将对这两个定理进行解读，并探讨其应用。

一、罗尔定理的解读罗尔定理是微积分中的一个基本定理，它是拉格朗日中值定理的特例。

罗尔定理的表述如下：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，且满足f(a)=f(b)，则存在一个点c∈(a, b)，使得f'(c)=0。

罗尔定理的证明思路是通过利用连续函数在闭区间上取得最大值和最小值的性质，结合导数的定义，找到一个点c使得f'(c)=0。

这个定理的意义在于，当一个函数在两个端点的函数值相等时，必然存在一个点使得其导数为零。

罗尔定理的应用非常广泛，例如在求解方程的根、证明函数的性质等问题中都可以使用罗尔定理。

通过罗尔定理，我们可以将一个复杂的问题转化为求解导数为零的方程，简化了问题的求解过程。

二、拉格朗日中值定理的解读拉格朗日中值定理是微积分中的另一个重要定理，它是基于罗尔定理而推广得到的。

拉格朗日中值定理的表述如下：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，则存在一个点c∈(a, b)，使得f'(c)=\frac{f(b)-f(a)}{b-a}。

拉格朗日中值定理的证明思路是通过构造辅助函数g(x)=f(x)-kx，其中k为常数，使得g(a)=g(b)，然后利用罗尔定理找到一个点c使得g'(c)=0。

由于g'(c)=f'(c)-k，因此可以得到f'(c)=k，进而得到f'(c)=\frac{f(b)-f(a)}{b-a}。

拉格朗日中值定理的应用也非常广泛，例如在求解函数的极值、证明函数的性质等问题中都可以使用拉格朗日中值定理。

通过拉格朗日中值定理，我们可以将一个函数在一个闭区间上的平均变化率与其导数联系起来，从而研究函数的变化趋势。

精心整理内容概要习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值ξ。

（1）]511[32)(2.,,x x x f ---=；（2）]30[3)(,,x x x f -=。

知识点：罗尔中值定理。

思路：根据罗尔定理的条件和结论，求解方程0)(/=ξf ，得到的根ξ便为所求。

解：)5.即为所（2∴f (f '★2.思路 解∴5(01)12,ξ±∃=，使(1)(0)()10f f f ξ-'=-，验证完毕。

★3.已知函数4)(x x f =在区间]21[,上满足拉格朗日中值定理的条件，试求满足定理的ξ。

解：要使(2)(1)()21f f f ξ-'=-，只要3415ξξ=⇒=(12)ξ,=即为满足定理的ξ。

★★4.试证明对函数r qx px y ++=2应用拉格朗日中值定理时所求得的点ξ总是位于区间的正中间。

证明：不妨设所讨论的区间为][a,b ，则函数r qx px y ++=2在][a,b 上连续，在)(a,b 内可导，从而有()()()f b f a f ξb a-'=-，即a b r qa pa r qb pb q ξ-++-++=+)()(222， 解得2ab ξ+=，结论成立。

★5.函数3)(x x f =与1)(2+=x x g 在区间]21[,上是否满足柯西定理的所有条件？如满足，请求出满足定理的数值ξ。

知识点：柯西中值定理。

思路解，所以满★★★6.存在ξ思路，然后再证明)0(F ()()()0F ξf ξξf ξ''=+=，即()()f ξf ξξ'=-。

注：辅助函数的构造方法一般可通过结论倒推，如：要使()()f x f x x'=-，只要 ∴只要设辅助函数)()(x xf x F =★★7.若函数)(x f 在)(a,b 内具有二阶导函数，且)()()(321x f x f x f ==)(321b x x x a <<<<，证明：在)(31,x x 内至少有一点ξ，使得()0f ξ''=。

微积分中的罗尔定理与拉格朗日中值定理微积分是数学中的一门重要学科，其中的罗尔定理和拉格朗日中值定理是两个基本定理，它们在求解函数的性质和证明其他定理时起到了至关重要的作用。

本文将详细介绍罗尔定理和拉格朗日中值定理的概念、原理和应用。

一、罗尔定理罗尔定理是微积分中的一个基本定理，它是导数与函数零点之间关系的一个重要联系。

罗尔定理的核心思想是：如果一个函数在某个区间两个端点处取得相同的函数值，并且在这个区间内是连续可导的，那么在这个区间内一定存在一个点，使得该点的导数等于零。

具体地，设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，并且f(a) = f(b)，那么在(a, b)内至少存在一个点c，使得f'(c) = 0。

罗尔定理的证明思路是通过构造一个辅助函数g(x)，使得g(x)满足罗尔定理的条件，然后利用导数的中值定理得到g'(c) = 0，进而推导出f'(c) = 0。

罗尔定理在实际应用中常用于证明函数的零点存在以及函数的极值点。

二、拉格朗日中值定理拉格朗日中值定理是微积分中的另一个基本定理，它是导数与函数增减性之间的一个重要联系。

拉格朗日中值定理的核心思想是：如果一个函数在某个区间内连续，并且在这个区间内可导，那么在这个区间内一定存在一个点，使得该点的导数等于函数在这个区间内的平均变化率。

具体地，设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)内可导，那么在(a, b)内至少存在一个点c，使得f'(c) = (f(b) - f(a))/(b - a)。

拉格朗日中值定理的证明思路是通过构造一个辅助函数g(x)，使得g(x)满足拉格朗日中值定理的条件，然后利用导数的介值性质得到g'(c) = (g(b) - g(a))/(b - a)，进而推导出f'(c) = (f(b) - f(a))/(b - a)。

拉格朗日中值定理在实际应用中常用于证明函数的性质和推导其他定理。

第三章 微分中值定理与导数的应用第一节 微分中值定理一、罗尔定理 1、 费马定理：设)()(0f D x U ⊂,)()(0x f x f ≤[或)()(0x f x f ≥],)(0x U x ∈，若)()(0x D x f ∈，则0)(0='x f .证明：由于0)()(0≤-x f x f ,)(0x U x ∈，那么0)()(lim )(0000≥--='-→x x x f x f x f x x ,(因00<-x x )0)()(lim )(0000≥--='+→x x x f x f x f x x ,(因00>-x x ) , 所以 0)(0='x f .2、罗尔定理：设],[)(b a C x f ∈,),()(b a D x f ∈,且)()(b f a f =，则),(b a ∈∃ξ,..t s 0)(='ξf . 证明：因],[)(b a C x f ∈,],[,b a x x M m ∈∃，..t s)}({min )(x f x f m bx a m ≤≤==, )}({max )(x f x f M bx a M ≤≤==.(1) 当M m =时,则],[,)(b a x M x f ∈≡,那么),(,0)(b a x x f ∈≡'.取 ),(2b a ba ∈+=ξ，有0)(='ξf . (2) 当M m <时, 因)()(b f a f =,),()(b a D x f ∈,① 若M a f <)(,有),(b a x M ∈, 取M x =ξ； ② 若M a f =)(,有),(b a x m ∈, 取m x =ξ；因),(b a ∈ξ,)()(ξD x f ∈,由费马定理知：0)(='ξf .3、几何意义x yO)(x f y =ξyC)(x f y =A Ba OxξyC)(x f y =A Ba Oxb曲线)(x f y =在两个端点等高，则曲线内必有一水平切线。

课后习题全解习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件如满足，请求出满足定理的数值ξ。

（1）]511[32)(2.,,x x x f ---=；（2）]30[3)(,,x x x f -=。

知识点：罗尔中值定理。

思路：根据罗尔定理的条件和结论，求解方程0)(/=ξf ，得到的根ξ便为所求。

解：（1）∵32)(2--=x x x f 在]511[.,-上连续，在)5.1,1(-内可导，且0)51()1(==-.f f ，∴32)(2--=x x x f 在]511[.,-上满足罗尔定理的条件。

令()410f ξξ'=-=得)511(41.,ξ-∈=即为所求。

（2）∵x x x f -=3)(在]30[,上连续，在)30(,内可导，且0)3()0(==f f ，∴xx x f -=3)(在]30[,上满足罗尔定理的条件。

令()0f ξ'==，得)30(2,ξ∈=即为所求。

★2.验证拉格朗日中值定理对函数25423-+-=x x x y 在区间]10[,上的正确性。

知识点：拉格朗日中值定理。

思路：根据拉格朗日中值定理的条件和结论，求解方程(1)(0)()10f f f ξ-'=-，若得到的根]10[,ξ∈则可验证定理的正确性。

解：∵32()452y f x x x x ==-+-在]10[,连续，在)10(,内可导，∴25423-+-=x x x y 在区间]10[,上满足拉格朗日中值定理的条件。

又2)0(2)1(-=-=,f f ，2()12101f x x x '=-+，∴要使(1)(0)()010f f f ξ-'==-，只要：(01),ξ=，∴5(01)12,ξ∃=∈，使(1)(0)()10f f f ξ-'=-，验证完毕。

★3.已知函数4)(x x f =在区间]21[,上满足拉格朗日中值定理的条件，试求满足定理的ξ。

解：要使(2)(1)()21f f f ξ-'=-，只要3415ξξ=⇒=从而(12)ξ,=即为满足定理的ξ。

罗尔中值定理和拉格朗日中值定理罗尔中值定理和拉格朗日中值定理是非常有用的数学定理，一般用于证明某些数学结论。

罗尔中值定理和拉格朗日中值定理都是几何学的重要组成部分，具有广泛的应用前景。

本文将从数学历史的角度研究这两个定理的演变，并介绍它们的使用以及它们在数学理论中的作用。

罗尔中值定理（Rolle Theorem）是由法国数学家保罗罗尔（Pierre de Fermat）在17世纪发现的。

罗尔中值定理的定义是：设函数y=f（x）在[a,b]上具有连续的导数，并且在边界点a处取值为f（a），在边界点b处取值为f（b），那么在[a,b]之间存在一个c，使得f（c）=0。

也就是说，一个连续函数在[a,b]范围内至少产生一次零点。

拉格朗日中值定理（Lagrange Mean Value Theorem）又被称为拉格朗日定理或拉格朗日中值定理，是法国数学家Joseph Louis Lagrange在1797年发现的。

这一定理明确说明：若函数y=f（x）在[a,b]上具有连续的二阶导数，则存在c∈（a,b），使得f （c）=[f（b）-f（a）] / [b-a]也就是说，拉格朗日中值定理认为函数在[a,b]范围内一定存在一个零点，而这个零点肯定处于[a,b]范围内的某个位置上（当然，这个点可能是a或b）。

罗尔中值定理和拉格朗日中值定理都在几何学和微积分中起着非常重要的作用。

在几何学中，它们可以帮助数学家从几何方面确定几何问题的解决方案，从而帮助人们解决实际的几何问题。

在微积分中，它们可以用来证明某些抽象数学结论，例如求解极限问题，求解微分方程等。

此外，罗尔中值定理和拉格朗日中值定理还有许多应用，尤其是在应用数学和专业硕士论文中，经常会用到这两个定理。

例如，下列句子中使用了罗尔中值定理：若f（x）是在区间[a,b]上具有连续的导数的函数，则在区间[a,b]内至少存在一个零点。

在专业硕士论文中，笔者经常使用拉格朗日中值定理来证明某些抽象的数学结论，例如证明极限的存在性，证明微分方程的解存在性等。

中值定理及其应用中值定理是微积分中的重要定理之一，它是高阶微积分的基础，被广泛应用于物理、经济、工程等领域。

在本文中，我们将介绍中值定理的概念、证明以及其在实际问题中的应用。

一、中值定理的概念中值定理是微积分中的一个基本定理，用来分析函数在某个区间上的平均变化率与瞬时变化率的关系。

它由罗尔定理、拉格朗日中值定理和柯西中值定理组成。

1. 罗尔定理罗尔定理是中值定理的基础，它主要用于研究函数在闭区间上连续且在开区间上可导的情况。

罗尔定理的表述为：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且满足f(a) = f(b)，则存在c∈(a,b)，使得f'(c) = 0。

2. 拉格朗日中值定理拉格朗日中值定理是中值定理的一种形式，它由罗尔定理推导而来。

拉格朗日中值定理的表述为：如果函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，则存在c∈(a, b)，使得f'(c) = (f(b) - f(a))/(b - a)。

3. 柯西中值定理柯西中值定理是中值定理的另一种形式，它由拉格朗日中值定理推导而来。

柯西中值定理的表述为：如果两个函数f(x)和g(x)在闭区间[a,b]上连续，在开区间(a, b)上可导，并且g'(x)≠0，则存在c∈(a, b)，使得[f(b) - f(a)]/g(b) - g(a) = f'(c)/g'(c)。

二、中值定理的证明中值定理的证明相对复杂，需要运用到微积分中的一些基本概念和定理。

在这里，我们将省略中值定理的详细证明过程。

三、中值定理的应用中值定理在实际问题中具有广泛的应用。

以下是几个常见的应用实例：1. 平均速度与瞬时速度根据拉格朗日中值定理，对于一段时间内的平均速度与某一时刻的瞬时速度，它们之间存在一个相等的关系。

这在物理学中有着重要的意义，可以通过计算平均速度来得到瞬时速度的近似值。

2. 函数求导与图像切线中值定理可以用于求解函数的导数以及函数图像的切线。