江苏省沭阳县怀文中学九年级数学下册 6.3二次函数与一元二次方程导学案(1)(无答案) 苏科版

二次函数与一元二次方程班级 姓名 【学习目标】1.经历探索二次函数与一元二次方程关系的过程，体会方程与函数之间的联系；2.理解抛物线与x 轴公共点的个数与相应的一元二次方程根的对应关系；3.会求抛物线与坐标轴的交点坐标. 【课前自习】1. 根据c bx ax y ++=2的图象和性质填表：函 数图 象a开口 对称轴顶 点增 减 性 c bx ax y ++=2向上当x 时，y 随x 的增大而减少.当x 时，y 随x 的增大而 .0<a当x 时，y 随x的增大而减少. 当x 时，y 随x 的增大而 .2.二次函数的顶点式是 ，其中顶点坐标是 ，对称轴是 .3.解以下一元二次方程：①0322=--x x ②0962=+-x x ③0322=+-x x4.对于任何一个一元二次方程02=++c bx ax ，我们可以通过表达式 的值判断方程的根的情况如下：当 >0时，方程有 实数根； 当 =0时，方程有 实数根； 当 <0时，方程 实数根.教师家长xyOxyOxy( , )( , )Oxy( , )xy【课堂助学】 一、探索归纳：1.观察二次函数的图象，写出它们与x 轴、y 轴的交点坐标： 函数 322--=x x y962+-=x x y322+-=x x y图象交 点与x 轴交点坐标是 与x 轴交点坐标是 与x 轴 与y 轴交点坐标是 与y 轴交点坐标是 与y 轴交点坐标是2.比照《课前自习》第3题各方程的解，你发现什么？3.归纳：⑴一元二次方程02=++c bx ax 的实数根就是对应的二次函数c bx ax y ++=2与x 轴交点的 .⑵二次函数与一元二次方程的关系如下：（一元二次方程的实数根记为21x x 、）二次函数c bx ax y ++=2与一元二次方程02=++c bx ax与x 轴有 个交点 ⇔ac b 42- 0，方程有 的实数根是 .与x 轴有 个交点 这个交点是 点⇔ac b 42- 0，方程有 的实数根是 .与x 轴有 个交点 ⇔ ac b 42- 0，方程 实数根. ⑶二次函数c bx ax y ++=2与y 轴交点坐标是 .练习.判断以下函数的图象与x 轴是否有公共点，有几个公共点，并说明理由. ⑴x x y -=2； ⑵962-+-=x x y ⑶11632++=x x y评价 签字xyy=x -6x+9Oxyy=x -2x-3Oxyy=x -2x+3O二、典型例题：例1、已知二次函数342+-=x x y .求该抛物线的图象与坐标轴的交点坐标.归纳：⑴求抛物线c bx ax y ++=2与x 轴的交点坐标只要令 ，转化为求对应方程 的解；假设对应方程的实数根为21x x 、，那么抛物线与x 轴的交点坐标是 ，特别当21x x =时，这个交点就是抛物线的 .⑵求抛物线c bx ax y ++=2与y 轴的交点坐标只要令 ，该交点坐标是 . 这也是求任意函数的图象与坐标轴交点坐标的一般方法.【课堂检测】1.抛物线22x x y --=与x 轴的交点坐标是 ，与y 轴的交点坐标是 .2.抛物线c bx ax y ++=2的图象都在x 轴的下方，那么函数值y 的取值范围是 .3.抛物线c bx ax y ++=2与x 轴只有一个交点（-3，0），那么它的顶点坐标是 . 4. 假设抛物线42++=bx x y 与x 轴只有1个交点，求b 的值.5. 求抛物线822--=x x y 与x 轴的交点之间的距离.【拓展提升】利用以下平面直角坐标系求例①中抛物线342+-=x x y 与坐标轴的交点围成的 △ABC 的周长和面积.yC y=x 2-4x+3抛物线上是否存在点D ，令△ABD 与△ABC 面积相等，如果有，请写出D 点坐标. 【课外作业】1.判断以下函数的图象与x 轴是否有公共点，有几个公共点，并说明理由. ①252+-=x x y ②122-+-=x x y ③322-+-=x x y2.二次函数的图象与一元二次方程的根的关系如下：抛物线与x 轴有 个公共点⇔ac b 42- 0，方程有 实数根； 抛物线与x 轴有 个公共点⇔ac b 42- 0，方程有 实数根； 抛物线与x 轴有 个公共点⇔ac b 42- 0，方程 实数根.3.抛物线c bx ax y ++=2的图象都在x 轴的上方，那么函数值y 的取值范围是 .4.假设抛物线92+-=bx x y 与x 轴只有1个交点，那么b = . 5.抛物线c bx ax y ++=2的顶点是（3，0），那么它与x 轴有 个交点. 6.已知二次函数1032--=x x y .⑴求该抛物线的图象与坐标轴的交点坐标. ⑵求抛物线与x 轴的交点之间的距离.。

2021届九年级数学下册第6章二次函数6.3二次函数与一元二次方程(1)导学案（无答案）苏科版二次函数与一元二次方程主题§二次函数和一元二次方程（）知识和技能：了解二次函数图像与轴的交点数与一元二次方程根数之间的关系。

学习过程和方法：体验二次函数与方程的关系，理解一元二次方程的情感态度和价值观：本节重点掌握二次函数图像与轴的交点数和一元二次方程的根。

自主空间目标过程的根是二次函数图像与轴交点的横坐标。

学习的主要困难在于理解一元二次方程的根是二次函数图像和轴之间交点的横坐标。

教学过程在同一坐标系中绘制二次函数，并回答以下问题：（）每个图像与轴有多少交点？（）一元二次方程？有多少验证一元二次方程是否有根？（）图像坐标和二次函数的轴交点与一元二次方程的根之间的关系是什么？新知识探究：合作探究2。

思考功能y？十、2倍？3和方程x？2倍？3.0 close 2如何预览导航系统？示例分析：[示例]假设二次函数的图像-与轴有两个交点，则的值范围为1/4为。

【例】抛物线＋＋与轴交于点（－，），对称轴为－，顶点到轴的距离为，求此抛物线表达式．三、展示交流：．求下列二次函数的图象与轴交点坐标，并作草图验证．（）－；（）－－．．已知二次函数与轴有公共点，求的取值范围.．你能利用、、之间的某种关系判断二次函数＋＋的图象与轴何时有两个交点、一个交点，何时没有交点？提炼总结：由一元二次方程的根的情况可以判断二次函数图象与轴的交点个数。

当δb?4ac>时，一元二次方程的根的情况是，此时二次函数图象与轴有交点；当δb?4ac时，一元二次方程的根的情况是，此时二次函数图象与轴有交点；当δb?4ac.抛物线是的值。

如果轴只有一个公共点。

判断以下函数与轴的位置关系：（）。

打高尔夫球时，球的飞行轨迹可以看作抛物线。

如果不考虑空气阻力，球的飞行高度（单位：m）和飞行距离（单位：100m）满足二次函数：，球的最大水平距离是多少？能达到球的飞行高度吗？当这个班达到标准时，有一个二次函数的图像。

x y o 新苏科版九年级数学下册第五章《二次函数与一元二次方程（1）》学案议一议：在同一坐标系中画出二次函数y=x 2+2x,y=x 2-2x+1,y=x 2-2x+2的图象并回答下列问 题：(1)每个图象与x 轴有几个交点？(2)一元二次方程? x 2+2x=0,x 2-2x+1=0有几个根?验证一下一元二次方程x 2-2x+2=0有根吗?(3)二次函数y=ax 2+bx+c 的图象和x 轴交点的坐标与一元二次方程ax 2+bx+c=0的根有什么关系?例1．已知二次函数y=kx 2－7x －7的图象与x 轴有两个交点，求k 的取值范围。

例2．K 取何值时，抛物线y=x 2-3x+k+2与x 轴相交？例3．抛物线y=-x 2+（m-1）x+m 与y 轴交于点（0，3）（1） 求m 的值并画出图象。

（2）求它与x 轴的交点和抛物线的顶点坐标。

（3）x 取何值时，抛物线在x 轴上方？ （4）x 取何值时，y 的值随x 的增大而减小？【当堂巩固】1．二次函数y ＝x 2＋2x ，y ＝x 2－2x ＋1，y ＝x 2－2x ＋2的图象与x 轴分别有 个交点， 个交点， 交点．2．抛物线y=3x 2＋5x 与两坐标轴交点的个数为（ ）A ．3个B ．2个C ．1个D ．无 3．抛物线y=a （x －2）（x ＋5）与x 轴的交点坐标为 ．4．抛物线y=2x 2＋8x ＋m 与x 轴只有一个交点，求m 的取值范围．5．二次函数y=kx 2＋3x －4的图象与x 轴有两个交点，求k 的取值范围．提高练习： 1．已知二次函数y=x 2＋mx ＋m －2．求证：无论m 取何实数，抛物线总与x 轴有两个交点．2.已知抛物线y=mx 2＋（3－2m ）x ＋m －2（m ≠0）与x 轴有两个不同的交点．求m 的取值范围；3.已知二次函数y=x 2－2kx ＋k 2＋k －2．（1）当实数k 为何值时，图象经过原点？（2）当实数k 在何范围取值时，函数图象的顶点在第四象限内？课外作业： 1、方程 的根是 ___ ；则函数 的图象与x 025102=-+-x x 25102-+-=x x y轴的交点有 个，其坐标是 ．2、若函数24y x x k =-++的最大值等于3，则k =_______。

初 三 数 学（第六章 二次函数复习1）知识点：１．概念：一般地，形如y=ax 2+bx+c(a,b,c,是常数，且a ≠0)的函数称为二次函数，其中x是自变量，y 是x 的函数．２．图像：是 ，上下平移得 ；左右平移得 ；既上下又左右平移得 ．３．性质：开口方向、顶点坐标、对称轴、最值、增减性4．三种表达形式：一般式 ；顶点式 ；交点式 ．５．二次函数与一元二次方程关系：一元二次方程是二次函数当 时的特殊情形．６．应用：求一元二次方程的近似解（图像法）；在实际问题中的应用．一、选择题1.在下列关系式中,y 是x 的二次函数的关系式是( )A.2xy+x 2=1B.y 2-ax+2=0C.y+x 2-2=0D.x 2-y 2+4=02．下列四个函数中, 图象的顶点在y 轴上的函数是( )A ．232y x x =-+B ．25y x =-C ．22y x x =-+D ．244y x x =-+3．把二次函数122--=x x y 配方成顶点式为( )A ．2)1(-=x yB ． 2)1(2--=x yC ．1)1(2++=x yD ．2)1(2-+=x y4．设等边三角形的边长为x(x>0），面积为y ，则y 与x 的函数关系式是( )A.212y x =B.214y x = C.2y x = D.2y x = 5．若直线y=ax ＋b (a ≠0）在第二．四象限都无图像，则抛物线y=ax 2+bx+c( )A.开口向上，对称轴是y 轴B.开口向下，对称轴平行于y 轴C.开口向上，对称轴平行于y 轴D.开口向下，对称轴是y 轴6．一次函数y=ax+b 与二次函数y=ax 2+bx+c 在同一坐标系中的图像可能是( )7．已知抛物线y=-x 2+mx+n 的顶点坐标是（-1，- 3 )，则m 和n 的值分别是( )A.2,4B.-2,-4C.2,-4D.-2,08．对于函数y=-x 2+2x-2使得y 随x 的增大而增大的x 的取值范围是 ( )A.x>-1B.x ≥0C.x ≤0D.x<-19．抛物线y=x 2-(m+2)x+3(m-1)与x 轴( )A.一定有两个交点； B ．只有一个交点； C ．有两个或一个交点； D ．没有交点10．二次函数y=2x 2+mx-5的图像与x 轴交于点A (x 1, 0）．B(x 2，0), 且x 12+x 22=294，则m 的值为( )A.3B.-3C.3或-3D.以上都不对11．对于任何的实数t ，抛物线 y=x 2 +(2-t) x + t 总经过一个固定的点，这个点是( )A . (1, 0) B.（-l, 0) C.（-1, 3) D. (l, 3)12．已知二次函数c bx ax y ++=2的图象过点A （1，2），B （3，2），C （5，7）．若点M （-2，y 1），N （-1，y 2），K （8，y 3）也在二次函数c bx ax y ++=2的图象上，则下列结论正确的是 ( )A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 3＜y 1＜y 2D ．y 1＜y 3＜y 2二、填空题13．抛物线y=-2x+x 2＋7的开口向 ，对称轴是 ，顶点是 .14．抛物线23y x =向右平移1个单位，再向下平移2个单位，所得到的抛物线是15.对于二次函数y=ax 2, 已知当x 由1增加到2时，函数值减少4，则常数a 的值是 .16.已知二次函数y=x 2-6x+n 的最小值为1，那么n 的值是 .17.抛物线在y=x 2-2x-3在x 轴上截得的线段长度是 .18.设矩形窗户的周长为6m ，则窗户面积S(m 2）与窗户宽x (m)之间的函数关系式是 ，自变量x 的取值范围是 .19．已知直线y=x 与二次函数y=ax 2－2x －1的图象的一个交点 M 的横标为1，则a 的值为20．已知二次函数b ax y +=2与432+-=x y 的图象关于x 轴对称，则=a ，=b21．二次函数432+=x y 与一次函数b x y +=只有唯一公共点，则=b三、解答题22．已知二次函数的图象以A （－1，4）为顶点，且过点B （2，－5）（1）求该函数的关系式；（2）求该函数图象与坐标轴的交点坐标；（3）将该函数图象向右平移，当图象经过原点时，A ．B 两点随图象移至A ′．B ′，求△O A ′B ′的面积.23．某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形一边长为x 米，面积为S 平方米.（1）求出S 与x 之间的函数关系式，并确定自变量x 的取值范围；（2）请你设计一个方案，使获得的设计费最多，并求出这个费用.24．如图，直线AB 过x 轴上的点A(2，0)，且与抛物线y=ax 2相交于B ．C 两点，B 点坐标为(1，1).(1)求直线和抛物线所表示的函数表达式;(2)在抛物线上是否存在一点D，使得S△OAD=S△OBC，若不存在，说明理由；若存在，请求出点D的坐标．。

6．2二次函数 第一课时班级： 学号： 姓名：学习目标： 1．经历探索二次函数y=x 2图象作法的过程，进一步感受应用图象发现函数性质的经验．2．会用描点法作出函数y=a x 2(a ≠0)的图象，能根据图象初步了解二次函数y=x 2的性质． 学习过程：一、自主探究：1． 回忆一次函数和反比例函数的图象及其作图方法．思考：二次函数的图象是直线吗？是双曲线吗？你打算怎样画出二次函数的图象？二、自主合作：2．用描点法画出二次函数y=x 2的图象，并观察图象的特征．（1）列表：函数y=x 2的自变量x 的取值范围是 ，根据函数y=x 2的特征，选x … -3 -2 -1 0 1 2 3 … y=x 2……(2)描点：以表中的每个x 值为点的横坐标、对应的y 值为点的纵坐标，在图（1）的直角坐标系中描出相应的点．（按x 的值从小到大，从左到右描点）（3）连线：用平滑的曲线顺次连接所描出的点，即得二次函数y =x 2的图象．（能用直线连接吗？）3．思考：二次函数y=x 2的图象有什么特征？（可从以下几方面考虑） (1)你能描述图象的形状吗?(2) 图象是轴对称图形吗? 如果是，它的对称轴是什么? 请你找出几对对称点，与同桌进行交流．4．在图（2）的直角坐标系中画出二次函数y=-x 2的图象．5．二次函数y =-x 的图象有什么特征？ 三、自主展示图（1） 图（2）6．二次函数y =x 2与y=-x 2的图象有什么共同特征？7．在平面直角坐标系中分别画出下列函数的图象：（1）y=221x ；(2)y=22x ．8．在平面直角坐标系中分别画出下列函数的图象：（1）y=-221x ； (2)y=-22x ．四、自主拓展：9．二次函数y=x 2的图象开口 ，对称轴是 ，顶点是 ．10．点A （2，-4）在函数y=-x 2的图象上，点A 在该图象上的对称点的坐标是 ．11．二次函数y=221x 与 y=-221x 的图象关于 对称． 12．若点A （1，a ）B （b ，9）在函数y=x 2的图象上，则a= ,b= ．。

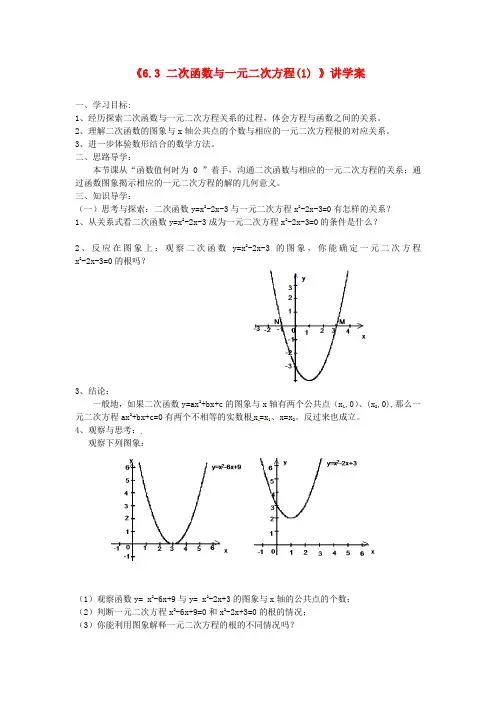
《6.3 二次函数与一元二次方程(1) 》讲学案一、学习目标:1、经历探索二次函数与一元二次方程关系的过程，体会方程与函数之间的关系。

2、理解二次函数的图象与x轴公共点的个数与相应的一元二次方程根的对应关系。

3、进一步体验数形结合的数学方法。

二、思路导学：本节课从“函数值何时为0 ”着手，沟通二次函数与相应的一元二次方程的关系；通过函数图象揭示相应的一元二次方程的解的几何意义。

三、知识导学：（一）思考与探索：二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系？1、从关系式看二次函数y=x2-2x-3成为一元二次方程x2-2x-3=0的条件是什么？2、反应在图象上：观察二次函数y=x2-2x-3的图象，你能确定一元二次方程x2-2x-3=0的根吗？3、结论：一般地，如果二次函数y=ax2+bx+c的图象与x轴有两个公共点（x1,0）、(x2,0),那么一元二次方程ax2+bx+c=0有两个不相等的实数根x=x1、x=x2。

反过来也成立。

4、观察与思考：观察下列图象：（1）观察函数y= x2-6x+9与y= x2-2x+3的图象与x轴的公共点的个数；（2）判断一元二次方程x2-6x+9=0和x2-2x+3=0的根的情况；（3）你能利用图象解释一元二次方程的根的不同情况吗？（二）归纳提高：一般地，二次函数y=ax 2+bx+c 图象与一元二次方程ax 2+bx+c=0的根有如下关系：1、如果二次函数y=ax 2+bx+c 图象与x 轴有两个交点（m,0）、(n,0),那么一元二次方程ax 2+bx+c=0有 实数根x 1= ,x 2= .2、如果二次函数y=ax 2+bx+c 图象与x 轴只有一个交点（m,0）,那么一元二次方程ax 2+bx+c=0有 实数根x 1=x 2= .3、如果二次函数y=ax 2+bx+c 图象与x 轴没有交点,那么一元二次方程ax 2+bx+c=0 实数根.反过来，由一元二次方程ax 2+bx+c=0的根的情况可以判断二次函数y=ax 2+bx+c 图象与x 轴的交点个数。

【目标】1.经历对实际问题情境分析确定二次函数表达式的过程，体会二次函数意义；2.了解二次函数关系式，会确定二次函数关系式中各项的系数。

【重点】1.经历探索二次函数关系的过程,获得用二次函数表示变量之间关系的体验.2.能够表示简单变量之间的二次函数。

【难点】确定实际问题中二次函数的关系式。

1.设在一个变化过程中有两个变量x 和y ，如果对于x 的每一个值， y 都有 唯一的值与它对应，那么就说y 是x 的 ，x 叫做 。

2.我们已经学过的函数有：一次函数、反比例函数，其中 的 图像是直线， 的图像是双曲线。

我们得到它们图像的方 法和步骤是：① ；② ；③ 。

3. 形如___________y =，（ ）的函数是一次函数，当______0=时，它是 函数，图像是经过 的直线； 形如ky x =，（ ）的函数是 函数，它的表达式还可 以写成：① 、②【探究问题】1．一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S 与半 径r 之间的函数关系式是 。

2．用16m 长的篱笆围成长方形圈养小兔，圈的面积y(㎡)与长方形的长x(m) 之间的函数关系式为 。

3．要给一个边长为x (m)的正方形实验室铺设地板，已知某种地板的价格 为每平方米240元，踢脚线价格为每米30元，如果其它费用为1000元，那么 总费用y （元）与x （m ）之间的函数关系式是 。

[讨论归纳] 观察上述函数函数关系有哪些共同之处？它们与一次函数、反比例函数的关 系式有什么不同？ 。

一般地，形如 ，（ ，且 ）的函数为二 次函数。

其中x 是自变量， 函数。

注意： 1、定义中只要求二次项系数a 不为零（必须存在二次项），一次项系数b 、常 数项c 可以为零。

最简单形式的二次函数：2(0)y ax a =≠。

例如 y ＝-5x 2+100x+60000和y=100x 2+200x+100都是二次函数．我们以前学过的正 方形面积S 与边长a 的关系S=a 2，圆面积s 与半径r 的关系2s r π=等也都 是二次函数的例子． 2、二次函数2y ax bx c =++中自变量x 的取值范围是 ，你 能说出上述三个问题中自变量的取值范围吗？ [例题精讲] 例1 函数y=（m ＋2）x 22-m ＋2x －1是二次函数，则m= ． 点拨：从二次函数的定义出发:看二次项的系数和次数确定m 的取值 例2．下列函数中是二次函数的有（ ） ①y=x ＋x 1；②y=3（x －1）2＋2；③y=（x ＋3）2－2x 2；④y=21x ＋x ． A ．1个 B ．2个 C ．3个 D ．4个 例3、写出下列各函数关系，并判断它们是什么类型的函数． ⑴圆的面积y （cm 2）与它的周长x （cm ）之间的函数关系； ⑵某种储蓄的年利率是1.98%，存入10000元本金，若不计利息税，求本息和y （元）与所存年数x 之间的函数关系； 课题 6.1 二次函数 时间课型 新授 课时 第 1 课时 主备人 审核人⑶菱形的两条对角线的和为26cm，求菱形的面积S（cm2）与一对角线长x （cm）之间的函数关系。

二次函数与一元二次方程
的
倚窗远眺，目光目光尽处必有一座山，那影影绰绰的黛绿色的影，是春天的颜色。

周遭流岚升腾，没露出那真实的面孔。

面对那流转的薄雾，我会幻想，那里有一个世外桃源。

在天阶夜色凉如水的夏夜，我会静静地，静静地，等待一场流星雨的来临…
许下一个愿望，不乞求去实现，至少，曾经，有那么一刻，我那还未枯萎的，青春的，诗意的心，在我最美的年华里，同星空做了一次灵魂的交流…
秋日里，阳光并不刺眼，天空是一碧如洗的蓝，点缀着飘逸的流云。

偶尔，一片飞舞的落叶，会飘到我的窗前。

斑驳的印迹里，携刻着深秋的颜色。

在一个落雪的晨，这纷纷扬扬的雪，飘落着一如千年前的洁白。

窗外，是未被污染的银白色世界。

我会去迎接，这人间的圣洁。

在这流转的岁月里，有着流转的四季，还有一颗流转的心，亘古不变的心。