PID控制算法

pid算法公式详解
PID算法，即比例（proportional）、积分（integral）、微分（derivative）控制算法，是一种应用广泛的控制算法。

它结合了比例、积分和微分三种环节于一体，适用于连续系统的控制。

在工业应用中，它是最广泛算法之一，如四轴飞行器、平衡小车、汽车定速巡航、温度控制器等场景均有应用。

PID算法的公式如下：
\[U(t)=K_p e(t)+K_i\int_{0}^{t}e(\tau)d\tau+K_d frac{de(t)}{dt}\]
其中，
-\(U(t)\)是控制器输出的控制信号；
-\(e(t))是控制器输入的误差信号；
-\(K_p\)、\(K_i\)和\(K_d\)是比例、积分和微分系数；
-(\int_{0}^{t}e(\tau)d\tau)是误差信号的累积值，即积分项；
-(\frac{de(t)}{dt}\)是误差信号的变化率，即微分项。

这个公式描述了PID控制器如何根据当前的误差以及过去的误差来计算出控制信号。

比例项反映了当前误差的大小，积分项反映了过去误差的累积，微分项反映了误差变化的趋势。

通过调整这三个参数，可以实现对系统的精确和快速控制。

电机控制pid算法电机控制PID算法引言：PID（Proportional-Integral-Derivative）算法是一种常用的控制算法，广泛应用于电机控制领域。

本文将详细介绍PID算法的原理和应用，并探讨其在电机控制中的作用和优势。

一、PID算法原理1. 比例控制（P）：比例控制是一种基本的反馈控制方法，其输出与误差成正比。

在电机控制中，比例控制可用于调整电机的速度或位置。

通过设置适当的比例增益，可以实现快速响应和准确控制。

2. 积分控制（I）：积分控制用于消除静态误差，通过对误差进行积分来修正系统偏差。

在电机控制中，积分控制可用于消除电机运行过程中的误差，提高控制精度和稳定性。

3. 微分控制（D）：微分控制用于抑制系统的超调和振荡，通过对误差的变化率进行微分来提前预测系统的响应。

在电机控制中，微分控制可用于提高系统的动态响应，减小系统的超调和振荡。

二、PID算法应用1. 电机速度控制：PID算法可用于电机的速度控制，通过测量电机的转速与设定值之间的误差，并根据比例、积分和微分系数对误差进行调整，控制电机的输出电压或电流，从而实现精确的速度控制。

2. 电机位置控制：PID算法也可用于电机的位置控制，通过测量电机的位置与设定值之间的误差，并根据比例、积分和微分系数对误差进行调整，控制电机的输出电压或电流，从而实现精确的位置控制。

3. 电机力矩控制：PID算法还可用于电机的力矩控制，通过测量电机的输出力矩与设定值之间的误差，并根据比例、积分和微分系数对误差进行调整，控制电机的输出电压或电流，从而实现精确的力矩控制。

三、PID算法的优势1. 简单易实现：PID算法是一种简单易实现的控制算法，只需调节比例、积分和微分系数即可实现对电机的控制。

算法结构简单，计算量小，适用于实时控制系统。

2. 鲁棒性强：PID算法具有较好的鲁棒性，能够适应不同的工作环境和负载变化。

通过合理调节PID参数，可以使电机控制系统具有较好的稳定性和鲁棒性。

pid电机控制算法
【原创实用版】
目录
1.PID 电机控制算法简介
2.PID 电机控制算法的工作原理
3.PID 电机控制算法的优点和缺点
4.PID 电机控制算法在实际应用中的案例
5.总结
正文
一、PID 电机控制算法简介
PID 电机控制算法，全称为比例 - 积分 - 微分电机控制算法，是一种广泛应用于电机控制的算法。

它是通过计算电机的误差，然后通过比例、积分、微分三个部分的调节，使电机达到或维持在期望的速度或位置。

二、PID 电机控制算法的工作原理
PID 电机控制算法的工作原理可以简单地概括为：计算误差，调节输入，使误差减小。

具体来说，就是通过测量电机的实际速度或位置与期望速度或位置的差值，即误差，然后通过比例、积分、微分三个部分的调节，使电机的输入电压或电流发生变化，从而改变电机的转速或转矩，使误差减小。

三、PID 电机控制算法的优点和缺点
PID 电机控制算法的优点主要有：调节速度快，稳定性好，适用于大多数电机控制场景。

其缺点主要是：对于非线性的电机系统，可能需要复杂的 PID 参数调节，而且对于突变的负载或环境变化，可能需要额外的控制策略来应对。

四、PID 电机控制算法在实际应用中的案例
PID 电机控制算法在实际应用中非常广泛，例如在电动汽车、机器人、自动化生产线等中都有应用。

以电动汽车为例，PID 电机控制算法可以精确地控制电机的转速和转矩，从而使电动汽车在行驶过程中能够保持稳定的速度和良好的驾驶性能。

五、总结
总的来说，PID 电机控制算法是一种成熟、有效的电机控制策略，它适用于大多数电机控制场景，同时也具有一定的局限性。

在过程控制中，由偏差的比例（P），积分（I）和微分（D）控制的PID控制器（也称为PID调节器）是使用最广泛的自动控制器。

具有原理简单，易于实现，应用范围广，控制参数独立，参数选择简单等优点。

从理论上可以证明，对于过程控制的典型对象“一阶滞后+纯滞后”，对于“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。

控制点目前包含三种比较简单的ＰＩＤ控制算法，分别是：增量式算法，位置式算法，微分先行。

这三种ＰＩＤ算法虽然简单，但各有特点，基本上能满足一般控制的大多数要求。

算法种类：1) PID增量式算法离散化公式：注：各符号含义如下u(t);;;;; 控制器的输出值。

e(t);;;;; 控制器输入与设定值之间的误差。

Kp;;;;;;; 比例系数。

Ti;;;;;;; 积分时间常数。

Td;;;;;;; 微分时间常数。

T;;;;;;;; 调节周期。

对于增量式算法，可以选择的功能有：(1) 滤波的选择可以对输入加一个前置滤波器，使得进入控制算法的给定值不突变，而是有一定惯性延迟的缓变量。

(2) 系统的动态过程加速在增量式算法中，比例项与积分项的符号有以下关系：如果被控量继续偏离给定值，则这两项符号相同，而当被控量向给定值方向变化时，则这两项的符号相反。

由于这一性质，当被控量接近给定值的时候，反号的比例作用阻碍了积分作用，因而避免了积分超调以及随之带来的振荡，这显然是有利于控制的。

但如果被控量远未接近给定值，仅刚开始向给定值变化时，由于比例和积分反向，将会减慢控制过程。

为了加快开始的动态过程，我们可以设定一个偏差范围v，当偏差|e(t)|< β时，即被控量接近给定值时，就按正常规律调节，而当|e(t)|>= β时，则不管比例作用为正或为负，都使它向有利于接近给定值的方向调整，即取其值为|e(t)-e(t-1)|，其符号与积分项一致。

利用这样的算法，可以加快控制的动态过程。

(3) PID增量算法的饱和作用及其抑制在PID增量算法中，由于执行元件本身是机械或物理的积分储存单元，如果给定值发生突变时，由算法的比例部分和微分部分计算出的控制增量可能比较大，如果该值超过了执行元件所允许的最大限度，那么实际上执行的控制增量将时受到限制时的值，多余的部分将丢失，将使系统的动态过程变长，因此，需要采取一定的措施改善这种情况。

pid电机控制算法的概念与基本原理
PID（Proportional-Integral-Derivative）控制算法是一种常用的电机控制算法，它结合了比例控制、积分控制和微分控制的特点，用于调节电机输出信号以使其接近或跟随给定的目标信号。

PID控制算法根据电机的运行状态和误差信号进行计算，并输出一个调节量作用于电机控制系统中的执行器（例如电机驱动器）。

以下是PID控制算法的基本原理：
1. 比例控制（Proportional Control）：比例控制根据当前误差信号的大小与设定目标值之间的差异来产生一个调节量。

调节量与误差成正比，即误差越大，调节量越大。

比例控制提供了快速的响应，但通常无法完全消除稳态误差（即最终误差）。

2. 积分控制（Integral Control）：积分控制通过累积误差信号的时间积分来产生一个调节量。

积分控制主要用于消除稳态误差，即使在达到目标值后仍然存在的小误差。

积分控制可以增加控制系统对慢速和渐变过程的响应能力。

3. 微分控制（Derivative Control）：微分控制根据误差信号的变化率来产生一个调节量。

微分控制用于提供控制系统对快速变化的过程的响应能力，并减少超调和震荡。

微分控制还可以提供对系统动力学行为的预测，以提前调整输出信号。

PID控制算法通过调节比例、积分和微分系数的数值来实现适当的控制性能。

选择合适的参数需要根据具体的电机和控制要求进行实验和调整，以获得稳定性、响应速度和误差补偿的平衡。

需要注意的是，PID控制算法是一种经典的控制算法，在实际应用中可能会因为系统的非线性、时变性等特性而需要进行改进或采用其他高级控制算法来提高性能。

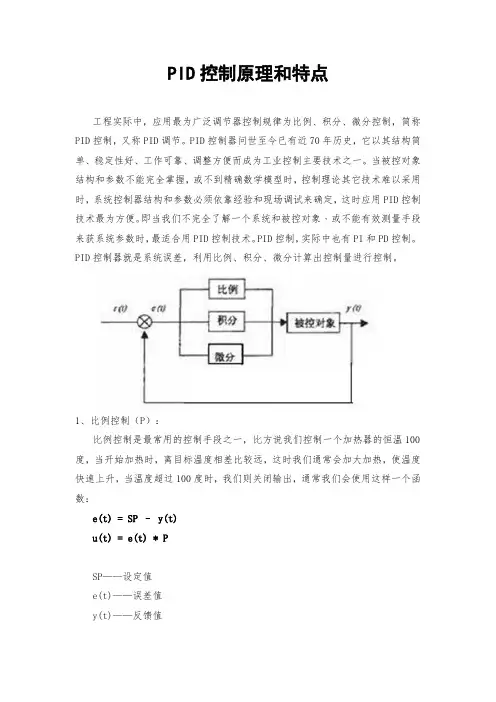
PID控制原理和特点工程实际中，应用最为广泛调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节。

PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制主要技术之一。

当被控对象结构和参数不能完全掌握，或不到精确数学模型时，控制理论其它技术难以采用时，系统控制器结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。

即当我们不完全了解一个系统和被控对象﹐或不能有效测量手段来获系统参数时，最适合用PID控制技术。

PID控制，实际中也有PI和PD控制。

PID控制器就是系统误差，利用比例、积分、微分计算出控制量进行控制。

1、比例控制（P）：比例控制是最常用的控制手段之一，比方说我们控制一个加热器的恒温100度，当开始加热时，离目标温度相差比较远，这时我们通常会加大加热，使温度快速上升，当温度超过100度时，我们则关闭输出，通常我们会使用这样一个函数：e(t) = SP – y(t)u(t) = e(t) * PSP——设定值e(t)——误差值y(t)——反馈值u(t)——输出值P——比例系数滞后性不是很大的控制对象使用比例控制方式就可以满足控制要求，但很多被控对象中因为有滞后性。

也就是如果设定温度是200度，当采用比例方式控制时，如果P选择比较大，则会出现当温度达到200度输出为0后，温度仍然会止不住的向上爬升，比方说升至230度，当温度超过200度太多后又开始回落，尽管这时输出开始出力加热，但温度仍然会向下跌落一定的温度才会止跌回升，比方说降至170度，最后整个系统会稳定在一定的范围内进行振荡。

如果这个振荡的幅度是允许的比方说家用电器的控制，那则可以选用比例控制。

2、比例积分控制（PI）：积分的存在是针对比例控制要不就是有差值要不就是振荡的这种特点提出的改进，它常与比例一块进行控制，也就是PI控制。

其公式有很多种，但大多差别不大，标准公式如下：u(t) = Kp*e(t) + Ki*∑e(t) + u0u(t)——输出Kp——比例放大系数Ki——积分放大系数e(t)——误差u0——控制量基准值（基础偏差）大家可以看到积分项是一个历史误差的累积值，如果光用比例控制时，我们知道要不就是达不到设定值要不就是振荡，在使用了积分项后就可以解决达不到设定值的静态误差问题，比方说一个控制中使用了PI控制后，如果存在静态误差，输出始终达不到设定值，这时积分项的误差累积值会越来越大，这个累积值乘上Ki后会在输出的比重中越占越多，使输出u(t)越来越大，最终达到消除静态误差的目的。

最优控制旨在寻找一种最优的控制策 略，使得系统性能达到最优。与PID 控制相比，最优控制具有更高的性能 指标和更好的全局优化能力。然而， 最优控制的实现需要精确的数学模型 和大量的计算资源，且对系统参数变 化较为敏感。
05
PID控制算法的应用实例
工业自动化领域的应用
要点一
温度控制
在工业生产过程中，PID控制算法被 广泛应用于温度控制系统中，如熔炼 炉、热处理炉等设备的温度控制。通 过实时采集温度数据，与设定值进行 比较，PID控制器能够自动调节加热 元件的功率，使温度稳定在设定值附 近。
该传递函数描述了PID控制器在频域中的特性，可用于分析系统的稳定性、动态性能和 稳态精度等。
通过调整Kp、Ki和Kd三个参数，可以实现对系统性能的优化。在实际应用中，常采用 试凑法、经验法或优化算法等方法来确定PID参数。
03
PID控制算法的参数整定
参数整定的意义
提高系统性能
通过调整PID控制器的参数，可以优化系统 的动态响应和稳态精度，从而提高系统的整 体性能。
适应不同应用场景
不同的被控对象和不同的应用场景需要不同的PID 参数配置，参数整定可以使PID控制器适应各种应 用场景。
保证系统稳定性
合理的参数配置可以保证系统的稳定性，避 免系统出现振荡或失控等不稳定现象。
参数整定的方法
试凑法
根据经验或实验数据，逐步调整 PID控制器的参数，观察系统的响 应情况，直到满足性能指标要求 。
PID控制算法由比例（P）、积分（I） 和微分（D）三个部分组成，每个部 分都有不同的作用，通过调整三个部 分的参数可以实现对系统的精确控制 。
PID控制算法的应用领域
01
02
03

PID控制算法控制算法1.PID控制算法的原理：-比例部分（P）：根据误差的大小，以比例系数的倍数调整控制器的输出。

一个较大的比例系数可以使系统的响应更加敏感，但可能引发过调和震荡；一个较小的比例系数可以减缓响应速度，但可能导致系统过于迟钝。

-积分部分（I）：根据误差累积的程度，以积分系数的倍数调整控制器的输出。

积分部分用来解决长时间累积误差的问题，减小系统的稳态误差。

但过大的积分系数可能导致系统不稳定。

-微分部分（D）：根据误差变化的速率，以微分系数的倍数调整控制器的输出。

微分部分用于预测误差变化的趋势，可以提前调整控制器的输出，减小过调和震荡的幅度。

2.PID控制算法的应用：-工业自动化：PID控制算法可以用来调节液位、温度、压力、流量等工业过程中的各种物理量。

通过对这些物理量的控制，可以实现生产过程的自动化和优化。

-机器人控制：PID控制算法可以用来控制机器人的位置、速度和力矩等。

通过对这些物理量的控制，可以使机器人实现准确的位置控制和运动轨迹规划。

-飞行器导航：PID控制算法可以用来控制飞行器的俯仰、横滚和偏航等。

通过对这些物理量的控制，可以使飞行器实现稳定的飞行和精确的导航。

3.PID控制算法的优缺点：-算法简单易于实现，计算量小。

-对被控制系统的响应速度快，可以实现快速稳定。

-可以通过调整比例、积分和微分系数来适应不同的控制要求。

然而，PID控制算法也存在以下缺点：-无法处理具有非线性特性的被控制系统。

-在存在模型不准确、系统参数变化较大等情况下，可能无法得到良好的控制效果。

-不适用于具有强耦合性的多变量系统。

为了解决这些问题，可以采用改进的PID控制算法，例如增加自适应性、模糊控制、神经网络控制等技术。

这些改进的算法可以更好地适应复杂的控制环境，并提高系统的鲁棒性和控制性能。

总结来说，PID控制算法是一种简单而有效的控制算法，具有广泛的应用领域。

虽然存在一些局限性，但通过改进和优化，可以进一步提高控制效果，满足不同的应用需求。

pid控制算法的原理
PID控制算法是一种经典的反馈控制算法，它基于对系统的测
量值进行连续监测和调整，使得系统的输出尽可能地接近期望值。

PID代表比例（Proportional）、积分（Integral）、微分（Derivative），它的原理可以简要概括为以下几个方面：
1. 比例控制：PID控制算法根据系统当前状态与期望状态之间
的误差，将误差乘以比例系数Kp得到一个修正量，然后将修
正量加到系统的控制量中。

这个修正量的大小与误差成正比，即越大的误差会产生越大的修正量。

2. 积分控制：PID控制算法对误差进行累积，直到误差归零。

通过积分系数Ki乘以误差的累积和，得到一个修正量，使得
系统能够更好地消除系统存在的稳态误差。

积分控制的作用是消除系统的静态偏差。

3. 微分控制：PID控制算法根据误差的变化率给出一个修正量，这个修正量的大小与误差变化率成正比。

微分系数Kd乘以误
差的变化率，得到修正量，可以使得系统更快地响应误差的变化，并避免系统的超调和震荡。

PID控制算法通过不断的调整比例、积分、微分系数来优化系
统的控制效果。

其中比例控制能够确保系统对误差的响应速度较快，积分控制能够确保系统消除稳态误差，微分控制能够确保系统对误差变化的响应平滑而稳定。

由于PID控制算法简
单易实现且效果良好，被广泛应用于各个领域的自动控制系统中。

pid算法公式
PID控制算法也称为PID表达式，是一种常用的闭环控制算法。

它在控制系统中的数学模型表示为一个三重积分运算：比例(P)、积分(I)和微分(D)。

它可以调节输出，使其与设定值保持一致，进而实现理想的调节结果，从而改善控制系统的性能。

PID算法可以模拟出人类操作的模式，将参与控制的变量结合起来，因此PID算法在自动控制领域有着重要的地位。

PID算法的公式如下：PID输出= Kp*e(t)+ Ki∫e(t)+ Kdde(t)/dt。

其中：Kp为比例系数，Ki为积分系数，Kd为微分系数；e(t)为反馈误差，t为时间。

Kp*e(t)表示比例控制，比例控制反馈误差大则输出值大，反馈误差小则输出值小；Ki∫e(t)，表示积分控制，误差积分增大，输出值越大，积分减小，输出值就越小；Kdde(t)/dt，表示微分控制，反馈误差快速减小时，相应的输出值减小，反馈误差减慢时，输出值加大，使控制系统的收敛增快。

通过调节Kp，Ki和Kd三个系数，可以控制系统的稳定性、精度和响应速度，从而实现更好的控制效果。

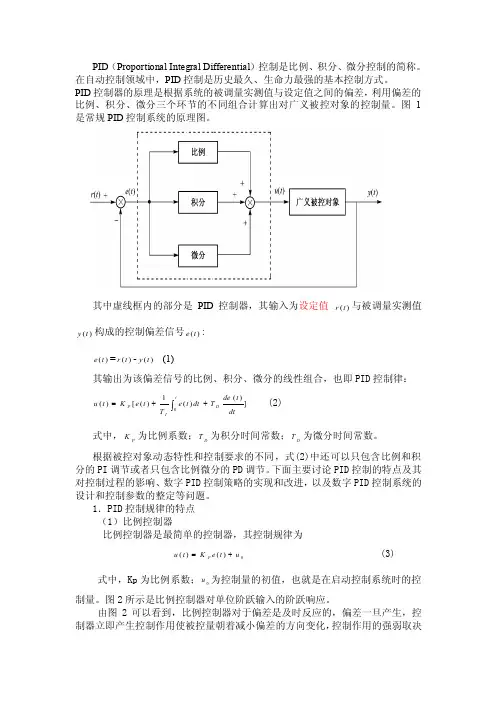
PID （Proportional Integral Differential ）控制是比例、积分、微分控制的简称。

在自动控制领域中，PID 控制是历史最久、生命力最强的基本控制方式。

PID 控制器的原理是根据系统的被调量实测值与设定值之间的偏差，利用偏差的比例、积分、微分三个环节的不同组合计算出对广义被控对象的控制量。

图1是常规PID 控制系统的原理图。

其中虚线框内的部分是PID 控制器，其输入为设定值)(t r 与被调量实测值)(t y 构成的控制偏差信号)(t e :)(t e =)(t r -)(t y (1)其输出为该偏差信号的比例、积分、微分的线性组合，也即PID 控制律：])()(1)([)(0⎰++=tDIP dtt de T dt t e T t e K t u (2)式中，P K 为比例系数；D T 为积分时间常数；D T 为微分时间常数。

根据被控对象动态特性和控制要求的不同，式(2)中还可以只包含比例和积分的PI 调节或者只包含比例微分的PD 调节。

下面主要讨论PID 控制的特点及其对控制过程的影响、数字PID 控制策略的实现和改进，以及数字PID 控制系统的设计和控制参数的整定等问题。

1．PID 控制规律的特点 （1）比例控制器比例控制器是最简单的控制器，其控制规律为0)()(u t e K t u P += (3)式中，Kp 为比例系数；0u 为控制量的初值，也就是在启动控制系统时的控制量。

图2所示是比例控制器对单位阶跃输入的阶跃响应。

由图2可以看到，比例控制器对于偏差是及时反应的，偏差一旦产生，控制器立即产生控制作用使被控量朝着减小偏差的方向变化，控制作用的强弱取决于比例系数Kp 。

图2 比例控制器的阶跃响应比例控制器虽然简单快速，但对于具有自平衡性（即系统阶跃响应终值为一有限值）的被控对象存在静差。

加大比例系数Kp 虽然可以减小静差，但当Kp 过大时，动态性能会变差，会引起被控量振荡，甚至导致闭环系统不稳定。

PID控制算法控制算法PID控制算法（Proportional-Integral-Derivative control algorithm）是一种常用的自动控制算法，用于调节系统的控制器参数，以实现系统的稳定控制。

它结合了比例项（P）、积分项（I）和微分项（D），根据系统的当前状态和误差的变化趋势进行调节。

在PID控制算法中，比例项（P）通过比较目标值与反馈值的差异来产生输出控制信号。

比例项的作用是根据误差大小来控制输出，当误差较大时，输出信号也会相应增大，以加快系统的响应速度。

然而，比例项单独使用容易导致系统产生振荡现象，因此还需要引入积分项和微分项。

积分项（I）用于校正系统的稳态误差，它积累了误差的累计值，并将其乘以一个系数后添加到输出信号中。

积分项的作用是通过减小稳态误差来提高系统的精度和稳定性。

当系统存在稳态误差时，积分项会不断累积，在逐渐减小误差的同时，输出信号也会逐渐增大。

微分项（D）通过测量误差变化的速率来预测下一时刻的误差趋势。

它的作用是根据误差变化的速率来调整输出信号，以减小系统的超调和振荡现象，提高系统的稳定性。

微分项的引入可以有效地减小系统的响应速度，避免系统出现过度调节问题。

PID控制算法的实现通常需要通过调节PID控制器的三个参数：比例增益（Kp）、积分时间常数（Ti）和微分时间常数（Td）。

参数的优化需要根据具体的系统需求和控制目标进行调节，一般通过实验和不断调整来找到最佳的参数组合。

需要注意的是，PID控制算法有一些局限性。

例如，当系统存在非线性和时变特性时，PID控制算法可能无法满足系统的要求。

此外，PID控制算法也对噪声和测量误差比较敏感，需要进行适当的滤波和校正。

总之，PID控制算法是一种简单且常用的自动控制算法。

通过比例项、积分项和微分项的结合调节，可以实现系统的稳定控制和误差校正。

在实际应用中，需要根据具体的控制需求和系统特性进行参数调整，以达到最佳的控制效果。

pid算法的原理和算法摘要：1.PID 算法的概念2.PID 算法的原理3.PID 算法的应用4.PID 算法的参数调整正文：一、PID 算法的概念PID 算法，即比例- 积分- 微分算法，是一种在自动控制原理中应用最为广泛的控制算法。

它主要由比例控制、积分控制和微分控制三部分组成，简称PID 控制，又称PID 调节。

二、PID 算法的原理1.比例控制：比例控制是根据系统偏差（实际值与期望值之间的差值）来调整控制量，其特点是控制作用与偏差成正比。

比例控制结构简单，易于实现，但不能消除系统的静差。

2.积分控制：积分控制是根据系统偏差的积分来调整控制量，其特点是控制作用与偏差的积分成正比。

积分控制可以消除系统的静差，但可能导致系统震荡。

3.微分控制：微分控制是根据系统偏差的变化速度来调整控制量，其特点是控制作用与偏差的变化速度成正比。

微分控制可以预测系统的变化趋势，从而减小系统的超调量和调整时间。

三、PID 算法的应用PID 算法广泛应用于工业控制、过程控制、航天航空、汽车工程等领域。

当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，PID 算法可以依靠经验和现场调试来确定控制器的结构和参数，从而实现较好的控制效果。

四、PID 算法的参数调整PID 算法的参数调整方法有很多，如试凑法、临界比例度法、扩充临界比例度法等。

参数调整的目的是使控制系统达到所需的性能指标，如超调量、调整时间、稳态误差等。

总结：PID 算法作为一种经典的自动控制算法，在实际应用中具有广泛的适用性和优越的性能。

通过比例、积分、微分三个环节的协同作用，PID 算法能够实现对被控对象的有效控制。

PID控制算法范文一、PID控制算法的基本原理1.比例控制（P控制）比例控制是根据被控对象的偏差信号与设定值之间的差异来调整控制量的大小。

当偏差信号较大时，控制量也会较大，用于缩小偏差；当偏差信号较小时，控制量也会较小，用于稳定系统。

2.积分控制（I控制）积分控制是根据偏差信号的积分累加量来调整控制量的大小。

积分控制可以消除静差，并增强控制系统的稳定性。

但是，过大的积分参数会导致系统的超调和震荡。

3.微分控制（D控制）微分控制是根据偏差信号的变化速率来调整控制量的大小。

微分控制可以减小系统的超调和快速抑制震荡，但是过大的微分参数会带来噪声放大和系统的不稳定。

二、PID控制算法的实现1.离散时间PID控制算法的实现在离散时间下，PID控制算法可以表示为：u(k)=Kp*[e(k)+T*(1/Ti)*∑(e(i))+Td*(e(k)-e(k-1))/T]其中，u(k)为当前时刻的控制量，e(k)为当前时刻的偏差信号，Kp 为比例系数，Ti为积分时间常数，Td为微分时间常数，T为采样周期。

2.连续时间PID控制算法的实现在连续时间下，PID控制算法可以表示为：u(t) = Kp * [e(t) + (1/Ti) * ∫(e(t))dt + Td * de(t)/dt]其中，u(t)为当前时刻的控制量，e(t)为当前时刻的偏差信号，Kp 为比例系数，Ti为积分时间常数，Td为微分时间常数。

三、PID控制算法的优化方法1.参数整定通过分析被控对象的特性，选择合适的比例系数、积分时间常数和微分时间常数。

常用的整定方法有经验整定、频域法和遗传算法等。

2.鲁棒控制为了使PID控制算法对被控对象的参数变化具有鲁棒性，可以采用鲁棒控制方法，如自适应PID控制、模糊PID控制等。

3.先进的控制算法除了传统的PID控制算法，还可以采用一些先进的控制算法来替代PID控制，如模型预测控制、自适应控制等。

综上所述，PID控制算法是一种经典的控制算法，在工业自动化控制系统中得到广泛应用。

PID控制算法
PID控制算法是一种广泛应用于工控领域的经典控制算法。

它是根据
被控对象的反馈信号与设定值之间的差异（称为误差）来计算控制器输出
的一种反馈控制算法。

PID控制算法的名称由三个参数所决定，分别是比
例增益（Proportional）、积分时间（Integral）、微分时间（Derivative），分别对应P、I、D三个字母。

PID控制算法的基本原理是通过对误差的比例、积分和微分分量的调节，实现对被控对象的控制。

比例增益参数决定了控制器输出与误差之间
的线性关系；积分时间决定了对误差的累加程度，可以消除系统静态误差；微分时间则可以预测误差变化的趋势，从而提前调整控制器输出，减小系
统的振荡。

在PID控制算法中，比例增益起到了主导作用。

较大的比例增益可以
使系统响应速度快，但也容易引起系统的振荡；较小的比例增益则可以减
小系统振荡，但响应速度较慢。

积分时间的主要作用是消除系统的静态误差，较大的积分时间可以减小静态误差，但也容易导致系统的超调；较小
的积分时间则会增大静态误差。

微分时间可以使系统对误差变化的趋势进
行预测，较大的微分时间可以减小系统振荡，但也容易使系统响应速度下降；较小的微分时间则会增大系统的振荡。

除了基本的PID控制算法之外，还可以通过改进或变种的方式来提高PID控制器的性能。

例如，增加反馈路径或前馈路径、引入自适应性、使
用模糊PID控制或模型预测控制等方法。

总之，PID控制算法是一种简单而有效的控制算法，具有广泛的应用价值。

通过调节PID控制器的参数，可以实现对被控对象的精确控制，满足不同应用场景的要求。

积分调节（I）
通过累积误差来进行调节。积分调节将不断累积误差，并根据累积误差 的大小来调整加热元件的功率输出，以消除误差。
03
微分调节（D）
根据温度误差的变化率来调节加热元件的功率输出。微分调节能够预测
温度的变化趋势，并根据变化趋势来调整加热元件的功率输出，以提前
调整，减小误差。
PID温度控制算法的应用场景
微分参数（D）的调整
总结词
微分参数用于抑制超调和减小调节时间，调整微分参数可以改变系统对误差变化的响应 速度。
详细描述
微分参数的调整主要影响系统对误差变化的响应速度。增大微分参数可以加快系统对误 差变化的响应速度，有助于抑制超调，减小调节时间；但过大的微分参数可能导致系统 对噪声和干扰过于敏感。减小微分参数则会使系统对误差变化的响应速度变慢，可能导
PID温度控制算法与其他控制算法的比较
模糊控制算法
模糊控制算法能够处理不确定性和非 线性问题，但在温度控制中，PID控 制算法具有更高的稳定性和可靠性。
神经网络控制算法
神经网络控制算法具有强大的自学习 和自适应能力，但在实际应用中， PID控制算法更加简单、易实现。
PID温度控制算法在智能家居领域的应用前景
pid温度控制算法
contents
目录
• PID温度控制算法简介 • PID温度控制算法的参数调整 • PID温度控制算法的实现 • PID温度控制算法的案例分析 • PID温度控制算法的未来发展
01
PID温度控制算法简介
PID温度控制算法的定义
01
PID温度控制算法是一种基于比例 -积分-微分控制的温度调控方法 。它通过调节加热元件的功率输 出，以达到对温度的精确控制。
积分参数（I）的调整

第一章PID控制算法PID控制算法是一种经典的反馈控制算法，它在自动控制领域被广泛应用于控制系统中。

PID控制算法的全称为比例-积分-微分控制算法，它通过比例控制、积分控制和微分控制的结合来实现对被控对象的稳定控制。

在PID控制算法中，比例控制（P）是指根据被控对象当前的偏差值与设定值之间的差异来进行控制。

比例控制的作用是使被控对象产生反馈力，使其逐渐接近设定值。

比例控制具有响应快的特点，但是容易出现超调现象，即被控对象距离设定值越远，输出力越大。

积分控制（I）是指根据被控对象历史的积累误差来进行控制。

积分控制的作用是消除系统静态误差，使被控对象最终达到设定值。

积分控制具有消除静态误差的作用，但是容易引起系统的振荡。

微分控制（D）是指根据被控对象当前的变化率来进行控制。

微分控制的作用是调整系统的响应速度，减轻超调现象。

微分控制具有抑制超调和提高系统稳定性的作用，但是容易受到噪声的干扰。

PID控制算法的基本原理是将比例控制、积分控制和微分控制的输出值进行加权求和，作为最终的控制输出信号。

以误差e(t)表示为被控对象的期望值与实际值的差异，比例部分的输出为Kp * e(t)，其中Kp为比例系数；积分部分的输出为Ki * ∫e(t)dt，其中Ki为积分系数；微分部分的输出为Kd * de(t)/dt，其中Kd为微分系数。

然后将这三个部分的输出进行相加，作为最终的控制输出信号，即u(t) = Kp * e(t) +Ki * ∫e(t)dt + Kd * de(t)/dt。

在实际应用中，对于不同的被控对象和控制要求，PID控制算法的参数需要进行调整。

常用的调参方法有手动调参和自动调参两种。

手动调参是通过观察被控对象的响应特性，逐步调整比例系数、积分系数和微分系数，以达到较好的控制效果。

自动调参是通过一些自适应调参算法，如遗传算法、粒子群算法等，自动最佳的参数组合。

总之，PID控制算法是一种简单而有效的控制算法，在工业自动控制领域有着广泛的应用。