下载文档原格式
第一篇 基础知识第一章 坐标、方向与距离第一节 地理坐标一、地球形体船舶在海上航行时，需要确定船舶的位置、航向和航程，这就要求在地球表面建立坐标系和确定方向的基准线，因此要对地球的形状有一定的了解。
地球的自然表面是不平坦的，是一个非常复杂而又不规则的曲面。
陆地上有高山、深谷和平地；海洋里有岛屿和海沟。
因此，地球的自然表面不是数学曲面，不能直接在其上进行运算，也不能直接在其上建立坐标系。
航海上所研究的地球形状，是指由假想的大地水准面所包围的闭合几何体——大地球体。
所谓大地水准面，是指与各地铅垂线相垂直且与完全均衡状态的海平面相一致的水准面，详细地说大地水准面是与平均海面相重合且延伸至大陆底部的一个连续的、无叠痕的、无棱角的闭合曲面。
大地球体仍是一个不规则的球体，不是数学曲面，不能直接在其上进行运算，也不能直接在其上建立坐标系，怎么办呢？一般在航海上，以大地球体的近似体代替大地球体来建立坐标系进行航海计算，以地球园球体作为它的第一近似体，而以地球椭园体作为它的第二近似体。
1． 第一近似体——地球圆球体在解决一般航海问题时，为了计算上的简便，通常是将大地球体当做地球园球体，其半径R =6，371，110M 。
2． 第二近似体——地球椭圆体 园体，如图1-1-1所示，地球椭园体是由椭圆P N QP S Q ′轴P N P S 轴a 、短半轴b 、扁率c 和偏心率e ,它们之间的相互关系是：a b a c -=； a b a e 22-=; c e 22≈ 在不同的历史时期，依据的测量结果不同，因而所推算出的地球椭圆体的参数也不相同。
我国从1954年开始采用前苏联克拉索夫斯基椭圆体参数，现在准备逐步采用IUGGl975年推荐的地球椭圆体参数，参见表1-1-1。
二、地球上的基本点、线、圈把地球看做第二近似体即椭圆体，如图1-1-2所示，O 为地球中心：地轴(axis of the earth)—地球自转的轴(S N P P )，即通过地球中心连结南极和北极的一条假想的线。
航海学航海学是一门研究船舶如何安全、经济地从一个港口（地点）航行到另一港口（地点）的实用性学科。
航海学主要研究下列课题：1．拟定一条安全、经济的航线和制定一个切实可行的航行计划。
2．航迹推算，包括航迹绘算和航迹计算两种方法。
航迹推算是指根据船上最基本的航海仪器（罗经和计程仪）所指示的航向和航程，结合海区内的风流要素和船舶操纵要素，不借助外界物标或航标，从某一已知船位起，推算出具有一定精度的航迹和某一时刻的船位的方法。
它是驾驶员在任何情况下，求取任何时刻的船位的最基本的方法，也是陆标定位、天文定位和电子定位的基础。
3．测定船位（简称定位），包括陆标定位、天文定位和电子定位三种。
陆标定位是指观测海图上标有准确位置的，并可供目视或雷达观测的山头、岛屿、岬角、灯塔等显著的固定物标与本船的某一（某些）相对位置关系，如方位、距离和方位差等，从而在海图上确定本船船位的方法和过程。
陆标定位一般可分为方位定位、距离定位、方位距离定位和移线定位等。
天文定位是指在海上利用航海六分仪观测天体（太阳、月亮和部分星体）高度来确定船舶位置的一种定位方法。
电子定位是指利用船舶所装备的无线电定位系统的接收机来测定本船位置的一种定位方法。
目前，普遍使用的有GPS定位系统和罗兰C定位系统。
船舶航行中，要求航海人员尽一切可能随时确定本船的船位所在。
这样，才可能结合海图，了解船舶周围的航行条件，及时采取适当、有效的航行方法和必要的航行措施，确保船舶安全、经济地航行。
航迹推算和定位是船舶在海上确定船位的两类主要方法。
4．航行方法，研究在各种航海条件下的航行方法，如沿岸航行、狭水道航行和特殊条件下的航行等。
为了研究上述课题，航海学还必须包括航海学基础知识和航路资料等基本内容。
其中，航海学基础知识主要包括坐标、方向和距离，以及海图两大部分内容；航路资料主要包括：潮汐与潮流、航标与《航标表》和航海图书资料等内容。
第一章坐标、方向和距离第一节地球形状和地理坐标一、地球形状航海上船舶和物标的坐标、方向和距离等，都是建立在一定形状的地球表面的，要研究坐标、方向和距离等航海基本问题，必须首先对地球的形状和大小作一定的了解。
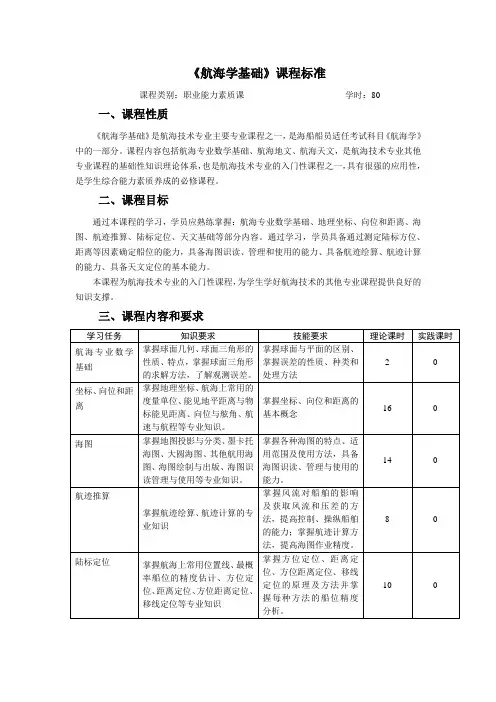
《航海学基础》课程标准课程类别：职业能力素质课学时：80一、课程性质《航海学基础》是航海技术专业主要专业课程之一，是海船船员适任考试科目《航海学》中的一部分。
课程内容包括航海专业数学基础、航海地文、航海天文，是航海技术专业其他专业课程的基础性知识理论体系，也是航海技术专业的入门性课程之一，具有很强的应用性，是学生综合能力素质养成的必修课程。
二、课程目标通过本课程的学习，学员应熟练掌握：航海专业数学基础、地理坐标、向位和距离、海图、航迹推算、陆标定位、天文基础等部分内容。
通过学习，学员具备通过测定陆标方位、距离等因素确定船位的能力，具备海图识读、管理和使用的能力、具备航迹绘算、航迹计算的能力、具备天文定位的基本能力。
本课程为航海技术专业的入门性课程，为学生学好航海技术的其他专业课程提供良好的知识支撑。
三、课程内容和要求四、实施要求1、教学要求（1）航海专业数学基础通过对比、联系实践等教学方法使学生掌握球面几何、球面三角形的性质、特点，掌握球面三角形的求解方法，了解观测误差。
以理论教学为主，加强与学员的互动。
（2）坐标、向位和距离坐标、向位和距离是航海学的基础知识，其中灯标射程为教学难点。
授课应以理论教学为主，联系航海工作实际并注意加强与学员之间的互动。
（3）海图海图是航海必备的航海资料和工具。
正确的了解海图的特点，熟悉海图上的资料，正确的使用、管理海图是船舶驾驶员的重要任务之一。
授课应理论联系实际，充分利用海图室的海图资源，使学生更好地掌握海图的相关知识。
（4）航迹推算航迹推算是驾驶员在任何情况下、在任何时刻求取船位的最基本方法，也是陆标定位、天文定位、电子定位等的基础。
航迹绘算是教学重点和难点，授课应以理论教学为主，对各种风流状态下的航迹推算进行分类、比对教学。
（5）陆标定位陆标定位是通过观测陆标与船舶之间的某种相互位置关系进行定位的方法和过程，是航海上获得船位的重要方法。
定位方法是教学重点、提高定位精度是教学难点。
第⼆节船舶定位⽅法.第⼆节船舶定位⽅法⼀、航迹推算(⼀)概述1.航海上确定船位的⽅法 1)航迹推算航迹推算是航⾏中求取船位的最基本⽅法。
它是根据船舶最基本的航海仪器(罗经和计程仪)指⽰的航向和航程，以及风流资料，在不借助于外界导航物标的条件下，从已知推算起点开始，推算出具有⼀定精度的航迹和船位。
2)定位定位是利⽤航海仪器，观测外界已确知其位置的物标，然后根据测量结果，求出观测时刻的船位。
陆标定位定位⽆线电航海仪器定位天⽂定位2.航迹推算的种类 1)航迹绘算法即海图作业法，是根据船舶航⾏时的真航向、航程和风流要素，在海图上绘画出推算航迹和推算船位；或者根据计划航线，预配风流压差，作图求出应驶的真航向和推算船位。
2)航迹计算法航迹计算法是根据推算起点的经纬度、航向和航程，利⽤查表或利⽤数学计算公式，求到达点推算船位经纬度的⽅法。
3.航迹推算的作⽤ 1)可随时确定船位；2)可预先推算出到达点的时间；3)估计船舶航⾏前⽅是否存在航⾏危险； 4)推算船位是天⽂定位和⽆线电定位的基础。
4.航迹推算的起、迄时间 1)起点：应在驶离引航⽔域或港界，定速航⾏后⽴即开始。
推算起点必须是准确的船位。
2)迄点抵达⽬的港领航⽔域或接近港界有物标或航标可供⽬测校验船位和导航时。
3)中断推算开始后不得⽆故中断。
但是，如果航经渔区或狭⽔道，由于转向频繁，可以暂时中⽌推算，但应将中断的起、迄点船位记⼊航海⽇志。
5.航迹推算中常⽤的名词术语1)计划航迹线简称计划航线，是根据安全、经济的原则在海图上拟定的航线，即船舶航⾏时计划要⾛的航线。
2)计划航迹向CA简称计划航向，是计划航迹前进的⽅向，由真北按顺时针⽅向计量到计划航迹线的⾓度。
3)推算航迹线通过航迹推算，预配风流压差后得到的航迹线，⼀般应与计划航线⼀致。
4)航迹线即实际航迹线，是船舶航⾏时所留下的航迹。
5)航迹向即实际航迹向，是由真北瞬时⽅向计量到航迹线的⾓度。
(⼆)航迹绘算1.⽆风流情况下的航迹绘算1)推算原则计划航向=真航向，即CG=TC推算航程=计程仪航程，即S G=S L(L2-L1)(1+?L)2)作图⽅法由推算起点画出计划航线，在其上截取计程仪航程S L得⼀点，即为积算船位，⽤DR表⽰。
课时授课计划课次序号：0001一、课题：第一章基础知识—坐标二、课型：解疑存疑型三、目的要求：掌握三种地球近似体的概念，理解地理坐标的定义和度量方法，理解大地坐标系的基本概念。
四、重点、难点：有关经纬度的计算五、教学方法及手段：PPT 教学六、参考资料：航海学，大连海事大学出版社航海学习题集，山东交通学院海运学院主编七、作业：航海学习题集相关练习八、授课记录：九、授课效果分析：通过习题反馈效果绪论：航海学概要简单介绍航海学这门学科的主要研究内容，让学生从宏观把握学习航海学对航海的重要意义。
航线拟定确定船位：航迹推算－－航迹绘算、航迹计算测定船位－－陆标定位(地文航海)－－天文定位(天文航海)－－无线电定位(电子航海)航行方法：大洋航行、沿岸航行、狭水道航行特殊条件下航行(雾中、冰区、岛礁区航行)航海学还包括：航海学基础知识：坐标、方向和距离；海图航路资料：潮汐与《潮汐表》航标和《航标表》航海图书资料第一篇基础知识第一章坐标、方向和距离1．1地球形状，地理坐标与大地坐标系1．1．1 地球形状概述：研究坐标、方向和距离等⇒地球的形状；地球自然表面⇒难以用数学公式描述；珠穆朗玛峰8 848 m，仅为地球半径的千分之一；可以用占地球表面约71％的海水面来描述地球形状。
大地水准面：设想一个与平均海面相吻合的水准面，并将其向陆地延伸，且保持该延伸面始终与当地的铅垂线相垂直，这样所形成的连续不断的、光滑的闭合水准面，叫作大地水准面。
大地球体：由上述大地水准面所包围的几何体称为大地球体，是理想的地球形状。
所以用大地球体描述地球形状，大地球体是大地水准面围成的球体。
大地球体的三种近似体：（航海上常用的前两种）第一近似体：地球圆球体 概念：地球圆球体参数：R = 3 437.746 8 n mile = 6 366 707m应用：计算简便、精度要求不高。
如航迹计算，简易墨卡托海图绘制，大圆航向和航程计算 第二近似体：地球椭圆体 概念：地球旋转椭圆体参数：长半轴a 、短半轴b 、扁率c 、偏心率e关系：aba c -=：=e ab a 22- 所以：c c c aba b e 2)2()1)(1(2≈-=+-=应用：用于较精确的航海计算等，如定义地理坐标，墨卡托海图绘制第三近似体：地球椭球体，精度高，多用于军事航天等尖端领域。
