2014东大真题解答

东北大学2014自控真题一、简答题（10分）1. 简述前馈控制可以改善线性系统哪方面性能，对线性系统稳定性有何影响？2. 简述频率特性的定义，最常用的频率特性表示方法有哪些？ 解：（1） 通过前馈补偿，提高了系统的控制精度，减小了稳态误差。

对于给定前馈，可以提高跟踪速度。

对于按扰动矫正，可在偏差对被控量产生影响前对系统进行校正。

由于输入取自闭环外，不影响系统的特征方程式，故不影响系统的稳定性。

（2） 当输入信号为谐波时，频率特性为输出信号的傅氏变换与输入信号的傅氏变换之比。

常见的表示法有幅相频率特性曲线、对数频率特性曲线、对数幅相频率特性曲线。

二、（20分）若某系统在单位阶跃输入作用时，系统在零初始条件下的输出响应为212t t e e -+,试求系统的单位阶跃响应。

解：12132[c(t)]21(s 2)(s 1)-+=-+=----s L s s s s 由于1Rs （S ）= 故(S)32(S)(S)(S 2)(S 1)B C S W R -+==-- 当(t)(t)r δ=，即R(S)1=32(S)W (S)*R(S)(S 2)(S 1)B SC -+==--， 进行拉氏反变换有11241[c(s)][]421---=+=-+--t t L L e e s s 三、（20分）已知系统的结构图如下图所示，若系统以2/n w rad s =的频率做等幅震荡，试确定震荡的k 、a 。

解：系统闭环特征方程：32(s)s as (k 2)s (k 1)0B D =+++++=由系统在2/n w rad s =的频率做等幅震荡，知2j ±为特征方程式的根。

令2s j =得“84(k 2)*2(k 1)0j a j --++++=整理得(2k 4)(k 14a)0j -++-=分别令实部为零，虚部为零，可得2k =，0.75a =四、（20分）已知单位负反馈系统的开环传递函数为，21(s a)4(s)(s 1)K W s +=+ 试绘制以a 为参数的根轨迹0a ≤<∞并确定使该单位负反馈系统稳定的a 的取值范围。

2014年辽宁省高考数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2014•辽宁）已知全集U=R，A={x|x≤0}，B={x|x≥1}，则集合∁U（A∪B）=（）A．{x|x≥0} B．{x|x≤1} C．{x|0≤x≤1} D．{x|0＜x＜1}考点：交、并、补集的混合运算．专题：集合．分析：先求A∪B，再根据补集的定义求C U（A∪B）．解答：解：A∪B={x|x≥1或x≤0}，∴C U（A∪B）={x|0＜x＜1}，故选：D．点评：本题考查了集合的并集、补集运算，利用数轴进行数集的交、并、补运算是常用方法．2．（5分）（2014•辽宁）设复数z满足（z﹣2i）（2﹣i）=5，则z=（）A．2+3i B．2﹣3i C．3+2i D．3﹣2i考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：把给出的等式两边同时乘以，然后利用复数代数形式的除法运算化简，则z可求．解答：解：由（z﹣2i）（2﹣i）=5，得：，∴z=2+3i．故选：A．点评：本题考查了复数代数形式的除法运算，是基础的计算题．3．（5分）（2014•辽宁）已知a=，b=log2，c=log，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a考点：对数的运算性质．专题：计算题；综合题．分析：利用指数式的运算性质得到0＜a＜1，由对数的运算性质得到b＜0，c＞1，则答案可求．解答：解：∵0＜a=＜20=1，b=log2＜log21=0，c=log=log23＞log22=1，∴c＞a＞b．故选：C．点评：本题考查指数的运算性质和对数的运算性质，在涉及比较两个数的大小关系时，有时借助于0、1这样的特殊值能起到事半功倍的效果，是基础题．4．（5分）（2014•辽宁）已知m，n表示两条不同直线，α表示平面，下列说法正确的是（）A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊂α，则m⊥nC．若m⊥α，m⊥n，则n∥αD．若m∥α，m⊥n，则n⊥α考点：空间中直线与直线之间的位置关系．专题：空间位置关系与距离．分析：A．运用线面平行的性质，结合线线的位置关系，即可判断；B．运用线面垂直的性质，即可判断；C．运用线面垂直的性质，结合线线垂直和线面平行的位置即可判断；D．运用线面平行的性质和线面垂直的判定，即可判断．解答：解：A．若m∥α，n∥α，则m，n相交或平行或异面，故A错；B．若m⊥α，n⊂α，则m⊥n，故B正确；C．若m⊥α，m⊥n，则n∥α或n⊂α，故C错；D．若m∥α，m⊥n，则n∥α或n⊂α或n⊥α，故D错．故选B．点评：本题考查空间直线与平面的位置关系，考查直线与平面的平行、垂直的判断与性质，记熟这些定理是迅速解题的关键，注意观察空间的直线与平面的模型．5．（5分）（2014•辽宁）设，，是非零向量，已知命题p：若•=0，•=0，则•=0；命题q：若∥，∥，则∥，则下列命题中真命题是（）A．p∨q B．p∧q C．（￢p）∧（￢q）D．p∨（￢q）考点：复合命题的真假；平行向量与共线向量．专题：简易逻辑．分析：根据向量的有关概念和性质分别判断p，q的真假，利用复合命题之间的关系即可得到结论．解答：解：若•=0，•=0，则•=•，即（﹣）•=0，则•=0不一定成立，故命题p为假命题，若∥，∥，则∥平行，故命题q为真命题，则p∨q，为真命题，p∧q，（￢p）∧（￢q），p∨（￢q）都为假命题，故选：A．点评：本题主要考查复合命题之间的判断，利用向量的有关概念和性质分别判断p，q的真假是解决本题的关键．6．（5分）（2014•辽宁）6把椅子排成一排，3人随机就座，任何两人不相邻的坐法种数为（）A．144 B．120 C．72 D．24考点：计数原理的应用．专题：应用题；排列组合．分析：使用“插空法“．第一步，三个人先坐成一排，有种，即全排，6种；第二步，由于三个人必须隔开，因此必须先在1号位置与2号位置之间摆放一张凳子，2号位置与3号位置之间摆放一张凳子，剩余一张凳子可以选择三个人的左右共4个空挡，随便摆放即可，即有种办法．根据分步计数原理可得结论．解答：解：使用“插空法“．第一步，三个人先坐成一排，有种，即全排，6种；第二步，由于三个人必须隔开，因此必须先在1号位置与2号位置之间摆放一张凳子，2号位置与3号位置之间摆放一张凳子，剩余一张凳子可以选择三个人的左右共4个空挡，随便摆放即可，即有种办法．根据分步计数原理，6×4=24．故选：D．点评：本题考查排列知识的运用，考查乘法原理，先排人，再插入椅子是关键．7．（5分）（2014•辽宁）某几何体三视图如图所示，则该几何体的体积为（）A．8﹣2πB．8﹣πC．8﹣D．8﹣考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：几何体是正方体切去两个圆柱，根据三视图判断正方体的棱长及切去的圆柱的底面半径和高，把数据代入正方体与圆柱的体积公式计算．解答：解：由三视图知：几何体是正方体切去两个圆柱，正方体的棱长为2，切去的圆柱的底面半径为1，高为2，∴几何体的体积V=23﹣2××π×12×2=8﹣π．故选：B．点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．8．（5分）（2014•辽宁）设等差数列{a n}的公差为d，若数列{}为递减数列，则（）A．d＜0 B．d＞0 C．a1d＜0 D．a1d＞0考点：数列的函数特性．专题：函数的性质及应用；等差数列与等比数列．分析：由于数列{2}为递减数列，可得=＜1，解出即可．解答：解：∵等差数列{a n}的公差为d，∴a n+1﹣a n=d，又数列{2}为递减数列，∴=＜1，∴a1d＜0．故选：C．点评：本题考查了等差数列的通项公式、数列的单调性、指数函数的运算法则等基础知识与基本技能方法，属于中档题．9．（5分）（2014•辽宁）将函数y=3sin（2x+）的图象向右平移个单位长度，所得图象对应的函数（）A．在区间[，]上单调递减B．在区间[，]上单调递增C．在区间[﹣，]上单调递减D．在区间[﹣，]上单调递增考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：直接由函数的图象平移得到平移后的图象所对应的函数解析式，然后利用复合函数的单调性的求法求出函数的增区间，取k=0即可得到函数在区间[，]上单调递增，则答案可求．解答：解：把函数y=3sin（2x+）的图象向右平移个单位长度，得到的图象所对应的函数解析式为：y=3sin[2（x﹣）+]．即y=3sin（2x﹣）．当函数递增时，由，得．取k=0，得．∴所得图象对应的函数在区间[，]上单调递增．故选：B．点评：本题考查了函数图象的平移，考查了复合函数单调性的求法，复合函数的单调性满足“同增异减”原则，是中档题．10．（5分）（2014•辽宁）已知点A（﹣2，3）在抛物线C：y2=2px的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，则直线BF的斜率为（）A．B．C．D．考点：直线与圆锥曲线的关系．专题：圆锥曲线的定义、性质与方程．分析：由题意先求出准线方程x=﹣2，再求出p，从而得到抛物线方程，写出第一象限的抛物线方程，设出切点，并求导，得到切线AB的斜率，再由两点的斜率公式得到方程，解出方程求出切点，再由两点的斜率公式求出BF的斜率．解答：解：∵点A（﹣2，3）在抛物线C：y2=2px的准线上，即准线方程为：x=﹣2，∴p＞0，=﹣2即p=4，∴抛物线C：y2=8x，在第一象限的方程为y=2，设切点B（m，n），则n=2，又导数y′=2，则在切点处的斜率为，∴即m=2m，解得=2（舍去），∴切点B（8，8），又F（2，0），∴直线BF的斜率为，故选D．点评：本题主要考查抛物线的方程和性质，同时考查直线与抛物线相切，运用导数求切线的斜率等，是一道基础题．11．（5分）（2014•辽宁）当x∈[﹣2，1]时，不等式ax3﹣x2+4x+3≥0恒成立，则实数a的取值范围是（）C．[﹣6，﹣2]D．[﹣4，﹣3] A．[﹣5，﹣3]B．[﹣6，﹣]考点：函数恒成立问题；其他不等式的解法．专题：综合题；导数的综合应用；不等式的解法及应用．分析：分x=0，0＜x≤1，﹣2≤x＜0三种情况进行讨论，分离出参数a后转化为函数求最值即可，利用导数即可求得函数最值，注意最后要对a取交集．解答：解：当x=0时，不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立；当0＜x≤1时，ax3﹣x2+4x+3≥0可化为a≥，令f（x）=，则f′（x）==﹣（*），当0＜x≤1时，f′（x）＞0，f（x）在（0，1]上单调递增，f（x）max=f（1）=﹣6，∴a≥﹣6；当﹣2≤x＜0时，ax3﹣x2+4x+3≥0可化为a≤，由（*）式可知，当﹣2≤x＜﹣1时，f′（x）＜0，f（x）单调递减，当﹣1＜x＜0时，f′（x）＞0，f（x）单调递增，f（x）min=f（﹣1）=﹣2，∴a≤﹣2；综上所述，实数a的取值范围是﹣6≤a≤﹣2，即实数a的取值范围是[﹣6，﹣2]．故选：C．点评：本题考查利用导数研究函数的最值，考查转化思想、分类与整合思想，按照自变量讨论，最后要对参数范围取交集；若按照参数讨论则取并集．12．（5分）（2014•辽宁）已知定义在[0，1]上的函数f（x）满足：①f（0）=f（1）=0；②对所有x，y∈[0，1]，且x≠y，有|f（x）﹣f（y）|＜|x﹣y|．若对所有x，y∈[0，1]，|f（x）﹣f（y）|＜m恒成立，则m的最小值为（）A．B．C．D．考点：函数恒成立问题；绝对值不等式的解法．专题：综合题；函数的性质及应用．分析：依题意，构造函数f（x）=（0＜k＜），分x∈[0，]，且y∈[0，]；x∈[0，]，且y∈[，1]；x∈[0，]，且y∈[，1]；及当x∈[，1]，且y∈[，1]时，四类情况讨论，可证得对所有x，y∈[0，1]，|f（x）﹣f（y）|＜恒成立，从而可得m≥，继而可得答案．解答：解：依题意，定义在[0，1]上的函数y=f（x）的斜率|k|＜，依题意，k＞0，构造函数f（x）=（0＜k＜），满足f（0）=f（1）=0，|f（x）﹣f（y）|＜|x﹣y|．当x∈[0，]，且y∈[0，]时，|f（x）﹣f（y）|=|kx﹣ky|=k|x﹣y|≤k|﹣0|=k×＜；当x∈[0，]，且y∈[，1]，|f（x）﹣f（y）|=|kx﹣（k﹣ky）|=|k（x+y）﹣k|≤|k（1+）﹣k|=＜；当y∈[0，]，且x∈[，1]时，同理可得，|f（x）﹣f（y）|＜；当x∈[，1]，且y∈[，1]时，|f（x）﹣f（y）|=|（k﹣kx）﹣（k﹣ky）|=k|x﹣y|≤k×（1﹣）=＜；综上所述，对所有x，y∈[0，1]，|f（x）﹣f（y）|＜，∵对所有x，y∈[0，1]，|f（x）﹣f（y）|＜m恒成立，∴m≥，即m的最小值为．故选：B．点评：本题考查函数恒成立问题，着重考查构造函数思想、分类讨论思想、函数方程思想与等价转化思想的综合运用，考查分析、推理及运算能力，属于难题．二、填空题：本大题共4小题，每小题5分。

一、选择题（15个小题45分）
二、4线-2线编码器设计，要求有输出有效信号标志（可使用与门、或门、非门）7分
三、时许逻辑电路给出电路图写状态转移方程画出时序图10分
四、根据PAL16L8图中的编程情况写出输出表达式用74153利用四选一实现
五、用面包板、发光二极管、电阻、导线、+5v电压源、峰值为+5v的方波、74195移位寄存器来设计直接反映其右移功能。

六、拉普拉斯变换的卷积性质证明9分
七、序列x(k)的双边z变换为x(Z)，收敛域为a<|z<|b，y(k)=x(k/2),k为偶数时y(k)=0,k为奇数时。

求y(k)的双边z变化及其收敛域。

10分
八、一个调制的题目，输入一个信号乘以p(t)，p(t)是一个周期矩形波（是奇信号的那种），有三问1）求p(t)傅里叶变化并画出频谱2）使得信号恢复出来，一些参数的要求3）忘了这个题目分值为18分不说了都是泪跟13年的那题很相似基本是原题
九、题目给出了一个RC网络图（是低通滤波器）。

1）写出其H(s)，2）画出其大致幅频曲线，3）给了e(t)=tε(t)（e(t)的形式可能不是这个）求零状态响应3）e(t)=1+sint求输出响应。

十、题目给出了一个系统框图（框图中有一个K），标明了A、B、C三点，题目要求将A、B、C三点处作为状态变量。

1）写出状态方程和输出方程2）求系统的H(s)3）求系统稳定是K的取值范围。

共 4 页 第 1 页南大学2014学年上学期工科数学分析期末考试卷（A 卷） 课程名称 考试学期 得分 适用专业 工科类 考试形式 闭卷 考试时间长度 150分钟 1．函数1()2d (0)x F x t x ⎫=->⎪⎭⎰的单调增加区间为 ； 2．已知2060arctan()d lim 1t t x ax x t →=⎰，则a = ； 3．曲线32635y x x x =-++上的拐点是 ； 4．曲线323(2)x y x =+的斜渐近线的方程是 ； 5．二阶常系数线性非齐次微分方程265e x y y y '''+-=的特解形式是*y = ； 6．设θ是常数，0x ∀>，若0ln d ln 2x x t t x θ⎛⎫= ⎪⎝⎭⎰，则θ= ； 7．240sin d x x π=⎰ ； 8．设21()cos d x f x t t =⎰，则10()d f x x =⎰ ； 9．用M ε-语言叙述极限lim ()x f x →-∞存在的Cauchy 收敛准则 .二.按要求计算下列各题（本题共5小题，每小题6分，满分30分）10．300sind lim (1cos )x x t tt x x →-⎰ 11. ()240(1)sin(1)d x x x x --⎰共 4 页 第 2 页12．已知()f x 的一个原函数为(1sin )ln x x +，求()d xf x x '⎰.13．设220sin ()2d ,()1xx t f x t p x ax bx c t+=+=+++⎰，求常数a 、b 、c ，使得 (0)(0),(0)(0),(0)(0)p f p f p f ''''''===.14。

x ⎰共 4 页 第 3 页 三（15）．（本题满分8分）求微分方程sin 2e x y y x ''+=+满足初值条件01x y ==， 00x y ='=的特解.四（16）．（本题满分7分）设函数()f x 定义在区间[0,)+∞上，恒取正值，若对(0,)x ∀∈+∞，()f x 在[0,)+∞上的积分平均值等于(0)f 与()f x 的几何平均值，试求()f x 的表达式.五（17）．（本题满分6分）1与(ln 1+的大小，并给出证明.共 4 页 第 4 页六（18）．（本题满分7分） 对参数,p q ，讨论反常积分0d 1p qx x x +∞+⎰的敛散性，并给出证明.七（19）．（本题满分6分）设()f x 在区间[0,2]上连续可导，(0)(2)0f f ==，求证：2002()d max ()x f x x f x ≤≤'≤⎰.。

东 南 大 学 考 试 卷 （A 卷）课程名称弹性力学考试学期 14-15-2得分适用专业 交通运输工程 考试形式闭卷考试时间长度 120分钟共3 页 第 1 页一、问答题（30分，每小题3分） 1. 弹性力学中的基本假定有哪些？2. 什么是边界条件？它可以分为哪几种类型？3. 什么是逆解法？4. 试叙述圣维南原理。

5．试写出极坐标系中用应力函数表达的相容方程。

6. 不计体力时，在极坐标中求平面应力问题，归结为求解一个应力函数()ρϕΦ，，它应满足那些条件？7. 产生轴对称应力状态的条件是什么？ 8. 小孔口问题的应力集中现象具有那些特点？ 9. 试叙述极小势能原理。

10. 试写出弹性力学的虚功方程。

二、计算题1. 试证明：发生最大与最小切应力的面上，正应力的数值都等于两个主应力的平均值。

（10分）2. 已知开孔矩形薄板在图示荷载作用下的应力解为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=2222223112cos 212ρρϕρσρr r q r q ⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+=4422312cos 212ρϕρσϕr q r q试求在孔边应力分量ϕσ达到的最大值及其位置。

（10分）3. 试检验223126y a y a +=Φ能否作为应力函数？若能，试求应力分量（不计体力），并画出图示杆件上的面力，求面力的合力并指出该应力函数所能解的问题。

（10分）4. 已知内半径为r ，外半径为R 的圆环受内压1q 作用时，圆环中的应力分别为1222211q r R R ---=ρσρ；1222211q r R R -+=ρσϕ试求具有圆形孔无限大弹性薄板内的应力。

（10分）5. 设半平面体在直边界上受集中力偶的作用，单位宽度上力偶矩为M ，如图所示，设应力函数为2=B sin +C ϕϕΦ，试求应力分量（15分）。

共3 页 第2页自觉 遵 守 考 场 纪 律 如 考 试 作 弊 此 答 卷 无效6. 图示的薄板，b a =，厚度为1个单位，两边固定，取泊松比0=μ，上边受到均布拉力q 的作用。

资料来源：中国教育在线 /
资料来源：中国教育在线 / 英语基础
一、单词全都是考单词，没有语法。

单词只有几题是专八单词里的，其他的都看不懂。

本人专八单词来回背了有6、7遍，可是做起来还是感觉困难。

每道题都像是在解释一种现象或者文化~总之就是单词要好好的背，尽可能多背写GRE 单词吧~~
二、阅读，阅读感觉不难，基本都是原文可以边度边做的，文章很短，之前看到说是GRE 类型的阅读，感觉蛮像的。

三、作文。

很简单，就专八类型的作文。

问ZF 该不该给那些考上大学但付不起学费的学生实行免学费政策。

至少300字。

翻译。

翻译这次改革，之前是一篇C-E 一篇E-C ，这次
第一大题是10个单句的E-C ，40分。

都不难。

第二题是C-E ，三段，蛮短的，讲科技的，感觉跟二笔的类型差不多，本人就是拿二笔来训练的。

所以做起来还蛮顺手的。

第三题是一整篇E-C ，也是讲科技的，说的是小行星的危害，使得欧洲国家发散探测器什么之类的上去获取信息。

百科。

一、10个名词解释，6分一个，一共60分。

看到的时候要很郁闷，之前是25个，2分一个，这次改革改得分值好大。

九州，五礼，三省六部制，玄学，古文运动，乾嘉学派，中体西用，软实力，避讳，还有一个忘了。

二、就最近发生的新闻，写一篇新闻评论。

600字
三、给了一大段钱钟书关于文学翻译的理论，就自拟题目写一篇作文，要有专业性，800字。

第三章 习题与答案 习题 A1.求向量123(4,1,3,2),(1,2,3,2),(16,9,1,3)T T T=--=-=-ααα的线性组合12335.+-ααα 解 12341161293535331223⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-=+- ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ααα1251613109491512561037⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪=+-= ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭. 2.从以下方程中求向量α1233()2()5()-++=+αααααα，其中123(2,5,1,3),(10,1,5,10),(4,1,1,1).TT T ===-ααα 解 由方程得1233322550-++--=αααααα，1232104651112632532515118310124⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=+-=+-= ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭αααα故1234⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭α,即(1,2,3,4)T =α.3.求证:向量组12i s α,α,,α,α 中的任一向量i α可以由这个向量组线性表出. 证 120010(1,2,,)i i s i s =+++++= ααααα4.证明: 包含零向量的向量组线性相关.证 设向量组为1211α,α,,α,0,α,,αi i s -+ ,则有12110α0αα00α0α0,0i i s k k -++++++++=≠而0,0,,0,,0,,0k 不全为0,故向量组线性相关.5.设有m 个向量12α,α,,αm ,证明: 若αα()i j i j =≠,则向量组12α,α,,αm 线性相关. 证 显然有1210α0αα0α()α0α0,0i i j m k k k +++++++-++=≠ , 而0,,0,,0,,0,,0,,0k k - 不全为0.故向量组线性相关.6.判断下列向量组的线性相关性(1) (1,1,0),(0,1,1,),(3,0,0,); (2) (2,0),(0,-1);(3) (-4,-5,2,6),(2,-2,1,3),(6,-3,3,9),(4,-1,5,6);(4) (1,0,0,2,5),(0,1,0,3,4),(0,0,1,4,7),(2,-3,4,11,12).解 (1)设有三个数123,,k k k ,使123(1,1,0)(0,1,1,) (3,0,0,)=(0,0,0)k k k ++则有方程组131223000k k k k k +=⎧⎪+=⎨⎪=⎩,因为系数行列式10311030010D =≠.方程组仅有零解,所以三个向量线性无关. (2)设有两个数12,k k 使12(2,0)(0,-1)=(0,0)k k + 则有方程组12200k k =⎧⎨-=⎩,由此解得120k k ==,所以两个向量线性无关.另外,也可由其分量不成比例看出两个向量线性无关. (3)设有四个数1234,,,k k k k ,使1234(-4,-5,2,6)(2,-2,1,3)(6,-3,3,9)(4,-1,5,6)=(0,0,0,0)k k k k +++,则有方程组1234123412341234426405230235063960k k k k k k k k k k k k k k k k +++=⎧⎪----=⎪⎨+++=⎪⎪+++=⎩,其系数行列式42645231021356396D ----==,所以方程组有非零解,向量组线性相关.(4) 设有四个数1234,,,k k k k ,使1234(1,0,0,2,5)(0,1,0,3,4)(0,0,1,4,7)(2,-3,4,11,12)=(0,0,0,0)k k k k +++则有方程组14243412341234203040234110547120k k k k k k k k k k k k k k +=⎧⎪-=⎪⎪+=⎨⎪+++=⎪⎪+++=⎩由前三个方程得1424342,3,4k k k k k k =-==-,代入第五个方程得4140k -=, 即40k =,从而1230k k k ===,所以向量组线性无关.7.设123α,α,α线性无关,证明:122331αα,αα,αα+++也线性无关. 证 设有三个数123,,k k k ,使()()()112223331αααααα0k k k +++++=, 则()()()131122233ααα0k k k k k k +++++=,因123α,α,α线性无关,故13122300k k k k k k +=⎧⎪+=⎨⎪+=⎩,因系数行列式10111020011D ==≠,所以只有1230k k k ===, 由此知122331αα,αα,αα+++线性无关.8.设12α,α,,αn 线性无关,问向量组122311αα,αα,,αα,ααn n n -++++ 是线性相关,还是线性无关?并给出证明. 解 设有n 个数12,,,,n k k k 使()()()()112223111αααααααα0n n n n n k k k k --++++++++= ,则得方程组1122310000n n n k k k k k k k k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩ 其系数行列式11000011100000110001(1),000110000011n n D +==+-可见,当n 为奇数时,20n D =≠,方程组仅有零解,向量组线性无关, 当n 为偶数时,0n D =,方程组有非零解,向量组线性相关.9.设12α(,,,)(1,2,,)i i i in a a a i n == ,证明:向量组12α,α,,αn 线性相关的充分必要条件是det()0ij a =.证 必要性:设12α,α,,αn 线性相关,则存在不全为0的n 个数12,,,,n k k k 使1122ααα0n n k k k +++= ,即有方程组()11121211212222112200*0n n n nn n nn n a k a k a k a k a k a k a k a k a k +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 该方程组有非零解,故系数行列式0n D =,即det()0ij a =,充分性: 对于方程组(*)当det()0ij a =时,系数行列式0n D =,所以有非零解,即存在不全为0的12,,,,n k k k 使1122ααα0n n k k k +++= 成立,故12α,α,,αn 线性相关.10.设12α,α,,αn 是一组n 维向量.已知n 维标准单位向量组12e ,e ,,e n 能由它们线性表出,证明: 12α,α,,αn 线性无关.证 设12α(,,,)(1,2,,)i i i in a a a i n == ,则有1122αe e e ,i i i in n a a a =+++可见12α,α,,αn 也能由12e ,e ,,e n 线性表出,从而两个向量组等价. 因为12e ,e ,,e n 线性无关,所以12α,α,,αn 也线性无关.11.设12α,α,,αn 是一组n 维向量.证明:它们线性无关的充分必要条件是:任一n 维向量都可由它们线性表出.证 必要性:设12α,α,,αn 线性无关,β为任一n 维向量,则12α,α,,αn ,β必线性相关.(个数大于维数),因此β可由12α,α,,αn 线性表出.充分性:设任一n 维向量β都可由12α,α,,αn 线性表出.因此12α,α,,αn 与12e ,e ,,e n 等价,从而12α,α,,αn 线性无关.12.判断下列向量是否线性相关,并求出一个极大线性无关组.(1)123α(1,2,1,4),α(9,100,10,4),α(2,4,2,8);T T T =-==--- (2) 123α(1,1,0),α(0,2,0),α(0,0,3);T T T ===(3) 1234α(1,2,1,3),α(4,1,5,6),α(1,3,4,7),α(2,1,1,0);T T T T ==---=---=- 解 (1)19221004A 1102448-⎛⎫ ⎪-⎪= ⎪- ⎪-⎝⎭ 192082001900320-⎛⎫ ⎪ ⎪→ ⎪ ⎪-⎝⎭192010000000-⎛⎫ ⎪ ⎪→ ⎪ ⎪⎝⎭102010000000-⎛⎫⎪ ⎪→⎪ ⎪⎝⎭, 向量组的秩为2, 12α,α为一个极大线性无关组.(2) 100A 120003⎛⎫ ⎪= ⎪ ⎪⎝⎭100020003⎛⎫ ⎪→ ⎪ ⎪⎝⎭向量组的秩为3, 123α,α,α为一个极大线性无关组.(3) 14122131A 15413670⎛⎫ ⎪--⎪= ⎪--- ⎪--⎝⎭141209530953018106⎛⎫ ⎪--- ⎪→ ⎪--- ⎪---⎝⎭1412095300000000⎛⎫ ⎪--- ⎪→ ⎪ ⎪⎝⎭向量组的秩为2, 12α,α为一个极大线性无关组.13.求一个秩是4的方阵,它的两个行向量是(1,0,3,0,0),(1,1,0,0,0)--. 解 所求方阵可写成1030011000A 001000001000000⎛⎫ ⎪-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,则1030001300A 00100000100000⎛⎫⎪- ⎪⎪→⎪⎪ ⎪⎝⎭显然(A)4R =.14.已知12α,α,,αs 的秩为r ,证明: 12α,α,,αs 中任意r 个线性无关的向量都构成它的一个极大线性无关组.证 设12α,α,,α,r i i i 为12α,α,,αs 中任意r 个线性无关的向量,因为向量组的秩为r ,故1212α,α,,α,α,(,,)r i i i i r i i i i ≠ 线性相关.可见12α,α,,αs 中的每个向量都可由12α,α,,α,r i i i 线性表出.因此, 12α,α,,α,r i i i 是12α,α,,αs 的一个极大线性无关组.15.用初等变换化下列矩阵为阶梯形,并判断其秩.(1)001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭; (2)1234110215610-⎛⎫ ⎪- ⎪ ⎪⎝⎭;(3)023*********-⎛⎫ ⎪- ⎪ ⎪--⎝⎭;(4)1725314353759413254759413420253248⎛⎫⎪⎪⎪⎪⎝⎭.解 (1) 001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭131********r r ↔⎛⎫ ⎪→ ⎪ ⎪⎝⎭,秩为3.(2) 1234110215610-⎛⎫ ⎪- ⎪ ⎪⎝⎭2131123403360336r r r r+-⎛⎫ ⎪→ ⎪ ⎪⎝⎭32123403360000r r -⎛⎫ ⎪→ ⎪ ⎪⎝⎭,秩为2.(3)023*********-⎛⎫ ⎪- ⎪⎪--⎝⎭12011203430471r r ---⎛⎫⎪→- ⎪ ⎪--⎝⎭213134011200130039r r r r ++--⎛⎫ ⎪→-- ⎪ ⎪--⎝⎭323011*********r r ---⎛⎫⎪→-- ⎪ ⎪⎝⎭, 秩为2.(4)1725314353759413254759413420253248⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭213143317253143201330153015r r r r r r ---⎛⎫ ⎪ ⎪→ ⎪ ⎪⎝⎭433217253143201310020000r r r r --⎛⎫⎪⎪→⎪ ⎪⎝⎭1310022013172531430000r r ↔⎛⎫ ⎪⎪→ ⎪ ⎪⎝⎭2131217100200110253190000r r r r --⎛⎫ ⎪- ⎪→ ⎪ ⎪⎝⎭23100202531900110000r r ↔⎛⎫⎪ ⎪→ ⎪- ⎪⎝⎭,秩为3. 16.证明: 两个矩阵和的秩不超过这两个矩阵秩的和,即 (A B)(A)(B)R R R +≤+.证 设1A (α,,α),(A),n R r == 1α,,αr 为一个极大线性无关组,1B (β,,β),(B),n R s == 1β,,βs 为一个极大线性无关组, 1A B (r ,,r )n += .因为1r ,,r n 可由1α,,αn ,1β,,βn 线性表出,从而也可由1α,,αr ,1β,,βs 线性表出.故()1A B (r ,,r )n R R +=≤ ()11α,,α,β,,βr s R r s =+=(A)(B)R R +.17.设A 与B 可乘,且AB 0=,证明: (A)(B)A R R +≤的列数. 证法一 设A 为m n ⨯矩阵,B 为n l ⨯矩阵 由AB 0=,有11111111n l m mn n nl m n n l a a b b a a b b ⨯⨯⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 0000m l⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭ 比较等式两边对应元素,有111111111100n n m mn n a b a b a b a b ++=⎧⎪⎨⎪++=⎩,11121211220,0n n m mn n a b a b a b a b ++=⎧⎪⎨⎪++=⎩ ,11111100l n nl m lmn nl a b a b a b a b ++=⎧⎪⎨⎪++=⎩ . 可见B 的列向量组为上述l 个齐次线性方程组的解向量,因此有 (B)(A)R n R ≤-, 移项得(A)(B)R R n +≤(A 的列数).证法二 设A 为m n ⨯矩阵,B 为n l ⨯矩阵, 12(A),(B)R r R r ==,因为1(A)R r =,则A 的标准形可写成1E 000r ⎛⎫⎪⎝⎭,即存在可逆阵P,Q 使得 PAQ 1E 000r ⎛⎫=⎪⎝⎭.又设()111B Q B B r m n r m ⨯--⨯⎛⎫= ⎪ ⎪⎝⎭, 则10(AB)(PAB)(PAQQ B)R R R -===,但()111111B E 0B PAQQ B Q B B 000r m r r m n r m ⨯⨯---⨯⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 可见11(B )(PAQQ B)0r m R R -⨯==,又因为12(Q B)(B)R R r -==,所以()12(B )n r m R r -⨯=,而()1B n r m -⨯共1n r -行,因此12n r r -≥,即12r r n +≤或(A)(B)R R n +≤.习题 B1.证明: 12α,α,,αs (其中1α0≠)线性相关的充要条件是至少有一个α(1)i i s <≤可被121α,α,,αi - 线性表出.证 必要性:设12α,α,,αs 线性相关(1α0≠),则存在不全为0的s 个数12,,,s k k k 使1122ααα0s s k k k +++= ,设i k 是12,,,s k k k 中最后一个不为零的数,即0i k ≠,而10i s k k +=== ,则1122ααα0i i k k k +++= ,因为1α0≠,所以1i >,即1i s <≤,(否则120,0s k k k ≠=== 则1α0k =不能成立),于是1111αααi i i i ik k k k --=--- ,即αi 可由121α,α,,αi - 线性表出.充分性:如果1111αααi i i k k --=++ ,则11111ααα0αα0i i i i s k k --+++-+++= ,而11,,,1,0,,0i k k -- 不全为0,所以12α,α,,αs 线性相关.2.证明:一个向量组的任一线性无关组都可扩充为一个极大线性无关组. 证 设有向量组12α,α,,αn 秩为s ,12α,α,,αr i i i 是它的任意一个线性无关组,如果r s =,则它就是12α,α,,αn 的一个极大线性无关组.如果r s <,则12α,α,,αn 的其余向量中一定可以选出向量1αr i +,使12α,α,,αr i i i ,1αr i +线性无关(否则与12α,α,,αn 秩s r >矛盾),只要1r s +<,重复上述过程,直到r i s +=时为止.这样121α,α,,α,α,,αr r s i i i i i + 就是由12α,α,,αr i i i 扩充成的一个极大线性无关组.3.已知两向量组有相同的秩,且其中之一可被另一个线性表出,证明:这两个向量组等价. 证 设12A :α,α,,α;s 12B:β,β,,βt 为两个秩为r 的向量组, 1212α,α,,α;β,β,,βr r 分别为A,B 极大线性无关组,设B 可由A 线性表出,则有()()1212β,β,,βα,α,,αTr r K = ,其中K 为组合系数构成的r 阶方阵,因为1212α,α,,α;β,β,,βr r 线性无关,所以K 可逆,()()11212α,α,,αβ,β,,βr r K -= ,从而12α,α,,αr 可由12β,β,,βr 线性表出,从而可由12β,β,,βt 线性表出,又12α,α,,αs 可由12α,α,,αr 线性表出,所以12α,α,,αs 可由12β,β,,βt 线性表出,即A 可由B 线性表出,因此向量组A ,B 等价.4.设向量组12α,α,,αs 的秩为r ,在其中任取m 个向量12α,α,,αm i i i ,证明:{}12α,α,,αm i i i R r m s ≥+- .证 设12α,α,,αm i i i 的秩为t ,从它的一个极大线性无关组(含t 个向量)可扩充为12α,α,,αs 的一个极大线性无关组(含r 个向量),所扩充向量的个数为r t -个.但12α,α,,αs 中除了12α,α,,αm i i i 外,还有s m -个向量,故r t s m -≤-,即t r m s ≥+-.5.设n m ⨯阶矩阵A 的秩为r ,证明:存在秩为r 的n r ⨯阶矩阵P 及秩为r 的r m ⨯阶矩阵Q ,使A PQ =.证 因(A)R r =,故可经有限次初等行变换和初等列变换化为标准形,即存在m 阶可逆阵F 和n 阶可逆阵G ,使得 E 0GAF 00r ⎛⎫=⎪⎝⎭,即11E 0A GF ,00r--⎛⎫= ⎪⎝⎭记111212122G G G ,G G -⎛⎫= ⎪⎝⎭111212122F F F F F -⎛⎫= ⎪⎝⎭,其中1111G ,F 均为r 阶方阵,则111211121121222122G G F F E0E 0A G F GG F F 0000rr--⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111112212122G 0F F G 0F F ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭=1111111221212122G F G F G F G F ⎛⎫ ⎪⎝⎭()11112121G F F G ⎛⎫= ⎪⎝⎭, 记1121G P G ⎛⎫=⎪⎝⎭,则P 为n r ⨯矩阵且(P )R r =(因1G -可逆,故其前r 列线性无关), ()1121Q F F =,则Q 为r m ⨯矩阵且(Q)R r =(因1F -可逆,故其前r 列线性无关),而A PQ =.。

s(s
1 1)(s
2)
，用描述函数法分析系统是否存
在稳定自振点，若存在，求自振 和 A。
八．
设有零阶保持器的离散系统如图所示，其中 r(t) = 1(t),T = 1s,K = 1。试求系统的上升时间、 峰值时间、调节时间。
R(s) -
1 eTs s
K
C(s)
s(s 1)
整理编辑 By 邵永 2014 年 1 月
+ -
Kp
+
1
s(s 1)
KdS
+
科目代码：839 Xc
(1) Kp =10,Kd =1,求相位裕度。 (2) 若 Wc=5，r=50o，求 Kp，Kd。
七．
（1）用描述函数法分析
W1=
2 s(0.1s
1)
、W2=
2 s(s 1)
，哪个更精确，为什么？
（2）非线性部分
N(A)=
4 A
,线性部分
W(s)=
东北大学
2014 年攻读硕士学位研究生入学考试试题
一．
科目代码：839
1.简述前馈控制可以改善线性系统哪方面性能，对线性系统稳定性有何影响？ 2.简述频率特性的定义，最常用的频率特性表示方法有哪些？
二．
若某系统在单位阶跃输入作用时，系统在零初始条件下的输出响应为：1-2e2t+et,试求系统的 单位脉冲响应。
五．
已知一最小相位系统开环对数幅频特性如下。其中实线为渐近线，虚线为精确线。试求系统 的开环传递函数8
0 -1
400
整理编辑 By 邵永 2014 年 1 月
东北大学
2014 年攻读硕士学位研究生入学考试试题

2014年普通高等学校招生全国统一考试英语辽宁卷第I卷第一部分：听力（共两节，满分30分）第一节（共5个小题，每小题1.5分，满分7.5分）1. What does the woman want to do?A. Find a place.B. Buy a map.C. Get an address.2. What will the man do for the woman?A. Repair the car.B. Give her a ride.C. Pick up her aunt.3. Who might Mr. Peterson be?A. A new professor.B. A department head.C. A company director.4. What does the man think of the book?A. Quite difficult.B. Very interesting.C. Too simple.5. What are the speakers talking about?A. Weather.B. Clothes.C. News.第二节（本节共15个小题，每小题1.5分，满分22.5分）听第6段材料，回答6、7题。

6. Why is Harry unwilling to join the woman?A. He has a pain in his knee.B. He wants to watch TV.C. He is too lazy.7. What will the woman probably do next?A. Stay at home.B. Take Harry to hospital.C. Do some exercise.听第7段材料，回答8、9题。

8. When will the man be home from work?A. At 5:45.B. At 6:15.C. At 6:509. Where will the speakers go?A. The Green House Cinema.B. The New State Cinema.C. The UME Cinema.听第8段材料，回答10至12题。

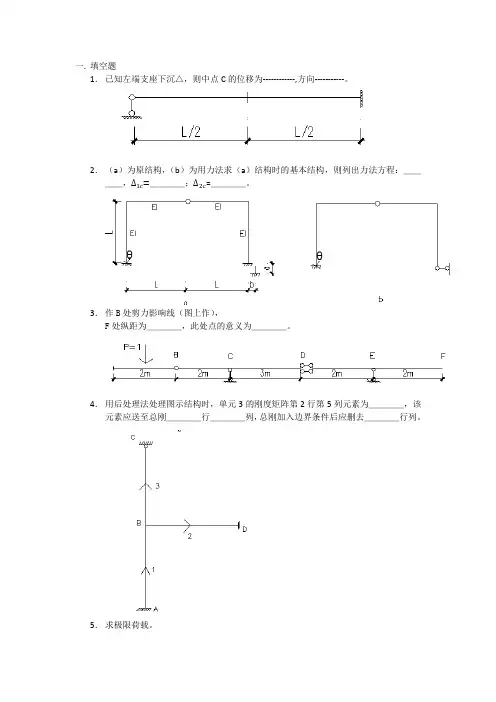
一.填空题
1．已知左端支座下沉△，则中点C的位移为------------,方向-----------。

2．（a）为原结构，（b）为用力法求（a）结构时的基本结构，则列出力法方程：＿＿＿＿，∆1c=＿＿＿＿；∆2c=＿＿＿＿。

3．作B处剪力影响线（图上作），
F处纵距为＿＿＿＿，此处点的意义为＿＿＿＿。

4．用后处理法处理图示结构时，单元3的刚度矩阵第2行第5列元素为＿＿＿＿，该元素应送至总刚＿＿＿＿行＿＿＿＿列，总刚加入边界条件后应删去＿＿＿＿行列。

5．求极限荷载。

二．几何组成分析。

三．作弯矩，轴力图。

EI=常数
四．h=l
，∝为常数，EI=常数，利用力法求解，作下图结构弯矩图，并写出求解过程。

10
五．EI=常数，利用位移法求解，写出方程，求出位移即可。

六．利用力矩分配法求解。

七．利用矩阵位移法（后处理法）作出下结构弯矩与剪力图（已知EA=EI=4）。

八．作最大动力弯矩图，并求出质点的最大动力位移，EI=常数。

2014年普通高等学校招生全国统一考试（辽宁卷）理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集,{|0},{|1}U R A x x B x x ==≤=≥，则集合()U C AB =（ ）A ．{|0}x x ≥B ．{|1}x x ≤C ．{|01}x x ≤≤D ．{|01}x x << 【答案】D 【解析】.).10()∪(∞).C 1[]0∞-(∴∞)1[],0-(R D B A B A B A 选，，，=+∪=∪+=∞=2.设复数z 满足(2)(2)5z i i --=，则z =（ ） A ．23i + B ．23i - C ．32i + D ．32i - 【答案】A 【解析】..3225252-25,5)-2)(2-(A i i i i i z i i z 选）（+=++=+=∴= 3.已知132a -=，21211log ,log 33b c ==，则（ ） A ．a b c >> B ．a c b >> C ．c a b >> D ．c b a >> 【答案】C 【解析】..∴).2,1(∈log ),1-2-(∈log ),121(∈2312131231-C b a c c b a 选，，>>===4.已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（ ）A ．若//,//,m n αα则//m nB ．若m α⊥，n α⊂，则m n ⊥C ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥ 【答案】B 【解析】..,..,.,B D C B A 选不用再看对平面上的直线直线垂直平面，则垂直对错，不一定平行平行同一平面的两直线对5.设,,a b c 是非零向量，学科 网已知命题P ：若0a b ∙=，0b c ∙=，则0a c ∙=；命题q ：若//,//a b b c ，则//a c ，则下列命题中真命题是（ ） A ．p q ∨ B ．p q ∧ C ．()()p q ⌝∧⌝ D ．()p q ∨⌝ 【答案】A 【解析】命题p 为假，命题q 为真，所以A 正确。

2014年东北大学化工原理真题部分答案一，概念题1.传质单元与传质单元高度2.沉降分离和沉降速度3.加热蒸汽和二次蒸汽4.热流量和热通量5.溶液沸点升高和杜林规则6.三传类比7.搅拌目的8.离心泵压头及其意义9.浓缩热和自蒸发（闪蒸）10.给热系数和传质系数二,简述题1.1试用瑞利法和π定理（布金汉定理）推导圆柱绕流的阻力FD的表达式，并说明瑞利法和布金汉π定理各适用于何种情况？已知圆柱绕流阻力FD与圆柱的直径为D，流体的流速为V，流体的密度和流体的动力粘滞系数有关。

2.为什么工业上气体的除尘常放在冷却之后进行而在悬浮液的过滤分离中,滤浆却不宜在冷却后才进行过滤？3.为什么离心泵可用出口阀来调节流量？往复泵可否采用同样方法调节流量？为什么？由离心泵的工作点知，改变泵出口阀的开度，使局部阻力改变，而管路特性曲线改变，流量随之改变，此法虽不经济，但对泵运转无其它影响；而往复泵属容积式泵，压头与流量基本无关，若关闭出口阀，则因泵内压力急剧升高，造成泵体。

管路和电机的损坏，故不宜用出口阀来调节流量。

4.流体的流动形态？判断依据？5温差损失及其原因？6.什么是过滤操作？过滤操作的优点？7. 何谓离心泵的“气缚”和“气蚀”现象，它们对泵的操作有何危害？应如何防止？三。

计算题1.如图的输水系统。

已知管内径d=50mm,在阀门全开时输送系统的Σ(L+L e)=50m,摩擦系数可取λ=0.03, 泵的性能曲线, 在流量为6m3/h至15m3/h范围内可用下式描述:H=18.92-0.82V 0.8，此处H e为泵的扬程m,V为泵的流量m3/h, 问: e⑴如要求流量为10m3/h，单位质量的水所需外加功为多少?单位重量的水所需外加功为多少?此泵能否完成任务?⑵如要求输送量减至8m3/h(通过关小阀门来达到)，泵的轴功率减少百分之多少?(设泵的效率变化忽略不计)(1)当V1=10m3/h，所需外加功W s=gz＋h f=9.81×10+8×0.03×50×(10/3600)2/(20.0505)=128.1 J/kgH e’=W s/g=128.1/9.81=13.06 J/N泵的扬程H e=18.92－0.82(10)0.8=13.75 J/N∵H e H e’，故此泵能完成任务。

2014年东南大学724预防基础综合考研真题（回忆版）流行病学一、名词解释1．二代发病率2．流行病学病因3．出生队列分析4．Population susceptibility人群易感性5．secular trend长期趋势（英文）6．hereditary susceptibility遗传易感性（英文）7．暴发8．流行二、连线题链霉素的发现是谁？应用了什么流行病学方法？结核杆菌是谁发现的？用了什么流行病学方法？海员出血的治疗是谁发现的？用了什么流行病学方法？脊髓灰质炎是谁发现的？使用什么流行病学发现的？三、大题队列研究，描述性研究，病例对照研究的特点及应用与意义？实验研究的特点及其应用与意义？实验研究的原则及其意义？队列研究的一个计算题：AR、AR%、RR的值及其意义病例对照研究的一个计算题：OR值及其意义筛检的一个计算题：计算上述表中的真实值与其预测值（真阳性，假阳性，真阴性，假阴性，约登指数，符合率，阳性预测值，阴性预测值）统计学只含有考点。

大题1．单样本量的t检验步骤及其计算2．配对t检验的过程及其计算3．两组独立样本的t检验过程及其计算4．两组独立样本方差不齐的t检验过程及其计算.为什么要用秩和检验，其应用条件，步骤及过程。

5．100个学生的身高与坐高的一组数据如何处理及其各指标的意义（可以分别从集中趋势的平均数，离散趋势的标准差，方差，变异系数。

身高与坐高的相关性，以及95%的参考值范围，95%的置信区间入手）6．偏回归系数－1.79与p＝0.137值相结合说明了什么，有什么意义？毒理学一、名词解释（中文译成英文，8个）1．毒物2．毒物动力学3．时间毒理学4．毒理学安全性评价5．生殖毒理学6．观察到损害作用最低水平7．遗传毒性致癌物8．质量控制二、大题1．外源化学的分布特点及其靶器官。

研究外源化学的分布与靶器官的意义。

2．致癌阶段及特点3．肝损害严重原因4．影响机体对毒物代谢因素及意义5．危险度特征分析内容6．实验动物选择原则7．安全性评价的内容。

2014年东南大学建筑学院建筑学免试硕士研究生建筑设计试题
时间：2014年10月14日，8:00——14:00
（注：每位考生在下列四题中任选三题作答，建筑技术方向的考生题目D为必选）
A、空间设计
成果要求
1、画出从A视角看的建筑轴测图，不开洞口，只表现体量，比例1:100
2、画出B视点看的室内透视图，自行设计室内及外墙面，并用2-3句话来阐述空间设
计特点。

（建议用时：2小时）
D、筒中筒结构，绘制标准层平面
成果要求
1、第一部分（分值80%）
布置外筒柱，并注明柱距
布置外筒梁（裙梁）
布置内外筒连梁
布置内外筒角柱、剪力墙
2、第二部分（分值2%）
画出标准层的立面图
B、厂房改建汽车展馆，不得改变主体结构
1、功能面积要求：总建筑面积1400平方米
展厅600平方米
多功能厅250平方米
咖啡厅100平方米
接待、办公各6间20平方米2、成果要求
画出体现功能和空间的轴侧图1:200
分析图若干
C、居住小区规划设计
1、设计要求：总建筑面积大于等于41600平方米
辅助用房小于等于6000平方米
容积率大于等于1.6
停车位0.5个/户
建筑间距1:1.25
布置多层住宅、12层及以下高层、辅助建筑
多层及辅助建筑退界6m，12层及以下高层退界15m 2、成果要求
总平面图1:1000
各类经济技术指标
分析图若干。

2014年普通高等学校招生全国统一考试（辽宁卷）理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集,{|0},{|1}U R A x x B x x ==≤=≥，则集合()U C AB =（ ）A ．{|0}x x ≥B ．{|1}x x ≤C ．{|01}x x ≤≤D ．{|01}x x << 2.设复数z 满足(2)(2)5z i i --=，则z =（ ） A ．23i + B ．23i - C ．32i + D ．32i - 3.已知132a -=，21211log ,log 33b c ==，则（ ） A ．a b c >> B ．a c b >> C ．c a b >> D ．c b a >> 4.已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（ ） A ．若//,//,m n αα则//m n B ．若m α⊥，n α⊂，则m n ⊥ C ．若m α⊥，m n ⊥，则//n α D ．若//m α，m n ⊥，则n α⊥5.设,,a b c 是非零向量，已知命题P ：若0a b ∙=，0b c ∙=，则0a c ∙=；命题q ：若//,//a b b c ，则//a c ，则下列命题中真命题是（ ）A ．p q ∨B ．p q ∧C ．()()p q ⌝∧⌝D ．()p q ∨⌝6. 6把椅子摆成一排，3人随机就座，任何两人不相邻的做法种数为（ ） A ．144 B ．120 C ．72 D ．247.某几何体三视图如图所示，则该几何体的体积为（ ） A ．82π- B ．8π- C ．82π-D ．84π-8.设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（ ） A ．0d < B ．0d > C ．10a d < D ．10a d > 9.将函数3sin(2)3y x π=+的图象向右平移2π个单位长度，所得图象对应的函数（ ） A ．在区间7[,]1212ππ上单调递减 B ．在区间7[,]1212ππ上单调递增C ．在区间[,]63ππ-上单调递减 D ．在区间[,]63ππ-上单调递增 10.已知点(2,3)A -在抛物线C ：22y px =的准线上，过点A 的直线与C 在第一象限相切于点B ，记C 的焦点为F ，则直线BF 的斜率为（ ） A ．12 B ．23 C ．34 D ．4311.当[2,1]x ∈-时，不等式32430ax x x -++≥恒成立，则实数a 的取值范围是（ ） A ．[5,3]-- B ．9[6,]8-- C ．[6,2]-- D ．[4,3]-- 12.已知定义在[0,1]上的函数()f x 满足： ①(0)(1)0f f ==；②对所有,[0,1x y ∈，且x y ≠，有1|()()|||2f x f y x y -<-.若对所有,[0,1x y ∈，|()()|f x f y k -<，则k 的最小值为（ ）A ．12 B ．14 C ．12π D ．18第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.执行右侧的程序框图，若输入9x =，则输出y = .14.正方形的四个顶点(1,1),(1,1),(1,1),(1,1)A B C D ----分别在抛物线2y x =-和2y x =上，如图所示，若将一个质点随机投入正方形ABCD 中，则质点落在阴影区域的概率是 .15.已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN += .16.对于0c >，当非零实数a ，b 满足224240a ab b c -+-=，且使|2|a b +最大时，345a b c-+的最小值为 .三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）在ABC ∆中，内角A ，B ，C 的对边a ，b ，c ，且a c >，已知2BA BC ∙=，1cos 3B =，3b =，求： （1）a 和c 的值； （2）cos()BC -的值. 18. （本小题满分12分）一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示：.（1）求在未来连续3天里，有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率；（2）用X 表示在未来3天里日销售量不低于100个的天数，求随机变量X 的分布列，期望()E X 及方差()D X .19. （本小题满分12分）如图，ABC ∆和BCD ∆所在平面互相垂直，且2AB BC BD ===，0120ABC DBC ∠=∠=，E 、F 分别为AC 、DC 的中点. （1）求证：EF BC ⊥；（2）求二面角E BF C --的正弦值.圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线22122:1x y C a b-=过点P （1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程.已知函数8()(cos )(2)(sin 1)3f x x x x x π=-+-+，2()3()cos 4(1sin )ln(3)xg x x x x ππ=--+-.证明：（1）存在唯一0(0,)2x π∈，使0()0f x =；（2）存在唯一1(,)2x ππ∈，使1()0g x =，且对（1）中的x 0有01x x π+<.请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑. 22. （本小题满分10分）选修4-1：几何证明选讲如图，EP 交圆于E 、C 两点，PD 切圆于D ，G 为CE 上一点且PG PD =，连接DG 并延长交圆于点A ，作弦AB 垂直EP ，垂足为F. （1）求证：AB 为圆的直径； （2）若AC=BD ，求证：AB=ED.：坐标系与参数方程将圆221x y +=上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C. （1）写出C 的参数方程；（2）设直线:220l x y +-=与C 的交点为12,P P ，以坐标原点为极点，x 轴正半轴为极坐标建立极坐标系，求过线段12PP 的中点且与l 垂直的直线的极坐标方程. 24. （本小题满分10分）选修4-5：不等式选讲设函数()2|1|1f x x x =-+-，2()1681g x x x =-+，记()1f x ≤的解集为M ，()4g x ≤的解集为N.（1）求M ； （2）当x MN ∈时，证明：221()[()]4x f x x f x +≤. 参考答案一、选择题1. D [解析] 由题意可知，A ∪B ＝{x |x ≤0或x ≥1}，所以∁U (A ∪B )＝{x |0＜x ＜1}．2. A [解析] 由(z －2i)(2－i)＝5，得z －2i ＝52－i，故z ＝2＋3i.3. C [解析] 因为0<a ＝2－13<1，b ＝log 213<0，c ＝log 1213>log 1212＝1，所以c >a >b .4. B [解析] B [解析] 由题可知，若m ∥α，n ∥α，则m 与n 平行、相交或异面，所以A 错误；若m ⊥α，n ⊂α，则m ⊥n ，故B 正确；若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，故C 错误．若m ∥α，m ⊥n ，则n ∥α或n ⊥α或n 与a 相交，故D 错误． 5. A [解析] 由向量数量积的几何意义可知，命题p 为假命题；命题q 中，当b ≠0时，a ，c 一定共线，故命题q 是真命题．故p ∨q 为真命题．6. D [解析] 这是一个元素不相邻问题，采用插空法，A 33C 34＝24.7. B [解析] 根据三视图可知，该几何体是正方体减去两个体积相等的圆柱的一部分⎝⎛⎭⎫占圆柱的14后余下的部分，故该几何体体积为2×2×2－2×14×π×2＝8－π8. C [解析] 令b n ＝2a 1a n ，因为数列{2a 1a n }为递减数列，所以b n ＋1b n ＝2a 1a n ＋12a 1a n＝2a 1(a n ＋1－a n )＝2a 1d <1，所得a 1d <0.9. B [解析] 由题可知，将函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图像向右平移π2个单位长度得到函数y ＝3sin ⎝⎛⎭⎫2x －23π的图像，令－π2＋2k π≤2x －23π≤π2＋2k π，k ∈Z ，即π12＋k π≤x ≤7π12＋k π，k ∈Z 时，函数单调递增，即函数y ＝3sin ⎝⎛⎭⎫2x －23π的单调递增区间为⎣⎡⎦⎤π12＋k π，7π12＋k π，k ∈Z ，可知当k ＝0时，函数在区间⎣⎡⎦⎤π12，7π12上单调递增10. D [解析] 因为抛物线C ：y 2＝2px 的准线为x ＝－p2，且点A (－2，3)在准线上，所以p ＝4.设直线AB 的方程为x ＋2＝m (y －3)，与抛物线方程y 2＝8x 联立得到y 2－8my ＋24m ＋16＝0，由题易知Δ＝0，解得m ＝－12(舍)或者m ＝2，这时B 点的坐标为(8，8)，而焦点F 的坐标为(2，0)，故直线BF 的斜率k BF ＝8－08－2＝43. 11. C C [解析] 当－2≤x <0时，不等式转化为a ≤x 2－4x －3x 3，令f (x )＝x 2－4x －3x 3(－2≤x <0)，则f ′(x )＝－x 2＋8x ＋9x 4＝－（x －9）（x ＋1）x 4，故f (x )在[－2，－1]上单调递减，在(－1，0)上单调递增，此时有a ≤1＋4－3－1＝－2.当x ＝0时，g (x )恒成立．当0<x ≤1时，a ≥x 2－4x －3x 3，令个g (x )＝x 2－4x －3x 3(0<x ≤1)，则g ′(x )＝－x 2＋8x ＋9x 4＝ －（x －9）（x ＋1）x 4，故g (x )在(0，1]上单调递增，此时有a ≥1－4－31＝－6.综上，－6≤a ≤－2.解法一：12. B [解析] 不妨设0≤y <x ≤1.当x －y ≤12时，|f (x )－f (y )|<12|x －y |＝12(x －y )≤14.当x －y >12时，|f (x )－f (y )|＝|f (x )－f (1)－(f (y )－f (0))|≤|f (x )－f (1)|＋|f (y )－f (0)|<12|x －1|＋12|y －0|＝－12(x －y )＋12<14.故k min ＝14.解法二：解法三：解法四：13.299[解析] 当x ＝9时，y ＝5，则|y －x |＝4；当x ＝5时，y ＝113，则|y －x |＝43；当x ＝113时，y ＝299，则|y －x |＝49<1.故输出y ＝299.14.23[解析] 正方形ABCD 的面积S ＝2×2＝4，阴影部分的面积S 1＝2⎠⎛－11(1－x 2)d x ＝2⎝⎛⎭⎫x －13x 31－1＝83，故质点落在阴影区域的概率P ＝834＝23. 15. 12 [解析] 取MN 的中点为G ，点G 在椭圆C 上．设点M 关于C 的焦点F 1的对称点为A ，点M 关于C 的焦点F 2的对称点为B ，则有|GF 1|＝12|AN |，|GF 2|＝12|BN |，所以|AN |＋|BN |＝2(|GF 1|＋|GF 2|)＝4a ＝12.16. 2- [解析] 由题知2c ＝－(2a ＋b )2＋3(4a 2＋3b 2)．(4a 2＋3b 2)⎝⎛⎭⎫1＋13≥(2a ＋b )2⇔4a 2＋3b 2≥34(2a ＋b )2，即2c ≥54(2a ＋b )2， 当且仅当4a 21＝3b213，即2a ＝3b ＝6λ(同号)时，|2a ＋b |取得最大值85c ，此时c ＝40λ2.3a －4b ＋5c ＝18λ2－1λ＝18⎝⎛⎭⎫1λ－42－2≥－2， 当且仅当a ＝34，b ＝12，c ＝52时，3a －4b ＋5c取最小值－2.17.（Ⅰ）由2BA BC ⋅=得，cos 2c a B ⋅=，又1cos 3B =，所以ac =6.由余弦定理，得2222cos a c b ac B +=+.又b =3，所以2292213ac +=+⨯=.解22613ac a c =⎧⎪⎨+=⎪⎩，得a =2，c =3或a =3，c =2. 因为a >c ,∴ a =3，c =2. （Ⅱ）在ABC ∆中，sin 3B ===由正弦定理，得2sin sin 339c CB b ==⋅=，又因为a b c =>，所以C 为锐角，因此7cos9C===.于是cos()cos cos sin sinB C B C B C-=+=1723393927⋅+⋅=.18.（Ⅰ）设1A表示事件“日销售量不低于100个”，2A表示事件“日销售量低于50个”，B表示事件“在未来连续3天里有连续2天日销售量不低于100个且另一天的日销售量低于50个”.因此1()(0.0060.0040.002)500.6P A=++⨯=.2()0.003500.15P A=⨯=.()0.60.60.1520.108P B=⨯⨯⨯=.（Ⅱ）X的可能取值为0,1,2,3.相应的概率为033(0)(10.6)0.064P X C==⋅-=,123(1)0.6(10.6)0.288P X C==⋅-=,223(2)0.6(10.6)0.432P X C==⋅-=,333(3)0.60.216P X C==⋅=,分布列为19.（Ⅰ）证明：（方法一）过E作EO⊥BC，垂足为O，连OF，由△ABC≌△DBC可证出△EOC≌△FOC，所以∠EOC=∠FOC=2π，即FO⊥BC，又EO⊥BC，因此BC⊥面EFO，又EF⊂面EFO，所以EF⊥BC.（方法二）由题意，以B为坐标原点，在平面DBC内过B左垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示的空间直角坐标系.易得B （0,0,0），A (0，-1，),D(,-1,0)，C (0,2,0),因而11(0,),,,0)22E F ,所以33(,0,),(0,2,0)22EF BC =-=，因此0EF BC ⋅=,从而EF BC ⊥，所以EF BC ⊥. （Ⅱ）（方法一）在图1中，过O 作OG ⊥BF ，垂足为G ，连EG ，由平面ABC ⊥平面BDC ，从而EO ⊥平面BDC ，又OG ⊥BF ，由三垂线定理知EG 垂直BF . 因此∠EGO 为二面角E -BF -C 的平面角； 在△EOC 中，EO =12EC=12BC ·cos 30°，由△BGO ∽△BFC 知，BO OG FC BC =⋅=,因此tan ∠EGO =2EO OG =,从而sin ∠EGO，即二面角E -BF -C （方法二）在图2中，平面BFC 的一个法向量为1(0,0,1)n =，设平面BEF 的法向量2(,,)n x y z =，又311(,,0),(0,,)2222BF BE ==,由220n BF nBE ⎧⋅=⎪⎨⋅=⎪⎩ 得其中一个2(1,n =，设二面角E -BF -C 的大小为θ，且由题意知θ为锐角，则121212cos |cos ,|||||||5n nn n n n θ⋅=<>==⋅因sin θ即二面角E -BF -C 20.（Ⅰ）设切点坐标为0000(,)(0,0)x y x y >>，则切线斜率为0x y -，切线方程为0000()x y y x x y -=--，即004x x y y +=，此时，两个坐标轴的正半轴与切线围成的三角形面积为000014482S x y x y =⋅⋅=.由22000042x y x y +=≥知当且仅当00x y =时00x y 有最大值，即S 有最小值，因此点P 得坐标为 ， 由题意知222222213a ba b a ⎧-=⎪⎨⎪+=⎩解得221,2a b ==，故1C 方程为2212y x -=. （Ⅱ）由（Ⅰ）知2C的焦点坐标为(，由此2C 的方程为22221113x y b b +=+，其中10b >.由P 在2C 上，得22112213b b +=+， 解得b 12=3，因此C 2方程为22163x y += 显然，l 不是直线y =0.设l 的方程为x =my1122(,),(,)A x y B x y由22163x my x y ⎧=⎪⎨+=⎪⎩得22(2)30m y ++-=，又12,y y 是方程的根，因此1212232y y y y m ⎧+=⎪⎪⎨-⎪=⎪+⎩①②，由12,3x y x m=+=+得12122221212122()266()32x x m y y m m x x m y y y y m ⎧+=++=⎪⎪+⎨-⎪=+++=⎪+⎩③④因1122(2,2),(2)AP x y BP x y =--=-由题意知0A P B P ⋅=，所以12121212))40x x x x y y y y ++++=⑤，将①，②，③，④代入⑤式整理得22110m -+=，解得12m =-或12m =-+，因此直线l 的方程为1)0x y --=，或1)0x y +-=. 21.（Ⅰ）当(0,)2x π∈时，2'()(1sin )(2)2cos 03f x x x x x π=-++--<，函数()f x 在(0,)2π上为减函数，又2816(0)0,()0323f f πππ=->=--<，所以存在唯一0(0,)2x π∈，使0()0f x =. （Ⅱ）考虑函数3()cos 2()4ln(3),[,]1sin 2x x h x x x x ππππ-=--∈+，令t x π=-，则[,]2x ππ∈时，[0,]2t π∈， 记3cos 2()()4ln(1)1sin t t u t h t t t ππ=-=-++，则3()'()(2)(1sin )f t u t t t π=++ ，由（Ⅰ）得，当0(0,)t x ∈时，'()0u t >，当0(,)2t x π∈时，'()0u t <.在0(0,)x 上()u t 是增函数，又(0)0u =，从而当0(0,]t x ∈时，()0u t >，所以()u t 在0(0,]x 上无零点. 在0(,)2x π上()u t 是减函数，由0()0,()4ln 202u x u π>=-<，存在唯一的10(,)2t x π∈ ，使1()0u t =.所以存在唯一的10(,)2t x π∈使1()0u t =.因此存在唯一的11(,)2x t πππ=-∈，使111()()()0h x h t u t π=-==.因为当(,)2x ππ∈时，1sin 0x +>，故()(1sin )()g x x h x =+与()h x 有相同的零点，所以存在唯一的1(,)2x ππ∈，使1()0g x =.因1110,x t t x π=->，所以01x x π+<请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑. 22.（Ⅰ）因为PD =PG ,所以∠PDG =∠PGD .由于PD 为切线，故∠PDA =∠DBA ,又由于∠PGD =∠EGA ,故∠DBA =∠EGA ,所以∠DBA +∠BAD =∠EGA +∠BAD ,从而∠BDA =∠PF A .由于AF 垂直EP ，所以∠PF A =90°，于是∠BDA =90°，故AB 是直径. (Ⅱ)连接BC ，DC .由于AB 是直径，故∠BDA =∠ACB =90°， 在Rt △BDA 与Rt △ACB 中，AB =BA ,AC =BD ， 从而Rt △BDA ≌Rt △ACB ，于是∠DAB =∠CBA . 又因为∠DCB =∠DAB ,所以∠DCB =∠CBA ，故DC ∥AB .由于,,AB EP DC EP DCE ⊥⊥∠所以为直角 于是ED 是直径，由（Ⅰ）得ED =AB .23.（Ⅰ）设11(,)x y 为圆上的点，在已知变换下位C 上点（x ，y ），依题意，得112x x y y =⎧⎨=⎩ 由22111x y +=得22()12y x +=，即曲线C 的方程为2214y x +=.，故C 得参数方程为 cos 2sin x t y t ⎧⎨⎩＝＝ （t 为参数）.(Ⅱ)由2214220y x x y ⎧+=⎪⎨⎪+-=⎩解得：10x y =⎧⎨=⎩，或02x y =⎧⎨=⎩. 不妨设12(1,0),(0,2)P P ,则线段12PP 的中点坐标为1(,1)2,所求直线的斜率为12k =，于是所求直线方程为111()22y x -=-， 化极坐标方程，并整理得2cos 4sin 3ρθρθ-=-，即34sin 2cos ρθθ=-.24.（Ⅰ）33,[1,)()1,(,1)x x f x x x -∈+∞⎧=⎨-∈-∞⎩当1x ≥时，由()331f x x =-≤得43x ≤，故413x ≤≤； 当1x <时，由()11f x x =-≤得0x ≥，故01x ≤<； 所以()1f x ≤的解集为4{|0}3M x x =≤≤.(Ⅱ)由2()16814g x x x =-+≤得2116()4,4x -≤解得1344x -≤≤，因此13{|}44N x x =-≤≤，故3{|0}4MN x x =≤≤.当x MN ∈时，()1f x x =-，于是22()[()]()[()]x f x x f x xf x x f x +⋅=+2111()(1)()424x f x x x x =⋅=-=--≤.。

东北大学考研试题及答案一、单项选择题（每题2分，共20分）1. 下列选项中，不属于东北大学特色专业的是：A. 材料科学与工程B. 机械工程C. 计算机科学与技术D. 法学答案：D2. 东北大学位于我国的哪个省份？A. 辽宁省B. 吉林省C. 黑龙江省D. 河北省答案：A3. 东北大学创建于哪一年？A. 1923年B. 1922年C. 1924年D. 1925年答案：A4. 东北大学的主要校区位于哪个城市？A. 沈阳市B. 大连市C. 长春市D. 哈尔滨市5. 东北大学在下列哪个方面具有显著优势？A. 艺术B. 体育C. 工程D. 文学答案：C6. 东北大学是否是“211工程”和“985工程”重点建设的大学？A. 是B. 否答案：A7. 东北大学是否拥有研究生院？A. 是B. 否答案：A8. 东北大学是否设有博士后流动站？A. 是B. 否答案：A9. 东北大学是否为教育部直属高校？A. 是B. 否答案：A10. 东北大学是否在国内外享有较高的声誉？A. 是答案：A二、多项选择题（每题3分，共15分）1. 东北大学在下列哪些领域有较强的研究实力？A. 材料科学B. 信息科学C. 管理科学D. 环境科学答案：A, B, C, D2. 东北大学的校训是：A. 求实创新B. 厚德博学C. 笃行致远D. 知行合一答案：A, B, C3. 东北大学是否与下列哪些机构有合作关系？A. 国家自然科学基金委员会B. 国家社会科学基金委员会C. 教育部D. 科技部答案：A, B, C, D三、简答题（每题5分，共10分）1. 请简述东北大学的历史沿革。

答案：东北大学始建于1923年，原名东北工学院，后经过多次更名和发展，成为今天的东北大学。

2. 东北大学在哪些方面为学生提供了良好的学习环境？答案：东北大学为学生提供了先进的教学设施、丰富的图书资源、优秀的师资队伍以及良好的校园文化氛围。

四、论述题（每题15分，共30分）1. 论述东北大学在国内外学术界的地位和影响。

2014年东北大学853管理学考研真题（回忆版，不完整）
东北大学
2014年硕士研究生入学考试试题
科目名称：管理学科目代码：853
一、概念题（每题5分）
1．企业资源计划
2．激励
3．虚拟团队
4．学习型组织
5．组织创新
二、简答题（第1～4题每题10分，第5题15分）
1．阐述服务、管理、领导三者之间的关系。

2．试述PEST分析的作用。

3．选择一个管理原理，进行分析。

4．
5．结合实际说说知识产权的重要性。

三、材料题
原书后面的关于三鹿奶粉的那段材料，进行分析三鹿集团破产的原因，以及给你的启示。

四、论述题
1．核心价值在组织文化中建设的重要性。

2．联系实际，你觉得你认为最重要的管理职能是什么？
五、计算题
讲的是原本有5000万元，进行投资的话成功率是95%，每年还能获利10%，不成功的话则血本无归；如果存进银行则会每年有5%的利息；如果****公司，付给**公司要5万元，**公司认为成功的话97%，不成功的话是50%。

有两问，第一问是说你觉得他应该用什么方法来管理她的5000万元。