差商与牛顿插值多项式
- 格式:ppt
- 大小:944.50 KB
- 文档页数:21



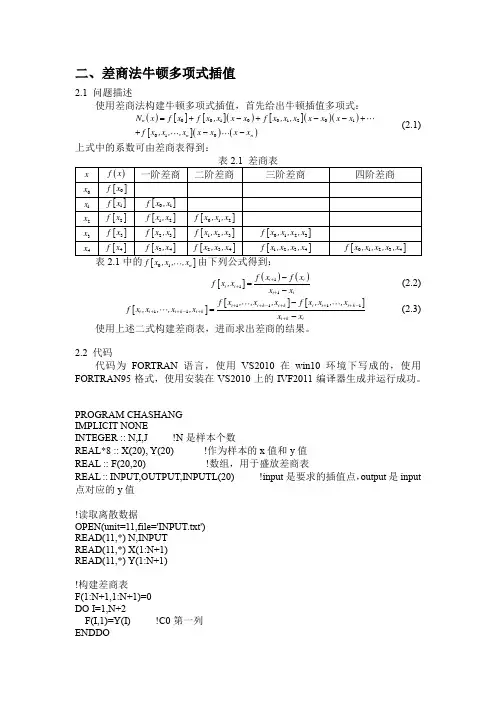
二、差商法牛顿多项式插值2.1 问题描述使用差商法构建牛顿多项式插值,首先给出牛顿插值多项式:()[][]()[]()()[]()()001001201010n n n N x f x f x ,x x x f x ,x ,x x x x x f x ,x ,,x x x x x =+-+--++-- (2.1)上式中的系数可由差商表得到:][01n f x ,x ,,x []()()111i i i i i if x f x f x ,x x x +++-=- (2.2)[][][]111111i i k i k i i i k i i i k i k i k if x ,,x ,x f x ,x ,,x f x ,x ,,x ,x x x ++-+++-++-++-=- (2.3)使用上述二式构建差商表,进而求出差商的结果。
2.2 代码代码为FORTRAN 语言,使用VS2010在win10环境下写成的,使用FORTRAN95格式,使用安装在VS2010上的IVF2011编译器生成并运行成功。
PROGRAM CHASHANG IMPLICIT NONEINTEGER :: N,I,J !N 是样本个数REAL*8 :: X(20), Y(20) !作为样本的x 值和y 值 REAL :: F(20,20) !数组,用于盛放差商表REAL :: INPUT,OUTPUT,INPUTL(20) !input 是要求的插值点,output 是input 点对应的y 值!读取离散数据OPEN(unit=11,file='INPUT.txt') READ(11,*) N,INPUT READ(11,*) X(1:N+1) READ(11,*) Y(1:N+1)!构建差商表F(1:N+1,1:N+1)=0 DO I=1,N+2F(I,1)=Y(I) !C0第一列 ENDDODO I=2,N+2,1 DO J=2,I,1F(I,J)=(F(I,J-1)-F(I-1,J-1))/(X(I)-X(I-J+1)) ENDDO ENDDO!输出差商表 DO I=1,N+2 DO J=1,N+1WRITE(*,*)F(I,J) ENDDO ENDDO!构建累乘表INPUTL INPUTL(1:N+1)=1 DO I=2,N+1INPUTL(I)=INPUTL(I-1)*(INPUT-X(I-1)) !分别求出公式2.1中的各项并存储在INPUTL(I)中,累乘n 次 ENDDO!计算结果OUTPUT=F(1,1)*INPUTL(1) DO I=2,N+2OUTPUT=OUTPUT+F(I,I)*INPUTL(I) !累加得到公式2.1中的N(x)值ENDDOOPEN(unit=22,file='OUTPUT.txt') WRITE(22,*) OUTPUTENDPROGRAM2.3 验证使用了沈艳等人《高等数值计算》(清华大学出版社出版的)一书中例6.1(P100)中的样本值开展了验证,将题目中的6π,4π,3π写为小数形式: 0.5235 0.7854 1.0472同样,其对应的函数值也写为小数形式:0.5 0.7071 0.8660 输入插值点518π,即0.8727,程序执行之后,得到该插值点对应的y 值: 0.765433667340945输入文件格式:—————————————— 2 0.872660.5236 0.7854 1.0472 0.5 0.7071 0.866得到的输出文件:——————————————0.7654179 ——————————————。

差商公式推导牛顿插值公式
设有n+1个数据点(x0,y0),(x1,y1),...,(xn,yn),要求通过
这些数据点构造一个n次多项式P(x),用于近似原函数的插值。
牛顿插值公式的一般形式为:
P(x)=f[x0]+f[x0,x1](xx0)+f[x0,x1,x2](xx0)(xx1)+...+f [x0,x1,...,xn](xx0)(xx1)...(xxn1)
其中f[x0]代表差商,f[x0,x1]代表二阶差商,以此类推。
1.一阶差商的计算:
f[xi]=(yiy0)/(xix0)
2.二阶差商的计算:
f[xi,xi+1]=(f[xi+1]f[xi])/(xi+1xi)
3.三阶及更高阶差商的计算:
f[xi,xi+1,...,xi+k]=(f[xi+1,xi+2,...,xi+k]f[xi,xi+1,...,xi
+k1])/(xi+kxi)
4.将差商代入牛顿插值公式中,得到:
P(x)=f[x0]+f[x0,x1](xx0)+f[x0,x1,x2](xx0)(xx1)+...+f [x0,x1,...,xn](xx0)(xx1)...(xxn1)
这样就得到了n次牛顿插值公式。
总结起来,差商公式的推导过程就是根据给定的数据点,计算不同阶次的差商,然后将差商代入牛顿插值公式中得到n次多项式。
通过这个多项式,我们可以在给定的数据点间进行插值,从而近似原函数的数值。






使⽤Python求⽜顿插值多项式及其差商表(附加⼀个拉格朗⽇插值多项式)闲话不多说,直接上代码。
import numpy as npfrom sympy import *# 定义⼀个求差商表的函数,使⽤递归求解差商表,返回值是差商的值# x是数组,表⽰样本点的x# f是数组,表⽰样本点的函数值f(x)# start是int类型,表⽰x数组的起始下标,# end是int类型,表⽰x数组的结束下标,# res是数组类型,表⽰差商表,对⾓线以下为各阶差商表def cs(x,f,start,end,res):# 当x中只有两个元素的时候,结束递归if((end-start)==1):# 将⼀阶差商填⼊差商表res[end-1][end-start-1]=(f[end]-f[start])/(x[end]-x[start])# 返回差商return res[end-1][end-start-1]# 当x中元素个数⼤于2时,根据公式递归调⽤此函数求差商,并将差商填⼊差商表res[end-1][end-start-1]=(cs(x,f,start+1,end,res)-cs(x,f,start,end-1,res))/(x[end]-x[start])# 返回差商return res[end-1][end-start-1]# 定义⼀个求⽜顿插值多项式的函数# x是数组,表⽰样本点的x# f是数组,表⽰样本点的函数值f(x)def Newton(x,f):res = np.ones([x.size - 1, x.size - 1])*np.inf # 初始化差商表⾻架结构cs(x, f, 0, x.size - 1, res) #调⽤差商表函数给差商表填值,对⾓线及以下才是差商表的值X=symbols("x") #定义x变量y=f[0] #初始化⽜顿插值多项式,它的第⼀项是常数项,正好是f[0]for i in range(x.size-1):temp=1 #临时变量,保存 f[x0,x1,...,xn]*(x-x1)(x-x2)...(x-xn-1)for j in range(i+1):temp=temp*(X-x[j]) #(x-x1)(x-x2)...(x-xn-1)temp=res[i,i]*temp #将差商表对⾓线元素作为系数y=y+temp #将temp添加到多项式中# 返回⽜顿插值多项式return yif__name__=="__main__":# 样本点x=np.array([2.0,2.1,2.2,2.3,2.4])f=np.array([1.414214,1.449138,1.483240,1.516575,1.549193])##### 可以直接得到差商表res = np.ones([x.size - 1, x.size - 1]) * np.inf # 初始化差商表⾻架结构# 调⽤差商表函数cs(x,f,0,x.size-1,res)print(res)#### 也可以直接得到⽜顿插值多项式X=symbols("x") #定义⾃变量xy=Newton(x,f) #调⽤函数得到⽜顿插值多项式,类型是<class 'sympy.core.add.Add'>print("N(x)=",y)# 给⾃变量x赋值,求出函数近似值print(y.evalf(subs={X:2.15})) #求给定⾃变量x值时函数f(x)的值 | 将表达式转化为函数得到的差商表:⽜顿插值多项式(⽐较长,就截取了部分):拉格朗⽇插值多项式代码(使⽤⽅法很简单,和⽜顿插值多项式⼀样): #拉格朗⽇插值法def L(x,f):X=symbols("x")m=x.size #x个数L=0for i in range(m):temp=1for j in range(m):if(i!=j):temp=temp*((X-x[j])/(x[i]-x[j]))L=L+temp*f[i]return L各位⼤哥点个赞呐(卑微)。