摆正方形

正方形组成的图形－多连块教学内容:课本第8页教学目标:1、引导学生探索用正方形拼组各种平面图形。

2、培养学生的几何思维能力和组合能力。

3、结合生活实际，培养学生收集信息、处理信息的能力。

教学重点：引导学生探索用正方形拼组各种平面图形。

教学难点：引导学生探索用正方形拼组各种平面图形。

教学过程:活动一：认识多连块媒体出示：一连块、两连块、三连块、四连块、五连块1、请学生仔细观察，每一个图形有什么特点？我们可以给它起个什么名称？它的含义是什么？活动二、用多连块搭图形1、媒体演示主题图师：图上的小伙伴们在干什么？说说他们搭的图形是由几个正方形连块组成的？同桌说一说。

2、小组活动，用正方形多连块搭自己喜欢的图形，，并说一说自己所搭的图形各是由几个正方形连块组成的？活动三、探究正方形多连块的组合种类1、学生操作学具，尝试摆出三连块的组合种类。

2、交流得出：三连块的2种组合种类。

3、两人合作：尝试摆出四连块的组合种类。

4、交流得出：四连块的5种组合种类。

5、小组合作：探究五连块的组合种类。

组长记录6、各小组交流，展示五连块的12种组合种类。

活动四、用多连块摆长方形和正方形1、媒体出示：小亚摆出的长方形（学生观察），同桌说一说小亚摆出的长方形是由几块怎样的多连块拼成的？（一连块、三连块、四连块各一种。

）2、学生操作学具，模仿小亚那样来拼出长方形。

3、师小结：小亚拼的这个长方形竖着看，每列有2个正方形，因为有四列，所以我们简单地把它称为2×4的长方形。

4、媒体出示：小巧摆出的长方形（学生观察），同桌说一说小亚摆出的长方形是由几块怎样的多连块拼成的？（两连块1块、三连块2块、四连块2块。

）5、学生操作学具，模仿小巧拼出长方形来。

6、这是一个怎样的长方形？学生小结：小亚拼的这个长方形竖着看，每列有4个正方形，因为有四列，所以我们简单地把它称为4×4的长方形。

活动五、用新图形片摆长方形1．媒体出示小胖的长方形：说一说这是一个怎样的长方形？你知道他是怎样摆的吗？2．利用学具找好朋友一起摆一摆这个3×5的长方形。

正方形点阵图的计算公式试题分享一第一大题填空题，共有8小题，考查了学生的计算能力和应变水平。

第1小题，用小棒摆正方形，摆1个正方形要4根，摆2个正方形要7根，摆3个正方形要10根……从这里我们可以发现：1个要4根，2个要7根，3个要10根……下一个都比前一个多3根，则第n个的规律是：3n+1，所以摆10个需要3×10+1＝31（根）。

第2小题通过观察发现，点数分别为6、9、12……以此类推，第9个点阵图有30个点，具体规律是：第一个图：6+3×0个第二个图：6+3×1个第三个图：6+3×2个第四个图：6+3×3第n个图有：6+3×（n-1）个，则求第9个有几个点时，可通过代入法知道，共有6+3×（9-1）＝6+24＝30（个）。

第3小题通过观察，我们知道了：1+3＝[（3+1）÷2]的平方，即规律是：第一个数加最后一个数的和除以2的平方，根据这个规律，我们得出了：1+3+5+7+9+11+13+15＝[（1+15）÷2]㎡＝8×8，因此计算1+3+5+7+9+5+3+1时，可以转换成：（1+3+5+7+9）+（5+3+1）＝5的平方+3的平方＝34。

试题分享二第4小题用拆分法，因为1/2×1＝1-1/2，1/2×3＝1/2-1/3，所以1/1×2+1/2×3+……1/2018×2019＝1-1/2+1/2-1/3+1/3+……1/2018-1/2019＝1-1/2019＝2018/2019。

第5小题的解法同样用拆分法：1/2+1/6+1/8+1/12+1/20+1/30+1/42+1/56＝1/1×2+1/2×3+1/8+1/3×4+1/4×5+1/5×6+1/7×8＝1-1/2+1/2-1/3+1/8-1/3-1/4+1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8 ＝1第6题底层的规律是：1个、3个、5个、7个、9个……奇数规律，所以第6个最底层为11个，小三角形总数的规律是：1个、4个、9个、16个、25个……其规律是1的平方、2的平方、3的平方、4的平方、5的平方……因此，第6个整个6层共有6的平方个小三角形，即36个。

例１.摆一个正方形，至少需要4根火柴棍.（1）摆两个大小相同的正方形，至少需要几根火柴棍? （2）摆三个大小相同的正方形，至少需要几根火柴棍? （3）摆五个正方形，最少需要几根火柴棍?1.（选择题）你能用10根火柴棒摆成3个相同的正方形吗？A、能B、不能C、A和B都有可能D、以上答案均不对2.（单选题）你能用9根火柴棒拼出4个相同的三角形吗？A、不能B、能C、A和B都有可能D、以上答案均不对例２.用四根火柴棍可以拼成1个边长是1根火柴棍的正方形，怎样用12根火柴棍拼出6个边长为1根火柴的正方形呢？1.（选择题）你能用7根火柴棒摆成3个相同的三角形吗？A、不能B、能C、A和B都有可能D、以上答案均不对2.（选择题）用6根火柴,拼出4个相同的三角形。

问能不能？A、能B、不能C、A和B都有可能D、以上答案均不对例３.移动3根火柴棒，使这条鱼的鱼头朝右，鱼尾朝左。

1.（单选题）由10根火柴棒摆成的两个倒扣杯子，如图所示，请你移动4根火柴，把杯口正过来。

问能不能？A、不能B、能C、A和B都有可能D、以上答案均不对2.（单选题）用10根火柴棍摆成向上飞的蝙蝠图形，如图所示。

试移动三根火柴，使它变成向下飞的蝙蝠图形。

问能不能？A、能B、不能C、A和B都有可能D、以上答案均不对例４.右图所示为一个倒放着且缺一条腿的椅子，请你移动两根火柴棍把椅子正过来。

1.（单选题）水井的计量单位是“口”，人们常说“一口井”、“两口井”等等，图中是用16根火柴排成的一个“井”字。

请移动6根火柴，使它变成两个同样大小的“口”字。

问能不能？A、能B、不能C、A和B都有可能D、以上答案均不对2.用火柴棒搭成小猪图，你能移动火柴棒使猪头、猪尾正好换一个方向吗？问你至少移动了____根火柴棒？例５.请移动左图中的3根火柴棍，使它变成右图的形状。

1.（单选题）左边是用6根火柴排成的金字塔，右边是用6根火柴排成的倒立的金字塔，能不能只移动2根火柴棍，就把左边的金字塔变成右边的倒立的金字塔？问能不能？A、不能B、能C、A和B都有可能D、以上答案均不对...2.（单选题）右图是用20根火柴棍组成的5个同样大小的正方形，请你移动三根火柴棍，使原图变为7个同样大小的小正方形。

数学小故事400字四年级
从前，有个叫小明的小学生，他非常喜欢数学，每天都会认真地学习数学知识。

有一天，小明和他的朋友小华一起玩耍，他们想出了一个有趣的问题：谁能用最少的火柴摆出一个正方形？
小明和小华分别拿起了 10 根和 9 根火柴，开始思考如何摆出正方形。

小明思考了一会儿，想到了一个办法：他用一根火柴作为正方形的一条边，另外 9 根火柴分别作为正方形的另外 9 条边，最后将火柴交叉连接起来，一个正方形就摆出来了。

小华也不甘示弱，他拿起了 9 根火柴，想了想，决定采用另外一种方式来摆出正方形。

他先将 4 根火柴交叉连接起来，形成一个十字形，然后再将另外 5 根火柴放在十字形的上面和下面，最后也形成了一个正方形。

小明和小华的正方形都有不同的摆法，但是它们都是正确的，因此他们都非常自豪地认为自己是最棒的数学高手。

通过这个小故事，我们可以看到数学的魅力所在，它不仅可以让我们学会解决问题的方法，还可以让我们的思维变得更加敏捷和有条理。

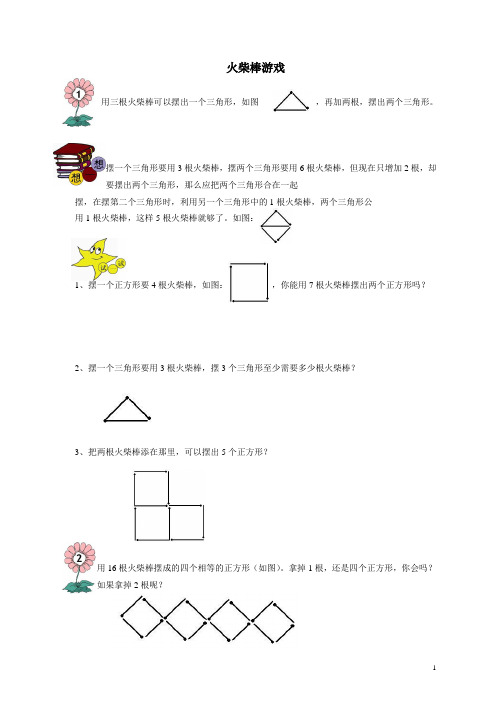
火柴棒游戏用三根火柴棒可以摆出一个三角形，如图，再加两根，摆出两个三角形。

摆一个三角形要用3根火柴棒，摆两个三角形要用6根火柴棒，但现在只增加2根，却要摆出两个三角形，那么应把两个三角形合在一起摆，在摆第二个三角形时，利用另一个三角形中的1根火柴棒，两个三角形公用1根火柴棒，这样5根火柴棒就够了。

如图：1、摆一个正方形要4根火柴棒，如图：，你能用7根火柴棒摆出两个正方形吗？2、摆一个三角形要用3根火柴棒，摆3个三角形至少需要多少根火柴棒？3、把两根火柴棒添在那里，可以摆出5个正方形？用16根火柴棒摆成的四个相等的正方形（如图）。

拿掉1根，还是四个正方形，你会吗？如果拿掉2根呢？注意火柴棒减少了，正方形不能减少。

减少1根火柴棒，第四个正方形少了一条边，可以让第三个正方形的一条边做两个正方形的公用边，如图：减少两根火柴棒，第四个正方形就少了两条边了，可以让第二个正方形的一条边和第三个正方形的一条边做第四个正方形的公用边，如图：还有其他摆法，你会吗？1、用12根火柴棒，摆成四个大小一样的正方形，怎么摆？2、图中有几个正方形？最少要添上几根火柴棒就能得到8个正方形？下图是由5根火柴棒摆成的图形，请你移动其中的3根，变成这样的图形：这是由5根火柴棒组成的图形，只移动其中的3根，就有2根火柴棒不需要移动，我们可以这样移：1、第一排有1根火柴棒，第二排有2根，第三排有3根，请你移动2根，变为第一排3根，第二排2根，第三排1根。

2、如下图，由火柴棒摆了两只倒扣的杯子，请移动4根火柴棒，把杯口正过来。

3、下图是由8根火柴棒组成的向北飞的小燕子，请你移动3根火柴棒，使小燕子掉头向南飞。

移动一根火柴棒，使等式成立。

左边结果是15，右边结果是11，所以通过火柴棒的移动，使左边与右边相等，我们可以把“14”十位上的“1”移到另一个加数“1”上，使“1”变成“7”，等式成立。

移动一根火柴棒可使算式成为正确的算式：你能移动两根火柴棒使等式成立吗？等式右边结果是8，可使左边变成9-1或7+1，9-1算式难以出现9，可选择7+1，这样经移动算式变为：1、你能移动其中两根火柴棒，使算式变成正确的吗？2、移动其中的一根火柴棒，使算式成立。

小学奥数知识点趣味学习——火柴棍游戏火柴除了可作火种外，人们常用它来摆图形、算式，做出许多有趣的游戏。

它不受场地和时间的限制，只要有几根火柴(或几根长短一样的细小木棍)就可以进行。

火柴游戏寓知识、技巧于游戏之中，启迪你的智慧，开阔你的思路，丰富你的课余生活。

火柴游戏大体分为两种：一种是摆图形和变换图形；一种是变换算式。

01摆图形游戏游戏1 用8根火柴棍可以摆成一个正方形。

现添两根，即用10根火柴能摆出与这个正方形同样大小的图形吗？分析与解：8根火柴摆一个正方形，每边必是两根火柴。

它可以分成四个小正方形(如右图)。

因此，只要用10根火柴摆出有四个同样大小的小正方形的图形即可。

下面的四个图形都符合题意。

游戏2 用8根火柴棍摆出八个大小一样的三角形和两个一样大小的正方形。

分析与解：4根火柴可摆出一个正方形，另4根火柴又可摆出一个同样大小的正方形。

把这两个正方形如右图所示交叉放在一起，就形成八个相同的三角形。

02移动火柴，变换图形游戏游戏3 右图是用10根火柴棍摆成的一座房子。

请移动2根火柴，使房子改变方向。

解：如左下图所示，除虚线表示的2根火柴外，其余火柴是左、右对称的，所以改变房子的方向与这些火柴无关，应移动虚线表示的2根火柴(见右下图)。

游戏4 在左下图中移动4根火柴棍，使图形成为只有三个正方形的图形。

解：因为只能移动4根火柴，所以图中较长的边(3根或4根火柴的边)都不能动。

把图中最里面的4根火柴移补到右上图的相关位置上即可。

游戏5 在左下图中移动4根火柴棍，使它变成3个三角形，并且这3个三角形的面积之和与原来的六边形面积相同。

解：原图中有6个三角形，变化后剩下3个三角形，这3个三角形与原来的6个三角形的面积相同，必然有一个三角形的面积要增大。

如右上图所示，移动虚线表示的4根火柴。

图中下面的大三角形面积等于小三角形面积的4倍。

03去掉火柴，变换图形游戏游戏6 在左下图中去掉尽量少的火柴棍，使得图中不存在任何正方形。

国庆期间,某广场用花盆摆成了一个正方形
描述一下
国庆期间，某广场用花盆摆置成一个美丽的正方形，令人眼前一亮。

花盆里面种满了鲜艳夺目的花，如粉红的牡丹，鲜艳的玫瑰，芬芳的茉莉，火红的月季，还有各种蔷薇、石竹等，五彩缤纷，犹如五彩斑斓的绚丽图案。

把整个广场围绕着的建筑，都涂抹上彩色的涂料，把它变成一幅像艺术画作一样的美丽画卷。

大量的灯光装点着广场周围，使这片景象更为美丽，显得广场里很是热闹，熙熙攘攘，来去的人们略显兴奋。

旁边的商家也把装饰把弄的非常好看，有大量的国旗、丝带、烟花等装置，衬托着芳草花海，增添当地气息，新奇有趣。

这让人怡然自得，所有去广场里的人都和愉快。

看着绚丽的花海，听着欢快的音乐，仿佛把节日的喜悦、团圆的温暖，都和这个城市的居民们分享。

在国庆节期间，某广场用花盆摆成的迷人正方形，令那里的人们流连忘返，玩得不亦乐乎。

摆火柴棒游戏☜知识要点小朋友，你们知道吗，小小的火柴棒可以用来做很多趣的数学游戏呢。

比如：用火柴棒可以摆成各种图形，如果拿掉或是移动火柴棒，就可以变成其它图形；还可以用火柴棒摆出数字和运算符号，在去掉、添加或是移动火柴棒后，也可以互相变化。

例如：这些都非常有趣，小朋友，你想试一试吗？☜精选例题【例1】：（1）用4根火柴棒摆成1个正方形。

（2）再加3根火柴棒，你能用7根火柴棒摆出2个相同的正方形吗？ 思路点拨：（1）一个正方形有四条边，用四根火柴棒摆出一个正方形很容易。

（2）要摆出2个独立的正方形，至少需要8根火柴棒。

现在在只有7根火柴棒，少了1根，那么就需要合用1根火柴棒，这样7根火柴棒就可以摆出2个正方形了。

摆的方法有很多种，可以自己试一试。

☝标准答案：（1）（2）✌活学巧用1．用3根火柴棒可以摆成1个三角形，用5根火柴棒，你能摆出2个相同的三角形吗？2．请添上3根火柴棒，使下图变成3个正方形？3.下图中有3个三角形，怎样移动火柴棒，使它变成含有4个同样大小的三角形的图形？【例2】：请你用12根火柴棒摆出的4个同样大小的正方形。

☝思路点拨：摆一个正方形需要4根火柴棒，那么，摆4个同样大小的独立的正方形需要16根火柴棒，现在只有12根火柴棒，少4根，所以需要4根火柴棒共用。

☝标准答案：✌活学巧用1．下图是用12根火柴棒摆出的4个同样大小的正方形。

请你移动3根火柴棒，使它变成3个同样大小的正方形，该怎样移？2.下图是用12根火柴棒摆出的4个同样大小的正方形。

请你去掉2根火柴棒，使它变成2个大小不一样的正方形，该怎样去？3.下图是用12根火柴棒摆出的4个同样大小的正方形。

请你去掉1根火柴棒，使它变成3个正方形，该怎样去？【例3】：下面的算式是不成立的，现只许移动一根火柴棒，使它成立。

☝思路点拨：首先算一算等式两边的结果各是多少，你会发现一边大一边小，那我们就要想办法把大的一边减小，或者把小的一边增大，移动后两边的结果都一样，这样就可以使等式成立了。