习题二解答

第一章习题解答（一）1．设z =z 及Arcz 。

解：由于3i z e π-==所以1z =，2,0,1,3Arcz k k ππ=-+=±。

2．设121z z =，试用指数形式表示12z z 及12z z 。

解：由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。

3．解二项方程440,(0)z a a +=>。

解：12444(),0,1,2,3k ii z a e aek πππ+====。

4．证明2221212122()z z z z z z ++-=+，并说明其几何意义。

证明：由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是：平行四边形对角线长平方和等于于两边长的和的平方。

5．设z 1，z 2，z 3三点适合条件：0321=++z z z ,1321===z z z 。

证明z 1，z 2，z 3是内接于单位圆1=z 的一个正三角形的顶点。

证 由于1321===z z z，知321z z z ∆的三个顶点均在单位圆上。

因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以， 12121-=+z z z z ，又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ，同理33231=-=-z z z z ，知321z z z ∆是内接于单位圆1=z 的一个正三角形。

机械制造工艺学部分习题解答2第二章：机械加工工艺规程设计（第3版P94）2-1何谓机械加工工艺规程？工艺规程在生产中起何作用？概念题，见教材P25.2-2简述机械加工工艺过程卡和工序卡的主要区别以及它们的应用场合？概念题，见教材P25.2-3简述机械加工工艺过程的设计原则、步骤和内容。

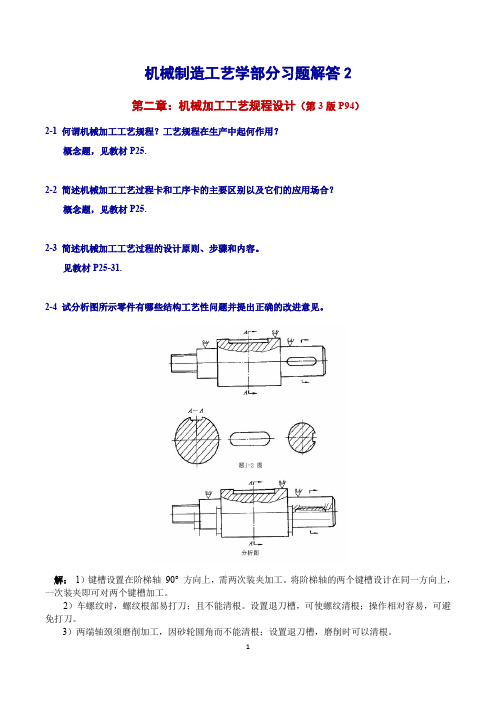
见教材P25-31.2-4试分析图所示零件有哪些结构工艺性问题并提出正确的改进意见。

解：1）键槽设置在阶梯轴90°方向上，需两次装夹加工。

将阶梯轴的两个键槽设计在同一方向上，一次装夹即可对两个键槽加工。

2）车螺纹时，螺纹根部易打刀；且不能清根。

设置退刀槽，可使螺纹清根；操作相对容易，可避免打刀。

3）两端轴颈须磨削加工，因砂轮圆角而不能清根；设置退刀槽，磨削时可以清根。

2-7何谓经济精度？选择加工方法时应考虑的主要问题有哪些？答：（P34）经济精度——在正常加工条件下（采用符合质量标准的设备、工艺装备和标准技术等级的工人，不延长加工时间）所能保证的加工精度和表面粗糙度。

选择加工方法时应考虑（P35）：根据零件表面、零件材料和加工精度以及生产率要求，考虑本厂现有的工艺条件，考虑加工经济精度等因素。

2-8在大批量生产条件下，加工一批直径为，长度为58mm的光轴，其表面粗糙度，材料为45钢，试安排其加工路线。

答：粗车——半精车——粗磨——精磨——精密磨削。

2-9图4-71所示箱体零件的两种工艺安排如下：(1)在加工中心上加工：粗、精铣底面；粗、精铣顶面；粗镗、半精镗、精镗Φ80H7孔和60H7孔；粗、精铣两端面。

(2)在流水线上加工：粗刨、半精刨底面，留精刨余量；粗、精铣两端面；粗镗削、半精镗Φ80H7孔和60H7孔，留精镗余量；粗刨、半精刨、精刨顶面；精镗Φ80H7孔和60H7孔；精刨底面。

试分别分析上述两种工艺安排有无问题，若有问题请提出改进意见。

答：(1)应在先加工底面、顶面之后，加工两端面，因为底面、端面是定位表面，定位表面加工之后，再进行镗孔。

第2章 逻辑门电路2.1解题指导[例2-1] 试用74LS 系列逻辑门，驱动一只V D =1.5V ，I D =6mA 的发光二极管。

解：74LS 系列与之对应的是T4000系列。

与非门74LS00的I OL为4mA ，不能驱动I D =6mA 的发光二极管。

集电极开路与非门74LS01的I OL 为6mA ，故可选用74LS01来驱动发光二极管，其电路如图所示。

限流电阻R 为Ω=--=--=k V V V R OL D CC 5.065.05.156[例2-2] 试分析图2-2所示电路的逻辑功能。

解：由模拟开关的功能知：当A =1时，开关接通。

传输门导通时，其导通电阻小于1k Ω，1k Ω与200k Ω电阻分压，输出电平近似为0V 。

而A =0时，开关断开，呈高阻态。

109Ω以上的电阻与200k Ω电阻分压，输出电平近似为V DD 。

故电路实现了非逻辑功能。

[例2-3] 试写出由TTL 门构成的逻辑图如图2-3所示的输出F 。

&≥1F≥1A B图2-3 例2-3门电路A BF图2-4 例2-4门电路解：由TTL 门输入端悬空逻辑上认为是1可写出 [例2-4] 试分别写出由TTL 门和CMOS 门构成的如图2-4所示逻辑图的表达式或逻辑值。

解：由TTL 门组成上面逻辑门由于10k Ω大于开门电阻R ON ，所以，无论 A 、B 为何值由CMOS 门组成上面逻辑门由于CMOS 无开门电阻和关门电阻之说，所以，2.2 习题解答2-1 一个电路如图2-5所示，其三极管为硅管，β=20，试求：ν1小于何值时，三极管T 截止，ν1大于何值时，三极管T 饱和。

解：设v BE =0V 时，三极管T 截止。

T 截止时，I B =0。

此时 10)10(020--=-I v v I =2VT 临界饱和时，v CE =0.7V 。

此时mA I BS 0465.010207.010=⨯-= mA v I I I BS B 0465.010)10(7.027.0=----==v I=4.2Vv I v O BB 图2-5三极管电路A BF 图2-1例2-1 OC 门驱动发光二极管FA 图2-2 例2-2 模拟开关ΩV V 020011DD F ≈+=DD DD 44DD599F 210101021010V V V V ≈+≈⨯+=AB A F =++⋅=110≡F AB F =上述计算说明v I <2V 时，T 截止；v I >4.2V 时，T 饱和。

第二章习题解答1、证明P.eE f的充要条件是对任意含有人的邻域U(P,》)(不一定以人 为中心)中，恒有异于人的点人屈于E (事实上，这样的人述有无穷多个)。

而 0 听E 的充要条件则是有含人的邻域U(P,小(同样，不一定以人为中心)存 在，使 U(P,5)uE 。

证明：(1)充分性，用反证法，若吒疋E',则儿的某一邻域U(£),心)中 至多有有限个异于人的点X" X 2,…，X “属于E ,令mind(^,旺)二 在U(£,夕)中不含异于人的点屈于E,这与条件矛盾。

必要性，设U(P, /)是任意一个含有人的邻域，则d(£), E)〈5,令岳二5 - d(£), P)〉0,则 U(«, Q)uU(P, 6)。

因为P {)eE\ 所以，在 U (人，$) 中含于无穷多个屈于E 的点，其中必有异于人的点用，即U(P, 5)中有异于人 的点片。

(2)必要性是显然的，下而证明充分性，设含有几的邻域U(P,》)uE, 则 d(£, P)C,令$Y-d(£, P),则 U(£), Q)uU(P, d),从而 U(£),o§ ) u E ,故 P {} e E oo2、设R" = R r是全体实数，厶是［0, 1］上的全部有理点，求E ：, E 「E 。

0 解：E ； = ［0, 1］, E\=e , E 二［0,3、设R n = R 2是普通的xoy 平而， 1] o £2 = {(X , y) 0 |x 2 + /<l},求 E ；, E 2 ,o 解：E ；二{(兀,y) x 2 + y 2^l},0 E 2={(X 9 y) %2+r<i}, E 2={(xt y) x 2 + y 2^l} o4、设R 性R?是普通的xoy 平面， 耳是函数y 二＜si 4当的图形上 0 当 x = 0的点作成的集合，求E ；, E 3 o解：E ；二{(兀，y)|xH0, y =siny } U {(0, y)卜 lWyWl}E 3=(/>0 _5、 在F 中看第2题的耳，E, , E 各是由哪些点构成的。

习题二1 •某人根据医嘱，每天需补充A、B、C三种营养，A不少于80单位，B不少于150单位，C不少于180单位.此人准备每天从六种食物中摄取这三种营养成分. 已知六种食物每百克的营养成分含量及食物价格如表2-22所示.（1）试建立此人在满足健康需要的基础上花费最少的数学模型；（2）假定有一个厂商计划生产一中药丸，售给此人服用，药丸中包含有A , B , C三种营养成分•试为厂商制定一个药丸的合理价格，既使此人愿意购买，又使厂商能获得最大利益，建立数学模型.表 2-221 X j jmin Z 0.5% 0.4X0.8X30 .9x40.3X50.2X613x125x214X3 40X48X5 11X6 8024x19x230X325X412X5 15X6 15018x17x221X3 34X410X5 180x1> x2、X、X4、X、X6 0(2 )设V i为第i种单位营养的价格，则数学模型为max w 80y1 150 y2180 y313V1 24 y2 18y3 0.525y1 9y2 7y30.414y1 30 y221y30.840y1 25y2 34 y3 0.98y1 12y2 10y3 0.311y1 15y2 0.5力，丫2”302 •写出下列线性规划的对偶问题max 2X14X2min w % 4y2八X1 3X2 1 ”y1 y2 2（1）X15X2 4 3y1 5y2 4X1,X2 0 y1, y2 0min w 9% 6y 2 2y 3+5y 4 10 y 5 3y i 6y 2 y 3 g 衣 2 对偶问题为：2y i 2y 2 3 y i 5y 2 出 6 6y i y 2 2y 37y i 无约束；y 2 0, y 3, 0, y 4 0, X 5 03 .考虑线性规划mi nZ 12X 120X 2X 1 4X 2 4 X 1 5X 22 2X 1 3X 27X 1, X 2 0(1) 说明原问题与对偶问题都有最优解； ⑵通过解对偶问题由最优表中观察出原问题的最优解; ⑶利用公式C B B^1求原问题的最优解； (4)利用互补松弛条件求原问题的最优解.【解】(1)原问题的对偶问题为maxw 4% 2y 2 7y 3 y i y 2 2y 312min Z 2x i X 2 3x 3 x 1 2X 210(2)1 2X i 3X 2 X 38X ,X 无约束，X 0maxw 10y i 8y 2 y i y 22 【解】2y i 3y 21y 2 3叶无约束；y 2 0maxZX 1 2X 24X 3 3X 410X 1X 2 X 3 4X 48(3)7X 1 6X 2 2X 3 5X 4 104X 1 8X 2 6X 3 X 4 6X 1,X 2 0,X 3 0,X 4无约束min w 8y 1 10y 2 6y 3【解】10 y 1 7y 2 4y 31 y 1 6y2 8y3 2 y 1 2y 2 6y 34 4y 1 5y 2 y 33y 1 无约束；y 2 0, y 3 0 max Z 2X -I 3X 2 6X 3 7X 43X -I 2X 2 X 3 6X 4 9 6X -I 5X 3 X 4X 1 2X 2 X 3 62X 45 X 1 10X 10, X 2,X 3, X 4无约束max Z2X -I 3X 2 6X 3 7X 43X 1 2X 2 X 3 6X 4 9 6X -| 5X 3 X 46【解】 X 1 2X 2 X 3 2X 42X -I 5 X -I10X - 0, X , X , X 无约束4y i 5y 3*20y j 0,j 1,2,3容易看出原问题和对偶问题都有可行解，女口X = (2, 1)、Y = (1 , 0, 1)，由定理2.4知都有最优解。