手拉手模型(修正1)
- 格式:ppt
- 大小:760.00 KB
- 文档页数:13
专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
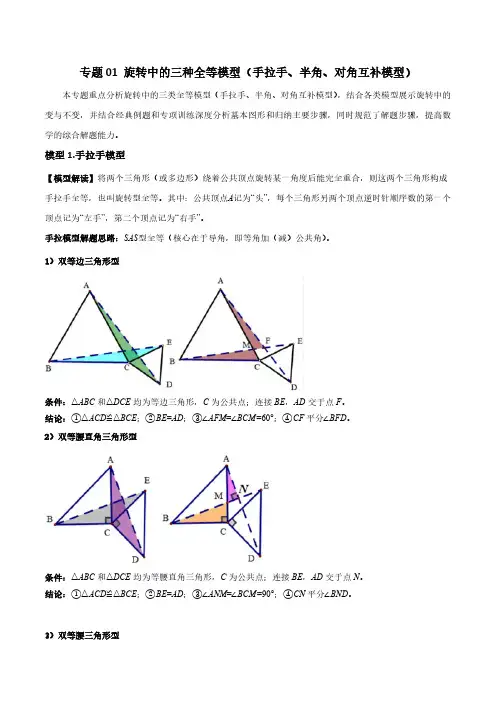
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。
3)双等腰三角形型条件:△ABC 和△DCE 均为等腰三角形,C 为公共点;连接BE ,AD 交于点F 。
结论:①△ACD ≌△BCE ;②BE =AD ;③∠ACM =∠BFM ;④CF 平分∠AFD 。
4)双正方形形型条件:△ABCFD 和△CEFG 都是正方形,C 为公共点;连接BG ,ED 交于点N 。
结论:①△△BCG ≌△DCE ;②BG =DE ;③∠BCM =∠DNM=90°;④CN 平分∠BNE 。
例1.(2022·黑龙江·中考真题)ABC V 和ADE V 都是等边三角形.(1)将ADE V 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE V 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE V 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC+=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,PA =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明CAP BAF ≌△△(SAS ),得CAP BAF Ð=Ð,AF AP =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明BAP CAF ≌△△(SAS ),得出CAF BAP Ð=Ð,AP AF =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∵△ABC 是等边三角形,∴AB =AC ,∵点P 与点A 重合,∴PB =AB ,PC =AC ,PA =0,∴PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC=+证明:在BP 上截取BF CP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AC =AB ,CP =BF , ∴CAP BAF ≌△△(SAS ),∴CAP BAF Ð=Ð,AF AP =,∴CAP CAF BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AB =AC ,BP =CF ,∴BAP CAF ≌△△(SAS ),∴CAF BAP Ð=Ð,AP AF =,∴BAF BAP BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.例2.(2023·湖南·长沙市八年级阶段练习)如图1,在Rt △ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE .(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长;(3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.例3.(2023·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B 重合时,如图2,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论.【详解】解:(1)CD 2+DB 2=2DF 2证明:∵DF =EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF = 连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =,CF AB ^,即90CFB Ð=° ∴45FCB FBC Ð=Ð=°,90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =,45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2 证明:连接CF 、BE∵CF =BF ,DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ,∠DCF =∠EBF =135°∵∠EBD =∠EBF -∠FBD =135°-45°=90° 在Rt △DBE 中,BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例4.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC V 和ADE V 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE V 均为等腰直角三角形,90ACB DCE Ð=Ð=°,点A ,D ,E 在同一条直线上,CM 为DCE V 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°;2AE AD DE BE CM=+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ≌△CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ≌△CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∵ABC V 和ADE V 是顶角相等的等腰三角形,∴AB AC =,AD AE =,BAC DAE Ð=Ð,∴BAC CAD DAE CAD Ð-Ð=Ð-Ð,∴BAD CAE Ð=Ð.在BAD V 和CAE V 中,AB AC BAD CAE AD AE =ìïÐ=Ðíï=î,∴()BAD CAE SAS ≌△△,∴BD CE =.(2)解:90AEB =°∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE V V ,∴AD BE =,ADC BEC ÐÐ=,∵CDE △是等腰直角三角形,∴45CDE CED Ð=Ð=°,∴180135ADC CDE Ð=°-Ð=°,∴135BEC ADC Ð=Ð=°,∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°.∵CD CE =,CM DE ^,∴DM ME =.∵90DCE Ð=°,∴DM ME CM ==,∴2DE CM =.∴2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ≌△BCE 是解本题的关键.3)15°模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④D AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。

《三角形证明》题型解读12 全等典型模型:“手拉手”模型【知识梳理】(一)“手拉手模型”的基本图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点在同一直线上。
解题方法:一定有以下六个结论(三组全等、一个60°、一个等边△、一组平行线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠2=∠3=60°,∴∠ABE=∠CBD=120°,∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②△ABH ≌△CBF证明过程:∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠1=∠2,∴△ABH ≌△CBF (SAS ) ③△BHE ≌△BFD证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,∵BE=BD ,∠2=∠3,∴△BHE ≌△BFD (SAS ) ④∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程:∵△BHE ≌△BFD (SAS ),∴BH=BF ,∵∠2=60°,∴△BHF 是等边三角形(有一个角是60°的等腰三角形是等边三角形) ⑥HF//AD证明过程:∵△BHF 是等边三角形,∴∠8=60°,∵∠3=60°,∴∠8=∠3,∴HF//AD (二)“手拉手模型”的变化图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点不在同一直线上。
图2M N 765431H GFEDCBA765431HG F ED CBA解题方法:一定有以下三个结论(一组全等,一个60°、一个角平分线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠3=60°,∴∠ABE=∠CBD (共角模型),∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程:作BM ⊥AE 于点M ,BN ⊥GD 于点N ,如图2,∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠AMB=∠CNB=90°,∴△ABM ≌△CBN (AAS ),∴BM=BN ,∴BG 平分∠HBF (到角两边的距离相等的点,在这个角的角平分线上) (三)常见“手拉手”变化图形【典型例题】例1.如图,C 为线段AE 上一动点(不与A 、E 重合),在AE 同侧分别作等边△ABC 和等 边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,以下五个结论: ①AD =BE ;②PQ ∥AE ;③CP =CQ ;④BO =OE ;⑤∠AOB =60°,恒成立的结论有( )。
1 手拉手模型
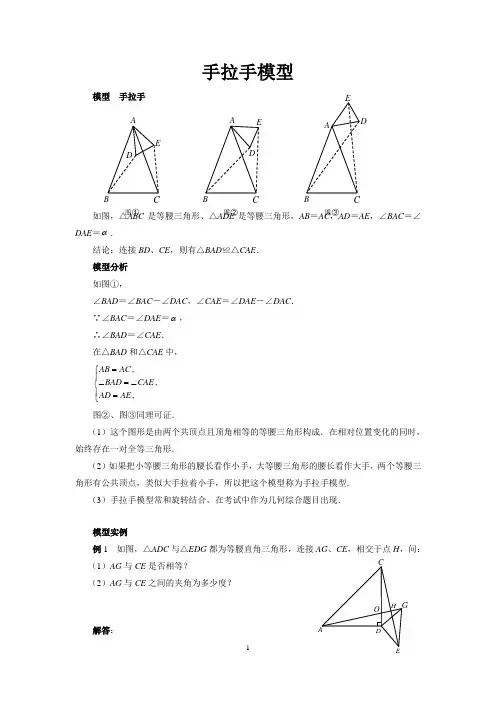
模型 手拉手
如图,△ABC 是等腰三角形、△ADE 是等腰三角形,AB =AC ,AD
=AE ,∠BAC =∠DAE =α.
结论:连接BD 、CE ,则有△BAD ≌△CAE .
模型分析
如图①,
∠BAD =∠BAC -∠DAC ,∠CAE =∠DAE -∠DAC .
∵∠BAC =∠DAE =α,
∴∠BAD =∠CAE .
在△BAD 和△CAE 中,
AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩
﹐﹐
﹐ 图②、图③同理可证.
(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.
(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型.
(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现.
模型实例
例1 如图,△ADC 与△EDG 都为等腰直角三角形,连接AG 、CE ,相交于点H ,问:
(1)AG 与CE 是否相等?
(2)AG 与CE 之间的夹角为多少度?
解答:
C D E A B 图① C D E A B 图② C
D E A B 图③ C D E G H A O。
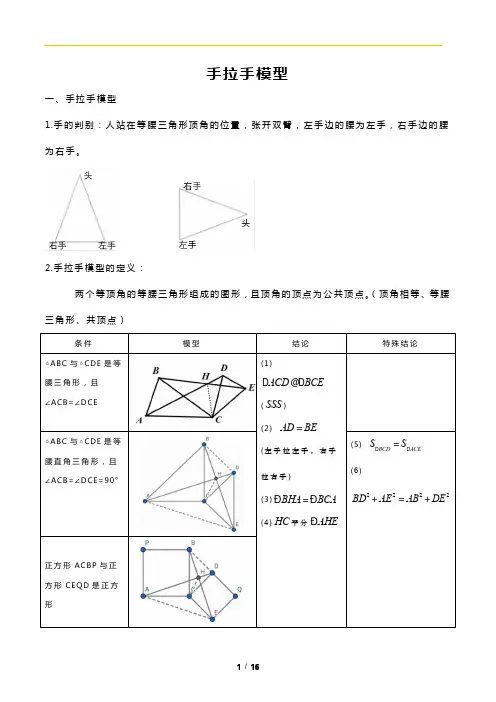
手拉手模型一、手拉手模型1.手的判别:人站在等腰三角形顶角的位置,张开双臂,左手边的腰为左手,右手边的腰为右手。
2.手拉手模型的定义:两个等顶角的等腰三角形组成的图形,且顶角的顶点为公共顶点。
(顶角相等、等腰三角形、共顶点)条件模型结论特殊结论△ABC与△CDE是等腰三角形,且∠ACB=∠DCE (1)D ACD@D BCE (SSS)(2)AD=BE(左手拉左手,右手拉右手)(3)ÐBHA=ÐBCA(4)HC平分ÐAHE△ABC与△CDE是等腰直角三角形,且∠ACB=∠DCE=90°(5)S D BCD=S D ACE(6)BD2+AE2=AB2+DE2正方形ACBP与正方形CEQD是正方形△ABC 与△CDE是等边三角形(5)D ACM@D BCND DCM@D ECN(6) CM=CN(7)D CMN是等边三角形(8)MN∥AE,CD∥AB, CB∥DE(9) BH+CH=AHDH+CH=EH二、手拉手模型的变形:(两三角形相似,且对应角共顶点)条件模型结论D BAC∽D DAE,且ÐDAE=ÐBAC (1)D BAD∽D CAE(两边对应成比例且夹角相等) (2)BDCE=BACA(3) ÐBHC=ÐBAC【巩固练习】1、如图所示,若△ABC、△ADE都是正三角形,试比较线段BD与线段CE的大小.2、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是()3、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,四边形ADEF是菱形?(4)当△ABC满足什么条件时,四边形ADEF是正方形?(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?4、问题情境:如图1,已知△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC=2,CD=CE=1,点D在AC 边上,点E 在BC 延长线上。

完整版)社会学模型手拉手模型1.引言社会学是研究人类社会行为、社会关系和社会机构的科学。
手拉手模型是社会学中一个重要的概念,用来描述人们在社会互动中相互协作、互惠互助的关系。
本文将介绍手拉手模型的定义、特点和应用,并探讨其在社会学研究中的意义和影响。
2.手拉手模型的定义手拉手模型是指人们在社会交往中通过相互支持、合作和互助,形成紧密的互联互动的关系。
它强调人与人之间的互惠和互助,是一种相互关联和相互依赖的社会联系模式。
3.手拉手模型的特点手拉手模型具有以下几个特点:相互支持:手拉手模型强调人们在社会交往中相互支持,通过共同的努力和帮助来实现目标。
合作互助:在手拉手模型中,人们通过相互合作和互助,共同解决问题和应对挑战。
互联互动:手拉手模型强调人与人之间的紧密联系和互动,通过交流和合作实现共同的利益。
4.手拉手模型的应用手拉手模型在社会学研究中有广泛的应用,例如:教育领域:手拉手模型可以用于描述学生之间的相互支持和合作学习的关系,促进学生的共同学习和发展。
社区发展:手拉手模型可以应用于社区组织和发展,通过组织居民之间的互助、合作和支持,提高社区的凝聚力和发展能力。
心理健康:手拉手模型可以用于描述亲密关系中的相互支持和互助,帮助个体在压力和困难时获得支持和帮助。
5.手拉手模型的意义和影响手拉手模型的应用和研究对社会学具有重要意义和积极影响:加强社会联系:手拉手模型强调人与人之间的相互关联和互助,可以加强社会联系和社区凝聚力。
促进社会发展:通过手拉手模型中的合作和互助,可以促进社会的发展和进步。
改善人际关系:手拉手模型强调相互支持和互助,有助于改善人际关系和促进个体的心理健康。
6.结论手拉手模型是社会学中的一个重要概念,用于描述人们在社会交往中相互协作、互惠互助的关系。
它强调人与人之间的相互支持、合作和互助,在教育、社区发展和心理健康等领域有广泛的应用。
手拉手模型的研究和应用对于加强社会联系、促进社会发展和改善人际关系具有重要意义和积极影响。

模型介绍共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。
寻找共顶点旋转模型的步骤如下: (1)寻找公共的顶点(2)列出两组相等的边或者对应成比例的边(3)将两组相等的边分别分散到两个三角形中去,证明全等或相似即可。
两等边三角形两等腰直角三角形两任意等腰三角形*常见结论:连接BD 、AE 交于点F ,连接CF ,则有以下结论:(1)BCD ACE≅△△(2)AE BD=(3)AFB DFE∠=∠(4)FC BFE∠平分【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
【知识总结】【基本模型】一、等边三角形手拉手-出全等图1图2图3图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有:①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;图1图2图3图4手拉手模型的定义:两个顶角相等且有共顶点的等腰三角形形成的图形。
手拉手模型特点:“两等腰,共顶点”模型探究:例题精讲考点一:等边三角形中的手拉手模型【例1】.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.有下列结论:①AD=BE;②AP=BQ;③∠AOB=60°;④DC=DP;⑤△CPQ为正三角形.其中正确的结论有_____________.解:∵△ABC和△DCE是正三角形,∴AC=BC,DC=CE,∠BCA=∠DCE=60°,∴∠BCA+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,在△ACD和△BCE中∴△ACD≌△BCE(SAS),∴AD=BE,∴①正确;∵△ACD≌△BCE,∴∠CBE=∠CAD,∵∠ACB=∠DCE=60°,∴∠BCD=60°=∠ACB,在△ACP和△BCQ中∴△ACP≌△BCQ(ASA),∴AP=BQ,∴②正确;PC=QC,∴△CPQ为正三角形∴⑤正确∵△ACD≌△BCE,∴∠ADC=∠BEC,∠DCE=60°=∠CAD+∠ADC,∴∠CAD+∠BEC=60°,∴∠AOB=∠CAD+∠BEC=60°,∴③正确;∵△DCE 是正三角形,∴DE =DC ,∵∠AOB =60°,∠DCP =60°,∠DPC >∠AOB ,∴∠DPC >∠DCP ,∴DP <DC ,即DP <DE ,∴④错误;所以正确的有①②③⑤变式训练【变式1-1】.如图,ABD ∆,AEC ∆都是等边三角形,则BOC ∠的度数是()A .135︒B .125︒C .120︒D .110︒解:ABD ∆ ,AEC ∆都是等边三角形,AD AB ∴=,AE AC =,60DAB CAE ∠=∠=︒,60ADB DBA ∠==︒,DAB BAC CAE BAC ∴∠+∠=∠+∠,DAC BAE ∴∠=∠,()DAC BAE SAS ∴∆≅∆,ADC ABE ∴∠=∠,BOC BDO DBA ABE∴∠=∠+∠+∠BDO DBA ADC =∠+∠+∠ADB DBA=∠+∠6060=︒+︒120=︒,BOC ∴∠的度数是120︒故选:C .【变式1-2】.如图,△DAC 和△EBC 均是等边三角形,AE 、BD 分别与CD 、CE 交于点M 、N ,有如下结论:①△ACE ≌△DCB ;②CM =CN ;③AC =DN ;④∠DAE =∠DBC .其中正确的有()A .②④B .①②③C .①②④D .①②③④解:∵△DAC 和△EBC 均是等边三角形,∴AC =DC ,BC =CE ,∠ACE =∠BCD ,∴△ACE≌△DCB,①正确由①得∠AEC=∠CBD,∴△BCN≌△ECM,∴CM=CN,②正确假使AC=DN,即CD=CN,△CDN为等边三角形,∠CDB=60°,又∵∠ACD=∠CDB+∠DBC=60°,∴假设不成立,③错误;∵∠DBC+∠CDB=60°∠DAE+∠EAC=60°,而∠EAC=∠CDB,∴∠DAE=∠DBC,④正确,∴正确答案①②④故选:C.【变式1-3】.如图,△ABC和△ADE都是等边三角形,点D在BC上,DE与AC交于点F,若AB=5,BD=3,则=.解:连接CE,过点F作FM⊥BC于点M,FN⊥CE于点N,∵△ABC和△ADE为等边三角形,∴AB=AC,AD=AE,∠BAC DAE=60°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=CE=3,∠ABD=∠ACE=60°,∵AB=BC=5,∴DC=2,∵∠ACB=∠ACE=60°,FM⊥BC,FN⊥CE,∴FM=FN,=DC•FM,S△FCE=CE•FN,∵S△DFC∴,∴,故答案为:.考点二:等腰直角三角形中的手拉手模型【例2】.如图,ACB∆和ECD∆都是等腰直角三角形,90ACB ECD∠=∠=︒,D为AB边上一点,若5AD=,12BD=,则DE的长为__________解:ACB∆和ECD∆都是等腰直角三角形,CD CE∴=,AC BC=,90ECD ACB∠=∠=︒,ACE BCD∴∠=∠,在ACE∆和BCD∆中,CE CDACE BCD AC BC=⎧⎪∠=∠⎨⎪=⎩,()ACE BCD SAS∴∆≅∆,12BD AE∴==,45CAE CBD∠=∠=︒,90EAD∴∠=︒,222212513DE AE AD∴=+=+=.变式训练【变式2-1】.如图,3AB=,2AC=,连结BC,分别以AC、BC为直角边作等腰Rt ACD∆和等腰Rt BCE∆,连结AE、BD,当AE最长时,BC的长为()A.22B.3C.11D.17解:90ACD BCE∠=∠=︒,ACD ACB BCE ACB∴∠+∠=∠+∠,即ACE DCB∠=∠,在ACE ∆和DCB ∆中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,()ACE DCB SAS ∴∆≅∆,AE BD ∴=,AC CD == ,90ACD ∠=︒,2AD ∴=,3AB = ,∴当点A 在BD 上时,BD 最大,最大值为325+=,如图,过C 作CE AD ⊥于E ,由等腰三角形“三线合一”得1DE AE ==,314BE AB AE ∴=+=+=,再由直角三角形斜边中线等于斜边一半得1DE =,BC ∴=.故选:D .【变式2-2】.如图,在Rt ABC ∆中,AB AC =,点D 为BC 中点,点E 在AB 边上,连接DE ,过点D 作DE 的垂线,交AC 于点F .下列结论:①AED CFD ∆≅∆;②EF AD =;③BE CF AC +=;④212AEDF S AD =四边形,其中正确的结论是(填序号).解:AB AC = ,90BAC ∠=︒,点D 为BC 中点,12BD CD AD BC ∴===,45BAD CAD C ∠=∠=∠=︒,AD BC ⊥,BC =,DF DE ⊥ ,90EDF ADC ∴∠=∠=︒,ADE CDF ∴∠=∠,AD CD = ,BAD C ∠=∠,()AED CFD ASA ∴∆≅∆,故①正确;当E 、F 分别为AB 、AC 中点时,12EF BC AD ==,故②不一定正确;ADE CDF ∆≅∆ ,AE CF ∴=,BE AE AB += ,BE CF AC ∴+=,故③正确;ADE CDF ∆≅∆ ,ADE CDF S S ∆∆∴=,212ADF CDF ADC AEDF S S S S AD ∆∆∆∴=+==⨯四边形,故④正确;故答案为:①③④.【变式2-3】.如图,△ABC 和△CEF 均为等腰直角三角形,E 在△ABC 内,∠CAE +∠CBE =90°,连接BF .(1)求证:△CAE ∽△CBF .(2)若BE =1,AE =2,求CE 的长.(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴==,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;(2)解:∵△CAE∽△CBF,∴∠CAE=∠CBF,==,又∵==,AE=2∴=,∴BF=,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴EF2=BE2+BF2=12+()2=3,∴EF=,∵CE2=2EF2=6,∴CE=.考点三:任意等腰三角形中的手拉手模型【例3】.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD =36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论是_____.解:∵∠AOB=∠COD=36°,∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,在△AOC和△BOD中,∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,故②正确;∵∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OBD=∠OAC+∠AOB,∴∠AMB=∠AOB=36°,故①正确;法一:作OG⊥AM于G,OH⊥DM于H,如图所示,则∠OGA=∠OHB=90°,∵△AOC≌△BOD,∴OG=OH,∴MO平分∠AMD,故④正确;法二:∵△AOC≌△BOD,∴∠OAC=∠OBD,∴A、B、M、O四点共圆,∴∠AMO=∠ABO=72°,同理可得:D、C、M、O四点共圆,∴∠DMO=∠DCO=72°=∠AMO,∴MO平分∠AMD,故④正确;假设MO平分∠AOD,则∠DOM=∠AOM,在△AMO与△DMO中,,∴△AMO≌△DMO(ASA),∴AO=OD,∵OC =OD ,∴OA =OC ,而OA <OC ,故③错误;变式训练【变式3-1】.如图,等腰ABC ∆中,120ACB ∠=︒,4AC =,点D 为直线AB 上一动点,以线段CD 为腰在右侧作等腰CDE ∆,且120DCE ∠=︒,连接AE ,则AE 的最小值为()A .23B .4C .6D .8解:连接BE 并延长交AC 延长线于F ,120ACB ∠=︒ ,AC BC =,30CAB CBA ∴∠=∠=︒,120DCE ACB ∠=︒=∠ ,ACD BCE ∴∠=∠,AC BC = ,CD CE =,()ACD BCE SAS ∴∆≅∆,30CBE CAD ∴∠=∠=︒,CB 为定直线,30CBE ∠=︒为定值,∴当D 在直线AB 上运动时,E 也在定直线上运动,当AE BE ⊥时,AE 最小,30CAB ABC CBE ∠=︒=∠=∠ ,90AFB ∴∠=︒,∴当E 与F 重合时,AE 最小,在Rt CBF ∆中,90CFB ∠=︒,30CBF ∠=︒,122CF CB ∴==,6AF AC CF ∴=+=,AE ∴的最小值为6AF =,故选:C .【变式3-2】.如图,在△ABC 中,AB =AC =5,∠BAC =120°,以CA 为边在∠ACB 的另一侧作∠ACM =∠ACB ,点D 为边BC (不含端点)上的任意一点,在射线CM 上截取CE =BD ,连接AD ,DE ,AE .设AC 与DE 交于点F ,则线段CF 的最大值为.解:∵∠BAC=120°,AB=AC,∴∠B=∠ACB=30°.∵∠ACM=∠ACB,∴∠B=∠ACM=30°.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴AD=AE,∠BAD=∠CAE.∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120°.即∠DAE=120°.∵AD=AE,∴∠ADE=∠AED=30°;∵∠ADE=∠ACB=30°且∠DAF=∠CAD,∴△ADF∽△ACD.∴=.∴AD2=AF•AC.∴AD2=5AF.∴AF=.∴当AD最短时,AF最短、CF最长.∵当AD⊥BC时,AF最短、CF最长,此时AD=AB=.∴AF最短==.∴CF最长=AC﹣AF最短=5﹣=.故答案为:.【变式3-3】.【问题背景】(1)如图1,等腰ABC ∆中,AB AC =,120BAC ∠=︒,AQ BC ⊥于点Q ,则BC AB =;【知识应用】(2)如图2,ABC ∆和ADE ∆都是等腰三角形,120BAC DAE ∠=∠=︒,D 、E 、C 三点在同一条直线上,连接BD .求证:ADB AEC ∆≅∆.(3)请写出线段AD ,BD ,CD之间的等量关系,并说明理由.(1)解:AB AC = ,120BAC ∠=︒,AQ BC ⊥,30B C ∴∠=∠=︒,BQ QC =,12AQ AB ∴=,由勾股定理得:32BQ AB ===,BC ∴=,∴BC AB ==(2)证明:BAC DAE ∠=∠ ,BAC BAE DAE BAE ∴∠-∠=∠-∠,即DAB EAC ∠=∠,在ADB ∆和AEC ∆中,AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩,()ADB AEC SAS ∴∆≅∆;(3)解:CD BD =+,理由如下:由(1)可知:DE =,ADB AEC ∆≅∆ ,EC BD ∴=,CD DE EC BD ∴=+=+.实战演练1.风筝为中国人发明,相传墨翟以木头制成木鸟,研制三年有成,是人类最早的风筝起源.如图,小飞在设计的“风筝”图案中,已知AB AD =,B D ∠=∠,BAE DAC ∠=∠,那么AC 与AE 相等.小飞直接证明ABC ADE ∆≅∆,他的证明依据是()A .SSSB .SASC .ASAD .AAS证明:BAE DAC ∠=∠ ,BAE EAC DAC EAC ∴∠+∠=∠+∠,BAC DAE ∴∠=∠,AB AD = ,B D ∠=∠,()ABC ADE ASA ∴∆≅∆,AC AE ∴=,故选:C .2.如图,ABD ∆,AEC ∆都是等边三角形,则BOC ∠的度数是()A .135︒B .125︒C .120︒D .110︒解:ABD ∆ ,AEC ∆都是等边三角形,AD AB ∴=,AE AC =,60DAB CAE ∠=∠=︒,60ADB DBA ∠==︒,DAB BAC CAE BAC ∴∠+∠=∠+∠,DAC BAE ∴∠=∠,()DAC BAE SAS ∴∆≅∆,ADC ABE ∴∠=∠,BOC BDO DBA ABE∴∠=∠+∠+∠BDO DBA ADC =∠+∠+∠ADB DBA=∠+∠6060=︒+︒120=︒,BOC ∴∠的度数是120︒,故选:C .3.如图,点A 是x 轴上一个定点,点B 从原点O 出发沿y 轴的正方向移动,以线段OB 为边在y 轴右侧作等边三角形,以线段AB 为边在AB 上方作等边三角形,连接CD ,随点B 的移动,下列说法错误的是()A .BOA BDC∆≅∆B .150ODC ∠=︒C .直线CD 与x 轴所夹的锐角恒为60︒D .随点B 的移动,线段CD 的值逐渐增大解:A .OBD ∆ 和ABC ∆都是等边三角形,60ABC OBD ODB BOD ∴∠=∠=∠=∠=︒,BO BD =,BC AB =,ABC DBA OBD DBA ∴∠-∠=∠-∠,CBD ABO ∴∠=∠,()BOA BDC SAS ∴∆≅∆,故A 不符合题意;B .BOA BDC ∆≅∆ ,90BDC BOA ∴∠=∠=︒,6090150ODC BDO BDC ∴∠=∠+∠=︒+︒=︒,故B 不符合题意;C .延长CD 交x 轴于点E ,150ODC ∠=︒ ,18030ODE ODC ∴∠=︒-∠=︒,90BOA ∠=︒ ,60BOD ∠=︒,30DOA BOA BOD ∴∠=∠-∠=︒,60DEA DOA ODE ∴∠=∠+∠=︒,∴直线CD 与x 轴所夹的锐角恒为60︒,故C 不符合题意;D .BOA BDC ∆≅∆ ,CD OA ∴=,点A 是x 轴上一个定点,OA ∴的值是一个定值,∴随点B 的移动,线段CD 的值不变,故D 符合题意;故选:D .4.如图,3AB =,2AC =BC ,分别以AC 、BC 为直角边作等腰Rt ACD ∆和等腰Rt BCE ∆,连结AE 、BD ,当AE 最长时,BC 的长为()A .22B .3C .11D .17解:90ACD BCE ∠=∠=︒ ,ACD ACB BCE ACB ∴∠+∠=∠+∠,即ACE DCB ∠=∠,在ACE ∆和DCB ∆中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,()ACE DCB SAS ∴∆≅∆,AE BD ∴=,2AC CD == ,90ACD ∠=︒,222AD AC CD ∴=+=,3AB = ,∴当点A 在BD 上时,BD 最大,最大值为325+=,如图,过C 作CE AD ⊥于E ,由等腰三角形“三线合一”得1DE AE ==,314BE AB AE ∴=+=+=,再由直角三角形斜边中线等于斜边一半得1DE =,2217BC CE BE ∴=+=.故选:D .5.如图,线段OA 绕点O 旋转,线段OB 的位置保持不变,在AB 的上方作等边PAB ∆,若1OA =,3OB =,则在线段OA 旋转过程中,线段OP 的最大值是()A 10B .4C .5D .5解:如图,以AO 为边,在AO 的左侧作等边AOH ∆,连接BH ,AOH ∆ ,ABP ∆是等边三角形,1AO AH OH ∴===,AB AP =,60OAH BAP ∠=∠=︒,OAP HAB ∴∠=∠,在OAP ∆和HAB ∆中,AO AH OAP HAB AP AB =⎧⎪∠=∠⎨⎪=⎩,()OAP HAB SAS ∴∆≅∆,OP BH ∴=,在OPH ∆中,BH OH OB <+,∴当点H 在BO 的延长线上时,BH 的最大值4OH OB =+=,OP ∴的最大值为4,故选:B .6.如图,O 是等边△ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,则∠AOB =150°.解:连接OO ′,如图,∵线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,∴BO ′=BO =4,∠O ′BO =60°,∴△BOO ′为等边三角形,∴∠BOO ′=60°,∵△ABC 为等边三角形,∴BA =BC ,∠ABC =60°,∴∠O ′BO ﹣∠ABO =∠ABC ﹣∠ABO ,即∠O ′BA =∠OBC ,在△O ′BA 和△OBC中,∴△O ′BA ≌△OBC (SAS ),∴O ′A =OC =5,在△AOO ′中,∵OA ′=5,OO ′=4,OA =3,∴OA 2+OO ′2=O ′A 2,∴∠AOO ′=90°,∴∠AOB =60°+90°=150°,故答案为:150°.7.如图,△ABC与△ADE均是等腰直角三角形,点B,C,D在同一直线上,AB=AC=2,AD=AE=3,∠BAC=∠DAE=90°,则CD=﹣.解:∵AB=AC=2,AD=AE=3,∠BAC=∠DAE=90°,∴BC=AB=2,DE=AE=3,∠BAD=∠CAE,∠ABC=45°=∠ACB,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴EC=BD,∠ABD=∠ACE=45°,∴∠ECB=∠ECD=90°,∴DE2=EC2+CD2,∴18=(2+CD)2+CD2,解得:CD=﹣,CD=﹣﹣(不合题意舍去),故答案为:﹣.8.如图,△ABC和△ADE均为等腰直角三角形,连接CD、BE,点F、G分别为DE、BE 的中点,连接FG.在△ADE旋转的过程中,当D、E、C三点共线时,若AB=3,AD=2,则线段FG的长为.解:连接BD,∠BAD=90°﹣∠BAE,∠CAE=90°﹣∠BAE,∴∠BAD=∠CAE.又AD=AE,AB=AC,∴△ADB≌△AEC(SAS).∴BD=CE,∠ADB=∠AEC=135°,∴∠BDC=135°﹣45°=90°.∵△ABC和△ADE均为等腰直角三角形,AB=3,AD=2,∴DE=2,BC=3.设BD=x,则DC=2+x,在Rt△BDC中,利用勾股定理BD2+DC2=BC2,所以x2+(2+x)2=18,解得x1=﹣﹣(舍去),x2=﹣+.∵点F、G分别为DE、BE的中点,∴FG=BD=.故答案为.9.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.解:猜测AE=BD,AE⊥BD;理由如下:∵∠ACD=∠BCE=90°,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,又∵△ACD和△BCE都是等腰直角三角形,∴AC=CD,CE=CB,在△ACE与△DCB中,∴△ACE≌△DCB(SAS),∴AE=BD,∠CAE=∠CDB;∵∠AFC=∠DFH,∠FAC+∠AFC=90°,∴∠DHF=∠ACD=90°,∴AE⊥BD.故线段AE和BD的数量相等,位置是垂直关系.10.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.证明:(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠E=45°,由(1)知△BAC≌△DAE,∴∠BCA=∠E=45°,∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF到G,使得FG=FB,∵AF⊥BG,∴∠AFG=∠AFB=90°,在△AFB和△AFG中,,∴△AFB≌△AFG(SAS),∴AB=AG,∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,∵∠GCA=∠DCA=45°,在△CGA和△CDA中,,∴△CGA≌△CDA(AAS),∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.11.已知△ABC和△ADE都是等边三角形,点D在射线BF上,连接CE.(1)如图1,BD与CE是否相等?请说明理由;(2)如图1,求∠BCE的度数;(3)如图2,当D在BC延长线上时,连接BE,△ABE、△CDE与△ADE的面积有怎样的关系?并说明理由.解:(1)BD=CE,理由如下:∵△ABC和△ADE是都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∠ABC=∠ACB=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;(2)∵△ABD≌△ACE,∴∠ABD=∠ACE=60°,∴∠BCE=120°;+S△CDE=S△ADE,理由如下:(3)S△ABE∵△ABC和△ADE是都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∠ABC=∠ACB=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),=S△ACE,∠ABC=∠ACE=60°,∴S△ABD∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ABC=∠ECD,∴AB∥CE,=S△ABC,∴S△ABE+S△CDE=S△ADE+S△ACD,∵S△ACE+S△CDE=S△ADE+S△ACD,∴S△ABD+S△ACD+S△CDE=S△ADE+S△ACD,∴S△ABC+S△CDE=S△ADE.∴S△ABE12.如图,在△ABC中,分别以AB、AC为腰向外侧作等腰Rt△ADB与等腰Rt△AEC,∠DAB=∠EAC=90°,连接DC、EB相交于点O.(1)求证:BE⊥DC;(2)若BE=BC.①如图1,G、F分别是DB、EC中点,求的值.②如图2,连接OA,若OA=2,求△DOE的面积.(1)证明:∵∠DAB=∠EAC=90°,∴∠EAB=∠CAD,在△BAE和△DAC中,,∴△BAE≌△DAC(SAS),∴∠ABE=∠ADC,∵∠BAD=90°,∴∠DOB=90°,即BE⊥DC;(2)解:①取DE的中点H,连接GH、FH,∵点G是BD的中点,∴GH∥BE,GH=BE,同理,FH∥CD,FH=CD,∵BE=CD.BE⊥DC,∴GH=FH,GH⊥FH,∴△HGF为等腰直角三角形,∴GF=GH,∵GH=BE,∴GF=BE,∵BE=BC,∴=;②作AM⊥BE于M,AN⊥CD于N,在△BAE和△BAC中,,∴△BAE≌△BAC(SSS),∴∠BAE=∠BAC=135°,∴∠DAE=135°﹣90°=45°,即∠OAD+∠OAE=45°,∵△BAE≌△DAC,∴AM=AN,又AM⊥BE,AN⊥CD,∴OA平分∠BOC,∴∠BOA=∠COA=45°,∴∠DOA=∠EOA=135°,∴∠ODA+∠OAD=45°,∴∠OAE=∠ODA,∴△ODA∽△OAE,∴=,即OD•OE=OA2=4,∴△DOE的面积=×OD•OE=2.13.如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD 为一边在AD的右侧作等腰直角△ADF,∠ADE=∠AED=45°,∠DAE=90°,AD=AE,解答下列问题:(1)如果AB=AC,∠BAC=90°,∠ABC=∠ACB=45°.①当点D在线段BC上时(与点B不重合),如图(2),线段CE、BD之间的数量关系为CE=BD;位置关系为CE⊥BD;(不用证明)②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,请写出结论并说明理由.(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?请写出条件,并借助图(4)简述CE⊥BD成立的理由.解:(1)①CE与BD位置关系是CE⊥BD,数量关系是CE=BD.理由:如图(2),∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,∴∠BAD=∠CAE.又BA=CA,AD=AE,∴△ABD≌△ACE(SAS),∴∠ACE=∠B=45°且CE=BD.∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即CE⊥BD.故答案为:CE=BD;CE⊥BD.②当点D在BC的延长线上时,①的结论仍成立.如图(3),∵∠DAE=90°,∠BAC=90°,∴∠DAE=∠BAC,∴∠DAB=∠EAC,又AB=AC,AD=AE,∴△DAB≌△EAC(SAS),∴CE=BD,且∠ACE=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD;(2)如图(4)所示,当∠BCA=45°时,CE⊥BD.理由:过点A作AG⊥AC交BC于点G,∴AC=AG,∠AGC=45°,即△ACG是等腰直角三角形,∵∠GAD+∠DAC=90°=∠CAE+∠DAC,∴∠GAD=∠CAE,又∵DA=EA,∴△GAD≌△CAE(SAS),∴∠ACE=∠AGD=45°,∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.14.(注意:本题中的说理过程中的每一步必须注明理由,否则不得分)如图1,在△ABC 中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°;①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为CF⊥BD,线段CF、BD的数量关系为CF=BD;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立?并说明理由;(2)如图4,如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.解:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC(SAS),∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.故答案为:CF⊥BD,CF=BD;②当点D在BC的延长线上时①的结论仍成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC(SAS),∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD;(2)当∠ACB=45°时,CF⊥BD.理由如下:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF(SAS),∴∠ACF=∠AGC=45°,∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.15.背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了下列三个问题,请你帮助解答:(1)将正方形AEFG绕点A按逆时针方向旋转(如图1),还能得到BE=DG吗?若能,请给出证明;若不能,请说明理由;(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图2),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)把背景中的正方形分别改写成矩形AEFG和矩形ABCD,且,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.(1)证明:∵四边形AEFG为正方形,∴AE=AG,∠EAG=90°,又∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠EAB=∠GAD,∴△AEB≌△AGD(SAS),∴BE=DG;(2)当∠EAG=∠BAD时,BE=DG,理由如下:∵∠EAG=∠BAD,∴∠EAB=∠GAD,又∵四边形AEFG和四边形ABCD为菱形,∴AE=AG,AB=AD,∴△AEB≌△AGD(SAS),∴BE=DG;(3)解:方法一:过点E作EM⊥DA,交DA的延长线于点M,过点G作GN⊥AB交AB于点N,由题意知,AE=4,AB=8,∵=,∴AG=6,AD=12,∵∠EMA=∠ANG,∠MAE=∠GAN,∴△AME∽△ANG,设EM=2a,AM=2b,则GN=3a,AN=3b,则BN=8﹣3b,∴ED2=(2a)2+(12+2b)2=4a2+144+48b+4b2,GB2=(3a)2+(8﹣3b)2=9a2+64﹣48b+9b2,∴ED2+GB2=13(a2+b2)+208=13×4+208=260.方法二:如图2,设BE与DG交于Q,BE与AG交于点P,∵,AE=4,AB=8∴AG=6,AD=12.∵四边形AEFG和四边形ABCD为矩形,∴∠EAG=∠BAD,∴∠EAB=∠GAD,∵,∴△EAB∽△GAD,∴∠BEA=∠AGD,∴A,E,G,Q四点共圆,∴∠GQP=∠PAE=90°,∴GD⊥EB,连接EG,BD,∴ED2+GB2=EQ2+QD2+GQ2+QB2=EG2+BD2,∴EG2+BD2=42+62+82+122=260.。

(完整版)心理学模型手拉手模型心理学模型手拉手模型概述心理学模型手拉手模型是一种有效的心理治疗方法,旨在帮助个人理解和管理自己的情绪和行为。
这种模型结合了心理学理论和实践,通过身体、情绪和思维三个层面的综合训练,促进个人的内在平衡和健康成长。
模型框架心理学模型手拉手模型基于以下几个关键要素:1.身体层面这一层面的训练旨在通过身体运动和呼吸练,促进身体的放松和平衡。
例如,深呼吸、瑜伽和身体冥想等练可以帮助个人减轻压力、放松身心,并提高自我意识。
2.情绪层面情绪是我们内在体验的一部分,而情绪的管理对心理健康至关重要。
手拉手模型通过情绪识别、表达和调节的训练,帮助个人更好地处理情绪,减少消极情绪的影响,提升积极情绪的体验。
3.思维层面思维是影响我们行为和情绪的关键因素之一。
手拉手模型通过认知重塑和思维模式的调整,帮助个人改善负面思维模式,培养积极的信念和态度,并在面对挑战时更加应对灵活。
实施过程心理学模型手拉手模型的实施过程一般包括以下几个步骤:1. 确定目标:与个人合作,明确希望达到的目标和所需改变的领域。
2. 认知评估:通过与个人的对话和评估工具,了解其目前的思维、情绪和行为模式,并识别不健康的模式和问题领域。
3. 训练计划制定:根据评估结果,制定个性化的训练计划,包括身体、情绪和思维层面的综合训练。
4. 实施训练:与个人合作,按照计划进行训练,定期评估进展,并根据需要进行调整。
5. 评估和总结:定期评估个人的进展和成效,为后续训练提供参考,并总结经验和教训。
适用范围心理学模型手拉手模型适用于各个年龄段的个人,无论是面对情绪困扰、心理压力或行为问题,都能从中受益。
此外,该模型还可用于个人成长发展、情绪管理、焦虑和抑郁症等心理疾病的治疗。
结论心理学模型手拉手模型通过综合训练身体、情绪和思维三个层面,帮助个人理解和管理自己的情绪和行为。
它是一种简单且有效的心理治疗方法,可以帮助个人实现内在平衡和健康成长。


百 度 文库本文为word 版资料,可以任意编辑修 本文为word 版资料,可以任意编辑修手拉手模型模型 手拉手如图,△ABC 是等腰三角形、△ADE 是等腰三角形,AB =AC ,AD =AE ,∠BAC =∠DAE =α.结论:连接BD 、CE ,则有△BAD ≌△CAE . 模型分析 如图①,∠BAD =∠BAC -∠DAC ,∠CAE =∠DAE -∠DAC . ∵∠BAC =∠DAE =α, ∴∠BAD =∠CAE . 在△BAD 和△CAE 中, AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩﹐﹐﹐ 图②、图③同理可证.(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型. (3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现. CDEAB图①CDEAB 图②CDEAB 图③模型实例例1 如图,△ADC 与△EDG 都为等腰直角三角形,连接AG 、CE ,相交于点H ,问: (1)AG 与CE 是否相等?(2)AG 与CE 之间的夹角为多少度?解答:(1)AG =CE .理由如下:∵∠ADG =∠ADC +∠CDG ,∠CDE =∠GDE +∠CDG ,∠ADC =∠EDG =90°, ∴∠ADG =∠CDE . 在△ADG 和△CDE 中, AD CD ADG CDE DG DE =⎧⎪∠=∠⎨⎪=⎩﹐﹐﹐ ∴△ADE ≌△CDE . ∴AG =CE . (2)∵△ADG ≌△CDE ,∴∠DAG =∠DCE . ∵∠COH =∠AOD , ∴∠CHA =∠ADC =90°. ∴AG 与CE 之间的夹角是90°.例2 如图,在直线AB 的同一侧作△ABD 和△BCE ,△ABD 和△BCE 都是等边三角形,连接AE 、CD ,二者交点为H .求证:(1)△ABE ≌△DBC ; (2)AE =DQ ; (3)∠DHA =60°; CDGH AODE H(5)△EGB ≌△CFB ; (6)连接GF ,GF ∥AC ; (7)连接HB ,HB 平分∠AHC .证明:(1)∠ABE =120°,∠CBD =120°, 在△ABE 和△DBC 中, BA BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩﹐﹐﹐ ∴△ABE ≌△DBC . (2)∵△ABE ≌△DBC , ∴AE =DC .(3)△ABE ≌△DBC , ∴∠1=∠2. ∴∠DGH =∠AGB . ∴∠DHA =∠4=60°.(4)∵∠5=180°-∠4-∠CBE =60°, ∴∠4=∠5. ∵△ABE ≌△DBC , ∴∠1=∠2. 又∵AB =DB ,∴△AGB ≌△DFB (ASA ).(5)同(4)可证△EGB ≌△CFB (ASA ). (6)如图①所示,连接GF . 由(4)得,△AGB ≌△DFB . ∴BG =BF . 又∵∠5=60°,∴△BGF 是等边三角形. ∴∠3=60°. ∴∠3=∠4. ∴GF ∥AC .(7)如图②所示,过点B 作BM ⊥DC 于M ,过点B 作BN ⊥AE 于点N . ∵△ABE ≌△DBC , ∴S △ABE =S △DBC . ∴12×AE ×BN =12×CD ×BM . CDE FG HAB51234图①D EHNM∴BM =BN .∵点B 在∠AHC 的平分线上. ∴HB 平分∠AHC . 练习:1. 在△ABC 中,AB =CB ,∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF .(1)求证:BE =BF ;(2)若∠CAE =30°,求∠ACF 度数.答案:(1)证明:∠ABC =90°. 在Rt △ABE 和Rt △CBF 中, CF AE AB CB =⎧⎨=⎩﹐﹐∴Rt △ABE ≌Rt △CBF (HL ). ∴BE =BF .(2)∵AB =CB ,∠ABC =90°, ∴∠BAC =∠BCA =45°. ∴∠CAE =30°.∴∠BAE =45°-30°=15°. ∵Rt △ABE ≌Rt △CBF , ∴∠BCF =∠BAE =15°.∴∠ACF =∠BCF +∠BCA =15°+45°=60°.2. 如图,△ABD 与△BCE 都为等边三角形,连接AE 与CD ,延长AE 交CD 于点H .求证:(1)AE =DC ; (2)∠AHD =60°;(3)连接HB ,HB 平分∠AHC .答案:(1)∵∠ABE =∠ABD -∠EBD ,∠DBC =∠EBC -∠EBD ,∠ABD =∠EBC =60°,∴∠ABE =∠DBC . 在△ABE 和△DBC 中, AB DB ABE DBC =⎧⎪∠=∠⎨﹐﹐C EFABCDE HAB∴△ABE ≌△DBC . ∴AE =DC .(2)∵△ABE ≌△DBC , ∴∠EAB =∠CDB .又∵∠OAB +∠OBA =∠ODH +∠OHD , ∴∠AHD =∠ABD =60°.(3)过B 作AH 、DC 的垂线,垂足分别为点M 、N . ∵△ABE ≌△DBC , ∴S △ABE =S △DBC . 即12AE ·BM =12CD ·BN . 又∵AE =CD , ∴BM =BN . ∴HB 平分∠AHC .3. 在线段AE 同侧作等边△ABC 和等边△CDE (∠ACE <120°),点P 与点M 分别是线段BE 和AD 的中点. 求证:△CPM 是等边三角形.答案:证明:∵△ABC 和△CDE 都是等边三角形, ∴AC =BC ,CD =CE . ∴∠ACB =∠ECD =60°. ∴∠BCE =∠ACD . ∴△BCE ≌△ACD .∴∠CBE =∠CAD ,BE =AD .又∵点P 与点M 分别是线段BE 和AD 的中点, ∴BP =AM .在△BCP 和△ACM 中, BC AC CBE CAD BP AM =⎧⎪∠=∠⎨⎪=⎩﹐﹐﹐ ∴△BCP ≌△ACM .∴PC =MC ,∠BCP =∠ACM . ∴∠PCM =∠ACB =60°. CDEABP4. 将等腰Rt △ABC 和等腰Rt △ADE 按图①方式放置,∠A =90°,AD 边与AB 边重合,AB =2AD =4.将△ADE 绕A 点逆时针方向旋转一个角度α(0°<α<180°),BD 的延长线交CE 于P .(1)如图②,求明:BD =CE ,BD ⊥CE ;(2)如图③,在旋转的过程中,当AD ⊥BD 时,求CP 长.答案:(1)∵等腰Rt △ABC 和等腰Rt △ADE , ∴AB =AC ,AD =AE ,∠BAC =∠DAE =90°. ∵∠DAB =90°-∠CAD ,∠CAE =90°-∠CAD , ∴∠DAB =∠CAE . ∴△ABD ≌△ACE . ∴BD =CE . ∴∠DBA =∠ECA .∴∠CPB =∠CAB .(8字模型) ∴BD ⊥CE .(2)由(1)得BP ⊥CE .又∵AD ⊥BD ,∠DAE =90°,AD =AE , ∴四边形ADPE 为正方形. ∴AD =PE =2.∴∠ADB =90°,AD =2,AB =4, ∴BD =CE =3∴CP =CE -PE =232. 图① CDEAB图② PCABDE图③CABDP赠送—高中数学知识点第一章空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。

初二数学手拉手模型(一)引言概述:初二数学手拉手模型是一种教学方法,旨在帮助学生更深入地理解和应用数学知识。
通过手拉手合作模式,学生可以互相学习、互相借鉴,共同提高数学学习的效果。
本文将介绍初二数学手拉手模型的基本原理和应用方法,并分别从创设情境、设计问题、组织合作、总结反思和评价几个大点,详细阐述每个大点下的细节。
正文内容:一、创设情境1. 选择适当的实际情境,激发学生的兴趣和动机。
2. 引导学生观察、思考和提出问题,培养他们的问题意识。
3. 确定学生需要解决的数学问题,并与实际情境相结合。
二、设计问题1. 设计能够引导学生思考和合作的问题。
2. 确定问题的难度和范围,确保学生能够通过合作解决问题。
3. 鼓励学生提出多种解决方法,并比较它们的优劣。
三、组织合作1. 将学生分为小组,并确保每个小组成员都能参与到合作中。
2. 引导学生学会倾听和表达自己的观点,培养良好的沟通能力。
3. 提供适当的教学资源和支持,帮助学生克服困难。
四、总结反思1. 引导学生归纳和总结问题的解决过程,发现其中的规律和方法。
2. 鼓励学生分享自己的思考和收获,促进彼此之间的学习交流。
3. 提供针对学生的个性化反馈,帮助他们更好地理解和应用数学知识。
五、评价1. 设计合适的评价标准,全面评价学生在手拉手模型中的表现。
2. 鼓励学生积极参与评价过程,反思自己的学习和合作经验。
3. 提供具体的建议和指导,帮助学生更好地改进自己的学习方式。
总结:初二数学手拉手模型以创设情境、设计问题、组织合作、总结反思和评价为主要内容,通过这种方式,学生可以在合作中相互学习、借鉴,共同提高数学学习的效果。
这种模型不仅可以增进学生的数学理解和应用能力,还能培养他们的问题意识、沟通能力和团队合作精神。
通过引导学生参与模型的各个环节,可以促进他们主动探索、思考和解决问题的能力,为进一步提高数学学习水平奠定良好的基础。
初中数学几何模型之——手拉手模型,跟我学-应对中考轻松自
如
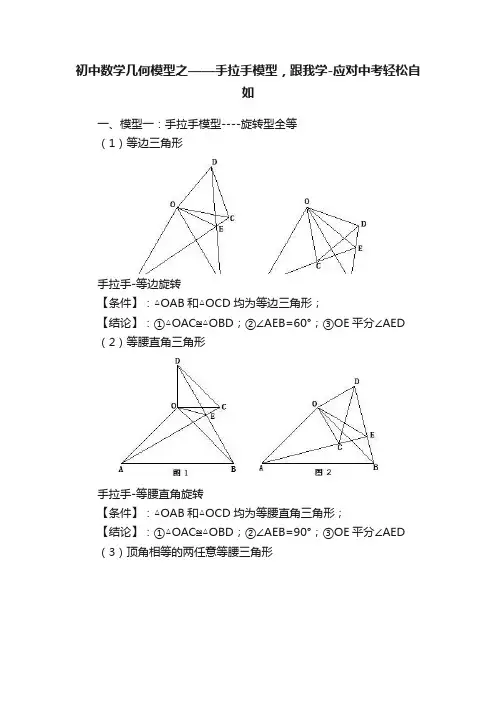
一、模型一:手拉手模型----旋转型全等
(1)等边三角形
手拉手-等边旋转
【条件】:△OAB和△OCD均为等边三角形;
【结论】:①△OAC≌△OBD;②∠AEB=60°;③OE平分∠AED
(2)等腰直角三角形
手拉手-等腰直角旋转
【条件】:△OAB和△OCD均为等腰直角三角形;
【结论】:①△OAC≌△OBD;②∠AEB=90°;③OE平分∠AED
(3)顶角相等的两任意等腰三角形
手拉手-等腰旋转
【条件】:△OAB和△OCD均为等腰三角形;且∠COD=∠AOB
【结论】:①△OAC≌△OBD;②∠AEB=∠AOB;③OE平分∠AED
二、模型二:手拉手模型----旋转型相似
(1)一般情况
【条件】:CD∥AB,将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA
(2)特殊情况
【条件】:CD∥AB,∠AOB=90° 将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA;
③BD/AC=OD/OC=OB/OA=tan∠OCD;
④BD⊥AC;
⑤连接AD、BC,必有AD2+BC2=AB2+CD2;
⑥S△BCD=1/2AC×BD。
最全⼿拉⼿模型⼿拉⼿是数学中最常见的⼀种⼏何图形。
属于共端点⼏何模型的⼀种类别。
在平时的考试之中,经常会遇到这样⼀类考题。
它是我们研究⼏何图形的基础。
当然,对于⼿拉⼿模型结论的研究,我们这⼀节也会提供⼀些⼿段。
⽐如旋转、全等都是我们的处理⼿段。
当然,说了那么多,我们来说下,什么是⼿拉⼿模型,我们看下什么样的图形叫做⼿拉⼿模型。
⼿拉⼿模型主要抓三个条件:1:共顶点2:等腰(等边,正⽅形等等,换句话讲共顶点的两边相等)3:顶⾓相等⼿拉⼿模型主要分为:“等边△+等边△”和“等腰△+等腰△”等边△+等边△类型⼀:等边类型⼀:前题条件:图中,B,C,D三点共线,有等边△ABC和等边△CDE.前题条件:(1)图中,B,C,D三点共线,有等边△ABC和等边△CDE.我们可以得到以下⼀些结论:结论⼀:△ACD≌△BCE(2)记AC、BE交点为M,AD、CE交点为N:结论⼆:△ACN≌△BCM;△MCE≌△NCD(3)连接MN:结论三:△MNC是等边三⾓形+MN//BC(4)记AD、BE交点为P,连接PC:因为△ACD≌△BCE所以过点C作CG⊥BE,CH⊥AD ∴CG与CH分别是BE与AD边上的⾼∵BE=AD ∴CG=CH 所以易知Rt△PGC≌Rt△PCH (HL)∴∠1=∠2结论四:PC平分∠BPD(5)∵∠CAD+∠CDA=∠ACB=60°∴∠DBE+∠CDA=60° ∴∠BPD=120° 由(4)可知∠BPC=∠CPD=60° ∴∠APB=∠BPC=∠CPD=∠DPE=60°.结论五:∠APB=∠BPC=∠CPD=∠DPE=60°.(6)连接AE:结论六:P点是△ACE的费马点(PA+PC+PE值最⼩)(7)因为∠APB=∠ACB=60°所以可以得到:△AMP∽△BMC同理可以得到以下⼏组相似三⾓形:△AMB∽△MPC,△PNC∽△END,△PNE∽△CND当然,我们也可以得到A、B、C、P四点共圆/P、C、D、E四点共圆结论七:△AMP∽△BMC,△AMB∽△MPC,△PNC∽△END,△PNE∽△CND+A、B、C、P四点共圆和P、C、D、E四点共圆(8) 如图,在PD上截取PF=PC, 由此可以知道△PCF为等边三⾓形∴易证:△PCE≌△FCD∴有PD=CP+PE同理可得:BP=AP+PC结论⼋:PD=CP+PE,BP=AP+PC注意:当然前⾯都是在B、C、D共线的时候得出的结论。
“手拉手”旋转模型一、模型解读【模型特征】如图1,O A =O A ’,O B =O B ’,且∠A O A ’=∠B O B ’,不妨将较长的边(如O B 、O B ’)称为“大手”,较短的边(如O A 、O A ’)称为“小手”,连结A B ,A ’B ’,容易证得图2中“大手拉小手”所形成的△A O B 与△A ’O B ’全等,于是我们将具有这种特征的图形俗称为“手拉手模型”.【基本性质】如,若O A =O A ’,O B =O B ’,设∠A O A ’=∠B O B ’=α,连结A B ,A ’B ’交于点C ,连结A A ’,B B ’,则:(1)△A O A ’∽△B O B ’,△A O B ≌△A ’O B ’;(2)A B =A ’B ’;(3)∠A B O =∠A ’B ’O ,∠B A O =∠B ’A ’O ,∠A C A ’=α;(4)O C 平分∠A C B ’;证明:(1)由已知易得:△A O A ’∽△B O B ’,又∠A O A ’=∠B O B ’,所以∠A O B =∠A ’O B ’,则△A O B ≌△A ’O B ’;(2)由(1)得:A B =A ’B ’;(3)由(1)得:∠A B O =∠A ’B ’O ,∠B A O =∠B ’A ’O ,又∠A D O =∠A ’D C ,所以∠A C A ’=∠A O A ’=α;(4)过点O 作O E ⊥A B 于E ,O F ⊥A ’B ’于点F ,由(1)得:S △A O B =S △A ’O B ’,即,所以O E =O F ,故O C 平分∠A C B ’.图1图3图2【重要结论】下面我们探讨“手拉手”旋转模型中两种特殊情形:α=60°或90°.1.共顶点等边三角形如图4,等边△A B C与等边△C D E,其中A,C,E三点共线,连结A D、B E相交于O,A D交B C于点F,B E交C D于点G,连结F G,O C,则:(1)△A C D≌△B C E,△B G C≌△A F C,△C F D≌△C G E;(2)A D=B E,B G=A F,F D=G E,C F=C G;图4(3)∠A O B=60°;(4)O C平分∠A O E;(5)△C F G为等边三角形;(6)F G//A E;(7)O C+O B=O A,O C+O D=O E;(8);(9).证明:(1)(2)(3)(4)由上面基本性质的证明可知:△A C D≌△B C E,A D=B E,∠A O B=60°,O C平分∠A O E,∠C A F=∠C B O,容易得到∠B C D=∠A C B=60°,又A C=B C,所以△B G C≌△A F C,同理可得△C F D≌△C G E,故B G=A F,F D=G E,C F=C G;(5)由∠B C D=60°,C F=C G,则△C F G为等边三角形;(6)由(5)得∠C F G=60°,所以∠C F G=∠A C B,故F G//A E;(7)在A O上取点H,使得O H=O C,又∠A O B=60°,且O C平分∠A O E,所以∠H O C=60°,那么△C H O为等边三角形,则C H =C O=O H,∠H C O=60°,又∠A C B=60°,所以∠A C H=∠B C O,于是△A H C≌△B O C,则A H=B O,故O A=O H+A H=O C+O B,同理可得O C+O D=O E;(8)由F G//A E,易得△B F G∽△B C E,则,容易得到C F//D E,则△A C F∽△A E D,那么,又,所以,进一步,故;(9)由∠B C D=∠A O C=∠E O C=60°得∠B O C=∠C O D=120°,∠B C O=∠C D O,于是△B O C∽△C O D,则,即.点评:本题的图形具有丰富的内涵,除了得到上述一般性结论,还能得到其他结论,比如图中三角形相似还有很多,另有多对四点共圆,再如还有类似(8)的结论:,等,有兴趣的读者可继续探究.2.共顶点等腰直角三角形(顺向)如图5,等腰直角△A B C与等腰直角△C D E,连结A D、B E相交于O,A D交B C于点F,B E交C D于点G,连结F G,O C ,则:(1)△A C D ≌△B C E ;(2)A D =B E 且A D ⊥B E ;(3)O C 平分∠A O E ;(4)O B +O C =O A ,O D +O C =O E ;(5)若∠B C D =45°,则.证明:(1)(2)(3)(5)的证明见共顶点等边三角形(1)(2)(3)(4)(9)的证明,(4)过点C 作C H ⊥O C 交A D 于点H ,由(3)得∠A O C =45°,所以C H =O C ,O H =O C ,又∠B C A =90°,所以∠B C O =∠A C H ,从而△B O C ≌△A H C ,于是O B =A H ,所以O A =O H +A H =O B +O C ,同理O E =O D +O C .点评:如果将连结A D 与B E 称为“顺向手拉手”,那么连结B D 与A E 我们称为“逆向手拉手”,那么它又有哪些漂亮的性质呢?3.共顶点等腰直角三角形(逆向)如图6,等腰直角△A B C 与等腰直角△C D E ,连结B D 、A E ,过点C 的直线分别交A E ,B D 于点H ,F ,则:(1)S △B C D =S △A C E;(2)若,垂足为H ,则B F =D F ,A E =2C F ;(3)若平分B D ,则,A E =2C F .证明:(1)延长B C 至点G ,使得C G =B C =A C ,则∠A C G =∠D C E =90°,于是∠A C E =∠G C D ,所以△A C E ≌△G C D ,可得S △A C E =S △G C D ,又C G =B C ,所以S △B C D =S △G C D ,故S △B C D=S △A C E;(2)由(1)得∠C D G =∠C E A ,容易得到D G ⊥A E ,又,所以,由B C =C G 得B F =D F ,进一步D G =2C F ,于是A E =2C F ;(3)与(2)证明类似.点评:①此题的证明方法多样,这里采用的这种证明方法有一定的代表性,即通过将“逆向手拉手”补成“顺向手拉手”的方式,也就是图中的C A ,C G ,C D ,C E 构成“顺向手拉手”,从而实现线段数量与位置的转移;②本题如果连接A D ,B E ,还能得到另外一些结论,如S 四边形A B C D =,等.4.“相似型手拉手”旋转模型如图7,O A ’=k O A ,O B ’=k O B ,且∠A O A ’=∠B O B ’=α,如图8,连结A A ’,B B ’,A B ,A ’B ’,则:(1)△A O A ’∽△B O B ’,△A O B ∽△A ’O B ’;(2)A ’B ’=k A B ;(3)∠A B O =∠A ’B ’O ,∠B A O =∠B ’A ’O ,∠A C A ’=α.证明:(1)由O A ’=k O A ,O B ’=k O B 得或,图6图7图8又∠A O A ’=∠B O B ’,所以∠A O B =∠A ’O B ’,△A O A ’∽△B O B ’,从而△A O B ∽△A ’O B ’;(2)由(1)中△A O B ∽△A ’O B ’得,即A ’B ’=k A B ;(3)由(1)容易得到∠A B O =∠A ’B ’O ,∠B A O =∠B ’A ’O ,∠A C A ’=α.二、例题评析1.题型分类例1、(2014武汉)如图1,在四边形A B C D 中,A D =4,C D =3,∠A B C =∠A C B =∠A D C =45°,则B D 的长为.解法分析:由∠A B C =∠A C B =45°得A B =A C ,可以从图中识别出以A 为顶点的一个“三爪图”,如图,此时我们可以通过补全图形,将其转化为“手拉手”旋转模型,如图,即将线段A D 绕着点A 顺时针旋转90°得到线段A E ,连接B D ,C E ,由上面“共顶点等腰直角三角形(顺向)”分析得B D =C E ,于是实现了线段的“转移”,成功的将条件“聚集”在△C D E 中,从而题目得解.解:如图,将线段A D 绕着点A 顺时针旋转90°得到线段A E ,连接C E ,D E ,则A D =A E ,A D ⊥A E ,由“手拉手”旋转模型得到∠A D E =45°且B D =C E ,又∠A D C =45°,所以∠C D E =90°,因为A D =4,由勾股定理得:D E =,又C D =3,在R t △C D E 中,C E ==,故B D =.点评:对于上面识别出“三爪图”然后补成“手拉手”旋转模型,我们可以用一句话总结辅助线特征——“等选段共顶点,旋转是首选”,本题还可以将线段A D 绕着点A 逆时针旋转90°,同样补成“手拉手”旋转模型,进而解决问题.例2、(2017河南)如图1,在R t △A B C 中,∠A =90°,A B =A C ,点D ,E 分别在边A B ,A C 上,A D =A E ,连接D C ,点M ,P ,N 分别为D E ,D C ,B C 的中点.(1)观察猜想图1中,线段P M 与P N 的数量关系是,位置关系是;(2)探究证明把△A D E 绕点A 逆时针方向旋转到图2的位置,连接M N ,B D ,C E ,判断△P M N 的形状,并说明理由;(3)拓展延伸把△A D E 绕点A 在平面内自由旋转,若A D =4,A B =10,请直接写出△P M N 面积的最大值.图1图2图4图3解法分析:(1)容易得到P M=P N,P M⊥P N;(2)从图2中容易识别出A B,A D,A C,A E构成“顺向手拉手”旋转模型,于是△A B D≌△A C E,那么B D=C E且B D⊥C E,由点M,P,N分别为D E,D C,B C的中点,得P M和P N分别为△C D E 和△B C D的中位线,所以P M =C E,P N =B D,且P M//C E,P N//B D,于是P M=P N,P M⊥P N,故△P M N为等腰直角三角形;(3)只要C E或B D最大时,△P M N的面积最大,从题中可以得到点E在以A为圆心,A E为半径的圆上运动,故当点E在C A的延长线上时,C E最大,由A D=4,A B=10得C E的最大值为14,此时P M=7,故△P M N面积的最大值为.解:(1)P M=P N,P M⊥P N;(2)△P M N为等腰直角三角形,理由如下:如图3,延长B D交C E于F,交A C于H,由∠D A E=∠B A C得∠B A D=∠C A E,又A B=A C,A D=A E,所以△A B D≌△A C E,那么B D=C E且∠A B D=∠A C E,又∠A H B=∠C H F,所以∠C F H=∠B A C=90°,即B D⊥C E,图3再由点M,P,N分别为D E,D C,B C的中点,得P M =C E,P N =B D,且P M//C E,P N//B D,于是P M=P N,P M⊥P N,故△P M N为等腰直角三角形;(3).变式训练:1.(2017淮安)【操作发现】如图①,在边长为1个单位长度的小正方形组成的网格中,△A B C 的三个顶点均在格点上.(1)请按要求画图:将△A B C绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接B B′;(2)在(1)所画图形中,∠A B ′B=.【问题解决】如图②,在等边三角形A B C中,A C=7,点P在△A B C内,且∠A P C=90°,∠B P C=120°,求△A P C的面积.小明同学通过观察、分析、思考,对上述问题形成了如下想法:想法一:将△A P C绕点A按顺时针方向旋转60°,得到△A P′B,连接P P′,寻找P A,P B,P C三条线段之间的数量关系;想法二:将△A P B 绕点A 按逆时针方向旋转60°,得到△A P ′C ′,连接P P ′,寻找P A ,P B ,P C 三条线段之间的数量关系.…请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)【灵活运用】如图③,在四边形A B C D 中,A E ⊥B C ,垂足为E ,∠B A E =∠A D C ,B E =C E =2,C D =5,A D =k A B (k 为常数),求B D 的长(用含k 的式子表示).2.(2016常德)已知四边形A B C D 中,A B =A D ,A B ⊥A D ,连接A C ,过点A 作A E ⊥A C ,且使A E =A C ,连接B E ,过A 作A H ⊥C D 于H 交B E 于F .(1)如图1,当E 在C D 的延长线上时,求证:①△A B C ≌△A D E ;②B F =E F ;(2)如图2,当E 不在C D 的延长线上时,B F =E F 还成立吗?请证明你的结论.2.拓展应用例3、(2015莆田)在R t △A C B 和R t △A E F 中,∠A C B =∠A E F =90°,若点P 是B F 的中点,连接P C ,P E .特殊发现:如图1,若点E ,F 分别落在边A B ,A C 上,则结论:P C =P E 成立(不要求证明).问题探究:把图1中的△A E F 绕着点A 顺时针旋转.(1)如图2,若点E 落在边C A 的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;(2)如图3,若点F 落在边A B 上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)记,当k 为何值时,△C P E 总是等边三角形?(请直接写出k 的值,不必说明理由)解法分析:如图4,图5,我们将图2和图3补成“顺向手拉手”旋转模型,我们将△A B C 和△A E F 分别关于A C 和A E 翻折得到△A B ’C 和△A E F ’,在图4中,出现特殊情形:点B ’,A ,F 在同一直线上,点F ’,A ,B 在同一直线上,所以B ’F =B F ’,图2图1图3图2图1容易证得C P ,E P 分别为△B B ’F 和△B F B ’的中位线,所以C P =B ’F ,E P =B F ’,于是C P =E P ;在图5中,可以看出A B ’,A B ,A F ,A F ’构成“顺向手拉手”旋转模型,于是△A B ’F ≌△A B F ’,从而B ’F =B F ’,延长B ’F 交B F ’的延长线于点H ,有∠B ’A F =∠B ’H B ,同理C P =E P ,且C P //B ’H ,E P //B F ’,若△C P E 是等边三角形,则∠C P E =60°,于是∠B ’H F ’=60°,所以∠B ’A F =∠B ’H B =120°,那么∠C A B =60°,故.解:如图4,图5,将△A B C 和△A E F 分别关于A C 和A E 翻折得到△A B ’C 和△A E F ’,则△A B C ≌△A B ’C ,△A E F ≌△A E F ’,(1)由点E 在C A 的延长线上,∠B A C =∠E A F 可得点B ’,A ,F 在同一直线上,点F ’,A ,B 在同一直线上,又A B =A B ’,A F =A F ’,所以B ’F =B F ’,因为点P 是B F 的中点,那么C P ,E P 分别为△B B ’F 和△B F B ’的中位线,所以C P =B ’F ,E P =B F ’,于是C P =E P ;(2)如图5,由A F =A F ’,A B ’=A B ,∠B ’A B =∠F A F ’=2∠C A B ,得△A B ’F ≌△A B F ’,从而B ’F =B F ’,有∠B ’A F =∠B ’H B ,同理C P =E P ;(3)当时,△C P E 总是等边三角形.变式训练:1.如图1,△A B C 与△A D E 均为等腰直角三角形,A B =A C ,A D =D E ,∠B AC =90°,∠ADE =90°,点F 为B E 的中点,连结C E ,D F ,问:CE 与DF 之间的关系?并证明.2.如图2,△A B C 与△A D E 为等腰三角形,A B =B C ,A D =D E ,且∠ABC +∠ADE =180°,连结C E ,F 为C E的中点,求证:(1)B F ⊥D F ;(2)t a n ∠A C B =.图5图4图1图2。
B专题01 手拉手模型大全等边三角形模型一、△ACE 与△DBC 是等边三角形。
当B 、C 、E 三点不共线时 1.△ACE ≅△BCD 2.BD=CE 3.∠APB=60°思路引领:由:∠ACB=∠E CD=60°⇒∠BCD=∠ACE 又∵AB=AC, CD=CE ∴△ACE ≅△BCD∴BD=AE, ∠CAE=∠CBD (法一)∴点A,B,C,P 四点共圆. ∴∠APB=∠ACB= 60°(法二) ∠APB+∠CAE=∠ACB +∠BCD=∠AGB ∴∠APB=∠ACB= 60°模型二、△ACE 与△DBC 是等边三角形。
当B 、C 、E 三点共线时,则有以下10个结论 (可借助右边备用图) 1.△ACE ≅△BCD 2.BD=CE 3.∠APB=60° 以上证法同一.4.△HCA ≅△BGC由△ACE ≅△BCD 可得∠CAE=∠CBD, 又∵AB=AC, ∠ACH=∠BCG=60°, ∴△HCA ≅△BGC5.△GCH 是等边三角形. △HCA ≅△BGC ⇒CG=CH 又由于∠BCG=60°,所以△GCH 是等边三角形. 6.△GDC ≅△HCE△HCA ≅△BGC ⇒CG=CH又由于DC=ED,∠ACH=∠BCG=60° 可得△GDC ≅△HCE 7.GH∥BE由△GCH 是等边三角形. 可得∠CHG=∠H CE=60° GH∥BEBB8.PC 平分∠EPB思路:过点C 作CM,CN 分别垂直于BD,AE,垂足为 M,N∵△ACE ≅△BCD ∴CM=CN ∴PC 平分∠EPB9.BP=AP+PC,EP=PD+PC 如图,截取BQ=AP 易证△APC ≅△BQC 得∠BCQ=∠ACP,CP=CQ 可证: ∠QCP=60° 得△CPQ 为等边三角形. 则CP=QP.∴BP=BQ+QP=AP+AC 同法可证: EP=PD+PC10.△GCB∽△APG,△DPH∽△HCE由上述结论中的:∠CBG=∠PAG, ∠APG=∠GCB,可证△GCB∽△APG 同理可证△DPH∽△HCE等腰篇模型三、若△ACE 与△DBC 是等腰三角形。
手拉手模型(等线段共端点模型)1、定义:两个顶角相等且共顶点的等腰三角形形成的图形。
2、四个固定结论:判断左右:将等腰三角形顶角(头)朝上,正对读者,读者左边为着手顶点,右边为右手顶点,如图1、图2(1)经典线段相等:左拉左=右拉右找经典全等:包含A.经典线段B.两对等腰(等线段共端点)(2)共顶点旋转模型(证明基本思想“SAS”)核心导角:∠A=∠C则得出∠B=∠D,(八字图模型)核心图形:AB`=AC`,AB=AC ∠B`AC=∠BAC以上给出了连续变化的图形,图中两个阴影部分的三角形全等,注意利用三角形全等性质进项转化边或转化角3、利用旋转思想构造辅助线(1)根据相等的边找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角画出旋转后的三角形4、旋转前后具有以下性质(1)对应线段和对应角分别相等(2)对应点位置的排列次序相同(3)任意两条对应线段的夹角都等于旋转角例题讲解:A类1:在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD,证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)BH平分∠AHC;解题思路:1:出现共顶点的等边三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;2:如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H.问(1)△ADG≌△CDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分∠AHE?等边三角形要得到哪些结论?要联想到什么模型?等腰直角三角形要得到哪些结论?要联想到什么模型?解题思路:1:出现共顶点的等腰直角三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;3:如图,分别以△ABC 的边AB、AC 同时向外作等腰直角三角形,其中 AB =AE ,AC =AD,∠BAE =∠CAD=90°,点G为BC中点,点F 为BE 中点,点H 为CD中点。
N M C B A BNC A B C N模型4 手拉手模型“手拉手”数学模型:1.如图,已知点C 为线段AB 上一点,ACM △、BCN △是等边三角形.⑴ 求证:AN BM =. ⑵ 将ACM △绕点C 按逆时针方向旋转180°,使点A 落在CB 上,请你对照原题图在图中画出符合要求的图形;⑶ 在⑵得到的图形中,结论“AN BM =”是否还成立,若成立,请证明;若不成立,请说明理由;【解析】⑴ ∵ACM △、BCN △是等边三角形∴AC CM =,BC CN = 60ACM BCN ∠=∠=°∴∠=∠ACN MCB在ACN △和MCB △中=⎧⎪∠=∠⎨⎪=⎩AC MC ACN MCB CN CB∴ACN MCB △≌△(SAS )∴AN BM =⑵ 将ACM △绕点C 旋转如图:⑶在⑵的情况,结论AN BM=仍然成立.证明:∵60=.=,CN CB∠=∠=°,CA CMBCM NCA∴CAN CMB△≌△(SAS),∴AN MB=.【方法总结】这是一个运动变化的探索题,是“手拉手”经典例题,证明方法类似,且在一定的条件下,探究原结论的存在性(不变性);解决此类题,需要画图分析、判断、猜想、推理论证.【随堂练习】(2015秋•川汇区期末)如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.【解答】证明:CD=BE,CD⊥BE,理由如下:因为∠BAD=∠CAE=90°,所以∠BAD+∠DAE=∠CAE+∠DAE,即∠BAE=∠DAC.因为,所以△BAE≌△DAC(SAS).所以BE=DC,∠BEA=∠DCA.如图,设AE与CD相交于点F,因为∠ACF+∠AFC=90°,∠AFC=∠DFE,所以∠BEA+∠DFE=90°.即CD⊥BE.。