偏置曲柄滑块机构计算

偏置曲柄滑块的运动方程式
偏置曲柄滑块是一种机械装置，由一个曲柄和一个滑块组成。

曲柄是一个旋转的杆状物体，而滑块是沿着曲柄轨迹移动的物体。

偏置曲柄滑块的运动方程式描述了滑块在不同时间点上的位置。

运动方程式可以通过几何关系和动力学原理推导得到。

下面是一个典型的偏置曲柄滑块运动方程式的示例：
假设曲柄长度为L，曲柄的角速度为ω，滑块的位置为(x, y)，滑块与曲柄连接处的角度为θ。

根据几何关系，我们可以得到以下关系式：
x = L*cos(θ)
y = L*sin(θ)
其中，θ的取值范围通常是从0到2π，表示一次完整的旋转。

根据动力学原理，我们可以推导出滑块的加速度与曲柄的角度加速度之间的关系。

假设滑块的质量为m，滑块的加速度为a，曲柄的角加速度为α，那么有以下关系式：
m*a_x = -m*L*α*sin(θ) - m*L*ω^2*cos(θ)
m*a_y = m*L*α*cos(θ) - m*g
其中，g表示重力加速度。

通过解这两个方程，我们可以得到滑块的加速度a_x和a_y，进而求解出滑块的速度v_x和v_y以及位置x和y随时间的变化。

综上所述，偏置曲柄滑块的运动方程式用于描述滑块在不同时间点上的位置。

通过几何关系和动力学原理，我们可以推导出滑块的位置、速度和加速度与曲柄的角度和角加速度之间的关系。

曲柄滑块机构的运动精度分析与计算宋亮;赵鹏兵【摘要】曲柄滑块机构是一种典型的四连杆机构,尽管设计时理论计算可以达到很高的精度,但是由于构件的制造误差及运动副的配合间隙等因素,会使机构在运动中产生输出误差,有时还会显著超出机构设计的允许误差.依据概率统计的相关理论进行机构设计,即考虑构件制造尺寸的随机误差,以保证机构运动的精度在允许的误差范围内.利用MATLAB进行仿真计算和实例研究,得出了理论设计和精度分析的计算结果.该方法准确、效率高、而且适合其它类型的机构设计,具有较大的工程实际应用价值.%Slider-crank mechanism is a typical four-bar linkage, in spite of the high precision when it' s calculated theoretically. The manufacturing error and kinematic pair clearance of the components will lead to the output error during the motion of the mechanism. Sometimes,it will significantly exceed the tolerance of the design. According to the probability and statistics theory, the mechanism is designed, that' s considering the random error of the component to make sure that the motion accuracy is in the allowed error range. Utilizing MATLAB to simulate and calculate based on case studies. and the theoretical design and accuracy analysis are obtained. This method is accurate and very efficiently, it also can be used in other kind of mechanism design, and it has much more practical value in engineering.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)010【总页数】5页(P2201-2205)【关键词】曲柄滑块机构;运动学;概率设计;等影响法;精度分析【作者】宋亮;赵鹏兵【作者单位】海军装备部,西安,710043;西北工业大学现代设计与集成制造技术教育部重点实验室,西安,710072【正文语种】中文【中图分类】TH112.1曲柄滑块机构是一种单移动副的四连杆机构，如图1和图2所示，分别为对心和偏心曲柄滑块机构。

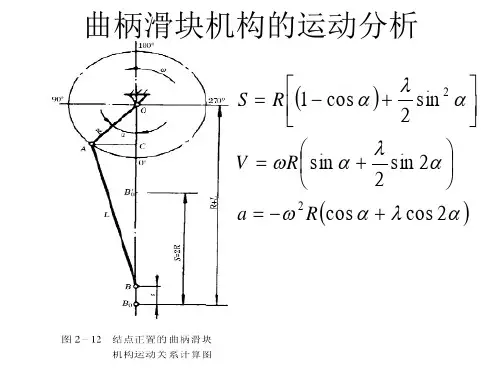
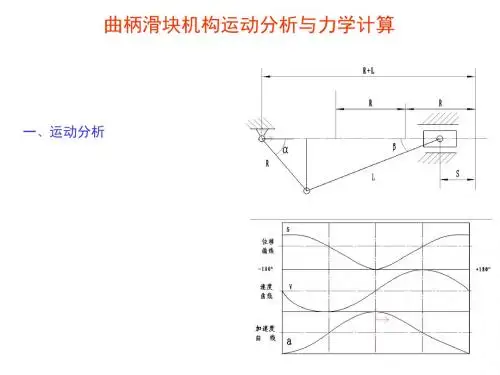
偏置曲柄滑块的运动方程式1. 引言偏置曲柄滑块机构是一种常见的机械传动装置，广泛应用于各个领域，如工业生产线、汽车发动机等。

它由一个旋转的偏置曲柄和一个在偏置曲柄上滑动的滑块组成。

通过改变偏置曲柄的旋转角度，可以控制滑块的运动轨迹和速度。

本文将介绍偏置曲柄滑块机构的基本原理和运动方程式，并通过数学推导和图示进行详细阐述。

2. 偏置曲柄滑块机构的基本原理偏置曲柄滑块机构由三个主要部分组成：偏置曲柄、连杆和滑块。

其中，偏置曲柄是一个固定在轴上并绕轴旋转的零件，连杆连接着偏置曲柄和滑块。

当偏置曲柄绕轴旋转时，连杆上的一端固定在偏置曲柄上，另一端连接着滑块。

由于连杆长度不变且固定在两个点上，所以当偏置曲柄旋转时，滑块被迫在一定的轨迹上运动。

3. 偏置曲柄滑块的运动方程式为了推导偏置曲柄滑块的运动方程式，我们需要定义一些参数和符号：•偏置曲柄长度：a•连杆长度：b•偏置曲柄旋转角度：θ•滑块位置：（x，y）根据几何关系，可以得到以下方程：x = a * cos(θ) + b * cos(φ) (1) y = a * sin(θ) + b * sin(φ) (2)其中，φ是连杆与x轴的夹角。

为了求解φ，我们可以利用三角形余弦定理：cos(φ) = (a^2 + b^2 - x^2 - y^2) / (2ab)将cos(φ)代入方程（1）和（2）中，即可得到偏置曲柄滑块的运动方程式。

4. 运动轨迹和速度分析根据运动方程式（1）和（2），我们可以分析偏置曲柄滑块机构的运动轨迹和速度。

4.1 运动轨迹通过改变偏置曲柄旋转角度θ，可以控制滑块的运动轨迹。

当θ=0时，滑块位于初始位置（a, 0）。

随着θ的增大，滑块将沿着一个椭圆轨迹运动，直到θ=π/2时达到最高点。

4.2 速度分析根据运动方程式（1）和（2），我们可以求解滑块的速度。

对x和y关于时间t求导数，即可得到滑块在x和y方向上的速度：v_x = -a * sin(θ) * θ’ - b * sin(φ) * φ’ (3) v_y = a * cos(θ) * θ’ + b * cos(φ) * φ’ (4)其中，θ’和φ’分别表示偏置曲柄旋转角度和连杆夹角随时间变化的导数。

偏置曲柄滑块机构是一种常用的机械传动装置，其行程速比系数是衡量其性能的重要指标之一。

本文将从以下几个方面对偏置曲柄滑块机构的行程速比系数进行探讨。

一、偏置曲柄滑块机构的基本结构和工作原理偏置曲柄滑块机构由曲柄、连杆和滑块三部分组成，通过曲柄的旋转驱动连杆运动，进而带动滑块进行直线往复运动。

其工作原理如下：当曲柄旋转时，连杆由于铰接在曲柄和滑块上，会受到离心力的作用而产生往复运动，最终带动滑块进行直线往复运动。

二、行程速比系数的定义和计算方法行程速比系数是指偏置曲柄滑块机构在工作过程中，滑块在两个极值点（即最大位移点和最小位移点）的速度比值。

行程速比系数可用公式表示如下：\[S = \frac{v_{max}}{v_{min}}\]其中，S为行程速比系数，v_{max}为滑块在最大位移点的速度，v_{min}为滑块在最小位移点的速度。

通过测量这两个速度并代入公式中，即可得到偏置曲柄滑块机构的行程速比系数。

三、影响偏置曲柄滑块机构行程速比系数的因素1. 曲柄长度：曲柄长度的不同会影响到曲柄的旋转角度和速度，进而影响到连杆的往复运动速度，从而影响到滑块的速度，最终影响行程速比系数。

2. 连杆长度：连杆长度的变化会改变连杆的往复运动轨迹，进而影响到滑块的速度变化，从而影响行程速比系数。

3. 滑块质量和摩擦系数：滑块的质量和摩擦系数的变化会影响滑块的运动阻力，进而影响到滑块的速度，最终影响行程速比系数。

四、优化偏置曲柄滑块机构行程速比系数的方法1. 优化设计曲柄和连杆：通过合理设计曲柄和连杆的长度和结构，可以使偏置曲柄滑块机构在运动过程中速度更加均匀，从而优化行程速比系数。

2. 采用低摩擦材料和润滑方式：选择低摩擦系数的材料，并采用合适的润滑方式，可以降低滑块的摩擦阻力，从而优化行程速比系数。

3. 控制滑块质量和惯性：通过控制滑块的质量和惯性，可以减小滑块的惯性力，使其运动更加平稳，从而优化行程速比系数。

曲柄滑块机构滑块位移计算1. 引言嘿，朋友们，今天我们来聊聊一个听起来有点复杂但其实非常有趣的东西——曲柄滑块机构。

这可不是某种高深的数学公式，而是我们生活中经常能见到的一个小玩意儿！想想看，汽车的发动机、一些机械手臂，甚至某些玩具里面都可能用到这个机构，真的是无处不在，像老百姓的热水器一样，虽然看不见，但却在默默为我们服务。

那么，什么是曲柄滑块机构呢？简单来说，它是通过一个曲柄和滑块的配合，实现直线运动和旋转运动的转化。

你可以想象一下，当你转动一个把手，里面的曲柄就开始摇摆，而滑块就像跟着节奏舞动的舞者，跟着曲柄的节奏在轨道上滑行。

这种奇妙的转换其实在很多地方都能看到，比如家里的榨汁机、打印机，甚至一些健身器材，都是它在“辛勤工作”。

2. 曲柄滑块机构的基本原理2.1 工作原理好，咱们接下来深入点，看看这个机构是怎么工作的。

曲柄滑块机构的核心就是一个固定的轴心，曲柄围绕这个轴心旋转，而滑块在轨道上来回滑动。

就像一个旋转的小风车，风车的叶子不断转动，而下面的小车子随着风的方向在轨道上奔跑。

这个原理不仅简单，而且巧妙。

要说到滑块的位移计算，咱们得用到一些简单的几何知识。

不过，别担心，我不会让你看那些复杂的公式。

我们可以通过一些简单的图形和推理来理解。

首先，我们需要知道曲柄的长度、滑块的初始位置以及转角度。

这就像你在做一道菜，得先准备好所有的食材，才能下锅。

2.2 位移的计算接下来，咱们来聊聊如何计算滑块的位移。

假设曲柄的长度是L，转动的角度是θ，那么滑块的位移可以通过一些简单的三角函数来算。

你可以把它想象成一个小三角形，曲柄的旋转就像三角形的一个边在转动，而滑块的移动就是另外一条边的变化。

通过这两条边，我们就能轻松找出滑块的位移。

要是你觉得这有点儿复杂，也不用太担心，咱们可以把它当作一种有趣的游戏，尝试不同的角度，看滑块怎么移动，仿佛是在看一场小型的机械表演，滑块的每一次移动都像是在跳舞，每个转动的角度都在为它的舞步伴奏。

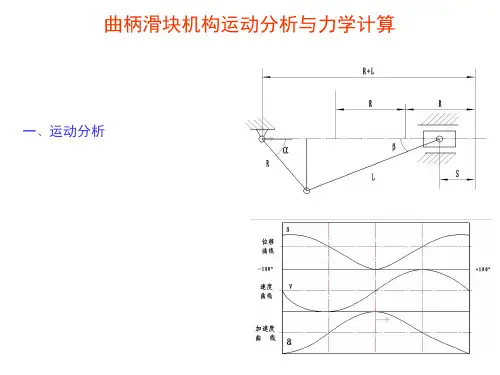
从偏置曲柄滑块机构运动方程式探析机械运
动规律
偏置曲柄滑块机构是机械领域中一种常见的转动与直线运动的结合机构，它常被应用于各种机械装置中，例如汽车发动机、压缩机、机床等。

在这篇文章中，我们将详细探索偏置曲柄滑块机构运动方程式的含义，以及机械运动的规律。

偏置曲柄滑块机构中的主要元件是曲柄、连杆和滑块。

当曲柄转动时，连杆便随之运动，滑块则产生直线运动。

而方程式中涉及的角度与长度等量则包括：曲柄转角、连杆长度、连杆转角、滑块位置等参数。

通过偏置曲柄滑块机构运动方程式的推导，我们可以得到其运动规律。

其中，连杆的角速度和加速度随曲柄转角变化而发生变化，在滑块运动过程中，其速度和加速度也随之变化。

在实际应用中，我们可以通过对机械元件尺寸和转动速度等参数的选择，来控制偏置曲柄滑块机构的运动规律，以满足不同的机械运动需求。

总的来说，偏置曲柄滑块机构是机械领域中一种常见而重要的结构，其运动方程式的探析有助于我们更深入地理解机械运动规律以及其应用。

而通过不断学习和实践，我们可以更好地应用偏置曲柄滑块机构，为机械领域的发展做出更大的贡献。