小学数学因数与倍数、质数与合数练习题答案

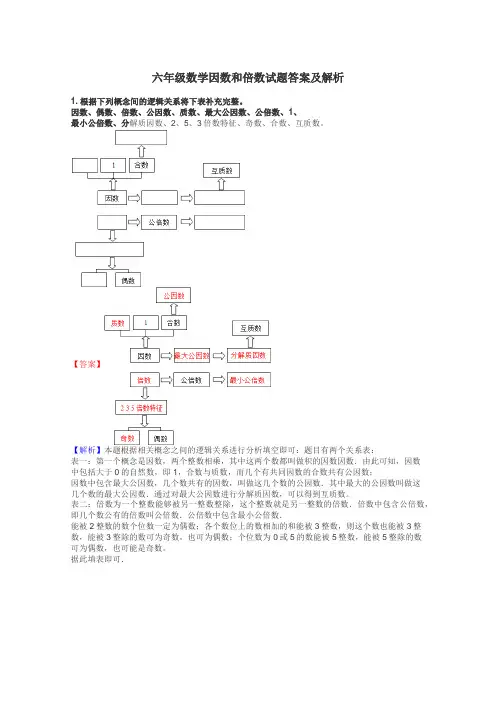
六年级数学因数和倍数试题答案及解析1.根据下列概念间的逻辑关系将下表补充完整。

因数、偶数、倍数、公因数、质数、最大公因数、公倍数、1、最小公倍数、分解质因数、2、5、3倍数特征、奇数、合数、互质数。

【答案】【解析】本题根据相关概念之间的逻辑关系进行分析填空即可：题目有两个关系表：表一：第一个概念是因数，两个整数相乘，其中这两个数都叫做积的因数因数．由此可知，因数中包括大于0的自然数，即1，合数与质数，而几个有共同因数的合数共有公因数；因数中包含最大公因数，几个数共有的因数，叫做这几个数的公因数．其中最大的公因数叫做这几个数的最大公因数．通过对最大公因数进行分解质因数，可以得到互质数。

表二：倍数为一个整数能够被另一整数整除，这个整数就是另一整数的倍数．倍数中包含公倍数，即几个数公有的倍数叫公倍数．公倍数中包含最小公倍数．能被2整数的数个位数一定为偶数；各个数位上的数相加的和能被3整数，则这个数也能被3整数，能被3整除的数可为奇数，也可为偶数；个位数为0或5的数能被5整数，能被5整除的数可为偶数，也可能是奇数。

据此填表即可．解：根据相关概念之间的逻辑关系可得：2.古希腊认为：如果一个数恰好等于它的所有因数（本身除外）相加之和，那么这个数就是“完全数”。

例如：6有四个因数1、2、3、6，除本身6以外，还有1、2、3三个因数。

6 = 1+2+3，恰好是所有因数之和，所以6就是“完全数”。

下面的数中是“完全数”的是（）。

A．12B．28C．36D．48【答案】B【解析】这道题能正确理解完全数的定义是关键。

根据题中叙述的完全数的定义，分别找出这四个数的因数后发现28的因数有1、2、4、7、14、28，除 28外 ,1＋2＋4＋7＋14=28，所以28是完全数。

3.（2011•武汉）某个四位数有如下特点：它加上1之后是15的倍数，它减去3之后是38的倍数．把它的各数位上的数字左右倒过来写，所得的新数与原数之和能被10整除，这个四位数是多少？【答案】所求的四位数是1409或1979【解析】原数加1后是15的倍数，所以这个四位数必是5的倍数，所以个位数字是4或9，又因为原数减去3后是38的倍数，是一个偶数，可得原数应该是奇数，所以原数的个位数字只能是9，再从条件（3）可知：原数的个位数字与千位数字之和是10，所以千位数字是10﹣9=1，设原数为38m+3（m为自然数），则有1009≤38m+3≤1996，据此可得26≤m≤53，据此再进行分析即可解答．解答：解：原数加1后是15的倍数，所以这个四位数必是5的倍数，所以个位数字是4或9，又因为原数减去3后是38的倍数，是一个偶数，可得原数应该是奇数，所以原数的个位数字只能是9，再从条件（3）可知：原数的个位数字与千位数字之和是10，所以千位数字是10﹣9=1，设原数为38m+3（m为自然数），则有1009≤38m+3≤1996，可得26≤m≤53，因为原数38m+3的个位数字是9，所以8m的个位数字是6．从而m的个位数字是2或7，在26到53之间，个位数字是2或7的数有27、32、37、42、47、52，又因为原数加上1后是15的倍数，则38m+3+1=38m+4是3的倍数，则19m+2必定是3的倍数，19m+2=3×6m+m+2，所以m+2是3的倍数，即m被3除余1，在27、32、37、42、47、52中，只有37和52被3除余1，所以m=37或52，所以38×37+3=1409，38×52+3=1979，经检验正好满足题意，答：所求的四位数是1409或1979．点评：根据题干，明确四位数的个位数字和千位数字分别是9和1，再根据被15整除的数的特征和偶数特征进行分析即可解答．4.（2014•长沙县）下面哪些数能被11整除（）A． 323532 B． 38380 C． 978768【答案】A【解析】能被11整除的数，奇数位（从左往右数）上的数字和与偶数位上的数字和之差（大数减小数）能被11整除，则该数就能被11整除．由此方法判定即可．解答：解：A．（3+3+3）﹣（2+5+2）=0，能被11整除，故A正确；B．（8+8）﹣（3+3+0）=10，不能被11整除，故B错误；C．（9+8+6）﹣（7+7+8）=2，不能被11整除，故C错误．故选：A．点评：掌握被一个数整除数的特征，牢记判定方法是解决问题的根本．5.（2011•武汉）某个四位数有如下特点：它加上1之后是15的倍数，它减去3之后是38的倍数．把它的各数位上的数字左右倒过来写，所得的新数与原数之和能被10整除，这个四位数是多少？【答案】所求的四位数是1409或1979．【解析】原数加1后是15的倍数，所以这个四位数必是5的倍数，所以个位数字是4或9，又因为原数减去3后是38的倍数，是一个偶数，可得原数应该是奇数，所以原数的个位数字只能是9，再从条件（3）可知：原数的个位数字与千位数字之和是10，所以千位数字是10﹣9=1，设原数为38m+3（m为自然数），则有1009≤38m+3≤1996，据此可得26≤m≤53，据此再进行分析即可解答．解答：解：原数加1后是15的倍数，所以这个四位数必是5的倍数，所以个位数字是4或9，又因为原数减去3后是38的倍数，是一个偶数，可得原数应该是奇数，所以原数的个位数字只能是9，再从条件（3）可知：原数的个位数字与千位数字之和是10，所以千位数字是10﹣9=1，设原数为38m+3（m为自然数），则有1009≤38m+3≤1996，可得26≤m≤53，因为原数38m+3的个位数字是9，所以8m的个位数字是6．从而m的个位数字是2或7，在26到53之间，个位数字是2或7的数有27、32、37、42、47、52，又因为原数加上1后是15的倍数，则38m+3+1=38m+4是3的倍数，则19m+2必定是3的倍数，19m+2=3×6m+m+2，所以m+2是3的倍数，即m被3除余1，在27、32、37、42、47、52中，只有37和52被3除余1，所以m=37或52，所以38×37+3=1409，38×52+3=1979，经检验正好满足题意，答：所求的四位数是1409或1979．点评：根据题干，明确四位数的个位数字和千位数字分别是9和1，再根据被15整除的数的特征和偶数特征进行分析即可解答．6.（2013•浦口区）甲、乙两个数，甲数除以乙数商2余17，乙数的10倍除以甲数商3余45．求甲、乙二数．【答案】甲数是 65，乙数是 24【解析】被除数、除数、商和余数的关系：被除数=除数×商+余数．如果设乙数为 x，则根据甲数除以乙数商 2 余 17，得甲数=2x+17．又根据乙数的 10 倍除以甲数商3余45得10x=3（2x+17）+45，列出方程并解方程，即可得解．解答：解：设乙数为x，则甲数为2x+1710x=3（2x+17）+4510x=6x+51+454x=96x=242x+17=2×24+17=65．答：甲数是 65，乙数是 24．点评：灵活应用余数的性质“被除数=除数×商+余数”来解决实际问题．7.我国著名的数学家陈景润要证明“哥德巴赫猜想”：“任何一个大于4的偶数，一定是两个奇素数的和．”俗称“1+1=2”．试将大于4且小于30的偶数分别写成2个奇素数的和．【答案】22=5+17，24=7+17，26=3+23，28=5+23．【解析】只有1和它本身两个约数的数是质数，除了1和它本身还有别的约数的数是合数，是2的倍数的数是偶数，不是2的倍数的数是奇数，由此即可得答案．解答：解：大于4且小于30的偶数分别写成2个奇素数的和有：22=5+17，24=7+17，26=3+23，28=5+23．点评：解答本题要明确自然数，质数，合数的概念，熟记30以内的质数表．要注意写出的两个数都要是质数．8.一个合数至少有（）个约数．A． 1 B． 2 C． 3【答案】C【解析】根据合数的概念即可解答．解答：解：一个数，如果除了1和它本身还有别的因数，这样的数叫做合数；由此一个合数至少有3个约数．答：一个合数至少有3个约数．故选：C．点评：此题考查的目的是理解和掌握合数的概念和内涵，据此解决有关的问题．9.把726分解质因数．【答案】726=3×2×11×11【解析】分解726，可以先用质数3去除，得242，再用质数2去除，再用质数11去除即可解答．解：726=3×2×11×11，故答案为：726=3×2×11×11．点评：考查了分解质因数的方法，一般要先用质数3、2、5去除．10.a口bc是一个四位数，已知a+b+c=15，且以a口bc是3的倍数，方框中可填的数有( )个。

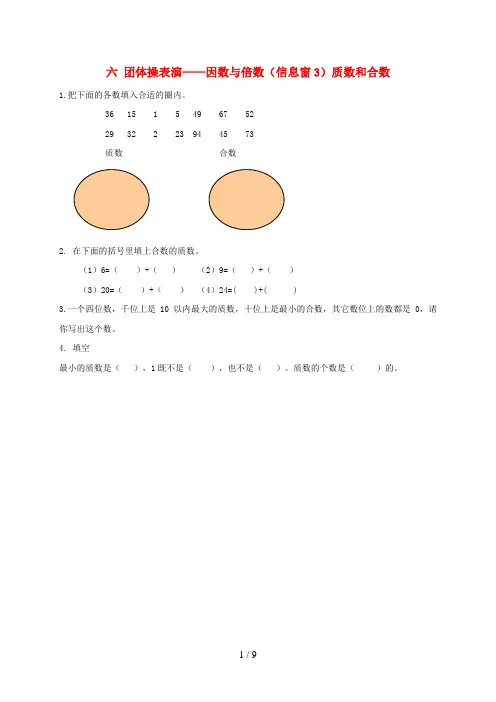
六团体操表演——因数与倍数（信息窗3）质数和合数1.把下面的各数填入合适的圈内。

36 15 1 5 49 67 5229 32 2 23 94 45 73质数合数2. 在下面的括号里填上合数的质数。

（1）6=（）+（）（2）9=（）+（）（3）20=（）+（）（4）24=( )+( )3.一个四位数，千位上是10以内最大的质数，十位上是最小的合数，其它数位上的数都是0，请你写出这个数。

4. 填空最小的质数是（），1既不是（），也不是（）。

质数的个数是（）的。

参考答案：1.质数合数2.（1）6=（ 3 ）+（ 3 ）（2）9=（ 2 ）+（ 7 ）（3）20=（ 3 ）+（ 17 ）（4）24=( 5 )+( 19 )或20=7+13 或24=( 11 )+( 13 )或24=( 17 )+( 7 )3. 70404.最小的质数是（ 2 ），1既不是（质数），也不是（合数）。

质数的个数是（无限的）的。

第三单元小数的意义和性质4 小数的大小比较内容1.在○里填上“>”“<”或“=”。

236○158 999○1100 799○80075○57 320○302 534○5342.比较0.48元和0.6元的大小。

1.都转化为几角几分进行比较。

0.6元是6角,0.48元是4角8分,6角( )4角,所以0.6( )0.48。

3.用小数的意义比较。

先用小数的( )将0.6转化为两位小数是( ),有( )个0.01;0.48有( )个0.01,所以0.6( )0.48。

4.小数的大小比较,先比较整数部分,整数部分大的那个数大。

如果整数部分相同,就比较小数部分,按照( )的顺序比较。

5.小数的大小比较和小数部分的位数( )。

(填“有关”或“无关”)6.在○里填上“>”“<”或“=”。

2○2.001 3.15○3.1460.08元○0.11元 4.50○4.5009.899○9.988 2元○1.98元7. 把下面各数按照从小到大的顺序填在框里。

倍数与因数经典例题答案班级小组姓名成绩（满分120）一、认识倍数和因数（共4小题，每题3分，共计12分）例1.判断。

(1)因为42÷7=6,所以42是倍数,7是因数。

(×)(2)51是17的倍数,17是51的因数。

(√)(3)1是1,2,3,4,5,…的因数。

(√)(4)4的倍数有无数个,4的因数只有2和4。

(×)(5)因为4×8=32,所以32是8的倍数,8是32的因数。

(√)(6)一个数的倍数一定比这个数大。

(×)(7)一个数的因数的个数是有限的,一个数的倍数的个数是无限的。

(√)例1.变式1.根据算式填数。

(1)10×2=20(10)和(2)是(20)的因数,(20)是(2)和(10)的倍数。

(2)28÷7=4(28)是(7)和(4)的倍数,(4)和(7)是(28)的因数。

(3)3×18=54(54)是(3)和(18)的倍数,(3)和(18)是(54)的因数。

(4)95÷5=19(5)和(19)是(95)的因数,(95)是(5)和(19)的倍数。

找一个数的倍数的方法例1.变式2.把4的倍数用“○”圈起来。

例1.变式3.小蜜蜂采蜜。

(连一连)二、倍数与因数（共4小题，每题3分，共计12分）例2.判断。

(1)0不是自然数。

(×)(2)自然数都是整数。

(✓)(3)8是倍数,1是因数。

(×)(4)32既是4的倍数,又是8的倍数。

(✓)(5)1是1,2,3的因数。

(✓)(6)12是12的倍数。

(✓)例2.变式1.体育课上,王老师为五年级(1)班的同学安排了一次有趣的跳绳活动,王老师将全班学生分成5个小组,每组7人。

跳绳的规则是这样的:每人只跳60秒,跳的次数是7的倍数的有效,否则无效。

下面表格展示了两组同学的成绩,找一找哪些成绩是有效的,填在表格里。

例2.变式2.爸爸每4天休息一次,妈妈每3天休息一次,5月6日爸爸、妈妈都休息,下一次爸爸、妈妈共同休息将在几月几日?4+1=5（天）3+1=4（天)4x5=206+20=26（日）答:下一次爸爸、妈妈共同休息将在5月26日.组数成绩有效成绩第一组14,43,56,70,85,62,42第二组39,63,78,98,47,90,9114567042639891例2.变式3.老师的年龄在20岁到40岁之间,既是6的倍数,又是9的倍数,请猜猜老师今年几岁。

人教版五年级数学下册第二单元《因数与倍数》质数和合数专项练习卷（全卷共4页，共19题，40分钟完成）1．在自然数1－10中，质数有（），合数有（），（）既不是质数，也不是合数。

2．最小的合数是（），最小的质数是（）。

3．在2、3、4、9、10、11、18、54这些数中，质数是（），合数是（），既是奇数又是合数的是（），既是质数又是偶数的是（）。

4．12的因数有（）个，在这些因数中，质数有（），合数有（），奇数有（），偶数有（）。

5．两个质数的和是15，则这两个质数是（）和（）。

6．在（）里填上合适的质数。

65＝（）×（）7．两个质数的积是15，这两个质数分别是（）和（）。

8．把20写成两个不同质数和的形式。

20＝（）＋（）＝（）＋（）9．将下列各数分别填入指定的圈里。

27、5、14、11、1、2、33、62、0、1910．平平今年的年龄是个两位数，个位上既是质数又是偶数，十位上既不是质数也不是合数。

他今年（）岁，至少再过（）年，他的年龄数同时是2、3、5的倍数。

11．一个九位数，最高位和万位上的数都是1，百位上的数是最小的合数，个位上的数既是一个奇数，又是一个合数，千万位上的数比十万位上的数多3，十万位上的数既是一个偶数，又是一个质数，其余各位上是0，这个数写作（ ）；这个数读作 （ ）。

31997852四舍五入到万位约是（ ）万。

577500改写成用“万”做单位的数是（ ）万。

12．所有合数都能写成几个质数相乘的形式，例如422=⨯，623=⨯，18233=⨯⨯。

23，42，36，93，101这几个数是不是合数？把合数照上面的样子写成质数相乘的形式。

13．下面是育才小学五年级各班的人数．哪几个班可以平均分成人数相同的小组？哪几个班不可以？为什么？（要求每组不止1人且不止1组）14．猜一猜：一个数左往右依次是：①是最小的合数；②最大因数是8；③因数只有1和5；④既不是质数也不是合数；⑤最大的一位数；⑥既是质数又是偶数⑦10以内最大的质数。

小学数学因数与倍数、质数与合数练习题一、判断题( √)1、任何自然数，它的最大因数和最小倍数都是它本身。

( X)2、一个数的倍数一定大于这个数的因数。

( X)3、个位上是0的数都是2和5的倍数。

( √)4、一个数的因数的个数是有限的，一个数的倍数的个数是无限的。

( X)5、5是因数，10是倍数。

( X)6、36的全部因数是2、3、4、6、9、12和18，共有7个。

( X)7、因为18÷9=2，所以18是倍数，9是因数。

( X)9、任何一个自然数最少有两个因数。

( √)10、一个数如果是24的倍数，则这个数一定是4和8的倍数。

( X)11、15的倍数有15、30、45。

( √)12、一个自然数越大，它的因数个数就越多。

( X)13、两个质数相乘的积还是质数。

( √)14、一个合数至少得有三个因数。

( √)15、在自然数列中，除2以外，所有的偶数都是合数。

( X)16、15的因数有3和5。

( X)17、在1—40的数中，36是4最大的倍数。

( √)18、16是16的因数，16是16的倍数。

( X)19、8的因数只有2，4。

( √)20、一个数的最大因数和最小倍数都是它本身，也就是说一个数的最大因数等于它的最小倍数。

( √)21、任何数都没有最大的倍数。

( √)22、1是所有非零自然数的因数。

( X )23、所有的偶数都是合数。

1( X)24、质数与质数的乘积还是质数。

( X)25、个位上是3、6、9的数都能被3整除。

( X)26、一个数的因数总是比这个数小。

( X)27、743的个位上是3，所以743是3的倍数。

( X)28、100以内的最大质数是99。

二、填空。

1、在50以内的自然数中，最大的质数是（47 ），最小的合数是（ 4 ）。

2、既是质数又是奇数的最小的一位数是（ 3 ）。

3、在20以内的质数中，（11、15、17 ）加上2还是质数。

4、如果有两个质数的和等于24，可以是（5 ）＋（19 ），（17 ）＋（7 ）或（11 ）＋（13 ）。

小学五年级下学期，数学练习50题（有答案）因数与倍数----质数与合数，测试题一、选择题1．a、b、c是100以内的3个质数，使得a＋b＝c成立的不同质数算式共有（）个。

A．6B．7C．8D．92．下面各组数中，三个连续自然数都是合数的是（）。

A．4、5、6B．8、9、10C．13、14、153．10以内既是奇数，也是合数的数是（）。

A．9B．2C．74．两个质数的积是（）。

A．质数B．合数C．不能确定5．下面说法正确的有（）句。

（1）所有的偶数都是合数（2）一个数的倍数有无数个（3）两个质数的和是偶数（4）9的倍数一定也是3的倍数A．1B．2C．3D．46．下列说法正确的是（）。

A．所有奇数都是质数B．3的所有倍数都是合数C．奇数都不是2的倍数D．自然数中除了质数就是合数7．下列各数或表示数的式子（x为整数）：3x＋4，4，x＋6，2x＋6，0，一定是偶数的共有（）个。

A．4B．3C．2D．18．一个两位数由3个不同的质数相乘得到，这个数的因数共有（）个。

A．3B．5C．89．下列说法正确的是（）。

A．6是12的倍数B．10的因数只有2和5C．能同时被2和5整除的最大的两位数是90D．互素的两个数一定都是素数10．几个质数的积一定是（）。

A．奇数B．偶数C．无法判断11．从1到2005连续自然数相加的和是（）。

A．奇数B．偶数12．一个质数（）。

A．没有因数B．只有1个因数C．只有2个因数13．一个数既是质数，又是偶数，它是（）。

A．2B．4C．5D．614．自然数可以分为（）两类。

A．质数和合数B．奇数和偶数C．因数和倍数D．1和合数15．下列数是质数的是（）。

A．9B．15C．21D．29二、解答题16．一个三位质数，各位数字也是质数且互不相同，个位数字等于前两位数字的和，这个质数是多少？17．一个长方形的长和宽都是以厘米为单位的质数，并且周长是36cm。

这个长方形的面积最大是多少平方厘米？18．如果a×（b＋c）＝209，并且a、b、c是不同的质数（c＜b），那么a、b、c各代表多少？19．一个长方形的长和宽是两个连续的合数，这个长方形的面积是72平方厘米，它的周长是多少厘米？20．用数字1，2，3，组成一位数、两位数和三位数，其中哪些是质数，哪些是合数？21．两个质数的和是20，积是91，这两个质数分别是多少？22．两个质数的积是202，这两个质数的和是多少？23．两个质数的和是39，求这两个质数的积。

人教版五年级数学下册第二单元《因数与倍数》测试题（含答案）一、选择题1．下面的说法正确的是（ ）。

A ．偶数与偶数的和一定是偶数B ．奇数与偶数的和一定是偶数C ．质数与质数的积一定是质数D ．质数与合数的积一定是质数2．小红买6支铅笔的总价可能是（ ）元．A ．4.8B ．5.2C ．5 3．一个奇数和一个偶数的积一定是（ ）．A ．奇数B ．偶数C ．质数D ．两种情况都有可能4．要使24□5是3的倍数，那么□中可能是（ ）。

A ．3或6B ．1、4或7C ．1或0D ．2或5 5．小军从一个物体的上面观察这个物体时，看到的是一个正方形，这个物体（ ）。

A ．一定是正方体B ．一定是长方体C ．只能是正方体或长方体D ．形状无法确定6．105可以分解成105=3×5×7．那么105的因数共有（ ）A ．3个B ．5个C ．6个D ．8个 7．两个奇数的和是（ ）。

两个偶数的和是（ ），奇数和偶数的和是（ ）。

每空分别填（ ）。

A ．偶数；偶数；奇数B ．奇数；奇数；奇数C ．奇数；奇数；偶数 8．m 表示不等于0的自然数，下面式子中所表示的数一定是偶数的是（ ）。

A ．31m - B ．31+m C ．21m +D ．22m + 9．同时是3和5的倍数的最大两位奇数是（ ）A ．90B ．75C ．30D ．1510．一个盒子里有红、白、黑三色珠子共27个，其中红色珠子的个数占白色珠子的61，那么盒子里最多有（ ）颗红珠子．A ．3B ．6C ．8D ．18二、其他计算11．把下面的各数分解质因数。

36 57 105三、填空题 12．在1-100的自然数中，既不是2的倍数，又不是3的倍数的数有（______）个． 13．7既是7的 ，又是7的 ．14．37□，如果是2和5的倍数，□里填（______），如果是3和5的倍数，□里填（______）。

15．一个数的最大因数是24，这个数是_____，这个数的所有因数有_____，这个数的最小倍数是_____．16．一个数的个位是质数，又是5的倍数，十位是最小的合数，这个数是（______）。

《因数与倍数--质数和合数》习题一．选择题1、下面表示分解质因数正确的是()A．2612=⨯⨯=⨯⨯D．18233⨯=B．17117=⨯C．101252、在下面四组数中，()组中的数都是质数．A．13，21，17 B．91，71，51 C．43，53，73 D．17，37，853、一个合数至少有()个因数．A．1 B．2 C．3 D．无数4、37(⨯)的积是质数．A．1 B．可以是1，也可以是别的数C．质数5、3个质数相加，结果()A．一定是奇数B．一定是偶数C．可能是奇数也可能是偶数6、把78分解质因数是()A．7832131=⨯=⨯⨯⨯B．783213=⨯⨯C．786137、把24分解质因数，下面的式子中，正确的是()A．242322=⨯⨯⨯⨯=⨯⨯C．2423221=⨯⨯⨯B．242628、下面四个数中，是合数．C.119DB.51A.97.83二、填空题9、在18的所有因数中，质数有，合数有．10、在连续的自然数中，两个都是质数的是和．11、最小的质数是，它与最小的合数的和是．12、从0，1，2，3四个数中，任选三个数字，组成一个同时是2和5的倍数，又含有因数3的最大三位数是，把它分解质因数是．13、两个质数的和是15，积是26，这两个质数分别是和．14、一个数的最小倍数是48，把这个数分解质因数是．三、判断题15、边长是质数的正方形，它的周长一定是合数．（判断对错）16、自然数中，最小的质数与最小的合数相差2．．（判断对错）17、两个质数相乘，积是合数．（判断对错）18、把一个数用质数相乘的形式表示出来，叫做分解质因数．（判断对错）19、两个不同数相乘的积一定是合数．（判断对错）四、应用题20、有三张写有数字7，8，9的卡片，从中抽取一张、两张、三张，分别组成一位数、两位数和三位数，其中哪些是质数？哪些是合数？21、有三个小朋友的年龄正好是三个连续自然数，且他们年龄之积是210，这三个小朋友年龄分别是多少？五、操作题22、先圈出下面的合数，再把它们分解质因数．23、送信，连一连．24、下面各数中哪些是质数？哪些是合数？分别填入指定的圈里．17、37、40、51、1、61、22、73、83、95、11、15、99、87六、解答题25、两个质数的乘积是91，这两个质数分别是多少？26、把下面的数分解质因数（从上到下，从左到右填写）．27、两个质数的和是18，积是65，这两个质数分别是多少？28、在横线里填上合适的质数：20=+=++39=+=-．29、数学辩论题．观察下面的数学现象：3与5互质，5与8互质，3与8也互质；4与7互质，7与9互质，4与9也互质⋯⋯正方：根据上述现象，可得出这样一个结论：若A与B互质，B与C互质，则A与C一定互质．你（作为反方）是否认同正方观点？如果不同意，请举例予以辩论．30、将下面合数分解质因数．（1）26 （2）18 （3）24 （4）3531、在11、18、33中，是质数，是的质因数，和是互质数．32、一个数的最大约数是42，把这个数分解质因数是．答案一、选择题1、解：A、2612⨯=，不符合分解质因数的书写形式．B、17117=⨯，其中1既不是质数，也不是合数，所以不正确；=⨯⨯，其中1既不是质数，也不是合数，所以不正确；C、10125D、18233=⨯⨯，符合要求，所以正确；故选：D ．2、解：A 组中21是合数；B 组中91、71、51都是合数；C 组中43、53、73都是质数；D 组中85是合数．故选：C ．3、解：一个合数至少有3个因数． 故选：C ．4、解：37137⨯=，37还是质数，所以371⨯的积是质数； 故选：A ．5、解：根据数和的奇偶性可知，两个质数的合可能是奇数，也可能是偶数；奇数中包含质数，偶数中除2之外全为合数，例如23510++=，10是偶数，35715++=，15是奇数，所以，3个质数相加，结果可能是奇数也可能是偶数； 故选：C ．6、解：782313=⨯⨯ 故选：B ．7、解：242223=⨯⨯⨯． 故选：A ．8、解：83、97都仅有1和它本身两个因素所以是质数； 51有因数1、3、17、51； 119有因数1、7、17、119． 所以51、119是合数． 故选：C 、D ． 二、填空题9、解：18的因数有：1，2，3，6，9，18．其中2，3为质数，即其中有2个质数，6、9、18为合数，即有3个合数． 故答案为：2、3、6、9、18．10、解：在连续的自然数中，两个都是质数的只有2和3．故答案为：2、3．+=；11、解：最小的质数是2，最小的合数是4，它们的和是246故答案为：2，6．12、解：符合条件的三位数有120、210，其中最大三位数是210；=⨯⨯⨯2102357=⨯⨯⨯．故答案为：210，2102357=⨯13、解：26213+=13215所以，这两个质数是2，13．故答案为：2，13．14、解：一个数的最大因数和最小最小倍数都是它本身，所以这个数是48，=⨯⨯⨯⨯；4822223=⨯⨯⨯⨯．故答案为：4822223三、判断题⨯；15、解：正方形的周长=边长4它的周长至少有三个约数：1，4，边长，所以说一定是合数；边长是质数的正方形，它的周长一定是合数，所以本题说法正确；故答案为：√．16、解：在自然数中最小的质数是2，最小的合数是4，最小的质数与最小的合数相差：422-=，所以原题说法正确；故答案为：√．17、解：质数⨯质数=积，积是两个质数的倍数，这两个质数也就是这个积的因数，这样积的因数除了1和它本身外还有这两个质数，所以它们的积一定是合数；故答案为：√．18、解：把一个数用质数相乘的形式表示出来，叫做分解质因数是正确的． 故答案为：√．19、解；1和2是大于零的自然数，它们的积122⨯=，2是质数，1和5是大于零的自然数，它们的积155⨯=，5是质数，所以两个不同数相乘的积一定是合数的说法是错误的； 故答案为：⨯． 四、应用题20、解；三张数字卡片7、8、9，从中抽一张，分别组成的一位数是7、8、9；从中抽两张组成的两位数有：78、79、87、89、97、98， 从中抽三张组成的三位数有：789、798、879、897、987、978；其中质数有：7、79、89、97；合数有：8、9、78、87、98、789、798、879、897、987、978． 21、解：因为2102357567=⨯⨯⨯=⨯⨯； 所以这三个自然数分别是5、6、7． 答：这三个小朋友年龄分别是5，6，7． 五、操作题 22、解：如图所示：20225=⨯⨯ 45335=⨯⨯ 91713=⨯23、解：24、解：质数有：17、37、61、73、83、11；合数有：40、51、22、95、15、99、87．故答案为：六、解答题25、解：因为91713=⨯，所以这两个质数分别是7、13．答：这两个质数分别是7和13．=⨯⨯26、解：18233故完成填空如下：27、解：把65分解质因数：=⨯，65513答：这两个质数是5和13．28、解：根据质数的意义可知，=+=++，203172513=+=-．39237412故答案为：3，17，2，5，13；2，37，41，2．29、解：若A与B互质，B与C互质，则A与C不一定互质，例如：3与5互质，5与9互质，但3与9不互质，3和9的公因数有：1、3．30、解：（1）26213=⨯； （2）18233=⨯⨯； （3）242223=⨯⨯⨯； （4）3557=⨯；故答案为：213=⨯；233=⨯⨯；2223=⨯⨯⨯；57=⨯．31、解：在11、18、33中，11是质数，11是33的质因数，11和18是互质数． 故答案为：11，11，33，11，18． 32、解：42237=⨯⨯ 故答案为：42237=⨯⨯．。

数学学科专属辅导讲义学员姓名教师姓名班主任上课日期上课时间年级课时教学内容因数与倍数2教学目标1、理解掌握质数和合数2、学会分解质因数教学重难点1、理解掌握质数和合数2、学会分解质因数教学内容1、理解掌握2、3、5的倍数的特征1、把55个橘子分给甲、乙、丙三人，甲得到的橘子数是乙的2 倍，且甲、乙得到的橘子数都比丙多，丙得到的橘子数比10 多，则甲、乙、丙三人各得多少个？2、一个数加3是5的倍数，减去3是6的倍数，这个数最小是多少？【课前导入1】写出3、5、7、8、10、12、13、15这7个数的所有因数观察以上数的因数，他们有什么特点。

总结：像2、3、5这几个数，只有1和它本身两个因数，这样的数叫作质数，也称为素数；像6，8、9这几个数，除了1和它本身还有别的因数，也就是有两个以上因数，这样的数叫作合数。

练习1：(1)质数只有( )个因数，合数至少有( )个因数。

(2) 自然数中，最小的质数是( )，最小的合数是( )。

(3) 比10小的数里，质数有( )个，合数有( )个。

(4) 20的因数有( )，其中是质数的有( )。

问题1：1是质数还是合数？说说想法。

问题2：可以将大于O的自然数还可以按什么分类，分成几类？问题3：按质数和合数的分类和偶数、奇数的分类比较，有什么不同？总结：20以内的质数是：2、3、5、7、1 1、1 3、1 7、19。

质数不都是奇数，因为2是质数。

【课前导入2】请把5和28分别写成两个数相乘的形式。

77=53+17+7再任取一个奇数461,那么461=449+7+5也是三个素数之和.461还可以写成257+199+5仍然是三个素数之和.这样,我就发现:任何大于5的奇数都是三个素数之和.1、30的所有因数有( )A.1、2、3、5和10B. 2、3、5、10和15C. 1、2、3、5、6、10、15和302、当两个数互质时，它们的最大公因数是( )。

A. 1B. 2C. 无法确定3、把20分解质因数应该写成（）A. 20=1×2×2×5B. 2×2×5=20C. 20=2×2×54、14和28的公倍数（）。

质数和合数练习题一、填空。

1、像2、3、5、7、19、13、23…只有1和它本身两个因数的数叫做质数或素数。

像 4、6、9、14…除了1和它本身外还有别的因数的数叫做合数。

2、最小的自然数是（0），最小的质数是（2），最小的合数是（4）。

3、在0、1、2、9、15、32、147、60、216中，自然数有 0、1、2、9、15、32、147、60、216，奇数有 1、9、15、147 ，偶数有0、2、32、60、216 ，质数有 2 ，合数有 9、15、32、147、60、216 ，是3的倍数的数有 9、15、60、216 。

既不是质数，又不是合数的有 1 。

4、 20以内既是合数又是奇数的数有 9、15 。

5、能同时是2、3、5倍数的最小两位数是30。

6、 18的因数有1、2、3、6、9、18，其中质数有2、3 ，合数有6、9、18 。

7、 50以内11的倍数有11、22、33、44 。

8、三个连续偶数的和是54，这三个偶数分别是16、18 、20 。

9、 40以内最大质数与最小合数的乘积是148 。

37乘410、从1、0、8、5四个数字中选三个数字，组成一个有因数5的最小三位数是105 。

11、一个三位数，能有因数2，又是5的倍数，百位上是最小的质数，十位上是10以内最大奇数，这个数是290 。

12、一个四位数，千位上是最小的质数，百位上是最小的合数，十位上既不是质数也不是合数，个位上既是奇数又是合数，这个数是2419 。

13、有两个数都是质数，这两个数的和是8，两个数的积是15，这两个数是3和 5 。

14、既不是质数，又不是合数的自然数是 1 ；既是质数，又是偶数的数是2 ；既是奇数又是质数的最小数是3；既是偶数，又是合数的最小数是 4 ；既是奇数，又是合数的最小的数是9 。

15、个位上是0 的数，既是2的倍数，也是5的倍数。

16、20以内的数中不是偶数的合数有 9、15 ，不是奇数的质数有 2 。

五年级数学倍数与因数试题答案及解析1.在1~20的自然数中，最大的质数是（）；最下的合数是（）；是偶数但不是合数的是（）；是奇数也是合数的是（）。

【答案】19、4、2、9和15【解析】略2.在35的因数中，有（）个不同的质数。

A.1B.2C.3【答案】B。

【解析】质数是只有1和它本身两个约数的数，合数是除了1和它本身，还有别的约数的数，35的因数有1、5、7、35，其中1既不是质数也不是合数，根据质数、合数的意义可知：35的因数中有5、7两个质数。

3.有一个数，它既是8的因数，又是8的倍数，这个数是（）。

A.8B.16C.24【答案】A。

【解析】根据找一个数的因数的方法：一个数的因数是有限的，最大的因数是它本身，最小的因数是1；根据找一个数的倍数的方法，一个数的倍数是无限的，最小的一个倍数是它本身，可见一个数的本身既是其最大约数又是其最小倍数。

4.在方格纸上画长方形，使它的面积是16cm2，边长是整厘米数。

（每个小方格的边长表示1cm）16的全部因数：________________________________。

【答案】1，2，4，8，16。

据此画图如下：【解析】先把16写出两个数相乘的形式，即可画出这个面积是16平方厘米的长方形，再根据求一个数的因数的方法，进行依次列举即可。

5.深圳大运会闭幕式体操队表演时有48人。

如果体操队排成长方形队形（每队人数和排数都不小于4），可以有几种排法？【解析】此题实际是求48的因数，然后根据题意即可解答。

6.要使1280是3的倍数，至少要加上（）。

A.1B.3C.4【答案】A。

【解析】根据能被3整除的数的特征：即该数各个数位上数的和能被3整除；进行解答即可。

7.解答。

（1）是3的倍数的有：______________________。

（2）同时是2和3的倍数的有：___________________________。

（3）同时是3和5的倍数的有：____________________________。

五年级因数与倍数试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个数是12的因数？A. 5B. 6C. 8D. 102. 如果a是b的倍数，那么下列哪个说法是正确的？A. b是a的因数B. a是b的因数C. a和b互为质数D. a和b互为倍数3. 下列哪个数既是3的倍数又是4的倍数？A. 12B. 15C. 18D. 204. 一个数的最大因数是它本身，这个数是？A. 1B. 质数C. 合数D. 任何数5. 下列哪个数有4个因数？A. 12B. 15C. 18D. 20二、判断题（每题1分，共5分）1. 任何数都有因数。

（）2. 一个数的倍数个数是无限的。

（）3. 质数只有两个因数。

（）4. 两个质数相乘，它们的乘积是合数。

（）5. 一个数的因数个数是有限的。

（）三、填空题（每题1分，共5分）1. 12的因数有：1、2、__、__、12。

2. 如果a是b的倍数，那么b是a的__。

3. 15的倍数有：15、30、__、__。

4. 一个数的最大因数是它__。

5. 18的因数个数是__。

四、简答题（每题2分，共10分）1. 请写出12的所有因数。

2. 请写出15的所有倍数。

3. 请问一个数的最大因数是多少？4. 请问一个数的倍数个数是有限的还是无限的？5. 请写出18的所有因数。

五、应用题（每题2分，共10分）1. 如果a是b的倍数，那么b是a的什么？2. 如果一个数的最大因数是它本身，那么这个数是什么？3. 如果一个数的倍数个数是无限的，那么这个数是什么？4. 如果两个质数相乘，它们的乘积是什么？5. 如果一个数的因数个数是有限的，那么这个数是什么？六、分析题（每题5分，共10分）1. 请分析一个数的因数和倍数之间的关系。

2. 请分析质数和合数的因数个数有什么不同。

七、实践操作题（每题5分，共10分）1. 请找出36的所有因数。

2. 请找出45的所有倍数。

八、专业设计题（每题2分，共10分）1. 设计一个算法，找出一个正整数所有的因数。

2022-2023学年度第二学期五年级数学测试卷因数与倍数学校:___________姓名：___________班级：___________考号：___________一、填空题（每空1分，共12分）1．20以内既是奇数又是合数的有___________。

2．一个数既是8的倍数又是24的因数，这个数是___________。

3．在11－100的自然数中，最大的质数是( )，最小的偶数是( )。

4．在2，3，5，9，13，23，33中，( )是质数，( )是合数。

5．一个数的最大因数和最小倍数都是36，这个数的因数有( )。

6．一个长方形的周长是16dm，且长和宽都是质数，则长是___________dm，宽是___________dm。

7．用3、0、6三个数组成的三位数中，能同时被2、3、5整除的数有( )个；能同时被2、3整除的数有( )个。

8．一个九位数，个位和百位是最小的质数，十万位是最小的奇数，最高位是最小的合数，其余数位上的数是最小的偶数，这个数是( )。

二、判断题（每题2分，共10分）9．两个质数的积不可能是偶数。

( )10．有7个小学生排成人数均等的队伍，只有一种排法。

( )11．两个奇数的和是偶数，积也是偶数。

( )12．一个自然数（0除外）不是质数就是合数。

( )13．a是c的倍数，b也是c的倍数，则a＋b的和一定是c的倍数。

( )三、选择题（每题2分，共10分）14．相邻两个自然数的和是（）。

A．奇数B．偶数C．不能确定15．两位数中既是3的倍数又是5的倍数最大的奇数是（）。

A．99B．95C．7516．按照（），可以把自然数分为奇数和偶数。

A．因数的个数B．是不是2的倍数C．是不是3的倍数17．一个数，它既是18的倍数，又是18的因数，这个数是（）。

A．9B．18C．36D．32418．1＋2＋3＋……＋88的和是（）数，2a＋a＋b＋b＋b＋a＋b的和是（）数。

A．奇；质B．偶；偶C．质；不确定D．质；奇四、文字题（每题4分，共16分）19．三个连续的偶数和是96，这三个数分别是多少？20．如果三个连续自然数的和150，这三个自然数分别是多少？21．最大的两位质数减去最小合数与最小的两位质数的积，差是多少？22．列式不计算。

姓名：年级：五年级上北师大版小学数学五年级上学期第三单元倍数与因数考点题型归纳考点题型一：奇数、偶数、质数、合数的概念要点：①奇数是单数，偶数是双数。

②质数是只有2个因数的数，合数是至少有3个因数的数。

练习一：1、最小的奇数是（），最小的质数是（），最小的合数是（）。

2、一个偶数加上（）数，结果是奇数。

3、偶数＋偶数=（）奇数×偶数=（）偶数÷奇数=（）4、在18的所有因数中，（）是质数，（）是合数，（）既不是质数，也不是合数。

5、两个连续偶数的和的平均数是17，这两个偶数分别是（）和（）。

6、有三个小朋友，他们的年龄一个比一个大1岁，他们三个人年龄的乘积是120，这三个小朋友年龄的和是（）。

7、10以内所有奇数的和是（）。

9、质数有（）个因数，合数最少有（）个因数，（）只有1个因数。

10、最小的合数和最小的质数的和是（）。

11、最小质数和最小合数的乘积是（），它的因数有（）。

12、两位数中最小的偶数是（），最小的奇数是（），最小的质数是（），最小的合数是（）。

13、24的因数共有（）个。

其中，质数有（）个，合数有（）个。

14、一个两位数，个位上数字和十位上数字都是质数，且这两个数字的和是8，这个两位数可能是（）或（）。

15、已知两个质数的和是12，这两个质数的积是（）。

16、如果a÷b=c……d，b是最小的合数，c是最小的质数，d最大是（），此时a的值是（）。

考点题型二：倍数与因数要点：①一个整数能够被另一个整数整除，那么这个整数就是另一整数的倍数。

②假如a*b=c（a、b、c都是整数），那么我们称a和b就是c的因数。

④最小公倍数：两个或多个整数的公倍数中最小的一个。

⑤最大公因数：两个或多个整数共有因数中最大的一个。

练习二：1、在60=12×5中，12和5是60的（）数。

2、因为4×9=36，36是9和4的（）数，9和4是36的（）数。

3、一个数既是6的倍数，又是36的因数，这个数可能是（）。

五年级数学因数和倍数试题答案及解析1.有3个连续自然数，已知中间一个数是n，那么其他两个自然数分别是（）和（）。

【答案】n-1；n+1【解析】主要考查了对自然数的认识。

自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

2.三个连续自然数的和是45，这三个自然数分别是（）、（）和（）。

【答案】14；15；16【解析】主要考查了对自然数的认识。

自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

3.下列哪些是自然数，请把他们写在下边的横线上。

0.34，45，26，435， 8.45， 6.54， 20， 6.01【答案】45，26，435，20【解析】主要考查了对自然数的认识。

自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

4.下列哪些是自然数，请把他们写在下边的横线上。

0.43，342，12，40， 324.9， 6.34， 13， 0.01【答案】342，12，40， 13【解析】主要考查了对自然数的认识。

自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

5.没有最大的自然数。

（）【答案】正确【解析】主要考查了对自然数的认识。

自然数用以计量事物的件数或表示事物次序的数。

即用数码0，1，2，3，4，……所表示的数。

6.13和26的最大公因数是，最小公倍数是。

考点：求几个数的最大公因数的方法；求几个数的最小公倍数的方法。

分析：13和26是倍数关系，所以这两个数的最大公因数就是较小的数13，最小公倍数是较大的那个数，即26。

解答：解：因为26÷13=2，即26是13的倍数，所以13和26的最大公因数是13，13和26的最小公倍数是26。

故答案为：13，26。

【答案】13，26【解析】【考点】求几个数的最大公因数的方法；求几个数的最小公倍数的方法。

人教版五年级下册《第2单元因数与倍数》小学数学-有答案-同步练习卷（4）一、想一想填一填1. 一个数，如果只有________和________两个因数，这样的数叫做质数。

2. 在自然数1∼10中，既是质数又是偶数的数是________，既是合数又是奇数的数是________．3. 9以内，相邻的两个自然数都是质数的是________和________，都是合数的是________和________．4. 18的因数有________，其中质数有________，合数有________．5. 10以内所有的质数的和是________．6. 最小的合数是________，最小的质数是________，________既不是合数也不是质数。

7. 奇数+奇数＝________ 偶数+偶数＝________ 奇数+偶数＝________．8. 两个质数的积是14，这两个质数的和是________．二、小法官判案．一个自然数不是质数就是合数。

________（判断对错）．所有的偶数都是合数，所有的质数都是奇数。

________．（判断对错）一个自然数至少有两个因数。

________．（判断对错）所有的质数加上1后都是合数。

________（判断对错）13，17，23，27都是质数。

________（判断对错）一个质数的最大因数和最小倍数都是质数。

________（判断对错）三、对号入座1，7，35，83，109都是（）A.偶数B.奇数C.质数一个合数至少有（）个因数。

几个不同质数的乘积一定是（）A.合数B.奇数C.偶数非零的自然数按因数的个数分，可以分为（）A.质数和合数B.奇数和偶数C.质数、合数和1D.因数和倍数两个连续自然数的积一定是（）A.偶数B.奇数C.质数四、解答题（共2小题，满分0分）猜猜我是谁。

分一分（把下列各数填在合适的圆圈里）2，4，5，7，9，31，40，57，61，70，83，102六、快乐提升他们今年多大？一、想一想，填一填根据算式24÷3＝8，24是3和8的________，3和8是24的________．在自然数1−20中，质数有________，偶数有________，既是奇数又是合数的有________．两个质数的乘积一定是________，两个偶数的差一定是________．三个连续奇数的和是45，这三个奇数分别是________、________和________．一个三位数，百位上的数是最小的奇数，个位上的数是最小的合数，十位上的数是比3大比7小的奇数，这个数是________．二、小法官判案因为36÷4＝9，所以36只有4和9两个因数。

板块一 因数倍数一、 因数的概念与最大公因数0被排除在因数与倍数之外1． 求最大公因数的方法①分解质因数法：先分解质因数，然后把相同的因数连乘起来．例如：2313711=⨯⨯，22252237=⨯⨯，所以(231,252)3721=⨯=； ②短除法：先找出所有共有的因数，然后相乘．例如：2181239632，所以(12,18)236=⨯=；③辗转相除法：每一次都用除数和余数相除，能够整除的那个余数，就是所求的最大公因数．用辗转相除法求两个数的最大公因数的步骤如下：先用小的一个数除大的一个数，得第一个余数；再用第一个余数除小的一个数，得第二个余数；又用第二个余数除第一个余数，得第三个余数；这样逐次用后一个余数去除前一个余数，直到余数是0为止．那么，最后一个除数就是所求的最大公因数．(如果最后的除数是1，那么原来的两个数是互质的)．例如，求600和1515的最大公因数：151********÷=；6003151285÷=；315285130÷=；28530915÷=；301520÷=；所以1515和600的最大公因数是15．2． 最大公因数的性质①几个数都除以它们的最大公因数，所得的几个商是互质数；②几个数的公因数，都是这几个数的最大公因数的因数；③几个数都乘以一个自然数n ，所得的积的最大公因数等于这几个数的最大公因数乘以n ．3． 求一组分数的最大公因数先把带分数化成假分数，其他分数不变；求出各个分数的分母的最小公倍数a ；求出各个分数的分子的最大公因数b ；b a即为所求． 二、倍数的概念与最小公倍数1. 求最小公倍数的方法①分解质因数的方法；例如：2313711=⨯⨯，22252237=⨯⨯，所以[]22231,252237112772=⨯⨯⨯=；②短除法求最小公倍数； 例如：2181239632，所以[]18,12233236=⨯⨯⨯=；知识点拨 第二讲 约数倍数③[,](,)a b a b a b ⨯=． 2. 最小公倍数的性质①两个数的任意公倍数都是它们最小公倍数的倍数．②两个互质的数的最小公倍数是这两个数的乘积．③两个数具有倍数关系，则它们的最大公因数是其中较小的数，最小公倍数是较大的数．3. 求一组分数的最小公倍数方法步骤先将各个分数化为假分数；求出各个分数分子的最小公倍数a ；求出各个分数分母的最大公因数b ；b a即为所求．例如：35[3,5]15[,]412(4,12)4== 注意：两个最简分数的最大公因数不能是整数，最小公倍数可以是整数.例如：[]()1,414,4232,3⎡⎤==⎢⎥⎣⎦ 三、最大公因数与最小公倍数的常用性质1． 两个自然数分别除以它们的最大公因数，所得的商互质。

五年级数学质数与合数试题答案及解析1.两个质数的积一定是合数。

（）【答案】√【解析】略2.把10以内所有的质数相乘，所得的积一定是( )。

A．奇数B．偶数C．质数D．无法确定【答案】B【解析】略3. 12的因数有( )，其中( )是质数，( )是合数。

【答案】1，2，3，4，6，12 2，3 4，6，12【解析】略4.在20以内的自然数中，是奇数又是质数的数是（）。

【答案】3,5,7,11,13,17,19【解析】略5.两个质数的差是2，这两个质数分别是( )和( )。

【答案】7 5【解析】略6.最小的质数是( )，最小的奇数是( )，( )既不是质数也不是合数。

【答案】2 1 1【解析】略7.两个质数的和一定是合数。

( )【答案】×【解析】例如2＋3＝5，5是质数。

8. 37是( )。

A．因数 B．质数 C．合数【答案】B【解析】略9.按要求写数。

24的因数：___________________________________________40以内6的倍数：______________________________________20以内的质数：________________________________________20以内的合数：_______________________________________20以内的奇数：_______________________________________20以内的偶数：_______________________________________【答案】24，2，12，3，8，4，66，12，18，24，30，362，3，5，7，11，13，17，194，6，8，9，10，12，14，15，16，18，201，3，5，7，9，11，13，15，17，192，4，6，8，10，12，14，16，18，20【解析】略10.如果n是自然数，那么2n＋2一定是偶数。

【六年级数学小升初】数的认识：质数、合数与分解质因数（含知识点、练习和答案）知识点：质数与合数：1、质数：一个数，如果只有1和它本身两个因数，那么这样的数叫做质数（或素数）。

例如：30以内的质数有：2、3、5、7、11、13、17、19、23、29。

注意：（1）质数又称素数，有无限个。

一个大于1的自然数，除了1和它本身外，不能被其他自然数整除。

（2）最简分数：当分数的分子和分母互质时（只有公因数1），即为最简分数。

2、合数：一个数，如果除了1和它本身之外，还有别的因数，这样的数就叫做合数。

例如：4、6、8、9、12、24都是合数。

3、特别的：1既不是质数也不是合数。

自然数除了0和1外，不是质数就是合数。

如果把自然数（0除外）按其因数的个数的不同分类，可分为质数、合数和1。

4、分解质因数：把一个合数用质因数相乘的形式表示出来，就叫做分解质因数。

注意：每个合数都能写成几个质数相乘的形式。

其中的每个质数都是这个合数的因数，叫做这个合数的质因数。

例如：12=2×2×3，2和3就叫做12的质因数。

同步练习：一、单选题1、在1～10中，是偶数但不是质数的有（）个。

A、2B、3C、92、两个合数相加后，和是（）。

A、合数B、偶数C、奇数3、23和（）的乘积是质数。

A、1B、任何自然数C、质数4、（）的最大公因数一定是1。

A、两个奇数B、两个偶数C、两个合数D、两个不同的质数5、相邻的两个自然数的和一定是（）。

A、奇数B、偶数C、质数D、合数6、若b是质数，那么下面说法正确的是（）。

A、b一定是奇数B、b一定不是2的倍数C、b只有两个因数7、分子、分母是两个不同的质数，那么这个分数（）最简分数。

A、不一定是B、一定是C、一定不是8、如果正方形的边长是质数，那么它的面积和周长都是（）。

A、奇数B、合数C、质数D、偶数9、关于“2”，下列说法正确的是（）。

A、奇数和质数B、偶数和质数C、奇数和合数D、偶数和合数10、20以内的自然数中有质数（）个。