下载文档原格式
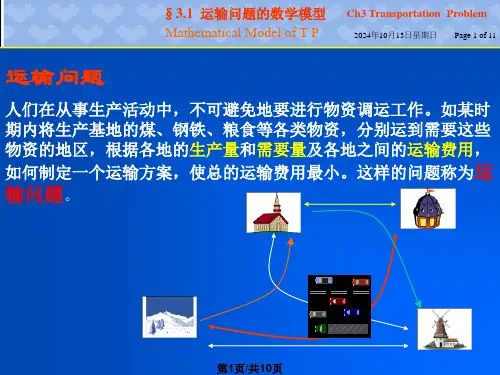
运输问题的数学模型例题运输问题是指在运输过程中，如何最优地分配资源，使得运输成本最小，运输效率最高。
运输问题的数学模型包括最小化成本、最大化效益等多种形式。
下面我们来看一个例题。
问题描述：某物流公司有3个仓库和4个客户，每个仓库和客户之间的距离已知。
现在需要将货物从仓库运送到客户，每个客户需要的货物量也已知。
假设每个仓库的货物量都足够满足所有客户的需求，如何安排运输方案，使得总运输成本最小？解题思路：我们可以用线性规划来解决这个问题。
设每个仓库和客户之间的运输量为$x_{ij}$，其中$i$表示仓库编号，$j$表示客户编号。
则总运输成本可以表示为：$$%min %sum_{i=1}^3%sum_{j=1}^4 c_{ij}x_{ij}$$其中$c_{ij}$表示从仓库$i$到客户$j$的单位运输成本。
同时，对于每个客户$j$，要求其所需货物量$q_j$必须满足：$$%sum_{i=1}^3 x_{ij}=q_j$$对于每个仓库$i$，要求其供应的货物量$y_i$必须满足：$$%sum_{j=1}^4 x_{ij}=y_i$$另外，由于$x_{ij}$必须非负，所以还要满足：$$x_{ij}%geq 0$$综上所述，我们可以得到如下线性规划模型：$$%min %sum_{i=1}^3%sum_{j=1}^4 c_{ij}x_{ij}$$$$s.t.% %sum_{i=1}^3 x_{ij}=q_j,% j=1,2,3,4$$$$% % % % % % % % % %sum_{j=1}^4 x_{ij}=y_i,% i=1,2,3$$ $$% % % % % % % % % x_{ij}%geq 0,% i=1,2,3,% j=1,2,3,4$$这是一个标准的线性规划模型，可以用常见的线性规划求解器求解。
求解结果就是每个仓库和客户之间的运输量$x_{ij}$，以及总运输成本。
总结：运输问题是一个常见的优化问题，在实际生产和物流中经常会遇到。
