求以下序列的z变换

1.2 教材第一章习题解答1. 用单位脉冲序列及其加权和表示题1图所示的序列。

解:2. 给定信号:(1)画出序列的波形，标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示序列;(3)令，试画出波形;(4)令，试画出波形;(5)令，试画出波形。

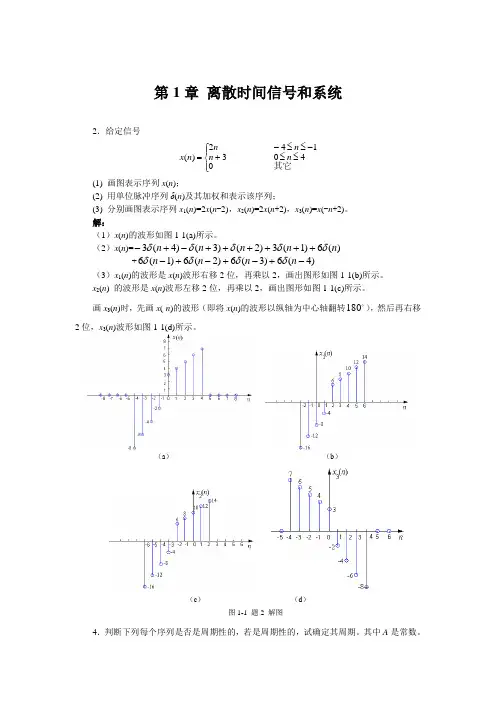
解:(1)x(n)的波形如题2解图(一)所示。

(2)(3)的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图(二)所示。

(4)的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图(三)所示。

(5)画时，先画x(-n)的波形，然后再右移2位，波形如题2解图(四)所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

(1)，A是常数;(2)。

解:(1)，这是有理数，因此是周期序列，周期是T=14;(2)，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，与分别表示系统输入和输出，判断系统是否是线性非时变的。

(1);(3)，为整常数;(5);(7)。

解:(1)令:输入为，输出为故该系统是时不变系统。

故该系统是线性系统。

(3)这是一个延时器，延时器是一个线性时不变系统，下面予以证明。

令输入为，输出为，因为故延时器是一个时不变系统。

又因为故延时器是线性系统。

(5)令:输入为，输出为，因为故系统是时不变系统。

又因为因此系统是非线性系统。

(7)令:输入为，输出为，因为故该系统是时变系统。

又因为故系统是线性系统。

6. 给定下述系统的差分方程，试判断系统是否是因果稳定系统，并说明理由。

(1);(3);(5)。

解:(1)只要，该系统就是因果系统，因为输出只与n时刻的和n时刻以前的输入有关。

如果，则，因此系统是稳定系统。

(3)如果，，因此系统是稳定的。

系统是非因果的，因为输出还和x(n)的将来值有关.(5)系统是因果系统，因为系统的输出不取决于x(n)的未来值。

如果，则，因此系统是稳定的。

7. 设线性时不变系统的单位脉冲响应和输入序列如题7图所示，要求画出输出输出的波形。

求以下序列的z 变换习题五 Z 变换1． 求以下序列的z 变换,并画出零极点图和收敛域.分析：Z 变换定义∑∞-∞=-==n nzn x z X n x Z )()()]([，n 的取值是)(n x 的有值范围。

Z 变换的收敛域 是满足∞<=∑∞-∞=-M zn x n n)(的z 值范围。

)(21)()2(n u n x n⎪⎭⎫⎝⎛=)1(21)()3(--⎪⎭⎫⎝⎛-=n u n x n)1(,1)()4(≥=n nn x 为常数）00(0,)sin()()5(ωω≥=n n n n x 10,)()cos()()6(0<<+=r n u n Ar n x n Φω)1||()()1(<=a a n x n求以下序列的z 变换解:（1） 由Z 变换的定义可知：∞====<<<<z z az a z az a z a az ,0 1, 11,1 零点为：极点为：即：且收敛域：解：(2) 由z 变换的定义可知:nn n z n u z X -∞-∞=∑=)()21()(∑∞=-=0)21(n n n z12111--=z211121 ><⋅z z 即：收敛域：0 21==z z 零点为：极点为：nn nzaz X -∞-∞=⋅=∑)(nn n nn n z a za-∞=---∞=-∑∑+=1nn n nn nz a z a -∞=∞=∑∑+=01))(1()1()1)(1(1111212a z az a z a az az a za az az ---=---=-+-=-)(21)()2(n u n x n⎪⎭⎫⎝⎛=)1(21)()3(--⎪⎭⎫⎝⎛-=n u n x n求以下序列的z 变换解:（3)nn n z n u z X -∞-∞=∑---=)1()21()(∑--∞=--=1)21(n n n z∑∞=-=12n n n z zz212--=12111--=z 21 12 <<z z 即：收敛域：0 21 ==z z 零点为：极点为：解： （4) ∑-⋅∞==11)(n nz nz X∑∞--=-=•••11)(1)(n n z n n dz z dX 21)(11z z z n n -=-=∑∞=-- ,1||>z 。

[数字信号处理]序列的z 变换序列的z 变换z 变换的定义z 变换的定义如下X (z )=∞∑n =−∞x (n )z −n其中z =e j ω,是⼀个复数.在复平⾯上,z 相当于单位圆上的⼀点.典型序列的z 变换单位脉冲序列的z 变换求序列δ(n )的z 变换X (z )=∞∑n =−∞δ(n )z −n =δ(0)z 0=1,0<|z |<∞最后的⼀句话是收敛域阶越序列的z 变换求序列u (n )的z 变换X (z )=∞∑n =−∞u (n )z −n =n =∞∑n =0z −n =11−z −1,|z |>1矩形序列的z 变换求序列R 4(n )的z 变换X (n )=∞∑n =∞R 4(n )z −n =3∑n =0z −n =1+z −1+z −2+z −3=1−z −41−z −1,0<|z |<∞收敛域z 变换的性质线性设x 1(n )的z 变换是X 1(z )x 2(n )的z 变换是X 2(z )如果x 3(n )=ax 1(n )+bx 2(n )那么X 3(z )=aX 1(z )+bX 2(z )X 3(z )的收敛域为X 1(z )的收敛域和X 2(z )的收敛域的交集移位性质双边序列x (n )为双边序列时设x (n )的z 变换是X (z )则x (n +n 0)的z 变换是z n 0X (z )序列移位不会改变z 变换的收敛域右边序列右移公式x (n )为右边序列设x (n )的z 变换是X (z )x (n −1)的z 变换是z −1X (z )+x (−1)x (n −2)的z 变换是z −2X (z )+z −1x (−1)+x (−2)如此类推右边序列左移公式x (n )为右边序列设x (n )的z 变换是X (z )x (n +1)的z 变换是z 1X (z )−x (1)x (n +2)的z 变换是z 2X (z )−z 1x (1)−x (2)如此类推序列乘实指数序列设x (n )的z 变换是X (z )y (n )=a n x (n )的z 变换Y (z )=X (a −1z )复共轭序列的z 变换设x (n )的z 变换是X (z )则x ∗(n )的z 变换是X ∗(z ∗)初值定理设x (n )的z 变换是X (z )则x (0)=lim终值定理设x(n)的z 变换是X(z) \\则x(\infty)=\lim_{z->1}(z-1)X(z)序列类型收敛域有限长序列$0<右边序列$左边序列$双边序列$R_{x-}<Loading [MathJax]/jax/element/mml/optable/BasicLatin.js帕斯维尔定理(能量定理)时域总能量等于z域总能量(能量守恒)E=\sum_{n=-\infty}^{\infty}|x(n)|^2=\frac{1}{2\pi}\int_{-\pi}^{\pi}|X(e^{j\omega})|^2d\omega。

z变换公式表范文1.基本变换：-原始序列：$x[n]$- Z变换：$X(z) = \sum_{n=-\infty}^{\infty} x[n] \cdot z^{-n}$2.常数乘法：- $ax[n]$ 的Z变换是 $aX(z)$3.基本序列变换：- 单位冲激序列：$\delta[n]$- $Z\{\delta[n]\} = 1$-单位步序列：$u[n]$- $Z\{u[n]\} = \frac{1}{1 - z^{-1}}$-递增指数序列：$n$- $Z\{n\} = \frac{z^{-1}}{(1 - z^{-1})^2}$-幂指数序列：$z^n$- 当 $，z， < 1$ 时，$Z\{z^n\} = \frac{1}{1- z^{-1}}$-当$，z，>1$时，$Z\{z^n\}$不收敛- 正弦序列：$\sin(\omega_0 n)$- $Z\{\sin(\omega_0 n)\} = \frac{\sin(\omega_0)}{1 - 2z^{-1}\cos(\omega_0) + z^{-2}}$- 余弦序列：$\cos(\omega_0 n)$- $Z\{\cos(\omega_0 n)\} = \frac{1 - z^{-1}\cos(\omega_0)}{1 - 2z^{-1}\cos(\omega_0) + z^{-2}}$4.线性运算：-前移：- $Z\{x[n-1]\} = z^{-1} \cdot X(z)$-后移：- $Z\{x[n+1]\} = z \cdot (X(z) - x[0])$-缩放：- $Z\{x[a \cdot n]\} = X(z^a)$-线性组合：- $Z\{a \cdot x[n] + b \cdot y[n]\} = a \cdot X(z) + b \cdot Y(z)$5.典型序列变换：-原始序列：$x[n]=a^nu[n]$- 当 $，a， < 1$ 时，$Z\{a^n u[n]\} = \frac{1}{1 - az^{-1}}$ - 当 $，a， > 1$ 时，$Z\{a^n u[n]\} = \frac{az^{-1}}{1 -az^{-1}}$-原始序列：$x[n]=n^mu[n]$- $Z\{n^m u[n]\} = \frac{b_m}{(1 - z^{-1})^{m+1}}$其中，$b_m$为常数，受初始条件影响。

数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。

解：2.给定信号：25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n序列；（3）令1()2(2)x n x n=-，试画出1()x n波形；（4）令2()2(2)x n x n=+，试画出2()x n波形；（5）令3()2(2)x n x n=-，试画出3()x n波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）（3）1()x n的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n时，先画x(-n)的波形，然后再右移2位，3()x n波形如题2解图（四）所示。

3.判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5.设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-； （3）0()()y n x n n =-，0n 为整常数； （5）2()()y n x n =； （7）0()()nm y n x m ==∑。

解：（1）令：输入为0()x n n -，输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。

第二章2.1 判断下列序列是否是周期序列。

若是，请确定它的最小周期。

（1）x(n)=Acos(685ππ+n ) （2）x(n)=)8(π-ne j（3）x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，得出=ω85π。

因此5162=ωπ是有理数，所以是周期序列。

最小周期等于N=)5(16516取k k =。

（2）对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。

因此πωπ162=是无理数，所以不是周期序列。

（3）对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，又x(n)=Asin(343ππ+n )＝Acos(-2π343ππ-n )＝Acos(6143-n π)，得出=ω43π。

因此382=ωπ是有理数，所以是周期序列。

最小周期等于N=)3(838取k k =2.2在图2.2中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。

计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。

(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 3333 3444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。

(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n)2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λnu(n)*u(n)解：(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联，已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n).解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=an-u(-n),0<a<1 用直接计算线性卷积的方法，求系统的单位阶跃响应。