实验12 父权指数与父权概率

实验十二父权指数与父权概率【实验目的】掌握父权指数与父权概率的计算方法，了解父权概率的意义。

【实验原理】亲子鉴定中，经过DNA分型后，若争议父亲与孩子之间的基因型不违反孟德尔遗传规律（Mendelian Law），就有两种可能：一种是该争议父亲就是孩子的亲生父亲（生物学父亲，简称生父）。

另一种是他是该人群中的随机男子，此人只是偶然具有孩子的生父基因型组合，以下称为随机男子。

将这两种可能进行比较就是似然率（likelihood ratio, LR），此数值即为父权指数（paternity index, PI）。

显然，父权指数是反映检验结果（基因型组合）不违反孟德尔遗传规律时，对“争议父亲是孩子的生父”这一主张的支持强度。

依据支持强度，可以评估他们之间是否存在亲生关系。

根据Bayes定理，PI可以转换成父权概率（probability of paternity），用以反映争议父亲是孩子生父可能性的高低，使结论容易被理解。

【仪器与方法】纸、笔、计算器、电脑及计算软件。

【检材】争议父、母亲、孩子复合STR基因座分型结果图谱。

【实验步骤】1. 三联体（母子亲生关系已经确定）案件PI和父权概率计算将已知实验结果的图谱进行分析，分别列出复合STR基因座分型结果，打开亲权鉴定软件，点击亲权鉴定菜单，选择三联体和试剂盒型号，按照方法输入父母子3人的基因型。

输入完毕后，在生成结果表中勾选，点击右下角的计算器计算PI。

2. 二联体（父子）案件PI和父权概率计算将已知实验结果的图谱进行分析，分别列出复合STR基因座分型结果，打开亲权鉴定软件，点击亲权鉴定菜单，选择二联体和试剂盒型号，按照方法输入父子3人的基因型。

输入完毕后，在生成结果表中勾选，点击右下角的计算器计算PI。

注意事项a. 性别基因座（AMEL）中的X和Y在程序中分别用1和2表示，在设置基因座时，基因座序号X请设为1，Y设为2。

b. 等位基因输入时，分隔符可为'/'、'-'、'+'，"13/15"或"13-15"或"13+15"都是正确的，纯合子可只输入一个等位基因，如"13/13"可输入为"13"，性别基因（AMEL）在输入时可不使用分隔符，如"X/Y"可直接输入为"XY"，"XX"可简化输入为"X"（"YY"或"Y"将不被程序所授），在偶合率计算时，AMEL的Pi值始终为0.5，而在亲权鉴定中，AMEL不列入计算。

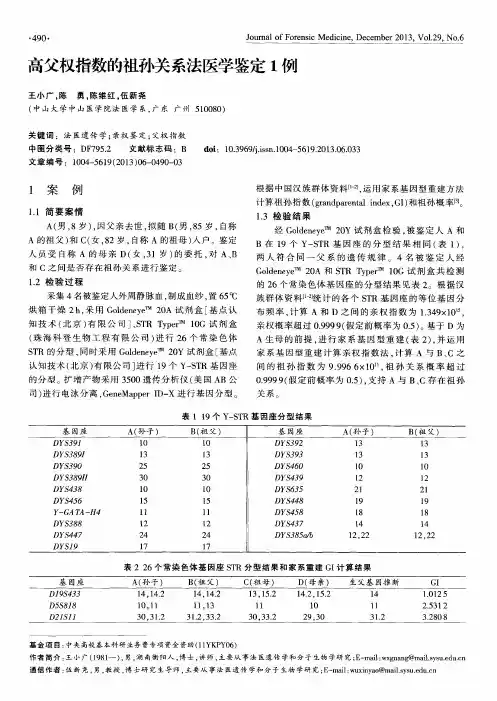
父权指数名词解释“父权指数”(父权支配子女的比例)是指父亲在家庭中施行暴力或其他形式控制(或威胁)的程度。

父权指数不是父亲统治或控制孩子的简单的加和，而是受文化、历史传统、家庭和亲子之间冲突的影响。

父权指数较高，并不意味着对孩子的暴力增加了，相反可能表明父母的感情更融洽，对孩子的管教也更有效。

据估计，美国1/3的妇女是独生子女，她们被看作掌上明珠，被父母的温暖包围着，很少挨打受骂，很少体验过精神或肉体上的痛苦，因此，她们的“父权指数”往往偏低。

父权指数与社会文化因素和心理学因素有关。

对暴力行为进行归因时，心理学上的解释是：由于个体的先天特质以及成长环境中经历的不同事件而导致某些人选择将暴力内容视为负性刺激。

例如，一些研究者提出，社会成员是否获得攻击型的人格特征主要取决于他们在幼年时期是否受到家庭的溺爱。

另外，个体经历过的那些负性事件或负性事件的重复，也都可能影响个体的负性事件解释模式。

有证据显示，母亲对儿童的虐待通常被视为对儿童身体造成的伤害;但是在文化发展比较慢的社会中，父亲对儿童的虐待就会被认为是对儿童身体和心理发育造成的严重影响。

一般认为，父权支配子女的形式随着社会结构的变迁而发生变化。

20世纪60年代之前，以高大壮男人统治小矮瘦弱儿童的父权形象占优势。

60年代后，伴随社会政治经济生活的发展，职业身份和社会角色的变化，妇女就业率增加，平均收入水平上升，妇女开始担当起社会职责，家庭的地位日益上升，特别是那些掌握着专业技术的知识女性的崛起，与父权家庭越来越难以协调，丈夫的社会职责被不断分工和取代，男人更倾向于把更多的时间放在挣钱养家上，夫妻矛盾增多。

而女性则越来越注重自己在职业领域的发展，希望获得和男人同样的经济收入，享受同等的生活水平。

家庭分工的不断变化以及女性的社会地位不断上升，使得男人再像过去那样对待自己的子女越来越不合适宜。

在这种背景下，父亲对儿童的管教方式、控制方式就更容易失控。

虽然大多数国家的法律没有对虐待儿童的父母进行惩罚的规定，但一旦子女被认为需要进行诉讼，父亲就面临着巨大的压力。

短串联重复序列(short tandem repeats,STR)是人类的一类重要遗传标记,因其多态性丰富,扩增片断长度短,广泛地应用于亲子鉴定中。

但是,STR 基因座在遗传的过程中发生突变的概率较高,因此在鉴定过程中是个不容忽视的问题,要值得注意。

笔者在工作中遇一例较罕见的母亲发生二步突变的羊水检材鉴定,现报道如下。

1 案例资料1.1 案情简介李某(孕17周+),自然受孕,未确定腹中胎儿父亲是否为其老公,特委托本鉴定所鉴定是否存在亲子关系。

1.2 检验方法胎儿羊水5m l 、男方带毛囊毛发2根、女方血样备用。

采用Chelex-100 法分别提取DNA。

经PowerPlex R21 (普洛麦格生物技术有限公司)、AGCU EX22(无锡中德美联生物技术有限公司)复合扩增系统以及Investigator Argus RX-12(德国QIAGEN公司)扩增系统进行扩增,扩增产物在ABI3500型DNA测序仪上电泳,由GeneMapper ID X1.3软件进行结果分析。

2 结果2.1 22个常染色体STR 基因座分型结果同时应用PowerPlex R21和AGCU EX22复合扩增系统,胎儿与孕妇在D5S818位点的分型结果一致,不符合遗传规律。

结果见表1。

2.2 12个位点X-STR 基因座分型结果分析12位点X-STR基因座检测结果,胎儿的X-STR分型均能从孕妇及可疑父的分型中找到来源,符合X染色体遗传规律,结果见表2。

2.3 STR 亲权指数,累计亲权指数及亲权概率的计算亲权指数(paternity index,PI)、累积亲权指数(cumulative paternity index,CPI)及相对父权概率(relative chance of paternity,RCP)的计算按文献报道的方法计算,计算所使用的相关等位基因分布频率数据来自文献［1-2］和司法部司法鉴定科学技术研究所2014年亲权鉴定能力验证资料中的相关数据,以及无锡中德美联生物技术有限公司所提供的频率表。

双亲皆疑亲子鉴定父权指数的计算方法高林林;任贺【期刊名称】《法医学杂志》【年(卷),期】2017(033)006【总页数】3页(P646-648)【关键词】法医遗传学;亲子关系;父权指数【作者】高林林;任贺【作者单位】杭州市公安局刑事科学技术研究所,浙江杭州 310002;北京警察学院,北京 102202【正文语种】中文【中图分类】DF795.2目前，《亲权鉴定技术规范》（SF/Z JD0105001—2016）对标准三联体及二联体父权指数（paternity index，PI）的计算方法进行了详细举例说明，其中标准三联体的PI计算方法与公安部发布的《法庭科学DNA亲子鉴定规范》（GA/T 965—2011）中的计算方法一致。

而对于在法庭科学亲子鉴定领域占有一定比例的未知名尸体身源认定、失踪孩子寻找父母等双亲皆疑案件PI的计算却均无明确规定。

因此，寻求一种科学、合理的双亲皆疑PI的计算方法对于法庭科学工作者来说非常重要。

双亲皆疑亲子鉴定是指鉴定某一对夫妇（或男女）是否为孩子的生物学父母，即可疑父-孩子-可疑母的组合形式。

计算这类亲子鉴定的方法在国际上也无统一标准。

本文通过10例双亲皆疑的亲子鉴定案例来探讨适合于法医实际案件鉴定中双亲皆疑PI计算及结果解释的方法，以供参考。

1 材料与方法1.1 样本与分型方法收集日常检案中未知名尸体及失踪孩子双亲皆疑的亲子鉴定案例共10例，依次编为1～10。

其中，未知名尸体及失踪孩子为女性5例，男性5例，共30份样本。

提取所有样本DNA后应用AmpFℓSTR®IdentifilerTM试剂盒（美国AB公司）及EX22试剂盒（无锡中德美联生物技术有限公司）在9700型PCR仪（美国AB 公司）上进行扩增，实验条件及步骤均按照试剂盒及仪器使用说明书操作。

扩增产物在3130xl基因分析仪（美国AB公司）上进行毛细管电泳，最后采用GeneMapper®ID-X软件（美国Thermo Fisher Scientific公司）进行等位基因分型。

１ ９ １ ８ １ ４ １ ２． ２ ２
ＤＹＳ １ ９
１ ７
１ ７
表２ ２ ６个 常 染 色体 基 因座 Ｓ Ｔ Ｒ分 型 结 果 和 家 系重 建 Ｇ Ｉ 计 算 结 果
基金项 目： 中央高校 基 本科研 业务 费专 项 资金 资助 （ １ １ Ｙ Ｋ Ｐ Ｙ ０ ６ ）
３ ０ １ Ｏ
１ ５ １ １ １ ２ ２ ４
ＤＹ￥ ４ ３ ９ Ｄｌ ， Ｓ ６ ３ ５
ＤＹＳ ４ ４ ８ Ｄｌ ， ＤＹ￥ ４ ３ ７ ＤＹＳ ３ ８ ５ ａ ／ ｂ
１ ２ ２ １
１ ９ １ ８ １ ４ １ ２． ２ ２
ｌ ２ ２ １
Ｂ在 １ ９个 Ｙ— Ｓ Ｔ Ｒ基 因 座 的分 型 结 果 相 同 （ 表 １ ） ． 两 人 符 合 同 一 父 系 的遗 传 规 律 。４名 被 鉴 定 人 经
Ｇ ｏ ｌ ｄ ｅ ｎ ｅ ｙ ｅ Ｍ Ｔ ２ ０ Ａ和 Ｓ Ｔ Ｒ Ｔ ｙ ｐ ｅ ｒ Ｍ Ｔ １ ０ Ｇ 试 剂 盒 共 检 测
家 系基 因型重 建 计算 亲 权 指数 法 ， 计 算 Ａ 与 Ｂ、 Ｃ之
（ 珠 海 科 登 生 物 工程 有 限公 司 ） 进行 ２ ６个 常 染 色 体 Ｓ Ｔ Ｒ的分 型 。 同 时采用 Ｇ ｏ ｌ ｄ ｅ ｎ ｅ ｙ ｅ Ｍ Ｔ ２ ０ Ｙ试 剂盒 『 基 点
认 知技 术 （ 北京） 有 限公 司 ］ 进行 １ ９个 Ｙ — Ｓ Ｔ Ｒ基 因 座
ＤＹＳ ４ ６ Ｄ
Ａ（ 孙子 ）
１ ３ １ ３
ｌ ０
Ｂ（ 祖父）
１ ３ １ ３
１ ０
ＤＹＳ ３ ８ ９ １ １ Ｄｌ ， ３ ８
ＤＹＳ ４ ５ ６ ｙ—Ｇ， ４ 一 日 ＤＹ￥ ３ ８ ８ ＤＹ￥ ４ ４７

HLA分型肯定父权的简易程序计算法蛔型煎H/-A~型害嘞../,7/7HLA分型肯定父权的简易程序计算法增足皖南医学院法医学系法医物证学教研室c芜Ⅲ为了解决用HLA分型作亲权鉴定时计算父权概率的困难,提出一种可用电子计算器的简易程序计算法,比一般逐步计算法为快,可供推广应用.材料和方法1.电子计算器CASIOfx--3600P型或180P型2.案例资料经用HLA—A,一B抗血清分型检验未排陈亲子关系案例共25倒?其中属于奉教研室的10例,引自文献.的lj例.3.程序计算法以赵桐茂提出的计算步骤并加以简化,依计算公式编成计算程序.以a,bIcId代表由HLA—A,一B两个座位上检出的抗原,x.Y为空白基因,有4种不同表型,须分别编成P1～P4四种程序,其计算程序清单附后.结果与讨论1.程序计算法的可|I性依文献"j表16—6中4种HLA表型和相应单倍型频率Yi值,按本文的计算公式和程序进行实例运算,回代验证,其传递各种可能的单倍型相对机会xi值与原文结果完全一致.应用文献"中的案例和单信型频率Yi值,按本文的程序运算,其x,Y值,PI和w值也都和原文一致,表明本文的程序计算法是准确可靠的.2.程序计算法的计算速度用计算器按公式进行逐步计算与用程序计算法对比,其结果如表l,后者比前者快6～lO倍,其中最常用的Pl程序,在3O秒内即可完成.裹1.计算速度比较(min)至重型盟堕::,里:一1234平均P1P2P3P4P5平均藏.ses黧.-s¨e108sssee3.案例计算表2列举了5例计算结果.例1为本室检验的离婚案,属于第一种表型,适用于按P1程序运算例2～4是以例1的检案结果为基础,模拟第2～4种表型,按P2~P4程序运算.这四种表型生母都是肯定的.例5为本室检验的家庭成员失散认亲案,父母双方都可疑,按程序P5计算备案例均按本文程序计算法计算出的PI和w值的大小,依文献判断亲子关系的参考标准,作出相应亲子关系鉴定结论.4.本文程序的适用范围P1～P4适用于强奸致孕,婚姻外生育或家庭纠纷离婚寨;P5适用于家庭成员失散认亲,遗弃婴儿及产房调错婴儿案.在实际检案中,尤以P1和P5为最常用.裹2亲权鉴定案例的计算结果倒1属于第一种表型,接程序P1运算表型:MA2A10:B5,B22CA10;A30:B5,B7FA9,A30:B7,B17单倍型:A2B5①A2B22②A1OB5①A10B7@AgB7①A9B17②A10B5③AlOB22④A30B5③Aa0B7④Aa0B7③A30B17④必需单倍型:A10B5③A30B7固统计值:MR=0.0000X=X3=0.2041Y:o.0001PI=2041W=O.9995肯定父权例2F和C属第二种表型,按程序P2运算表型:MA2,A10IB5,B22CA10?AXIB5,B7FA9,AXIB7,BI7单倍型:A2B5①A2B22②AIOB5⑨AlOB22④A20B5①AlOB7②AXB5⑤AXB7④必需单倍型:AIOB5③统计值:MR=0.0010x:x3一O.0187YO.0044PIA9B7①AgB17@AXB7@AxB17@AXB7@4.25w=0.8095不排除父权例3M属第一种表型t按程序P1求出MXI各值.F.C属第三种表型,按程序P3运算表型:MA2.A10:B5,B22CA10,A30;B5,BYFA9,A30B7.BY单倍型A2B5①A2B22②A1017,5①AI~BY②A9B7④AgBY@AIOB5@AlOB22④A30B5@A3OBY④A30B7@A3OBY④必需单倍型:AIOB5③A3OBY④统计值:MMR=0.0002MX1=MX4=0.0098MX2=Mx3=0.4902FMR—O.O∞OFXl—O.2I79FX2=O.2521FX3=O.3761FX4=0.1239X—o?2500Y—o.0069PI=36.23W=o.9731非常可能有父权例4Ftc属第四种表型,按程序P4运算表型:MA2.A10;B5,B22CA10,AN{B5,BY单倍型rA2B5①A2B22②A10B5①A10BY②A10B5③A10B22④AXB5③AXBY④必需单倍型:A10B5⑤AXRV④FA9.AXtB7,BYAgB7①AgBY②AXB7③AXBY@统计值:FMR一0.0012XI=05088X2=O.2719x3=O.0695x—x4=0.1499Y=0.0395PI=3.79w一0.7912不排除父权倒5F,M双方都有疑问的案例,按P5计算表型:MA1,A10}B5.B17CA2,A10;B5,B22FA2,A11lB5.B22单倍型:A1B5?①A1B17②A2B5①A2B22②A2B5①A2B22②A10B5@A10B17④A10B5@A10B22④AllB5③A11B22④必需单倍型:A10B5③A2B22②统计值:MMR—O0001MX=MX3一O.4736FMR=0.0012FX=FX2=O.3331x一0.1578Y:O.0002PI=888.20w一0.9988肯定父权(跗单倍型频率).AgBT=.0116AgB17一0080A30B7~.0001A30B17.00001AXB7一.00Z4AXBl7一.0347A10B7=.0020A2B5=.0186A2B22一.0160A1DB5一0058A1OB22.000lAl.BY一.0057A30B5一.0024A30BY一.0001A9BY一.0236AxB5一.O123AXBY.0157A1B=.0020AIBI7一.0068A10B17=.0011Al1B5一.0242A¨B22一.0105HLA分型计算程序jI单程序中代号说明:ON:开机.,为按键.MODE,.:执行计算.MODE,7,4:数值取小数4位.INV.KAC;清除常数存储器中数值.INVtMin:存显示数于独立存储器,已存旧数自动消除.MR:由独立存储器调出存^的显示数.Kin:向常数存储器翰^Kout:由常数存储器呼出.INV.RND:自动四舍五^.INV,1/X:取倒数.F:父或可疑被控父M母.C:子女OG:必需基因或单倍型.)【j:传递单倍型的相对机会PI:父权指数.w:父权概率.168运算前操作:0?MODE…M0DE,7,4,INV.KAC,0,IV.Min,程序】rP1):用于第一种表型a,bd计算,其单倍型有4种:ac①+ad②,bc@bd④(1)求FMRj【ac).Kin.1,(&d】,Kin,2,(bc),Kin.3,(bd),Kin.":,kout,1,×,kout,4.+,kout.2.×,kout3,,×,2,=,(MR)INV,Min.(2)求FXi:kout,l,×,kout,4,-?-.MR.一,(X1或X4)kout,2,×,kout.3,-?-,MR,,(X2或X3)1x值一FOG的值;若OG多于1种则取2xi.'Y值一FOG的随机人群频率Yi;若OG多于1种则取2Yi.将x,Y值代人下式. (3)求PI值:(x),kin@(Y),Kin,6,kout,5,÷.kout,6,],MODE,7.2,INV,RND,一,(PI)Kin.6.+,】,一(PI一1)(4)求W值:INV,I/X,:l,(P1+】)}×,kout.6,MODE,7.4,一.(w)程序2(P2):用于第二种表型a,x【c_d计算,其单倍型有4种①,ad@.xc③,xd④(】)求FMR:(ac),kin,1.(ad),kin,2,(xc),kin.3,(xd),kin,4.[,[,kout.2,+.kout,4,],×,kout.1,一.kout●●～2,×.kout.3,].×,2,=,(MR)INV,Min,(2)求FXi.1l,kout.2,'-,kout,4,],×,kout,1.÷,MR,[,kout.1,一.kout,3.],×.kout,2.÷,MR,kout,2.×,kout.3,--?-,MR,=,(X3)kort,l,×,kout,4.-F,MR,一,(X4)'x值一FOG的值:若OG多于】种则取己Xi.则Y值一c(yl+y3)或Y值=c(y2+y4)(3)求PI值,w值:同Pl之(3).:,tX1)=,(X2)若FOG为子之①(或@),与②(或④)程序3(P3):用于第三种表型a,bY计算t其单倍型有4种:ac①.ay②,be@,by@ c为第三种表型.则x=FX1×M(XI+x2)~-FX2×M(X3+x4).M为第一种表型,则X~F(XI斗X2)/2.若F和M表型都是第一型或都是第三型,则x:0.5./20.25 (1)求FMR:(ac).kin,l,(ay),kin}2,(bc),kin.3,(by),kin,4,[,[,kout,3,+.kout,4-.×,kout.1.一,kout,2,×,kout.3,],×,2.一,(MR)INV.Min,(2)求FXil『,kout,3,+,kout,4,],×,kout,l,-F,MR,一,(X】)kout,2,×,kout,3.÷.MR.=,(X2)[,kout,1.+,kout.2,],×,kout,3,÷,MR.一.(x3)kout,1.×,kout,4.-F,MR.一,(X4)(3)先就M表型额率,按程序PI求出MXi各值,然后求x值:(MXI),kin.1,(MX2),kin,2t(MX3).kin,3,(MX4),Kin.4,(Fx】),kint5, (FX2),kin,6,[.kout,j,+,kout,2.],×,kout,5,+,[.kout,3,+,kout,4,],×,kout,6.一,(x)(4)求Y值:(Cy1),kin.1,(Cy2)&in,2.(CY3)?kin,3.(Cy4),kin,4?(MX1),kin,5, (Mx2),kin,6,[,kout,3,+.kout,4,,×,kout.5,一.kout,3,×,kout,6.=INV.Min.(MX3),kin,5.(MX4),kin,6,[,kout,1,+,kout,2,],×,kout5,kout,1.×,kout.6,+,MR,一,(Y)(5)求PI,W值:同Pl之(3)程序4(P4):用于第四种表型atxmy计算,其单倍型有4种①,ay②rxc③txy④169(1)求FMR:(ac),kin,1,(ay).kin,2,(xc),kin,3,(xy).kin,4,kout.L.INV,,r,[,kout.2.+,kout,8.十,kout,4,],×,kout,1,+,kout,2,×kout.3,,×.2,一.(MR)INV,Min,(2)求FXi;[,kout,I,INV,x.+,.kout,2,+,kout.3,十,kout,41,×.kout,I.],÷.MR,一.(XI)[,kout,1,十.kout,3.],×.kout,2,÷,MR,,(x2)[,kout,1.+,kout.2,].×.kout.3,÷,MR,=,(X3)kout.1,×,kout,4.÷,MR.一,(X4)x值:c为第四种表型-则X=FOGRXi值:或取25Xi.Y值;F为第四种表型,则Y=C(yl+y2+y3+y4)F为第一种表型.则Y=FOG的随机人群频率Y'或乙Yi(3)求PI,w值:同P1之(3).程序5(P5):用于MtF,职方与C的关系均有疑问的案例.根据F.M双方表型所属类型,选择相应的程序计出FXitMXi值,求出FX,MX代人下式.(1):(CyI),kin,1,(Cy2),kin,2.(CyS),kin.3,(Cy4),kin.4,(FX),kin,5,(MX),kin.6,(2)求Y值:[,kout,1t×,kout,4,+.kout,2,×,kout,3.],×,2,一,(Y)INV,Mn,求x,PItw值:kout,5.×kout,6,一.(x)÷,MR,MODE.7,2,一,(P1)kin,6.+,1.=.(PI+1)INV,I/X.《I/(PI+1))×,kout,6,MODE.7.4,一,(w)(致谢:本文曹先后承蒙郭景元教授,曼梅筠教授,贾静涛教授和席永昌主任涪医师等热情帮助;本教研室方单华技师参加HLA血型榜验,特一井在此深致谢意!)参考室峨1.郭景元等.HLA及其在法医学上的应用.中国法医学杂志1986}1(2):lll2.昊梅筠.亲权鉴定(续二).中国法医学杂志1989;2(t):2493.贾静涛.法医血型血清学.第1版沈阳:辽宁科学技术出版社,1988:29～304.赵桐茂.HLA分型原理和应用.第1版.上海科学技术出版社,1984:245～255,124～1265.赵桐茂,亲子鉴定.北京:人民卫生出版杜,1988:32.67～92,133～119.2365.MartinW,etaI.IntroductionofastandardizedPater—n[tyIndexforthestatisticalevnhtionofbloodgroupfindingsinDatern[tytesting.ForSeiInt1983:21:717.HummelK.OnthetheoryandpracticeofEs窖en—Moiler'sWV alueandGtlrtler,sPaternityIndexfPI). ForSolIntl984;25:1(1992年1O月收稿I993年9月謦回)(上接164页)讨论自发性食道破裂多见于剧烈呕吐和急剧运动.因食道内腔压力骤然增高而发生破裂本例死者食道原无任何病变t左胸腔,纵焉及胃内未发现鱼刺等硬性物质,餐后呕吐即感腹痛,呼吸困难,赦呕吐应是破裂的原因.食道破裂部位可发生在颈部,食道下段及食道170与胃交界处或其它部位.而自发性食道破裂常发生在食道下部,破裂口大小不等.这可能由于(1)食道牯膜上皮在贲门连接处由20～25层复层扁平上皮突变为单层柱状上皮(2)剧烈呕吐导致食道内压力突然增高.食道最先受该压力冲击的部位是食道下部.(1992年i2月收稿-1993年5月謦回,本文编辑麻采昌)。

03
三、STR分型技术亲权关系鉴定的标准
单击此处添加大标题内容
三联体判断
不对实验室的要求和分析技术体系的要求进行总结，只总结STR分型结果。 STR 分型结果符合下述条件者可做出否定亲生关系的结论： 出现4个或更多矛盾 STR 基因座 累计PI值＜1／1000
三联体判断
01
STR分型结果符合下述条件者可以描述为肯定或支持亲生关系：
添加标题
二联体判断
STR 分型结果符合下述条件者可做出否定亲生关系的结论：
出现3个或更多矛盾 STR 基因座
单击此处添加小标题
累计PI值＜1／1000
单击此处添加小标题
二联体判断
STR分型结果符合下述条件者可以描述为肯定或支持亲生关系：
起码检测18个STR基因座争议父与孩子之间没有发现矛盾基因座；
添加标题
02
起码检测15个STR基因座争议父与孩子之间没有发现矛盾基因座；
添加标题
03
或检测19个STR基因座只发现1个矛盾基因座；
添加标题
04
或检测28个STR基因座只发现2个矛盾基因座；
添加标题
05
或检测35个STR基因座只发现3个矛盾基因座；
添加标题
06
累计PI值≥10000，（亲权概率W≥0.9999假定前概率＝0.5）
PQ
PQ
QR
PI=1/[2(p+q)]
PQ
PQ
PQ
PI=1/(p+q)
例如第一种情况时 X=0.5*0.5+0*0 Y=0.5*q+0*p 故PI=1/（2q）
2.父权指数的计算
2.2二联体父权指数的计算 PI=X/Y，母亲没有参加检验，基因型不确定，看成一个随机个体。

法医物证学：是以法医物证为研究对象，以提供科学证据为目的，研究应用生命科学技术解决案件中与人体有关的生物检材鉴定的一门科学。

法医物证鉴定：鉴定是指在诉讼过程中，司法机关指派或聘请具有专门知识的人就案件中的专门性问题做出判断性结论的科学活动。

遗传多态性：指控制遗传标记的基因座上存在有两个或两个以上等位基因，并且等位基因的频率大于0.01。

序列多态性（sequence polymorphism）：指某基因座碱基排列方式的个体差异。

PCR-ASO技术（等位基因特异性寡核苷酸探针杂交分析法）：根据碱基互补的原则，制备识别特定寡核苷酸序列的单链DNA探针，并标记示踪物，在高强度条件下与变性DNA样品杂交，检测示踪物，阳性者为检出相应的等位基因。

DNA分子杂交：是指来源于不同DNA分子的两条非同源DNA单链，因部分碱基互补，在退火条件下，局部碱基配对结合形成一条双链核苷酸的过程。

DNA探针（DNA probe）：是指经示踪物标记的，能与互补的寡核苷酸序列实现退火杂交的已知核苷酸片段。

小卫星重复单位变异分型（MVR）:是指VNTR基因座的重复序列同时存在内部的碱基序列的变异，根据碱基差异设计了上游5，端为共同的引物，下游3，端有两种引物，两组引物的PCR产物在相邻的2条泳道上电泳，比较相对应位置上有无谱带，进行数字编码分型。

等位基因特异性PCR（ASPCR）：是指在确定某一碱基是该等位基因所特有的基础上，设计一对引物，两引物3，端的第一碱基均与等位基因特有碱基相对应，待扩增的位点上有多少等位基因便有多少引物。

在反应体系中，只有完全碱基对应的引物才得以扩增，不对应的引物则得不到扩增或扩增效率较低。

由于各等位基因引物长度不同，通过分析扩增引物长度，确定等位基因。

规则抗体：ABO血型抗体恒定存在于正常人的血清中，可以预测其存在。

又称为天然抗体。

孟买型：红细胞上及唾液中全无A、B、H抗原，血清中含有抗A、抗B、抗H抗体的变异型。

一、单选题1、亲子鉴定中，需要确定与小孩有无亲子关系的男子称为A.被控母亲B.被控父亲C.被控叔叔D.被控爷爷正确答案：B2、根据亲子鉴定基本原理，以ABO血型为例，母亲的血型是O型，孩子的血型是O型，被控父亲的血型是AB型，则下列说法正确的是A.被控母亲与孩子不符合遗传规律B.被控父亲与孩子不符合遗传规律C.被控父亲与孩子符合遗传规律D.被控父亲与被控母亲符合遗传规律正确答案：B3、根据亲子鉴定基本原理，以STR为例，母亲的基因型是7-9，孩子的基因型是5-7，被控父亲与孩子符合遗传规律时，被控父亲的基因型是A.11-12B.5-8C.8-10D.8-11正确答案：B4、在一个双等位基因遗传标记系统中，符合和不符合遗传规律的格局下列描述错误的是A.如果母亲的基因型是aa，孩子的基因型是aa，被控父亲的基因型是AA，则不符合遗传规律B.如果母亲的基因型是Aa，孩子的基因型是Aa，被控父亲的基因型是aa，则不符合遗传规律C.如果母亲的基因型是AA，孩子的基因型是AA，被控父亲的基因型是aa，则不符合遗传规律D.如果母亲的基因型是AA，孩子的基因型是Aa，被控父亲的基因型是AA，则不符合遗传规律正确答案：B5、根据遗传规律，描述错误的是A.D7S820基因座中，母亲的基因型是9-11，孩子的基因型是9-11，被控父亲的基因型是8-12，则符合遗传规律B.MN血型系统中，母亲的血型是MN型，孩子的血型是N型，被控父亲的血型是M型，则不符合遗传规律C.vWA基因座中，母亲的基因型是15-17，孩子的基因型是14-17，被控父亲的基因型是16-18，则不符合遗传规律D.ABO血型系统中，母亲的血型是A型，孩子的血型是O型，被控父亲的血型是AB型，则不符合遗传规律正确答案：A6、评估遗传分析系统效能的指标是A.非父排除概率B.母权指数C.父权相对机会D.父权指数正确答案：A7、根据遗传规律，排除父子关系的类型中，属于直接排除的是A.母亲的血型是Rh（E+）型，孩子的血型是Rh（EE）型，被控父亲的血型是Rh（E-）型B.母亲的在D20S161基因座基因型是15-18型，孩子在D20S161基因座基因型是15-18型，被控父亲在D20S161基因座基因型是17-20型C.母亲的血型是MN型，孩子的血型是N型，被控父亲的血型是MM 型D.母亲的血型是O型，孩子的血型是O型，被控父亲的血型是AB型正确答案：B8、非父排除概率计算原理描述错误的是A.排除概率依据遗传标记是否为显隐性或共显性遗传方式有不同的计算方法B.主要取决于遗传标记的等位基因数目和基因频率分布C.非父排除概率的大小与遗传标记的遗传方式及多态性程度有关D.排除概率依据遗传标记，无论为显隐性还是共显性遗传方式的计算方法相同正确答案：D9、关于排除父权，下列说法正确的是A.遗传标记在两代人之间传递是不可能有遗传例外的B.只要有一个遗传标记不符合遗传规律就可以排除父权C.无血缘关系的男子与小孩的遗传标记偶然也会符合遗传规律D.遗传标记在两代人之间传递是不可能有突变的正确答案：C10、根据下列基因座非父排除概率值，遗传标记排除假父亲的能力最强的是A.0.302B.0.413C.0.510D.0.683正确答案：D11、下列不属于遗传变异的是A.受外伤留在额头的刀疤B.基因突变C.沉默基因D.基因缺失正确答案：A12、关于基因突变，描述错误的是A.突变是导致亲代与子代的遗传标记不符合遗传规律的重要原因B.在细胞的减数分裂过程中，存在有基因的交换和重组，或由于某些外界影响因素的作用，导致基因的核苷酸顺序和数目发生改变C.突变可能影响亲子鉴定结果的正确性D.突变对亲子鉴定结果的正确性毫无影响正确答案：D13、关于无效等位基因，描述错误的是A.对常规使用的STR基因座进行观察，无效基因的出现率大约为0.01%~0.5%B.对常规使用的STR基因座进行观察，无效基因的出现率大约为1%~5%C.STR序列内出现点突变一般不会干扰对片段长度的分型D.如果单个碱基变异正好在模板上引物3’末端的结合处，将会直接影响该引物退火和延伸，导致这个等位基因没有扩增产物，这个没有扩增产物而漏检的基因叫做无效等位基因正确答案：B14、亲子鉴定需要掌握的知识不包括A.能解决操作方法所引起的一系列问题B.掌握不同群体或不同民族血型的基因与单倍型频率C.无需专业知识，任何人都可承担D.血液遗传学、免疫血液学及分子生物学知识正确答案：C15、当只有1个遗传标记不符合遗传规律时，需A.否定父权B.检测更多遗传标记C.重新采集样本D.放弃检测正确答案：B16、亲子关系鉴定中判断遗传证据强度的指标是A.父权指数B.非父排除率C.个人识别能力D.杂合度正确答案：A17、父权指数计算公式PI=X/Y描述正确的是A.是判断亲子关系所需的两个条件概率的似然比B.PI是指随机男子是孩子生物学父亲的概率C.PI是指具有被控父亲遗传表型的男子是孩子生物学父亲的概率D.PI取值范围是0~1正确答案：A18、有母亲参与的共显性遗传标记计算父权指数，描述错误的是A.检测遗传标记结果孩子的表型为PQ，母亲的表型为P, 被控父亲表型为Q。

亲权指数 (PI) 计算上例中假设父 2 不能排除父子亲生关系 , 但他不一定是孩子的生父，因为人群中 FGA-25 基因频率为 0.0958 。

虽然生父必须有生父基因，但有 FGA-25 基因的男人不一定就是孩子的生父。

按照概率理论，具有生父基因的假设父和具有生父基因的随机男人都有成为孩子生父的可能性。

假设父提供生父基因成为孩子生父的可能性和随机男人提供生父基因成为孩子生父的可能性的比值叫作亲权指数（ paternity index,PI ）。

前一种可能性假设为 X; 后一种可能性假设为Y 。

上例中的假设父 2 基因型为 24/25 杂合子，他提供生父基因 FGA-25 的可能性为 1/2 ，即 X=1/2 。

随机男人提供生父基因 FGA-25 的机会为该基因的频率，即 Y=0.0958 。

因此，此例的 PI 值为 0.5/0.0958=5.22 。

如果假设父 2 的确是孩子的生父，则不论检测多少位点，均不会排除他与孩子的亲生关系，在所有检测的位点，每一个位点就可以计算出一个 PI 值，多个位点的累计 PI 值等于各个位点 PI 值的乘积，但前提条件是所检测的各位点之间没有遗传连锁关系。

三联体基因型组合的可归纳为三条原则：（ 1 ）当假设父为纯合子时， X=1 ；假设父为杂合子时， X=1/2 ，但杂合子假设父的 2 个基因均可能是生父基因时， X=1 。

（ 2 ）只涉及 1 个生父基因时， Y 值等于生父基因的频率。

（ 3 ）若涉及 2 个生父基因时， Y 值为 2 个生父基因频率之和。

非父排除率孩子的非亲生父亲的男子，能够被遗传标记系统排除的概率。

这是判断试剂盒系统效能的重要指标。

通俗点讲：这代表了试剂盒在亲子鉴定中的能力；非父排除率越高，代表试剂盒能力越强；试剂盒能力越强，代表把不是孩子父亲的男人认定为是孩子父亲的可能性越小。

ID试剂盒的系统累计非父排除率为0.99999872，SN试剂盒的系统累计非父排除率为0.999999763，DM试剂盒的系统累计非父排除率更高。

利用微卫星标记对绵羊进行亲子鉴定刘龙腾;贾春旸;努尔力·阿不力孜;张文祥;赵宗胜【摘要】采用微卫星DNA分子标记方法,通过对132只父系半同胞中国美利奴羊在BM4621、BM143、OarHH55、OarJMP8、BM6438、BM6506、BM1824、OarDB6、ILSTS0049个微卫星位点的分析,计算出了中国美利奴羊在这9个位点的等位基因频率及其分布规律,并对其中7组亲子进行了亲子鉴定.结果表明,这9个微卫星位点均表现为高度或中度多态性；9个微卫星位点在选择的7组亲子中,获得了0.999 8～0.999 9的父权概率,说明这9个微卫星位点即使在亲缘关系较近的群体中进行亲子鉴定也是可行的.【期刊名称】《江苏农业学报》【年(卷),期】2014(030)001【总页数】5页(P135-139)【关键词】STR基因座;分子标记;绵羊;亲子鉴定【作者】刘龙腾;贾春旸;努尔力·阿不力孜;张文祥;赵宗胜【作者单位】石河子大学动物科技学院,新疆石河子832003;石河子大学动物科技学院,新疆石河子832003;石河子大学动物科技学院,新疆石河子832003;石河子大学动物科技学院,新疆石河子832003;石河子大学动物科技学院,新疆石河子832003【正文语种】中文【中图分类】S826.8+6在现代动物育种中，由于要利用各种亲属的表型信息，准确的系谱记录十分重要，然而在有些情况下，不能准确地确认某些个体的父本，不能准确地判断个体的亲缘关系，从而影响绵羊育种工作的顺利开展。

因此对家畜特别是种公畜的系谱确证就显得更为重要。

用微卫星DNA 进行亲子鉴定是一新兴的生物技术，在国内外多种家畜和动物上做过试验并取得较好的结果。

Glowatek-Mullis 等［1］用分属不同染色体的多态微卫星位点成功解决了以前用血型无法解决的35 头牛的血缘控制问题。

Fredholm 等［2］用6 ～9 个分属不同染色体的多态微卫星位点鉴定了来源于12 个品种狗的血缘，此外还利用微卫星位点对一个有争议的母本进行了确认(概率99.99%)。

亲权指数计算公式
【原创实用版】
目录
1.亲权指数的定义和意义
2.亲权指数的计算公式
3.亲权指数的应用和举例
正文
1.亲权指数的定义和意义
亲权指数，又称亲子关系指数，是一种衡量亲子间遗传相似程度的指标。

在法医学、遗传学以及亲权鉴定等领域具有重要意义。

通过计算亲权指数，可以判断两个个体之间是否存在亲子关系，以及亲子关系的概率。

2.亲权指数的计算公式
亲权指数的计算公式为：
亲权指数 = (1/N) * ∑(Fij/Pij)
其中，N 为比较的基因位点数，Fij 为子代基因位点 i 和 j 的等位基因频率，Pij 为双亲基因位点 i 和 j 的等位基因频率。

在实际计算过程中，通常采用 Log 变换以消除频率的平方效应，并使用最大似然估计法来计算亲权指数。

3.亲权指数的应用和举例
亲权指数在亲权鉴定中有着广泛应用。

例如，在法庭科学中，通过比较已知亲子的基因型和待鉴定亲子的基因型，可以计算亲权指数，从而判断待鉴定亲子之间是否存在亲子关系。

在遗传学研究中，亲权指数可用于分析亲属间的遗传相似性，探究家族遗传病的传播规律等。

总之，亲权指数作为一种衡量亲子间遗传相似程度的重要指标，在多
个领域具有广泛的应用。

排除母系亲属父权概率的计算
罗冬梅;胡跃清
【期刊名称】《数学理论与应用》
【年(卷),期】2009(000)002
【摘要】在许多案例中，特别是在遗产继承和移民案例中，要排除父权的更可能是小孩的亲属而不是与其无任何血缘关系的男性。

本文给出了小孩母系男性亲属排父率的简洁且通用的计算公式。

结合2组汉族地区数据，计算出4类小孩母系男性亲属的排父率。

数值结果表明：母系男性亲属的排父率接近或达到随机男子的排父率，并且母亲的亲兄弟是最容易被排除父权的。

【总页数】5页(P9-13)
【作者】罗冬梅;胡跃清
【作者单位】安徽工业大学数理学院,安徽马鞍山243002;东南大学数学系,江苏南京210096
【正文语种】中文
【中图分类】O211
【相关文献】
1.双亲皆疑亲子鉴定父权指数的计算方法 [J], 高林林;任贺
2.亲子鉴定中HLA分型母子对排除概率的简易计算法 [J], 梅善宗
3.学习《概率论与数理统计》应该注意的若干问题(1)——概率概念的内涵与概率的分解计算 [J], 许道云;秦永彬;刘长云
4.短片段优先扩增引起D1S80基因座错误排除父权1例 [J], 刘显智;夏凤珍;李剑
平
5.河南汉族人群11个STR基因座在排除父权方面的应用 [J], 刘永波;陈辉;李晓雯;连建华;宋国英;程晓丽
因版权原因，仅展示原文概要，查看原文内容请购买。

计 算 亲权 指数 （ｐａｔｅｒｎｉｔｙ ｉｎｄｅｘ，ＰＩ）、累积 亲 权 指 数 （ｃｕｍｕｌａｔｉｖｅ ｐａｔｅｒｎｉｔｙ ｉｎｄｅｘ，ＣＰＩ）。根 据 司 法 部 《亲 权鉴 定技 术 规 范 》（ＳＦ／ＺＪＤ０１０５００１—２０１０）和 《法庭 科 学 ＤＮＡ 亲 子 鉴 定 规 范 》（ＧＡ／Ｔ９６５—２０１１） 判断是 否 存在 亲缘 关 系 。 ２ 结 果
遗传 分 析 仪 进 行 毛 细 管 电 泳 ，通 过 Ｇｅｎｅ Ｍａｐｐｅｒ ＩＤ．Ｖ３．２软 件进 行结 果分 析 。 １．２．３ 父权 指 数计 算方 法 ：在 亲 子鉴 定 中 ，父 权 指 数 是判 断亲 子关 系所 需 的 两个 概率 的似 然 比，即 具 有 假设 父遗 传 表 型 的男 子 是 孩 子 生 物 学 父 亲 的 概 率 （Ｘ ）与 随机 男子 是孩 子 生 物学 父 亲 的概 率 （Ｙ ）
的 比值 。亲权 指数 （ｐａｔｅｒｎｉｔｙ ｉｎｄｅｘ，ＰＩ）ＰＩ＝＝＝ Ｖ 一
筹 ，ｘ（具有假设父遗传表型的男子是孩子生
物 学父 亲 的概率 ）一 ｆ（生母 提 供生 母基 因概 率 ）×Ｃ （假 设 父提 供生 父 基 因概 率 ）。Ｙ （随机 男 子 是 孩 子 生 物学 父 亲 的概率 ）一 ｆ（生母 提供 生母 基 因概 率 ） ×ｇ（随机 男 子 提供 生 父 基 因 概 率 ）。 由于 ＳＴＲ 基 因突变 一 步 约 占 ９０ 以上 ，Ｂｒｅｎｎｅｒ假 设 ：５０ ９／６的 一 步 向 上 突 变 或 ５Ｏ 的 一 步 向 下 突 变 ；５Ｖ０的 二 步 向上 突 变 或 ５ 的 二 步 向 下 突 变 ，以 此 类 推 。 Ｐｒ
ＤＯＩ：１０．３９６９／ｊ．ｉｓｓｎ．０２５３—９９２６．２０１８．０４．０３９ 作 者 单 位 ：０３０００１太 原 ，山 西 医科 大 学 法 医 学 院 （牛 蕾 蕾 ）；广 东 省 汕 头 市公 安 局 刑 事 技 术 中心 （窦 定 所 （康 永 红 ）

浅谈高中生物概率题的解题技巧作者：沈洁来源：《读天下》2020年第19期摘;要：《遗传与进化》是生物学科必须二课本也是三本必修里面最让学生头疼的一本，从这届学生开始我把关于概率的计算系统的进行讲解，相关知识点进行分类归纳，结果收效不错，现在就和大家分享一下我的教学心得。

关键词：高中生物;概率题;解题技巧一、联系有关章节分析原理假说演绎法的四个步骤——实验、假说、验证、结论，孟德尔研究过程是按照这个步骤进行的，对于孟德尔第一定律常规的讲解让学生知道如何书写遗传图解，知道雌雄配子随机结合，知道第一定律是针对一对相对性状，最重要的一点让学生知道两个比例即可：Dd×Dd（杂合子自交）后代显性∶隐性=3∶1，Dd×dd（杂合子测交）后代显性∶隐性=1∶1，这两个比例十分重要，知道这两个比例可以解百题，以下例题我会做详细解释。

对于第二定律孟德尔针对的是二对及二对以上的相对性状，第二定律最终的目的还是解决生产实践上的问题正如有两种奶牛，一种是生长快产奶量低一种是生长慢产奶量高，这里出现了两对相对性状，这节课我淡化了常规讲解，分析孟（二）实验过程中我才去让学生发现孟（二）和孟（一）之间的通性看看能否发现有关概率计算的捷径，比如在假说（纸上谈兵）的这个步骤把两对相对性状分开研究：黄色和绿色、圆粒和皱粒，顺势把孟（一）概率引入，黄色和圆粒是显性，根据分离定律F2代黄色∶绿色=3∶1，圆粒∶皱粒=3∶1，得出两对实际上可以理解为（3∶1）×（3∶1）正好符合9∶3∶3∶1，由此得出不管几对相对性状都可以一对一对看，化繁为简，认识到孟德尔第二定律实际上就是第一定律的结合体同时深入分析9∶3∶3∶1这个概率实际上可以演变为9∶6∶1、9∶3∶4、9∶7、12∶3∶1等情况为接下来难一些的概率题做准备。

二、针对典型题目发现解题技巧（一）简单题目解题方法——3∶1、1∶1是关键1. 利用基因型算概率典型例题1：将基因型为AaBb和AABb的玉米杂交，按基因的自由组合规律，后代中基因型为AABB的个体占1/8。

我的父母是我父母的概率
1.亲子鉴定百分之多少是亲生的含义
亲子鉴定的99.99%说的是两者之间的亲权概率。

一般亲子鉴定否定的100%，肯定是99.99%以上。

肯定的不会达到100%。

只会无限接近100%。

99.99%是亲子鉴定这项技术的固有亲权概率。

根据标准：一般16个位点是大于99.95%以上，20个位点的大于99.99%以上，40个位点大于99.9999%以上。

这些是位点数固有的最小概率。

有时候根据两者间的DNA数据比较20位点也有很大是大于
99.9999%以上的。

2.亲子鉴定达到百分之多少可以证明两个人是亲兄妹？百分之九十五到百分之九十八。

3.亲权概率达到百分之多少可以断定是亲生的？百分之九十如果是亲生的一般都是百分之九十九的
4.亲子鉴定百分之多少就算有血缘关系？若符合亲子关系，亲子关系概率会达99.99%以上；当结果是排除亲子关系时，则至少会出现两个以上之点位不吻合，亲子关系概率值也会趋近于0，而否定亲子关系时准确度是100%。

不能确定血缘关系，那个确定的是亲子关系，也就是父母与子女。

一、选择题1．在不透明的布袋中，装有三个颜色分别为红色、白色、绿色的小球，所有小球除颜色外其他都相同，若分别从两个布袋中随机各取出一个小球，则所取出的两个小球颜色相同的概率是（）A．13B．12C．23D．1A解析：A【分析】先画出树状图，从而可得从两个布袋中各取出一个小球的所有可能结果，再找出所取出的两个小球颜色相同的结果，然后利用概率公式进行计算即可得．【详解】由题意，画树状图如下：由此可知，从两个布袋中各取出一个小球的所有可能结果共有9种，它们每一种出现的可能性都相等，其中，所取出的两个小球颜色相同的结果共有3种，则所求的概率为3193P==，故选：A．【点睛】本题考查了利用列举法求概率，依据题意，正确画出树状图是解题关键．2．甲、乙、丙三个小朋友玩滑梯，他们通过抽签的方式决定玩滑梯的先后顺序，则顺序恰好是甲→乙→丙的概率是（）A．13B．14C．15D．16D解析：D【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与出场顺序恰好是甲、乙、丙的情况，再利用概率公式求解即可求得答案．【详解】画出树状图得：∵共有6种等可能的结果，其中出场顺序恰好是甲、乙、丙的只有1种结果，∴出场顺序恰好是甲、乙、丙的概率为16，故选：D．【点睛】本题考查了用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．3．由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘，如果一个转盘转出了红色，另一转盘转出了蓝色，游戏者就配成了紫色，下列说法正确的是（）A．两个转盘转出蓝色的概率一样大B．如果A转盘转出了蓝色，那么B转盘转出蓝色的可能性变小了C．游戏者配成紫色的概率为1 6D．先转动A转盘再转动B转盘和同时转动两个转盘，游戏者配成紫色的概率不同C 解析：C【分析】根据古典概率模型的定义和列树状图求概率分别对每个选项逐一判断可得．【详解】解：A、A盘转出蓝色的概率为12、B盘转出蓝色的概率为13，此选项错误；B、如果A转盘转出了蓝色，那么B转盘转出蓝色的可能性不变，此选项错误；C、画树状图如下：由于共有6种等可能结果，而出现红色和蓝色的只有1种，所以游戏者配成紫色的概率为16，D、由于A、B两个转盘是相互独立的，先转动A转盘再转动B转盘和同时转动两个转盘，游戏者配成紫色的概率相同，此选项错误；故选：C．【点睛】此题考查了列表法或树状图法求概率．注意用到的知识点为：概率＝所求情况数与总情况数之比．4．下列说法中正确的是（）A．“打开电视，正在播放《新闻联播》”是必然事件B．“x2＜0（x是实数）”是随机事件C．掷一枚质地均匀的硬币10次，可能有5次正面向上D．为了了解夏季冷饮市场上冰淇淋的质量情况，宜采用普查方式调查C解析：C【解析】试题分析：选项A中的事件是随机事件，故选项A错误；．选项B中的事件是不可能事件，故选项B错误；．选项C中的事件是随机事件，故选项C正确；．选项D中的事件应采取抽样调查，普查不合理，故选D错误；．故选C．考点：概率的意义；全面调查与抽样调查；随机事件；探究型．5．布袋中有红、黄、蓝三种颜色的球各一个，从中摸出一个球之后不放回布袋，再摸第二个球，这时得到的两个球的颜色中有“一红一黄”的概率是（）A．16B．29C．13D．23C解析：C【解析】解：画树状图如下：一共有6种情况，“一红一黄”的情况有2种，∴P（一红一黄）=26=13．故选C．6．某班四个小组进行辩论比赛，赛前三位同学预测比赛结果如下：甲说：“第二组得第一，第四组得第三”；乙说：“第一组得第四，第三组得第二”；丙说：“第三组得第三，第四组得第一”；赛后得知，三人各猜对一半，则冠军是（）A．第一组B．第二组C．第三组D．第四组B解析：B【解析】试题分析：因为三人都猜对了一半，假设甲说的前半句正确，来看看后面的说法有没有矛盾，有矛盾就是错误的没矛盾就是正确的．假设甲说的“第二组得第一”是正确的，那么丙说的“第四组得第一”是错误的，“第三组得第三”就是正确的，那么乙说的“第三组得第二”是错误的，“第一组得第四”是正确的，这样三人都猜对了一半，且没矛盾．故猜测是正确的．故选B．考点：推理与论证点评：此类问题是初中数学的难点，解题关键往往假设一个正确或错误，来推看看有没有矛盾．7．下列说法：①“明天的降水概率为80%”是指明天有80%的时间在下雨；②连续抛一枚硬币50次，出现正面朝上的次数一定是25次（）A．只有①正确B．只有②正确C．①②都正确D．①②都错误D解析：D【分析】概率是反映事件发生机会的大小的概念，只是表示发生的机会的大小，机会大也不一定发生，机会小也有可能发生．【详解】①“明天的降水概率为80%”是指是指明天下雨的可能性是80%，不是有80%的时间在下雨，故①错误；②“连续抛一枚硬币50次，出现正面朝上的次数一定是25次”，这是一个随机事件，抛一枚硬币，出现正面朝上或者反面朝上都有可能，但事先无法预料，故②错误；①和②都是错误的．故选D．【点睛】本题考查概率的相关概念．不确定事件是可能发生也可能不发生的事件．正确理解随机事件、不确定事件的概念是解决本题的关键．8．下列事件是必然事件的是()A．阴天一定会下雨B．购买一张体育彩票，中奖C．打开电视机，任选一个频道，屏幕上正在播放新闻联播D．任意画一个三角形，其内角和是180°D解析：D【分析】根据必然事件的概念可得答案．【详解】A、阴天下雨是随机事件；B、购买一张体育彩票，中奖是随机事件；C、打开电视机，任选一个频道，屏幕上正在播放新闻联播是随机事件；D、任意画一个三角形，其内角和是180°是必然事件；故选：D．【点睛】本题考查了必然事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．9．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．若3枚鸟卵全部成功孵化，则3只雏鸟中恰有2只雄鸟的概率是（）A．23B．58C．38D．16C解析：C【分析】根据题意列举出所有情况，看三只雏鸟中恰有2只雄鸟的情况数占总情况数的多少即可．【详解】根据题意画图如下：共8种情况，三只雏鸟中恰有两只雄鸟有3种情况，所以概率为38．故选C．【点睛】此题考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比；得到三只雏鸟中恰有两只雄鸟的情况数是解决本题的关键．10．有下列事件：①367人中必有2人的生日相同；②抛掷一枚均匀的骰子两次，朝上一面的点数之和一定不小于2；③在标准大气压下，温度低于0℃时冰融化；④如果a，b 为实数，那么a+b＝b+a．其中是必然事件的有( )A．1个B．2个C．3个D．4个C解析：C【分析】必然事件指的是一定发生的事件，据此分别判断即可．【详解】①中，一年最多366天，则367人中，必有2人生日相同，是必然事件；②中，骰子朝上面最小为1，两次之和最小为2，即一定不小于2，是必然事件；③中，标准大气压下，低于0℃，冰不会融化，不是必然事件；④中，根据加法交换律，a+b＝b+a一定成立，是必然事件故选：C【点睛】本题考查必然事件的判定，注意事件可分为3类：随机事件，必然事件，不可能事件．二、填空题11．如图，点O为正方形的中心，点E、F分别在正方形的边上，且∠EOF＝90°，随机地往图中投一粒米，则米粒落在图中阴影部分的概率是___________．【分析】先证△OAE≌△OBF四边形EOFC的面积=三角形AOE面积+四边形AOFC面积=三角形BOF面积+四边形AOFC面积=正方形AOBC的面积=S大正方形米粒落在图中阴影部分的概率就是阴影部分解析：1 4【分析】先证△OAE≌△OBF，四边形EOFC的面积=三角形AOE面积+四边形AOFC面积=三角形BOF面积+四边形AOFC面积=正方形AOBC的面积=14S大正方形，米粒落在图中阴影部分的概率就是阴影部分的面积同正方形总面积的比．【详解】解：过O作OA⊥CE于A，OB⊥CF交CF延长线于B，∵点O为正方形的中心，∴OA=OB，∠OAE=∠OBF=90º=∠AOB ，∵∠EOF＝90°，∴∠EOA+∠AOF=90º,∠AOF+∠FOB=90º，∴∠EOA=∠FOB，∴△EOA≌△FOB，Ｓ四边形EOFC =Ｓ△AOE+Ｓ四边形AOFC =Ｓ△BOF+Ｓ四边形AOFC=Ｓ正方形AOBC=14S大正方形，S四边形EOFC=S正方形AOBC=14S大正方形，如图所示：， P=EOFC AOBC S 1=S S 4S 四边形正方形大正方形大正方形， 因此米粒落在图中阴影部分的概率是14． 故答案为：14 【点睛】本题考查点投阴影部分的概率，掌握利用几何图形面积来确定概率的方法，不规则图形用全等三角形转化为正方形规则图形是解题关键．12．在一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球，随机从中摸出一个球，不再放回袋中，充分搅匀后再随机摸出一球，则两次都摸到红球的概率是_____．【分析】先画树状图展示所有20种等可能的结果数再找出两次都摸到红球的结果数然后根据概率公式求解【详解】解：画树状图为：共有20种等可能的结果数其中两次都摸到红球的结果数为6种所以两次都摸到红球的概率 解析：310【分析】先画树状图展示所有20种等可能的结果数，再找出两次都摸到红球的结果数，然后根据概率公式求解．【详解】解：画树状图为：共有20种等可能的结果数，其中两次都摸到红球的结果数为6种，所以两次都摸到红球的概率＝620＝310． 故答案为310． 【点睛】 此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．13．有4根细木棒，长度分别为2cm、3cm、4cm、5cm，从中任选3根，恰好能搭成一个三角形的概率是__________．【分析】根据题意使用列举法可得从有4根细木棒中任取3根的总共情况数目以及能搭成一个三角形的情况数目根据概率的计算方法计算可得答案【详解】根据题意从有4根细木棒中任取3根有234；345；235；24解析：3 4【分析】根据题意，使用列举法可得从有4根细木棒中任取3根的总共情况数目以及能搭成一个三角形的情况数目，根据概率的计算方法，计算可得答案．【详解】根据题意，从有4根细木棒中任取3根，有2、3、4；3、4、5；2、3、5；2、4、5，共4种取法，而能搭成一个三角形的有2、3、4；3、4、5，2、4、5，三种，得P=3 4 .故其概率为：34．【点睛】本题考查概率的计算方法，使用列举法解题时，注意按一定顺序，做到不重不漏．用到的知识点为：概率=所求情况数与总情况数之比．14．在不透明的口袋中有若干个完全一样的红色小球，现放入10个仅颜色不同的白色小球，均匀混合后，有放回的随机摸取，经过大量重复实验摸到白色小球的频率稳定在0.2，据此估计该口袋中原有红色小球个数为_________ ．40【分析】利用频率估计概率设原来红球个数为x个现放入10个仅颜色不同的白色小球均匀混合后有放回的随机摸取经过大量重复实验摸到白色小球的频率稳定在02根据概率公式可得关于x的方程解方程即可得【详解】解析：40【分析】利用频率估计概率，设原来红球个数为x个，现放入10个仅颜色不同的白色小球，均匀混合后，有放回的随机摸取，经过大量重复实验摸到白色小球的频率稳定在0.2，根据概率公式可得关于x的方程，解方程即可得．【详解】设原来红球个数为x个，则有100.2 10x=+，解得：x=40，经检验x=40是原方程的根．故答案为40．【点睛】本题考查了利用频率估计概率和概率公式的应用，熟练掌握概率的求解方法以及分式方程的求解方法是解题的关键．15．一个不透明的盒子中装有9个大小相同的乒乓球，其中3个是黄球，6个是白球，从该盒子中任意摸出一个球，摸到白球的概率是_________．【分析】用白球的个数除以球的总个数即可确定摸到白球的概率【详解】解：盒子中装有9个大小相同的乒乓球其中3个是黄球6个是白球则摸到白球的概率是：故答案为【点睛】本题考查概率的求法与运用正确应用概率公式 解析：23【分析】用白球的个数除以球的总个数，即可确定摸到白球的概率．【详解】解：盒子中装有9个大小相同的乒乓球，其中3个是黄球，6个是白球， 则摸到白球的概率是：6293=． 故答案为23． 【点睛】本题考查概率的求法与运用，正确应用概率公式是解答本题的关键．16．已知a 为正整数，且二次函数()273y x a x =+-+的对称轴在y 轴右侧，则a 使关于y 的分式方程4211ay y y y--=--有正整数解的概率为_______．【分析】利用二次函数对称轴公式求得从而确定a 所有的正整数解然后解关于y 的方程得然后确定符合题意的a 的值然后根据概率公式求解【详解】解：由题意可知：解得因为为正整数∴a 可以取123456共6种等可能结 解析：13【分析】 利用二次函数对称轴公式求得702a -->，从而确定a 所有的正整数解，然后解关于y 的方程，得21y a =-，然后确定符合题意的a 的值，然后根据概率公式求解． 【详解】 解：由题意可知：702a -->，解得7a < 因为a 为正整数，∴a 可以取1，2，3，4，5，6共6种等可能结果解4211ay yy y--=--化为：42(1)ay y y---=-解得：21 ya=-当a=2或3时，y有正整数解，符合题意共2种∴a使关于y的分式方程4211ay yy y--=--有正整数解的概率为21=63故答案为：13．【点睛】本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．也考查了根的判别式和分式方程的解．17．在x2□2xy□y2的空格□中，分别填上“+”或“﹣”，在所得的代数式中，能构成完全平方式的概率是_______．50【分析】能构成完全平方式的情况有++；-+两种情况共有的情况为++；--；+-；-+共四种情况【详解】能有的共有4种情况能构成平方式的有两种情况＝＝50故能构成完全平方式的概率是50故答案为：5解析：50%【分析】能构成完全平方式的情况有+，+；-，+两种情况，共有的情况为+，+；-，-；+，-；-，+共四种情况．【详解】能有的共有4种情况，能构成平方式的有两种情况．2 4＝12＝50%．故能构成完全平方式的概率是50%．故答案为：50%．【点睛】本题考查完全平方式的概念，求出构成完全平方式有几种情况，能填几种情况，从而可求出概率．18．在一个不透明的盒子中，装有红、黄、绿三种只有颜色不同、其余均相同的小球各2个，从中任取一个球，取出的球为红色的概率为_____．【分析】直接利用概率公式求解【详解】摸出的一个球是红球的概率＝＝故答案为：【点睛】此题考查了概率公式的应用用到的知识点为：概率=所求情况数与总情况数之比解析：1 3【分析】直接利用概率公式求解．【详解】摸出的一个球是红球的概率＝223⨯＝13． 故答案为：13． 【点睛】此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比． 19．完全相同的4个小球，上面分别标有数字1、-1、2、-2，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次(第一次摸出球后放回摇匀)．把第一次、第二次摸到的球上标有的数字分别记作m ，n ，以m ，n 分别作为一个点的横坐标与纵坐标，定义点(),m n 在反比例函数ky x=上为事件k Q （44,k k -≤≤为整数），当k Q 的概率最大时，则k 的所有可能的值为__________．±2【分析】首先根据题意列出表格然后根据表格求得k 取不同值时的概率比较大小即可确定k 的所有可能的值【详解】列表得：（1−2）（−1−2）（2−2）（−2−2）（12）（−12）（22）解析：±2． 【分析】首先根据题意列出表格，然后根据表格求得k 取不同值时的概率，比较大小即可确定k 的所有可能的值． 【详解】 列表得：∵若点（m ，n ）在反比例函数ky x=上， 则k ＝mn ，∵P （k ＝−4）＝21168=，P （k ＝−1）＝21168=，P （k ＝−2）＝41164=，P （k ＝1）＝21168=，P （k ＝2）＝41164=，P （k ＝4）＝21168=，∴当Q k 的概率最大时，k ＝±2． 故答案为：±2． 【点睛】此题考查了列表法或树状图法求概率与反比例函数的性质．此题难度适中，解题时注意列表法与树状图法可以不重不漏的列出所有等可能的情况，然后根据概率公式求得概率．20．某种油菜籽在相同条件下的发芽试验结果如下表：请用频率估计概率的方法来估计这批油菜籽在相同条件下的发芽概率是_______（精确到0.01）.090【分析】对于不同批次的某种菜籽的发芽率往往误差会比较大为了减少误差我们经常采用多批次计算求平均数的方法【详解】解：=（4+9+60+116+282+639+1339+1806+2715）÷（5解析：0.90【分析】对于不同批次的某种菜籽的发芽率往往误差会比较大，为了减少误差，我们经常采用多批次计算求平均数的方法．【详解】解：x =（4+9+60+116+282+639+1339+1806+2715）÷（5+10+70+130+310+700+1500+2000+3000）=6970÷7725≈0.90．当n足够大时，发芽的频率逐渐稳定于0.90，故用频率估计概率，这批油菜籽在相同条件下的发芽概率是0.90．故答案为0.90．【点睛】本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．三、解答题21．为贯彻落实全市城乡“清爽行动”暨生活垃圾分类攻坚大会精神，积极创建垃圾分类示范单位，我校举行了一次“垃圾分类”模拟活动. 我们将常见的生活垃圾分为四类：可回收垃圾、厨余垃圾、有害垃圾、其他垃圾，且应分别投放于4种不同颜色的对应垃圾桶中. 若在这次模拟活动中，某位同学将两种不同类型的垃圾先后随意投放于2种不同颜色的垃圾桶．（1）请用列表或画树状图表示所有可能的结果数；（2）求这位同学将两种不同类型的垃圾都正确投放的概率.解析：（1）答案见解析；（2）1 12.【分析】（1）根据题意画出树状图得出所有情况数即可；（2）根据（1）中的数据，求出概率即可．【详解】解：（1）根据题意，画树状图得：由列表可知，一共有12种结果.（2）跟据（1）中的数据可知，正确的投放，只有一种，所以这位同学将两种不同类型的垃圾都正确投放的概率为112． 【点睛】考查用列树状图的方法解决概率问题，熟悉相关性质是解决本题的关键． 22．如图，一个质地均匀的转盘分为A 、B 两个扇形区域，A 区域的圆心角为120° （1）随意转动转盘一次，指针指在B 区域的概率是多少.（2）随意转动两次转盘，指针第一次指在B 区域，第二次指在A 区域的概率是多少，用树状图或列表方法来说明理由．解析：（1）23；（2）29【分析】（1）算出B 所在的圆心角度数，进行计算即可； （2）将转盘分成三等分，列树状图计算即可； 【详解】（1）360120240︒-︒=︒， ∴24023603︒=︒， ∴指针指在B 区域的概率为23． （2）将转盘分成三等分，一共有三种等分区域，列树状图如下，一共有9种结果，其中第1次是B，第2次是A的有2种，∴概率为：29．【点睛】本题主要考查了列表法与树状图法求概率，准确画图计算是解题的关键．23．交大附中各班举行了“垃圾分类，从我做起”的主题班会，九年级三班的同学在班会课上进行了一个有关垃圾分类知识竞答的活动，他们上网查阅了相关资料，收集到如下四个图标，并将其制成编号为,,,A B C D的四张卡片(除编号和内容外，其余完全相同) ，他们将这四张卡片背面朝上，洗匀放好．（1）从中随机抽取一张，恰好抽到“可回收物”的概率是（2）从中随机抽取一张(不放回)，再从中随机抽一张，请用列表或画树状图的方法求抽到的两张卡片恰好是“其他垃圾”和“有害垃圾”的概率(这四张卡片分别用它们的编号,,,A B C D表示)解析：（1）14；（2）16．【分析】（1）根据概率公式直接得出答案；（2）根据题意先画出树状图列出所有等可能结果数，根据概率公式求解即可．【详解】解：（1）有其他垃圾、可回收物、有害垃圾、厨房垃圾，共四张卡片，恰好抽到“可回收物”的概率是14；（2）根据题意画图如下：共12种等可能的结果数，其中抽到“其他垃圾”和“有害垃圾”的结果数为2，∴抽到的两张卡片恰好是“其他垃圾”和“有害垃圾”的概率21 126 ==．【点睛】本题考查了列表法或树状图法求概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题时放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．24．某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：（为了方便记录，把a≤x＜b记作：[a，b）．）最高气温[10，15)[15，20)[20，25)[25，30)[30，35)[35，40)天数216362574（1）求六月份这种酸奶一天的需求量不超过300瓶的概率；（2）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量为450瓶时，写出Y的所有可能值，并估计Y大于零的概率．解析：（1）35；（2）900元，300元，-100元，45【分析】（1）由前三年六月份各天的最高气温数据，求出最高气温位于区间[20，25）ºC和最高气温低于20ºC的天数，由此能求出六月份这种酸奶一天的需求量不超过300瓶的概率．（2）当温度大于等于25°C时，需求量为500，求出Y=900元；当温度在[20，25）°C时，需求量为300，求出Y=300元；当温度低于20°C时，需求量为200，求出Y=-100元，从而当温度大于等于20ºC时，Y＞0，由此能估计估计Y大于零的概率．【详解】解：（1）由前三年六月份各天的最高气温数据，得到最高气温位于区间[20，25）ºC和最高气温低于20的天数为2+16+36＝54，根据往年销售经验，每天需求量与当天最高气温（单位：ºC）有关．如果最高气温不低于25ºC，需求量为500瓶，如果最高气温位于区间[20，25）ºC，需求量为300瓶，如果最高气温低于20ºC，需求量为200瓶，∴六月份这种酸奶一天的需求量不超过300瓶的概率p＝543905=；（2）∵当温度大于等于25ºC时，需求量为500瓶，Y＝450×2＝900元；当温度在[20，25）ºC时，需求量为300瓶，Y＝300×2﹣（450﹣300）×2＝300元；当温度低于20ºC时，需求量为200瓶，Y＝400﹣（450﹣200）×2＝﹣100元；∴当温度大于等于20ºC时，Y＞0，∵由前三年六月份各天的最高气温数据，得当温度大于等于20ºC的天数有：90﹣（2+16）＝72，∴估计Y大于零的概率P＝724905=．【点睛】本题考查概率的求法，考查利润的所有可能取值的求法，用运算作出推理论证，找出Y>0的天数是解决问题的关键．25．甲、乙两人玩“锤子、石头、剪子、布”游戏．他们在不透明的袋子中放入形状、大小均相同的19张卡片，其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7，两人各随机摸出一张卡片（先摸者不放回）来比胜负，并约定：“锤子”胜“石头”和“剪子”，“石头”胜“剪子”，“剪子”胜“布”，“布”胜“锤子”和“石头”，同种卡片不分胜负．(1)若甲先摸，他摸出“石头”的概率是多少？(2)若甲先摸出了“石头”，则乙获胜的概率是多少？(3)若甲先摸，则他先摸出哪种卡片获胜的可能性最大？解析：（1）419；（2）59；（3）甲摸锤子获胜的可能性最大.【分析】(1)共有19张牌，石头的有4张，用4÷19即可得；(2)甲先摸出“石头”后，还有18张牌，而锤子有3种情况，布有7种情况，共有10种情况乙可以获胜，用10÷18即可；(3)分别算出各种卡片获胜占总情况的多少，比较即可得出答案．【详解】(1)P（甲摸石头）=4 19；(2)P（乙胜）=375 1919 +=-；(3)P（甲摸锤子胜）=451 1912 +=-，P（甲摸石头胜）=55 19118=-，P（甲摸剪子胜）=718，P（甲摸布胜）=347 19118 +=-，。