圆和扇形练习的的题目

实用标准文案圆和扇形练习题1(如无特别说明，题目中n取3.14 )姓名：____________________一、填空题1. 如果用d表示圆的直径，那么圆的周长C = _______________ .2. 如果已知圆的周长为C,那么求圆的半径用公式_______________ .3. n叫做 ___________ ，它是_______________ 禾廿 __________ 的比值，即n = _______4•我国南北朝时期的数学家将圆周率计算到七位小数.5•如果已知圆的半径为r,那么半圆的周长公式为C半圆= __________________ .6.已知圆环的外圆半径为r i,内圆半径为r2，那么圆环的宽度d= ___________ .7•已知圆的周长为C,那么圆心角为n°的弧长1 = _______________ .&半径为r,圆心角为n°勺弧长I = _________________ .9. __________________________ 120。

的圆心角是360。

的_________________ 分之一，它所对的弧是相应圆周长的 _____ 分之一.10. _____________________________________________________ 将长为12 cm的圆周平均分为四份，每一份的弧长为 _______________________________ cm .11. 已知60。

的圆心角所对的弧长为3 cm,它所在的圆的周长是____________12. _______________________________________________ 半径为2 cm,圆心角为90°勺弧长为 ________________________________________ .、选择题cm.1.圆的周长是直径的(A) 3.14159 倍； (B) 3.14 倍；(C) 3 倍； (D) n 倍2. 圆的半径扩大为原来的3倍.......................... ( )(A)周长扩大为原来的9倍(B)周长扩大为原来的6倍(C)周长扩大为原来的3倍(D)周长不变3. 圆的半径不变，圆心角扩大为原来的2倍，则...... ()(A)弧长扩大为原来的4倍(B)弧长扩大为原来的2倍(C)弧长不变(D )弧长缩小为原来的一半三、简答题1.求下图中圆的周长2、一个圆形花坛的直径为5米,要在它的边上镶一圈合金，需要合金多少米？3、用18.84 cm的铁丝做一个圆, 求这个圆的半径.5、如果圆环的外圆周长为 30 cm,内圆周长为20 cm,求圆环的宽度.(结果 保留两位小数)8. 半径为6 cm 的圆，一圆心角所对的弧长为 6.28 cm,这个圆心角多少度?9、一辆自行车的车轮直径是 0.76米，那么 (1) 它在地面上转一圈行了多少路程？(2) 如果它每分钟转 200圈，那么它每分钟可以行驶多少路程？ (3) 按上面的速度，小明从家到学校要 5分钟，求小明家到学校的距离10.某海关大楼的大钟时针长 1.8米，从上午11点到下午4点，时针的尖端移动了多 少米？6. 半径为5 cm,圆心角为72°勺 弧长是多少？7. 直径为9 cm 的圆，圆心角 40°勺弧长是多少？圆和扇形练习题2(如无特别说明，题目中n取3.14 )姓名：______________________一、填空题1. 如果用r表示圆的半径，那么圆的面积S= .2. __________________________________ 半径为1米的圆的面积为______，半径为2米的圆面积为_________________________________ •3. 直径为1米的圆的面积为____________ ，直径为6米的圆面积为 ______________ .4. _______________________________________ 面积为12.56平方米的圆，半径为米，直径为___________________________________________ 米.5•如果已知圆的半径为r,那么半圆的面积公式为S半圆= ________________.6•外滩海关大钟钟面的直径是 5.8米，面积是 ________ 平方米(结果保留一位小数)(C)不变;三、简答题1、求下列圆的面积(1) r=2cm(A) 扩大为原来的两倍; (B) 扩大为原来的四倍;(D )缩小一半⑵ d=10cm2、上海体育馆圆形比赛场地的 半径是55米，求它的周长和面积4、在一个边长为20 cm 的正方形内画一个最大的圆，这个圆的面积又是多少?6. 如下图，在半径为 5米的圆形花坛周 围修一条宽1米的小路，求小路的面积7•图中正方形的边长为 2 cm,求下图中阴影部分的面积9.直径为18 cm 的圆中，圆心角 40°勺 扇形面积是多少？ 10.半径为6 cm 的扇形面积为18.84cm 2,它的圆心角是多少度?5.已知电风扇的叶片长约 50 cm, 风扇转动时叶片扫过的面积•&半径为15 cm,圆心角为72°勺 扇形面积是多少？3、求下图中半圆的面积11.某海关大楼的大钟时针长 1.8米，从上午11点到下午4点，时针扫过的面积是多 少平方米？13 .下列每个正方形的边长为2, 求下图中阴影部分的面积14•已知正方形的边长为 2，求右图中阴影部分的面积12.求下图中扇形的周长和面积第四章圆和扇形测试卷(时间45分钟，满分100分)姓名：_______________一、填空题(每小题3分，满分36分)1、___________________________________ 圆的直径为30,则圆的周长= .2、______________________________________________________ 圆半径为2cm，那么180°的圆心角所对的弧长1= ____________________________________ cm.3、________________________________________________________________ 如果圆的半径r = 12cm，那么18°的圆心角所对的弧长I = ____________________________________ cm.4、把边长为2分米的正方形剪成一个最大的圆，则这个圆的面积= ____ m2.5、大圆的半径是小圆的半径的2倍，则大圆面积是小圆面积的 ________ 倍•6、一个半圆面的半径是r,则它的面积是________ .7、圆的面积扩大到原来的9倍，则它的半径扩大到原来的_______ 倍.8、一个圆的半径从2cm增加到3cm，则周长增加了_______ cm.9、120°的圆心角所对的弧长是15.072米，弧所在的圆的半径是 _______ 米.1 、10、一个扇形面积是它所在圆面积的，这个扇形的圆心角是度.611、一个圆环的外半径是5cm，内半径是3cm,这圆环的面积是 _______ cm2.12、把直径为18厘米的圆等分成9个扇形，每个扇形的周长是 __________ 厘米.二、选择题(每题3分，满分12分)13、下列结论中正确的是................................. ( )(A) 任何圆的周长与半径之比不是一个常数；(B) 任何两个圆的周长之比等于它们的半径之比；(C) 任何两个圆的周长之比是一个常数；(D称圆的周长与半径之比为圆周率.14、下列判断中正确的是.................................. ( )(A) 半径越大的弧越长；(B) 所对圆心角越大的弧越长；(C) 所对圆心角相同时，半径越大的弧越长；(D) 半径相等时，无论圆心角怎么改变弧长都不会改变15、下列判断中正确的是.................................. ( )(A) 半径越大的扇形面积越大；(B) 所对圆心角越大的扇形面积越大；(C) 所对圆心角相同时，半径越大的扇形面积越大；(D) 半径相等时，所对圆心角越大的扇形面积越小16、一个圆的半径增加2cm,则这个圆......................... ( )(A)周长增加4cm ；(B)周长增加4 cm ；(C)面积增加4cm2；(D)面积增加.4 cm2.三、简答题(17〜20每题5分，21〜24每题6分，25题8分，满分52分)17、一辆汽车的轮子直径1米，若行驶时车轮转速为8周/秒,取3,试计算这辆汽车的行驶速度为每小时多少千米？18、取3，试计算当上述汽车以120千米/小时的速度行使时，车轮的转速是每秒多少周•(结果保留整数位)19、如图，一个圆环的外圆半径为 4cm ，内圆半径为3cm ，取 试计算圆环的面积•20、如图，半径为6的圆恰容于一个正方形内， 试用 表示正方形内圆以外部分的面积21、某建筑物上大钟的分针长1.2米，时针长0.9米，取 3.14，试计算一小时分针和时针的针尖运动的弧长.22、已知正方形边长为 2，分别以正方形两个对角顶点为圆心，以边长为半径作两段圆23、已知C 、D 两点在以AB 为直径的半圆周上且把半圆三等分，若已知AB 长为10，试用表示阴影部分面积.24、如图，四个圆的半径都是1,四个圆的圆心恰好是正方形的四个顶点，试用 表示阴影部分面积25、小红用4根各长1米的绳子围成4个圆，小蓝用2根各长2米的绳子围成2个圆, 小白用1根长4米的绳子围成1个圆，试求他们围得图形的面积之比 .7. 半径为3 cm 的圆的面积是 ________ ，直径为2 cm 的圆面积为 _____ . 8. 面积为3.14怦的圆半径是 _________ 米，直径是 ____ 米.29. ____________________________________________ 分针长6 cm,它一小时扫过的面积为3.14，弧，试用 表示两弧所夹叶形部分的面积________________________________________________________ cm .10. 某圆的周长是12.56米，那么它的半径是，面积是.11 .已知外圆的面积为5 m* 2 3,内圆的面积为 3 m2,圆环的面积是 _______ .12. ____________________________________________________________ 已知外圆的半径为 2 cm,内圆半径为 1 cm,圆环的面积为___________________________________ .13. 已知圆面积为S,那么圆心角为n°的扇形面积S扇= ________________ .14. _____________________________________________ 半径为r,圆心角为n°勺扇形面积S扇= ______________________________________________________ .15. __________________________ 120。

圆和扇形单元练习题一、填空1、圆的半径为4厘米, 它的周长是________厘米2、圆的周长是9.42cm, 则它的半径是________3、圆的直径为5cm, 则它的面积是________4、若36°的圆心角所对的弧长为12.56cm, 则此弧所对的圆的半径为_________cm5、一弧长为18.84cm, 这弧的半径为4cm, 则弧所对的圆心角为_______度6、圆心角为45°, 半径为8厘米的扇形, 它的周长是________厘米7、已知圆心角为120°的扇形弧长为12.56厘米, 则扇形的面积是________一条弧长是圆周长的, 则此弧所对的圆心角是_________度10、一个圆环的面积是小圆面积的8倍, 则大圆半径是小圆半径的_________倍11.甲圆的半径是乙圆半径的, 那么乙圆面积是甲圆面积的________12.一段弧长是12.56厘米, 占圆周长的, 则这段弧所在圆的周长是__________13.一个圆的面积扩大到原来的9倍, 那么圆的周长扩大到原来的_________倍14、一个扇形的面积是15.7平方厘米, 圆心角是90°, 则这个扇形所在圆的面积是_______平方厘米。

15.把一个圆分成两个不等的扇形, 且大扇形的面积是小扇形面积的倍, 则小扇形的圆心角是________16.在一个面积为10平方厘米的正方形纸上剪下一个最大的圆, 这个圆的面积是______17、一半圆的周长为10.28m, 则半圆的面积为_______三、简答题1.如图, 已知r=2cm；求阴影部分的周长及面积2.已知一个扇形的面积为37.68平方厘米, 这个扇形的圆心角为270度, 这个扇形的半径和周长各是多少？3.如图, 已知OC=4cm,OD=2cm；∠AOC=60°,求阴影部分的周长和面积。

4.正方形的边长为4cm , 求阴影部分的周长及面积5.求阴影部分的周长和面积6如图, 图中长方形面积和圆面积相等, 已知圆周长为9.42cm, 求阴影部分的周长及面积。

圆与扇形专练1、如，求阴影部分的面积。

（单位：㎝）【参考答案】3.14×3×3÷4+3.14×2×2÷4-3×2=4.205（平方厘米）答：阴影部分的面积为4.205平方厘米。

2、求下列图形中阴影部分的面积（单位：㎝）【参考答案】1×2=2（平方厘米）答：阴影部分的面积为2平方厘米。

3、已知正方形的面积为12平方厘米，求阴影部分的面积。

【参考答案】3.14×12×3/4 =28.26（平方厘米）答：阴影部分的面积为28.26平方厘米4、已经半圆的直径为9㎝，求阴影部分的面积。

6÷2=3（cm）3.14×3×3÷2-6×3÷2=5.13（cm）5.13×2=10.26（平方厘米）答：阴影部分的面积是10.26平方厘米。

5、如图3，求阴影部分的面积。

（单位：㎝）（12+8）÷2=10（cm）12÷2=6（cm）8÷2=4（厘米）阴影部分的面积：3.14×102×1/2-3.14×62×1/2+3.14×42×1/2=157-56.52+25.12=125.6（平方厘米）答：阴影部分面积是125.6平方厘米。

6、图中阴影部分甲的面积比阴影部分乙的面积大57平方厘米,AB=20厘米,CB 垂直于AB，求BC的长。

解：(S甲+S空白)-(S乙+S空白)=57S△ABC=157-57=100(平方厘米)100×2÷20=10(厘米)答：BC的长是10厘米。

7、下图三角形ABC是直角三角形，阴影①的面积比阴影②的面积小23平方厘米，求BC的长。

1/2 ×3.14 ×10 ×10=157 （平方厘米）（157+23）×2÷20=18 （平方厘米）答：BC的长是18平方厘米。

圆与扇形练习题（一）1、下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？2、下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？3、如图，在18 8的方格纸上，画有1，9，9，8四个数字．那么，图中的阴影面积占整个方格纸面积的几分之几？4、在4×7的方格纸板上面有如阴影所示的”6”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几？5、(人大附中分班考试题)如图，正方形边长为1，正方形的4个顶点和4条边分别为4个圆的圆心和半径，求阴影部分面积．(π取3.14)6、图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心．如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米？圆与扇形练习题（二）1．如右图，有8个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．则花瓣图形的面积是多少平方厘米？ (π取3)42.如图中三个圆的半径都是5cm，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取3.14)3．如图，大圆半径为小圆的直径，已知图中阴影部分面积为1S ，空白部分面积为2S ，那么这两个部分的面积之比是多少？(圆周率取3.14)4.计算图中阴影部分的面积(单位：分米)．A5、如图，阴影部分的面积是多少？6、请计算图中阴影部分的面积．圆与扇形练习题（三）1、 求图中阴影部分的面积．2、求如图中阴影部分的面积．(圆周率取3.14)(2)ba(1)10343、求下列各图中阴影部分的面积．4、求下列各图中阴影部分的面积(图中长度单位为cm ，圆周率按3计算)：5、 如图，ABCD 是正方形，且1FA AD D E ===，求阴影部分的面积．(取π3=)6、求图中阴影部分的面积(单位：cm )．2圆与扇形练习题（四）1、 如图，长方形ABCD 的长是8cm ，则阴影部分的面积是 2cm ．(π 3.14=)5cm 7.5cm3cm 2cm ④③②①E2、 (2007年西城实验期末考试题)如图所示，在半径为4cm 的图中有两条互相垂直的线段，阴影部分面积A与其它部分面积B 之差(大减小)是 2cm ．3、一块圆形稀有金属板平分给甲、乙二人．但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块．现甲取②、③两块，乙取①、④两块．如果这种金属板每平方厘米价值1000元，问：甲应偿付给乙多少元？4、 求右图中阴影部分的面积．(π取3)5、 (第四届走美决赛试题)如图，边长为3的两个正方形BDKE 、正方形DCFK 并排放置，以BC 为边向内侧作等边三角形，分别以B 、C 为圆心，BK 、CK 为半径画弧．求阴影部分面积．(π 3.14=)圆与扇形练习题（五）1、如图，已知扇形BAC 的面积是半圆ADB 面积的34倍，则角CAB 的度数是________．DCBA3、 如下图，直角三角形ABC 的两条直角边分别长6和7，分别以,B C 为圆心，2为半径画圆， 已知图中阴影部分的面积是17，那么角A 是多少度(π3=)4、 如图，大小两圆的相交部分(即阴影区域)的面积是大圆面积的415，是小圆面积的35．如果量得小圆的半径是5厘米，那么大圆半径是多少厘米？5、 有七根直径5厘米的塑料管，用一根橡皮筋把它们勒紧成一捆(如图)，此时橡皮筋的长度是多少厘米？(π取3)6、 如图，边长为12厘米的正五边形，分别以正五边形的5个顶点为圆心， 12厘米为半径作圆弧，请问：中间阴影部分的周长是多少？(π 3.14=)7、 如图是一个对称图形．比较黑色部分面积与灰色部分面积的大小，得：黑色部分面积________灰色部分面积．圆与扇形练习题（六）1、 用一块面积为36平方厘米的圆形铝板下料，从中裁出了7个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？2、 如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是1．求阴影部分的面积．3、 如图所示，求阴影面积，图中是一个正六边形，面积为1040平方厘米，空白部分是6个半径为10厘米的小扇形．(圆周率取3.14)4、 (09年第十四届华杯赛初赛)如下图所示，AB 是半圆的直径，O 是圆心，AC CD DB ==，M 是 CD 的中点，H 是弦CD 的中点．若N 是OB 上一点，半圆的面积等于12平方厘米，则图中阴影部分的面积是 平方厘米．5、如图，C 、D 是以AB 为直径的半圆的三等分点，O 是圆心，且半径为6．求图中阴影部分的面积．6、如图，两个半径为1的半圆垂直相交，横放的半圆直径通过竖放半圆的圆心，求图中两块阴影部分的面积之差．(π取3)圆与扇形练习题（七）1、 如图，两个正方形摆放在一起，其中大正方形边长为12，那么阴影部分面积是多少？(圆周率取3.14)2、 如右图，两个正方形边长分别是10和6，求阴影部分的面积．(π取3)3、 如图，ABC 是等腰直角三角形，D 是半圆周的中点，BC 是半圆的直径．已知10AB BC ==，那么阴影部分的面积是多少？(圆周率取3.14)4、 图中给出了两个对齐摆放的正方形，并以小正方形中右上顶点为圆心，边长为半径作一个扇形，按图中所给长度阴影部分面积为 ；(π 3.14=)5、 如图，图形中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的．问：涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少？圆与扇形练习题（八）1、 (2008年西城实验考题)奥运会的会徽是五环图，一个五环图是由内圆直径为6厘米，外圆直径为8厘米的五个环组成，其中两两相交的小曲边四边形(阴影部分)的面积都相等，已知五个圆环盖住的面积是77.1平方厘米，求每个小曲边四边形的面积．(π 3.14=)DC B2、 已知正方形ABCD 的边长为10厘米，过它的四个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连擎起来得右图．那么，图中阴影部分的总面积等于______方厘米．(π 3.14=)3、 如图，ABCD 是边长为a 的正方形，以AB 、BC 、CD 、DA 分别为直径画半圆，求这四个半圆弧所围成的阴影部分的面积．(π取3)4、如图，正方形ABCD 的边长为4厘米，分别以B 、D 为圆心以4厘米为半径在正方形内画圆．求阴影部分面积．(π取3)B5、(2008年四中考题)已知三角形ABC 是直角三角形，4cm AC =，2cm BC =，求阴影部分的面积．6、（奥林匹克决赛试题）在桌面上放置3个两两重叠、形状相同的圆形纸片.它们的面积都是100平方厘米，盖住桌面的总面积是144平方厘米，3张纸片共同重叠的面积是42平方厘米.那么图中3个阴影部分的面积的和 是平方厘米.圆与扇形练习题（九）1、(2008年国际小学数学竞赛)如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点．以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -(其中m 、n 为正整数)，请问m n +之值为何？S 2S 1G HFE DCBAC332、在图中，两个四分之一圆弧的半径分别是2和4，求两个阴影部分的面积差．(圆周率取3.14)3、如图，矩形ABCD 中，AB =6厘米，BC =4厘米，扇形ABE 半径AE =6厘米，扇形CBF 的半径CB =4厘米，求阴影部分的面积．(π取3)4、求图中阴影部分的面积．5、如右图，正方形的边长为5厘米，则图中阴影部分的面积是 平方厘米，(π 3.14=)6、如图所示，阴影部分的面积为多少？(圆周率取3)圆与扇形练习题（十）1、已知右图中正方形的边长为20厘米，中间的三段圆弧分别以1O 、2O 、3O 为圆心，求阴影部分的面积．(π3=)I IAB CIO32、 一个长方形的长为9，宽为6，一个半径为l 的圆在这个长方形内任意运动，在长方形内这圆无法运动到的部分，面积的和是_____．(π取3)3、 已知半圆所在的圆的面积为62.8平方厘米，求阴影部分的面积．(π 3.14=)B4、 如图，等腰直角三角形ABC 的腰为10；以A 为圆心，EF 为圆弧，组成扇形AEF ；两个阴影部分的面积相等．求扇形所在的圆面积．5、 如图，直角三角形ABC 中，AB 是圆的直径，且20AB =，阴影甲的面积比阴影乙的面积大7，求BC长．(π 3.14=)6、三角形ABC 是直角三角形，阴影I 的面积比阴影II 的面积小225cm ，8cm AB =，求BC 的长度．圆与扇形练习题（十一）1、 如图，三角形ABC 是直角三角形，阴影部分①比阴影部分②的面积小28平方厘米，AB 长40厘米．求BC 的长度？(π取3.14)2、 (2009年十三分入学测试题)图中的长方形的长与宽的比为8:3，求阴影部分的面积．3、 如图，求阴影部分的面积．(π取3)4、 如图，直角三角形的三条边长度为6,8,10，它的内部放了一个半圆，图中阴影部分的面积为多少？65、 大圆半径为R ，小圆半径为r ，两个同心圆构成一个环形．以圆心O 为顶点，半径R 为边长作一个正方形：再以O 为顶点，以r 为边长作一个小正方形．图中阴影部分的面积为50平方厘米，求环形面积．(圆周率取3.14)6、图中阴影部分的面积是225cm ，求圆环的面积．圆与扇形练习题（十二）1、已知图中正方形的面积是20平方厘米，则图中里外两个圆的面积之和是 ．(π取3.14)2、图中小圆的面积是30平方厘米，则大圆的面积是平方厘米．(π取3.14)3、图中大正方形边长为a，小正方形的面积是．4、一些正方形内接于一些同心圆，如图所示．已知最小圆的半径为1cm，请问阴影部分的面积为多少平方厘米？(取22π7 =)5.图中大正方形边长为6，将其每条边进行三等分，连出四条虚线，再将虚线的中点连出一个正方形(如图)，在这个正方形中画出一个最大的圆，则圆的面积是多少？(π 3.14=)6.如下图所示，两个相同的正方形，左图中阴影部分是9个圆，右图中阴影部分是16个圆．哪个图中阴影部分的面积大？为什么？圆与扇形练习题（十三）1、如图，在33⨯方格表中，分别以A、E、F为圆心，半径为3、2、1，圆心角都是90°的三段圆弧与正方E O DC BA DA形ABCD 的边界围成了两个带形，那么这两个带形的面积之比12:?S S2、 如图中，正方形的边长是5cm ，两个顶点正好在圆心上，求图形的总面积是多少？(圆周率取3.14)3、 如下图，AB 与CD 是两条垂直的直径，圆O 的半径为15厘米，AEB 是以C 为圆心，AC 为半径的圆弧，求阴影部分面积．4、 如图，AB 与CD 是两条垂直的直径，圆O 的半径为15， AEB是以C 为圆心，AC 为半径的圆弧． 求阴影部分面积．ACB5、 如下图所示，曲线PRSQ 和ROS 是两个半圆．RS 平行于PQ ．如果大半圆的半径是1米，那么阴影部分是多少平方米？(π取3.14)6、 在右图所示的正方形ABCD 中，对角线AC 长2厘米．扇形ADC 是以D 为圆心，以AD为半径的圆的一部分． 求阴影部分的面积．圆与扇形练习题（十四）1、某仿古钱币直径为4厘米，钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图)．求钱币在桌面上能覆盖的面积为多少？9631293GDA2、 传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米．每当太阳西下，钟面就会出现奇妙的阴影(如右图)．那么，阴影部分的面积是 平方米．3、图中是一个钟表的圆面，图中阴影部分甲与阴影部分乙的面积之比是多少？4已知三角形GHI 是边长为26厘米的正三角形，圆O 的半径为15厘米．90AOB COD EOF ∠=∠=∠=︒．求阴影部分的面积．5.如下图，两个半径相等的圆相交，两圆的圆心相距正好等于半径，AB 弦约等于半径为10厘米，求阴影部分的面积．6、 下图中，3AB =，阴影部分的面积是圆与扇形练习题（十五）1、如图，ABCD 是平行四边形，8cm AD =，10cm AB =，30DAB ∠=︒，高4cm CH =，弧BE 、DF 分别以AB 、CD 为半径，弧DM 、BN 分别以AD 、CB 为半径，则阴影部分的面积为多少？(精确到0.01)DA760︒30︒B1C1C2A2CBAⅢⅡⅠⅣⅢⅡⅠEDCBAA2、如图所示，两条线段相互垂直，全长为30厘米．圆紧贴直线从一端滚动到另一端(没有离开也没有滑动)．在圆周上设一个定点P，点P从圆开始滚动时是接触直线的，当圆停止滚动时也接触到直线，而在圆滚动的全部过程中点P是不接触直线的．那么，圆的半径是多少厘米？(设圆周率为3．14，除不尽时，请四舍五入保留小数点后两位．如有多种答案请全部写出)P3、(第三届希望杯)将一块边长为12厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮，求剪成的正方形铁皮的面积的最大值.4、正三角形ABC的边长是6厘米，在一条直线上将它翻滚几次，使A点再次落在这条直线上，那么A点在翻滚过程中经过的路线总长度是多少厘米？如果三角形面积是15平方厘米，那么三角形在滚动过程中扫过的面积是多少平方厘米？(结果保留π)5、直角三角形ABC放在一条直线上，斜边AC长20厘米，直角边BC长10厘米．如下图所示，三角形由位置Ⅰ绕A点转动，到达位置Ⅱ，此时B，C点分别到达1B，1C点；再绕1B点转动，到达位置Ⅲ，此时A，1C点分别到达2A，2C点．求C点经1C到2C走过的路径的长．6、如图，一条直线上放着一个长和宽分别为4cm和3cm的长方形Ⅰ．它的对角线长恰好是5cm．让这个长方形绕顶点B顺时针旋转90°后到达长方形Ⅱ的位置，这样连续做三次，点A到达点E的位置．求点A走过的路程的长．圆与扇形练习题（十六）1、草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊(见如图)．问：CB A2、一只狗被拴在底座为边长3m 的等边三角形建筑物的墙角上(如图)，绳长是4m ，求狗所能到的地方的总面积．(圆周率按3.14计算)3、如图是一个直径为3cm 的半圆，让这个半圆以A 点为轴沿逆时针方向旋转60︒，此时B 点移动到'B 点，求阴影部分的面积．(图中长度单位为cm ，圆周率按3计算)．4、如图所示，直角三角形ABC 的斜边AB 长为10厘米，60ABC ∠=︒，此时BC 长5厘米．以点B 为中心，将ABC ∆顺时针旋转120︒，点A 、C 分别到达点E 、D 的位置．求AC 边扫过的图形即图中阴影部分的面积．(π取3)E5、如右图，以OA 为斜边的直角三角形的面积是24平方厘米，斜边长10厘米，将它以O 点为中心旋转90︒，问：三角形扫过的面积是多少？(π取3)6、如图，直角三角形ABC 中，B ∠为直角，且2BC =厘米，4AC = 厘米，则在将ABC ∆绕C 点顺时针旋转120︒的过程中，AB 边扫过图形的面积为 ．(π 3.14=)圆与扇形练习题（十七）1、如图，ABC ∆是一个等腰直角三角形，直角边的长度是1米．现在以C 点为圆心，把三角形ABC 顺时针转90度，那么，AB 边在旋转时所扫过的面积是 平方米．(π 3.14=)ABC2、 (祖冲之杯竞赛试题)如图，ABCD 是一个长为4，宽为3，对角线长为5的正方形，它绕C 点按顺时针方向旋转90︒，分别求出四边扫过图形的面积．CBD A3、 (2004年第九届华杯赛初赛)半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？⑵⑴A O A O4、如果半径为25厘米的小铁环沿着半径为50厘米的大铁环的外侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？⑴O A⑵OA5、如图所示，大圆周长是小圆周长的n (1n >)倍，当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又回到原来的位置，小圆绕自己的圆心转动了几周？6.如图，15枚相同的硬币排成一个长方形，一个同样大小的硬币沿着外圈滚动一周，回到起始位置．问：这枚硬币自身转动了多少圈？圆与扇形练习题（十八）1、12个相同的硬币可以排成下面的4种正多边形(圆心的连线)．用一个同样大小的硬币，分别沿着四个正多边形的外圈无滑动地滚动一周．问：在哪个图中这枚硬币自身转动的圈数最多，最多转动了多少圈？2、 一枚半径为1cm 的圆形硬币相互紧靠着平放在桌面上，让一枚硬币沿着它们的外轮廓滚过后回到原来的位置，那么与原A 点重合的点是______．硬币自己转动______，硬币圆心的运动轨迹周长为_______．3、 先做一个边长为2cm 的等边三角形，再以三个顶点为圆心，2cm 为半径作弧，形成曲边三角形(如左图)．再准备两个这样的图形，把一个固定住(右图中的阴影)，另一个围绕着它滚动，如右图那样，从顶点相接的状态下开始滚动．请问此图形滚动时经过的面积是多少平方厘米？(π 3.14=)CBA 2224、如图：求中间阴影面积与四边阴影的面积差。

圆的弧长与扇形面积综合练习题题1：已知一个半径为3cm的圆的弧长为12πcm，求扇形的面积。

题解：求扇形的面积时，需要知道扇形的圆心角和半径。

已知圆的弧长是12πcm，可以计算出圆心角的大小。

因为弧长等于半径乘以圆心角的弧度，所以可以得到12π = 3cm × 圆心角。

解方程可以得到圆心角为4π/3弧度。

扇形的面积等于圆心角占据的比例乘以整个圆的面积，所以扇形的面积为(4π/3)(π(3)^2) = 12π平方cm。

题2：若一个圆的半径是5cm，那么它的弧长和扇形面积各是多少？题解：已知圆的半径是5cm，它的弧长可以计算得出。

弧长等于半径乘以圆心角的弧度，所以弧长等于5cm ×圆心角。

圆心角的弧度可以通过圆弧长除以半径得到。

假设圆心角为θ弧度，则弧长为5θ。

要求扇形的面积，也需要知道圆心角的大小。

同样，我们可以利用扇形的面积公式，并确认圆心角的弧度为θ。

扇形的面积等于圆心角占据的比例乘以整个圆的面积。

所以扇形的面积为θ(π(5)^2) = 25θπ平方cm。

题3：已知一个扇形的半径是8m，扇形的面积是12π平方m，求圆心角和弧长各是多少？题解：已知扇形的半径是8m，扇形的面积是12π平方m。

要求圆心角的大小，可以利用扇形面积的公式，并确认圆心角的弧度为θ。

扇形的面积等于圆心角占据的比例乘以整个圆的面积，所以12π平方m = θ(π(8)^2)。

解方程可以得到θ = 3π/4。

要求弧长的大小，同样可以利用扇形的面积公式，但是需要先计算出圆心角的弧度。

扇形的面积等于圆心角占据的比例乘以整个圆的面积，所以12π平方m = (3π/4)(π(8)^2)。

解方程可以得到弧长为6πm。

题4：一个扇形的圆心角是π/2，弧长是4，求扇形的面积。

题解：已知扇形的圆心角是π/2，弧长是4。

要求扇形的面积，需要用到圆心角和半径的关系。

圆心角所占的比例乘以整个圆的面积就是扇形的面积。

所以扇形的面积等于(π/2)(πr^2)，其中r表示圆的半径。

圆与扇形常见题型1、圆的半径扩大 3 倍，面积扩大（）A. 3 倍B. 6 倍C. 9 倍D. 12 倍2、扇形的圆心角是60°，半径为 6 厘米，扇形的面积是（）平方厘米。

A. 6πB. 9πC. 12πD. 36π3、一个圆的周长是 18.84 厘米，它的面积是（）平方厘米。

A. 9.42B. 18.84C. 28.26D. 113.04填空题1、圆的直径是 8 厘米，周长是（）厘米，面积是（）平方厘米。

2、扇形的半径是 5 厘米，圆心角是90°，面积是（）平方厘米。

3、一个圆的面积是 50.24 平方厘米，它的半径是（）厘米。

计算题1、已知圆的半径为 4 厘米，求圆的周长和面积。

2、扇形的半径为 10 厘米，圆心角为120°，求扇形的面积。

应用题1、一个圆形花坛的周长是 37.68 米，这个花坛的面积是多少平方米？2、在一个半径为 8 厘米的圆中，剪去一个圆心角为90°的扇形，剩下的面积是多少平方厘米？答案及解析：选择题1、C 圆的面积公式为S = πr²，半径扩大 3 倍，面积扩大 9 倍。

2、A 扇形面积公式为S = (n/360)πr²，n 为圆心角度数，r 为半径，代入可得面积为6π 平方厘米。

3、C 先根据周长求出半径，再求面积，可得面积为 28.26 平方厘米。

填空题1、25.12 50.24 周长= 8×π = 25.12 厘米，面积= 16π = 50.24 平方厘米。

2、19.625 扇形面积 = （90/360）×25π = 19.625 平方厘米。

3、4 由面积公式可得半径 = 4 厘米。

计算题1、周长= 8π 厘米，面积 = 16π 平方厘米。

2、扇形面积= 100π/3 平方厘米。

应用题1、半径 = 6 米，面积= 36π 平方米。

先根据周长求出半径，再求面积。

2、圆的面积为64π 平方厘米，扇形面积为16π 平方厘米，剩下的面积为48π 平方厘米。

圆和扇形练习题圆和扇形练习题圆和扇形是几何学中常见的图形，也是数学学习中的重要内容。

通过练习题的形式，我们可以更好地理解和掌握圆和扇形的性质和计算方法。

下面，我将给大家介绍一些有趣的圆和扇形练习题。

1. 题目：一个圆的半径为5cm，求其周长和面积。

解析：圆的周长公式为C=2πr，面积公式为A=πr²。

代入半径r=5cm，即可计算得到周长C=2π×5≈31.42cm，面积A=π×5²≈78.54cm²。

2. 题目：一个扇形的半径为8cm，弧长为12cm，求其圆心角和面积。

解析：扇形的圆心角公式为θ=（L/r）×180°/π，面积公式为A=（θ/360°）×πr²。

代入半径r=8cm，弧长L=12cm，即可计算得到圆心角θ=（12/8）×180°/π≈68.18°，面积A=（68.18°/360°）×π×8²≈36.76cm²。

3. 题目：一个扇形的半径为10cm，圆心角为60°，求其弧长和面积。

解析：扇形的弧长公式为L=θ/360°×2πr，面积公式为A=θ/360°×πr²。

代入半径r=10cm，圆心角θ=60°，即可计算得到弧长L=60°/360°×2π×10≈10.47cm，面积A=60°/360°×π×10²≈52.36cm²。

4. 题目：一个圆的周长为18πcm，求其半径和面积。

解析：圆的周长公式为C=2πr，面积公式为A=πr²。

代入周长C=18πcm，即可计算得到半径r=18/2=9cm，面积A=π×9²=81πcm²。

圆与扇形练习题一一、判断题：1、圆的面积和圆的半径成正比例。

（）2、圆的面积和圆的半径的平方成正比例。

（）3、圆的面积和圆的周长的平方成正比例。

（）4、正方形的面积和边长成正比例。

（）5、正方形的周长和边长成正比例。

（）6、长方形的面积一定时，长和宽成反比例。

（）7、长方形的周长一定时，长和宽成反比例。

（）8、三角形的面积一定时，底和高成反比例。

（）9、梯形的面积一定时，上底和下底的和与高成反比例。

（）10、圆的周长和圆的半径成正比例。

（）1、两个圆的周长相等，它们的直径也相等（）2、圆的周长总是该圆直径的∏倍。

（）3．大圆的圆周率比小圆的圆周率大。

（）4、大圆的直径是小圆半径的4倍，那么大圆的周长是小圆周长的4倍。

（）5、半圆的周长就是圆周长的一半。

（）6、圆的半径扩大2倍，它的直径也扩大2倍，它的周长将会增加一倍。

（）二、填空。

1。

在同一个圆里，半径是5厘米，直径是（）厘米。

2．圆是平面上的一种（）图形。

3、圆的半径是3厘米，直径是（）厘米，周长是（）厘米。

4．圆的周长是28．26米，它的直径是（）厘米，半径是（）厘米。

5、一台时钟的分针长6厘米，它走过2圈走了（）厘米6。

一圆的周长是12．56厘米，如果用圆规画这个圆，圆规两脚的距离是（）厘米。

7、一个圆环，外圆半径是3厘米，内圆半径是2厘米，这个圆环的面积是（）8、8、圆心角是90度的扇形面积是所在圆面积的（）分之（）三、圆的面积1．个圆的周长一个正方形的周长相等，这个正方形的边长是6．28厘米，圆的面积是多少平方厘米？2．圆形水池，周长是18．84米，面积是多少平方厘米？20cm5．直径是1.5米，每分转8圈，压路机每分前进多少米？6．圆形养鱼池，直径是4米，这个养鱼池的周长是多少米？8．自动旋转喷灌装置半径是10米，它的最大喷灌面积是多少平方米？9．草坪周长是50.24米，这块草坪占地多少平方米？10．画一个直径2cm的圆。

圆与扇形练习题二1.填空题（每题2分，共24分）（1）一个半圆，半径为r，半圆周长是（）。

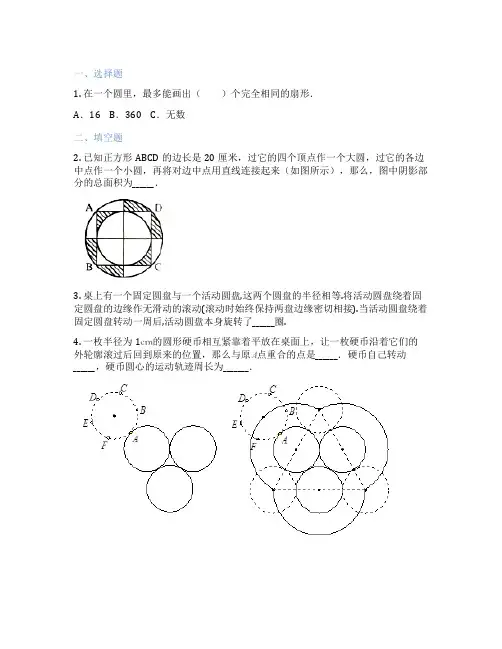
一、选择题1. 在一个圆里，最多能画出（）个完全相同的扇形．A．16 B．360 C．无数二、填空题2. 已知正方形ABCD的边长是20厘米，过它的四个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来（如图所示），那么，图中阴影部分的总面积为______．3. 桌上有一个固定圆盘与一个活动圆盘,这两个圆盘的半径相等.将活动圆盘绕着固定圆盘的边缘作无滑动的滚动(滚动时始终保持两盘边缘密切相接).当活动圆盘绕着固定圆盘转动一周后,活动圆盘本身旋转了______圈.4. 一枚半径为1的圆形硬币相互紧靠着平放在桌面上，让一枚硬币沿着它们的外轮廓滚过后回到原来的位置，那么与原点重合的点是______．硬币自己转动______，硬币圆心的运动轨迹周长为_______．5. 一个闹钟内圆的面积是30平方厘米，阴影部分的面积是________平方厘米．（取3.14）6. 如图所示，将半径分别为5厘米和4厘米的两个半圆如图放置，那么阴影部分的周长是______．三、解答题7. 正三角形的边长是6厘米，在一条直线上将它翻滚几次，使点再次落在这条直线上，那么点在翻滚过程中经过的路线总长度是多少厘米？如果三角形面积是15平方厘米，那么三角形在滚动过程中扫过的面积是多少平方厘米？(结果保留)8. 如图，是平行四边形，，，，高，弧、分别以、为半径，弧、分别以、为半径，则阴影部分的面积为多少？(精确到)9. 如图所示，直角三角形的斜边长为10厘米，，此时长5厘米．以点为中心，将顺时针旋转，点、分别到达点、的位置．求边扫过的图形即图中阴影部分的面积．(取3)10. 如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是1．求阴影部分的面积．。